Redes neurais em trading: Representação linear por partes de séries temporais

Introdução

Normalmente, ao falarmos sobre a representação de uma série temporal, imaginamos dados que são uma sequência de pontos registrados em ordem cronológica. No entanto, à medida que o volume de informações brutas cresce, aumenta também a complexidade de sua análise, o que reduz a eficiência do uso das informações disponíveis. Isso é especialmente relevante no mercado financeiro, onde a perda de tempo na análise da informação e na tomada de decisões aumenta o risco de não obter lucro ou até mesmo ter prejuízos. Nesse contexto, a redução da dimensionalidade dos dados é essencial para aumentar a eficiência e a eficácia da análise de dados inteligente. Um dos métodos de redução da dimensionalidade é a representação linear por partes de séries temporais.

A representação linear por partes de séries temporais é um método de aproximação de séries temporais usando funções lineares em pequenos intervalos. Neste artigo, quero apresentar a vocês o algoritmo de Representação Linear por Partes Bidirecional (Bidirectional Piecewise Linear Representation — BPLR), que foi apresentado no trabalho "Bidirectional piecewise linear representation of time series with application to collective anomaly detection". Este método foi proposto para resolver o problema da detecção de anomalias em séries temporais.

A detecção de anomalias em séries temporais é uma subárea importante da análise inteligente de dados de séries temporais. Seu objetivo é identificar comportamentos inesperados em todo o conjunto de dados. Como as anomalias são geralmente causadas por diferentes mecanismos, elas não têm critérios específicos para sua definição. Na prática, os dados que apresentam comportamentos esperados tendem a atrair mais atenção, enquanto os dados anômalos são frequentemente vistos como ruído e, posteriormente, ignorados ou removidos. No entanto, as anomalias podem conter informações valiosas, tornando sua detecção muito importante. A detecção precisa de anomalias pode ajudar a mitigar consequências indesejadas em várias áreas, como meio ambiente, indústria, finanças e outras.

As anomalias em séries temporais podem ser divididas nas seguintes três categorias:

1. Anomalias pontuais: um ponto de dado é considerado anômalo em relação aos outros pontos. Essas anomalias são geralmente causadas por erros de medição, falhas de sensores, erros de entrada de dados ou outros eventos excepcionais;
2. Anomalias contextuais: em um determinado contexto, um ponto de dado é considerado anômalo, mas, fora dele, não;
3. Anomalias coletivas: uma subsequência de séries temporais que exibe um comportamento anômalo. Essa é uma tarefa bastante complexa, porque tais anomalias não podem ser consideradas anômalas em uma análise individual. Pelo contrário, é o comportamento coletivo do grupo que é considerado anômalo.

As anomalias coletivas podem fornecer informações valiosas sobre o sistema ou processo analisado, pois podem indicar problemas ao nível de grupo que precisam ser resolvidos. Assim, a detecção de anomalias coletivas pode ser uma tarefa essencial em diversas áreas, como cibersegurança, finanças e saúde. Os autores do método BPLR concentraram-se especificamente na identificação de anomalias coletivas em sua pesquisa.

A alta dimensionalidade dos dados de séries temporais exige significativos recursos computacionais quando se usa dados brutos para a detecção de anomalias. Entretanto, para aumentar a eficiência na detecção de anomalias, uma abordagem típica envolve primeiro a redução da dimensionalidade e, em seguida, o uso de medidas de distância para realizar a tarefa no subespaço transformado. Portanto, os autores do método propõem um novo algoritmo de segmentação bidirecional para a representação linear por partes BPLR. Com este método, é possível transformar a série temporal original em uma forma de expressão de baixa dimensionalidade, adequada para uma análise eficiente.

Além disso, o trabalho propõe um novo algoritmo de medição de similaridade, baseado na ideia de integração por partes (PI). Este algoritmo realiza o cálculo eficiente da medida de similaridade com custos computacionais relativamente baixos.

1. O Algoritmo

A detecção de anomalias com base no método BPLR proposto consiste em duas etapas principais:

1. Representação das séries temporais;
2. Medição de similaridade.

Antes de descrever o algoritmo de representação de séries temporais no método BPLR, é importante destacar que o método foi projetado para a tarefa de detecção de anomalias. Supõe-se que a série temporal analisada possui algum grau de ciclicidade, cujo tamanho pode ser obtido experimentalmente ou a partir de conhecimento prévio. Assim, a série temporal original é dividida em subsequências não sobrepostas, cujo tamanho corresponde ao ciclo presumido dos dados originais. A comparação dessas subsequências permite que os autores identifiquem regiões anômalas. A seguir, descreveremos o algoritmo de representação de uma única subsequência, que é repetido para todos os elementos da série temporal analisada.

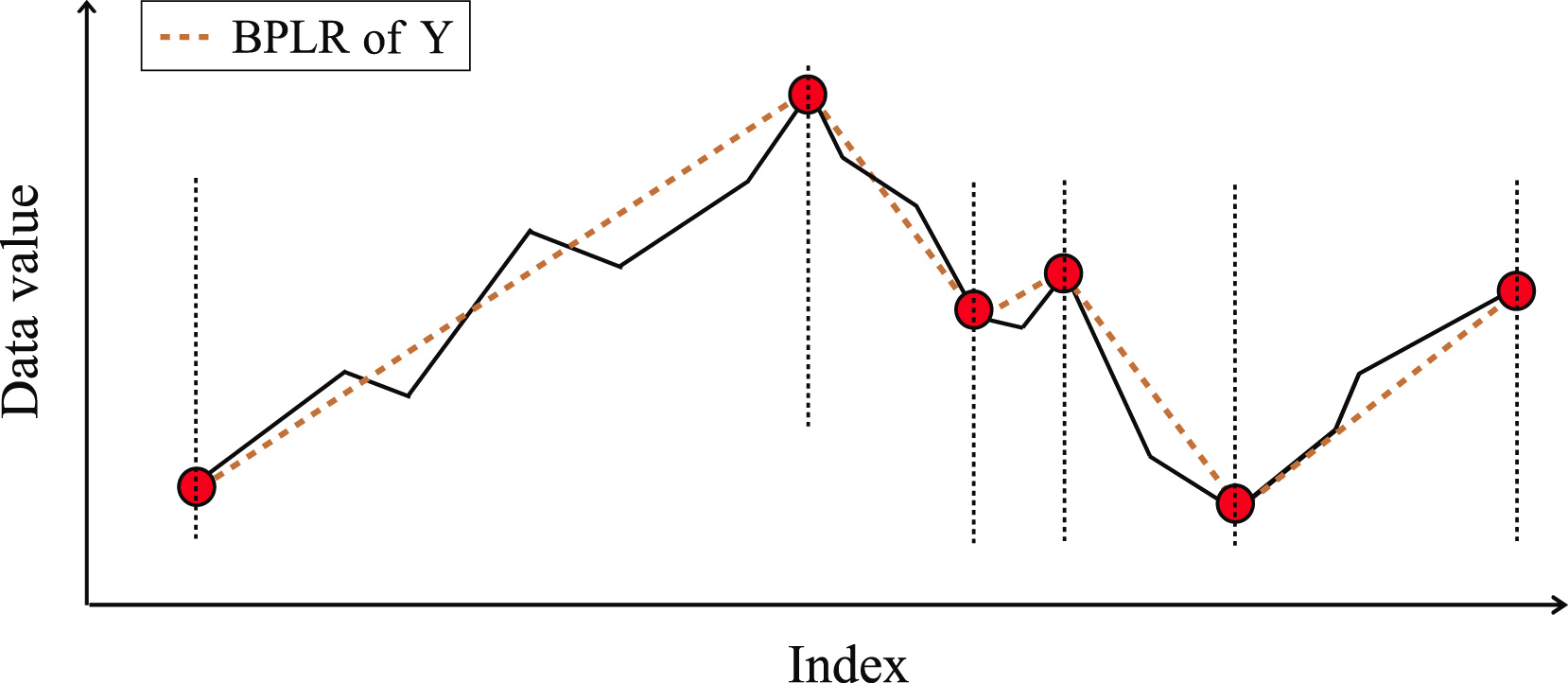
Para representar a série temporal, é necessário identificar vários conjuntos de pontos de segmentação em cada subsequência e, em seguida, transformar a subsequência original em um conjunto de segmentos lineares.

Inicialmente, para encontrar os pontos de separação prováveis da subsequência em segmentos distintos, identificamos todos os possíveis Pontos de Reversão de Tendência (Trend Turning Points — TTP). Os autores do método destacam seis tipos de pontos de reversão de tendência.

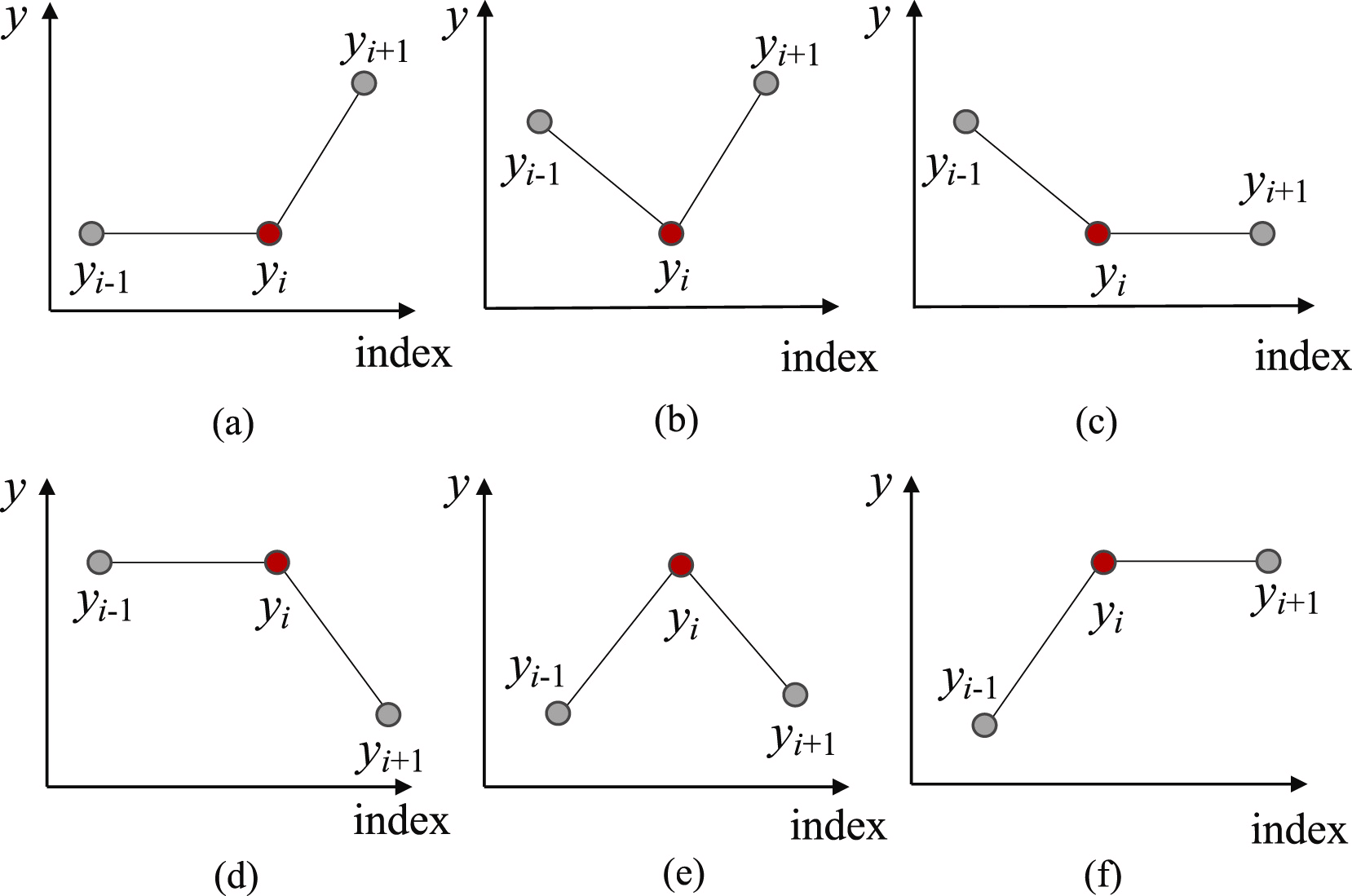
Vale mencionar que os primeiros e últimos elementos de cada subsequência são automaticamente considerados Pontos de Reversão de Tendência.

O próximo passo é determinar a importância de cada ponto de reversão de tendência encontrado. Como medida de importância dos TTP, os autores propõem o uso do desvio em relação ao valor médio da subsequência.

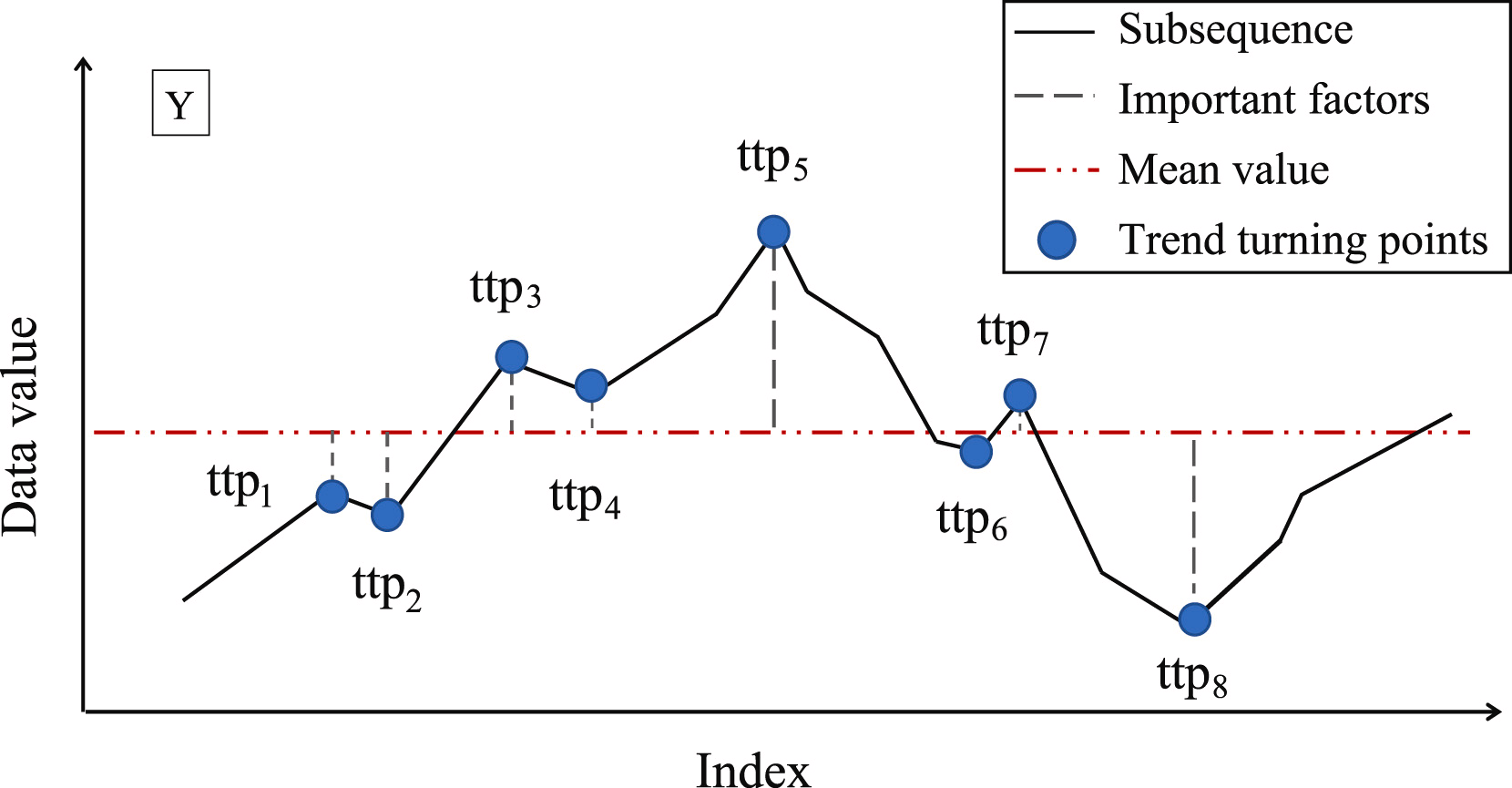
Em seguida, os Pontos de Reversão de Tendência (TTP) são ordenados conforme sua importância. A definição dos segmentos é realizada de forma iterativa, partindo do TTP1 com a maior importância em duas direções: antes e depois do TTP1. Para determinar a qualidade de um segmento, é introduzido um hiperparâmetro adicional, δß, que define o desvio máximo permitido dos pontos da sequência em relação à linha do segmento.

Para determinar o ponto inicial do segmento anterior, percorremos os elementos da sequência original em ordem reversa a partir do TTP1 analisado, até que todos os elementos entre o TTP1 e o candidato ao início do segmento estejam dentro do limite δß. Quando encontramos um ponto que excede essas margens, a iteração é interrompida, e o segmento é armazenado. Se outros pontos de reversão de tendência previamente encontrados caírem na área do segmento, eles são removidos.

Da mesma forma, é realizado o processo de busca pelo término do segmento na direção após o TTP1. É esse processo de busca de segmentos em ambas as direções a partir do extremo que confere ao método o nome de bidirecional.

Após a determinação dos pontos finais de ambos os segmentos, as operações são repetidas com o próximo extremo em ordem de importância. As iterações terminam quando não há mais pontos de reversão de tendência não processados na matriz.

Para calcular a similaridade entre duas subsequências, é determinada a área da figura formada pelos segmentos das sequências analisadas.

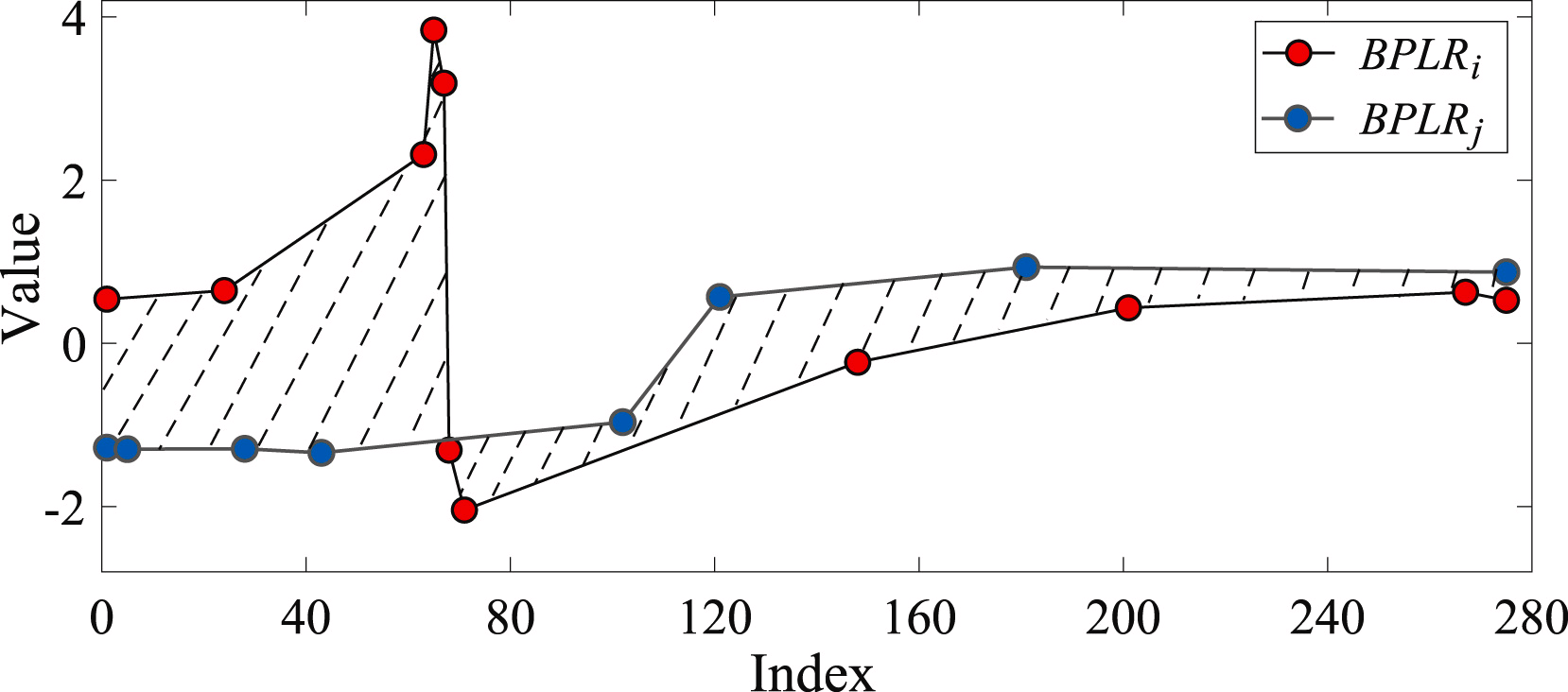
Para resolver o problema da detecção de anomalias, os autores do método criam uma matriz de desvios Mdist. Em seguida, para cada subsequência, é calculado o desvio total em relação às outras subsequências da série temporal analisada, denominado Di. Na prática, Di representa a soma dos elementos da matriz Mdist na linha i. Uma subsequência é considerada anômala se o seu desvio total exceder um limiar de erro pré-determinado em relação à média desse indicador das demais subsequências.

Os autores do método BPLR apresentam resultados experimentais com dados sintéticos e reais, demonstrando a eficácia da solução proposta.

2. Implementação em MQL5

Acima, discutimos a representação teórica do método BPLR para a detecção de subsequências anômalas em séries temporais. Na parte prática deste artigo, implementaremos nossa interpretação das abordagens propostas utilizando MQL5. Vale mencionar que utilizaremos apenas parcialmente as soluções sugeridas.

Desde já, adianto que, no escopo deste trabalho, não buscaremos anomalias em séries temporais. Os mercados financeiros são extremamente dinâmicos e multifacetados, portanto é perfeitamente esperado que surjam desvios significativos entre quaisquer duas subsequências não sobrepostas.

Por outro lado, a representação alternativa de uma série temporal como uma sequência linear por partes pode ser bastante útil. Em nossos trabalhos anteriores, já discutimos os benefícios de segmentar dados. A questão da definição do tamanho dos segmentos continua sendo um tema muito relevante. Até agora, sempre utilizamos tamanhos de segmentos uniformes. No entanto, o método de representação linear por partes permite usar tamanhos de segmentos dinâmicos, ajustados com base na série temporal dos dados brutos, o que de certa forma resolve o problema de extrair características de diferentes escalas da série temporal. Ao mesmo tempo, a representação linear por partes mantém um tamanho fixo, independentemente do tamanho do segmento, o que a torna prática para análises subsequentes.

Vale ressaltar também a forma de representar os segmentos. O próprio nome "representação linear por partes" indica que o segmento é representado como uma função linear:

Consequentemente, especificamos explicitamente a direção da tendência principal no intervalo de tempo do segmento. A capacidade de compactar dados é um bônus adicional, ajudando a reduzir a complexidade do modelo.

E, claro, não iremos dividir a série temporal analisada em subsequências. Em vez disso, representaremos todos os dados brutos como uma sequência linear por partes. Nossa abordagem prevê que o modelo, a partir da análise dos dados representados, deverá tirar conclusões e propor a "única solução correta".

Começaremos nossa implementação desenvolvendo o programa no lado OpenCL.

2.1 Implementação no lado OpenCL

Como vocês sabem, para otimizar os custos de treinamento e operação de nossos modelos, movemos a maioria dos cálculos para o contexto dos dispositivos OpenCL, permitindo a organização das computações em um espaço multidimensional de fluxos paralelos. Esta implementação segue o mesmo princípio.

Para segmentar a série temporal analisada, criaremos um kernel chamado PLR.

__kernel void PLR(__global const float *inputs,
                  __global float *outputs,
                  __global int *isttp,
                  const int transpose,
                  const float min_step
                 )
  {
   const size_t i = get_global_id(0);
   const size_t lenth = get_global_size(0);
   const size_t v = get_global_id(1);
   const size_t variables = get_global_size(1);

Nos parâmetros do kernel, planejamos passar ponteiros para três buffers de dados:

• inputs — resultados brutos
• outputs — resultados
• isttp — buffer auxiliar para registrar os Pontos de Reversão de Tendência (TTP)

Além disso, incluiremos duas constantes:

• transpose — flag que indica a necessidade de transpor os dados brutos e os resultados
• min_step — desvio mínimo necessário dos elementos da sequência para registrar um TTP

Planejamos invocar o kernel em um espaço de tarefas bidimensional, considerando o número de elementos na sequência analisada e a quantidade de sequências unitárias no conjunto multidimensional da série temporal. Assim, no corpo do kernel, identificaremos imediatamente o fluxo atual no espaço de tarefas e, em seguida, determinaremos as constantes de deslocamento no buffer dos dados brutos.

//--- constants
   const int shift_in = ((bool)transpose ? (i * variables + v) : (v * lenth + i));
   const int step_in = ((bool)transpose ? variables : 1);

Após uma breve etapa de preparação, identificaremos a presença de um Ponto de Reversão de Tendência na posição do elemento analisado. Os pontos extremos da série temporal analisada automaticamente recebem o status de ponto de reversão, pois são, por definição, os extremos do segmento.

   float value = inputs[shift_in];
   bool bttp = false;
   if(i == 0 || i == lenth - 1)
      bttp = true;

Em casos específicos, primeiro procuramos a menor variação necessária no valor da série temporal em relação ao elemento atual da sequência. Durante este processo, registramos os valores mínimos e máximos no intervalo percorrido.

   else
     {
      float prev = value;
      int prev_pos = i;
      float max_v = value;
      float max_pos = i;
      float min_v = value;
      float min_pos = i;
      while(fmax(fabs(prev - max_v), fabs(prev - min_v)) < min_step && prev_pos > 0)
        {
         prev_pos--;
         prev = inputs[shift_in - (i - prev_pos) * step_in];
         if(prev >= max_v && (prev - min_v) < min_step)
           {
            max_v = prev;
            max_pos = prev_pos;
           }
         if(prev <= min_v && (max_v - prev) < min_step)
           {
            min_v = prev;
            min_pos = prev_pos;
           }
        }

Em seguida, de maneira semelhante, procuramos o elemento subsequente com o desvio mínimo necessário.

      //---
      float next = value;
      int next_pos = i;
      while(fmax(fabs(next - max_v), fabs(next - min_v)) < min_step && next_pos < (lenth - 1))
        {
         next_pos++;
         next = inputs[shift_in + (next_pos - i) * step_in];
         if(next > max_v && (next - min_v) < min_step)
           {
            max_v = next;
            max_pos = next_pos;
           }
         if(next < min_v && (max_v - next) < min_step)
           {
            min_v = next;
            min_pos = next_pos;
           }
        }

E verificamos se o valor atual é um extremo.

      if(
         (value >= prev && value > next) ||
         (value > prev && value == next) ||
         (value <= prev && value < next) ||
         (value < prev && value == next)
      )
         if(max_pos == i || min_pos == i)
            bttp = true;
     }

É importante lembrar que, ao buscar elementos com o desvio mínimo necessário, podemos formar um corredor de valores que consiste em vários elementos da sequência, criando um certo platô de extremo. Por isso, o elemento recebe o status de Ponto de Reversão de Tendência (TTP) apenas se for de fato o extremo dentro desse corredor.

Salvamos o status determinado e limpamos o buffer de resultados. Nesse momento, sincronizamos os fluxos do grupo local.

//---
   isttp[shift_in] = (int)bttp;
   outputs[shift_in] = 0;
   barrier(CLK_LOCAL_MEM_FENCE);

A sincronização dos fluxos é necessária para garantir que todos os fluxos da sequência unitária do tempo atual tenham registrado seus respectivos status de TTP antes das operações seguintes.

As operações subsequentes são realizadas apenas pelos fluxos que identificaram um Ponto de Reversão de Tendência. Os demais fluxos não atendem às condições especificadas e praticamente finalizam suas operações.

Primeiro, calculamos a posição do extremo atual. Para isso, contamos a quantidade de flags positivos na posição do elemento atual e, de forma prudente, armazenamos em uma variável local a posição do TTP anterior no buffer de dados brutos.

//--- calc position
   int pos = -1;
   int prev_in = 0;
   int prev_ttp = 0;
   if(bttp)
     {
      pos = 0;
      for(int p = 0; p < i; p++)
        {
         int current_in = ((bool)transpose ? (p * variables + v) : (v * lenth + p));
         if((bool)isttp[current_in])
           {
            pos++;
            prev_ttp = p;
            prev_in = current_in;
           }
        }
     }

Depois, definimos os parâmetros da aproximação linear da tendência do segmento atual.

//--- cacl tendency
   if(pos > 0 && pos < (lenth / 3))
     {
      float sum_x = 0;
      float sum_y = 0;
      float sum_xy = 0;
      float sum_xx = 0;
      int dist = i - prev_ttp;
      for(int p = 0; p < dist; p++)
        {
         float x = (float)(p);
         float y = inputs[prev_in + p * step_in];
         sum_x += x;
         sum_y += y;
         sum_xy += x * y;
         sum_xx += x * x;
        }
      float slope = (dist * sum_xy - sum_x * sum_y) / (dist > 1 ? (dist * sum_xx - sum_x * sum_x) : 1);
      float intercept = (sum_y - slope * sum_x) / dist;

Os resultados obtidos são armazenados no buffer de resultados.

      int shift_out = ((bool)transpose ? ((pos - 1) * 3 * variables + v) : (v * lenth + (pos - 1) * 3));
      outputs[shift_out] = slope;
      outputs[shift_out + 1 * step_in] = intercept;
      outputs[shift_out + 2 * step_in] = ((float)dist) / lenth;
     }

Aqui, vale destacar que caracterizamos cada segmento com três parâmetros:

• slope — o ângulo de inclinação da linha da tendência;
• intercept — o deslocamento da linha da tendência no subespaço dos dados brutos;
• dist — o comprimento do segmento.

Talvez seja necessário dizer algumas palavras sobre a representação da duração do segmento. Imagino que vocês perceberam que usar um valor inteiro para indicar a duração da sequência não seria a melhor opção neste caso. Para que a modelagem funcione de forma eficiente, é preferível utilizar um formato normalizado de representação dos dados. Por isso, decidimos representar a duração do segmento como uma fração do tamanho total da sequência unitária analisada. Dividimos a quantidade de elementos no segmento pelo número total de elementos na sequência do conjunto unitário. Para evitar erros decorrentes de operações inteiras, previamente convertimos a quantidade de elementos do segmento de int para float.

Além disso, criamos uma ramificação específica de operações para o último segmento. Isso ocorre porque não sabemos quantos segmentos serão formados em determinado momento. Hipoteticamente, se houver grandes oscilações nos elementos da série temporal e pontos de reversão de tendência em cada elemento, poderíamos acabar com um aumento de valores em vez de uma compactação por um fator de 3. Embora esse cenário seja improvável, não queremos um aumento no volume de dados, mas também não desejamos perder informações.

Portanto, partimos do conhecimento prévio sobre a representação de séries temporais no MQL5 e do entendimento da estrutura dos dados analisados — os dados mais recentes são posicionados no início da série temporal. Por isso, damos maior atenção a esses dados, enquanto os elementos no final da janela analisada, que possuem maior profundidade histórica, tendem a ter um impacto reduzido nos eventos subsequentes. Apesar disso, não ignoramos completamente sua influência.

Consequentemente, para registrar os resultados, usamos um buffer de dados do mesmo tamanho que o tensor de valores originais da série temporal. Isso nos permite armazenar segmentos que são três vezes menores que o comprimento da sequência (3 elementos para registrar 1 segmento). Acreditamos que essa capacidade é mais do que suficiente. No entanto, para evitar a perda de dados caso haja mais segmentos do que o esperado, combinamos os dados dos últimos segmentos em um único segmento.

   else
     {
      if(pos == (lenth / 3))
        {
         float sum_x = 0;
         float sum_y = 0;
         float sum_xy = 0;
         float sum_xx = 0;
         int dist = lenth - prev_ttp;
         for(int p = 0; p < dist; p++)
           {
            float x = (float)(p);
            float y = inputs[prev_in + p * step_in];
            sum_x += x;
            sum_y += y;
            sum_xy += x * y;
            sum_xx += x * x;
           }
         float slope = (dist * sum_xy - sum_x * sum_y) / (dist > 1 ? (dist * sum_xx - sum_x * sum_x) : 1);
         float intercept = (sum_y - slope * sum_x) / dist;
         int shift_out = ((bool)transpose ? ((pos - 1) * 3 * variables + v) : (v * lenth + (pos - 1) * 3));
         outputs[shift_out] = slope;
         outputs[shift_out + 1 * step_in] = intercept;
         outputs[shift_out + 2 * step_in] = ((float)dist) / lenth;
        }
     }
  }

Geralmente, esperamos ter um número menor de segmentos, o que resultará no preenchimento dos elementos finais do nosso buffer de resultados com valores zero.

É importante observar que o algoritmo descrito anteriormente não contém parâmetros treináveis e pode ser utilizado na fase de pré-processamento dos dados brutos. Isso significa que não há necessidade de um processo de propagação reversa ou de distribuição de gradientes de erro. Mesmo assim, planejamos integrar esse algoritmo em nossas redes neurais. Como consequência, precisaremos implementar o algoritmo de propagação reversa para distribuir o gradiente de erro dos camadas neurais posteriores até as camadas anteriores. Ao mesmo tempo, a ausência de parâmetros treináveis elimina a necessidade de algoritmos de otimização.

Assim, como parte da implementação dos algoritmos de propagação reversa, criaremos o kernel de distribuição de gradiente de erro chamado PLRGradient.

__kernel void PLRGradient(__global float *inputs_gr,
                          __global const float *outputs,
                          __global const float *outputs_gr,
                          const int transpose
                         )
  {
   const size_t i = get_global_id(0);
   const size_t lenth = get_global_size(0);
   const size_t v = get_global_id(1);
   const size_t variables = get_global_size(1);

Nos parâmetros desse kernel, também passaremos ponteiros para três buffers de dados. Desta vez, esses serão dois buffers de gradientes de erro (um para os dados brutos e outro para os resultados) e o buffer dos resultados da propagação para frente da camada atual. Além disso, incluiremos o já conhecido flag de transposição de dados, que é usado para definir os deslocamentos nos buffers.

Planejamos invocar o kernel no mesmo espaço bidimensional de tarefas. A primeira dimensão será limitada pelo tamanho da sequência da série temporal, enquanto a segunda será pelo número de séries temporais unitárias nos dados multimodais brutos. No corpo do kernel, identificamos imediatamente o fluxo atual no espaço de tarefas em todas as dimensões.

Em seguida, definiremos as constantes de deslocamento nos buffers de dados.

//--- constants
   const int shift_in = ((bool)transpose ? (i * variables + v) : (v * lenth + i));
   const int step_in = ((bool)transpose ? variables : 1);
   const int shift_out = ((bool)transpose ? v : (v * lenth));
   const int step_out = 3 * step_in;

A preparação, no entanto, não termina aqui. O próximo passo será identificar o segmento em que o elemento analisado dos dados brutos está localizado. Para isso, faremos um loop no qual somaremos os tamanhos dos segmentos, começando pelo primeiro. Repetiremos as iterações até encontrar o segmento que contenha o elemento buscado dos dados brutos.

//--- calc position
   int pos = -1;
   int prev_in = 0;
   int dist = 0;
   do
     {
      pos++;
      prev_in += dist;
      dist = (int)fmax(outputs[shift_out + pos * step_out + 2 * step_in] * lenth, 1);
     }
   while(!(prev_in <= i && (prev_in + dist) > i));

Após a conclusão das iterações, obteremos:

• pos — o índice do segmento que contém o elemento buscado dos dados brutos;
• prev_in — o deslocamento no buffer de dados brutos até o primeiro elemento do segmento;
• dist — o número de elementos no segmento.

Para calcular as derivadas de primeira ordem das operações de propagação para frente, precisaremos também da soma das posições dos elementos do segmento e da soma dos seus valores quadráticos.

//--- calc constants
   float sum_x = 0;
   float sum_xx = 0;
   for(int p = 0; p < dist; p++)
     {
      float x = (float)(p);
      sum_x += x;
      sum_xx += x * x;
     }

Com a preparação finalizada, podemos prosseguir com o cálculo do gradiente de erro. Primeiro, extrairemos o gradiente de erro para o ângulo de inclinação e o deslocamento.

//--- get output gradient
   float grad_slope = outputs_gr[shift_out + pos * step_out];
   float grad_intercept = outputs_gr[shift_out + pos * step_out + step_in];

Lembremos da fórmula utilizada durante a propagação para frente para calcular o deslocamento vertical da linha de tendência.

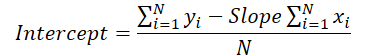
Observamos que o valor do ângulo de inclinação é utilizado para o cálculo do deslocamento. Portanto, é necessário ajustar o gradiente de erro do ângulo de inclinação, levando em consideração seu impacto na correção do deslocamento. Para isso, derivamos a função de deslocamento em relação ao ângulo de inclinação.

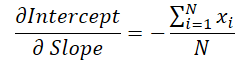
Multiplicamos o valor obtido pelo gradiente de erro do deslocamento e somamos o resultado ao gradiente de erro do ângulo de inclinação.

//--- calc gradient
   grad_slope -= sum_x / dist * grad_intercept;

Agora, vamos considerar a fórmula usada para definir o ângulo de inclinação.

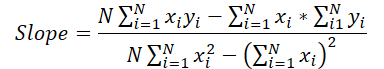
Percebe-se que o denominador é uma constante, permitindo que ajustemos o gradiente de erro do ângulo de inclinação de acordo com essa constante.

   grad_slope /= fmax(dist * sum_xx - sum_x * sum_x, 1);

Por fim, analisaremos a influência dos dados brutos em ambas as fórmulas.

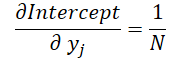
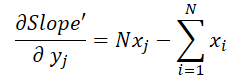
onde 1 ≤ j ≤ N e

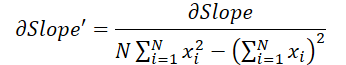
Com base nessas fórmulas, determinamos o gradiente de erro no nível dos dados brutos.

   float grad = grad_intercept / dist;
   grad += (dist * (i - prev_in) - sum_x) * grad_slope;
   if(isnan(grad) || isinf(grad))
      grad = 0;

O resultado é então armazenado no elemento correspondente do buffer de gradientes dos dados brutos.

//--- save result
   inputs_gr[shift_in] = grad;
  }

Com isso, concluímos o trabalho no contexto OpenCL, o código completo do programa OpenCL pode ser encontrado no anexo.

2.2 Implementação da Nova Classe

Após finalizar o trabalho no contexto OpenCL, passamos para o código da aplicação principal. Aqui, criaremos uma nova classe chamada CNeuronPLROCL, que nos permitirá integrar o algoritmo descrito anteriormente em nossos modelos, na forma de uma camada neural convencional.

Como geralmente semelhantes, o novo objeto herda sua funcionalidade principal da nossa classe base de camadas neurais, CNeuronBaseOCL. Abaixo, apresentamos a estrutura dessa nova classe.

class CNeuronPLROCL  :  public CNeuronBaseOCL
  {
protected:
   bool              bTranspose;
   int               icIsTTP;
   int               iVariables;
   int               iCount;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL)  { return true; }

public:
                     CNeuronPLROCL(void)  : bTranspose(false) {};
                    ~CNeuronPLROCL(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window_in, uint units_count, bool transpose, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronPLROCL;   }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

Na estrutura apresentada, é possível observar a redefinição de um conjunto padrão de métodos, além da adição de algumas variáveis, cujos nomes indicam claramente suas funções:

• bTranspose — flag que indica a necessidade de transpor os dados brutos e os resultados;
• iCount — tamanho da sequência analisada (profundidade histórica);
• iVariables — número de parâmetros analisados no conjunto multimodal da série temporal (sequências unitárias).

Vale destacar que, apesar da presença de um buffer auxiliar nos parâmetros do kernel da propagação para frente, não criamos um buffer adicional na aplicação principal. Em vez disso, apenas armazenamos o ponteiro correspondente em uma variável local chamada icIsTTP.

A ausência de objetos internos permite que o construtor e o destrutor da classe permaneçam vazios. A inicialização do objeto ocorre no método Init.

bool CNeuronPLROCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                         uint window_in, uint units_count, bool transpose, 
                         ENUM_OPTIMIZATION optimization_type, uint batch
                        )
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_in * units_count, optimization_type, batch))
      return false;

O método recebe como parâmetros as principais constantes que definem a arquitetura do objeto. No corpo da classe, imediatamente chamamos o método homônimo da classe pai, que já implementa os controles necessários e a inicialização dos objetos e variáveis herdadas.

Em seguida, armazenamos os parâmetros de configuração do objeto criado.

   iVariables = (int)window_in;
   iCount = (int)units_count;
   bTranspose = transpose;

Por fim, no método, criaremos um buffer auxiliar de dados no contexto OpenCL.

   icIsTTP = OpenCL.AddBuffer(sizeof(int) * Neurons(), CL_MEM_READ_WRITE);
   if(icIsTTP < 0)
      return false;
//---
   return true;
  }

Após a inicialização do objeto, prosseguimos com a construção do algoritmo de propagação para frente, implementado no método feedForward. Aqui, basta chamarmos o kernel de propagação para frente PLR, criado anteriormente. No entanto, há um detalhe importante: precisamos configurar grupos locais para sincronizar os fluxos dentro de cada sequência temporal unitária.

bool CNeuronPLROCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!OpenCL || !NeuronOCL || !NeuronOCL.getOutput())
      return false;
//---
   uint global_work_offset[2] = {0};
   uint global_work_size[2] = {iCount, iVariables};
   uint local_work_size[2] = {iCount, 1};

Para isso, definimos um espaço global de tarefas bidimensional. No primeiro eixo, especificamos o tamanho da sequência analisada, e no segundo eixo, o número de sequências temporais unitárias. O tamanho do grupo local também é definido em um espaço de tarefas bidimensional, onde o primeiro eixo corresponde ao valor global, e no segundo eixo definimos 1. Dessa forma, cada grupo local trabalha com sua própria sequência unitária.

Depois, passamos os parâmetros necessários para o kernel.

   ResetLastError();
   if(!OpenCL.SetArgumentBuffer(def_k_PLR, def_k_plr_inputs, NeuronOCL.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_PLR, def_k_plr_outputs, getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_PLR, def_k_plt_isttp, icIsTTP))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_PLR, def_k_plr_transpose, (int)bTranspose))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_PLR, def_k_plr_step, (float)0.3))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

E, em seguida, adicionamos o kernel à fila de execução.

//---
   if(!OpenCL.Execute(def_k_PLR, 2, global_work_offset, global_work_size, local_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }
//---
   return true;
  }

Em cada etapa, lembramos de monitorar o processo de execução das operações. Ao final do método, retornamos um valor lógico indicando o sucesso ou falha da execução para o programa chamador.

O método de distribuição do gradiente de erro, calcInputGradients, é construído de forma semelhante. Porém, ao contrário da propagação para frente, aqui não criamos grupos locais, e cada fluxo realiza suas operações independentemente. O código completo deste método pode ser encontrado no anexo.

Como mencionado anteriormente, o objeto que estamos criando não possui parâmetros treináveis. Portanto, o método de otimização updateInputWeights foi redefinido apenas para manter a estrutura dos objetos e garantir a compatibilidade durante a implementação. Esse método sempre retorna true.

Com isso, concluímos a explicação sobre os algoritmos dos métodos da nova classe. O código completo de todos os métodos, incluindo aqueles que não foram detalhados nesta parte do artigo, está disponível no anexo.

2.3 Arquitetura do Modelo

Nesta parte do artigo, implementamos um dos algoritmos de representação linear por partes de séries temporais, que agora pode ser integrado à arquitetura dos nossos modelos.

Para testar a eficácia da implementação proposta, incorporamos a nova classe na estrutura de um modelo de Codificador de estado do ambiente. Simplicidade foi a nossa prioridade na arquitetura do modelo, visando avaliar o impacto da decomposição da série temporal em tendências lineares distintas.

Como de costume, a arquitetura do modelo é descrita no método CreateEncoderDescriptions.

bool CreateEncoderDescriptions(CArrayObj *encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }

O método recebe como parâmetro um ponteiro — objeto de array dinâmico para registrar a arquitetura do modelo em construção. No corpo do método, imediatamente verificamos a validade do ponteiro recebido. Se necessário, criamos uma nova instância do array dinâmico.

Alimentamos o modelo com informações sobre o estado do ambiente, fornecendo uma profundidade histórica definida, sem qualquer pré-processamento dos dados.

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Aqui é importante mencionar que o algoritmo de representação linear por partes funciona igualmente bem com dados normalizados e com dados "brutos". Mas há algumas nuances.

Em primeiro lugar, na nossa implementação, utilizamos o parâmetro de desvio mínimo necessário dos valores da série temporal para registrar os Pontos de Reversão de Tendência (TTP). É desnecessário dizer que é preciso ajustar cuidadosamente este hiperparâmetro para analisar cada série temporal de forma adequada. O uso do algoritmo para analisar séries temporais multimodais, cujas sequências unitárias possuem distribuições diferentes, complica consideravelmente essa tarefa e, geralmente, torna inviável o uso de um único hiperparâmetro para todas as sequências unitárias.

Em segundo lugar, planejamos utilizar os resultados do PLR em modelos cuja eficiência é significativamente maior quando se usam dados normalizados.

Claro, podemos aplicar a normalização aos resultados do PLR antes de fornecê-los ao modelo, mas a quantidade dinâmica de segmentos dificulta essa tarefa.

Por outro lado, normalizar os dados brutos antes de passá-los para o modelo que usa o algoritmo de representação linear por partes simplifica bastante essas questões. Unificar as distribuições de todas as sequências unitárias permite o uso de um único hiperparâmetro para a análise de séries temporais multimodais. Além disso, a normalização das distribuições dos dados brutos possibilita o uso de hiperparâmetros médios, adequados para diferentes sequências de entrada. 

Ao receber dados normalizados no início da camada, obtemos sequências normalizadas na saída. Por isso, a próxima camada do nosso modelo é a camada de normalização em lote.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Em seguida, para operar no contexto das sequências unitárias, transpomos os dados brutos.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Vale notar que, em nossa implementação do algoritmo PLR, é mais eficiente usar um parâmetro de transposição em vez de uma camada de transposição. No entanto, o uso da camada de transposição é justificado pelo design subsequente da arquitetura do modelo.

Após preparar os dados, dividimos em segmentos lineares.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronPLROCL;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   descr.step = int(false);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Em seguida, utilizamos um MLP de três camadas para fazer previsões das sequências unitárias, com base em um horizonte de previsão definido.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = BarDescr;
   descr.window = HistoryBars;
   descr.step = HistoryBars;
   descr.window_out = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = BarDescr;
   descr.window = LatentCount;
   descr.step = LatentCount;
   descr.window_out = LatentCount;
   descr.optimization = ADAM;
   descr.activation = SIGMOID;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = BarDescr;
   descr.window = LatentCount;
   descr.step = LatentCount;
   descr.window_out = NForecast;
   descr.optimization = ADAM;
   descr.activation = TANH;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Observe que usamos camadas convolucionais com janelas não sobrepostas para realizar a previsão condicionalmente independente dos valores de cada sequência unitária. Utilizo o termo "previsão condicionalmente independente" porque as trajetórias preditivas de todas as sequências unitárias utilizam as mesmas matrizes de coeficientes de peso.

Os valores preditivos são então transpostos para o formato dos dados brutos.

//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = BarDescr;
   descr.window = NForecast;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Em seguida, adicionamos a eles os parâmetros estatísticos da distribuição, que foram extraídos durante a normalização dos dados brutos.

//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRevInDenormOCL;
   descr.count = BarDescr*NForecast;
   descr.activation = None;
   descr.optimization = ADAM;
   descr.layers=1;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Na saída do modelo, aplicamos técnicas do método FreDF para alinhar os passos individuais das trajetórias preditivas das sequências unitárias da série temporal analisada.

//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFreDFOCL;
   descr.window = BarDescr;
   descr.count =  NForecast;
   descr.step = int(true);
   descr.probability = 0.7f;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

Assim, construímos o modelo de Codificador de estado do ambiente, que essencialmente integra o PLR e o MLP para previsão de séries temporais.

3. Testes

Na parte prática deste artigo, implementamos o algoritmo de representação linear por partes de séries temporais (PLR). O algoritmo proposto não contém parâmetros treináveis, servindo apenas para converter a série temporal analisada em uma representação alternativa. Também apresentamos uma modelo de previsão de séries temporais relativamente simples, utilizando a camada CNeuronPLROCL que criamos. Agora é o momento de avaliar a eficácia das abordagens descritas.

Para treinar o modelo de Codificador de estado do ambiente na previsão dos valores futuros da série temporal analisada, utilizamos um conjunto de dados de treinamento compilado durante o trabalho da nossa publicação anterior.

Lembro que, para o treinamento de nossos modelos, usamos dados históricos reais do instrumento EURUSD no time frame H1, coletados ao longo de todo o ano de 2023. Durante o treinamento, o modelo de Codificador de estado do ambiente trabalha apenas com dados históricos de movimentação de preços e indicadores analisados. Assim, treinamos o modelo até obter os resultados desejados, sem a necessidade de atualizar o conjunto de dados de treinamento.

Quanto ao treinamento do modelo, vale ressaltar a estabilidade do processo. O modelo é treinado de maneira bastante rápida, sem grandes oscilações no erro de previsão.

No final, apesar da simplicidade relativa da estrutura do modelo, os resultados obtidos foram bastante satisfatórios. Por exemplo, abaixo está um gráfico comparativo entre a movimentação de preços alvo e a trajetória prevista.

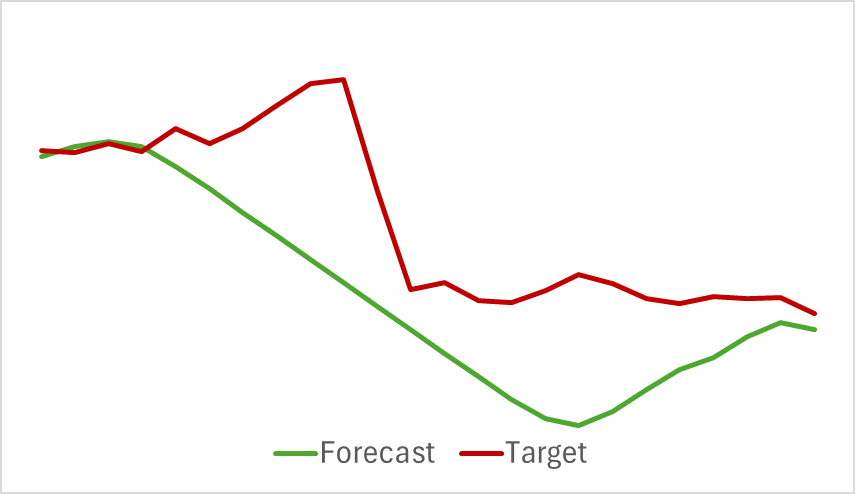
No gráfico, observa-se que o modelo conseguiu capturar as principais tendências do movimento futuro do preço. É interessante notar que, para um horizonte de previsão de 24 horas, os valores previstos são bastante próximos dos reais no início e no fim da trajetória de previsão. Apenas o impulso da trajetória prevista apresenta uma extensão maior ao longo do tempo.

Adicionalmente, as trajetórias de previsão dos indicadores analisados também apresentam bons resultados. Abaixo, mostramos o gráfico de previsão do indicador RSI.

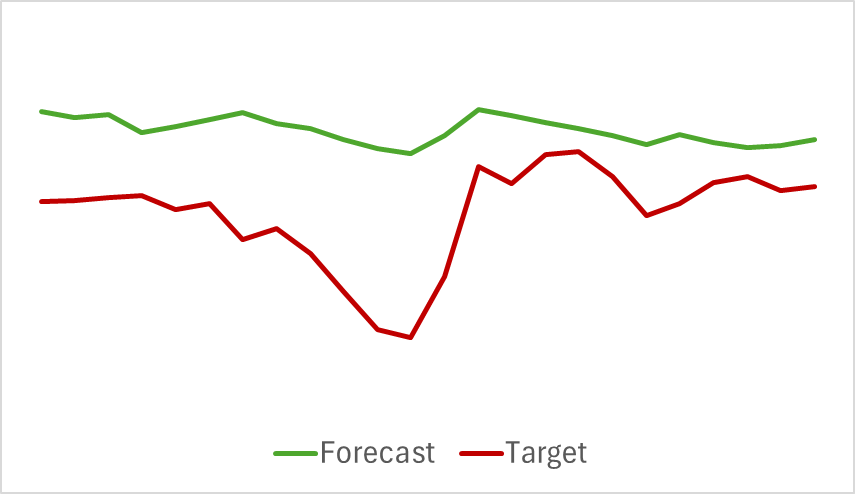
Os valores previstos do RSI estão ligeiramente acima dos valores reais e apresentam uma amplitude menor, mas ainda assim é possível observar uma correspondência temporal e direcional com os principais impulsos.

Quero destacar que as previsões do movimento de preços e dos indicadores apresentadas se referem ao mesmo intervalo de tempo. Ao comparar os dois gráficos, nota-se que o impulso principal nos valores previstos e reais dos indicadores coincide, em termos de tempo, com o impulso principal da movimentação real do preço.

Considerações finais

Neste artigo, exploramos métodos de representação alternativa de séries temporais por meio de segmentação linear por partes. Na parte prática, implementamos uma das variações dos métodos propostos. Os resultados dos experimentos realizados indicam o potencial dos métodos discutidos.

Referências

Representação linear por partes bidirecional de séries temporais com aplicação na detecção de anomalias coletivas

Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA para coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA para coleta de exemplos pelo método Real-ORL
3	Study.mq5	Expert Advisor	EA para treinamento de Modelos
4	StudyEncoder.mq5	Expert Advisor	EA para treinamento do Codificador
5	Test.mq5	Expert Advisor	EA para testar o modelo
6	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema
7	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação de redes neurais
8	NeuroNet.cl	Biblioteca	Biblioteca de código do programa OpenCL