
Redes neurais de maneira fácil (Parte 96): Extração multinível de características (MSFformer)
Introdução
Os dados de séries temporais são amplamente utilizados no mundo real e desempenham um papel fundamental em diversas áreas, incluindo finanças. Esses dados representam sequências de observações coletadas em diferentes pontos no tempo. A análise e modelagem profundas das séries temporais permitem aos pesquisadores prever tendências e padrões futuros, o que é utilizado no processo de tomada de decisões.
Nos últimos anos, muitos pesquisadores se concentraram no estudo de séries temporais utilizando modelos de aprendizado profundo. Esses métodos se mostraram eficazes na captura de relações não lineares e no tratamento de dependências de longo prazo, sendo especialmente úteis para modelar sistemas complexos. No entanto, apesar dos avanços significativos, ainda existem desafios substanciais para a extração e integração eficazes dessas dependências de longo prazo com características de curto prazo. A compreensão e a integração corretas desses dois tipos de dependência são imprescindíveis para construir modelos preditivos precisos e confiáveis.
Uma das soluções propostas para esse problema foi apresentada no trabalho "Time Series Prediction Based on Multi-Scale Feature". Extraction". Nele, é apresentada a MSFformer (Multi-Scale Feature Transformer), uma arquitetura baseada em um mecanismo aprimorado de atenção piramidal. Este modelo é projetado para a extração e integração eficazes de características multinível.
Os autores do método destacam as seguintes inovações da MSFformer:
- Introdução do mecanismo Skip-PAM, que permite ao modelo capturar de maneira eficaz tanto as características de longo prazo quanto as de curto prazo em séries temporais extensas.
- Um módulo aprimorado para a criação de uma estrutura piramidal de dados, o CSCM.
Os autores apresentaram resultados experimentais em três conjuntos de dados de séries temporais, demonstrando o desempenho superior do modelo proposto. Os mecanismos sugeridos permitem que a MSFformer processe dados complexos de séries temporais com maior precisão e eficiência, garantindo previsões altamente precisas e confiáveis.
1. Algoritmo MSFformer
Os autores da MSFformer propõem uma arquitetura inovadora de mecanismo de atenção piramidal aplicada a diferentes intervalos de tempo, que constitui a base do método. Além disso, para construir a informação temporal multinível nos dados brutos, eles utilizam a convolução de características no módulo de construção de grande escala, o CSCM (Coarser-Scale Construction Module), que permite a extração de informações temporais em um nível mais bruto.
No CSCM módulo, é construída uma árvore de características da série temporal analisada. Aqui, inicialmente, os dados brutos passam por uma camada totalmente conectada, que converte a dimensionalidade das características em um tamanho fixo. Em seguida, são utilizados vários blocos de convolução de características FCNN.
No bloco FCNN, vetores de características são formados a partir da extração de dados da sequência original com um passo cruzado especificado. Esses vetores são combinados. E, então, são realizadas sobre eles operações de convolução. A visualização autoral do bloco FCNN é apresentada abaixo.
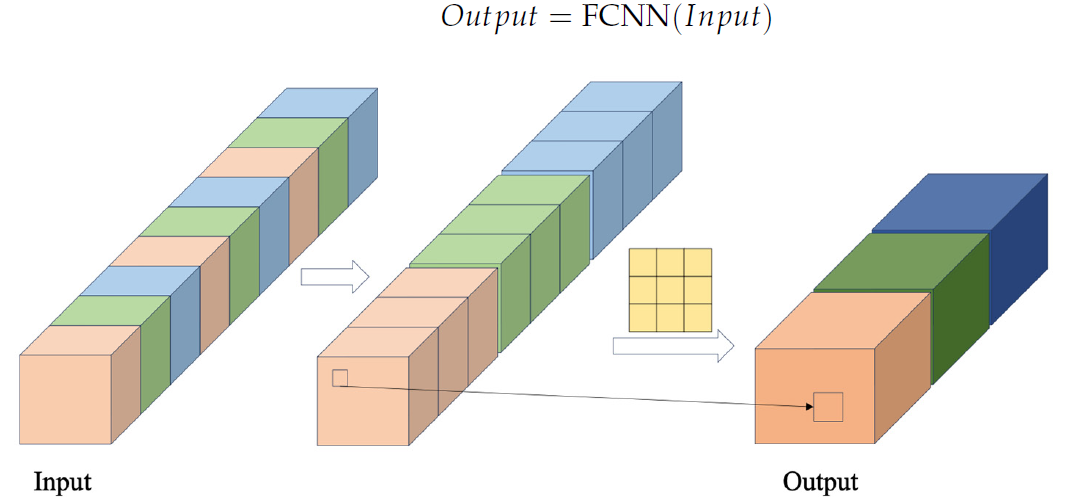
O módulo CSCM proposto pelos autores utiliza vários blocos FCNN consecutivos. E cada um deles, usando os resultados do bloco anterior como dados de entrada, extrai características de uma escala maior.
As características em diferentes escalas obtidas dessa forma são combinadas em um único vetor, cujo tamanho é reduzido por uma camada linear ao nível dos dados originais.
A visualização autoral do módulo CSCM é apresentada abaixo.
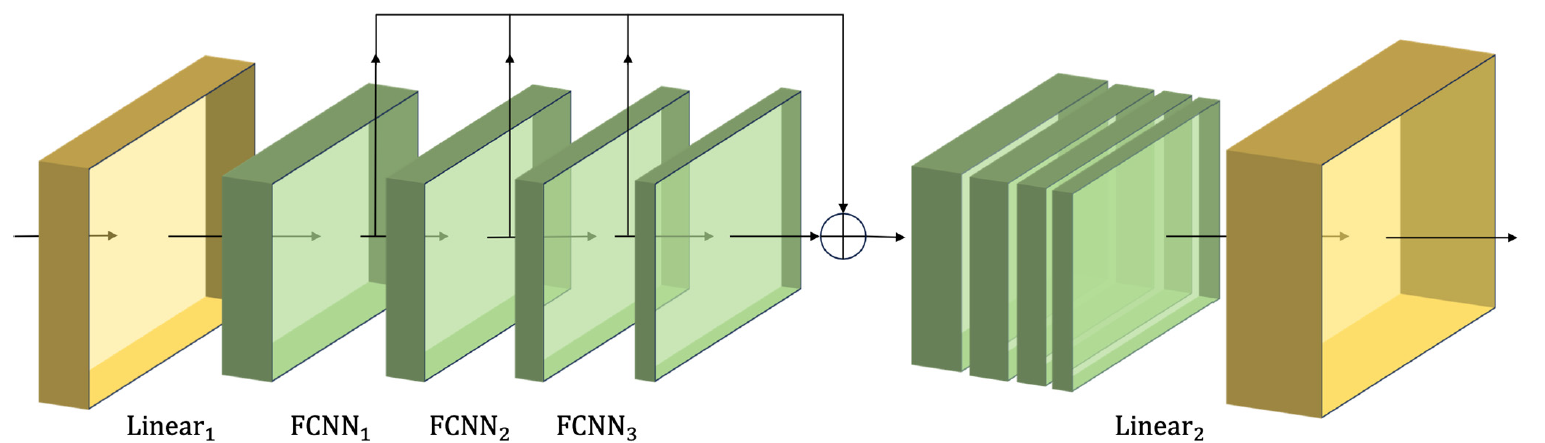
Ao passarmos os dados da série temporal analisada por meio de tal CSCM, obtemos informações temporais sobre as características em diferentes níveis de detalhamento. Construímos uma árvore piramidal de características sobrepondo camadas FCNN. Isso permite compreender os dados em múltiplos níveis e fornece uma base sólida para a implementação da estrutura inovadora de atenção piramidal Skip-PAM(Skip-Pyramidal Attention Module).
A ideia principal do Skip-PAM é processar os dados originais em vários intervalos de tempo, o que permite ao modelo capturar dependências temporais em diferentes níveis de detalhamento. Nos níveis inferiores, o modelo pode se concentrar em padrões detalhados de curto prazo. Enquanto isso, os níveis superiores conseguem capturar tendências e periodicidades mais amplas. O Skip-PAM proposto dá maior ênfase a dependências periódicas, como a cada segunda-feira ou no início de cada mês. Essa abordagem multinível permite que o modelo capture diversas inter-relações temporais em diferentes níveis.
O Skip-PAM extrai informações de séries temporais em múltiplas escalas através de um mecanismo de atenção baseado na árvore de características temporais. Esse processo inclui conexões intraescalares e interescalares. As conexões intraescalares envolvem o cálculo da atenção entre um nó e seus nós vizinhos no mesmo nível. As conexões interescalares envolvem cálculos de atenção entre um nó e seu nó pai.
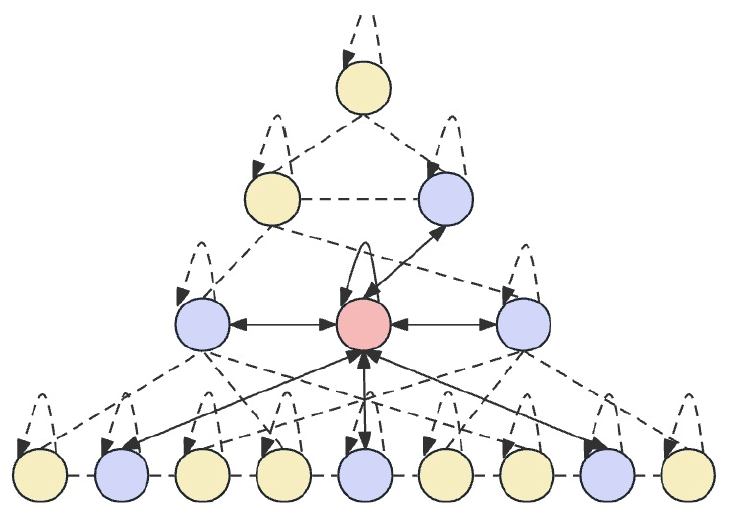
Por meio desse mecanismo de atenção piramidal, o Skip-PAM, combinado com a convolução multinível de características no CSCM, forma uma rede poderosa de extração de características capaz de se adaptar a mudanças dinâmicas em várias escalas temporais, sejam flutuações de curto prazo ou evoluções de longo prazo.
Os dois módulos descritos acima são combinados pelos autores do método em um modelo robusto chamado MSFformer, cuja visualização autoral é apresentada abaixo.
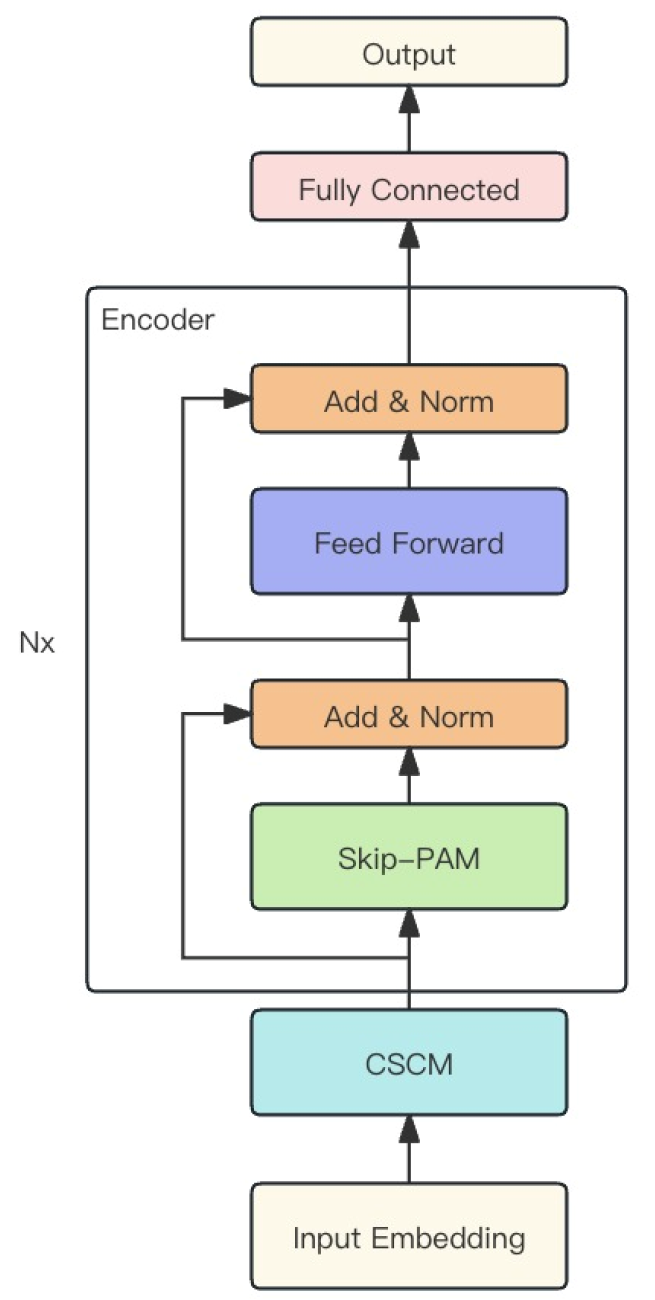
2. Implementação com MQL5
Após compreender os aspectos teóricos do método MSFformer, passamos para a parte prática de nosso artigo, na qual implementamos nossa visão dos métodos propostos utilizando MQL5.
Como mencionado anteriormente, a base do método MSFformer é composta por 2 módulos: CSCM e Skip-PAM. Estes são os módulos que implementaremos neste artigo. O trabalho será extenso, então o dividimos em 2 partes, conforme os módulos a serem implementados.
2.1. Construção do módulo CSCM
Começaremos com a construção do módulo CSCM. Para implementar a arquitetura deste módulo, criaremos a classe CNeuronCSCMOCL, que herdará as funcionalidades principais da classe base de camadas neurais CNeuronBaseOCL. A estrutura da nova classe é apresentada abaixo.
class CNeuronCSCMOCL : public CNeuronBaseOCL { protected: uint i_Count; uint i_Variables; bool b_NeedTranspose; //--- CArrayInt ia_Windows; CArrayObj caTranspose; CArrayObj caConvolutions; CArrayObj caMLP; CArrayObj caTemp; CArrayObj caConvOutputs; CArrayObj caConvGradients; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); //--- virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronCSCMOCL(void) {}; ~CNeuronCSCMOCL(void) {}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint &windows[], uint variables, uint inputs_count, bool need_transpose, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronCSCMOCL; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
Na estrutura apresentada da classe CNeuronCSCMOCL, podemos notar um conjunto relativamente padrão de métodos sobrescrevíveis e uma grande quantidade de arrays dinâmicos, que nos ajudarão a organizar a estrutura multicamada de extração de características. Conheceremos a finalidade dos arrays dinâmicos e das variáveis declaradas durante a implementação dos métodos.
Todos os objetos da classe são declarados estaticamente, o que nos permite deixar o construtor e o destrutor da classe "vazios". A inicialização direta de todos os objetos e variáveis incorporadas é feita no método Init.
Como de costume, nos parâmetros do método Init, recebemos as constantes principais que definem de forma inequívoca a arquitetura do objeto a ser criado.
Para dar ao usuário a flexibilidade de definir o número de camadas de extração de características e o tamanho da janela de convolução, utilizamos o array dinâmico windows. O número de elementos no array indica o número de blocos de extração de características FCNN a serem criados. E o valor de cada elemento indica o tamanho da janela de convolução do respectivo bloco.
O número de sequências temporais unitárias na série temporal multivariada dos dados brutos, assim como o tamanho da sequência original, são indicados nos parâmetros variables e inputs_count, respectivamente.
Além disso, adicionaremos uma variável lógica chamada need_transpose, que indicará a necessidade de transpor os dados brutos antes da extração das características.
bool CNeuronCSCMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint &windows[], uint variables, uint inputs_count, bool need_transpose, ENUM_OPTIMIZATION optimization_type, uint batch) { const uint layers = windows.Size(); if(layers <= 0) return false; if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, inputs_count * variables, optimization_type, batch)) return false;
No corpo do método, criamos um pequeno bloco de controle. Primeiro, verificamos a necessidade de criar pelo menos um bloco de extração de características. Em seguida, chamamos o método homônimo da classe base, no qual já estão implementadas algumas funções de controle e a inicialização dos objetos herdados. O resultado das operações do método da classe base é verificado pelo valor lógico retornado.
Na próxima etapa, salvamos os parâmetros recebidos nas variáveis internas e arrays correspondentes.
if(!ia_Windows.AssignArray(windows)) return false; i_Variables = variables; i_Count = inputs_count / ia_Windows[0]; b_NeedTranspose = need_transpose;
Depois, começamos o processo de inicialização dos objetos incorporados. E, neste ponto, caso seja necessário transpor os dados brutos, criaremos 2 camadas incorporadas de transposição de dados. A primeira para transpor os dados brutos.
if(b_NeedTranspose) { CNeuronTransposeOCL *transp = new CNeuronTransposeOCL(); if(!transp) return false; if(!transp.Init(0, 0, OpenCL, inputs_count, i_Variables, optimization, iBatch)) { delete transp; return false; } if(!caTranspose.Add(transp)) { delete transp; return false; }
E a segunda para transpor os resultados, devolvendo-os à dimensionalidade original.
transp = new CNeuronTransposeOCL(); if(!transp) return false; if(!transp.Init(0, 1, OpenCL, i_Variables, inputs_count, optimization, iBatch)) { delete transp; return false; } if(!caTranspose.Add(transp)) { delete transp; return false; } if(!SetOutput(transp.getOutput()) || !SetGradient(transp.getGradient()) ) return false; }
Vale notar que, se for necessário transpor os dados, redefinimos os buffers de resultados e gradientes da nossa classe para os buffers correspondentes da camada de transposição de resultados. Essa abordagem nos permitirá evitar operações desnecessárias de cópia de dados.
Em seguida, criaremos uma camada de alinhamento do tamanho dos dados brutos dentro das sequências unitárias separadas.
uint total = ia_Windows[0] * i_Count; CNeuronConvOCL *conv = new CNeuronConvOCL(); if(!conv.Init(0, 0, OpenCL, inputs_count, inputs_count, total, 1, i_Variables, optimization, iBatch)) { delete conv; return false; } if(!caConvolutions.Add(conv)) { delete conv; return false; }
E, em um laço, criaremos a quantidade necessária de camadas convolucionais de extração de características.
total = 0; for(uint i = 0; i < layers; i++) { conv = new CNeuronConvOCL(); if(!conv.Init(0, i + 1, OpenCL, ia_Windows[i], ia_Windows[i], (i < (layers - 1) ? ia_Windows[i + 1] : 1), i_Count, i_Variables, optimization, iBatch)) { delete conv; return false; } if(!caConvolutions.Add(conv)) { delete conv; return false; } if(!caConvOutputs.Add(conv.getOutput()) || !caConvGradients.Add(conv.getGradient()) ) return false; total += conv.Neurons(); }
Observe que, no array caConvolutions, combinamos a camada de alinhamento do tamanho dos dados brutos com as camadas de convolução de extração de características. Portanto, o array contém um objeto a mais do que o número especificado de blocos FCNN.
Lembro que o algoritmo do módulo CSCM prevê a concatenação das características de todos os níveis de escala analisados em um único tensor. Assim, paralelamente à criação das camadas convolucionais, calculamos o tamanho total do tensor de resultados. Além disso, armazenamos em arrays dinâmicos separados os ponteiros para os buffers de dados de resultados e gradientes de erro das camadas de extração de características criadas, o que proporcionará acesso mais rápido a seus conteúdos durante o treinamento e a utilização do modelo.
Agora, com o valor necessário em mãos, criaremos uma camada para armazenar o tensor concatenado.
CNeuronBaseOCL *comul = new CNeuronBaseOCL(); if(!comul.Init(0, 0, OpenCL, total, optimization, iBatch)) { delete comul; return false; } if(!caMLP.Add(comul)) { delete comul; return false; }
Também prevemos um caso particular: a criação de apenas uma camada de extração de características. Neste caso, não há nada a concatenar, e o tensor concatenado será uma cópia completa do único tensor de extração de características. Portanto, para evitar operações desnecessárias de cópia, redefiniremos os buffers de resultados e gradientes de erro.
if(layers == 1) { comul.SetOutput(conv.getOutput()); comul.SetGradient(conv.getGradient()); }
Depois disso, criaremos uma camada para ajustar linearmente o tamanho do tensor concatenado de características ao tamanho da sequência original.
conv = new CNeuronConvOCL(); if(!conv.Init(0, 0, OpenCL, total / i_Variables, total / i_Variables, inputs_count, 1, i_Variables, optimization, iBatch)) { delete conv; return false; } if(!caMLP.Add(conv)) { delete conv; return false; }
Anteriormente, redefinimos os buffers de dados brutos e resultados de nossa classe quando necessário para transpor os dados brutos. Caso contrário, fazemos essa redefinição neste momento.
if(!b_NeedTranspose) { if(!SetOutput(conv.getOutput()) || !SetGradient(conv.getGradient()) ) return false; }
Dessa forma, eliminamos operações desnecessárias de cópia de dados em ambos os cenários: quando é necessário transpor os dados brutos ou não.
Para finalizar o método, criaremos 3 buffers auxiliares para armazenar dados intermediários, que usaremos ao concatenar as características e deconcatenar os gradientes de erro correspondentes.
CBufferFloat *buf = new CBufferFloat(); if(!buf) return false; if(!buf.BufferInit(total, 0) || !buf.BufferCreate(OpenCL) || !caTemp.Add(buf)) { delete buf; return false; } buf = new CBufferFloat(); if(!buf) return false; if(!buf.BufferInit(total, 0) || !buf.BufferCreate(OpenCL) || !caTemp.Add(buf)) { delete buf; return false; } buf = new CBufferFloat(); if(!buf) return false; if(!buf.BufferInit(total, 0) || !buf.BufferCreate(OpenCL) || !caTemp.Add(buf)) { delete buf; return false; } //--- caConvOutputs.FreeMode(false); caConvGradients.FreeMode(false); //--- return true; }
Lembramos de monitorar o processo de criação de todos os objetos incorporados. Após a inicialização bem-sucedida de todos os objetos, retornamos o resultado lógico das operações para o programa chamador.
Após construir o método de inicialização do objeto da nossa classe CNeuronCSCMOCL, passamos a realizar seu método de propagação para frente. Vale ressaltar que, dentro desta classe, não executamos operações do lado do programa OpenCL. Toda a implementação se baseia no uso de métodos dos objetos incorporados, cujo algoritmo já foi implementado no OpenCL. Nestas condições, basta estruturarmos um algoritmo de alto nível usando os métodos dos objetos incorporados e herdados da classe base.
Como você sabe, a propagação para frente é feita no método feedForward, cujos parâmetros incluem um ponteiro para o objeto da camada anterior fornecido pelo programa chamador.
bool CNeuronCSCMOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { CNeuronBaseOCL *inp = NeuronOCL; CNeuronBaseOCL *current = NULL;
No corpo do método, declararemos 2 variáveis para armazenar ponteiros para os objetos das camadas neurais. Neste estágio, o ponteiro recebido do programa chamador será atribuído à variável dos dados brutos, enquanto a segunda variável permanecerá vazia.
Em seguida, verificamos a necessidade de transpor os dados brutos. Se for o caso, realizamos essa operação.
if(b_NeedTranspose) { current = caTranspose.At(0); if(!current || !current.FeedForward(inp)) return false; inp = current; }
Depois disso, passamos a série temporal original através das camadas convolucionais de extração de características de diferentes escalas, cujos ponteiros armazenamos no array caConvolutions.
int layers = caConvolutions.Total() - 1; for(int l = 0; l <= layers; l++) { current = caConvolutions.At(l); if(!current || !current.FeedForward(inp)) return false; inp = current; }
Lembro que a primeira camada nesse array é destinada ao alinhamento do tamanho da sequência dos dados brutos. E o resultado dessa camada não será usado na concatenação das características extraídas, que será realizada na etapa seguinte.
Vale mencionar que o algoritmo é projetado sem um limite superior rigoroso para o número de camadas convolucionais de extração de características. No mínimo, é permitido até mesmo um único bloco de extração. O algoritmo mais simples que poderíamos usar aqui seria criar um laço que adicionasse, de forma sequencial, um array de características por vez ao tensor. Contudo, esse método levaria a múltiplas cópias redundantes dos mesmos dados, aumentando significativamente os custos computacionais durante a propagação para frente. Para minimizar essas operações, desenvolvemos uma bifurcação no algoritmo baseada no número de blocos de extração de características.
Como mencionado anteriormente, deve haver ao menos uma camada de extração de características. Se não houver, retornamos um sinal de erro ao programa chamador, indicando o resultado negativo.
current = caMLP.At(0); if(!current) return false; switch(layers) { case 0: return false;
Com um único bloco de extração, não há o que concatenar. Como você se lembra, no método de inicialização da classe, ajustamos os buffers de dados para esse caso específico, eliminando operações desnecessárias de cópia. Assim, podemos prosseguir com as operações subsequentes sem complicações.
case 1: break;
Se houver entre 2 e 4 blocos de extração de características, escolhemos o método apropriado para realizar a concatenação dos dados.
case 2: if(!Concat(caConvOutputs.At(0), caConvOutputs.At(1), current.getOutput(), ia_Windows[1], 1, i_Variables * i_Count)) return false; break; case 3: if(!Concat(caConvOutputs.At(0), caConvOutputs.At(1), caConvOutputs.At(2), current.getOutput(), ia_Windows[1], ia_Windows[2], 1, i_Variables * i_Count)) return false; break; case 4: if(!Concat(caConvOutputs.At(0), caConvOutputs.At(1), caConvOutputs.At(2), caConvOutputs.At(3), current.getOutput(), ia_Windows[1], ia_Windows[2], ia_Windows[3], 1, i_Variables * i_Count)) return false;
Quando existem mais de 4 blocos, concatenamos as características dos primeiros 4 blocos e armazenamos o resultado em um buffer temporário.
default: if(!Concat(caConvOutputs.At(0), caConvOutputs.At(1), caConvOutputs.At(2), caConvOutputs.At(3), caTemp.At(0), ia_Windows[1], ia_Windows[2], ia_Windows[3], ia_Windows[4], i_Variables * i_Count)) return false; break; }
Preste atenção que, durante as operações de concatenação, não acessamos os objetos das camadas convolucionais diretamente pelo array caConvolutions, mas sim os buffers de resultados, cujos ponteiros foram armazenados no array dinâmico caConvOutputs.
A partir daí, definimos um laço que começa com a 4ª camada de extração de características, avançando em passos de 3 camadas. No corpo deste laço, primeiro calculamos o tamanho da janela dos dados já armazenados no buffer temporário.
uint last_buf = 0; for(int i = 4; i < layers; i += 3) { uint buf_size = 0; for(int j = 1; j <= i; j++) buf_size += ia_Windows[j];
Depois, implementamos uma lógica semelhante para escolher a função de concatenação, como mencionamos anteriormente. Neste caso, o buffer temporário com os dados já acumulados é sempre usado primeiro, ao qual são adicionadas as próximas características extraídas.
switch(layers - i) { case 1: if(!Concat(caTemp.At(last_buf), caConvOutputs.At(i), current.getOutput(), buf_size, 1, i_Variables * i_Count)) return false; break; case 2: if(!Concat(caTemp.At(last_buf), caConvOutputs.At(i), caConvOutputs.At(i + 1), current.getOutput(), buf_size, ia_Windows[i + 1], 1, i_Variables * i_Count)) return false; break; case 3: if(!Concat(caTemp.At(last_buf), caConvOutputs.At(i), caConvOutputs.At(i + 1), caConvOutputs.At(i + 2), current.getOutput(), buf_size, ia_Windows[i + 1], ia_Windows[i + 2], 1, i_Variables * i_Count)) return false; break; default: if(!Concat(caTemp.At(last_buf), caConvOutputs.At(i), caConvOutputs.At(i + 1), caConvOutputs.At(i + 2), caTemp.At((last_buf + 1) % 2), buf_size, ia_Windows[i + 1], ia_Windows[i + 2], ia_Windows[i + 3], i_Variables * i_Count)) return false; break; } last_buf = (last_buf + 1) % 2; }
Note que, ao adicionar as últimas camadas de características (de 1 a 3), o resultado é salvo diretamente no buffer da camada de concatenação. Nos demais casos, utilizamos outro buffer temporário. Em cada iteração do laço, alternamos os buffers para evitar distorções e perdas de dados.
Após a concatenação de todas as características em um único tensor, resta ajustar o tamanho do tensor de resultados.
inp = current; current = caMLP.At(1); if(!current || !current.FeedForward(inp)) return false;
E, se necessário, transpor o tensor para que corresponda à dimensionalidade original dos dados.
if(b_NeedTranspose) { inp = current; current = caTranspose.At(1); if(!current || !current.FeedForward(inp)) return false; } //--- return true; }
Lembro que, no método de inicialização, definimos a substituição automática dos buffers de dados. Portanto, a cópia dos resultados das operações para o buffer herdado da nossa classe é automática.
Depois de construir o método de propagação para frente, passamos à implementação dos algoritmos de propagação reversa. O primeiro passo será criar o método para distribuir o gradiente do erro a todos os objetos, conforme sua influência no resultado geral (calcInputGradients). Como de costume, os parâmetros deste método incluem um ponteiro para o objeto da camada neural anterior. Neste caso, precisaremos transmitir a ele a parte apropriada do gradiente do erro.
bool CNeuronCSCMOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(!prevLayer) return false;
No corpo do método, verificamos imediatamente a validade do ponteiro recebido. Em seguida, criamos ponteiros locais para os dois neurônios com os quais trabalharemos de forma sequencial.
CNeuronBaseOCL *current = caMLP.At(0); CNeuronBaseOCL *next = caMLP.At(1);
Lembro que, ao distribuir o gradiente do erro, seguimos o mesmo algoritmo da propagação para frente, mas em ordem inversa. Consequentemente, passamos o gradiente através da camada de transposição de dados, se essa operação for necessária.
if(b_NeedTranspose) { if(!next.calcHiddenGradients(caTranspose.At(1))) return false; }
Em seguida, transmitimos o gradiente do erro para a camada concatenada das características extraídas em diferentes escalas.
if(!current.calcHiddenGradients(next.AsObject())) return false; next = current;
Depois, distribuímos o gradiente do erro para as camadas de extração de características correspondentes.
Não devemos esquecer o caso particular de ter apenas uma camada de extração de características. Nesse caso, basta ajustar o gradiente do erro pela derivada da função de ativação.
int layers = caConvGradients.Total(); if(layers == 1) { next = caConvolutions.At(1); if(next.Activation() != None) { if(!DeActivation(next.getOutput(), next.getGradient(), next.getGradient(), next.Activation())) return false; } }
No caso geral, primeiro separamos o gradiente do erro da última camada de extração de características e ajustamos o gradiente pela derivada da função de ativação.
else { int prev_window = 0; for(int i = 1; i < layers; i++) prev_window += int(ia_Windows[i]); if(!DeConcat(caTemp.At(0), caConvGradients.At(layers - 1), next.getGradient(), prev_window, 1, i_Variables * i_Count)) return false; next = caConvolutions.At(layers); int current_buf = 0;
A seguir, criamos um laço que percorre as camadas de extração de características em ordem inversa.
for(int l = layers; l > 1; l--) { current = caConvolutions.At(l - 1); if(!current.calcHiddenGradients(next.AsObject())) return false;
No corpo deste laço, primeiro obtemos o gradiente do erro da camada de extração subsequente.
int window = int(ia_Windows[l - 1]); prev_window -= window; if(!DeConcat(caTemp.At((current_buf + 1) % 2), caTemp.At(2), caTemp.At(current_buf), prev_window, window, i_Variables * i_Count)) return false;
Depois, extraímos a parte do gradiente correspondente à camada em análise a partir do buffer de gradientes do tensor concatenado.
if(current.Activation() != None) { if(!DeActivation(current.getOutput(), caTemp.At(2), caTemp.At(2), current.Activation())) return false; }
Ajustamos esse gradiente pela derivada da função de ativação.
if(!SumAndNormilize(current.getGradient(), caTemp.At(2), current.getGradient(), 1, false, 0, 0, 0, 1)) return false; next = current; current_buf = (current_buf + 1) % 2; } }
E somamos os gradientes de erro provenientes dos dois fluxos de dados.
Depois, prosseguimos para a próxima iteração do laço. Assim, distribuímos o gradiente do erro por todas as camadas de extração de características.
current = caConvolutions.At(0); if(!current.calcHiddenGradients(next.AsObject())) return false; next = current;
Em seguida, transmitimos o gradiente até a camada de alinhamento do tamanho dos dados brutos.
if(b_NeedTranspose) { current = caTranspose.At(0); if(!current.calcHiddenGradients(next.AsObject())) return false; next = current; }
Se necessário, passamos o gradiente do erro através da camada de transposição de dados.
if(!prevLayer.calcHiddenGradients(next.AsObject())) return false; //--- return true; }
Para finalizar as operações deste método, transmitimos o gradiente do erro para a camada neural anterior, conforme o ponteiro recebido nos parâmetros. Como você sabe, a distribuição do gradiente do erro não é o objetivo final do treinamento do modelo. Trata-se apenas de uma forma de determinar a direção e a magnitude da correção dos parâmetros do modelo. Assim, após distribuir o gradiente do erro com sucesso, precisamos ajustar os parâmetros do modelo para minimizar o erro de maneira geral. Essa funcionalidade é implementada no método updateInputWeights.
bool CNeuronCSCMOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { CObject *prev = (b_NeedTranspose ? caTranspose.At(0) : NeuronOCL); CNeuronBaseOCL *current = NULL;
Nos parâmetros do método, assim como anteriormente, recebemos um ponteiro para o objeto da camada neural anterior. Contudo, neste caso, não verificamos a validade do ponteiro recebido. Simplesmente o armazenamos em uma variável local. Aqui há uma particularidade: a camada de transposição de dados não possui parâmetros. Portanto, não chamaremos o método de ajuste de parâmetros do modelo para ela. Já para a camada de alinhamento do tamanho dos dados brutos, selecionaremos a camada anterior com base no parâmetro de necessidade de transposição dos dados, b_NeedTranspose.
A seguir, estruturamos um laço para corrigir os parâmetros das camadas convolucionais, incluindo a camada de ajuste do tamanho da sequência original e os blocos de extração de características.
for(int i = 0; i < caConvolutions.Total(); i++) { current = caConvolutions.At(1); if(!current || !current.UpdateInputWeights(prev) ) return false; prev = current; }
Em seguida, ajustamos os parâmetros da camada responsável pelo alinhamento da dimensionalidade dos resultados.
current = caMLP.At(1); if(!current || !current.UpdateInputWeights(caMLP.At(0)) ) return false; //--- return true; }
Os demais objetos incorporados em nossa classe CNeuronCSCMOCL não contêm parâmetros que possam ser treinados.
Com isso, consideramos concluída a implementação dos principais algoritmos do módulo CSCM. É claro que a funcionalidade de nossa classe não estará completa sem a implementação adicional de algoritmos para métodos auxiliares. No entanto, para manter o artigo conciso, deixaremos essa parte para estudo independente. O código completo de todos os métodos desta classe está disponível em um anexo. Nele, você encontrará também o código integral de todas as classes e programas utilizados na preparação deste artigo. Agora, vamos à construção dos algoritmos do próximo módulo — Skip-PAM.
2.2 Implementação dos algoritmos do módulo Skip-PAM
A segunda parte do trabalho envolve a implementação do algoritmo de atenção piramidal. A inovação dos autores do método MSFformer está na aplicação de algoritmos de atenção à árvore de características em diferentes intervalos. Os autores utilizam intervalos fixos entre as características dentro de um único nível de atenção. Nossa abordagem, porém, será um pouco diferente. E se permitirmos que o modelo aprenda sozinho quais características cada pirâmide de atenção deve analisar em cada nível de atenção? Parece promissor. E, na minha opinião, a implementação é óbvia e simples: basta adicionar uma camada S3 antes de cada nível de atenção.
Os algoritmos de nossa implementação do módulo Skip-PAM serão estruturados na classe CNeuronSPyrAttentionOCL, cuja estrutura é apresentada abaixo.
class CNeuronSPyrAttentionOCL : public CNeuronBaseOCL { protected: uint iWindowIn; uint iWindowKey; uint iHeads; uint iHeadsKV; uint iCount; uint iPAMLayers; //--- CArrayObj caS3; CArrayObj caQuery; CArrayObj caKV; CArrayInt caScore; CArrayObj caAttentionOut; CArrayObj caW0; CNeuronConvOCL cFF1; CNeuronConvOCL cFF2; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool AttentionOut(CBufferFloat *q, CBufferFloat *kv, int scores, CBufferFloat *out, int window); virtual bool AttentionInsideGradients(CBufferFloat *q, CBufferFloat *q_g, CBufferFloat *kv, CBufferFloat *kv_g, int scores, CBufferFloat *gradient); //--- virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); virtual void ArraySetOpenCL(CArrayObj *array, COpenCLMy *obj); public: CNeuronSPyrAttentionOCL(void) {}; ~CNeuronSPyrAttentionOCL(void) {}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window_in, uint window_key, uint heads, uint heads_kv, uint units_count, uint pam_layers, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronSPyrAttentionMLKV; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
Na estrutura mostrada, percebe-se que a nova classe contém ainda mais arrays dinâmicos e parâmetros. Os nomes deles são semelhantes aos objetos de outros módulos de atenção, e isso não é por acaso. Vamos nos familiarizar com esses objetos e variáveis à medida que implementarmos o código.
Como de costume, começamos a análise dos algoritmos da nova classe pelo método de inicialização do objeto Init.
bool CNeuronSPyrAttentionOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window_in, uint window_key, uint heads, uint heads_kv, uint units_count, uint pam_layers, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_in * units_count, optimization_type, batch)) return false;
Nos parâmetros do método, recebemos as constantes principais que definem a arquitetura do objeto criado. No corpo do método, imediatamente chamamos o método homônimo da classe base, onde foram implementados os controles mínimos necessários e a inicialização dos objetos herdados.
Devemos também considerar que, neste método, analisaremos etapas temporais individuais dentro de uma sequência temporal multimodal geral. Embora, neste caso, talvez não seja completamente apropriado chamar os dados de entrada do módulo Skip-PAM de sequência temporal multimodal. Afinal, os resultados do módulo CSCM anterior consistem em um conjunto de características extraídas em diferentes escalas, e não em uma sequência temporal convencional.
Após a execução bem-sucedida do método de inicialização dos objetos da classe base, armazenamos as constantes recebidas em variáveis locais.
iWindowIn = window_in; iWindowKey = MathMax(window_key, 1); iHeads = MathMax(heads, 1); iHeadsKV = MathMax(heads_kv, 1); iCount = units_count; iPAMLayers = MathMax(pam_layers, 2);
É importante destacar a introdução do novo parâmetro iPAMLayers, que determina o número de níveis de atenção piramidal. Os demais parâmetros mantêm o mesmo funcional descrito nos métodos de atenção discutidos anteriormente. Continuamos com o parâmetro iHeadsKV, permitindo a flexibilidade de usar um número de cabeças Key-Value diferente da quantidade de cabeças de atenção Query, conforme abordado no método MLKV.
Em seguida, limpamos os arrays dinâmicos.
caS3.Clear(); caQuery.Clear(); caKV.Clear(); caScore.Clear(); caAttentionOut.Clear(); caW0.Clear();
Criamos as variáveis locais necessárias.
CNeuronBaseOCL *base = NULL; CNeuronConvOCL *conv = NULL; CNeuronS3 *s3 = NULL;
E estabelecemos um laço para inicializar os objetos do bloco de atenção piramidal. Como você pode imaginar, o número de iterações do laço corresponde ao número de níveis de atenção a serem criados.
for(uint l = 0; l < iPAMLayers; l++) { //--- S3 s3 = new CNeuronS3(); if(!s3) return false; if(!s3.Init(0, l, OpenCL, iWindowIn, iCount, optimization, iBatch) || !caS3.Add(s3)) return false; s3.SetActivationFunction(None);
Dentro do laço, começamos criando a camada S3, responsável por reorganizar a sequência analisada. Neste caso, utilizamos apenas uma camada de embaralhamento de dados com uma janela correspondente ao número de parâmetros analisados na sequência multimodal original.
Depois disso, criamos os objetos para a geração das entidades Query, Key e Value. Vale ressaltar que, ao gerar essas entidades, usamos o mesmo objeto de dados brutos, mas com diferentes parâmetros para as cabeças de atenção.
//--- Query conv = new CNeuronConvOCL(); if(!conv) return false; if(!conv.Init(0, 0, OpenCL, iWindowIn, iWindowIn, iWindowKey*iHeads, iCount, optimization, iBatch) || !caQuery.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(None); //--- KV conv = new CNeuronConvOCL(); if(!conv) return false; if(!conv.Init(0, 0, OpenCL, iWindowIn, iWindowIn, 2*iWindowKey*iHeadsKV, iCount, optimization, iBatch) || !caKV.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(None);
A matriz de coeficientes de dependência será criada no contexto do OpenCL. Aqui, armazenamos apenas o ponteiro para o buffer.
//--- Score int temp = OpenCL.AddBuffer(sizeof(float) * iCount * iCount * iHeads, CL_MEM_READ_WRITE); if(temp < 0) return false; if(!caScore.Add(temp)) return false;
O próximo passo é criar a camada para armazenar os resultados da atenção multi-cabeças.
//--- MH Attention Out base = new CNeuronBaseOCL(); if(!base) return false; if(!base.Init(0, 0, OpenCL, iWindowKey * iHeadsKV * iCount, optimization, iBatch) || !caAttentionOut.Add(conv)) { delete base; return false; } base.SetActivationFunction(None);
Por fim, encerramos cada iteração do laço com uma camada que reduz a dimensionalidade ao nível dos dados brutos.
//--- W0 conv = new CNeuronConvOCL(); if(!conv) return false; if(!conv.Init(0, 0, OpenCL, iWindowKey * iHeadsKV, iWindowKey * iHeadsKV, iWindowIn, iCount, optimization, iBatch) || !caW0.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(None); }
Após completar todas as iterações de criação dos níveis de atenção piramidal, adicionamos uma camada que armazena a soma dos resultados do bloco de atenção piramidal com os dados brutos.
//--- Residual base = new CNeuronBaseOCL(); if(!base) return false; if(!base.Init(0, 0, OpenCL, iWindowIn * iCount, optimization, iBatch) || !caW0.Add(conv)) { delete base; return false; } base.SetActivationFunction(None);
Agora, precisamos inicializar as camadas do bloco FeedForward.
//--- FeedForward if(!cFF1.Init(0, 0, OpenCL, iWindowIn, iWindowIn, 4 * iWindowIn, iCount, optimization, iBatch)) return false; cFF1.SetActivationFunction(LReLU); if(!cFF2.Init(0, 0, OpenCL, 4 * iWindowIn, 4 * iWindowIn, iWindowIn, iCount, optimization, iBatch)) return false; cFF2.SetActivationFunction(None); if(!SetGradient(cFF2.getGradient())) return false;
No final do método, removemos de forma explícita a função de ativação desta camada.
SetActivationFunction(None); //--- return true; }
Após a inicialização dos objetos de nossa classe, partimos para a implementação dos algoritmos de propagação para frente. Vale destacar que será necessário realizar um pequeno trabalho preparatório no programa OpenCL. Criamos um novo kernel chamado MH2PyrAttentionOut, que é, essencialmente, uma versão ajustada do kernel MH2AttentionOut.
__kernel void MH2PyrAttentionOut(__global float *q, __global float *kv, __global float *score, __global float *out, const int dimension, const int heads_kv, const int window ) { //--- init const int q_id = get_global_id(0); const int k = get_global_id(1); const int h = get_global_id(2); const int qunits = get_global_size(0); const int kunits = get_global_size(1); const int heads = get_global_size(2);
A diferença principal, além do nome, está na adição de um parâmetro extra: a janela de atenção window. Planejamos invocar este kernel em um espaço de tarefas tridimensional. Como de costume, iniciamos o kernel identificando o fluxo em todas as dimensões do espaço de tarefas.
Em seguida, calculamos as constantes necessárias.
const int h_kv = h % heads_kv; const int shift_q = dimension * (q_id * heads + h); const int shift_k = dimension * (2 * heads_kv * k + h_kv); const int shift_v = dimension * (2 * heads_kv * k + heads_kv + h_kv); const int shift_s = kunits * (q_id * heads + h) + k; const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE); const int delta_win = (window + 1) / 2; float koef = sqrt((float)dimension); if(koef < 1) koef = 1;
E inicializamos um array local para armazenar valores intermediários.
__local float temp[LOCAL_ARRAY_SIZE];
Primeiro, precisamos determinar os coeficientes de dependência para cada elemento da sequência. Como você sabe, no bloco de atenção, esses coeficientes são normalizados pela função SoftMax. Para isso, começamos calculando a soma dos valores exponenciais dos coeficientes de dependência.
Na etapa inicial, cada fluxo reunirá sua parcela da soma dos valores exponenciais no elemento correspondente do array local. Aqui, há um detalhe importante: calculamos os coeficientes de dependência apenas dentro da janela de atenção do elemento atual. Para os elementos fora dessa janela, o coeficiente de dependência é definido como "0".
//--- sum of exp uint count = 0; if(k < ls) do { if((count * ls) < (kunits - k)) { float sum = 0; if(abs(count * ls + k - q_id) <= delta_win) { for(int d = 0; d < dimension; d++) sum = q[shift_q + d] * kv[shift_k + d]; sum = exp(sum / koef); if(isnan(sum)) sum = 0; } temp[k] = (count > 0 ? temp[k] : 0) + sum; } count++; } while((count * ls + k) < kunits); barrier(CLK_LOCAL_MEM_FENCE);
Para sincronizar os fluxos do grupo local, usamos uma barreira.
Na etapa seguinte, reunimos a soma de todos os elementos do array local. Para isso, implementamos um laço adicional, com sincronização dos fluxos locais em cada iteração. É importante garantir que cada fluxo passe pelo mesmo número de barreiras, para evitar que alguns fluxos "trave".
count = min(ls, (uint)kunits); //--- do { count = (count + 1) / 2; if(k < ls) temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : 0); if(k + count < ls) temp[k + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Com a soma dos valores exponenciais determinada, calculamos os coeficientes de dependência normalizados. E, claro, mantemos a consideração de que as dependências existem apenas dentro da janela de atenção.
//--- score float sum = temp[0]; float sc = 0; if(sum != 0 && abs(k - q_id) <= delta_win) { for(int d = 0; d < dimension; d++) sc = q[shift_q + d] * kv[shift_k + d]; sc = exp(sc / koef) / sum; if(isnan(sc)) sc = 0; } score[shift_s] = sc; barrier(CLK_LOCAL_MEM_FENCE);
Sincronizamos novamente os fluxos locais após calcular os coeficientes de dependência.
Depois, determinamos o valor dos elementos levando em conta as dependências. Utilizamos o mesmo algoritmo de soma em fluxos paralelos, que aplicamos ao calcular a soma exponencial dos coeficientes. Primeiro, reunimos as somas individuais nos elementos do array local.
//--- out for(int d = 0; d < dimension; d++) { uint count = 0; if(k < ls) do { if((count * ls) < (kunits - k)) { float sum = 0; if(abs(count * ls + k - q_id) <= delta_win) { sum = kv[shift_v + d] * (count == 0 ? sc : score[shift_s + count * ls]); if(isnan(sum)) sum = 0; } temp[k] = (count > 0 ? temp[k] : 0) + sum; } count++; } while((count * ls + k) < kunits); barrier(CLK_LOCAL_MEM_FENCE);
Em seguida, coletamos a soma dos valores dos elementos do array.
//--- count = min(ls, (uint)kunits); do { count = (count + 1) / 2; if(k < ls) temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : 0); if(k + count < ls) temp[k + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); //--- out[shift_q + d] = temp[0]; } }
A soma resultante é armazenada no elemento correspondente do buffer de resultados.
Assim, criamos um novo kernel de atenção dentro da janela especificada. Vale notar que para os elementos fora da janela de atenção, os coeficientes de dependência foram definidos como "0". Essa abordagem simples nos permite reutilizar o kernel MH2AttentionInsideGradients já existente para distribuir o gradiente do erro durante a propagação reversa.
Para enfileirar esses kernels para execução no programa principal, criamos os métodos AttentionOut e AttentionInsideGradients, respectivamente. O algoritmo desses métodos não difere muito dos métodos similares discutidos em artigos anteriores desta série, então não entraremos em detalhes agora. Recomendo que você os consulte no anexo. Agora, vamos à implementação dos algoritmos do método de propagação para frente, feedForward.
O método feedForward recebe um ponteiro para o objeto da camada neural anterior, que contém os dados brutos.
bool CNeuronSPyrAttentionOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { CNeuronBaseOCL *prev = NeuronOCL; CNeuronBaseOCL *current = NULL; CBufferFloat *q = NULL; CBufferFloat *kv = NULL;
No corpo do método, criaremos várias variáveis locais para armazenar os ponteiros dos objetos dos neurônios das camadas incorporadas.
Depois, estabelecemos um laço para percorrer os níveis de atenção. Dentro do laço, começamos embaralhando os dados brutos.
for(uint l = 0; l < iPAMLayers; l++) { //--- Mix current = caS3.At(l); if(!current || !current.FeedForward(prev.AsObject()) ) return false; prev = current;
Em seguida, geramos os tensores das entidades Query, Key e Value para aplicar o algoritmo de atenção multi-cabeças.
//--- Query current = caQuery.At(l); if(!current || !current.FeedForward(prev.AsObject()) ) return false; q = current.getOutput(); //--- Key and Value current = caKV.At(l); if(!current || !current.FeedForward(prev.AsObject()) ) return false; kv = current.getOutput();
E executamos o algoritmo do kernel de atenção para o nível atual.
//--- PAM current = caAttentionOut.At(l); if(!current || !AttentionOut(q, kv, caScore.At(l), current.getOutput(), iPAMLayers - l)) return false; prev = current;
Observe que, a cada nível subsequente, reduzimos o tamanho da janela de atenção, criando assim o efeito de uma pirâmide. Para isso, utilizamos a diferença "iPAMLayers - l".
Ao final das iterações do laço, reduzimos a dimensionalidade do tensor de resultados da atenção multi-cabeças ao nível do tamanho original dos dados.
//--- W0 current = caW0.At(l); if(!current || !current.FeedForward(prev.AsObject()) ) return false; prev = current; }
Após a execução bem-sucedida de todos os níveis de atenção piramidal, somamos e normalizamos os resultados da atenção com os dados originais.
//--- Residual current = caW0.At(iPAMLayers); if(!SumAndNormilize(NeuronOCL.getOutput(), prev.getOutput(), current.getOutput(), iWindowIn, true)) return false;
O bloco FeedForward completa o módulo de atenção piramidal, funcionando de forma similar ao Transformer padrão.
//---FeedForward if(!cFF1.FeedForward(current.AsObject()) || !cFF2.FeedForward(cFF1.AsObject()) ) return false;
Em seguida, somamos e normalizamos novamente os dados provenientes das duas séries de operações.
//--- Residual if(!SumAndNormilize(current.getOutput(), cFF2.getOutput(), getOutput(), iWindowIn, true)) return false; //--- return true; }
Não nos esquecemos de monitorar o andamento das operações. No final do método, retornamos o resultado lógico para o programa chamador.
Como de costume, após implementar a propagação para frente, passamos à construção dos algoritmos de propagação reversa, que são compostos por duas etapas: a distribuição do gradiente de erro e a otimização dos parâmetros do modelo.
A distribuição dos gradientes de erro é realizada no método calcInputGradients.
bool CNeuronSPyrAttentionOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(!prevLayer) return false;
Nos parâmetros desse método, recebemos um ponteiro para o objeto da camada neural anterior, cujo buffer precisa ser atualizado com o gradiente de erro, de acordo com a influência dos dados brutos no resultado geral.
Em seguida, criamos algumas variáveis locais para armazenar temporariamente os ponteiros para os objetos internos.
CNeuronBaseOCL *next = NULL; CNeuronBaseOCL *current = NULL; CNeuronBaseOCL *q = NULL; CNeuronBaseOCL *kv = NULL;
A distribuição dos gradientes de erro segue a ordem inversa das operações da propagação para frente. Primeiro, passamos o gradiente de erro pelo bloco FeedForward.
//--- FeedForward current = caW0.At(iPAMLayers); if(!current || !cFF1.calcHiddenGradients(cFF2.AsObject()) || !current.calcHiddenGradients(cFF1.AsObject()) ) return false; next = current;
Depois, somamos os gradientes de erro provenientes das duas séries de operações.
//--- Residual current = caW0.At(iPAMLayers - 1); if(!SumAndNormilize(getGradient(), next.getGradient(), current.getGradient(), iWindowIn, false)) return false; CBufferFloat *residual = next.getGradient(); next = current;
A seguir, organizamos um laço que percorre os níveis de atenção de forma reversa, realizando a descida do gradiente de erro em sequência.
for(int l = int(iPAMLayers - 1); l >= 0; l--) { //--- W0 current = caAttentionOut.At(l); if(!current || !current.calcHiddenGradients(next.AsObject()) ) return false;
Dentro do laço, começamos distribuindo o gradiente de erro pelas cabeças de atenção. Em seguida, propagamos o gradiente até as entidades Query, Key e Value.
//--- MH Attention q = caQuery.At(l); kv = caKV.At(l); if(!q || !kv || !AttentionInsideGradients(q.getOutput(), q.getGradient(), kv.getOutput(), kv.getGradient(), caScore.At(l), current.getGradient()) ) return false;
O próximo passo é fazer a descida do gradiente de erro até a camada de embaralhamento de dados. Nesse ponto, precisamos unir os dados dos dois fluxos — de Query e de Key-Value. Primeiro, extraímos o gradiente de erro de Query. E o armazenamos em um buffer temporário.
//--- Query current = caS3.At(l); if(!current || !current.calcHiddenGradients(q.AsObject()) || !Concat(current.getGradient(), current.getGradient(), residual, iWindowIn,0, iCount) ) return false;
Depois, pegamos o gradiente de Key-Value e somamos os resultados dos dois fluxos de dados.
//--- Key and Value if(!current || !current.calcHiddenGradients(kv.AsObject()) || !SumAndNormilize(current.getGradient(), residual, current.getGradient(), iWindowIn, false) ) return false; next = current;
Passamos o gradiente de erro pela camada de embaralhamento de dados e seguimos para a próxima iteração do laço.
//--- S3 current = (l == 0 ? prevLayer : caW0.At(l - 1)); if(!current || !current.calcHiddenGradients(next.AsObject()) ) return false; next = current; }
Ao final das operações do método, basta combinar os gradientes de erro dos dois fluxos. Primeiro, ajustamos o gradiente de erro das conexões residuais com a derivada da função de ativação da camada anterior. Ao descer o gradiente de erro até o nível da camada, o ajuste para a função de ativação é realizado automaticamente.
current = caW0.At(iPAMLayers - 1); if(!DeActivation(prevLayer.getOutput(), current.getGradient(), residual, prevLayer.Activation()) || !SumAndNormilize(prevLayer.getGradient(), residual, prevLayer.getGradient(), iWindowIn, false) ) return false; //--- return true; }
Por fim, somamos os gradientes de erro de ambos os fluxos.
Após a distribuição dos gradientes de erro, partimos para o ajuste dos parâmetros do modelo. Essa funcionalidade é implementada no método updateInputWeights. O algoritmo desse método é relativamente simples e direto: chamamos, de forma sequencial, os métodos de mesmo nome nos objetos incorporados que contêm parâmetros treináveis.
bool CNeuronSPyrAttentionOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { CNeuronBaseOCL *prev = NeuronOCL; CNeuronBaseOCL *current = NULL; for(uint l = 0; l < iPAMLayers; l++) { //--- S3 current = caS3.At(l); if(!current || !current.UpdateInputWeights(prev) ) return false; //--- Query prev = current; current = caQuery.At(l); if(!current || !current.UpdateInputWeights(prev) ) return false; //--- Key and Value current = caKV.At(l); if(!current || !current.UpdateInputWeights(prev) ) return false; //--- W0 prev = caAttentionOut.At(l); current = caW0.At(l); if(!current || !current.UpdateInputWeights(prev) ) return false; prev = current; } //--- FeedForward prev = caW0.At(iPAMLayers); if(!cFF1.UpdateInputWeights(prev) || !cFF2.UpdateInputWeights(cFF1.AsObject()) ) return false; //--- return true; }
Não se esqueça de monitorar cuidadosamente a execução de todas as operações do método e retornar o resultado lógico das operações para o programa chamador.
Com isso, concluímos a implementação dos métodos propostos do MSFformer. O código completo das classes criadas e seus métodos está disponível no anexo.
Considerações finais
Neste artigo, exploramos um método promissor e interessante de previsão de séries temporais chamado MSFformer (Multi-Scale Feature Transformer), apresentado no estudo "Time Series Prediction Based on Multi-Scale Feature Extraction". O algoritmo proposto é baseado em uma arquitetura aprimorada de atenção piramidal e em um novo método para a extração multinível de características em diferentes escalas a partir dos dados brutos.
Na parte prática do artigo, implementamos os dois módulos principais do algoritmo proposto. Os resultados dessa implementação serão analisados na próxima publicação.
Referências
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA de coleta de exemplos |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA de coleta de exemplos pelo método Real-ORL |
| 3 | Study.mq5 | Expert Advisor | EA para treinamento de Modelos |
| 4 | StudyEncoder.mq5 | Expert Advisor | EA para treinamento do Codificador |
| 5 | Test.mq5 | Expert Advisor | EA para teste do modelo |
| 6 | Trajectory.mqh | Biblioteca de classe | Estrutura de descrição do estado do sistema |
| 7 | NeuroNet.mqh | Biblioteca de classe | Biblioteca de classes para criação de rede neural |
| 8 | NeuroNet.cl | Biblioteca | Biblioteca de código para OpenCL |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/15156
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Algoritmo de busca através de vizinhança — Across Neighborhood Search (ANS)
Algoritmo de busca através de vizinhança — Across Neighborhood Search (ANS)
 Do básico ao intermediário: União (II)
Do básico ao intermediário: União (II)
 Redes neurais de maneira fácil (Parte 97): Treinamento do modelo usando o MSFformer
Redes neurais de maneira fácil (Parte 97): Treinamento do modelo usando o MSFformer
 Desenvolvimento de robô em Python e MQL5 (Parte 3): Implementação do algoritmo de negociação baseado em modelo
Desenvolvimento de robô em Python e MQL5 (Parte 3): Implementação do algoritmo de negociação baseado em modelo
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso