Redes neurais de maneira fácil (Parte 93): Previsão adaptativa nas áreas de frequência e tempo (Conclusão)
Introdução
No artigo anterior, conhecemos o algoritmo ATFNet, que é um conjunto de 2 modelos de previsão de séries temporais. Um deles trabalha no domínio temporal e faz previsões dos valores da série temporal estudada com base na análise da amplitude do sinal. O segundo modelo trabalha com as características de frequência da série temporal analisada, capturando suas dependências globais, periodicidade e espectro. A combinação adaptativa das duas previsões independentes, segundo os autores do método, permite alcançar resultados impressionantes.
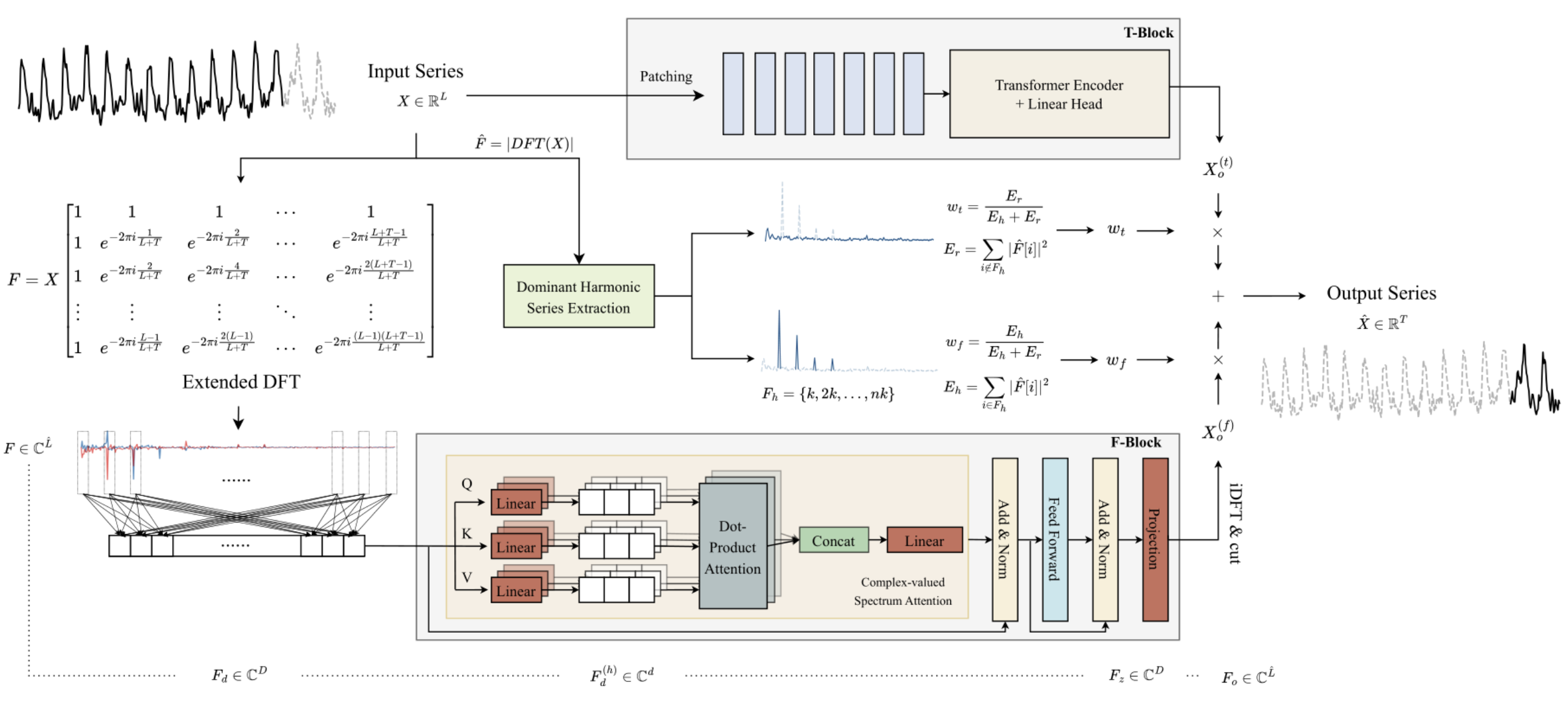
A principal característica do bloco frequencial F- é a construção completa do algoritmo utilizando matemática de números complexos. Para atender a esse requisito, no artigo anterior, criamos a classe CNeuronComplexMLMHAttention, na qual reproduzimos totalmente o algoritmo do Codificador multilayer do Transformer, com elementos de Self-Attention multicoabeça. A classe de atenção complexa que criamos é a base do bloco F. Neste artigo, continuaremos a implementar as abordagens propostas pelos autores do método ATFNet.
1. Criação da classe ATFNet
Após a implementação da base do bloco frequencial F — a classe de atenção complexa CNeuronComplexMLMHAttention, subimos um nível e criamos a classe CNeuronATFNetOCL, na qual todo o algoritmo ATFNet será implementado.
Devo admitir que a implementação de um algoritmo tão complexo como o ATFNet, em uma única classe de camada neural, talvez não seja a solução mais otimizada. No entanto, o modelo sequencial de rede neural que construímos anteriormente não permite a realização de vários processos paralelos, como os blocos T e F, neste caso. E a implementação de tal funcionalidade exigiria mudanças mais profundas. Foi decidido seguir o caminho de menor custo e implementar todo o algoritmo como uma única classe de camada neural. A estrutura da classe CNeuronATFNetOCL é apresentada abaixo.
class CNeuronATFNetOCL : public CNeuronBaseOCL { protected: uint iHistory; uint iForecast; uint iVariables; uint iFFT; //--- T-Block CNeuronBatchNormOCL cNorm; CNeuronTransposeOCL cTranspose; CNeuronPositionEncoder cPositionEncoder; CNeuronPatching cPatching; CLayer caAttention; CLayer caProjection; CNeuronRevINDenormOCL cRevIN; //--- F-Block CBufferFloat *cInputs; CBufferFloat cInputFreqRe; CBufferFloat cInputFreqIm; CNeuronBaseOCL cInputFreqComplex; CBufferFloat cMainFreqWeights; CNeuronBaseOCL cNormFreqComplex; CBufferFloat cMeans; CBufferFloat cVariances; CNeuronComplexMLMHAttention cFreqAtteention; CNeuronBaseOCL cUnNormFreqComplex; CBufferFloat cOutputFreqRe; CBufferFloat cOutputFreqIm; CBufferFloat cOutputTimeSeriasRe; CBufferFloat cOutputTimeSeriasIm; CBufferFloat cOutputTimeSeriasReGrad; CBufferFloat cReconstructInput; CBufferFloat cForecast; CBufferFloat cReconstructInputGrad; CBufferFloat cForecastGrad; CBufferFloat cZero; //--- virtual bool FFT(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im, bool reverse = false); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); virtual bool ComplexNormalize(void); virtual bool ComplexUnNormalize(void); virtual bool ComplexNormalizeGradient(void); virtual bool ComplexUnNormalizeGradient(void); virtual bool MainFreqWeights(void); virtual bool WeightedSum(void); virtual bool WeightedSumGradient(void); virtual bool calcReconstructGradient(void); public: CNeuronATFNetOCL(void) {}; ~CNeuronATFNetOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint history, uint forecast, uint variables, uint heads, uint layers, uint &patch[], ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronATFNetOCL; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); virtual CLayerDescription* GetLayerInfo(void); virtual bool WeightsUpdate(CNeuronBaseOCL *net, float tau); virtual void SetOpenCL(COpenCLMy *obj); virtual CBufferFloat *getWeights(void); };
Na estrutura apresentada da classe CNeuronATFNetOCL, podemos destacar 4 variáveis internas:
- iHistory — profundidade da história analisada;
- iForecast — horizonte de previsão;
- iVariables — número de variáveis analisadas (séries temporais unitárias);
- iFFT — tamanho do tensor da Transformada Rápida de Fourier (DFT).
Lembro que o algoritmo DFT exige que o tamanho do vetor de dados de entrada seja uma potência de "2". Portanto, complementamos o tensor de dados de entrada com valores nulos até o tamanho necessário.
Os objetos internos do método são divididos em dois blocos, conforme sua pertinência aos blocos do algoritmo ATFNet. Com sua designação e o funcionamento dos métodos da classe, nos familiarizaremos ao longo da implementação do algoritmo.
Todos os objetos internos foram declarados como estáticos, o que nos permite deixar o construtor e o destrutor da classe CNeuronATFNetOCL vazios.
1.1 Inicialização do objeto
A inicialização dos objetos internos da nossa nova classe é feita no método Init. Aqui encontramos a primeira consequência da decisão de implementar todo o algoritmo ATFNet em uma única classe — a necessidade de passar inúmeros parâmetros do programa chamador.
Basicamente, dentro da classe CNeuronATFNetOCL, precisamos construir dois modelos multicamada paralelos usando mecanismos de atenção tanto no bloco temporal T- quanto no bloco frequencial F-. E para cada modelo, precisamos especificar a arquitetura.
Para resolver esse problema, decidimos usar, quando possível, parâmetros "universais", onde o mesmo parâmetro é utilizado em ambos os modelos. Sem dúvida, temos parâmetros que descrevem o tensor de dados de entrada e os resultados: profundidade da história analisada, número de séries temporais unitárias e horizonte de previsão. Acredito que seja evidente que esses parâmetros são igualmente usados tanto no bloco T- quanto no bloco F-.
Além disso, ambos os modelos são construídos em torno do Codificador Transformer e utilizam a arquitetura de Self-Attention multicabeça com várias camadas. Decidimos usar o mesmo número de cabeças de atenção e camadas do Codificador em ambos os blocos.
No entanto, para a camada de segmentação de dados, que é usada no bloco T- e não tem análogo no bloco F-, precisaremos passar parâmetros adicionais. Para não aumentar muito a quantidade de parâmetros do método, decidimos utilizar um array com 3 elementos. O primeiro elemento desse array contém o tamanho da janela de um segmento, o segundo, o passo dessa janela no buffer de dados de entrada. O último elemento do array armazenará o tamanho de um patch na saída da camada de segmentação de dados.
bool CNeuronATFNetOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint history, uint forecast, uint variables, uint heads, uint layers, uint &patch[], ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, forecast * variables, optimization_type, batch)) return false;
No corpo do método, como de costume, chamamos o método de inicialização homônimo da classe pai. Aqui, é importante notar que, para o método da classe pai, especificamos o tamanho da camada como o produto do número de variáveis analisadas (séries temporais unitárias) pelo horizonte de previsão. Em outras palavras, planejamos obter na saída da camada CNeuronATFNetOCL o resultado pronto da previsão da continuação da série temporal analisada.
Após a inicialização bem-sucedida dos objetos herdados, salvamos nas variáveis os principais parâmetros da arquitetura.
iHistory = MathMax(history, 1); iForecast = forecast; iVariables = variables;
E calculamos o tamanho do tensor para a Transformada Rápida de Fourier. Aqui, gostaria de lembrar que os autores do ATFNet propõem uma decomposição de Fourier estendida, que define as características de frequência da série temporal completa, levando em consideração os dados históricos e previstos.
uint size = iHistory + iForecast; int power = int(MathLog(size) / M_LN2); if(MathPow(2, power) < size) power++; iFFT = uint(MathPow(2, power));
A próxima etapa será inicializar os objetos internos da nossa classe. Aqui, devemos começar com a representação esperada dos dados de entrada. Como nosso modelo prevê a análise de séries temporais unitárias nas áreas temporal e frequencial, esperamos que a entrada para nossa camada seja uma tupla de séries temporais unitárias. E na saída, a classe CNeuronATFNetOCL retornará uma tupla análoga com os valores previstos.
Outro ponto importante é a normalização dos dados. Ambos os blocos do modelo utilizam normalização dos dados de entrada. A diferença é que o bloco T- normaliza os dados no domínio temporal, enquanto o bloco F- faz isso no domínio frequencial. Por isso, nesta implementação, foi decidido que os dados de entrada do layer seriam não normalizados. A normalização e a reintrodução das características estocásticas são realizadas dentro dos blocos separados, de acordo com as dimensões correspondentes.
Para facilitar a leitura e a transparência do código, a inicialização dos objetos internos será feita em blocos, conforme o uso e a ordem do algoritmo. Começaremos pelo bloco T-.
Como mencionado anteriormente, os dados de entrada para a camada são não normalizados. Portanto, primeiro é necessário trazer os dados recebidos para um formato compatível.
//--- T-Block if(!cNorm.Init(0, 0, OpenCL, iHistory * iVariables, batch, optimization)) return false;
Os autores do ATFNet não usam codificação posicional no domínio frequencial, mas mantiveram-na na análise de dados no domínio temporal. Vamos adicionar uma camada de codificação posicional.
if(!cPositionEncoder.Init(0, 1, OpenCL, iVariables, iHistory, optimization, batch)) return false;
Em seguida, ao construir a camada de segmentação de dados, incluímos um tipo de transposição no algoritmo. Agora precisamos preparar os dados de entrada antes de enviá-los para a camada CNeuronPatching. Para realizar essa operação, foi adicionada uma camada de transposição de dados.
if(!cTranspose.Init(0, 2, OpenCL, iHistory, iVariables, optimization, batch)) return false; cTranspose.SetActivationFunction(None);
Agora precisamos calcular o número de patches na saída da camada de segmentação com base no tamanho da janela de um segmento e seu passo, recebidos nos parâmetros do método da aplicação externa.
uint count = (iHistory - patch[0] + 2 * patch[1] - 1) / patch[1];
Após a preparação necessária, iniciamos a camada de segmentação de dados.
if(!cPatching.Init(0, 3, OpenCL, patch[0], patch[1], patch[2], count, iVariables, optimization, batch)) return false;
Ao construir o método PatchTST, utilizamos Conformer como bloco de atenção. Aqui, seguiremos a mesma solução. O próximo passo será criar o número necessário de camadas do CNeuronConformer.
caAttention.SetOpenCL(OpenCL); for(uint l = 0; l < layers; l++) { CNeuronConformer *temp = new CNeuronConformer(); if(!temp) return false; if(!temp.Init(0, 4 + l, OpenCL, patch[2], 32, heads, iVariables, count, optimization, batch)) { delete temp; return false; } if(!caAttention.Add(temp)) { delete temp; return false; } }
Após o bloco de atenção, que analisa a série temporal original, adicionaremos um bloco de 3 camadas convolucionais, que fará a previsão dos dados subsequentes para toda a profundidade de planejamento, no contexto de séries temporais unitárias separadas.
int total = 3; caProjection.SetOpenCL(OpenCL); uint window = patch[2] * count; for(int l = 0; l < total; l++) { CNeuronConvOCL *temp = new CNeuronConvOCL(); if(!temp) return false; if(!temp.Init(0, 4+layers+l, OpenCL, window, window, (total-l)*iForecast, iVariables, optimization, batch)) { delete temp; return false; } temp.SetActivationFunction(TANH); if(!caProjection.Add(temp)) { delete temp; return false; } window = (total - l) * iForecast; }
Observe que, em cada camada, especificamos o mesmo número de elementos de sequência, igual ao número de séries temporais unitárias na série temporal analisada. Ao mesmo tempo, em cada camada subsequente, o número de filtros na saída da camada neural diminui, chegando, na última camada, ao valor da profundidade de previsão definida.
Na saída do bloco T-, adicionaremos aos valores previstos os parâmetros estatísticos da série temporal original usando a camada CNeuronRevINDenormOCL.
if(!cRevIN.Init(0, 4 + layers + total, OpenCL, iForecast * iVariables, 1, cNorm.AsObject())) return false;
Nesta etapa, inicializamos todos os objetos internos referentes ao bloco T- de previsão no domínio temporal. Agora, passamos a trabalhar com os objetos do bloco frequencial F-.
De acordo com o algoritmo ATFNet, os dados de entrada recebidos pelo bloco F- são convertidos para o domínio frequencial usando a Transformada Rápida de Fourier (DFT). Como você deve lembrar, nossa implementação anterior do algoritmo DFT grava o espectro de frequência em dois buffers de dados. Um buffer será utilizado para a parte real do espectro, e outro para a parte imaginária.
//--- F-Block if(!cInputFreqRe.BufferInit(iFFT * iVariables, 0) || !cInputFreqRe.BufferCreate(OpenCL)) return false; if(!cInputFreqIm.BufferInit(iFFT * iVariables, 0) || !cInputFreqIm.BufferCreate(OpenCL)) return false;
Para facilitar o processamento posterior, uniremos as informações do espectro em um único buffer.
if(!cInputFreqComplex.Init(0, 0, OpenCL, iFFT * iVariables * 2, optimization, batch)) return false;
Neste momento, também prepararemos um buffer para registrar a fração da frequência dominante. Vale notar que a frequência dominante é determinada separadamente para cada série temporal unitária.
if(!cMainFreqWeights.BufferInit(iVariables, 0) || !cMainFreqWeights.BufferCreate(OpenCL)) return false;
Lembremos que os dados de entrada fornecidos para nossa camada são dados brutos, que geram espectros bastante diferentes para as séries temporais unitárias. Para tornar os espectros comparáveis antes do processamento posterior, os autores do método recomendam normalizar as características frequenciais. Os dados normalizados serão armazenados nos buffers da camada cNormFreqComplex.
if(!cNormFreqComplex.Init(0, 1, OpenCL, iFFT * iVariables * 2, optimization, batch)) return false;
Ao mesmo tempo, as características estatísticas do espectro original serão armazenadas nos buffers de dados correspondentes.
if(!cMeans.BufferInit(iVariables, 0) || !cMeans.BufferCreate(OpenCL)) return false; if(!cVariances.BufferInit(iVariables, 0) || !cVariances.BufferCreate(OpenCL)) return false;
As características frequenciais dos dados de entrada, assim preparadas, serão processadas com o bloco de atenção complexa. No artigo anterior, realizamos uma grande implementação da classe CNeuronComplexMLMHAttention. Agora, resta apenas inicializar o objeto interno dessa classe.
if(!cFreqAtteention.Init(0, 2, OpenCL, iFFT, 32, heads, iVariables, layers, optimization, batch)) return false;
Após processar o espectro dos dados de entrada no bloco de atenção complexa, o algoritmo prevê a execução de procedimentos inversos. Primeiro, adicionamos ao espectro processado os indicadores estatísticos das características frequenciais originais.
if(!cUnNormFreqComplex.Init(0, 1, OpenCL, iFFT * iVariables * 2, optimization, batch)) return false;
Separaremos a parte real e a parte imaginária do espectro.
if(!cOutputFreqRe.BufferInit(iFFT*iVariables, 0) || !cOutputFreqRe.BufferCreate(OpenCL)) return false; if(!cOutputFreqIm.BufferInit(iFFT*iVariables, 0) || !cOutputFreqIm.BufferCreate(OpenCL)) return false;
Em seguida, retornamos os dados para o domínio temporal.
if(!cOutputTimeSeriasRe.BufferInit(iFFT*iVariables, 0) || !cOutputTimeSeriasRe.BufferCreate(OpenCL)) return false; if(!cOutputTimeSeriasIm.BufferInit(iFFT*iVariables, 0) || !cOutputTimeSeriasIm.BufferCreate(OpenCL)) return false;
Para o processo de propagação reversa, criaremos um buffer de gradientes para a parte real da série temporal.
if(!cOutputTimeSeriasReGrad.BufferInit(iFFT*iVariables, 0) || !cOutputTimeSeriasReGrad.BufferCreate(OpenCL)) return false;
Aqui, vale observar que não criamos um buffer de gradientes para a parte imaginária da série temporal. Isso ocorre porque os valores-alvo da parte imaginária da série temporal são "0". Assim, o gradiente de erro da parte imaginária é igual aos valores da parte imaginária com o sinal invertido. Durante o processo de propagação reversa, podemos usar o buffer de resultados da propagação para frente para a parte imaginária da série temporal processada.
Após a Transformada Inversa de Fourier DFT (iDFT), esperamos obter a série temporal completa processada, composta pela reconstrução dos dados de entrada e os valores previstos para o horizonte de planejamento definido. Para isolar a parte necessária dos valores previstos, dividiremos a série temporal completa em dois buffers: dados reconstruídos e valores previstos.
if(!cReconstructInput.BufferInit(iHistory*iVariables, 0) || !cReconstructInput.BufferCreate(OpenCL)) return false; if(!cForecast.BufferInit(iForecast*iVariables, 0) || !cForecast.BufferCreate(OpenCL)) return false;
Além disso, adicionaremos buffers para os gradientes de erro correspondentes.
if(!cReconstructInputGrad.BufferInit(iHistory*iVariables, 0) || !cReconstructInputGrad.BufferCreate(OpenCL)) return false; if(!cForecastGrad.BufferInit(iForecast*iVariables, 0) || !cForecastGrad.BufferCreate(OpenCL)) return false;
É importante destacar que o método proposto pelos autores do ATFNet não prevê a análise das discrepâncias entre os dados reconstruídos e os valores originais da série temporal analisada. No entanto, estamos adicionando essa funcionalidade na tentativa de realizar um ajuste mais refinado do bloco de atenção complexa. Potencialmente, uma compreensão mais detalhada dos dados analisados permitirá melhorar a qualidade das previsões da nossa modelo.
Adicionalmente, criaremos um buffer de valores nulos, que será usado para preencher os valores ausentes nos dados de entrada e nos gradientes de erro.
if(!cZero.BufferInit(iFFT*iVariables, 0) || !cZero.BufferCreate(OpenCL)) return false; //--- return true; }
Não devemos esquecer de controlar o processo em cada etapa das operações. Ao concluir a inicialização de todos os objetos declarados, retornamos um valor lógico à aplicação chamadora para indicar o sucesso das operações do método.
1.2 Propagação para frente
Após concluirmos a inicialização dos objetos da classe, passamos à construção do algoritmo de propagação. Começamos criando kernels adicionais no programa OpenCL.
Primeiro, vamos relembrar a normalização dos espectros das características frequenciais das séries temporais unitárias. O uso de algoritmos de normalização de dados reais previamente implementados pode distorcer os dados. Por isso, precisamos de um mecanismo de normalização de dados no domínio complexo. Esse funcionalidade será implementada no kernel ComplexNormalize. Nos parâmetros do kernel, passaremos ponteiros para 4 buffers de dados e a dimensionalidade da sequência unitária. Pretendemos usar esse kernel em um espaço unidimensional de tarefas, no contexto dos espectros das séries temporais unitárias.
__kernel void ComplexNormalize(__global float2 *inputs, __global float2 *outputs, __global float2 *means, __global float *vars, int dimension) { if(dimension <= 0) return;
Vale notar como os buffers de dados são declarados. Os buffers de dados de entrada, resultados e médias possuem o tipo vetorial float2. Decidimos usar esse tipo de dado no lado do OpenCL para lidar com valores complexos. Diferenciando-se dos demais, o buffer de variâncias é declarado com o tipo real float. Aqui, é importante lembrar que as variâncias indicam o desvio quadrático médio do valor em relação à média. E a distância entre dois pontos é uma magnitude real.
No corpo do método, verificamos a dimensionalidade do vetor a ser normalizado. É claro que ela deve ser maior que "0". Em seguida, identificamos o fluxo atual no espaço de tarefas, definimos o deslocamento nos buffers de dados e criamos uma representação complexa da dimensionalidade da sequência analisada.
size_t n = get_global_id(0); const int shift = n * dimension; const float2 dim = (float2)(dimension, 0);
Depois, realizamos um ciclo em que determinamos o valor médio do espectro analisado.
float2 mean = 0; for(int i = 0; i < dimension; i++) { float2 val = inputs[shift + i]; if(isnan(val.x) || isinf(val.x) || isnan(val.y) || isinf(val.y)) inputs[shift + i] = (float2)0; else mean += val; } means[n] = mean = ComplexDiv(mean, dim);
O resultado obtido é imediatamente armazenado no elemento correspondente do buffer de médias.
Na próxima etapa, geramos um ciclo para determinar a variância da sequência analisada.
float variance = 0; for(int i = 0; i < dimension; i++) variance += pow(ComplexAbs(inputs[shift + i] - mean), 2); vars[n] = variance = sqrt((isnan(variance) || isinf(variance) ? 1.0f : variance / dimension));
Aqui, é importante observar dois pontos. Primeiro: apesar de armazenarmos o valor médio no buffer de dados externos, usamos o valor de uma variável local ao realizar as operações, pois o acesso a um elemento de buffer na memória global do contexto é significativamente mais lento do que o acesso a uma variável local do kernel.
Segundo ponto: metodologicamente, ao calcular a variância de uma sequência de números complexos, diferente dos números reais, elevamos ao quadrado o valor absoluto da diferença entre o elemento da sequência complexa e o valor médio. É o valor absoluto da magnitude complexa que mostra a distância entre os pontos no espaço bidimensional das partes real e imaginária. Enquanto a simples diferença entre os valores complexos mostraria apenas o deslocamento das coordenadas.
Na última etapa do kernel, criamos um ciclo final para normalizar os dados do espectro de entrada. Os valores obtidos são gravados nos elementos correspondentes do buffer de resultados.
float2 v=(float2)(variance, 0); for(int i = 0; i < dimension; i++) { float2 val = ComplexDiv((inputs[shift + i] - mean), v); if(isnan(val.x) || isinf(val.x) || isnan(val.y) || isinf(val.y)) val = (float2)0; outputs[shift + i] = val; } }
Aqui, também trabalhamos com variáveis locais para o valor médio e o desvio quadrático médio.
Por fim, criaremos o kernel de desnormalização ComplexUnNormalize, no qual restauraremos os indicadores estatísticos extraídos do espectro original.
__kernel void ComplexUnNormalize(__global float2 *inputs, __global float2 *outputs, __global float2 *means, __global float *vars, int dimension) { if(dimension <= 0) return;
É fácil perceber que este kernel recebe o mesmo conjunto de parâmetros, com 4 ponteiros para buffers de dados e uma variável. Também planejamos executar o kernel em um espaço de tarefas unidimensional, segundo o número de séries temporais unitárias.
No corpo do kernel, identificamos o fluxo no espaço de tarefas e determinamos os deslocamentos nos buffers de dados.
size_t n = get_global_id(0); const int shift = n * dimension;
Carregamos os indicadores estatísticos dos buffers e imediatamente transformamos o desvio padrão em uma magnitude complexa.
float v= vars[n]; float2 variance=(float2)((v > 0 ? v : 1.0f), 0) float2 mean = means[n];
Em seguida, fazemos o único ciclo no kernel para converter os dados.
for(int i = 0; i < dimension; i++) { float2 val = ComplexMul(inputs[shift + i], variance) + mean; if(isnan(val.x) || isinf(val.x) || isnan(val.y) || isinf(val.y)) val = (float2)0; outputs[shift + i] = val; } }
Os valores obtidos são gravados nos elementos correspondentes do buffer de resultados.
Para chamar os kernels criados anteriormente no lado do programa principal, usamos os métodos ComplexNormalize e ComplexUnNormalize. O algoritmo para sua construção não difere dos métodos de criação de kernels OpenCL já discutidos, que colocam os kernels na fila de execução. Portanto, não vamos nos aprofundar no código desses métodos agora e adiante. No entanto, você pode acessá-lo diretamente no anexo.
Além disso, para a fusão adaptativa dos resultados de previsão temporais e frequenciais, precisaremos de coeficientes de influência, que os autores do método ATFNet sugerem determinar com base na fração da frequência dominante no espectro geral. Consequentemente, no programa OpenCL, criaremos dois kernels:
- MainFreqWeight — para determinar a fração da frequência dominante;
- WeightedSum — para calcular a soma ponderada das previsões nas áreas frequencial e temporal.
Ambos os kernels serão executados em um espaço de tarefas unidimensional, com base no número de séries temporais unitárias analisadas.
Nos parâmetros do kernel MainFreqWeight, passamos ponteiros para dois buffers de dados (características frequenciais e resultados) e a dimensionalidade da série analisada.
__kernel void MainFreqWeight(__global float2 *freq, __global float *weight, int dimension ) { if(dimension <= 0) return; //--- size_t n = get_global_id(0); const int shift = n * dimension;
No corpo do kernel, identificamos o fluxo atual de operações no espaço de tarefas e determinamos o deslocamento nos buffers de dados. Em seguida, preparamos variáveis locais.
float max_f = 0; float total = 0; float energy;
Depois, criamos um ciclo em que calculamos a energia da frequência dominante e de todo o espectro.
for(int i = 0; i < dimension; i++) { energy = ComplexAbs(freq[shift + i]); total += energy; max_f = fmax(max_f, energy); }
No final das operações do kernel, dividimos a energia da frequência dominante pela energia total do espectro. O valor obtido é armazenado no elemento correspondente do buffer de resultados.
weight[n] = max_f / (total > 0 ? total : 1); }
O algoritmo do kernel para calcular a soma ponderada das previsões nas áreas temporal e frequencial, WeightedSum, é bastante simples. Nos parâmetros, o kernel recebe 4 ponteiros para buffers de dados e a dimensão do vetor de uma sequência (no nosso caso, a profundidade da previsão).
__kernel void WeightedSum(__global float *inputs1, __global float *inputs2, __global float *outputs, __global float *weight, int dimension ) { if(dimension <= 0) return; //--- size_t n = get_global_id(0); const int shift = n * dimension;
No corpo do kernel, identificamos o fluxo atual no espaço de tarefas unidimensional e determinamos o deslocamento nos buffers de dados. Em seguida, realizamos o ciclo de somatório ponderado dos elementos. Os resultados das operações são imediatamente gravados no elemento correspondente do buffer de resultados.
float w = weight[n]; for(int i = 0; i < dimension; i++) outputs[shift + i] = inputs1[shift + i] * w + inputs2[shift + i] * (1 - w); }
Para colocar os kernels na fila de execução, foram criados métodos com os mesmos nomes no lado do programa principal, cujo código você pode consultar no anexo.
Após a conclusão da preparação, passamos à construção do método de propagação para frente feedForward da nossa classe CNeuronATFNetOCL. Nos parâmetros deste método, assim como no método equivalente da classe pai, recebemos um ponteiro para o objeto da camada neural anterior, que neste caso atua como os dados de entrada para as operações subsequentes.
bool CNeuronATFNetOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL || !NeuronOCL.getOutput()) return false;
No corpo do método, primeiro verificamos a validade do ponteiro recebido. Em seguida, armazenamos na variável interna do objeto atual o ponteiro para o buffer de resultados da camada neural recebida.
if(cInputs != NeuronOCL.getOutput())
cInputs = NeuronOCL.getOutput();
Depois, realizamos as operações de previsão dos valores subsequentes da série temporal analisada no domínio temporal. Primeiro, normalizamos os dados recebidos.
//--- T-Block if(!cNorm.FeedForward(NeuronOCL)) return false;;
Após isso, adicionamos a codificação posicional.
if(!cPositionEncoder.FeedForward(cNorm.AsObject())) return false;
Transpomos o tensor obtido e dividimos os dados em patches.
if(!cTranspose.FeedForward(cPositionEncoder.AsObject())) return false; if(!cPatching.FeedForward(cTranspose.AsObject())) return false;
Os dados assim preparados passam pelo bloco de atenção.
int total = caAttention.Total(); CNeuronBaseOCL *prev = cPatching.AsObject(); for(int i = 0; i < total; i++) { CNeuronBaseOCL *att = caAttention.At(i); if(!att.FeedForward(prev)) return false; prev = att; }
A previsão dos valores subsequentes é realizada.
total = caProjection.Total(); for(int i = 0; i < total; i++) { CNeuronBaseOCL *proj = caProjection.At(i); if(!proj.FeedForward(prev)) return false; prev = proj; }
Na saída do bloco T-, adicionamos os parâmetros estatísticos da série temporal original aos valores previstos.
if(!cRevIN.FeedForward(prev)) return false;
Após obter os valores previstos no domínio temporal, passamos a trabalhar com o domínio frequencial. Aqui, a primeira coisa que fazemos é transformar a série temporal recebida no espectro das características frequenciais. Para isso, utilizamos o algoritmo FFT.
//--- F-Block if(!FFT(cInputs, cInputs, GetPointer(cInputFreqRe), GetPointer(cInputFreqIm), false)) return false;
Após obter os dois buffers para as partes real e imaginária do espectro frequencial, unimos ambos em um único tensor.
if(!Concat(GetPointer(cInputFreqRe), GetPointer(cInputFreqIm), cInputFreqComplex.getOutput(), 1, 1, iFFT * iVariables)) return false;
Note que, ao concatenar os buffers de dados, usamos um tamanho de janela de apenas 1 elemento. Dessa forma, criamos um tensor no qual a parte real e a parte imaginária da característica frequencial correspondente ficam lado a lado.
Esse tensor das características frequenciais dos dados de entrada é então normalizado.
if(!ComplexNormalize()) return false;
Também determinamos a fração da frequência dominante.
if(!MainFreqWeights()) return false;
Os dados preparados das características frequenciais são passados pelo bloco de atenção. Para isso, basta chamar o método de propagação para frente da classe de atenção complexa multicamada, criada no artigo anterior.
if(!cFreqAtteention.FeedForward(cNormFreqComplex.AsObject())) return false;
Após a execução bem-sucedida das operações do bloco de atenção, retornamos os parâmetros estatísticos das características frequenciais dos dados originais para os dados processados.
if(!ComplexUnNormalize()) return false;
Dividimos o tensor do espectro frequencial nas suas partes real e imaginária.
if(!DeConcat(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), cUnNormFreqComplex.getOutput(), 1, 1, iFFT * iVariables)) return false;
Por fim, transformamos o espectro das características frequenciais de volta em uma série temporal.
if(!FFT(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), GetPointer(cOutputTimeSeriasRe), GetPointer(cOutputTimeSeriasIm), true)) return false;
Aqui, vale a pena dar algumas explicações sobre as operações descritas acima do bloco F-. À primeira vista, pode parecer estranho realizar tantas transformações da série temporal para as características frequenciais, normalizá-las e depois executar operações inversas, apenas para realizar as operações de atenção. Especialmente porque todas essas operações, exceto a atenção, não possuem parâmetros treináveis e, teoricamente, deveriam devolver a mesma série temporal original. Mas o ponto-chave está no bloco de atenção.
Lembro que os autores do método propuseram o uso de uma versão estendida da Transformada Discreta de Fourier. Na prática, usamos a base exponencial complexa DFT da série temporal completa. No entanto, ao transformar a série temporal original nas suas características frequenciais, não temos os valores previstos e simplesmente os substituímos por valores nulos. Consequentemente, a execução da Transformada Inversa de Fourier (DFT) provavelmente retornaria valores previstos próximos a "0", o que não é aceitável para nós. Por isso, tornamos os espectros das séries temporais unitárias comparáveis por meio da normalização. Ao compará-los no bloco de atenção, tentamos ensinar o modelo a restaurar os dados faltantes nas características frequenciais analisadas.
Assim, na saída do bloco de atenção complexa, esperamos obter espectros das características frequenciais ajustados e harmonizados das séries temporais completas, com os dados ausentes restaurados. A reconstrução da série temporal a partir dos espectros modificados nos permitirá obter valores previstos diferentes de "0" para as séries temporais analisadas.
Para concluir as operações de propagação para frente, resta apenas extrair os valores previstos da série temporal completa.
if(!DeConcat(GetPointer(cReconstructInput), GetPointer(cForecast), GetPointer(cOutputTimeSeriasReGrad), GetPointer(cOutputTimeSeriasRe), iHistory, iForecast, iFFT - iHistory - iForecast, iVariables)) return false;
E somar as previsões feitas nos domínios temporal e frequencial, levando em consideração o coeficiente de importância.
//--- Output if(!WeightedSum()) return false; //--- return true; }
Não nos esquecemos de verificar os resultados das operações em cada etapa. Após a conclusão das operações do método, retornamos um valor lógico que indica o sucesso de todas as operações para o programa chamador.
1.3 Distribuição do Gradiente de Erro
Após a propagação para frente, é necessário distribuir o gradiente de erro para todos os parâmetros treináveis do modelo. Em nossa nova classe, esses parâmetros estão presentes tanto no bloco T- quanto no bloco F-. Portanto, precisamos implementar um mecanismo de propagação do gradiente de erro através dos blocos T e F. Depois, combinamos o gradiente de erro dos dois fluxos e transmitimos o gradiente somado para o nível anterior da camada.
Assim como na propagação para frente, antes de construir o método calcInputGradients, precisamos fazer algumas preparações. Na propagação para frente, no lado do programa OpenCL, criamos os kernels de normalização e retorno dos indicadores estatísticos de distribuição ComplexNormalize e ComplexUnNormalize, respectivamente. Na propagação reversa, precisamos criar os kernels de distribuição do gradiente de erro para essas operações: ComplexNormalizeGradient e ComplexUnNormalizeGradient.
No kernel de distribuição do gradiente de erro através do bloco de normalização das características frequenciais, simplesmente dividimos o gradiente de erro recebido pelo desvio quadrático médio do espectro correspondente.
__kernel void ComplexNormalizeGradient(__global float2 *inputs_gr, __global float2 *outputs_gr, __global float *vars, int dimension) { if(dimension <= 0) return; //--- size_t n = get_global_id(0); const int shift = n * dimension; //--- float v = vars[n]; float2 variance = (float2)((v > 0 ? v : 1.0f), 0); for(int i = 0; i < dimension; i++) { float2 val = ComplexDiv(outputs_gr[shift + i], variance); if(isnan(val.x) || isinf(val.x) || isnan(val.y) || isinf(val.y)) val = (float2)0; inputs_gr[shift + i] = val; } }
Devo dizer que esta é uma abordagem simplificada para resolver esta tarefa. Aqui, tratamos o valor médio e o desvio quadrático médio como constantes. Embora, na realidade, eles sejam funções, e pelas regras da descida do gradiente, também precisaríamos corrigir sua influência e transmitir o gradiente de erro para os elementos que influenciam o modelo. No entanto, como a prática mostra que a influência desses elementos nos dados de entrada é mínima, para reduzir os custos de treinamento do modelo, omitimos essas operações.
O kernel de distribuição do gradiente através das operações de desnormalização é construído de maneira semelhante, exceto que, neste caso, multiplicamos o gradiente de erro recebido pelo desvio quadrático médio.
__kernel void ComplexUnNormalizeGradient(__global float2 *inputs_gr, __global float2 *outputs_gr, __global float *vars, int dimension) { if(dimension <= 0) return; //--- size_t n = get_global_id(0); const int shift = n * dimension; //--- float v = vars[n]; float2 variance = (float2)((v > 0 ? v : 1.0f), 0); for(int i = 0; i < dimension; i++) { float2 val = ComplexMul(outputs_gr[shift + i], variance); if(isnan(val.x) || isinf(val.x) || isnan(val.y) || isinf(val.y)) val = (float2)0; inputs_gr[shift + i] = val; } }
Em seguida, precisamos implementar um kernel para distribuir o gradiente de erro total entre os blocos de previsão nos domínios temporal e frequencial. Essa funcionalidade será implementada no kernel WeightedSumGradient. Nos parâmetros, o kernel recebe ponteiros para 4 buffers de dados e 1 parâmetro, de maneira semelhante ao kernel correspondente de propagação para frente.
__kernel void WeightedSumGradient(__global float *inputs_gr1, __global float *inputs_gr2, __global float *outputs_gr, __global float *weight, int dimension ) { if(dimension <= 0) return; //--- size_t n = get_global_id(0); const int shift = n * dimension;
No corpo do kernel, identificamos o fluxo atual no espaço de tarefas unidimensional e determinamos os deslocamentos nos buffers de dados. Depois, preparamos variáveis locais para os pesos das previsões no domínio frequencial e temporal.
float w = weight[n]; float w1 = 1 - weight[n];
Em seguida, fazemos o ciclo de distribuição do gradiente de erro nos buffers de dados correspondentes.
for(int i = 0; i < dimension; i++) { float grad = outputs_gr[shift + i]; inputs_gr1[shift + i] = grad * w; inputs_gr2[shift + i] = grad * w1; } }
A colocação dos kernels de distribuição do gradiente de erro na fila de execução é feita por métodos com os mesmos nomes no programa principal. Você pode consultar o código desses métodos no anexo.
Outro ponto a ser destacado é o cálculo do gradiente de erro do valor reconstruído da série temporal dos dados históricos. Essa funcionalidade será executada no método calcReconstructGradient.
Aqui, vale mencionar que, embora as operações sejam realizadas no contexto do OpenCL, não criaremos um novo kernel para essas operações. Em vez disso, utilizaremos o kernel existente para determinar o gradiente de erro com base nos valores-alvo. Basta criarmos um método que insira o kernel na fila de execução, utilizando os buffers de dados do nosso bloco F-.
O kernel utilizado será executado em um espaço de tarefas unidimensional, segundo o número de elementos no tensor. No nosso caso, o tamanho do vetor analisado é igual ao produto da profundidade da história analisada pelo número de séries temporais unitárias.
bool CNeuronATFNetOCL::calcReconstructGradient(void) { uint global_work_offset[1] = {0}; uint global_work_size[1]; global_work_size[0] = iHistory * iVariables;
Os dados-alvo serão os valores dos dados de entrada que obtivemos durante a propagação para frente da camada neural anterior. Durante a propagação para frente, de forma antecipada, armazenamos o ponteiro para o buffer de dados necessário.
if(!OpenCL.SetArgumentBuffer(def_k_CalcOutputGradient, def_k_cog_matrix_t, cInputs.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
O gradiente de erro será determinado para os dados reconstruídos a partir do espectro processado.
if(!OpenCL.SetArgumentBuffer(def_k_CalcOutputGradient, def_k_cog_matrix_o, cReconstructInput.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Os resultados das operações serão gravados no buffer de gradientes dos dados reconstruídos.
if(!OpenCL.SetArgumentBuffer(def_k_CalcOutputGradient, def_k_cog_matrix_ig, cReconstructInputGrad.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Durante a propagação para frente, não utilizamos funções de ativação.
if(!OpenCL.SetArgument(def_k_CalcOutputGradient, def_k_cog_activation, (int)None)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Colocamos o kernel na fila de execução, verificamos o resultado das operações e concluímos o método, retornando um valor lógico de sucesso para o programa chamador.
if(!OpenCL.SetArgument(def_k_CalcOutputGradient, def_k_cog_error, 1)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } ResetLastError(); if(!OpenCL.Execute(def_k_CalcOutputGradient, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel CalcOutputGradient: %d", GetLastError()); return false; } //--- return true; }
Após a conclusão da preparação, passamos à construção do método de distribuição do gradiente de erro calcInputGradients.
Nos parâmetros desse método, assim como no método equivalente da classe pai, recebemos um ponteiro para o objeto da camada anterior, ao qual devemos transmitir o gradiente de erro.
bool CNeuronATFNetOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL || !NeuronOCL.getGradient() || !cInputs) return false;
No corpo do método, verificamos imediatamente a validade do ponteiro recebido. Em seguida, distribuímos o gradiente de erro recebido da camada subsequente em dois fluxos, entre os blocos de previsão nos domínios temporal e frequencial.
//--- Output if(!WeightedSumGradient()) return false;
Primeiro, propagamos o gradiente de erro através do bloco T- de previsão no domínio temporal. Aqui, na ordem inversa da propagação para frente, chamamos os métodos correspondentes dos objetos internos.
//--- T-Block if(cRevIN.Activation() != None && !DeActivation(cRevIN.getOutput(), cRevIN.getGradient(), cRevIN.getGradient(), cRevIN.Activation())) return false; CNeuronBaseOCL *next = cRevIN.AsObject(); for(int i = caProjection.Total() - 1; i >= 0; i--) { CNeuronBaseOCL *proj = caProjection.At(i); if(!proj || !proj.calcHiddenGradients((CObject *)next)) return false; next = proj; } for(int i = caAttention.Total() - 1; i >= 0; i--) { CNeuronBaseOCL *att = caAttention.At(i); if(!att || !att.calcHiddenGradients((CObject *)next)) return false; next = att; } if(!cPatching.calcHiddenGradients((CObject*)next)) return false; if(!cTranspose.calcHiddenGradients(cPatching.AsObject())) return false; if(!cPositionEncoder.calcHiddenGradients(cTranspose.AsObject())) return false; if(!cNorm.calcHiddenGradients(cPositionEncoder.AsObject())) return false; if(!NeuronOCL.calcHiddenGradients(cNorm.AsObject())) return false;
O algoritmo de distribuição do gradiente no bloco de previsão frequencial é um pouco mais complexo. Primeiro, determinamos o gradiente de erro para a parte imaginária da série temporal reconstruída. Como mencionado anteriormente, o valor-alvo para a parte imaginária da série temporal é "0". Portanto, para determinar o gradiente de erro, simplesmente invertemos o sinal dos resultados da propagação para frente.
//--- F-Block if(!CNeuronBaseOCL::SumAndNormilize(GetPointer(cOutputTimeSeriasIm), GetPointer(cOutputTimeSeriasIm), GetPointer(cOutputTimeSeriasIm), iFFT*iVariables, false, 0, 0, 0, -0.5)) return false;
Em seguida, calculamos o gradiente de erro para a reconstrução dos dados históricos.
if(!calcReconstructGradient()) return false;
Depois, combinamos os tensores de gradientes de erro da reconstrução dos dados históricos (calculados no método calcReconstructGradient), o gradiente de erro da previsão da série temporal (obtido ao dividir o gradiente de erro da camada subsequente em dois fluxos), e completamos com valores nulos até o tamanho do espectro da série completa.
if(!Concat(GetPointer(cReconstructInputGrad), GetPointer(cForecastGrad), GetPointer(cZero), GetPointer(cOutputTimeSeriasReGrad), iHistory, iForecast, iFFT - iHistory - iForecast, iVariables)) return false;
Adicionamos esses valores nulos ao final do tensor de gradientes de erro da série temporal completa, pois não temos dados de valores-alvo além do horizonte de planejamento, e, portanto, não os corrigimos.
O gradiente de erro obtido para a série temporal completa, construído a partir dos dados do bloco de previsão frequencial, é transformado para o domínio frequencial por meio da aplicação da Transformada Rápida de Fourier (FFT).
if(!FFT(GetPointer(cOutputTimeSeriasReGrad), GetPointer(cOutputTimeSeriasIm), GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), false)) return false;
Os dados obtidos, tanto da parte real quanto da parte imaginária do espectro do gradiente de erro, são combinados em um único tensor.
if(!Concat(GetPointer(cOutputFreqRe), GetPointer(cOutputFreqIm), cUnNormFreqComplex.getGradient(), 1, 1, iFFT * iVariables)) return false;
Em seguida, ajustamos o gradiente de erro pela derivada das operações de desnormalização dos dados.
if(!ComplexUnNormalizeGradient()) return false;
O gradiente de erro passa então pelo bloco de atenção complexa.
if(!cNormFreqComplex.calcHiddenGradients(cFreqAtteention.AsObject())) return false;
Após isso, ajustamos o gradiente de erro pela derivada da função de normalização dos dados.
if(!ComplexNormalizeGradient()) return false;
Separamos as partes real e imaginária do espectro.
if(!DeConcat(GetPointer(cInputFreqRe), GetPointer(cInputFreqIm), cInputFreqComplex.getGradient(), 1, 1, iFFT * iVariables)) return false;
Finalmente, o gradiente de erro é retornado ao domínio temporal por meio da Transformada Inversa de Fourier (IFFT).
if(!FFT(GetPointer(cInputFreqRe), GetPointer(cInputFreqIm), GetPointer(cOutputTimeSeriasRe), GetPointer(cOutputTimeSeriasIm), false)) return false;
Aqui, vale destacar que obtivemos o gradiente de erro para a série temporal completa. No entanto, devemos transmitir para a camada anterior apenas o gradiente de erro dos dados históricos. Portanto, primeiro extraímos os dados do horizonte de análise histórica.
if(!DeConcat(GetPointer(cInputFreqRe), GetPointer(cOutputTimeSeriasIm), GetPointer(cOutputTimeSeriasRe), iHistory, iFFT-iHistory, iVariables)) return false;
Em seguida, somamos os valores obtidos aos resultados da distribuição do gradiente de erro do bloco T-.
if(!CNeuronBaseOCL::SumAndNormilize(NeuronOCL.getGradient(), GetPointer(cInputFreqRe), NeuronOCL.getGradient(), iHistory*iVariables, false, 0, 0, 0, 0.5)) return false; //--- return true; }
Lembro que, em cada iteração, monitoramos o processo de execução das operações. Após a conclusão bem-sucedida de todas as operações, retornamos um valor lógico para o programa chamador, indicando o sucesso do método.
1.4 Atualização dos parâmetros do modelo
O gradiente de erro de cada parâmetro treinável do modelo determina sua influência no resultado. O próximo passo é ajustar os parâmetros do modelo para minimizar o erro. Essa funcionalidade é realizada no método updateInputWeights. Na implementação da nossa classe, a atualização dos parâmetros consiste em chamar os métodos correspondentes dos objetos internos que contêm parâmetros treináveis. No bloco F, isso se aplica apenas à classe de atenção complexa.
bool CNeuronATFNetOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { //--- F-Block if(!cFreqAtteention.UpdateInputWeights(cNormFreqComplex.AsObject())) return false;
No bloco T-, há mais objetos com parâmetros treináveis.
//--- T-Block if(!cPatching.UpdateInputWeights(cPositionEncoder.AsObject())) return false; int total = caAttention.Total(); CNeuronBaseOCL *prev = cPatching.AsObject(); for(int i = 0; i < total; i++) { CNeuronBaseOCL *att = caAttention.At(i); if(!att.UpdateInputWeights(prev)) return false; prev = att; } total = caProjection.Total(); for(int i = 0; i < total; i++) { CNeuronBaseOCL *proj = caProjection.At(i); if(!proj.UpdateInputWeights(prev)) return false; prev = proj; } //--- return true; }
Com isso, concluímos a análise dos algoritmos para a implementação das abordagens propostas pelos autores do ATFNet. Você pode consultar o código completo da classe CNeuronATFNetOCL e de todos os seus métodos no anexo.
2. Arquitetura do modelo
Após concluir o trabalho com a nossa nova classe de implementação das abordagens do método ATFNet, passamos à construção da arquitetura dos nossos modelos. Como você já deve ter adivinhado, vamos implementar a nova camada neural no Codificador do estado do ambiente. Claro, é difícil chamar a classe CNeuronATFNetOCL de uma camada neural simples. Ela implementa uma arquitetura bastante complexa para a construção de um modelo integrado.
Na entrada do nosso codificador, forneceremos o conjunto de dados brutos, da mesma forma que fizemos com os modelos anteriores.
bool CreateEncoderDescriptions(CArrayObj *encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; } //--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
No entanto, neste caso, não normalizamos os dados recebidos. Lembro que tanto o bloco T- quanto o bloco F- em sua arquitetura realizam a normalização dos dados. Portanto, omitimos essa etapa. No entanto, nossos dados de entrada são formados por vetores que descrevem estados individuais do ambiente. Antes de prosseguir com o processamento, transporremos os dados de entrada para permitir a análise em termos de séries temporais unitárias.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTransposeOCL; descr.count = HistoryBars; descr.window = BarDescr; if(!encoder.Add(descr)) { delete descr; return false; }
Em seguida, usaremos nossa nova classe para prever os dados subsequentes da série temporal analisada.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronATFNetOCL; descr.count = BarDescr; descr.window = HistoryBars; descr.window_out = NForecast; descr.step = 8; descr.layers = 4; { int temp[] = {5, 1, 16}; ArrayCopy(descr.windows, temp); } descr.activation = None; descr.batch = 10000; if(!encoder.Add(descr)) { delete descr; return false; }
Essencialmente, toda a nossa modelo está contida nesta camada. Na saída, obtemos os valores previstos necessários para toda a profundidade do planejamento. Nos resta apenas transpor esses valores para a dimensionalidade necessária.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTransposeOCL; descr.count = BarDescr; descr.window = NForecast; descr.activation = None; if(!encoder.Add(descr)) { delete descr; return false; }
Para harmonizar o espectro dos valores previstos, usaremos as abordagens do método FreDF.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast; descr.step = int(false); descr.probability = 0.8f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
Os modelos do Ator e do Crítico foram deixados inalterados.
Os programas de treinamento e teste dos modelos treinados também foram transferidos sem alterações das publicações anteriores. Você pode consultar o código desses programas no anexo.
3. Testes
Realizamos um extenso trabalho de implementação das abordagens propostas pelos autores do método ATFNet usando MQL5. O volume do trabalho realizado até ultrapassou o de uma única publicação. E, finalmente, passamos para a etapa final do nosso trabalho — o treinamento e teste dos modelos.
Para treinar os modelos, utilizaremos o EA (Expert Advisor) previamente criado para o treinamento dos modelos anteriores. Portanto, podemos usar também os dados de treinamento coletados anteriormente.
Lembro que o treinamento dos modelos é realizado com dados históricos do instrumento EURUSD, time frame H1, para todo o ano de 2023.
Na primeira etapa, treinamos o modelo do Codificador para prever os estados subsequentes do ambiente em um horizonte de planejamento determinado pela constante NForecast.
Como anteriormente, o modelo do Codificador analisa apenas os movimentos de preço, então, durante a primeira fase do treinamento, não é necessário atualizar o conjunto de dados de treinamento.
Na segunda fase do nosso processo de treinamento, realizamos a busca pela política de ações mais otimizada do nosso Ator. Aqui, já realizamos o treinamento iterativo dos modelos do Ator e do Crítico, alternando com a atualização do conjunto de dados de treinamento. O processo de atualização do conjunto de dados nos permite ajustar as recompensas do ambiente na região da política atual do Ator, o que, por sua vez, ajuda a realizar um ajuste mais refinado da política desejada.
Durante o treinamento, conseguimos obter uma política do Ator que é capaz de gerar lucro tanto nos dados de treinamento quanto nos dados de teste. Os resultados dos testes do modelo são apresentados abaixo.
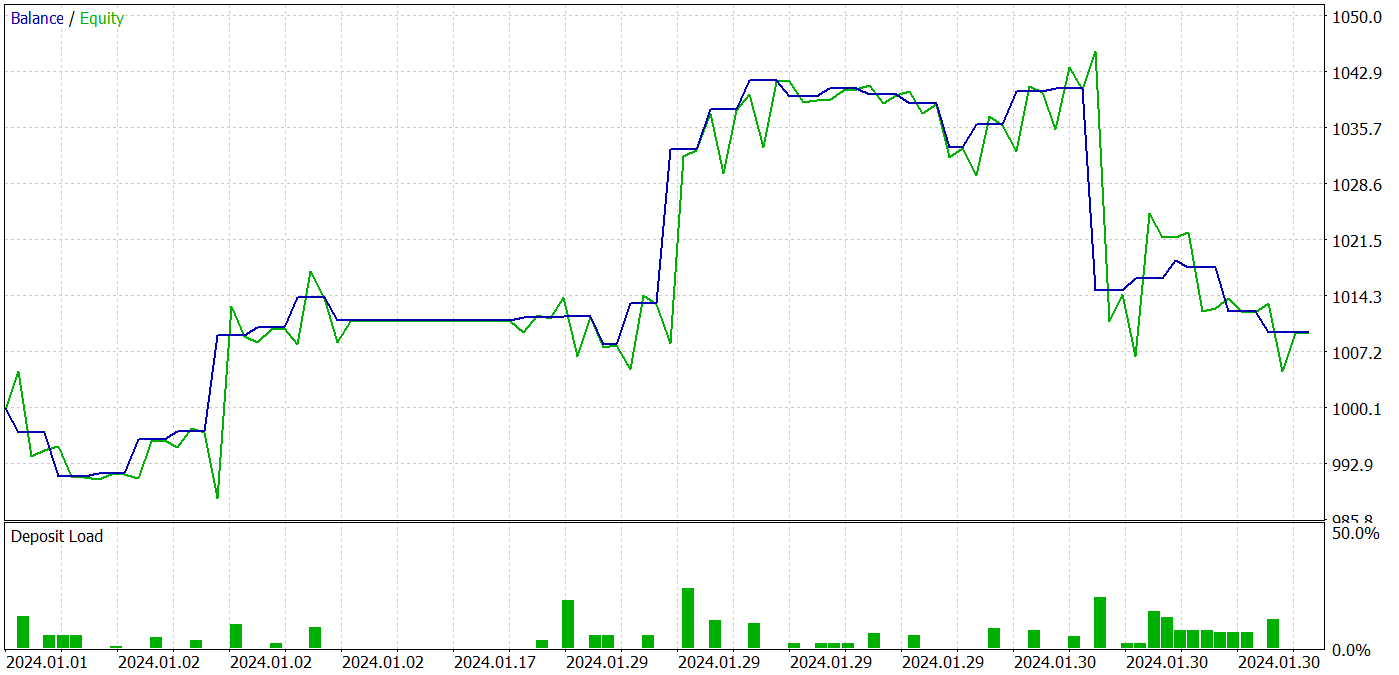
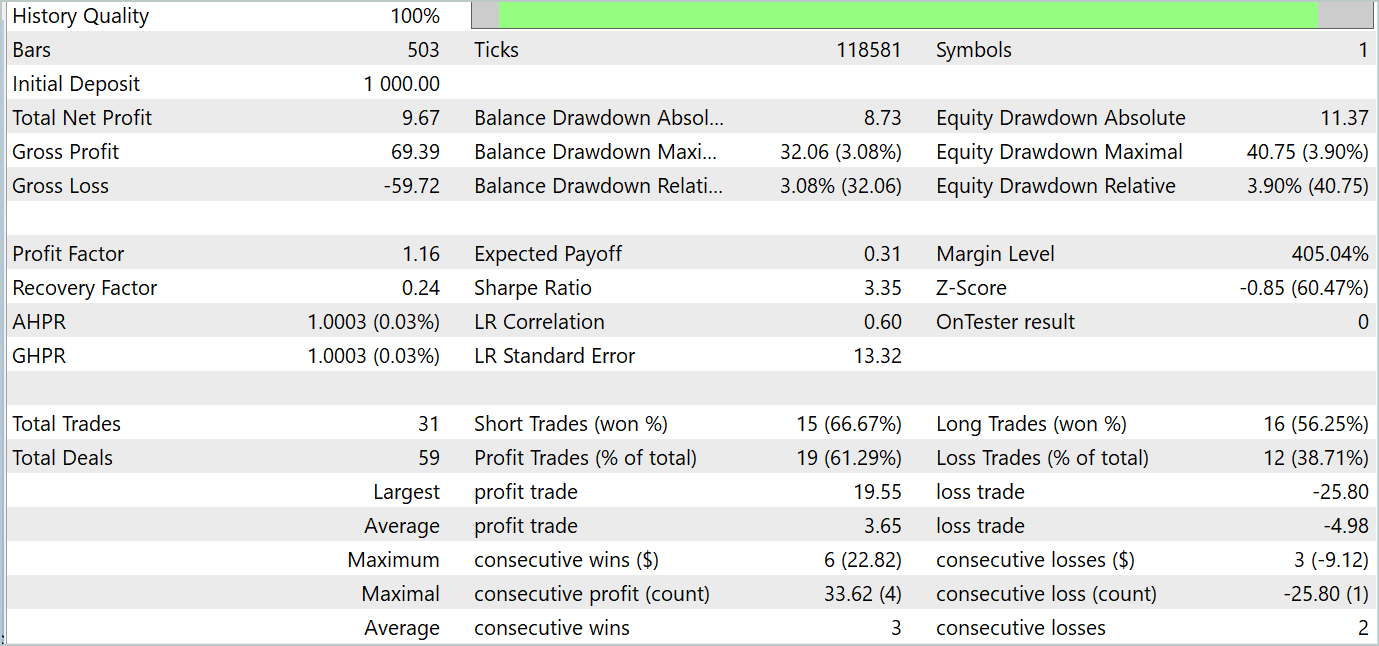
Durante o período de teste, o modelo realizou 31 operações, das quais 19 foram fechadas com lucro. A porcentagem de negociações lucrativas foi superior a 61%. É notável que o modelo realizou praticamente o mesmo número de posições longas e curtas (15 contra 16).
Considerações finais
Os dois últimos artigos foram dedicados ao método ATFNet, proposto no artigo "ATFNet: Adaptive Time-Frequency Ensembled Network for Long-term Time Series Forecasting", para a previsão de séries temporais multivariadas. O modelo ATFNet combina módulos dos domínios temporal e frequencial para analisar as dependências nas séries temporais. Ele utiliza o T-Block para capturar dependências locais no domínio temporal e o F-Block para analisar ciclicidades das séries no domínio frequencial.
O ATFNet aplica o ponderamento da energia da série harmônica dominante, a Transformada de Fourier estendida e a atenção ao espectro complexo para se adaptar à periodicidade e ao deslocamento de frequências nas séries temporais de entrada.
Na parte prática do nosso trabalho, implementamos nossa visão das abordagens propostas usando MQL5. Realizamos o treinamento e teste dos modelos com dados reais. Os resultados dos testes indicam o potencial das abordagens propostas para a construção de estratégias de trading lucrativas.
Referências
- ATFNet: Adaptive Time-Frequency Ensembled Network for Long-term Time Series Forecasting
- Outros artigos da série
Programas utilizados no artigo:
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA para coleta de exemplos |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA para coleta de exemplos usando o método Real-ORL |
| 3 | Study.mq5 | Expert Advisor | EA para treinamento de modelos |
| 4 | StudyEncoder.mq5 | Expert Advisor | EA para treinamento do Codificador |
| 5 | Test.mq5 | Expert Advisor | EA para teste do modelo |
| 6 | Trajectory.mqh | Biblioteca de classe | Estrutura para descrever o estado do sistema |
| 7 | NeuroNet.mqh | Biblioteca de classe | Biblioteca de classes para criação de redes neurais |
| 8 | NeuroNet.cl | Biblioteca | Biblioteca de código OpenCL. |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/15024
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Um Guia Passo a Passo sobre a Estratégia de Quebra de Estrutura (BoS)
Um Guia Passo a Passo sobre a Estratégia de Quebra de Estrutura (BoS)
 Algoritmo de Busca Cooperativa Artificial (Artificial Cooperative Search, ACS)
Algoritmo de Busca Cooperativa Artificial (Artificial Cooperative Search, ACS)
 Construindo um Modelo de Restrição de Tendência de Candlestick (Parte 4): Personalizando o Estilo de Exibição para Cada Onda de Tendência
Construindo um Modelo de Restrição de Tendência de Candlestick (Parte 4): Personalizando o Estilo de Exibição para Cada Onda de Tendência
 Redes neurais de maneira fácil (Parte 92): Previsão adaptativa nas áreas de frequência e tempo
Redes neurais de maneira fácil (Parte 92): Previsão adaptativa nas áreas de frequência e tempo
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Olá, Dmitry!
Como você treina e reabastece o banco de dados de exemplos para um ano de histórico? Tenho um problema com a reposição de novos exemplos no arquivo bd em seus Expert Advisors dos artigos mais recentes (onde você usa um ano de histórico). O problema é que, quando esse arquivo atinge o tamanho de 2 GB, ele aparentemente começa a ser salvo de forma incorreta e o Expert Advisor de treinamento de modelos não consegue lê-lo e apresenta um erro. Ou o arquivo bd começa a diminuir drasticamente de tamanho, com cada nova adição de exemplos de até vários megabytes, e o consultor de treinamento ainda apresenta um erro. Esse problema ocorre em até 150 trajetórias se você fizer o histórico por um ano e em cerca de 250 se fizer o histórico por 7 meses. O tamanho do arquivo bd cresce muito rapidamente. Por exemplo, 18 trajetórias pesam quase 500 Mb. 30 trajetórias têm 700 MB.
Como resultado, para treinar, temos de excluir esse arquivo com um conjunto de 230 trajetórias ao longo de 7 meses e criá-lo novamente com um Expert Advisor pré-treinado. Mas, nesse modo, o mecanismo de atualização de trajetórias ao reabastecer o banco de dados não funciona. Presumo que isso se deva à limitação de 4 GB de RAM para um thread no MT5. Em algum lugar da ajuda, eles escreveram sobre isso.
O interessante é que em artigos anteriores (em que o histórico era de 7 meses e a base para 500 trajetórias pesava cerca de 1 GB) esse problema não estava presente. Não estou limitado pelos recursos do PC, pois a RAM tem mais de 32 GB e a memória da placa de vídeo é suficiente.
Dmitry, como você ensina com esse ponto em mente ou talvez tenha configurado o MT5 com antecedência?
Eu uso arquivos de artigos sem nenhuma modificação.
Como resultado, para treinar, temos que excluir esse arquivo com um conjunto de 230 trajetórias ao longo de 7 meses e criá-lo novamente com um Expert Advisor pré-treinado. Mas, nesse modo, o mecanismo de atualização de trajetórias ao reabastecer o banco de dados não funciona. Presumo que isso se deva à limitação de 4 GB de RAM para um thread no MT5. Em algum lugar da ajuda, eles escreveram sobre isso.
O interessante é que em artigos anteriores (em que o histórico era de 7 meses e a base para 500 trajetórias pesava cerca de 1 GB) esse problema não existia. Não estou limitado pelos recursos do PC, pois a RAM tem mais de 32 GB e a placa de vídeo tem memória suficiente.
Dmitry, como você ensina com isso em mente ou talvez tenha configurado o MT5 com antecedência?
Eu uso arquivos de artigos sem nenhuma modificação.
Victor,

Não sei o que lhe responder. Eu trabalho com arquivos maiores.
Olá, li este artigo e é interessante. Entendi um pouco, mas vou ler novamente depois de ler o artigo original.
Deparei-me com este artigo https://www.mdpi.com/2076-3417/14/9/3797#
ele afirma que eles obtiveram 94% de sucesso na classificação de imagens de bitcoin, isso é realmente possível?