Integração de Modelos Ocultos de Markov no MetaTrader 5

Introdução

É bem conhecido que uma das características fundamentais das séries temporais financeiras é que elas exibem memória. No contexto da análise de séries temporais, memória refere-se à estrutura de dependência dentro dos dados, onde valores passados influenciam os valores atuais e futuros. Compreender a estrutura da memória ajuda na escolha do modelo apropriado para a série temporal. Neste artigo, discutimos um tipo diferente de memória: o tipo que assume a forma de um Modelo Oculto de Markov (HMM). Exploraremos os fundamentos dos HMMs e demonstraremos como construir um HMM utilizando o módulo hmmlearn do Python. Por fim, apresentaremos códigos em Python e MQL5 que permitem a exportação de HMMs para uso em programas MetaTrader 5.

Compreendendo os Modelos Ocultos de Markov

Os Modelos Ocultos de Markov são uma poderosa ferramenta estatística utilizada para modelar dados de séries temporais, onde o sistema modelado é caracterizado por estados não observáveis (ocultos). Uma premissa fundamental dos HMMs é que a probabilidade de estar em um determinado estado em um momento específico depende do estado do processo no instante anterior. Essa dependência representa a memória de um HMM.

No contexto das séries temporais financeiras, os estados poderiam representar se uma série está em tendência de alta, em tendência de baixa ou oscilando dentro de um intervalo específico. Qualquer pessoa que tenha usado qualquer indicador financeiro está familiarizada com o efeito "whipsaw" causado pelo ruído inerente às séries temporais financeiras. Um HMM pode ser utilizado para filtrar esses falsos sinais, fornecendo uma compreensão mais clara das tendências subjacentes.

Para construir um HMM, precisamos de observações que capturem a totalidade do comportamento que define o processo. Essa amostra de dados é usada para aprender os parâmetros do HMM apropriado. Esse conjunto de dados seria composto por várias características do processo que está sendo modelado. Por exemplo, se estivermos estudando os preços de fechamento de um ativo financeiro, também poderíamos incluir outros aspectos relacionados ao preço de fechamento, como vários indicadores que, idealmente, ajudam a definir os estados ocultos de nosso interesse.

O processo de aprendizado dos parâmetros do modelo é realizado sob a suposição de que a série modelada estará sempre em um de dois ou mais estados. Os estados são simplesmente rotulados de 0 a S-1. Para esses estados, devemos atribuir um conjunto de probabilidades que capturam a probabilidade do processo mudar de um estado para outro. Essas probabilidades são geralmente chamadas de matriz de transição. A primeira observação tem um conjunto especial de probabilidades iniciais para estar em cada estado possível. Se uma observação está em um determinado estado, espera-se que siga uma distribuição específica associada a esse estado.

Um HMM é, portanto, totalmente definido por quatro propriedades:

• O número de estados assumidos
• As probabilidades iniciais para a primeira observação estar em qualquer um dos estados
• A matriz de transição de probabilidades
• As funções de densidade de probabilidade para cada estado.
  

No início, temos as observações e o número assumido de estados. Queremos encontrar os parâmetros de um HMM que se ajustem ao conjunto de dados que temos. Isso é feito observando a verossimilhança usando uma técnica estatística chamada estimativa de máxima verossimilhança. Neste contexto, a estimativa de máxima verossimilhança é o processo de buscar as propriedades do modelo que mais provavelmente correspondem às nossas amostras de dados. Isso é alcançado calculando a verossimilhança de cada amostra estar em um estado específico em um momento específico. Isso é feito utilizando os algoritmos forward e backward, que percorrem todas as amostras, respectivamente para frente e para trás no tempo.

O algoritmo forward

Começamos com a primeira observação em nosso conjunto de dados antes de calcular as probabilidades para as amostras subsequentes. Para a primeira amostra, utilizamos as probabilidades do estado inicial, que, neste momento, são consideradas parâmetros de teste para um HMM candidato. Se nada é conhecido sobre o processo sendo modelado, é perfeitamente aceitável definir todas as probabilidades de estado inicial para 1/S, onde S representa o número total de estados assumidos. Aplicando o Teorema de Bayes, temos a seguinte equação geral:

Onde "lk" é a probabilidade de uma amostra no tempo "t" estar no estado "i", e "p" é a probabilidade de estar no estado "i" no tempo "t", dado as amostras até o tempo "t". "O" é uma amostra individual, uma única linha no conjunto de dados.

A probabilidade da primeira amostra é calculada de acordo com a regra de probabilidade condicional, P(A) = P(A|B)P(B). Portanto, para a primeira amostra, a probabilidade de estar no estado i é calculada multiplicando a probabilidade do estado inicial de estar no estado i com a função de densidade de probabilidade da primeira amostra.

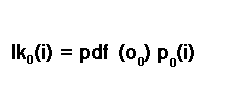
Este é outro parâmetro de teste do HMM candidato. Na literatura, às vezes é referido como probabilidade de emissão. Exploraremos mais detalhadamente as probabilidades de emissão posteriormente no texto. Por enquanto, basta saber que este é outro parâmetro de teste nesta fase. Não devemos esquecer que não estamos certos do estado em que estamos. Temos que considerar a possibilidade de que poderíamos estar em qualquer um dos estados possíveis. Isso resulta na probabilidade inicial final sendo a soma de todas as probabilidades de todos os estados possíveis.

 

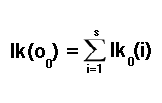
Para calcular as probabilidades para as observações subsequentes, devemos considerar a possibilidade de transição para um estado específico a partir de qualquer um dos estados possíveis no instante anterior. É aqui que as probabilidades de transição entram em jogo, que neste ponto são outro parâmetro de teste. A probabilidade de chegar a um estado específico no próximo instante, dado que calculamos a probabilidade para o instante atual, é estimada multiplicando a probabilidade do estado conhecido com a probabilidade de transição correspondente.

Este é um bom momento para falar sobre probabilidades de transição ou a matriz de transição.

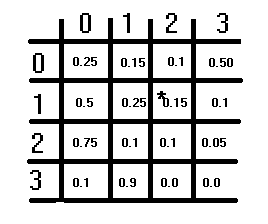
A ilustração acima mostra uma matriz de transição hipotética. Ela tem uma estrutura S×S, com S sendo o número de estados assumidos. Cada elemento representa uma probabilidade, e as probabilidades em cada linha devem somar 1. Essa condição não se aplica às colunas. Para obter a probabilidade de transição correspondente para mudar de um estado para outro, você se refere primeiro às linhas e depois às colunas. O estado atual do qual se está mudando corresponde ao índice da linha, e o estado para o qual se está mudando corresponde ao índice da coluna. O valor nesses índices é a probabilidade de transição correspondente. A diagonal da matriz descreve as probabilidades do estado não mudar.

Retornando à tarefa de calcular as probabilidades para as demais observações em nossa amostra de dados escolhida, estávamos multiplicando a probabilidade de um estado pela probabilidade de transição. No entanto, para obter uma visão completa, devemos considerar a possibilidade de transição para qualquer um dos estados possíveis. Fazemos isso somando todas as possibilidades, de acordo com a equação a seguir:

            

Isso conclui o cálculo das probabilidades individuais para cada amostra em nosso conjunto de dados. Essas probabilidades individuais podem ser combinadas por meio de multiplicação para obter a probabilidade para o conjunto de dados inteiro. O cálculo descrito é chamado de algoritmo forward, devido ao método de recursão temporal para frente. sso contrasta com o algoritmo backward, que discutiremos na próxima seção.

O algoritmo backward

Também é possível calcular as probabilidades individuais movendo-se para trás no tempo, começando da última amostra de dados para a primeira. Começamos definindo a probabilidade para todos os estados como 1 para a última amostra de dados. Para cada amostra de dados, se em um estado específico, calculamos a probabilidade do conjunto subsequente de amostras, considerando que podemos transitar para qualquer um dos estados. Fazemos isso calculando a soma ponderada das probabilidades de cada estado: a probabilidade de estar naquele estado multiplicada pela função de densidade de probabilidade da amostra estar no mesmo estado. O resultado deste cálculo é então ajustado usando a probabilidade de transição do estado atual para o próximo como fator de ponderação. Tudo isso está encapsulado na fórmula abaixo:

As funções de densidade de probabilidade

Nas discussões sobre os algoritmos forward e backward, houve menção de funções de densidade de probabilidade (pdf) como parâmetros de um HMM. Surge então a pergunta: Que distribuição estamos assumindo? Como mencionado anteriormente, os parâmetros pdf de um HMM são geralmente chamados de probabilidades de emissão. São referidas como probabilidades quando os dados modelados consistem em valores discretos ou categóricos. Quando lidamos com variáveis contínuas, usamos a pdf.

Neste texto, demonstramos HMMs que modelam conjuntos de dados de variáveis contínuas seguindo uma distribuição normal multivariada. É possível implementar outras distribuições; na verdade, o módulo Python que veremos mais adiante possui implementações de HMM para diferentes distribuições dos dados sendo modelados. Por extensão, os parâmetros da distribuição assumida tornam-se um dos parâmetros do HMM. No caso da distribuição normal multivariada, seus parâmetros são as médias e covariâncias.

O algoritmo de Baum-Welch

O algoritmo de Baum-Welch é uma técnica de maximização de expectativa usada para testar diferentes parâmetros para HMMs candidatos e chegar ao ideal. O valor maximizado neste processo de otimização é a probabilidade para o conjunto completo de amostras. O algoritmo de Baum-Welch é conhecido por ser eficiente e confiável, mas possui suas limitações. Uma limitação evidente é sua natureza não convexa. Funções não convexas em relação à otimização são funções com inúmeros mínimos ou máximos locais.

Isso significa que, quando a convergência é alcançada, o máximo ou mínimo global do espaço de parâmetros pode não ter sido encontrado. A função basicamente não garante convergir para o ponto ideal. A melhor maneira de mitigar essa limitação é testar parâmetros que tenham uma probabilidade alta em comparação com outros no espaço de parâmetros. Para isso, precisaríamos testar vários valores de parâmetros aleatórios para encontrar o melhor espaço de parâmetros inicial para iniciar o processo de otimização.

Calculando probabilidades de estado

Uma vez que temos o HMM ideal e seus parâmetros, podemos usá-lo para calcular as probabilidades de estado para amostras de dados não vistas. O resultado de tal cálculo seria um conjunto de probabilidades, uma para cada estado, indicando a probabilidade de estar em cada estado. As probabilidades individuais do algoritmo forward são multiplicadas pelas probabilidades do algoritmo backward, resultando na probabilidade de um estado específico. De acordo com a regra de Bayes, a probabilidade de que uma observação esteja em um estado específico é calculada como:

Calculando probabilidades de estado usando o Algoritmo de Viterbi

Além das probabilidades de estado, também podemos inferir o estado provável em que uma observação está usando o Algoritmo de Viterbi. O cálculo começa pela primeira observação, cujas probabilidades de estado são calculadas usando as probabilidades iniciais de estado multiplicadas pelas probabilidades de emissão.

Para cada observação da segunda até a última, cada probabilidade de estado é calculada usando a probabilidade do estado anterior, a probabilidade de transição correspondente e sua probabilidade de emissão. O estado mais provável será aquele com a maior probabilidade.

Examinamos todos os componentes de um Modelo Oculto de Markov. Agora, abordaremos sua implementação prática. Começamos analisando uma implementação baseada em Python de HMMs fornecida pelo pacote hmmlearn. Discutiremos o uso da implementação do HMM Gaussiano do hmmlearn antes de mudar para o código MQL5 para demonstrar como integrar um modelo treinado em Python usando o hmmlearn em aplicações MetaTrader 5.

Pacote hmmlearn do Python

A biblioteca hmmlearn no Python fornece ferramentas para trabalhar com modelos ocultos de Markov. As ferramentas para treinar HMMs são encontradas no namespace hmm. Dentro do hmm, várias classes especiais são declaradas para trabalhar com processos de diferentes distribuições. Nomeadamente:

• MultinomialHMM: Modela HMMs onde as observações são discretas e seguem uma distribuição multinomial
• GMMHMM: Modela HMMs onde as observações são geradas a partir de uma mistura de distribuições gaussianas
• PoissonHMM: Modela HMMs onde as observações são assumidas como seguindo uma distribuição de PoissonRegressor
• Por último, temos a classe GaussianHMM que lida com conjuntos de dados que tendem a seguir uma distribuição Gaussiana (normal) multivariada. Esta é a classe que demonstraremos e cujo modelo resultante vincularemos ao MetaTrader 5.

Para instalar o pacote, você pode usar o seguinte comando:

pip install hmmlearn

Após instalar o pacote, você pode importar a classe GaussianHMM usando a instrução de importação a seguir:

from hmmlearn.hmm import GaussianHMM

Alternativamente, você pode importar o módulo hmm, que contém todas as classes listadas acima, juntamente com outras utilidades úteis. Se este método for usado, então os nomes das classes devem ser prefixados por hmm, assim:

from hmmlearn import hmm

Você pode inicializar um objeto GaussianHMM com vários parâmetros:

model = GaussianHMM(n_components=3, covariance_type='diag', n_iter=100, tol=0.01)

onde:

• "n_components": Número de estados no modelo
• "covariance_type": Tipo de parâmetros de covariância a serem usados ('spherical', 'diag', 'full', 'tied').. O tipo de covariância usado se relaciona com as características do conjunto de dados. Uma covariância esférica deve ser escolhida se as características ou variáveis no conjunto de dados modelado tiverem variança semelhante, sem possibilidade de serem correlacionadas. Caso contrário, se as variáveis tiverem variâncias contrastantes, a melhor opção é escolher um tipo de covariância diagonal. Se as variáveis estiverem correlacionadas, então uma covariância completa ou amarrada deve ser escolhida. Selecionar covariância completa fornece a maior flexibilidade, mas também pode ser computacionalmente caro. É a escolha mais segura, pois limita o número de suposições feitas sobre o processo modelado. Covariância amarrada faz a suposição adicional de que os estados compartilham uma estrutura de covariância semelhante. É um pouco mais eficiente em relação à covariância completa
• "n_iter": Número máximo de iterações a serem realizadas durante o treinamento
• "tol": Limite de convergência.

Para explorar todos os parâmetros que especificam um modelo, você pode consultar a documentação da biblioteca hmmlearn. Essa documentação fornece informações detalhadas sobre os vários parâmetros e seu uso. Você pode acessá-la online no site oficial da biblioteca hmmlearn ou através da documentação incluída com a instalação da biblioteca, utilizando a utilidade de ajuda embutida no Python.

help(GaussianHMM)

Para treinar um modelo, chamamos o método "fit()". Ele espera pelo menos um array bidimensional como entrada.

model.fit(data)

Após o treinamento ser concluído, podemos obter os estados ocultos de um conjunto de dados chamando "predict()" ou "decode()". Ambos esperam um array bidimensional com o mesmo número de características do conjunto de dados usado para treinar o modelo. O método "predict()" retorna um array de estados ocultos calculados, enquanto "decode()" retorna a verossimilhança logarítmica junto com o array de estados ocultos em uma tupla.

Chamar "score_samples()" retorna a verossimilhança logarítmica, bem como as probabilidades de estado para o conjunto de dados fornecido como entrada. Novamente, os dados devem ter o mesmo número de características dos dados usados para treinar o modelo.

Exportando um modelo oculto de Markov

Exportar um modelo treinado em Python usando o pacote hmmlearn para uso no MetaTrader 5 envolve a implementação de dois componentes personalizados:

• Componente Python: Este componente é responsável por salvar os parâmetros de um modelo treinado em um formato legível a partir de uma aplicação MetaTrader. Isso envolve exportar os parâmetros do modelo para um formato de arquivo que pode ser analisado pelas aplicações MetaTrader 5
• Componente MQL5: O componente MQL5 compreende código escrito em MQL5. Este componente deve incluir funcionalidades para ler os parâmetros do HMM exportados pelo componente Python. Além disso, precisa implementar os algoritmos forward, backward e Viterbi para calcular os estados ocultos e as probabilidades de estado para um conjunto de dados com base em um HMM especificado.
  

Implementar esses componentes envolve uma consideração cuidadosa dos formatos de serialização de dados, operações de entrada e saída de arquivos e implementações algorítmicas tanto em Python quanto em MQL5. É essencial garantir a compatibilidade entre as implementações em Python e MQL5 para transferir com precisão o modelo treinado e realizar tarefas de inferência no MetaTrader 5.

O pacote hmmlearn fornece a capacidade de salvar um HMM treinado usando o módulo pickle. O problema é que arquivos em formato pickle não são fáceis de trabalhar fora do Python. Portanto, uma opção melhor seria usar o formato json. Os parâmetros do HMM serão escritos em um arquivo JSON estruturado que pode ser lido usando código MQL5. Essa funcionalidade é implementada na função Python abaixo.

def hmm2json(hmm_model, filename):
    """
    function save a GaussianHMM model to json format 
    readable from MQL5 code.
    param: hmm_model should an instance of GaussianHMM
    param: string. filename or path to file where HMM 
    parameters will be written to
    """
    if hmm_model.__class__.__name__ != 'GaussianHMM':
        raise TypeError(f'invalid type supplied')
    if len(filename) < 1 or not isinstance(filename,str):
        raise TypeError(f'invalid filename supplied')
    jm  = {
            "numstates":hmm_model.n_components,
            "numvars":hmm_model.n_features,
            "algorithm":str(hmm_model.algorithm),
            "implementation":str(hmm_model.implementation), 
            "initprobs":hmm_model.startprob_.tolist(),
            "means":hmm_model.means_.tolist(),
            "transitions":hmm_model.transmat_.tolist(),
            "covars":hmm_model.covars_.tolist()
          }
    with open(filename,'w') as file:
        json.dump(jm,file,indent=None,separators=(',', ':')) 
    return 

Essa função recebe uma instância da classe GaussianHMM e um nome de arquivo como entrada, e grava os parâmetros do HMM em um arquivo JSON em um formato estruturado que pode ser lido usando código MQL5.

No código MQL5, a funcionalidade para ler modelos HMM salvos no formato JSON está incluída em hmmlearn.mqh. O arquivo inclui a definição da classe HMM.

//+------------------------------------------------------------------+
//|                                                     hmmlearn.mqh |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<Math\Alglib\dataanalysis.mqh>
#include<Math\Stat\Uniform.mqh>
#include<Math\Stat\Math.mqh>
#include<JAson.mqh>
#include<Files/FileTxt.mqh>
#include<np.mqh>

//+------------------------------------------------------------------+
//|Markov model estimation method                                    |
//+------------------------------------------------------------------+
enum ENUM_HMM_METHOD
  {
   MODE_LOG=0,
   MODE_SCALING
  };
//+------------------------------------------------------------------+
//| state sequence decoding algorithm                                |
//+------------------------------------------------------------------+
enum ENUM_DECODE_METHOD
  {
   MODE_VITERBI=0,
   MODE_MAP
  };
//+------------------------------------------------------------------+
//| Hidden Markov Model class                                        |
//+------------------------------------------------------------------+
class HMM
  {
private:
   ulong m_samples ;       // Number of cases in dataset
   ulong m_vars ;        // Number of variables in each case
   ulong m_states ;      // Number of states
   vector            m_initprobs;   // vector of probability that first case is in each state
   matrix            m_transition;  // probability matrix
   matrix m_means ;                 //state means
   matrix m_covars[] ;              // covariances
   matrix densities ;              // probability densities
   matrix alpha ;       // result of forward algorithm
   matrix beta ;        // result of backward algorithm
   matrix m_stateprobs ; // probabilities of state
   double likelihood ;  //  log likelihood
   matrix            trial_transition;
   bool              trained;
   double            m_mincovar;
   ENUM_HMM_METHOD   m_hmm_mode;
   ENUM_DECODE_METHOD m_decode_mode;
   //+------------------------------------------------------------------+
   //| normalize array so sum(exp(a)) == 1                              |
   //+------------------------------------------------------------------+
   matrix            log_normalize(matrix &in)
     {
      matrix out;
      if(in.Cols()==1)
         out = matrix::Zeros(in.Rows(), in.Cols());
      else
         out = logsumexp(in);
      return in-out;
     }
   //+------------------------------------------------------------------+
   //| log of the sum of exponentials of input elements                 |
   //+------------------------------------------------------------------+
   matrix            logsumexp(matrix &in)
     {
      matrix out;

      vector amax = in.Max(1);

      for(ulong i = 0; i<amax.Size(); i++)
         if(fpclassify(MathAbs(amax[i])) == FP_INFINITE)
            amax[i] = 0.0;

      matrix ama(amax.Size(),in.Cols());
      for(ulong i=0; i<ama.Cols();i++)
         ama.Col(amax,i);

      matrix tmp = exp(in - ama);

      vector s = tmp.Sum(1);

      out.Init(s.Size(),in.Cols());
      for(ulong i=0; i<out.Cols();i++)
         out.Col(log(s),i);

      out+=ama;

      return out;
     }

   //+------------------------------------------------------------------+
   //| normarlize vector                                                |
   //+------------------------------------------------------------------+
   vector            normalize_vector(vector &in)
     {
      double sum = in.Sum();
      return in/sum;
     }
   //+------------------------------------------------------------------+
   //|  normalize matrix                                                |
   //+------------------------------------------------------------------+
   matrix            normalize_matrix(matrix &in)
     {
      vector sum = in.Sum(1);

      for(ulong i = 0; i<sum.Size(); i++)
         if(sum[i] == 0.0)
            sum[i] = 1.0;

      matrix n;
      n.Init(sum.Size(), in.Cols());
      for(ulong i =0; i<n.Cols(); i++)
         n.Col(sum,i);

      return in/n;
     }
   //+------------------------------------------------------------------+
   //|   Set up model from JSON object                                  |
   //+------------------------------------------------------------------+
   bool              fromJSON(CJAVal &jsonmodel)
     {

      if(jsonmodel["implementation"].ToStr() == "log")
         m_hmm_mode = MODE_LOG;
      else
         m_hmm_mode = MODE_SCALING;

      if(jsonmodel["algorithm"].ToStr() == "Viterbi")
         m_decode_mode = MODE_VITERBI;
      else
         m_decode_mode = MODE_MAP;

      m_states = (ulong)jsonmodel["numstates"].ToInt();
      m_vars = (ulong)jsonmodel["numvars"].ToInt();


      if(!m_initprobs.Resize(m_states) || !m_means.Resize(m_states,m_vars) ||
         !m_transition.Resize(m_states,m_states) || ArrayResize(m_covars,int(m_states))!=int(m_states))
        {
         Print(__FUNCTION__, " error ", GetLastError());
         return false;
        }

      for(uint i = 0; i<m_covars.Size(); i++)
        {
         if(!m_covars[i].Resize(m_vars,m_vars))
           {
            Print(__FUNCTION__, " error ", GetLastError());
            return false;
           }

         for(int k = 0; k<int(m_covars[i].Rows()); k++)
            for(int j = 0; j<int(m_covars[i].Cols()); j++)
               m_covars[i][k][j] = jsonmodel["covars"][i][k][j].ToDbl();
        }

      for(int i =0; i<int(m_initprobs.Size()); i++)
        {
         m_initprobs[i] = jsonmodel["initprobs"][i].ToDbl();
        }

      for(int i=0; i<int(m_states); i++)
        {
         for(int j = 0; j<int(m_vars); j++)
            m_means[i][j] = jsonmodel["means"][i][j].ToDbl();
        }

      for(int i=0; i<int(m_states); i++)
        {
         for(int j = 0; j<int(m_states); j++)
            m_transition[i][j] = jsonmodel["transitions"][i][j].ToDbl();
        }

      return true;
     }

   //+------------------------------------------------------------------+
   //|  Multivariate Normal Density function                            |
   //+------------------------------------------------------------------+
   double            mv_normal(ulong nv,vector &x, vector &mean, matrix &in_covar)
     {
      matrix cv_chol;
      vector vc = x-mean;

      if(!in_covar.Cholesky(cv_chol))
        {
         matrix ncov = in_covar+(m_mincovar*matrix::Eye(nv,nv));
         if(!ncov.Cholesky(cv_chol))
           {
            Print(__FUNCTION__,": covars matrix might not be symmetric positive-definite, error ", GetLastError());
            return EMPTY_VALUE;
           }
        }

      double cv_log_det = 2.0 * (MathLog(cv_chol.Diag())).Sum();
      vector cv_sol = cv_chol.Solve(vc);

      return -0.5*((nv*log(2.0 * M_PI)) + (pow(cv_sol,2.0)).Sum() + cv_log_det);

     }


   //+------------------------------------------------------------------+
   //|logadd exp                                                        |
   //+------------------------------------------------------------------+
   double            logaddexp(double a, double b)
     {
      return a==-DBL_MIN?b:b==-DBL_MIN?a:MathMax(a,b)+log1p(exp(-1.0*MathAbs(b-a)));
     }
   //+------------------------------------------------------------------+
   //| scaled trans calculation                                         |
   //+------------------------------------------------------------------+
   matrix            compute_scaling_xi_sum(matrix &trans, matrix &dens,matrix &alf, matrix &bta)
     {
      matrix logdens = exp(dens).Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      matrix out;
      out.Resize(nc,nc);
      out.Fill(0.0);

      for(ulong t =0; t<ns-1; t++)
        {
         for(ulong i = 0; i<nc; i++)
           {
            for(ulong j = 0; j<nc; j++)
              {
               out[i][j] += alf[t][i] * trans[i][j] * logdens[t+1][j]*bta[t+1][j];
              }
           }
        }
      return out;
     }
   //+------------------------------------------------------------------+
   //| log trans calculation                                            |
   //+------------------------------------------------------------------+
   matrix            compute_log_xi_sum(matrix &trans, matrix &dens,matrix &alf, matrix &bta)
     {
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      vector row = alf.Row(ns-1);
      double logprob = (log(exp(row-row[row.ArgMax()]).Sum()) + row[row.ArgMax()]);

      matrix out;
      out.Init(nc,nc);

      out.Fill(-DBL_MIN);

      for(ulong t = 0 ; t<ns-1; t++)
        {
         for(ulong i =0; i<nc; i++)
           {
            for(ulong j =0; j<nc; j++)
              {
               double vl = alf[t][i] + logtrans[i][j]+ logdens[t+1][j]+bta[t+1][j] - logprob;
               out[i][j] = logaddexp(out[i][j], vl);
              }
           }
        }

      return out;

     }
   //+------------------------------------------------------------------+
   //| forward scaling                                                  |
   //+------------------------------------------------------------------+
   double            forwardscaling(vector &startp, matrix &trans, matrix &dens,matrix &out, vector&outt)
     {
      double minsum = 1.e-300;
      vector gstartp = startp;
      matrix gtrans = trans;
      matrix gdens = exp(dens).Transpose();

      ulong ns = gdens.Rows();
      ulong nc = gdens.Cols();

      if(out.Cols()!=nc || out.Rows()!=ns)
         out.Resize(ns,nc);

      if(outt.Size()!=ns)
         outt.Resize(ns);

      out.Fill(0.0);

      double logprob = 0.0;

      for(ulong i = 0; i<nc; i++)
         out[0][i] = gstartp[i]*gdens[0][i];

      double sum  = (out.Row(0)).Sum();

      if(sum<minsum)
         Print("WARNING: forward pass failed with underflow consider using log implementation ");

      double scale = outt[0] = 1.0/sum;
      logprob -= log(scale);

      for(ulong i=0; i<nc; i++)
         out[0][i] *=scale;

      for(ulong t =1; t<ns; t++)
        {
         for(ulong j=0; j<nc; j++)
           {
            for(ulong i=0; i<nc; i++)
              {
               out[t][j]+=out[t-1][i] * gtrans[i][j];
              }
            out[t][j]*=gdens[t][j];
           }
         sum = (out.Row(t)).Sum();
         if(sum<minsum)
            Print("WARNING: forward pass failed with underflow consider using log implementation ");

         scale = outt[t] = 1.0/sum;
         logprob -= log(scale);
         for(ulong j = 0; j<nc; j++)
            out[t][j] *= scale;

        }
      return logprob;
     }
   //+------------------------------------------------------------------+
   //|backward scaling                                                  |
   //+------------------------------------------------------------------+
   matrix            backwardscaling(vector &startp, matrix &trans, matrix &dens,vector &scaling)
     {
      vector gstartp = startp;
      vector scaled = scaling;
      matrix gtrans = trans;
      matrix gdens =  exp(dens).Transpose();

      ulong ns = gdens.Rows();
      ulong nc = gdens.Cols();

      matrix out;
      out.Init(ns,nc);

      out.Fill(0.0);
      for(ulong i = 0; i<nc; i++)
         out[ns-1][i] = scaling[ns-1];

      for(long t = long(ns-2); t>=0; t--)
        {
         for(ulong i=0; i<nc; i++)
           {
            for(ulong j =0; j<nc; j++)
              {
               out[t][i]+=(gtrans[i][j]*gdens[t+1][j]*out[t+1][j]);
              }
            out[t][i]*=scaling[t];
           }
        }
      return out;
     }
   //+------------------------------------------------------------------+
   //| forward log                                                      |
   //+------------------------------------------------------------------+
   double            forwardlog(vector &startp, matrix &trans, matrix &dens,matrix &out)
     {
      vector logstartp = log(startp);
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      if(out.Cols()!=nc || out.Rows()!=ns)
         out.Resize(ns,nc);

      vector buf;
      buf.Init(nc);

      for(ulong i =0; i<nc; i++)
         out[0][i] = logstartp[i] + logdens[0][i];

      for(ulong t =1; t<ns; t++)
        {
         for(ulong j =0; j<nc; j++)
           {
            for(ulong i =0; i<nc; i++)
              {
               buf[i] = out[t-1][i] + logtrans[i][j];
              }
            out[t][j] = logdens[t][j] + (log(exp(buf-buf[buf.ArgMax()]).Sum()) + buf[buf.ArgMax()]);
           }
        }

      vector row = out.Row(ns-1);

      return (log(exp(row-row[row.ArgMax()]).Sum()) + row[row.ArgMax()]);
     }
   //+------------------------------------------------------------------+
   //|  backwardlog                                                     |
   //+------------------------------------------------------------------+
   matrix            backwardlog(vector &startp, matrix &trans, matrix &dens)
     {
      vector logstartp = log(startp);
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      matrix out;
      out.Init(ns,nc);

      vector buf;
      buf.Init(nc);

      for(ulong i =0; i<nc; i++)
         out[ns-1][i] = 0.0;

      for(long t = long(ns-2); t>=0; t--)
        {
         for(long i =0; i<long(nc); i++)
           {
            for(long j =0; j<long(nc); j++)
              {
               buf[j] = logdens[t+1][j] + out[t+1][j] + logtrans[i][j];
              }
            out[t][i] = (log(exp(buf-buf[buf.ArgMax()]).Sum()) + buf[buf.ArgMax()]);
           }
        }
      return out;
     }
   //+------------------------------------------------------------------+
   //| compute posterior state probabilities scaling                    |
   //+------------------------------------------------------------------+
   matrix            compute_posteriors_scaling(matrix &alf, matrix &bta)
     {
      return normalize_matrix(alf*bta);
     }
   //+------------------------------------------------------------------+
   //| compute posterior state probabilities log                        |
   //+------------------------------------------------------------------+
   matrix            compute_posteriors_log(matrix &alf, matrix &bta)
     {
      return exp(log_normalize(alf+bta));
     }
   //+------------------------------------------------------------------+
   //|calculate the probability of a state                              |
   //+------------------------------------------------------------------+
   double            compute_posteriors(matrix &data, matrix &result, ENUM_HMM_METHOD use_log=MODE_LOG)
     {
      matrix alfa,bt,dens;
      double logp=0.0;
      dens = find_densities(m_vars,m_states,data,m_means,m_covars);
      if(use_log == MODE_LOG)
        {
         logp = forwardlog(m_initprobs,m_transition,dens,alfa);
         bt = backwardlog(m_initprobs,m_transition,dens);
         result = compute_posteriors_log(alfa,bt);
        }
      else
        {
         vector scaling_factors;
         logp = forwardscaling(m_initprobs,m_transition,dens,alfa,scaling_factors);
         bt = backwardscaling(m_initprobs,m_transition,dens,scaling_factors);
         result = compute_posteriors_scaling(alfa,bt);
        }
      return logp;
     }
   //+------------------------------------------------------------------+
   //| map  implementation                                              |
   //+------------------------------------------------------------------+
   double            map(matrix &data,vector &out, ENUM_HMM_METHOD use_log=MODE_LOG)
     {
      matrix posteriors;
      double lp = compute_posteriors(data,posteriors,use_log);
      lp = (posteriors.Max(1)).Sum();
      out = posteriors.ArgMax(1);
      return lp;
     }
   //+------------------------------------------------------------------+
   //| viterbi implementation                                           |
   //+------------------------------------------------------------------+
   double            viterbi(vector &startp, matrix &trans, matrix &dens, vector &out)
     {
      vector logstartp = log(startp);
      matrix logtrans = log(trans);
      matrix logdens = dens.Transpose();

      double logprob = 0;
      ulong ns = logdens.Rows();
      ulong nc = logdens.Cols();

      if(out.Size()<ns)
         out.Resize(ns);

      matrix vit(ns,nc);
      for(ulong i = 0; i<nc; i++)
         vit[0][i] = logstartp[i] + logdens[0][i];

      for(ulong t = 1; t<ns; t++)
        {
         for(ulong i =0; i<nc; i++)
           {
            double max = -DBL_MIN;
            for(ulong j = 0; j<nc; j++)
              {
               max = MathMax(max,vit[t-1][j]+logtrans[j][i]);
              }
            vit[t][i] = max+logdens[t][i];
           }
        }
      out[ns-1] = (double)(vit.Row(ns-1)).ArgMax();
      double prev = out[ns-1];
      logprob = vit[ns-1][long(prev)];
      for(long t = long(ns-2); t>=0; t--)
        {
         for(ulong i =0; i<nc; i++)
           {
            prev = ((vit[t][i]+logtrans[i][long(prev)])>=-DBL_MIN && i>=0)?double(i):double(0);
           }
         out[t] = prev;
        }
      return logprob;
     }
   //+------------------------------------------------------------------+
   //| Calculate the probability density function                       |
   //+------------------------------------------------------------------+
   matrix              find_densities(ulong variables,ulong states,matrix &mdata,matrix &the_means, matrix &covs[])
     {
      matrix out;
      out.Resize(states,mdata.Rows());

      for(ulong state=0 ; state<states ; state++)
        {
         for(ulong i=0 ; i<mdata.Rows() ; i++)
            out[state][i] = mv_normal(variables, mdata.Row(i), the_means.Row(state), covs[state]) ;
        }

      return out;
     }
   //+------------------------------------------------------------------+
   //| Forward algorithm                                                |
   //+------------------------------------------------------------------+

   double            forward(matrix &_transitions)
     {
      double sum, denom, log_likelihood;

      denom = 0.0 ;
      for(ulong i=0 ; i<m_states ; i++)
        {
         alpha[0][i] = m_initprobs[i] * densities[i][0] ;
         denom += alpha[0][i] ;
        }

      log_likelihood = log(denom) ;
      for(ulong i=0 ; i<m_states ; i++)
         alpha[0][i] /= denom ;


      for(ulong t=1 ; t<m_samples ; t++)
        {
         denom = 0.0 ;
         for(ulong i=0 ; i<m_states ; i++)
           {
            ulong trans_ptr = i;
            sum = 0.0 ;
            for(ulong j=0 ; j<m_states ; j++)
              {
               sum += alpha[t-1][j] * _transitions.Flat(trans_ptr);
               trans_ptr += m_states ;
              }
            alpha[t][i] = sum * densities[i][t] ;
            denom += alpha[t][i] ;
           }
         log_likelihood += log(denom) ;
         for(ulong i=0 ; i<m_states ; i++)
            alpha[t][i] /= denom ;
        }

      return log_likelihood ;

     }
   //+------------------------------------------------------------------+
   //| Backward algorithm                                               |
   //+------------------------------------------------------------------+
   double            backward(void)
     {
      double sum, denom, log_likelihood ;

      denom = 0.0 ;
      for(ulong i=0 ; i<m_states ; i++)
        {
         beta[(m_samples-1)][i] = 1.0 ;
         denom += beta[(m_samples-1)][i] ;
        }

      log_likelihood = log(denom) ;
      for(ulong i=0 ; i<m_states ; i++)
         beta[(m_samples-1)][i] /= denom ;

      for(long t=long(m_samples-2) ; t>=0 ; t--)
        {
         denom = 0.0 ;
         for(ulong i=0 ; i<m_states ; i++)
           {
            sum = 0.0 ;
            for(ulong j=0 ; j<m_states ; j++)
               sum += m_transition[i][j] * densities[j][t+1] * beta[(t+1)][j] ;
            beta[t][i] = sum ;
            denom += beta[t][i] ;
           }
         log_likelihood += log(denom) ;
         for(ulong i=0 ; i<m_states ; i++)
            beta[t][i] /= denom ;
        }

      sum = 0.0 ;
      for(ulong i=0 ; i<m_states ; i++)
         sum += m_initprobs[i] * densities[i][0] * beta[0][i] ;

      return log(sum) + log_likelihood ;
     }

public:
   //+------------------------------------------------------------------+
   //| constructor                                                      |
   //+------------------------------------------------------------------+

                     HMM(void)
     {
      trained =false;

      m_hmm_mode = MODE_LOG;
      m_decode_mode = MODE_VITERBI;
      m_mincovar = 1.e-7;
     }
   //+------------------------------------------------------------------+
   //| desctructor                                                      |
   //+------------------------------------------------------------------+

                    ~HMM(void)
     {

     }

   //+------------------------------------------------------------------+
   //| Load model data from regular file                                |
   //+------------------------------------------------------------------+
   bool               load(string file_name)
     {
      trained = false;
      CFileTxt modelFile;
      CJAVal js;
      ResetLastError();

      if(modelFile.Open(file_name,FILE_READ|FILE_COMMON,0)==INVALID_HANDLE)
        {
         Print(__FUNCTION__," failed to open file ",file_name," .Error - ",::GetLastError());
         return false;
        }
      else
        {
         if(!js.Deserialize(modelFile.ReadString()))
           {
            Print("failed to read from ",file_name,".Error -",::GetLastError());
            return false;
           }
         trained = fromJSON(js);
        }
      return trained;
     }
   //+------------------------------------------------------------------+
   //|Predict the state given arbitrary input variables                 |
   //+------------------------------------------------------------------+

   matrix            predict_state_probs(matrix &inputs)
     {
      ResetLastError();

      if(!trained)
        {
         Print(__FUNCTION__, " Call fit() to estimate the model parameters");
         matrix::Zeros(1, m_states);
        }

      if(inputs.Rows()<2 || inputs.Cols()<m_vars)
        {
         Print(__FUNCTION__, " invalid matrix size ");
         matrix::Zeros(1, m_states);
        }

      matrix probs;
      compute_posteriors(inputs,probs,m_hmm_mode);

      return probs;
     }
   //+------------------------------------------------------------------+
   //|Predict the state sequence of arbitrary input variables           |
   //+------------------------------------------------------------------+
   vector            predict_state_sequence(matrix &inputs, ENUM_DECODE_METHOD decoder=WRONG_VALUE)
     {
      ResetLastError();

      if(!trained)
        {
         Print(__FUNCTION__, " Call fit() to estimate the model parameters");
         matrix::Zeros(1, m_states);
        }

      if(inputs.Rows()<2 || inputs.Cols()<m_vars)
        {
         Print(__FUNCTION__, " invalid matrix size ");
         vector::Zeros(1);
        }

      vector seq = vector::Zeros(inputs.Rows());
      ENUM_DECODE_METHOD decm;
      if(decoder!=WRONG_VALUE)
         decm = decoder;
      else
         decm = m_decode_mode;

      switch(decm)
        {
         case MODE_VITERBI:
           {
            matrix d = find_densities(m_vars,m_states,inputs,m_means,m_covars);
            viterbi(m_initprobs,m_transition,d,seq);
            break;
           }
         case MODE_MAP:
           {
            map(inputs,seq,m_hmm_mode);
            break;
           }
        }

      return seq;
     }
   //+------------------------------------------------------------------+
   //| get the loglikelihood of the model                             |
   //+------------------------------------------------------------------+

   double            get_likelihood(matrix &data)
     {
      ResetLastError();

      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return EMPTY_VALUE;
        }

      matrix dens = find_densities(m_vars,m_states,data,m_means,m_covars);
      matrix alfa;
      vector sc;

      switch(m_hmm_mode)
        {
         case MODE_LOG:
            likelihood = forwardlog(m_initprobs,m_transition,dens,alfa);
            break;
         case MODE_SCALING:
            likelihood = forwardscaling(m_initprobs,m_transition,dens,alfa,sc);
            break;
        }

      return likelihood;
     }
   //+------------------------------------------------------------------+
   //| get the initial state probabilities of the model          |
   //+------------------------------------------------------------------+

   vector            get_init_probs(void)
     {
      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return vector::Zeros(1);
        }
      return m_initprobs;
     }
   //+------------------------------------------------------------------+
   //| get the probability transition matrix                            |
   //+------------------------------------------------------------------+

   matrix            get_transition_matrix(void)
     {
      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return matrix::Zeros(1,1);
        }
      return m_transition;
     }
   //+------------------------------------------------------------------+
   //|get the state means matrix                                        |
   //+------------------------------------------------------------------+

   matrix            get_means(void)
     {
      if(!trained)
        {
         Print(__FUNCTION__," invalid call ");
         return matrix::Zeros(1,1);
        }
      return m_means;
     }

   //+------------------------------------------------------------------+
   //| get the covariance matrix for a particular state                 |
   //+------------------------------------------------------------------+

   matrix            get_covar_matrix_for_state_at(ulong state_index)
     {
      if(!trained || state_index>m_states)
        {
         Print(__FUNCTION__," invalid call ");
         return matrix::Zeros(1,1);
        }
      return m_covars[state_index];
     }
   //+------------------------------------------------------------------+
   //|  get the number of features for the model                |
   //+------------------------------------------------------------------+
   ulong             get_num_features(void)
     {
      return m_vars;
     }
  };


//+------------------------------------------------------------------+

Após criar uma instância da classe HMM, chamaríamos o método "load()" com um nome de arquivo específico.

//---declare object
   HMM hmm;
//--load exampleHMM model from json file
   if(!hmm.load("exampleHMM.json"))
     {
      Print("error loading model");
      return;
     }

Se os parâmetros do modelo forem lidos com sucesso, o método retornará verdadeiro.

Depois que um modelo for carregado, podemos obter os estados ocultos e as probabilidades de estado para um conjunto específico de observações. No entanto, é importante notar que a implementação de todos os algoritmos descritos anteriormente no texto é ligeiramente diferente. Em vez de usar verossimilhanças brutas, o código utiliza o log dos valores brutos para garantir a estabilidade numérica. Portanto, temos log-verossimilhanças em vez de verossimilhanças. Isso também significa que em qualquer lugar onde a multiplicação é necessária, devemos usar adição, já que estamos lidando com o log dos valores.

O método get_likelihood() da classe HMM retorna a log-verossimilhança para um conjunto de observações com base nos parâmetros do modelo carregado. É calculado usando o algoritmo forward. O método "predict_state_probs()" calcula as probabilidades de estado para cada observação fornecida como entrada. Este método retorna uma matriz onde cada linha representa as probabilidades de estado para uma observação.

Por outro lado, o método "predict_state_sequence()" retorna um vetor representando o estado para cada amostra fornecida como entrada. Por padrão, ele usa o algoritmo de Viterbi para calcular a sequência de estados mais provável. No entanto, também é possível selecionar a técnica simples "map", imitando o comportamento do método "decode()" do GaussianHMM.

A classe "HMM" fornece métodos getter para extrair os parâmetros de um modelo carregado:

• "get_means()": Retorna a matriz de médias usada para determinar as densidades de probabilidade
• "get_covar_matrix_for_state_at()": Obtém a matriz de covariância completa para um estado específico
• "get_transition_matrix()": Retorna as probabilidades de transição como uma matriz
• "get_init_probs()": Retorna um vetor das probabilidades iniciais de estado do modelo
• "get_num_features()": Retorna um valor unsigned long representando o número de variáveis esperadas como entrada para o modelo. Isso significa que qualquer matriz fornecida como entrada para "predict_state_probs()", "predict_state_sequence()" e "get_likelihood()" deve ter esse número de colunas e pelo menos 2 linhas.

O script saveHMM.py treina um HMM com base em um conjunto de dados aleatório.. Inclui a definição da função "hmm2json()", que é responsável por salvar os parâmetros do modelo final em um arquivo json. Os dados consistem em 10 linhas e 5 colunas. Uma instância da classe GaussianHMM é criada e o HMM é treinado nos dados aleatórios. Após ajustar o modelo, "hmm2json()" é chamado para salvar os parâmetros do modelo em um arquivo json. Em seguida, a log-verossimilhança, os estados ocultos e as probabilidades de estado são impressos.

# Copyright 2024, MetaQuotes Ltd.
# https://www.mql5.com
from hmmlearn import hmm
import numpy as np
import pandas as pd
import json 


assumed_states = 2 #number of states of process
maxhmm_iters = 10000 #maximum number of iterations for optimization procedure

def hmm2json(hmm_model, filename):
    """
    function save a GaussianHMM model to json format 
    readable from MQL5 code.
    param: hmm_model should an instance of GaussianHMM
    param: string. filename or path to file where HMM 
    parameters will be written to
    """
    if hmm_model.__class__.__name__ != 'GaussianHMM':
        raise TypeError(f'invalid type supplied')
    if len(filename) < 1 or not isinstance(filename,str):
        raise TypeError(f'invalid filename supplied')
    jm  = {
            "numstates":hmm_model.n_components,
            "numvars":hmm_model.n_features,
            "algorithm":str(hmm_model.algorithm),
            "implementation":str(hmm_model.implementation), 
            "initprobs":hmm_model.startprob_.tolist(),
            "means":hmm_model.means_.tolist(),
            "transitions":hmm_model.transmat_.tolist(),
            "covars":hmm_model.covars_.tolist()
          }
    with open(filename,'w') as file:
        json.dump(jm,file,indent=None,separators=(',', ':')) 
    return 
#dataset to train model on    
dataset = np.array([[0.56807844,0.67179966,0.13639585,0.15092627,0.17708295],
                   [0.62290044,0.15188847,0.91947761,0.29483647,0.34073613],
                   [0.47687505,0.06388765,0.20589139,0.16474974,0.64383775],
                   [0.25606858,0.50927144,0.49009671,0.0284832,0.37357852],
                   [0.95855305,0.93687549,0.88496015,0.48772751,0.10256193],
                   [0.36752403,0.5283874 ,0.52245909,0.77968798,0.88154157],
                   [0.35161822,0.50672902,0.7722671,0.56911901,0.98874104],
                   [0.20354888,0.82106204,0.60828044,0.13380222,0.4181293,],
                   [0.43461371,0.60170739,0.56270993,0.46426138,0.53733481],
                   [0.51646574,0.54536398,0.03818231,0.32574409,0.95260478]])  
#instantiate an HMM and train on dataset
model = hmm.GaussianHMM(assumed_states,n_iter=maxhmm_iters,covariance_type='full',random_state=125, verbose=True).fit(dataset)  
#save the model to the common folder of Metatrader 5 install
hmm2json(model,r'C:\Users\Zwelithini\AppData\Roaming\MetaQuotes\Terminal\Common\Files\exampleHMM.json')
#get the state probabilities and log likelihood
result = model.score_samples(dataset)
print("log_likelihood " ,result[0]) #print the loglikelihood
print("state sequence ", model.decode(dataset)[1]) #print the state sequence of dataset
print("state probs ", result[1]) #print the state probabilities 

O script correspondente do MetaTrader 5, testHMM.mq5, foi projetado para carregar o arquivo JSON criado por saveHMM.py. A ideia é reproduzir a log-verossimilhança, os estados ocultos e as probabilidades de estado gerados por saveHMM.py.

//+------------------------------------------------------------------+
//|                                                      TestHMM.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<hmmlearn.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- random dataset equal to that used in corresponding python script saveHMM.py
   matrix dataset =
     {
        {0.56807844,0.67179966,0.13639585,0.15092627,0.17708295},
        {0.62290044,0.15188847,0.91947761,0.29483647,0.34073613},
        {0.47687505,0.06388765,0.20589139,0.16474974,0.64383775},
        {0.25606858,0.50927144,0.49009671,0.0284832,0.37357852},
        {0.95855305,0.93687549,0.88496015,0.48772751,0.10256193},
        {0.36752403,0.5283874,0.52245909,0.77968798,0.88154157},
        {0.35161822,0.50672902,0.7722671,0.56911901,0.98874104},
        {0.20354888,0.82106204,0.60828044,0.13380222,0.4181293},
        {0.43461371,0.60170739,0.56270993,0.46426138,0.53733481},
        {0.51646574,0.54536398,0.03818231,0.32574409,0.95260478}
     };
//---declare object
   HMM hmm;
//--load exampleHMM model from json file
   if(!hmm.load("exampleHMM.json"))
     {
      Print("error loading model");
      return;
     }
//--get the log likelihood of the model
   double lk = hmm.get_likelihood(dataset);
   Print("LL ", lk);
//-- get the state probabilities for a dataset
   matrix probs = hmm.predict_state_probs(dataset);
   Print("state probs ", probs);
//---get the hidden states for the provided dataset
   vector stateseq = hmm.predict_state_sequence(dataset);
   Print("state seq ", stateseq);
  }
//+------------------------------------------------------------------+

Os resultados da execução de ambos os scripts são mostrados abaixo.

Saída de saveHMM.py.

KO      0       15:29:18.866    saveHMM (DEX 600 UP Index,M5)   log_likelihood  47.90226114316213
IJ      0       15:29:18.866    saveHMM (DEX 600 UP Index,M5)   state sequence  [0 1 1 1 1 0 0 1 0 0]
ED      0       15:29:18.866    saveHMM (DEX 600 UP Index,M5)   state probs  [[1.00000000e+000 1.32203104e-033]
RM      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
JR      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
RH      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
JM      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
LS      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [1.00000000e+000 5.32945369e-123]
EH      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [1.00000000e+000 8.00195599e-030]
RN      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [0.00000000e+000 1.00000000e+000]
HS      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [1.00000000e+000 1.04574121e-027]
RD      0       15:29:18.867    saveHMM (DEX 600 UP Index,M5)    [9.99999902e-001 9.75116254e-008]]

Conteúdo do arquivo JSON salvo.

{"numstates":2,"numvars":5,"algorithm":"viterbi","implementation":"log","initprobs":[1.0,8.297061845628157e-28],"means":[[0.44766002665812865,0.5707974904960126,0.406402863181157,0.4579477485782787,0.7074610252191268],[0.5035892002511225,0.4965970189510691,0.6217412486192438,0.22191983002481444,0.375768737249644]],"transitions":[[0.4999999756220927,0.5000000243779074],[0.39999999999999913,0.6000000000000008]],"covars":[[[0.009010166768420797,0.0059122234200326374,-0.018865453701221935,-0.014521967883281419,-0.015149047353550696],[0.0059122234200326374,0.0055414217505728725,-0.0062874071503534424,-0.007643976931274206,-0.016093347935464856],[-0.018865453701221935,-0.0062874071503534424,0.0780495488091017,0.044115693492388836,0.031892068460887116],[-0.014521967883281419,-0.007643976931274206,0.044115693492388836,0.04753113728071052,0.045326684356283],[-0.015149047353550696,-0.016093347935464856,0.031892068460887116,0.045326684356283,0.0979523557527634]],[[0.07664631322010616,0.01605057520615223,0.042602194598462206,0.043095659393111246,-0.02756159799208612],[0.01605057520615223,0.12306893856632573,0.03943267795353822,0.019117932498522734,-0.04009804834113386],[0.042602194598462206,0.03943267795353822,0.07167474799610704,0.030420143149584727,-0.03682040884824712],[0.043095659393111246,0.019117932498522734,0.030420143149584727,0.026884283954788642,-0.01676189860422705],[-0.02756159799208612,-0.04009804834113386,-0.03682040884824712,-0.01676189860422705,0.03190589647162701]]]}

Saída de testHMM.mq5.

HD      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)   LL 47.90226114316213
EO      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)   state probs [[1,1.322031040402482e-33]
KP      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
KO      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
KF      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
KM      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
EJ      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [1,5.329453688054051e-123]
IP      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [1,8.00195599043147e-30]
KG      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0,1]
ES      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [1,1.045741207369424e-27]
RQ      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)    [0.999999902488374,9.751162535898832e-08]]
QH      0       15:30:51.727    TestHMM (DEX 600 UP Index,M5)   state seq [0,1,1,1,1,0,0,1,0,0]

Conclusão

Os HMMs são ferramentas estatísticas poderosas para modelagem e análise de dados sequenciais. Sua capacidade de capturar os estados ocultos subjacentes que impulsionam as sequências observadas os torna valiosos para tarefas envolvendo séries temporais, como dados financeiros. Apesar de suas vantagens, os HMMs não estão isentos de limitações. Eles dependem da suposição de Markov de primeira ordem, que pode ser excessivamente simplista para dependências complexas. As demandas computacionais para treinamento e inferência, especialmente para grandes espaços de estados, e o potencial para sobreajuste são desafios significativos.. Além disso, selecionar o número ideal de estados e inicializar os parâmetros do modelo requer uma consideração cuidadosa e pode impactar o desempenho. No entanto, os HMMs continuam sendo um método fundamental na modelagem de sequências, oferecendo uma estrutura robusta para muitas aplicações práticas. Com os avanços contínuos e abordagens híbridas que combinam HMMs com modelos mais flexíveis, sua utilidade continua a evoluir. Para os praticantes, entender tanto as capacidades quanto as limitações dos HMMs é essencial para aproveitar efetivamente seu potencial no desenvolvimento de negociações automatizadas.

Todo o código descrito no artigo está anexado abaixo. Cada um dos arquivos de código-fonte é descrito na tabela.

Arquivo	Descrição
Mql5\Python\script\saveHMM.py	Demonstra o treinamento e salvamento de um modelo oculto de Markov, contendo a definição da função hmm2json()
Mql5\include\hmmlearn.mqh	Contém a definição da classe HMM que permite a importação de HMMs treinados em Python para uso em MQL5
Mql5\script\testHMM.mq5	Script MT5 demonstrando como carregar um HMM salvo