
Redes neurais de maneira fácil (Parte 92): Previsão adaptativa nas áreas de frequência e tempo
Introdução
As áreas de tempo e frequência são duas representações fundamentais usadas para análise de dados de séries temporais. Na área de tempo, a análise se concentra nas mudanças de amplitude ao longo do tempo, o que permite identificar dependências locais e processos transitórios dentro do sinal. Por outro lado, a análise na área de frequência foca na representação das séries temporais em termos de seus componentes de frequência, proporcionando uma compreensão das dependências globais e características espectrais dos dados. Combinar as vantagens de ambas as áreas é uma abordagem promissora para resolver o problema da mistura de diferentes propriedades periódicas em séries temporais reais. E aqui enfrentamos o desafio de combinar eficazmente as vantagens das áreas de tempo e frequência.
Em comparação com os avanços na área de tempo, a área de frequência ainda possui muitas áreas inexploradas. Nos últimos artigos, conhecemos alguns exemplos de uso da área de frequência para um melhor tratamento das dependências globais das séries temporais. A previsão direta na área de frequência permite utilizar mais informações espectrais para aumentar a precisão das previsões de séries temporais. No entanto, existem alguns problemas associados à previsão direta do espectro na área de frequência. Um desses problemas é a possível incompatibilidade das características de frequência entre o espectro dos dados analisados conhecidos e o espectro completo da série temporal estudada, que surge do uso da Transformada Discreta de Fourier (DFT). Essa incompatibilidade dificulta a representação exata de informações sobre frequências específicas em todo o espectro dos dados brutos, o que leva a imprecisões nas previsões.
Outro problema é como extrair de forma eficaz informações sobre combinações de frequências. A extração das características espectrais é uma tarefa complexa, pois as séries harmônicas, que surgem em grupos dentro do espectro, contêm um volume significativo de informações.
Para resolver os problemas mencionados acima, no artigo "ATFNet: Adaptive Time-Frequency Ensembled Network for Long-term Time Series Forecasting" foi proposto o método ATFNet. Ele inclui módulos nas áreas de tempo e frequência para tratar simultaneamente das dependências locais e globais. Além disso, o artigo apresentou um novo mecanismo de ponderação, que distribui dinamicamente os pesos entre os dois módulos.
Os autores do método propuseram uma ponderação energética das séries harmônicas dominantes, capaz de gerar pesos adequados para os módulos nas áreas de tempo e frequência com base no nível de periodicidade demonstrado pelos dados brutos. Isso permite utilizar de maneira eficaz as vantagens de ambas as áreas ao lidar com séries temporais com diferentes padrões periódicos.
Além disso, os autores do método introduzem o DFT expandido para alinhar o espectro das frequências discretas dos dados brutos com a série temporal completa, o que melhora a precisão da representação de frequências específicas.
Os autores do método implementam um mecanismo de atenção na área de frequência e propõem a atenção espectral complexa (CSA). Essa abordagem permite coletar informações de várias combinações de características de frequência, proporcionando uma maneira eficiente de direcionar a atenção para representações na área de frequência.
O artigo apresenta resultados de experimentos com oito conjuntos de dados reais, segundo os quais o ATFNet apresenta resultados promissores, superando em muitos casos outros métodos modernos de previsão de séries temporais.
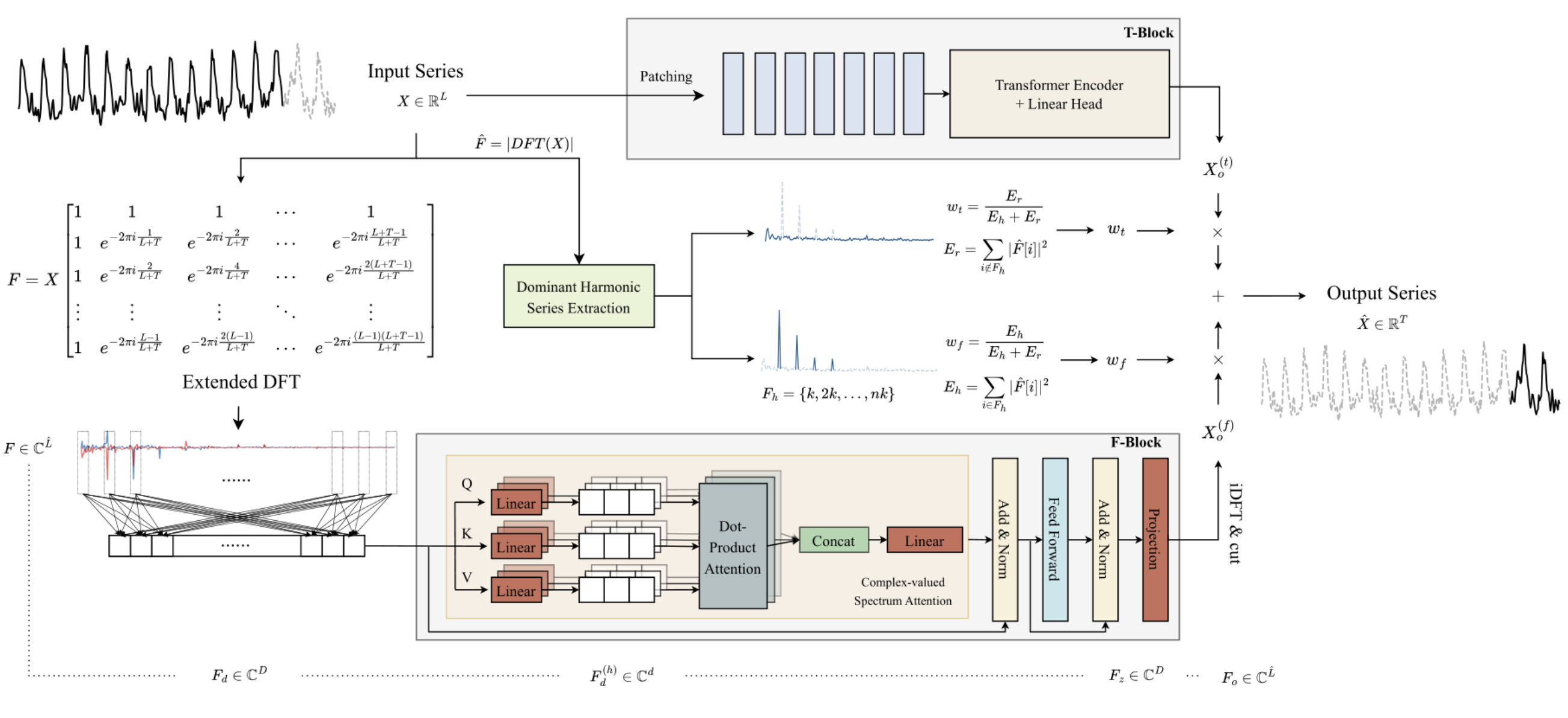
1. Algoritmo ATFNet
Os autores do ATFNet utilizam um esquema de canais independentes, o que impede a mistura dos espectros de diferentes canais. Como os canais podem ter diferentes padrões globais, misturar seus espectros pode prejudicar a eficiência do modelo.
Os dados brutos de uma série temporal unificada são processados diretamente no T-bloco na área de tempo. Como resultado, obtém-se um valor previsto dos próximos pontos da série temporal analisada.
Os autores do método usam a Transformada Discreta de Fourier expandida (DFT) para transformar os dados brutos da série temporal unificada na área de frequência, gerando um espectro de frequências expandido. Em seguida, ocorre a transformação reversa do espectro de volta para a área de tempo utilizando a DFT inversa (iDFT). Como resultado, o F-bloco retorna os valores previstos da série temporal com base nas características de frequência.
Os resultados das previsões dos blocos T e F são combinados usando coeficientes de ponderação adaptativos para obter o resultado final das previsões da série temporal analisada. Esses pesos são determinados com base na ponderação da energia da série de harmônicas dominantes.
O algoritmo pode ser resumido da seguinte forma:
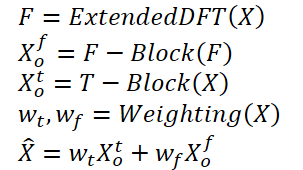
O uso da DFT tradicional pode levar a uma incompatibilidade entre as frequências dos espectros dos dados brutos e da série analisada. Portanto, modelos de previsão baseados na análise de pequenos blocos de dados brutos podem não ter acesso a informações completas e precisas sobre as características de frequência de toda a série temporal analisada. Isso resulta em previsões menos precisas ao construir a série temporal completa.
Para resolver esse problema, os autores do método propõem um DFT expandido, que supera a limitação imposta pelo tamanho dos dados analisados. Isso permite obter o espectro original que corresponde ao grupo de frequências do DFT de toda a série. Em particular, os autores do ATFNet substituem a base exponencial complexa original pela base DFT da série completa:
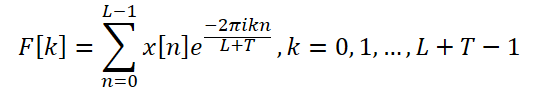
Assim, obtemos um espectro de características de frequência com comprimento L + T, que coincide com o espectro do DFT da série completa analisada (dados brutos + dados previstos). Para séries temporais reais, a simetria conjugada do espectro de saída é uma propriedade importante do DFT. Usando essa propriedade, é possível reduzir os custos computacionais, considerando apenas a primeira metade do espectro das características de frequência dos dados brutos, pois a segunda metade fornece informações redundantes.
A arquitetura do F-Block é baseada no Codificador do Transformer, cujos parâmetros possuem valores complexos. Vale ressaltar que todos os cálculos no F-bloco são realizados no campo dos números complexos.
Além disso, os autores do método utilizam o RevIN para tratar o espectro original das características de frequência do F. Embora o RevIN tenha sido originalmente desenvolvido para eliminar o deslocamento de distribuição na área de tempo, os autores descobriram sua eficácia também na área de frequência. Essa abordagem permite transformar espectros de séries com diferentes características globais em uma distribuição comparável. Antes da análise, as características de frequência do F são normalizadas. Após o processamento dos dados, as características estatísticas da distribuição de frequências são adicionadas de volta.
Como no espectro da área de frequência há poucas dependências cronológicas, os autores não utilizam codificação posicional no F-bloco.
Adicionalmente, os autores aplicaram um mecanismo de atenção modificado com múltiplas cabeças. Para cada cabeça h = 1, 2, ..., H, o espectro incorporado Fd é projetado na dimensão do espectro por meio de projeções treináveis. Em seguida, em cada cabeça é realizado o produto escalar complexo da atenção.
O ATFNet também utiliza camadas de LayerNorm e FeedForward com conexões residuais, similar ao Transformer, que foram expandidas para o campo dos números complexos.
Após M camadas do Codificador, o resultado do bloco de atenção é projetado linearmente ao longo de toda a série. As características de frequência obtidas são projetadas de volta na área de tempo usando a iDFT. Os últimos T pontos (a parte de previsão) são considerados como o resultado do F-bloco.
É importante notar que o F-bloco utiliza uma arquitetura de rede neural totalmente complexa (CVNN).
O T-bloco é responsável por capturar as dependências locais nas séries temporais, que são mais fáceis de tratar na área de tempo. Neste bloco, os autores utilizam o método já conhecido de segmentação de séries temporais. O PatchTST é uma forma intuitiva e eficiente de capturar as dependências locais nas séries temporais. Aqui também é utilizado o RevIN para resolver o problema do deslocamento de distribuição.
As séries temporais periódicas demonstram frequentemente a existência de pelo menos um grupo harmônico em seu espectro de frequência, sendo que o grupo harmônico dominante apresenta a maior concentração de energia do espectro. E, inversamente, essa característica é raramente observada no espectro de séries temporais não periódicas, onde a distribuição de energia é mais uniforme. Os autores do ATFNet mostram que o grau de concentração de energia em uma série harmônica dominante no espectro de frequência pode refletir a periodicidade da série temporal. A relação da energia da série harmônica dominante com a energia total do espectro pode servir como um indicador quantitativo da concentração de energia. Intuitivamente, quando uma série temporal demonstra uma estrutura periódica mais evidente, ela pode ser decomposta em componentes. Consequentemente, tal série temporal possui uma maior concentração de energia dentro da série harmônica dominante.
Com base nessa propriedade, os autores do ATFNet utilizam a fração de energia da série harmônica dominante como um indicador para quantificar o grau de periodicidade da série temporal. Para identificar a série harmônica dominante, a tarefa mais importante é a determinação da frequência fundamental. Aqui, é possível utilizar diversas abordagens:
- Método ingênuo, que determina a frequência com o maior valor de amplitude como a frequência fundamental.
- Algoritmos de determinação de altura com base em regras.
- Algoritmos de determinação de altura com base em dados.
O algoritmo ATFNet permite o uso de qualquer abordagem para determinação da frequência fundamental. Os autores do método consideram esse componente junto com suas harmônicas e calculam a energia total Eh. Em seguida, são determinados os pesos do F-Block, calculando a relação entre a energia da frequência dominante e a energia total do espectro.
Em seu trabalho, os autores realizaram uma série de experimentos para avaliar a eficácia de diferentes métodos de determinação da frequência dominante. Eles concluíram que, em termos de relação entre precisão dos resultados e custos computacionais, o método ingênuo é o líder. Ele demonstra uma precisão admirável na maioria dos conjuntos de dados reais de séries temporais, ao mesmo tempo em que mantém baixos custos computacionais.
Por outro lado, abordagens alternativas enfrentam a questão da complexidade computacional. Além disso, métodos baseados em dados exigem dados marcados sobre o passo, que são muitas vezes difíceis de obter, criando um obstáculo significativo para seu uso prático. Portanto, em seus experimentos, os autores do ATFNet adotam o método ingênuo como padrão para a detecção da frequência fundamental.
A visualização do método ATFNet pelos autores é apresentada abaixo.
2. Implementação de operações básicas com números complexos
Em artigos anteriores, já tivemos uma breve introdução aos números complexos. Eles são convenientes para descrever o espectro de características de frequência. Usamos a parte real para representar a amplitude do sinal e a parte imaginária para registrar o deslocamento de fase. No entanto, ao obter o sinal em forma complexa a partir da DFT, trabalhamos separadamente com as partes real e imaginária. E então, usando a iDFT, transformamos as características de frequência obtidas de volta para a área de tempo.
Apesar da simplicidade de implementação da abordagem de análise das partes real e imaginária como entidades separadas, esse método não é o mais eficiente. Os autores do ATFNet examinam detalhadamente ambas as abordagens para o tratamento de números complexos e concluem que a análise das partes real e imaginária separadamente leva à perda de informações. Portanto, para implementar o método proposto, precisaremos modificar o bloco de atenção para trabalhar com números complexos.
Infelizmente, o OpenCL não oferece suporte nativo para números complexos. Portanto, precisaremos implementar manualmente as operações básicas da álgebra complexa.
Como já mencionado, um número complexo é composto pelas partes real e imaginária:
![]()
onde a é a parte real,
b é a parte imaginária,
i é a unidade imaginária.
E para armazenar um número complexo no OpenCL, é conveniente usar um vetor de 2 elementos float2.
A adição e subtração de números complexos seguem praticamente as mesmas operações vetoriais já implementadas no OpenCL. Portanto, não focaremos nesses pontos.
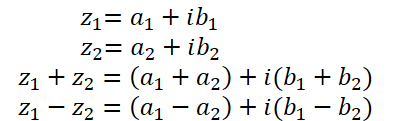
No entanto, a multiplicação de números complexos é um pouco mais complicada.
![]()
Para implementar essa operação, criaremos a função ComplexMul no programa OpenCL.
float2 ComplexMul(const float2 a, const float2 b) { float2 result = 0; result.x = a.x * b.x - a.y * b.y; result.y = a.x * b.y + a.y * b.x; return result; }
Observe que a função recebe como parâmetros dois vetores float2, e retorna o resultado no mesmo formato. Assim, criamos o maior grau possível de verossimilhança no trabalho com variáveis complexas.
A divisão de números complexos é ainda mais complexa:
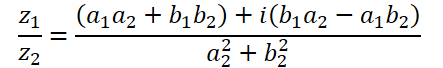
Para essa operação, criaremos a função ComplexDiv.
float2 ComplexDiv(const float2 a, const float2 b) { float2 result = 0; float z = pow(b.x, 2) + pow(b.y, 2); if(z > 0) { result.x = (a.x * b.x + a.y * b.y) / z; result.y = (a.y * b.x - a.x * b.y) / z; } return result; }
O valor absoluto de um número complexo é um número real que indica a energia da componente de frequência:
![]()
Implementaremos isso na função ComplexAbs.
float ComplexAbs(float2 a) { return sqrt(pow(a.x, 2) + pow(a.y, 2)); }
A fórmula para a extração da raiz quadrada de um número complexo é um pouco mais complicada:
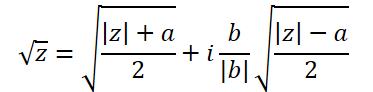
Para isso, criaremos a função ComplexSqrt.
float2 ComplexSqrt(float2 a)
{
float2 result = 0;
float z = ComplexAbs(a);
result.x = sqrt((z + a.x) / 2);
result.y = sqrt((z - a.x) / 2);
if(a.y < 0)
result.y *= (-1);
//---
return result;
}
Lembro que, no processo de implementação do algoritmo de Self-Attention, normalizamos os coeficientes de dependência usando a função SoftMax. E para implementá-la no domínio dos números complexos, precisaremos da exponencial de um número complexo:
![]()
O código será implementado da seguinte forma:
float2 ComplexExp(float2 a)
{
float2 result = exp(clamp(a.x, -20.0f, 20.0f));
result.x *= cos(a.y);
result.y *= sin(a.y);
return result;
}3. Camada de atenção complexa
Acima, realizamos o trabalho preparatório para implementar as operações matemáticas básicas com valores complexos. Agora passamos para a próxima etapa, onde criaremos uma classe de camada de atenção neural usando matemática de números complexos CNeuronComplexMLMHAttention.
A nova classe será baseada na camada de atenção correspondente para valores reais CNeuronMLMHAttentionOCL. A vantagem dessa abordagem é que podemos aproveitar ao máximo o funcional existente e já ajustado do nível superior. Precisamos apenas redefinir os métodos no nível inferior para possibilitar o trabalho com valores complexos. A estrutura da nova classe está apresentada abaixo.
class CNeuronComplexMLMHAttention : public CNeuronMLMHAttentionOCL { protected: virtual bool ConvolutionForward(CBufferFloat *weights, CBufferFloat *inputs, CBufferFloat *outputs, uint window, uint window_out, ENUM_ACTIVATION activ, uint step = 0); virtual bool AttentionScore(CBufferFloat *qkv, CBufferFloat *scores, bool mask = false); virtual bool AttentionOut(CBufferFloat *qkv, CBufferFloat *scores, CBufferFloat *out); virtual bool ConvolutuionUpdateWeights(CBufferFloat *weights, CBufferFloat *gradient, CBufferFloat *inputs, CBufferFloat *momentum1, CBufferFloat *momentum2, uint window, uint window_out, uint step = 0); virtual bool ConvolutionInputGradients(CBufferFloat *weights, CBufferFloat *gradient, CBufferFloat *inputs, CBufferFloat *inp_gradient, uint window, uint window_out, uint activ, uint shift_out = 0, uint step = 0); virtual bool AttentionInsideGradients(CBufferFloat *qkv, CBufferFloat *qkv_g, CBufferFloat *scores, CBufferFloat *gradient); virtual bool SumAndNormilize(CBufferFloat *tensor1, CBufferFloat *tensor2, CBufferFloat *out, int dimension, bool normilize = true, int shift_in1 = 0, int shift_in2 = 0, int shift_out = 0, float multiplyer = 0.5f); public: CNeuronComplexMLMHAttention(void) {}; ~CNeuronComplexMLMHAttention(void) {}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint layers, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronComplexMLMHAttentionOCL; } };
A estrutura apresentada chama a atenção por não declarar nenhum objeto interno ou variável. Durante a implementação da funcionalidade, utilizaremos completamente os objetos e variáveis herdados.
Além disso, na estrutura da classe, apenas a sobrescrita de métodos é declarada no bloco protected. Entre esses métodos, não há nenhum que não tenha sido previamente declarado na classe pai. Aqui, você não encontrará os métodos de alto nível para propagação para frente e reversa, feedForward, calcInputGradients, e updateInputWeights, nos quais geralmente estruturamos o algoritmo da classe. Isso ocorre porque mantemos completamente a sequência de ações do algoritmo da classe pai. No entanto, para trabalhar com valores complexos, precisamos dobrar o tamanho dos buffers de dados, já que a cada valor real é adicionada uma parte imaginária do número complexo. Além disso, é necessário incorporar a matemática dos números complexos no algoritmo. Como você sabe, quase todas as operações matemáticas são realizadas no lado do OpenCL. Portanto, além de sobrescrever os métodos de baixo nível, precisaremos também fazer alterações nos kernels do programa OpenCL.
3.1 Método de inicialização da classe
O trabalho de cada classe começa com sua inicialização. Como já foi dito, não declaramos objetos e variáveis internas na nossa nova classe. Portanto, o construtor e o destrutor da classe permanecem vazios. A inicialização dos objetos herdados é feita no método Init. Como de costume, os parâmetros desse método são recebidos do programa chamador e definem as principais constantes que determinam a arquitetura da classe. E aqui pode-se observar que a estrutura dos parâmetros do método foi totalmente transferida do método equivalente na classe pai. Isso não é surpreendente, pois mantemos completamente o algoritmo básico de atenção e a estrutura da classe pai. No entanto, reescreveremos o corpo do método por completo.
bool CNeuronComplexMLMHAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint layers, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, 2 * window * units_count, optimization_type, batch)) return false;
Dentro do método, chamamos normalmente o método de inicialização da classe pai. Aqui, é importante notar dois pontos:
- Chamamos o método de inicialização, não da classe CNeuronMLMHAttentionOCL diretamente, mas da classe base das nossas camadas neuronais, CNeuronBaseOCL. Isso ocorre porque a inicialização dos objetos internos da classe CNeuronMLMHAttentionOCL seria redundante, já que precisamos sobrescrever todos os buffers com tamanho aumentado para acomodar números complexos.
- Ao chamar o método da classe pai, aumentamos o tamanho da camada em duas vezes, o que está relacionado ao resultado esperado de trabalhar com números complexos.
E, claro, não nos esquecemos de verificar o resultado lógico da execução do método da classe pai.
Após a inicialização bem-sucedida dos objetos herdados da classe base da camada neural, armazenamos os principais parâmetros da arquitetura da camada que estamos criando.
iWindow = window; iWindowKey = fmax(window_key, 1); iUnits = units_count; iHeads = fmax(heads, 1); iLayers = fmax(layers, 1);
O próximo passo é calcular os tamanhos de todos os buffers que serão criados. Aqui, não esquecemos de que estamos trabalhando com números complexos. Portanto, todos os buffers são aumentados em 2 vezes em relação à classe pai.
uint num = 2 * 3 * iWindowKey * iHeads * iUnits; //Size of QKV tensor uint qkv_weights = 2 * 3 * (iWindow + 1) * iWindowKey * iHeads; //Size of weights' matrix of QKV tenzor uint scores = 2 * iUnits * iUnits * iHeads; //Size of Score tensor uint mh_out = 2 * iWindowKey * iHeads * iUnits; //Size of multi-heads self-attention uint out = 2 * iWindow * iUnits; //Size of our tensore uint w0 = 2 * (iWindowKey + 1) * iHeads * iWindow; //Size W0 tensor uint ff_1 = 2 * 4 * (iWindow + 1) * iWindow; //Size of weights' matrix 1-st feed forward layer uint ff_2 = 2 * (4 * iWindow + 1) * iWindow; //Size of weights' matrix 2-nd feed forward layer
Depois, realizamos um loop pelo número de camadas de atenção a serem criadas, no qual inicializamos os objetos internos.
for(uint i = 0; i < iLayers; i++) { CBufferFloat *temp = NULL;
Aqui, começamos criando um loop aninhado de 2 iterações, no qual inicializamos os objetos para gravar os dados da propagação para frente e os gradientes de erro correspondentes.
for(int d = 0; d < 2; d++) { //--- Initilize QKV tensor temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(num, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Tensors.Add(temp)) return false;
Primeiro, criamos o buffer concatenado das entidades Query, Key e Value. Em seguida, conforme o algoritmo de Self-Attention, precisaremos de um buffer para armazenar a matriz dos coeficientes de dependência.
//--- Initialize scores temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(scores, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!S_Tensors.Add(temp)) return false;
No próximo buffer, serão armazenados os resultados da atenção multicabeça:
//--- Initialize multi-heads attention out temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(mh_out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!AO_Tensors.Add(temp)) return false;
O tamanho destes será reduzido posteriormente ao nível do buffer de dados de entrada.
//--- Initialize attention out temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false;
Após o bloco de Atenção, segue o bloco FeedForward, composto por 2 camadas totalmente conectadas:
//--- Initialize Feed Forward 1 temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(4 * out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false; //--- Initialize Feed Forward 2 if(i == iLayers - 1) { if(!FF_Tensors.Add(d == 0 ? Output : Gradient)) return false; continue; } temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false; }
Neste ponto, inicializamos os buffers para gravar os resultados da propagação para frente e os gradientes de erro correspondentes. No entanto, para realizar as operações, precisaremos dos parâmetros de pesos treináveis. Primeiro, preenchemos a matriz de parâmetros treináveis para gerar as entidades Query, Key e Value.
//--- Initilize QKV weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(qkv_weights)) return false; float k = (float)(1 / sqrt(iWindow + 1)); for(uint w = 0; w < qkv_weights; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Weights.Add(temp)) return false;
Depois, geramos os parâmetros da camada de redução dimensional da atenção multicabeça:
//--- Initilize Weights0 temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(w0)) return false; for(uint w = 0; w < w0; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
E adicionamos os parâmetros do bloco FeedForward.
//--- Initilize FF Weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(ff_1)) return false; for(uint w = 0; w < ff_1; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; //--- temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(ff_2)) return false; k = (float)(1 / sqrt(4 * iWindow + 1)); for(uint w = 0; w < ff_2; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
Durante o treinamento dos parâmetros do modelo, serão necessários buffers para armazenar os momentos do treinamento. A quantidade desses buffers depende do método de treinamento dos parâmetros utilizado.
for(int d = 0; d < (optimization == SGD ? 1 : 2); d++) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(qkv_weights, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Weights.Add(temp)) return false; temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(w0, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; //--- Initilize FF Weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(ff_1, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(ff_2, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; } } //--- return true; }
Certificamo-nos de verificar o resultado de cada iteração deste método, pois, durante o treinamento e a execução do modelo, a ausência de qualquer um dos buffers necessários resultará em um erro crítico de execução do programa.
Após a inicialização de todos os objetos internos, finalizamos o método e retornamos o valor lógico das operações concluídas para o programa chamador.
3.2 Propagação para frente
Concluída a inicialização da classe, geralmente passamos para os métodos de propagação para frente. Embora o algoritmo de alto nível seja herdado da classe pai, ainda precisamos realizar alguns ajustes nos métodos de propagação para frente no nível inferior. Aqui, seguiremos a sequência do algoritmo Self-Attention.
Os dados de entrada da camada são primeiro transformados em entidades Query, Key e Value. Para gerá-las, utilizamos no passado o kernel de propagação para frente da camada convolucional na classe pai. Nesta implementação, seguiremos a mesma abordagem. No entanto, para trabalhar com variáveis complexas, precisaremos criar um novo kernel FeedForwardComplexConv no lado do programa OpenCL.
Nos parâmetros do kernel, passamos ponteiros para 3 buffers de dados: a matriz de parâmetros treináveis, os dados de entrada e o buffer para armazenar os resultados.
__kernel void FeedForwardComplexConv(__global float2 *matrix_w, __global float2 *matrix_i, __global float2 *matrix_o, int inputs, int step, int window_in, int activation ) { size_t i = get_global_id(0); size_t out = get_global_id(1); size_t w_out = get_global_size(1);
Observe que, no lado do programa principal, continuamos a usar buffers de dados do tipo float, mas com tamanho aumentado. Porém, no kernel do lado do OpenCL, os buffers de dados são declarados como tipo float2. Esse é o mesmo tipo de dados que utilizamos anteriormente ao criar as funções para variáveis complexas.
No corpo do método, identificamos o fluxo atual no espaço bidimensional de tarefas. A primeira dimensão se refere ao elemento na sequência de resultados, e a segunda dimensão ao filtro utilizado. No nosso caso, ele apontará para a posição no vetor concatenado das entidades, descrevendo um elemento da sequência analisada.
Com base nos dados recebidos, determinamos o deslocamento nos buffers de dados:
int w_in = window_in; int shift_out = w_out * i; int shift_in = step * i; int shift = (w_in + 1) * out; int stop = (w_in <= (inputs - shift_in) ? w_in : (inputs - shift_in));
E configuramos o loop para calcular o produto dos vetores:
float2 sum = matrix_w[shift + w_in]; for(int k = 0; k <= stop; k ++) sum += ComplexMul(matrix_i[shift_in + k], matrix_w[shift + k]);
Observe que, para calcular o produto de duas variáveis complexas, utilizamos a função ComplexMul criada anteriormente. A soma dos valores é realizada com operações vetoriais básicas.
Além disso, devido à declaração do tipo vetorial float2 para o buffer de dados, acessamos os elementos como se fossem buffers de dados reais, sem a necessidade de ajuste de deslocamento. Em cada operação, dois elementos — a parte real e a parte imaginária do número complexo — são extraídos do buffer simultaneamente.
Em seguida, verificamos o valor calculado. E, em caso de estouro da variável, alteramos seu valor para "0":.
if(isnan(sum.x) || isnan(sum.y) || isinf(sum.x) || isinf(sum.y)) sum = (float2)0;
Agora, resta-nos calcular a função de ativação e salvar o valor no buffer de resultados.
switch(activation) { case 0: sum = ComplexTanh(sum); break; case 1: sum = ComplexDiv((float2)(1, 0), (float2)(1, 0) + ComplexExp(-sum)); break; case 2: if(sum.x < 0) sum.x *= 0.01f; if(sum.y < 0) sum.y *= 0.01f; break; default: break; } matrix_o[out + shift_out] = sum; }
Para chamar o kernel criado no lado do programa principal, sobrescreveremos o método CNeuronComplexMLMHAttention::ConvolutionForward. É importante notar que estamos sobrescrevendo o método, e não criando um novo. Portanto, é crucial manter a estrutura completa dos parâmetros do método equivalente na classe pai. A sobrescrita do método nos permitirá chamá-lo a partir do método de propagação para frente da classe pai, sem realizar ajustes adicionais.
bool CNeuronComplexMLMHAttention::ConvolutionForward(CBufferFloat *weights, CBufferFloat *inputs, CBufferFloat *outputs, uint window, uint window_out, ENUM_ACTIVATION activ, uint step = 0) { if(CheckPointer(OpenCL) == POINTER_INVALID || CheckPointer(weights) == POINTER_INVALID || CheckPointer(inputs) == POINTER_INVALID || CheckPointer(outputs) == POINTER_INVALID) return false;
Dentro do método, primeiro verificamos a validade dos ponteiros recebidos para os objetos. Em seguida, verificamos a presença dos buffers de dados no contexto OpenCL.
if(weights.GetIndex() < 0) return false; if(inputs.GetIndex() < 0) return false; if(outputs.GetIndex() < 0) return false; if(step == 0) step = window;
Após a passagem bem-sucedida pelo bloco de controle, definimos o espaço de tarefas para o kernel e o deslocamento correspondente:
uint global_work_offset[2] = {0, 0}; uint global_work_size[2]; global_work_size[0] = outputs.Total() / (2 * window_out); global_work_size[1] = window_out;
Depois, passamos todos os parâmetros necessários para o kernel, com controle rigoroso da execução das operações:
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardComplexConv, def_k_ffc_matrix_w, weights.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardComplexConv, def_k_ffc_matrix_i, inputs.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardComplexConv, def_k_ffc_matrix_o, outputs.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardComplexConv, def_k_ffc_inputs, (int)(inputs.Total() / 2))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardComplexConv, def_k_ffc_step, (int)step)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardComplexConv, def_k_ffc_window_in, (int)window)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardComplexConv, def_k_ffс_window_out, (int)window_out)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardComplexConv, def_k_ffc_activation - 1, (int)activ)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Em seguida, colocamos o kernel na fila de execução e concluímos o método:
if(!OpenCL.Execute(def_k_FeedForwardComplexConv, 2, global_work_offset, global_work_size)) { string error; CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error); printf("Error of execution kernel %s: %s", __FUNCSIG__, error); return false; } //--- return true; }
O algoritmo para colocar os kernels na fila de execução é bastante padronizado. As variações podem ocorrer no tamanho do espaço de tarefas e em variáveis específicas. Para economizar seu tempo e reduzir o volume deste artigo, não entraremos em detalhes sobre os métodos de enfileiramento de kernels. O código completo está disponível no anexo. Agora, daremos mais atenção aos algoritmos de construção dos próprios kernels.
Continuando com o algoritmo Self-Attention. Após a definição das entidades Query, Key e Value, passamos para a determinação dos coeficientes de dependência. Para isso, precisamos multiplicar a matriz Query pela matriz transposta de Key. A matriz resultante é normalizada utilizando a função SoftMax.
Essa funcionalidade é executada no kernel ComplexMHAttentionScore, que será chamado a partir do método CNeuronComplexMLMHAttention::AttentionScore.
__kernel void ComplexMHAttentionScore(__global float2 *qkv, __global float2 *score, int dimension, int mask ) { int q = get_global_id(0); int h = get_global_id(1); int units = get_global_size(0); int heads = get_global_size(1);
Nos parâmetros, o kernel recebe ponteiros para dois buffers de dados: O buffer concatenado das entidades como dados de entrada. E um buffer para armazenar os resultados.
O kernel é executado em um espaço de tarefas bidimensional. A primeira dimensão define a linha da matriz Query, enquanto a segunda se refere à cabeça de atenção ativa. Assim, cada instância do kernel em execução realiza operações para calcular uma linha da matriz de coeficientes de dependência em uma cabeça de atenção.
No corpo do kernel, identificamos o fluxo atual em ambas as dimensões do espaço de tarefas e determinamos os deslocamentos nos buffers de dados:
int shift_q = dimension * (h + 3 * q * heads); int shift_s = units * (h + q * heads);
Em seguida, definimos o coeficiente de normalização dos dados:
float2 koef = (float2)(sqrt((float)dimension), 0); if(koef.x < 1) koef.x = 1;
E realizamos o loop para calcular os coeficientes de dependência:
float2 sum = 0; for(int k = 0; k < units; k++) { if(mask > 0 && k > q) { score[shift_s + k] = (float2)0; continue; }
Aqui, é importante destacar que o algoritmo implementa o mascaramento de dados, o que impede o "vazamento de informações futuras", ou seja, garante que o modelo só analise os coeficientes de dependência em relação aos tokens anteriores. Para os tokens subsequentes, os coeficientes de dependência são ajustados para 0, evitando que o modelo acesse informações do "futuro" durante o treinamento. Esse funcional é ativado por meio de uma flag mask, passado nos parâmetros do kernel.
No loop aninhado, calculamos o próximo elemento do vetor de dependência multiplicando dois vetores.
float2 result = (float2)0; int shift_k = dimension * (h + heads * (3 * k + 1)); for(int i = 0; i < dimension; i++) result += ComplexMul(qkv[shift_q + i], qkv[shift_k + i]);
Calculamos a exponencial do resultado da multiplicação:
result = ComplexExp(ComplexDiv(result, koef));
É crucial verificar o estouro da variável:
if(isnan(result.x) || isnan(result.y) || isinf(result.x) || isinf(result.y)) result = (float2)0;
O resultado é armazenado no buffer de resultados e adicionado à soma total para a normalização posterior.
score[shift_s + k] = result; sum += result; }
No final do kernel, normalizamos a linha calculada da matriz de coeficientes de dependência:
if(ComplexAbs(sum) > 0) for(int k = 0; k < units; k++) score[shift_s + k] = ComplexDiv(score[shift_s + k], sum); }
A matriz de coeficientes de dependência Score assim obtida é usada para calcular os resultados do bloco de atenção. Agora, precisamos multiplicar a matriz de coeficientes obtida pela matriz de entidades Value. Essa operação é realizada no kernel ComplexMHAttentionOut. Semelhante ao anterior, este kernel opera no mesmo espaço de tarefas bidimensional.
__kernel void ComplexMHAttentionOut(__global float2 *scores, __global float2 *qkv, __global float2 *out, int dimension ) { int u = get_global_id(0); int units = get_global_size(0); int h = get_global_id(1); int heads = get_global_size(1);
No corpo do kernel, identificamos o fluxo atual no espaço de tarefas e determinamos os deslocamentos nos buffers de dados:
int shift_s = units * (h + heads * u); int shift_out = dimension * (h + heads * u);
Em seguida, fazemos um sistema de loops aninhados para realizar as operações matemáticas de multiplicação da matriz Value pela linha correspondente de coeficientes de dependência:
for(int d = 0; d < dimension; d++) { float2 result = (float2)0; for(int v = 0; v < units; v++) { int shift_v = dimension * (h + heads * (3 * v + 2)) + d; result += ComplexMul(scores[shift_s + v], qkv[shift_v]); } out[shift_out + d] = result; } }
O resultado da atenção multicabeça assim obtido é consolidado em um único tensor e reduzido em dimensão até o tamanho do tensor de dados brutos. Então, as operações do bloco FeedForward são executadas. Essas operações são realizadas pelo kernel FeedForwardComplexConv, descrito anteriormente. Com isso, concluímos a descrição dos algoritmos dos kernels para as operações de propagação para frente. O código completo de todos os kernels, assim como os métodos que os chamam, pode ser encontrado no anexo.
3.3 Propagação reversa
Após concluir o a funcionalidade da propagação para frente, iniciamos a implementação dos algoritmos de propagação reversa. Esse trabalho é semelhante ao que fizemos anteriormente para a propagação para frente. Aproveitamos os algoritmos de alto nível herdados da classe pai e sobrescrevemos os métodos de baixo nível.
Como mencionado anteriormente, não abordaremos a descrição dos algoritmos de enfileiramento dos kernels para execução. Todos esses processos são bastante padronizados. Vamos dedicar mais atenção à análise dos algoritmos dos kernels no lado do programa OpenCL.
É fácil perceber que o kernel mais utilizado na propagação para frente foi o FeedForwardComplexConv. Esse é um bloco universal, utilizado em várias etapas. Portanto, faz sentido que comecemos a construção dos algoritmos de propagação reversa com o kernel de distribuição do gradiente de erro através desse bloco. Esse funcional será implementado no kernel CalcHiddenGradientComplexConv.
__kernel void CalcHiddenGradientComplexConv(__global float2 *matrix_w, __global float2 *matrix_g, __global float2 *matrix_o, __global float2 *matrix_ig, int outputs, int step, int window_in, int window_out, int activation, int shift_out ) { size_t i = get_global_id(0); size_t inputs = get_global_size(0);
O kernel é executado em um espaço de tarefas unidimensional, com base no número de elementos no buffer de dados de entrada. Cada fluxo individual desse kernel coleta os gradientes de erro de todos os elementos que influenciam o elemento de dados de entrada analisado.
No corpo do kernel, identificamos o fluxo atual e determinamos os deslocamentos nos buffers de dados. Em seguida, declaramos as variáveis locais necessárias:
float2 sum = (float2)0; float2 out = matrix_o[shift_out + i]; int start = i - window_in + step; start = max((start - start % step) / step, 0); int stop = (i + step - 1) / step; if(stop > (outputs / window_out)) stop = outputs / window_out;
Depois, realizamos um sistema de loops, no qual acumulamos o gradiente de erro total, levando em consideração a influência do elemento analisado no resultado geral:
for(int h = 0; h < window_out; h ++) { for(int k = start; k < stop; k++) { int shift_g = k * window_out + h; int shift_w = (stop - k - 1) * step + i % step + h * (window_in + 1); if(shift_g >= outputs || shift_w >= (window_in + 1) * window_out) break; sum += ComplexMul(matrix_g[shift_out + shift_g], matrix_w[shift_w]); } }
Após sair do loop, verificamos o estouro da variável:
if(isnan(sum.x) || isnan(sum.y) || isinf(sum.x) || isinf(sum.y)) sum = (float2)0;
E ajustamos o gradiente de erro com a derivada da função de ativação:
switch(activation) { case 0: sum = ComplexMul(sum, (float2)1.0f - ComplexMul(out, out)); break; case 1: sum = ComplexMul(sum, ComplexMul(out, (float2)1.0f - out)); break; case 2: if(out.x < 0.0f) sum.x *= 0.01f; if(out.y < 0.0f) sum.y *= 0.01f; break; default: break; } matrix_ig[i] = sum; }
O resultado é armazenado no buffer de gradientes de erro da camada anterior.
O próximo kernel que vamos analisar é o kernel de distribuição de gradientes de erro através do bloco de atenção ComplexMHAttentionGradients. Este kernel implementa um algoritmo bastante complexo, que pode ser dividido em três blocos, com base no número de entidades para as quais é calculado o gradiente de erro.
__kernel void ComplexMHAttentionGradients(__global float2 *qkv, __global float2 *qkv_g, __global float2 *scores, __global float2 *gradient) { size_t u = get_global_id(0); size_t h = get_global_id(1); size_t d = get_global_id(2); size_t units = get_global_size(0); size_t heads = get_global_size(1); size_t dimension = get_global_size(2);
Este kernel executa muitas operações. Para reduzir o tempo total de execução durante o treinamento do modelo, tentamos maximizar o paralelismo nas operações de cálculo das variáveis individuais. Para tornar a identificação do fluxo o mais transparente e intuitiva possível, criamos um espaço de tarefas tridimensional para esse kernel. Assim como nos métodos de propagação para frente do bloco de atenção, utilizamos o elemento da sequência e a cabeça de atenção. No entanto, no terceiro eixo do espaço de tarefas, inserimos a posição do elemento no tensor que descreve o elemento da sequência. Assim, apesar do grande número de operações, cada fluxo individual gravará apenas três valores no buffer de resultados. Nesse caso, estamos falando do buffer concatenado de gradientes de erro para as entidades Query, Key e Value.
No corpo do kernel, primeiro identificamos o fluxo no espaço de tarefas e determinamos os deslocamentos nos buffers de dados:
float2 koef = (float2)(sqrt((float)dimension), 0); if(koef.x < 1) koef.x = 1; //--- init const int shift_q = dimension * (heads * 3 * u + h); const int shift_k = dimension * (heads * (3 * u + 1) + h); const int shift_v = dimension * (heads * (3 * u + 2) + h); const int shift_g = dimension * (heads * u + h); int shift_score = h * units; int step_score = units * heads;
Em seguida, calculamos o gradiente de erro para o elemento analisado da matriz Value. Para isso, multiplicamos a coluna correspondente do tensor de gradientes de erro na saída do bloco de atenção pela coluna correspondente da matriz de coeficientes de dependência:
//--- Calculating Value's gradients float2 sum = (float2)0; for(int i = 0; i < units; i++) sum += ComplexMul(gradient[(h + i * heads) * dimension + d], scores[shift_score + u + i * step_score]); qkv_g[shift_v + d] = sum;
No próximo passo, calculamos o gradiente de erro para o elemento analisado da entidade Query. No entanto, é importante lembrar que essa entidade não exerce influência direta sobre o resultado. Sua influência é indireta, por meio da matriz de coeficientes de dependência. Portanto, precisamos primeiro encontrar o gradiente de erro para a linha correspondente da matriz de coeficientes de dependência. A normalização dos dados com a função SoftMax complica ainda mais o processo.
//--- Calculating Query's gradients shift_score = h * units + u * step_score; float2 grad = 0; float2 grad_out = gradient[shift_g + d]; for(int k = 0; k < units; k++) { float2 sc_g = (float2)0; float2 sc = scores[shift_score + k]; for(int v = 0; v < units; v++) sc_g += ComplexMul( ComplexMul(scores[shift_score + v], ComplexMul(qkv[dimension * (heads * (3 * v + 2) + h)], grad_out)), ((float2)(k == v, 0) - sc) );
O gradiente de erro encontrado para um coeficiente de dependência específico é multiplicado pelo elemento correspondente da matriz de entidades Key. Os valores obtidos são somados para acumular o gradiente de erro total:
grad += ComplexMul(ComplexDiv(sc_g, koef), qkv[dimension * (heads * (3 * k + 1) + h) + d]); }
O gradiente de erro acumulado é então gravado no buffer de resultados:
qkv_g[shift_q + d] = grad;
Da mesma forma, determinamos o gradiente de erro para os elementos da entidade Key, que também exerce influência indireta sobre o resultado por meio da matriz de coeficientes de dependência. Neste caso, estamos lidando com uma coluna dessa matriz:
//--- Calculating Key's gradients grad = 0; for(int q = 0; q < units; q++) { shift_score = h * units + q * step_score; float2 sc_g = (float2)0; float2 sc = scores[shift_score + u]; float2 grad_out = gradient[dimension * (heads * q + h) + d]; for(int v = 0; v < units; v++) sc_g += ComplexMul( ComplexMul(scores[shift_score + v], ComplexMul(qkv[dimension * (heads * (3 * v + 2) + h)], grad_out)), ((float2)(u == v, 0) - sc) ); grad += ComplexMul(ComplexDiv(sc_g, koef), qkv[dimension * (heads * 3 * q + h) + d]); } qkv_g[shift_k + d] = grad; }
Com isso, concluímos a análise dos algoritmos de construção dos kernels de propagação reversa para a funcionalidade da camada de atenção complexa. O código completo de todos os métodos e kernels dessa classe está disponível no anexo.
Considerações finais
Neste artigo, abordamos os aspectos teóricos da construção do método ATFNet, que combina abordagens de previsão de séries temporais tanto nas áreas de frequência quanto de tempo.
Na parte prática, realizamos um extenso trabalho de construção da camada de atenção utilizando operações complexas. No entanto, este é apenas um dos objetos do F-bloco do método proposto. No próximo artigo, continuaremos a construção do algoritmo do método ATFNet e analisaremos seus resultados com dados reais.
Referências
- ATFNet: Adaptive Time-Frequency Ensembled Network for Long-term Time Series Forecasting
- Outros artigos da série
Programas usados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA para coleta de exemplos |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA para coleta de exemplos com o método Real-ORL |
| 3 | Study.mq5 | Expert Advisor | EA para treinamento de modelos |
| 4 | StudyEncoder.mq5 | Expert Advisor | EA para treinamento de Codificador |
| 5 | Test.mq5 | Expert Advisor | EA para teste de modelo |
| 6 | Trajectory.mqh | Biblioteca de classes | Estrutura de descrição do estado do sistema |
| 7 | NeuroNet.mqh | Biblioteca de classes | Biblioteca de classes para criação de redes neurais |
| 8 | NeuroNet.cl | Biblioteca | Biblioteca de código do programa OpenCL |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/14996
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Algoritmo de Busca Cooperativa Artificial (Artificial Cooperative Search, ACS)
Algoritmo de Busca Cooperativa Artificial (Artificial Cooperative Search, ACS)
 Integração de Modelos Ocultos de Markov no MetaTrader 5
Integração de Modelos Ocultos de Markov no MetaTrader 5
 Redes neurais de maneira fácil (Parte 93): Previsão adaptativa nas áreas de frequência e tempo (Conclusão)
Redes neurais de maneira fácil (Parte 93): Previsão adaptativa nas áreas de frequência e tempo (Conclusão)
 Visualizações de negociações no gráfico (Parte 1): Escolha do período para análise
Visualizações de negociações no gráfico (Parte 1): Escolha do período para análise
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
As redes neurais são fáceis. Parte 92 😅
É acessível a todos. E o número de artigos mostra a versatilidade e o desenvolvimento constante.