MetaTrader 5 / Sistemas de negociação
English Русский 中文 Español Deutsch 日本語
preview
Redes neurais em trading: Modelo de dupla atenção para previsão de tendências

Redes neurais em trading: Modelo de dupla atenção para previsão de tendências

MetaTrader 5 — Sistemas de negociação |
149 0
Dmitriy Gizlyk
Dmitriy Gizlyk

Introdução

O preço de um instrumento financeiro é uma série temporal altamente volátil. São diversos os fatores que o influenciam, como taxas de juros, inflação, política monetária e o sentimento dos investidores. Modelar a relação entre o preço do instrumento financeiro e esses fatores, bem como prever sua dinâmica, representa um desafio complexo para pesquisadores e investidores.

Há uma vasta quantidade de estudos dedicados à previsão e à análise de séries temporais financeiras. Métodos estatísticos de análise frequentemente pressupõem que as séries temporais sejam geradas por processos lineares, o que os torna pouco eficazes para previsões não lineares. Métodos de aprendizado de máquina e aprendizado profundo têm demonstrado maior sucesso na modelagem de séries temporais financeiras, devido à sua capacidade de representação não linear. Um grande número de estudos foi realizado para extrair características em momentos específicos e utilizá-las para modelagem e previsão de resultados. No entanto, essas abordagens ignoram a interação dos dados e a continuidade de curto prazo das oscilações.

Com o objetivo de suprir essas lacunas, o estudo "A Dual-Attention-Based Stock Price Trend Prediction Model With Dual Features" propôs um método de extração dupla de dados. Ele se baseia tanto em pontos temporais individuais quanto em múltiplos momentos ao longo do tempo. Esse método combina características de mercado de curto prazo com características temporais de longo prazo para melhorar a precisão da previsão. O modelo proposto é baseado na arquitetura "Codificador-Decodificador" e utiliza um mecanismo de atenção nas etapas do Codificador e do Decodificador, que permite identificar as características mais relevantes em séries temporais longas.

Nesse estudo, foi apresentado um novo modelo de previsão de tendências de preços de ações (Trend Prediction Model — TPM), que emprega mecanismos de extração dupla de características e atenção dupla. O objetivo do modelo TPM é prever a direção e a duração dos movimentos de preços das ações. Os autores do método destacam as seguintes principais contribuições das abordagens propostas:

  1. Trata-se de um novo método de extração dupla de características, baseado em diferentes intervalos de tempo, que extrai eficientemente informações importantes do mercado e otimiza os resultados da previsão. No TPM, o método de regressão linear por partes e uma rede neural convolucional são utilizados, respectivamente, para extrair características de mercado de longo e curto prazo de séries temporais financeiras. A descrição das informações do mercado por meio de características duplas melhora o desempenho do modelo de previsão.
  2. Modelo de previsão de tendências de preços de ações (TPM) utilizando a estrutura "Codificador-Decodificador" e o mecanismo de atenção dupla. A facilitade adição de mecanismos de atenção nas etapas do Codificador e do Decodificador permite que o modelo TPM selecione, de forma adaptativa, as características de mercado de curto prazo mais relevantes e as combine com características temporais de longo prazo, aumentando a precisão da previsão.


1. Algoritmo TPM

Após analisar os métodos existentes de previsão de séries temporais, os autores do algoritmo TPM chegaram às seguintes conclusões:

  1. Uma série temporal financeira unidimensional contém informações insuficientes para prever o movimento de preços futuro com um nível necessário de confiança.
  2. Os métodos tradicionais de extração de características são limitados na análise do comportamento do mercado.
  3. O estudo de uma série temporal por meio de uma única rede neural é incompleto.

No método TPM, esses problemas são resolvidos pelo uso dos mecanismos de extração dupla de características e atenção dupla. O algoritmo proposto possui duas fases. Primeiro, é utilizada a regressão linear por partes para segmentar a série temporal financeira e extrair características temporais históricas de longo prazo com base em subsequências de diferentes intervalos de tempo. Já as características espaciais de mercado de curto prazo, baseadas em cada ponto temporal, são geradas por meio de uma rede neural convolucional.

Na segunda fase do TPM, as características duplas extraídas anteriormente são analisadas pelo modelo de previsão de tendências, que tem como base o mecanismo de atenção dupla. O modelo proposto é construído sobre a arquitetura Codificador-Decodificador.

O Codificador é baseado em um bloco LSTM-bloco recorrente, com a adição de um mecanismo de atenção aplicado para extrair adaptativamente as características de mercado de curto prazo mais relevantes.

O Decodificador também é construído utilizando um LSTM-bloco e um mecanismo de atenção, que seleciona e decodifica as características combinadas mais relevantes para prever a tendência dos preços das ações.

Como as informações fornecidas por uma série temporal financeira unidimensional são insuficientes, torna-se difícil modelar e prever a tendência dos preços das ações com base nesses dados. Os autores do método TPM utilizam dados básicos do mercado, como preços de abertura e fechamento do candle, preços máximos e mínimos e volume. E os transformam em uma série de indicadores técnicos.

Ao considerar a continuidade das variações dos dados, o TPM extrai características temporais de longo prazo por meio do método de regressão linear por partes (PLR). Esse método (PLR) reduz a dimensionalidade dos dados e melhora o desempenho computacional.

É evidente que o resultado da segmentação da série temporal depende do limite máximo de erro δ. Tomando os dados do CSI 300 como exemplo, os autores do método utilizam o PLR para segmentar sua série histórica de preços de fechamento. Com um limite de δ igual a 2,0, a série temporal pode ser dividida em 16 subsequências. No entanto, com um limite de δ igual a 4,0, essa mesma série temporal pode ser segmentada em apenas quatro subsequências. Assim, à medida que o valor do limite aumenta, mais oscilações dos dados são ignoradas, resultando em um número menor de subsequências. O valor do limite afeta a confiabilidade das características históricas da série temporal. Cada subsequência representa as oscilações dos dados em um determinado período. A inclinação sm e a duração dm de cada uma são geradas como características temporais de longo prazo para a previsão da tendência dos preços das ações.

Ao considerar a interação entre diferentes dados em um mesmo momento, as características espaciais de mercado de curto prazo em cada passo temporal são extraídas por meio de uma rede neural convolucional (CNN). Para a série temporal financeira analisada, é construída uma matriz de mercado que descreve o mercado de ações. Nessa matriz, cada linha representa uma dimensão dos dados analisados, e o número de linhas é n. enquanto cada coluna representa um ponto temporal. Como a CNN preserva as relações de vizinhança e a localização espacial dos dados originais, ela consegue capturar a relação não linear entre a matriz de mercado e a tendência das ações. e extrair características espaciais da série temporal histórica de curto prazo.

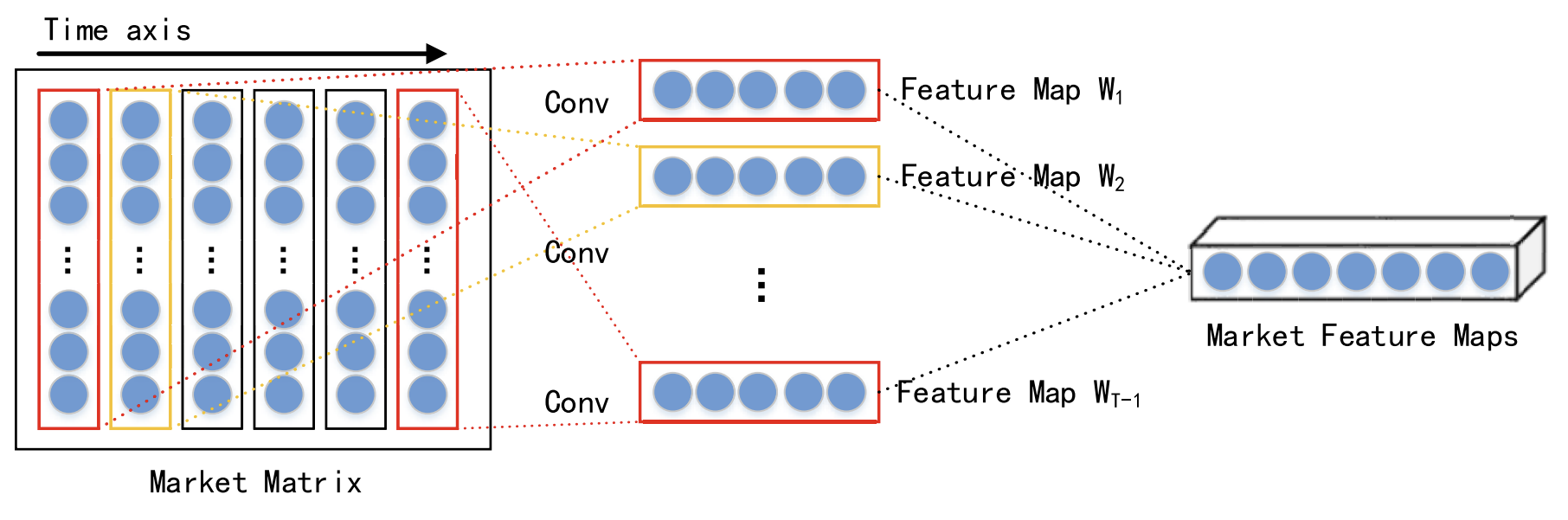
Os autores do método escolhem convoluções de diferentes tamanhos, como 1 × 3 e 1 × 5, para extrair características espaciais de mercado abstratas em múltiplos níveis. A função de ativação não linear escolhida é a ReLU.

Após as camadas de convolução, é aplicada uma camada de agrupamento máximo (max pooling), que reduz o tamanho dos mapas de características e previne o sobreajuste.

Os resultados das várias camadas de convolução e agrupamento máximo são transmitidos para a camada de projeção.

Como mencionado anteriormente, as características de curto e longo prazos extraídas são processadas pelo modelo utilizando a estrutura Codificador-Decodificador. Dentro dessa estrutura, o Codificador comprime as informações originais em um vetor de tamanho fixo, enquanto o Decodificador processa esses vetores para obter o resultado final. No entanto, quando há um excesso de informações de entrada, o Codificador não consegue identificar eficientemente todas as informações relevantes, o que resulta em um pior desempenho do modelo. O mecanismo de atenção pode otimizar esse problema, decodificando o estado oculto dos neurônios correspondentes.

É evidente que o Decodificador com mecanismo de atenção possui uma limitação — ele não consegue selecionar explicitamente os dados de entrada mais relevantes, por isso os autores do método TPM adicionam um mecanismo de atenção tanto na etapa do Codificador quanto na etapa do Decodificador.

A segunda fase do algoritmo TPM baseia-se no mecanismo de atenção dupla. A estrutura Codificador-Decodificador é dividida em duas etapas. Na primeira etapa, o Codificador baseado em LSTM com mecanismo de atenção analisa as características espaciais de mercado de curto prazo extraídas pela CNN. As características de curto prazo relevantes em cada ponto temporal são selecionadas de forma adaptativa e codificadas em vetores.

Na segunda etapa, os vetores codificados e as características temporais de longo prazo extraídas pelo PLR são inseridos no Decodificador baseado em LSTM, que decodifica os vetores e características correspondentes usando o mecanismo de atenção para prever a tendência do mercado de ações. Graças ao mecanismo de atenção dupla, o TPM consegue selecionar, de forma adaptativa, as características espaciais e temporais mais relevantes para a modelagem e a previsão de tendências.

Em cada ponto temporal t, o Codificador analisa a relação entre a característica original Wt e o estado oculto Ht:

onde Ht é o estado oculto do Codificador no momento t, fen(•) é uma função não linear, e ʘen representa os parâmetros do Codificador.

Os autores do método utilizam LSTM como função não linear fen para capturar dependências temporais e formar o Codificador de características de curto prazo. O LSTM é capaz de modelar eficientemente o comportamento dinâmico de séries temporais e evitar problemas de dissipação ou explosão de gradientes em RNN.

Os autores do método introduzem o mecanismo de atenção na etapa do Codificador e dividem as características de entrada WMarket de acordo com a dimensionalidade das características m. O estado oculto Ht-1 e o estado da célula (contexto) Ct-1, calculados no momento t-1, correspondentes à dimensionalidade das características de entrada, são identificados e usados para atualizar as características de entrada no próximo instante t.

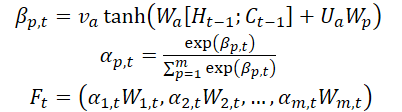
onde va, Wa e Ua são parâmetros, e a função SoftMax é utilizada para calcular a importância αm,t de cada dimensão da característica.

Todas as dimensões de Wt são atualizadas para Ft e inseridas no Codificador. Em seguida, o estado oculto do ponto temporal t é atualizado.

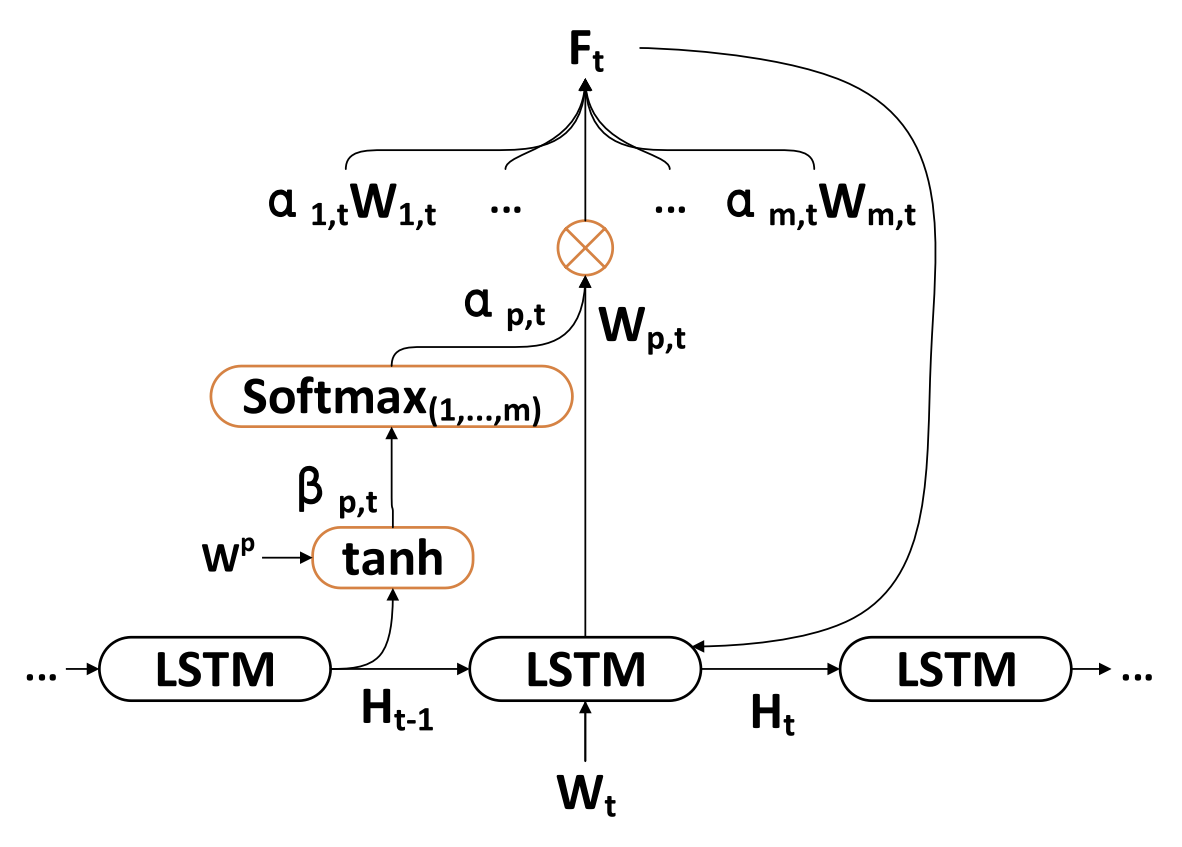
Assim, a cada momento t, é possível selecionar as dimensões relevantes das características espaciais do mercado. atualizar sequencialmente as características de entrada e o estado oculto do Codificador. e gerar o vetor de codificação mais relevante para as características de curto prazo.

O Decodificador é um bloco LSTM utilizado para prever a tendência do mercado de ações. As características temporais de longo prazo ZT-1 são extraídas pelo método PLR.

Em cada momento t, o Decodificador analisa a relação entre o vetor de codificação Wt, a característica de longo prazo Lt e o estado oculto Ht:

onde H't é o estado oculto do Decodificador no instante t, fde(•) é uma função não linear, e ʘde representa os parâmetros do Decodificador.

Os autores do TPM utilizam LSTM como a função não linear fde para capturar dependências temporais e formar o Decodificador de características de longo prazo. O procedimento de cálculo é semelhante ao da etapa do Codificador.

Os autores do TPM introduzem o mecanismo de atenção na etapa do Decodificador para obter estados ocultos relacionados de todas as instâncias temporais do Codificador.

O vetor de contexto, que é inserido no Decodificador, é obtido a partir de todos os estados ocultos do Codificador.

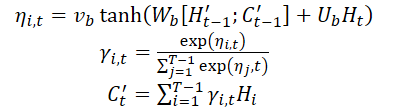
Após obter o vetor de contexto C't, ele é combinado com as características temporais de longo prazo Lt para gerar a característica mista yt:

Com as fórmulas descritas acima, em cada instante t, são escolhidos os estados ocultos mais relevantes do Codificador em todos os pontos temporais e as características temporais de longo prazo para gerar vetores mistos de características.

Em seguida, analisa-se a função de mapeamento não linear F(•) entre a tendência do mercado de ações e as características duplas. Por fim, uma função linear é utilizada para obter a previsão da tendência do mercado de ações no instante T.

Para treinar o modelo, foi utilizado o método de descida do gradiente estocástico com um otimizador de momento. O tamanho do lote de treinamento foi 64 e a taxa de aprendizado foi 0,001.

Como função de perda, foi utilizada a função do erro quadrático com termos de regularização.

A visualização do método TPM desenvolvido pelos autores é apresentada abaixo.


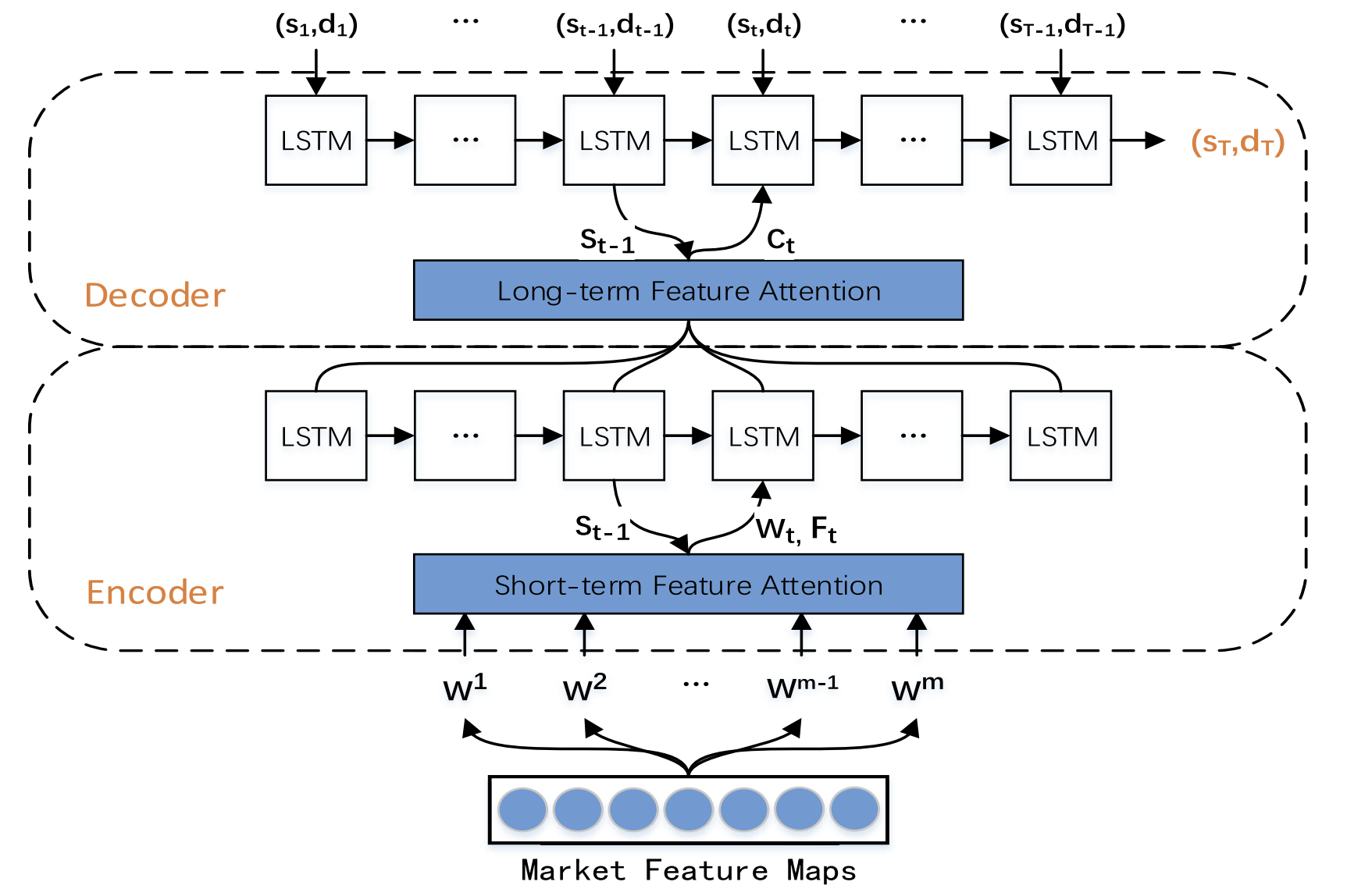
2. Implementação em MQL5

Após analisarmos os aspectos teóricos do método TPM, passamos à parte prática do nosso trabalho, na qual implementamos nossa visão dos conceitos propostos. Como de costume, mantivemos a ideia geral do método apresentado, mas permitimos algumas variações nos detalhes da execução. Naturalmente, isso pode afetar os resultados finais do modelo em diferentes graus.

Começamos, então, com a construção do Codificador.

2.1 Codificador TPM


Implementamos o Codificador de nosso modelo na classe CNeuronTPMCodificador, que herda a funcionalidade base do bloco LSTM previamente criado, CNeuronLSTMOCL. A escolha dessa classe como classe-mãe não é aleatória. Pois, como vimos, o Codificador do TPM é baseado em um bloco LSTM com a adição de mecanismos de atenção.

Além disso, decidimos incluir a extração de características de curto prazo diretamente no Codificador. E essa extração será realizada utilizando o bloco de criação de estrutura piramidal de dados CSCM. No entanto, há um detalhe: anteriormente, usávamos o bloco CSCM para extrair características de séries temporais unitárias. Agora, precisamos modificar ligeiramente o fluxo de dados para extrair características de pontos temporais individuais.

A estrutura geral do Codificador está apresentada abaixo.

class CNeuronTPMEncoder :  public CNeuronLSTMOCL
  {
protected:
   bool                 bTSinRow;
   //---
   CNeuronCSCMOCL       cFeatureExtraction;
   CNeuronBaseOCL       cMemAndHidden;
   CNeuronConcatenate   cConcatenated;
   CNeuronSoftMaxOCL    cSoftMax;
   CNeuronBaseOCL       cAttentionOut;
   CNeuronTransposeOCL  cTranspose;
   CBufferFloat         cTemp;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   //---
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronTPMEncoder(void){};
                    ~CNeuronTPMEncoder(void){};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint variables, uint lenth, uint hidden_size, bool ts_in_row, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual int       Type(void) override       const                      {  return defNeuronTPMEncoder; }
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

Aqui, observamos o conjunto familiar de métodos que podem ser sobrescritos, além de alguns objetos internos, cujo propósito será esclarecido no decorrer da implementação.

Como anteriormente, declaramos todos os objetos internos como estáticos, o que nos permite deixar "vazios" o construtor e o destrutor da classe. A inicialização da instância da nova classe ocorre no método Init.

bool CNeuronTPMEncoder::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                             uint variables, uint lenth, uint hidden_size, bool ts_in_row, 
                             ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronLSTMOCL::Init(numOutputs, myIndex, open_cl, hidden_size, optimization_type, batch))
      return false;
   if(!SetInputs(variables * lenth))
      return false;

Esse método recebe como parâmetros os principais atributos do objeto a ser criado. No nosso caso, são três:

  • variables — número de sequências unitárias na série temporal multimodal analisada;
  • lenth — tamanho da sequência analisada (profundidade do histórico);
  • hidden_size — tamanho do espaço oculto do bloco LSTM.

Além disso, adicionamos a flag ts_in_row, que indica a disposição das sequências unitárias em linhas do tensor de dados de entrada.

No corpo do método, chamamos o método de mesmo nome da classe-mãe, que executa um bloco mínimo de controle dos parâmetros do nível criado e inicializa os objetos herdados.

Aqui também passamos o tamanho do tensor de dados de entrada da classe-mãe, que é o produto do tamanho da sequência unitária pelo número de sequências nos dados de entrada.

Vale destacar que, dentro do bloco LSTM, utilizamos camadas totalmente conectadas e, nesse caso, a forma do tensor de entrada não tem relevância.

O próximo passo é inicializar o bloco de extração de características de curto prazo.

   uint windows[] = {variables, 6, 5, 4};
   if(!cFeatureExtraction.Init(0, 0, OpenCL, windows, lenth, variables, ts_in_row, optimization, batch))
      return false;

Para isso, primeiro definimos os tamanhos das janelas das camadas convolucionais responsáveis pela extração das características e chamamos o método de inicialização do bloco CSCM.

É importante observar que, ao chamar o método de inicialização do bloco CSCM, invertemos os parâmetros referentes ao tamanho das sequências unitárias e ao seu número. Isso se deve à necessidade de extrair características de etapas temporais individuais (barras), em vez de sequências unitárias, conforme originalmente previsto pelo método MSFformer.

O próximo passo é a inicialização dos objetos internos do bloco de atenção. Aqui, primeiro criamos uma camada cujos buffers armazenam a concatenação do estado oculto e do contexto do bloco LSTM da etapa anterior.

   if(!cMemAndHidden.Init(0, 1, OpenCL, hidden_size * 2, optimization, batch))
      return false;

Para calcular os coeficientes de importância das características individuais, utilizamos uma camada de concatenação, cujos resultados são normalizados pela função SoftMax.

   if(!cConcatenated.Init(0, 2, OpenCL, variables * lenth, variables * lenth, hidden_size * 2, optimization, batch))
      return false;
   cConcatenated.SetActivationFunction(TANH);
   if(!cSoftMax.Init(0, 3, OpenCL, variables * lenth, optimization, batch))
      return false;
   cSoftMax.SetHeads(variables);

Vale ressaltar que, neste estágio, a normalização dos dados é realizada dentro das sequências unitárias.

Em seguida, adicionamos uma camada para armazenar os resultados da atenção.

   if(!cAttentionOut.Init(0, 4, OpenCL, variables * lenth, optimization, batch))
      return false;

Se necessário, inicializamos uma camada de transposição dos dados.

   bTSinRow = ts_in_row;
   if(!bTSinRow)
     {
      if(!cTranspose.Init(0, 5, OpenCL, variables, lenth, optimization, iBatch))
         return false;
     }

Também adicionamos um buffer auxiliar para armazenar valores intermediários.

//---
   if(!cTemp.BufferInit(variables * lenth, 0) || !cTemp.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

Após a inicialização bem-sucedida de todos os objetos internos, retornamos o resultado lógico das operações executadas para o programa chamador e finalizamos a execução do método.

Concluída a inicialização do objeto, passamos à construção do algoritmo de propagação para frente da nova classe, que implementamos no método feedForward.

bool CNeuronTPMEncoder::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
//--- FEATURE EXTRACTION
   if(!cFeatureExtraction.FeedForward(NeuronOCL))
      return false;

Como de costume, esse método recebe como parâmetro um ponteiro para o objeto da camada neural anterior. No entanto, neste caso, não verificamos o ponteiro recebido, mas simplesmente o passamos para o método de propagação para frente da camada interna de extração de características de curto prazo. O controle do ponteiro recebido já está implementado no corpo do método chamado.

A próxima etapa é combinar o estado oculto e o contexto do nosso objeto, que foram armazenados após a propagação para frente anterior.

//--- Memory and Hidden
   if(!Concat(m_iHiddenState, m_iMemory, m_iHiddenState, m_iMemory, 
              cMemAndHidden.getOutputIndex(), 1, 1, 0, 0, Neurons()))
      return false;

Com isso, concluímos a etapa de preparação e passamos ao bloco de atenção. onde calculamos os coeficientes de importância das características individuais.

   if(!cConcatenated.FeedForward(cFeatureExtraction.AsObject(), cMemAndHidden.getOutput()))
      return false;
   if(!cSoftMax.FeedForward(cConcatenated.AsObject()))
      return false;
   int map = cSoftMax.getOutputIndex();

Se necessário, transpomos o tensor dos coeficientes de importância.

   if(!bTSinRow)
     {
      if(!cTranspose.FeedForward(cSoftMax.AsObject()))
         return false;
      map = cTranspose.getOutputIndex();
     }

Por fim, multiplicamos os coeficientes calculados elemento a elemento pelas respectivas características de curto prazo. Para essa multiplicação, utilizamos o kernel de propagação para frente da camada Dropout.

Vale lembrar que esse kernel foi originalmente criado para multiplicar os dados de entrada por uma máscara de exclusão de neurônios. Neste caso, usamos os coeficientes de importância como máscara.

Definimos a dimensionalidade do espaço de tarefas.

   uint global_work_offset[1] = {0};
   uint global_work_size[1];
   global_work_size[0] = int(cSoftMax.Neurons() + 3) / 4;

Passamos os parâmetros para o kernel.

   ResetLastError();
   if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_input, cFeatureExtraction.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_map, map))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_out, cAttentionOut.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_Dropout, def_k_dout_dimension, cSoftMax.Neurons()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

E o colocamos na fila de execução.

   if(!OpenCL.Execute(def_k_Dropout, 1, global_work_offset, global_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }

Após a execução do kernel, o buffer da camada cAttentionOut contém as características de curto prazo ajustadas pelos seus respectivos coeficientes de importância. Agora, podemos utilizar a funcionalidade básica do bloco LSTM para representar o tensor de características na saída do nosso Codificador.

//--- LSTM
   if(!CNeuronLSTMOCL::feedForward(cAttentionOut.AsObject()))
      return false;
//---
   return true;
  }

Não nos esquecemos de monitorar o processo de execução das operações em cada etapa. Após a conclusão bem-sucedida, retornamos o resultado lógico para o programa chamador e finalizamos o método.

Depois de implementar os algoritmos de propagação para frente, normalmente passamos à construção dos métodos de propagação reversa. E este caso não é exceção. O próximo passo é implementar o método de distribuição do gradiente do erro para todos os objetos internos e para o tensor de dados de entrada, conforme sua influência no resultado final do modelo. Essa funcionalidade é implementada no método calcInputGradients.

Assim como discutido anteriormente, esse método recebe como parâmetro um ponteiro para o objeto da camada neural anterior.

bool CNeuronTPMEncoder::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

Dentro do método, verificamos imediatamente a validade do ponteiro recebido.

Em seguida, utilizamos a funcionalidade herdada para propagar o gradiente do erro através do algoritmo do bloco LSTM até os resultados do nosso bloco de atenção.

   if(!CNeuronLSTMOCL::calcInputGradients(cAttentionOut.AsObject()))
      return false;

Depois disso, distribuímos o gradiente do erro em duas direções: coeficientes de importância das características e as próprias características. O algoritmo para colocar o kernel na fila de execução é semelhante ao já discutido.

//---
   uint global_work_offset[1] = {0};
   uint global_work_size[1];
   global_work_size[0] = cSoftMax.Neurons();
   ResetLastError();
   if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_f, cFeatureExtraction.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_fg, cTemp.GetIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_s, 
                                 (bTSinRow ? cSoftMax.getOutputIndex() : cTranspose.getOutputIndex())))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_sg, 
                             (bTSinRow ? cSoftMax.getGradientIndex() : cTranspose.getGradientIndex())))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_g, cAttentionOut.getGradientIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_CGConv_HiddenGradient, def_k_cgc_activationf, NeuronOCL.Activation()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_CGConv_HiddenGradient, def_k_cgc_activations, int(None)))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.Execute(def_k_CGConv_HiddenGradient, 1, global_work_offset, global_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }

No entanto, há dois pontos importantes a serem considerados. Primeiro, o buffer para a distribuição dos gradientes dos coeficientes de atenção depende da necessidade de usar a camada de transposição dos coeficientes de importância. E segundo, as características de curto prazo são utilizadas tanto na multiplicação pelos coeficientes de importância quanto no cálculo desses coeficientes. Portanto, nesta fase, armazenamos temporariamente o gradiente do erro das características de curto prazo em um buffer auxiliar.

O próximo passo é transpor, se necessário, o gradiente do erro dos coeficientes de importância das características individuais.

   if(bTSinRow)
     {
      if(!cSoftMax.calcHiddenGradients(cTranspose.AsObject()))
         return false;
     }

Em seguida, propagamos o gradiente do erro pelo bloco de atenção até o nível das características de curto prazo.

   if(!cConcatenated.calcHiddenGradients((CObject*)cSoftMax.AsObject(),(CBufferFloat *)NULL,(CBufferFloat *)NULL) ||
      !DeActivation(cConcatenated.getOutput(), cConcatenated.getGradient(), cConcatenated.getGradient(), 
                                                                            cConcatenated.Activation()))
      return false;
   if(!cFeatureExtraction.calcHiddenGradients(cConcatenated.AsObject(), cMemAndHidden.getOutput(), 
                                                                        cMemAndHidden.getGradient()))
      return false;

E somamos o gradiente do erro das características de curto prazo provenientes dos dois fluxos de informação.

   if(!DeActivation(cFeatureExtraction.getOutput(), GetPointer(cTemp), GetPointer(cTemp), NeuronOCL.Activation()) ||
      !SumAndNormilize(cFeatureExtraction.getGradient(), GetPointer(cTemp), cFeatureExtraction.getGradient(), 1, false))
      return false;

Por fim, propagamos o gradiente do erro até o nível da camada anterior e retornamos o resultado lógico da execução das operações para o programa chamador.

   if(!NeuronOCL.calcHiddenGradients(cFeatureExtraction.AsObject()))
      return false;
//---
   return true;
  }

Após a distribuição do gradiente do erro, resta otimizar os parâmetros do modelo para minimizar o erro total. Essa funcionalidade é implementada no método updateInputWeights, chamando métodos de mesmo nome nos objetos internos que contêm parâmetros treináveis.

bool CNeuronTPMEncoder::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(!CNeuronLSTMOCL::updateInputWeights(cAttentionOut.AsObject()))
      return false;
   if(!cFeatureExtraction.UpdateInputWeights(NeuronOCL))
      return false;
   if(!cConcatenated.UpdateInputWeights(cFeatureExtraction.AsObject(), cMemAndHidden.getOutput()))
      return false;
//---
   return true;
  }

Com isso, concluímos a análise dos algoritmos que implementam a funcionalidade principal da classe do nosso Codificador. O código completo de todos os métodos dessa classe pode ser consultado no anexo. Nele, você também encontrará o código completo de todos os programas utilizados na preparação deste artigo.

2.2 Decodificador TPM


Após a implementação dos algoritmos do Codificador TPM, passamos para a segunda etapa: a construção do Decodificador. Ao analisar os aspectos teóricos do método TPM, você deve ter notado uma grande semelhança entre os algoritmos do Codificador e do Decodificador. No entanto, mesmo pequenas diferenças exigem a criação de uma nova classe.

Assim como o Codificador, a nova classe do nosso Decodificador CNeuronTPM herda da classe do bloco LSTM. Sua estrutura é apresentada a seguir.

class CNeuronTPM :  public CNeuronLSTMOCL
  {
protected:
   CNeuronTPMEncoder    cEncoder;
   CNeuronPLROCL        cFeatureExtraction;
   CNeuronBaseOCL       cMemAndHidden;
   CNeuronConcatenate   cConcatenated;
   CNeuronSoftMaxOCL    cSoftMax;
   CNeuronBaseOCL       cAttentionOut;
   CNeuronConcatenate   cAttAndFeature;
   CBufferFloat         cTemp;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   //---
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronTPM(void){};
                    ~CNeuronTPM(void){};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,

                          uint variables, uint lenth, uint hidden_size, bool ts_in_row, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual int       Type(void) override       const                      {  return defNeuronTPM; }
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

A semelhança com a classe do Codificador discutida anteriormente é facilmente perceptível. Foram adicionados apenas dois objetos internos. E houve uma alteração no tipo da camada de extração de características — no Decodificador, utilizamos PLR para a extração de características de longo prazo.

Você deve ter notado que a classe do Codificador contém uma indicação de sua identidade, mas isso não ocorre no Decodificador. Há um motivo para isso. O Codificador e o Decodificador utilizam os dados de entrada para extrair características de diferentes níveis. Para evitar complicações na estrutura do modelo no nível superior, foi decidido unir o Codificador e o Decodificador em um único bloco. A classe do Codificador, construída anteriormente, foi incorporada como uma camada interna da nova classe, integrando assim o algoritmo TPM a esta estrutura. Isso justifica a nomenclatura CNeuronTPM.

Os parâmetros do método de inicialização da nova classe são idênticos aos do método de inicialização do Codificador discutido anteriormente.

bool CNeuronTPM::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                      uint variables, uint lenth, uint hidden_size, bool ts_in_row, 
                      ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronLSTMOCL::Init(numOutputs, myIndex, open_cl, hidden_size, optimization_type, batch))
      return false;
   if(!SetInputs(hidden_size))
      return false;

No corpo do método, também chamamos o método de inicialização da classe pai, só que o tamanho do tensor de entrada agora corresponde ao tamanho do estado oculto do Codificador. Pois o Decodificador recebe um vetor de características ponderado proveniente do Codificador.

Neste ponto, inicializamos o objeto Codificador.

   if(!cEncoder.Init(0, 0, OpenCL, variables, lenth, hidden_size, ts_in_row, optimization, iBatch))
      return false;

E a camada de extração de características.

   if(!cFeatureExtraction.Init(0, 1, OpenCL, variables, lenth, !ts_in_row, optimization, iBatch))
      return false;

O algoritmo de inicialização dos objetos do bloco de atenção segue o mesmo princípio da inicialização do Codificador, mas há diferenças nos tamanhos dos tensores de entrada.

   if(!cMemAndHidden.Init(0, 2, OpenCL, hidden_size * 2, optimization, iBatch))
      return false;
   if(!cConcatenated.Init(0, 3, OpenCL, hidden_size, hidden_size, hidden_size * 2, optimization, iBatch))
      return false;
   cConcatenated.SetActivationFunction(TANH);
   if(!cSoftMax.Init(0, 4, OpenCL, hidden_size, optimization, iBatch))
      return false;
   cSoftMax.SetHeads(1);
   if(!cAttentionOut.Init(0, 5, OpenCL, hidden_size, optimization, iBatch))
      return false;

Como mencionado anteriormente, utilizamos camadas totalmente conectadas no bloco LSTM. Portanto, o tensor de características de curto prazo recebido do Codificador pode ser considerado "despersonalizado" no contexto das sequências unitárias do conjunto de dados multimodal analisado. Isso nos permite normalizar os coeficientes de importância em todo o tensor. E neste estágio, a orientação do tensor de dados de entrada não é relevante.

Adicionamos uma camada de projeção das características de curto e longo prazo ponderadas do conjunto de dados analisado, que será passada como entrada para o bloco LSTM.

   if(!cAttAndFeature.Init(0, 6, OpenCL, hidden_size, hidden_size, variables * lenth, optimization, iBatch))
      return false;

Para finalizar as operações de inicialização da classe, adicionamos um buffer para armazenar os dados temporários.

   if(!cTemp.BufferInit(variables * lenth, 0) || !cTemp.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

O resultado lógico da inicialização dos objetos internos é retornado ao programa chamador.

Após inicializar os objetos internos, passamos à implementação do algoritmo de propagação para frente no método feedForward. Assim como nos demais métodos com o mesmo nome, recebemos como parâmetro um ponteiro para o objeto da camada neural anterior.

bool CNeuronTPM::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
//--- Encoder
   if(!cEncoder.FeedForward(NeuronOCL))
      return false;

Esse ponteiro é então passado diretamente para o método de propagação para frente do nosso Codificador.

Em seguida, utilizamos esse mesmo ponteiro para extrair as características de longo prazo do conjunto de dados analisado.

//--- FEATURE EXTRACTION
   if(!cFeatureExtraction.FeedForward(NeuronOCL))
      return false;

O funcionamento do bloco de atenção é semelhante ao do bloco equivalente no Codificador.

//--- Memory and Hidden
   if(!Concat(m_iHiddenState, m_iMemory, m_iHiddenState, m_iMemory, 
              cMemAndHidden.getOutputIndex(), 1, 1, 0, 0, Neurons()))
      return false;
//--- Attention
   if(!cConcatenated.FeedForward(cEncoder.AsObject(), cMemAndHidden.getOutput()))
      return false;
   if(!cSoftMax.FeedForward(cConcatenated.AsObject()))
      return false;

Multiplicamos os coeficientes de importância pelo vetor de características de curto prazo do Codificador.

   uint global_work_offset[1] = {0};
   uint global_work_size[1];
   global_work_size[0] = int(cSoftMax.Neurons() + 3) / 4;
   ResetLastError();
   if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_input, cEncoder.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_map, cSoftMax.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_out, cAttentionOut.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_Dropout, def_k_dout_dimension, cSoftMax.Neurons()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.Execute(def_k_Dropout, 1, global_work_offset, global_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }

O vetor ponderado das características de curto prazo é combinado com as características de longo prazo na camada de concatenação.

//--- Attention and Features
   if(!cAttAndFeature.FeedForward(cAttentionOut.AsObject(), cFeatureExtraction.getOutput()))
      return false;

Os dados assim preparados são enviados para a entrada do bloco LSTM.

//--- LSTM
   if(!CNeuronLSTMOCL::feedForward(cAttAndFeature.AsObject()))
      return false;
//---
   return true;
  }

Verificamos o resultado lógico da execução das operações e o retornamos ao programa chamador.

Normalmente, o próximo passo seria a construção dos métodos de propagação reversa. No entanto, você deve ter percebido a semelhança entre os métodos de propagação para frente do Codificador e do Decodificador. Claro, há algumas diferenças. Essas diferenças também existem nos métodos de propagação reversa. No entanto, os algoritmos são bastante semelhantes, no geral. Portanto, sugiro que você os consulte diretamente no anexo.

2.3 Arquitetura dos modelos treináveis


Acima, analisamos os algoritmos de implementação do método TPM utilizando MQL5. Esse método foi desenvolvido para prever tendências no movimento dos preços das ações. Naturalmente, o incorporamos ao nosso Codificador de estado do ambiente, cuja arquitetura é definida no método CreateCodificadorDescriptions.

O método recebe como parâmetro um ponteiro para um array dinâmico, onde armazenamos a arquitetura do modelo.

bool CreateEncoderDescriptions(CArrayObj *encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }

No corpo do método, verificamos a validade do ponteiro recebido e, se necessário, criamos uma nova instância do objeto do array dinâmico.

Como entrada do modelo, utilizamos os dados brutos da descrição do estado do ambiente. Para registrar os dados de entrada, usamos uma camada totalmente conectada básica, cujo tamanho deve ser suficiente para armazenar o tensor analisado. 

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Os dados brutos recebidos passam por um pré-processamento na camada de normalização em lote.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Em seguida, os dados preparados são enviados para o nosso módulo TPM.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTPM;
   descr.count = LatentCount;
   descr.window = BarDescr;
   descr.window_out = HistoryBars;
   descr.step = int(false);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Os dados obtidos do módulo TPM passam por um MLP de 3 camadas, do qual esperamos obter os valores previstos da série temporal analisada.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.optimization = ADAM;
   descr.activation = SIGMOID;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = BarDescr * NForecast;
   descr.optimization = ADAM;
   descr.activation = TANH;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Aos valores previstos, adicionamos os indicadores estatísticos da série temporal original, que haviam sido removidos na camada de normalização em lote.

//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRevInDenormOCL;
   descr.count = BarDescr * NForecast;
   descr.activation = None;
   descr.optimization = ADAM;
   descr.layers = 1;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

E então ajustamos os resultados previstos para a representação no domínio da frequência.

//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFreDFOCL;
   descr.window = BarDescr;
   descr.count =  NForecast;
   descr.step = int(true);
   descr.probability = 0.7f;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

Os modelos do Ator e do Crítico foram reaproveitados de trabalhos anteriores sem alterações. Você pode consultá-los diretamente no anexo.  

2.4 Consultores de treinamento dos modelos


Durante o treinamento dos modelos recorrentes, devemos prestar atenção às suas particularidades. Como você sabe, a principal característica desses modelos é a sensibilidade à ordem de apresentação dos dados de entrada. Sendo assim, durante o treinamento, é necessário utilizar os dados do conjunto de treinamento mantendo sua sequência histórica. Por outro lado, essa abordagem reduz a eficácia do treinamento da maioria dos modelos, pois favorece o sobreajuste em pequenos intervalos de tempo, prejudicando sua capacidade de generalização ao longo de todo o período de treinamento.

Para minimizar o impacto negativo desses fatores, durante o treinamento vamos extrair aleatoriamente, a partir do buffer de replay de experiência, pequenos subconjuntos com sequência histórica preservada para treinar o modelo. Em seguida, um novo lote de treinamento será amostrado. Vamos analisar a implementação dessa abordagem no método de treinamento do codificador de estado do ambiente (EA "...\Experts\TPM\StudyCodificador.mq5").

void Train(void)
  {
//---
   vector<float> probability = GetProbTrajectories(Buffer, 0.9);

No corpo do método, primeiro geramos um vetor de probabilidades para a seleção de passagens do conjunto de treino, ranqueado de acordo com a rentabilidade das passagens. Em seguida, declaramos as variáveis locais necessárias.

   vector<float> result, target, state;
   bool Stop = false;

Aqui também adicionamos uma variável indicando o tamanho do lote de treinamento para cada subconjunto.

   int Batch = 100;

Depois, estruturamos o sistema de laços aninhados. No laço externo, amostramos uma trajetória do conjunto de treino e o estado inicial do subconjunto de treino ao longo da trajetória escolhida.

   uint ticks = GetTickCount();
//---
   for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter += Batch)
     {
      int tr = SampleTrajectory(probability);
      int st = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - NForecast));
      if(st <= 0)
        {
         iter -= Batch;
         continue;
        }

Limpamos os buffers do estado oculto e do contexto do bloco LSTM.

      Encoder.Clear();

E então organizamos um laço interno para percorrer sequencialmente os estados em sua ordem histórica, a partir do estado do ambiente selecionado.

      for(int i = st; (i < MathMin(st + Batch, Buffer[tr].Total - NForecast) && !IsStopped() && !Stop); i++)
        {
         state.Assign(Buffer[tr].States[i].state);
         if(MathAbs(state).Sum() == 0)
           {
            iter += i - st - Batch;
            break;
           }
         bState.AssignArray(state);

No corpo do laço interno, transferimos o estado do ambiente analisado para o buffer de dados. Com os dados obtidos, prevemos a trajetória subsequente do movimento de preços.

         //--- State Encoder
         if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Em seguida, carregamos os valores-alvo da trajetória futura a partir do buffer de reprodução de experiência.

         //--- Collect target data
         if(!Result.AssignArray(Buffer[tr].States[i + NForecast].state))
            continue;
         if(!Result.Resize(BarDescr * NForecast))
            continue;

Verificamos a precisão das nossas previsões. No processo de propagação reversa, ajustamos os parâmetros do modelo buscando minimizar o erro na previsão do movimento subsequente.

         if(!Encoder.backProp(Result, (CBufferFloat*)NULL))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Informamos o usuário sobre o andamento do processo de treinamento e seguimos para a próxima iteração da estrutura de laços.

         if(GetTickCount() - ticks > 500)
           {
            double percent = double(iter + i - st) * 100.0 / (Iterations);
            string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Encoder", 
                                            percent, Encoder.getRecentAverageError());
            Comment(str);
            ticks = GetTickCount();
           }
        }
     }

Após a execução bem-sucedida de todas as iterações, limpamos o campo de comentários no gráfico do ativo. Exibimos os resultados do treinamento no diário do terminal e iniciamos o encerramento do EA.

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Encoder", Encoder.getRecentAverageError());
   ExpertRemove();
//---
  }

Alterações semelhantes foram feitas no EA de treinamento dos modelos do Ator e do Crítico. Apesar de esses modelos não conterem blocos recorrentes, tais ajustes são necessários para garantir o funcionamento adequado do codificador de estado do ambiente. Afinal, tanto o Ator quanto o Crítico utilizam os estados processados como dados de entrada.

Você pode consultar o código completo dos EAs de treinamento dos modelos no anexo. Lá também estão disponíveis os códigos integrais de todos os programas, classes e seus métodos utilizados na preparação deste artigo.


3. Testes

Nesta parte do artigo, conhecemos o método de previsão de trajetórias futuras de ações TPM e implementamos nossa própria versão dos conceitos propostos. Agora é hora de verificar os resultados do nosso trabalho com dados reais. Como sempre, treinaremos os modelos apresentados com dados históricos reais do instrumento EURUSD no timeframe H1, referentes ao ano de 2023.

Começamos treinando o codificador de estado do ambiente. Este modelo analisa apenas os dados históricos do movimento de preços, sem considerar as ações do Ator. Isso nos permite treinar totalmente o modelo com o conjunto de treino original, sem necessidade de reatualização. Podemos dizer que o modelo é treinado de forma bastante rápida e apresentou bons resultados. Abaixo está o gráfico comparando a trajetória prevista com a trajetória real do movimento de preços.

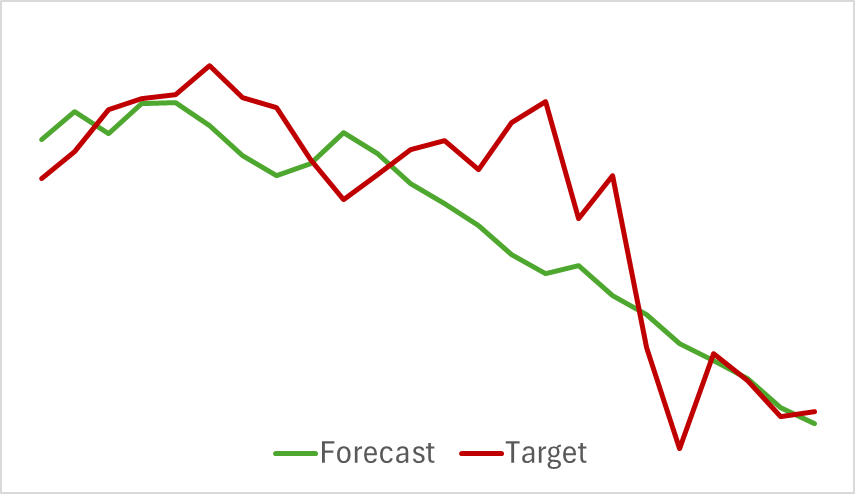
No gráfico, observamos uma sobreposição próxima entre as duas linhas. Nota-se que a trajetória prevista apresenta um aspecto mais suavizado. Potencialmente, isso pode contribuir para um treinamento mais estável do Ator.

No entanto, como você sabe, nosso objetivo principal é encontrar a política ótima do ator. Após treinar o codificador de estado do ambiente, passamos à segunda etapa do processo de treinamento — o treinamento da política do ator. Esse processo é iterativo. Como as ações do Ator tendem a se desviar durante o treinamento, podendo sair do espaço coberto pela amostragem original do conjunto de treinamento, precisamos atualizar periodicamente o buffer de reprodução da experiência, preenchendo-o com estados e recompensas que reflitam ações próximas à política atual do Ator.

Após uma série de iterações alternadas de treinamento dos modelos do Ator e do Crítico, com atualizações do conjunto de treinamento, conseguimos obter uma política capaz de gerar lucro no período histórico da amostragem de treinamento.

Com o objetivo de verificar a eficácia do modelo fora da amostra de treinamento (em dados novos), realizamos um teste com dados históricos de janeiro de 2024, mantendo os demais parâmetros inalterados.

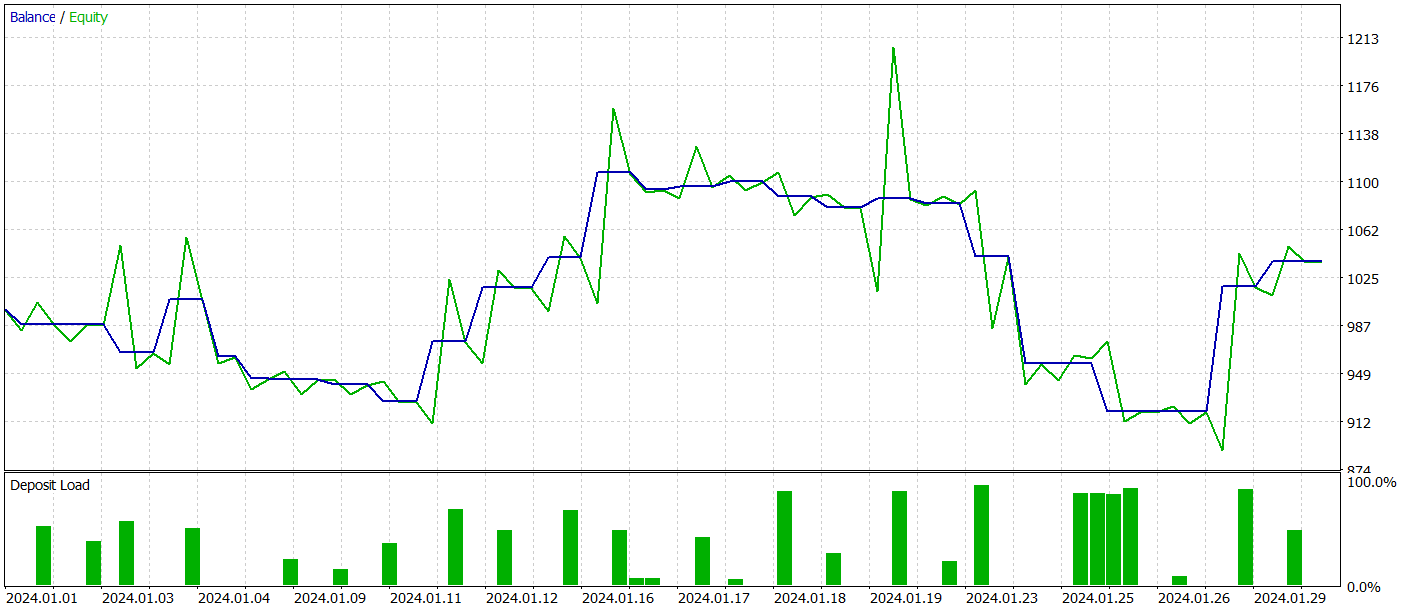
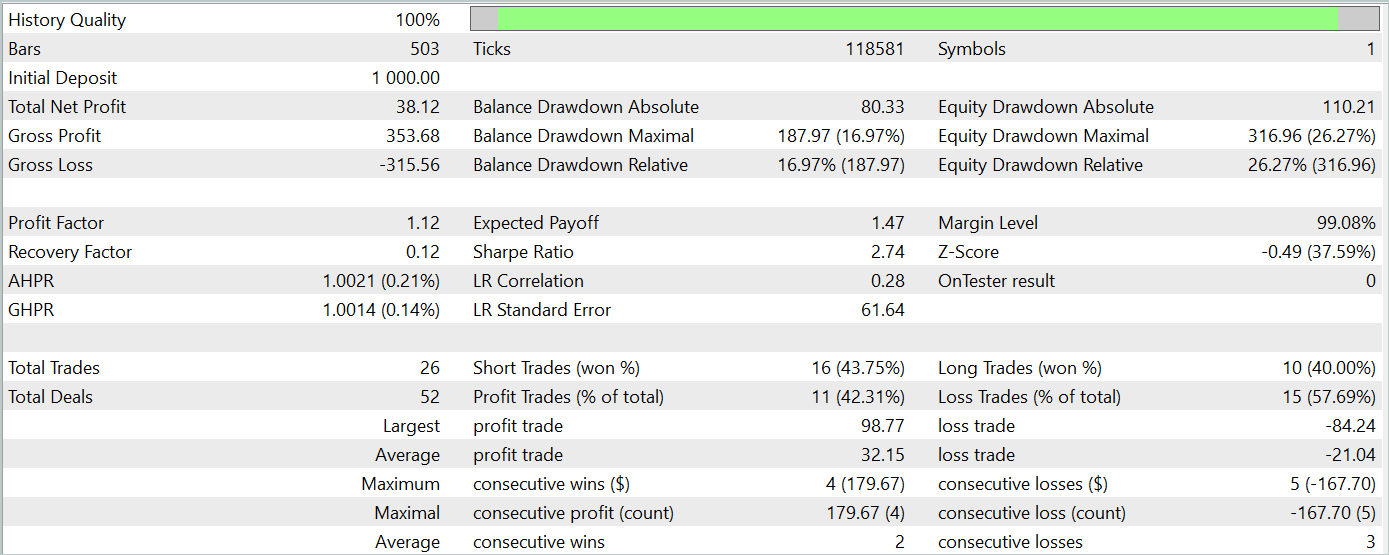
Durante o período de teste, o modelo executou 26 operações, das quais apenas 11 foram encerradas com lucro, representando pouco mais de 42%. No entanto, tanto o lucro máximo quanto o lucro médio por operação foram superiores às respectivas perdas. Isso permitiu alcançar lucro total no período de teste. O profit factor calculado a partir dos resultados do teste foi de 1,12.

Ainda assim, ao observar o gráfico de saldo, nota-se uma retração significativa no início da terceira dezena do mês. E isso levanta preocupações. Apesar do lucro obtido, o modelo ainda requer ajustes.


Considerações finais

Nesta matéria, exploramos o método TPM para previsão de tendências nos movimentos de preços. Esse método combina de forma eficaz as vantagens das redes convolucionais para análise de dependências de curto prazo e PLR para identificação de tendências de longo prazo.

Na parte prática do artigo, implementamos nossa própria interpretação das abordagens propostas utilizando MQL5. Treinamos e testamos os modelos apresentados. Com base nos testes, o modelo treinado obteve lucro com dados fora da amostra. No entanto, o gráfico de saldo não apresentou o comportamento ascendente ideal e mostrou sinais de retrações.

Em resumo, o método proposto possui potencial, mas o modelo que treinamos ainda necessita de aprimoramentos.

Links

  • A Dual-Attention-Based Stock Price Trend Prediction Model With Dual Features
  • Outros artigos da série

    • Programas utilizados no artigo

    # Nome Tipo Descrição
    1 Research.mq5 EA EA de coleta de amostras
    2 ResearchRealORL.mq5
    		 EA
    		 EA de coleta de amostras com método Real-ORL
    3 Study.mq5 EA EA de treinamento de modelos
    4 StudyCodificador.mq5 EA
    		 EA de treinamento do codificador
    5 Test.mq5 EA EA para teste do modelo
    6 Trajectory.mqh Biblioteca de classe Estrutura de descrição do estado do sistema
    7 NeuroNet.mqh Biblioteca de classe Biblioteca de classes para criação de rede neural
    8 NeuroNet.cl Biblioteca Biblioteca de código OpenCL

    Traduzido do russo pela MetaQuotes Ltd.
    Artigo original: https://www.mql5.com/ru/articles/15255

    Arquivos anexados |
    Baixar como ZIP
    MQL5.zip (1446.2 KB)

    Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.

    Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.

    Outros artigos do autor

    Ir para discussão
    Algoritmo do Campo Elétrico Artificial — Artificial Electric Field Algorithm (AEFA) Algoritmo do Campo Elétrico Artificial — Artificial Electric Field Algorithm (AEFA)
    Este artigo apresenta o Algoritmo do Campo Elétrico Artificial (AEFA), inspirado na lei de Coulomb da força eletrostática. Por meio de partículas carregadas e suas interações, o algoritmo simula fenômenos elétricos para resolver tarefas complexas de otimização. O AEFA demonstra propriedades únicas em relação a outros algoritmos baseados em leis da natureza.
    Técnicas do MQL5 Wizard que você deve conhecer (Parte 33): Kernels de Processos Gaussianos Técnicas do MQL5 Wizard que você deve conhecer (Parte 33): Kernels de Processos Gaussianos
    Os Kernels de Processos Gaussianos são a função de covariância da Distribuição Normal que pode desempenhar um papel em previsões. Exploramos esse algoritmo único em uma classe de sinal personalizada em MQL5 para ver se pode ser utilizado como um sinal principal de entrada e saída.
    Do básico ao intermediário: Indicador (III) Do básico ao intermediário: Indicador (III)
    Neste artigo iremos ver como declarar diversos indicadores de plotagem, como DRAW_COLOR_LINE e DRAW_FILLING. Além é claro, aprender como plotar indicadores múltiplos de uma forma muito simples, prática e pouco trabalhosa. Agora que realmente pode mudar a sua forma de enxergar o MetaTrader 5 e o mercado em geral.
    Integrando o MQL5 com pacotes de processamento de dados (Parte 2): Aprendizado de Máquina e Análise Preditiva Integrando o MQL5 com pacotes de processamento de dados (Parte 2): Aprendizado de Máquina e Análise Preditiva
    Na nossa série sobre integração do MQL5 com pacotes de processamento de dados, mergulhamos na poderosa combinação de aprendizado de máquina e análise preditiva. Exploraremos como conectar o MQL5 de forma perfeita com bibliotecas populares de aprendizado de máquina, para possibilitar modelos preditivos sofisticados para os mercados financeiros.