交易中的神经网络:基于双注意力的趋势预测模型
概述
金融工具的价格代表一串高度波动的时间序列,其会受到多种因素影响,包括利率、通货膨胀、货币政策、及投资者情绪。针对金融工具价格与这些因素之间的关系建模,并预测它们的动向,对于研究人员和投资者来说是一项重大挑战。
大量研究致力于金融时间序列的预测和分析。传统的统计方法往往假设时间序列是由线性过程生成的,这限制了它们在非线性预测中的有效性。机器学习和深度学习方法有能力捕获非线性关系,由此在金融时间序列建模方面已展现出极大成功。许多研究都专注于提取特定时间点的特征,并将其用于建模和预测。然而,这种方式往往忽视了数据交互,和短期波动连续性。
为了解决这些局限性,研究《基于双注意力并配以双特征的股价趋势预测模型》提出了一种双特征提取方法。该方法利用了单时间点和多时态间隔两者。它将短期行情特征、与长期时态特征集成在一起,从而提高预测准确性。所提议模型基于编码器-解码器架构,并在编码器和解码器阶段都采用了注意力机制,能够识别长期时间序列中最具相关性的特征。
本研究引入了一种新的趋势预测模型(TPM),设计用于通过运用双特征提取、和双注意力机制来预测股价趋势。TPM 旨在预测股价走势的方向、及持续时间。所提议方式的主要贡献如下:
- 基于不同时间范围的一种新型双特征提取方法,有效提取重要的市场信息,并优化预测结果。TPM 使用分段线性回归和卷积神经网络,分别从金融时间序列中提取长期和短期行情特征。通过双特征表示市场信息可显著提高模型的预测性能。
- 股票价格趋势预测模型(TPM),使用了编码器-解码器结构、和双注意力机制。通过在编码器和解码器阶段添加注意力机制,TPM 自适应选择最相关的短期行情特征,并将它们与长期时态特征相结合,从而提高预测准确性。
1. TPM 算法
在现有的分析时间序列预测方法后,TPM 的作者得出了以下结论:
- 单变量金融时间序列,对于预测未来的价格走势缺乏足够的信息。
- 传统的特征提取方法在捕获复杂的市场行为时受到限制。
- 使用单个神经网络的时间序列分析则是不完整的。
TPM 方法通过采用双特征提取、和双注意力机制来解决这些问题。所提议算法由两个阶段组成。首先,采用分段线性回归方法对金融时间序列进行切分,并在不同时间间隔的子序列基础上提取历史长期时态特征。使用卷积神经网络从独立的时间点提取短期空间市场特征。
然后,在第二个 TPM 阶段,基于双注意力机制的趋势预测模型,分析先前提取的双特征。所提议模型建立在编码器-解码器架构之上。
该编码器基于递归 LSTM 模块,并添加了一个注意力机制,可自适应提取最相关的短期行情特征。
解码器也是使用 LSTM 模块和注意力机制构建的,其选择并解码最相关的组合特征,从而预测股票价格趋势。
由于一维金融时间序列提供的信息不足,故很难基于这些数据对股票价格的趋势进行建模和预测。TPM 方法作者采用基本的市场数据进行分析,例如柱线的开盘价和收盘价、最高价和最低价、以及交易量,将它们转化为一系列技术指标。
鉴于数据的连续变化,TPM 使用分段线性回归(PLR)提取长期时态特征。PLR 方法抹平了短期波动噪声,降低了数据维度,并提高了计算性能。
时间序列的分段取决于 δ 最大误差阈值。以 CSI 300 数据为例,该方法的作者采用 PLR 来将其历史收盘价分段。当 δ 等于 2.0 时,时间序列可以切分为 16 个子序列。不过,如果阈值 δ 等于 4.0,则相同的时间序列只能分段为 4 个子序列。因此,随着阈值的增加,会忽略更多的数据波动,且形成的子序列会更少。阈值会影响历史时间序列特征的可靠性。每个子序列表示给定时间段内数据的波动。生成的每个子序列的斜率 sm 和持续时间 dm,作为趋势预测的长期时态特征。
考虑同一时间点会有不同数据的交互,每个时间步骤的短期空间市场特征会经由卷积神经网络(CNN)提取。为所分析金融时间序列构建市场矩阵。在市场矩阵中,每行代表所分析数据的一个维度,行数为 n。然后每列代表一个时间点。由于 CNN 保留了原始数据的邻域关系和空间定位,故它可捕获市场矩阵、和股票趋势之间的非线性关系。成果则是短期历史时间序列的空间特征。
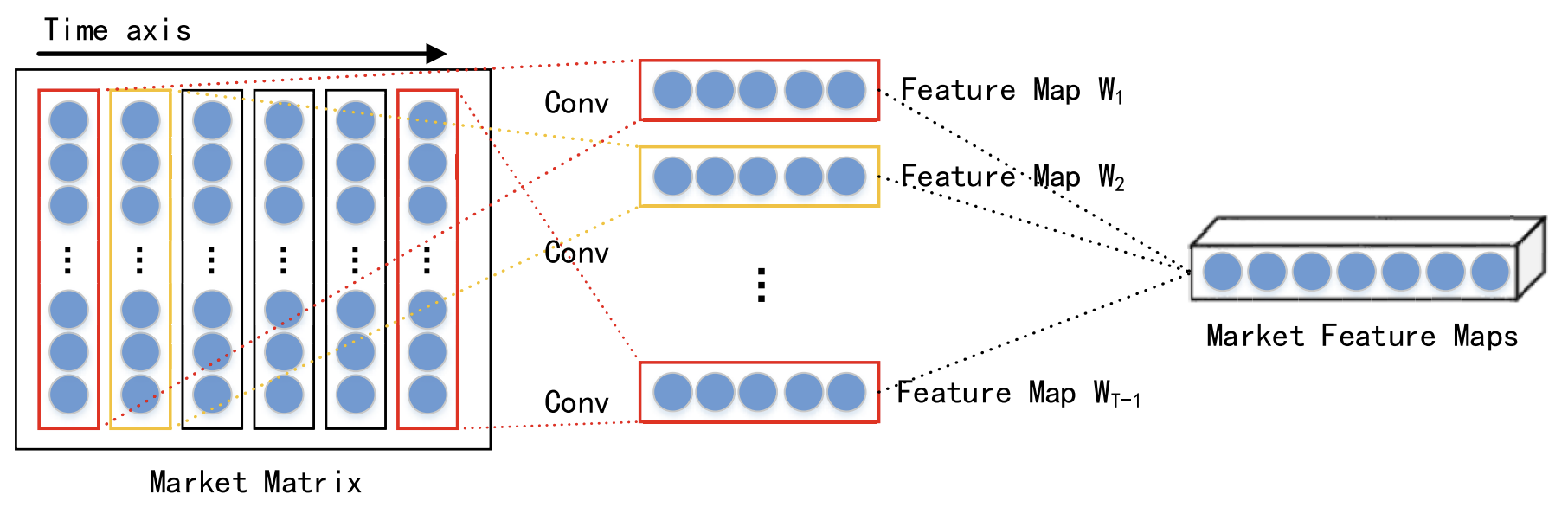
在他们的工作中,作者采用不同内核大小的卷积层,例如 1 × 3 到 1 × 5,来提取抽象的、多层级的空间市场特征。选择 ReLU 函数作为非线性激活函数。
在卷积层之后,应用最大池化层。这降低了特征映射的维度,并有助于防止过度拟合。
然后,来自多个卷积层、和最大池化层的输出被传递到预测层进一步处理。
如早前所述,提取的短期和长期特征在编码器-解码器架构中进行处理。在该结构中,编码器将输入信息压缩为固定大小的向量,而解码器处理这些向量,从而生成最终输出。不过,当输入数据很广泛时,编码器也许难以有效地捕获所有相关信息,从而导致模型性能下降。注意力机制通过解码相关神经元的隐藏状态来解决这一限制。
重点要注意,具有注意力机制的解码器缺乏显式选择最相关输入特征的能力。为了克服这一点,TPM 方法作者在编码器和解码器阶段都添加了注意力机制。
TPM 算法的第二阶段基于双注意力机制。编码器-解码器结构切分为两个阶段。在第一阶段,编码器基于搭配注意力机制的 LSTM,分析运用 CNN 提取的短期空间市场特征。自适应选择每个时间点对应的短期特征,并编码为向量。
在第二阶段,使用 PLR 提取的编码向量、和长期时间特征被投喂到基于 LSTM 的解码器,其基于注意力机制针对相应的向量和特征进行解码,从而预测股市趋势。通过运用双注意力机制,TPM 模型自适应识别最关键的空间市场和时态特征,以便建模、并预测趋势。
在每个时间点 t,编码器学习输入特征 Wt、与隐藏状态 Ht 之间的关系:
![]()
其中 Ht 是编码器在时间 t 的隐藏状态, fen(•) 是非线性函数,ʘen 表示编码器参数。
该方法作者使用 LSTM 作为非线性函数 fen,捕获时间依赖性,并形成一个短期特征编码器。LSTM 能够有效地模拟时间序列的动态时态行为,并避免 RNN 中的梯度消失或暴涨问题。
方法作者在编码器阶段引入了一种注意力机制,并根据它们的维度 m,切分初始特征 WMarket。在时间步骤 t-1 计算出的隐藏状态 Ht-1、和单元状态(上下文)Ct-1,及对应的输入特征维度,将用于在下一个时间点 t 更新原始特征。
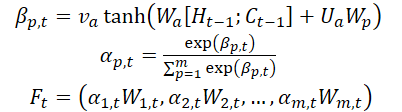
其中 va、Wa、和 Ua 是参数,SoftMax 函数用于计算每个特征维度的重要性 αm,t。
所有维度 Wt 都更新为 Ft,并投喂到编码器之中。之后,更新时间点 t 的隐藏状态。
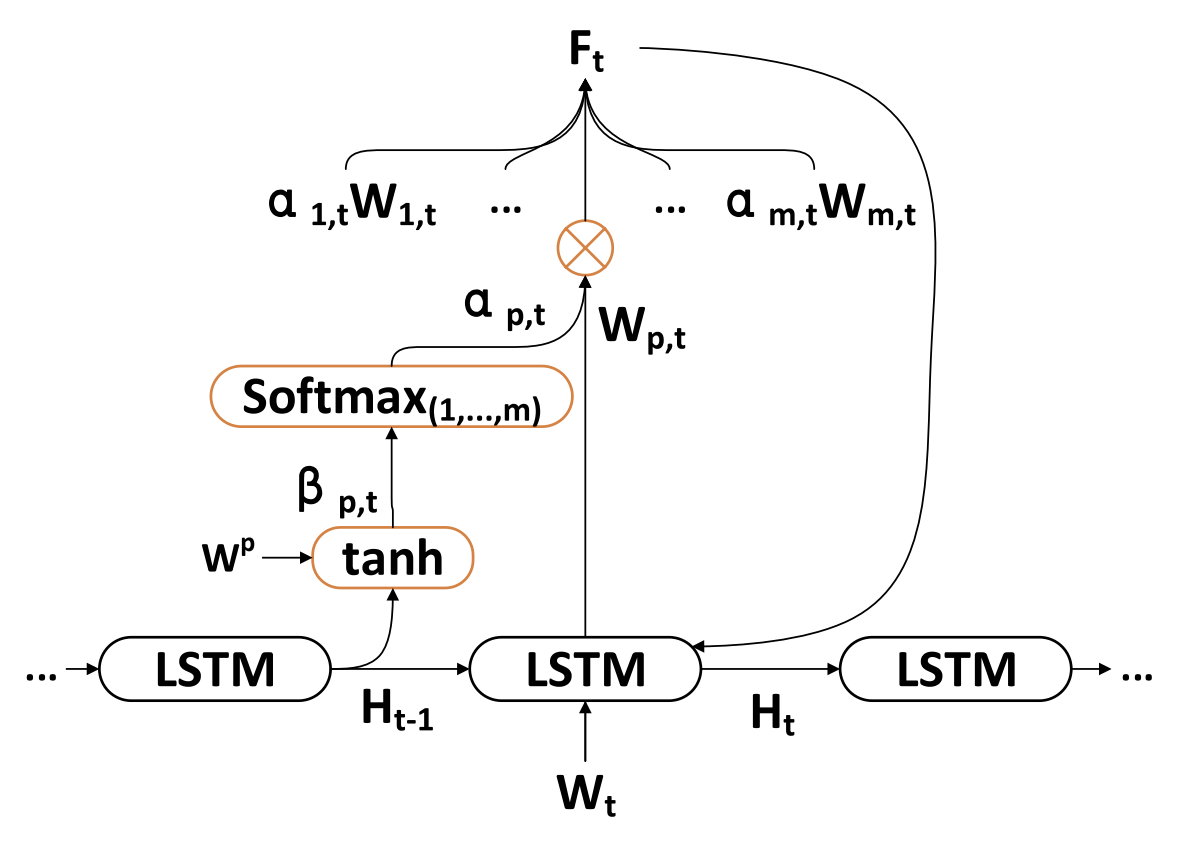
因此,在每个时间步骤 t 处,我们都可以选择空间市场特征的相关维度,迭代更新编码器的原始特征、和隐藏状态,并为短期特征生成最相关的编码向量。
解码器是专为预测股票市场趋势而设计的 LSTM 模块。通过 PLR 方法提取长期时间特征 ZT-1。
在每个时间步 t 处,解码器学习编码向量 Wt、长期特征 Lt、和隐藏状态 Ht 之间的关系:
![]()
其中 H't 是解码器在时间步骤 t 处的隐藏状态,fde(•) 是非线性函数,而 ʘde 表示解码器参数。
TPM 的作者使用 LSTM 作为非线性函数 fde 来捕获时间依赖性,并形成长期特征解码器。计算过程类似于编码器阶段。
TPM 的作者在解码器阶段引入了注意力机制,从而获取所有时间点处与编码器关联的隐藏状态。
投喂到解码器的上下文向量,是遍历编码器的所有隐藏状态获得的。
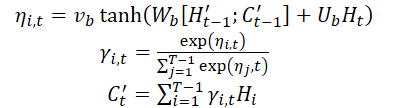
一旦获得上下文向量 C't,它与长期时态特征 Lt 相结合,生成一个混合特征 yt:
![]()
利用上述公式,在每个时间步 t 处,算法选择所有时间点、和长期时态特征中最相关的编码器隐藏状态,生成混合特征向量。
接下来,研究股票市场趋势和对偶特征之间的非线性映射函数 F(•)。最后,应用一个线性函数来生成时刻 T 的股票市场趋势预测。
该模型是经随机梯度下降法、和动量优化器训练的。训练批次大小为 64,学习率为 0.001。
使用具有正则化项的二次误差函数作为损失函数。
下面呈现的是作者对 TPM 方法的可视化。
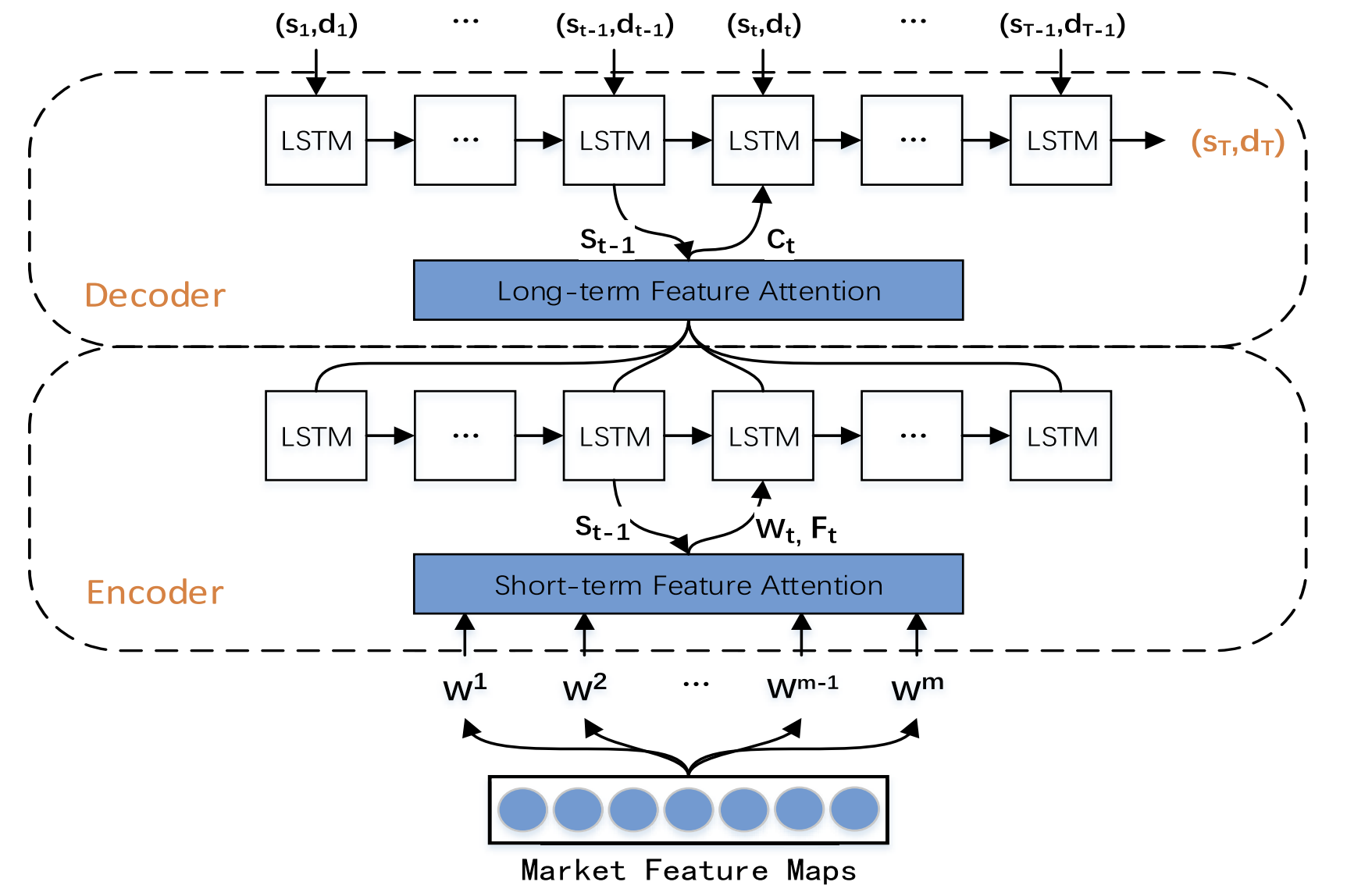
2. 利用 MQL5 实现
在研究过所提议 TPM 方法的理论层面之后,我们现在转到方法的实施,其中体现出我们对所提议方式的解释。如常,我们保留了所提议方法的一般框架,但在实现细节中引入了一些偏差。自然而然,这些调整也许会对模型的最终性能产生不同的影响。
我们将从构造编码器开始。
2.1TPM 编码器
我们在 CNeuronTPMEncoder 类中为我们的模型实现了编码器,该类继承了之前创建的 LSTM 模块 CNeuronLSTMOCL 的基本功能。选择这个父类是有意为之的。您也许能回想到,TPM 方法中的编码器基于附加了注意力机制的 LSTM 模块。
此外,我们决定将短期特征的特征提取过程直接合并到编码器当中。将利用先前开发的数据金字塔结构构建器 CSCM 执行特征提取。然而,有一个重要的细微差别:以前,CSCM 模块从单变量时间序列中提取特征。现在,我们需要稍微修改数据流,以便从独立时间点提取特征。
编码器的整体结构如下所示。
class CNeuronTPMEncoder : public CNeuronLSTMOCL { protected: bool bTSinRow; //--- CNeuronCSCMOCL cFeatureExtraction; CNeuronBaseOCL cMemAndHidden; CNeuronConcatenate cConcatenated; CNeuronSoftMaxOCL cSoftMax; CNeuronBaseOCL cAttentionOut; CNeuronTransposeOCL cTranspose; CBufferFloat cTemp; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronTPMEncoder(void){}; ~CNeuronTPMEncoder(void){}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint variables, uint lenth, uint hidden_size, bool ts_in_row, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual int Type(void) override const { return defNeuronTPMEncoder; } virtual void SetOpenCL(COpenCLMy *obj); };
此处,我们看到了一组熟悉的覆盖方法,和若干个嵌套对象,随着我们的实现持续,它们的用途将变得越来越清晰。
如前,所有嵌套对象都声明为静态。这种方式允许我们将类的构造函数和析构函数都保留为“空”。一个新类实例的实际初始化是在 Init 方法中进行的。
bool CNeuronTPMEncoder::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint variables, uint lenth, uint hidden_size, bool ts_in_row, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronLSTMOCL::Init(numOutputs, myIndex, open_cl, hidden_size, optimization_type, batch)) return false; if(!SetInputs(variables * lenth)) return false;
在参数中,该方法接收所创建对象的主要参数。在这种情况下,有 3 个这样的参数:
- variables — 所分析多模态时间序列中的单变量序列的数量。
- lenth — 所分析序列的大小(历史深度)。
- hidden_size ― LSTM 模块中隐藏空间的大小。
此外,我们还添加了标志 ts_in_row,它表示独立单变量序列在输入数据张量中所在行里的位置。
在方法主体中,我们调用父类中的同名方法,该方法提供了一个必需的控制模块,可验证所创建层的参数,并初始化继承对象。
于此,我们还传递父类的输入张量的大小,它等于单变量序列的大小、与输入数据中此类序列数量的乘积。
请注意,在 LSTM 模块中,我们用到了全连接层,而输入数据张量在这种情况下无关紧要。
下一步是初始化短期特征提取模块。
uint windows[] = {variables, 6, 5, 4}; if(!cFeatureExtraction.Init(0, 0, OpenCL, windows, lenth, variables, ts_in_row, optimization, batch)) return false;
为此,我们首先设置卷积特征提取层的窗口大小,并调用 CSCM 模块初始化方法。
请注意,在调用 CSCM 模块初始化方法时,我们重新排列了单变量序列的大小和数量的参数。这是因为需要从单个时间步长(柱线)中提取特征,而非像 MSFformer 方法那样从单变量序列中提取特征。
接下来,我们初始化注意力模块的嵌套对象。此处,我们首先创建一个层,我们在其缓冲区中连接了上一步中 LSTM 模块的隐藏状态和上下文。
if(!cMemAndHidden.Init(0, 1, OpenCL, hidden_size * 2, optimization, batch)) return false;
为了计算单个特征的重要性系数,我们将用到连接层,我们调用 SoftMax 函数对其结果进行归一化。
if(!cConcatenated.Init(0, 2, OpenCL, variables * lenth, variables * lenth, hidden_size * 2, optimization, batch)) return false; cConcatenated.SetActivationFunction(TANH); if(!cSoftMax.Init(0, 3, OpenCL, variables * lenth, optimization, batch)) return false; cSoftMax.SetHeads(variables);
注意,在该阶段,数据归一化是在单变量序列中执行的。
接下来,我们添加一个层来记录注意力输出。
if(!cAttentionOut.Init(0, 4, OpenCL, variables * lenth, optimization, batch)) return false;
如有必要,我们初始化数据转置层。
bTSinRow = ts_in_row; if(!bTSinRow) { if(!cTranspose.Init(0, 5, OpenCL, variables, lenth, optimization, iBatch)) return false; }
我们还添加了一个辅助缓冲区来记录中间值。
//--- if(!cTemp.BufferInit(variables * lenth, 0) || !cTemp.BufferCreate(OpenCL)) return false; //--- return true; }
成功初始化所有嵌套对象之后,我们将所执行作的逻辑结果传递给调用者,并终止该方法。
对象的初始化完成后,我们转到为新类构造前馈通验算法,我们在 feedForward 方法中实现该算法。
bool CNeuronTPMEncoder::feedForward(CNeuronBaseOCL *NeuronOCL) { //--- FEATURE EXTRACTION if(!cFeatureExtraction.FeedForward(NeuronOCL)) return false;
如常,在该方法的参数中,我们收到一个指向前一个神经层对象的指针。然而,在这种情况下,我们不检查接收到的指针,但将其传递给内部短期特征提取层的前馈方法。被调用方法本身的主体实现了所接收指针的控制。
下一步是将对象的隐藏状态、和上下文组合在一起,这些状态和上下文是从上一个前馈通验中保留的。
//--- Memory and Hidden if(!Concat(m_iHiddenState, m_iMemory, m_iHiddenState, m_iMemory, cMemAndHidden.getOutputIndex(), 1, 1, 0, 0, Neurons())) return false;
我们的准备工作到此结束。现在,我们转到讨论注意力模块。在该模块中,我们计算各个特征的重要性系数。
if(!cConcatenated.FeedForward(cFeatureExtraction.AsObject(), cMemAndHidden.getOutput())) return false; if(!cSoftMax.FeedForward(cConcatenated.AsObject())) return false; int map = cSoftMax.getOutputIndex();
如有必要,我们转置重要性系数张量。
if(!bTSinRow) { if(!cTranspose.FeedForward(cSoftMax.AsObject())) return false; map = cTranspose.getOutputIndex(); }
然后我们需要针对获得的系数,执行逐个元素乘以相应的短期特征。对于 2 个张量的逐元素乘法,我们将用到 Dropout 层的前馈通验内核。
我们创建这个内核是为了输入数据乘以神经元排斥掩码。在这种情况下,我们取用重要性系数作为掩码。
我们定义任务空间的维度。
uint global_work_offset[1] = {0}; uint global_work_size[1]; global_work_size[0] = int(cSoftMax.Neurons() + 3) / 4;
将参数传递给内核。
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_input, cFeatureExtraction.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_map, map)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_out, cAttentionOut.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_Dropout, def_k_dout_dimension, cSoftMax.Neurons())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
之后,我们将其放入执行队列之中。
if(!OpenCL.Execute(def_k_Dropout, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; }
在 AttentionOut 层缓冲区中执行内核以后,我们获得的短期特征已考虑到它们的重要性系数。现在,我们能够用 LSTM 模块的基本功能来表示编码器输出端的特征张量。
//--- LSTM if(!CNeuronLSTMOCL::feedForward(cAttentionOut.AsObject())) return false; //--- return true; }
不要忘记监控每个阶段的操作过程。成功执行之后,我们将所执行操作的逻辑结果传递给调用者,并完结该方法。
在实现前馈通验之后,我们通常会转到构造反向传播方法。这个类也不例外。在下一步中,我们根据它们对模型最终结果的影响,将误差梯度传播到所有嵌套对象、及输入数据张量。我们在 calcInputGradients 方法中实现指定的功能。
在该方法参数中,与上面讨论的类似,我们接收到一个指向前一个神经层对象的指针。
bool CNeuronTPMEncoder::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
在方法主体中,我们首先检查接收指针的相关性。
然后,使用继承的功能,我们经由 LSTM 模块算法,将误差梯度传播到注意力模块的输出级。
if(!CNeuronLSTMOCL::calcInputGradients(cAttentionOut.AsObject())) return false;
之后,我们将误差梯度分派在 2 个方向上:特征重要性系数,和特征本身。将内核放入队列的算法与上面讨论过的算法类似。
//--- uint global_work_offset[1] = {0}; uint global_work_size[1]; global_work_size[0] = cSoftMax.Neurons(); ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_f, cFeatureExtraction.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_fg, cTemp.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_s, (bTSinRow ? cSoftMax.getOutputIndex() : cTranspose.getOutputIndex()))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_sg, (bTSinRow ? cSoftMax.getGradientIndex() : cTranspose.getGradientIndex()))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_g, cAttentionOut.getGradientIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_CGConv_HiddenGradient, def_k_cgc_activationf, NeuronOCL.Activation())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_CGConv_HiddenGradient, def_k_cgc_activations, int(None))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.Execute(def_k_CGConv_HiddenGradient, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; }
于此,我们应当注意两点。首先,对于注意力系数的误差梯度传播缓冲区,取决于是否需要使用重要性系数转置层。其次,我们在乘以重要性系数,并计算这些系数时都是用短期特征本身。因此,在该阶段,我们将短期特征的误差梯度保存在一个临时数据缓冲区之中。
在下一步中,如有必要,我们转置独立特征的重要性系数的误差梯度。
if(bTSinRow) { if(!cSoftMax.calcHiddenGradients(cTranspose.AsObject())) return false; }
之后,我们经由注意力模块算法将误差梯度传播到短期特征级。
if(!cConcatenated.calcHiddenGradients((CObject*)cSoftMax.AsObject(),(CBufferFloat *)NULL,(CBufferFloat *)NULL) || !DeActivation(cConcatenated.getOutput(), cConcatenated.getGradient(), cConcatenated.getGradient(), cConcatenated.Activation())) return false; if(!cFeatureExtraction.calcHiddenGradients(cConcatenated.AsObject(), cMemAndHidden.getOutput(), cMemAndHidden.getGradient())) return false;
然后,我们汇总来自 2 条信息线程的短期特征级别的误差梯度。
if(!DeActivation(cFeatureExtraction.getOutput(), GetPointer(cTemp), GetPointer(cTemp), NeuronOCL.Activation()) || !SumAndNormilize(cFeatureExtraction.getGradient(), GetPointer(cTemp), cFeatureExtraction.getGradient(), 1, false)) return false;
在方法结尾处,我们将误差梯度向下传播到前一层的级别,并将操作的逻辑结果传递给调用者。
if(!NeuronOCL.calcHiddenGradients(cFeatureExtraction.AsObject())) return false; //--- return true; }
在分派了误差梯度之后,我们只需朝着把整体误差最小化方向优化模型参数。我们在 updateInputWeights 方法中实现此功能,即调用包含可训练参数的嵌套对象的同名方法。
bool CNeuronTPMEncoder::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(!CNeuronLSTMOCL::updateInputWeights(cAttentionOut.AsObject())) return false; if(!cFeatureExtraction.UpdateInputWeights(NeuronOCL)) return false; if(!cConcatenated.UpdateInputWeights(cFeatureExtraction.AsObject(), cMemAndHidden.getOutput())) return false; //--- return true; }
讲述编码器主要功能的算法实现到此结束。附件中提供了该类所有方法的完整代码,以及准备本文时用到的所有程序完整代码。
2.2TPM 解码器
实现 TPM 编码器算法后,我们转到第二阶段 — 构建解码器。在回顾 TPM 方法的理论层面期间,您或许会注意到编码器和解码器算法之间的显著相似之处。然而,即使有微小的差异,我们也需要开发一个新的类。
与编码器类似,新的解码器类 CNeuronTPMDecoder 派生自 LSTM 模块类。新类结构如下所示。
class CNeuronTPM : public CNeuronLSTMOCL { protected: CNeuronTPMEncoder cEncoder; CNeuronPLROCL cFeatureExtraction; CNeuronBaseOCL cMemAndHidden; CNeuronConcatenate cConcatenated; CNeuronSoftMaxOCL cSoftMax; CNeuronBaseOCL cAttentionOut; CNeuronConcatenate cAttAndFeature; CBufferFloat cTemp; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronTPM(void){}; ~CNeuronTPM(void){}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint variables, uint lenth, uint hidden_size, bool ts_in_row, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual int Type(void) override const { return defNeuronTPM; } virtual void SetOpenCL(COpenCLMy *obj); };
很容易看出与上面讨论的编码器类的相似之处。仅添加了 2 个嵌套对象。您还能注意到特征提取层类型的变化:在解码器中,我们用到 PLR 来提取长期特征。
您也许已留意到,编码器类包含所有权规范,而解码器中没有该规范。这种区别是有原因的。编码器和解码器在相同输入数据上进行操作,但在不同抽象级别上提取特征。为了避免上层的模型结构过于复杂,我决定将编码器和解码器合并为一个统一的模块。以前开发的编码器类已加入新类,作为内层,将 TPM 算法合并到单个实体之中。该决定反映在新类的名称中:CNeuronTPM。
新类的初始化方法的参数与上面讨论的编码器初始化方法完全相同。
bool CNeuronTPM::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint variables, uint lenth, uint hidden_size, bool ts_in_row, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronLSTMOCL::Init(numOutputs, myIndex, open_cl, hidden_size, optimization_type, batch)) return false; if(!SetInputs(hidden_size)) return false;
在方法主体中,我们还调用了父类的初始化方法。不过,其输入数据张量的大小已与编码器的隐藏状态的大小相对应。这是因为解码器的投喂数据,是从编码器接收的特征加权向量。
我们还初始化了编码器对象
if(!cEncoder.Init(0, 0, OpenCL, variables, lenth, hidden_size, ts_in_row, optimization, iBatch)) return false;
以及特征提取层。
if(!cFeatureExtraction.Init(0, 1, OpenCL, variables, lenth, !ts_in_row, optimization, iBatch)) return false;
初始化注意力模块对象的进一步算法,类似于编码器初始化期间的操作,但输入数据张量的大小存在差异。
if(!cMemAndHidden.Init(0, 2, OpenCL, hidden_size * 2, optimization, iBatch)) return false; if(!cConcatenated.Init(0, 3, OpenCL, hidden_size, hidden_size, hidden_size * 2, optimization, iBatch)) return false; cConcatenated.SetActivationFunction(TANH); if(!cSoftMax.Init(0, 4, OpenCL, hidden_size, optimization, iBatch)) return false; cSoftMax.SetHeads(1); if(!cAttentionOut.Init(0, 5, OpenCL, hidden_size, optimization, iBatch)) return false;
如早前所述,LSTM 模块使用全连接层。因此,在所分析输入多模态时间序列的单变量序列的上下文中,从编码器获得的短期特征张量可被认为是“匿名的”。这令我们能够对整个张量的重要性系数进行归一化。在该阶段,输入张量的方向对我们来说并不重要。
我们添加一个预测层,其中包含所分析时间序列的加权短期和长期特征,我们将将其馈送到 LSTM 模块之中。
if(!cAttAndFeature.Init(0, 6, OpenCL, hidden_size, hidden_size, variables * lenth, optimization, iBatch)) return false;
在类初始化作结尾处,我们添加一个缓冲区来存储临时数据。
if(!cTemp.BufferInit(variables * lenth, 0) || !cTemp.BufferCreate(OpenCL)) return false; //--- return true; }
我们将初始化嵌套对象的逻辑结果返回给调用者。
嵌套对象初始化之后,我们转到 feedForward 方法中实现前馈算法。与其它同名方法类似,在参数中,我们接收一个指向前一个神经层对象的指针。
bool CNeuronTPM::feedForward(CNeuronBaseOCL *NeuronOCL) { //--- Encoder if(!cEncoder.FeedForward(NeuronOCL)) return false;
然后我们将接收到的指针传递给编码器的前馈方法。
接下来,我们传递相同的指针来提取所分析时间序列的长期特征。
//--- FEATURE EXTRACTION if(!cFeatureExtraction.FeedForward(NeuronOCL)) return false;
注意力模块的操作类似于上面讨论过的编码器模块。
//--- Memory and Hidden if(!Concat(m_iHiddenState, m_iMemory, m_iHiddenState, m_iMemory, cMemAndHidden.getOutputIndex(), 1, 1, 0, 0, Neurons())) return false; //--- Attention if(!cConcatenated.FeedForward(cEncoder.AsObject(), cMemAndHidden.getOutput())) return false; if(!cSoftMax.FeedForward(cConcatenated.AsObject())) return false;
我们将重要性系数乘以编码器的短期特征向量。
uint global_work_offset[1] = {0}; uint global_work_size[1]; global_work_size[0] = int(cSoftMax.Neurons() + 3) / 4; ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_input, cEncoder.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_map, cSoftMax.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_out, cAttentionOut.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_Dropout, def_k_dout_dimension, cSoftMax.Neurons())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.Execute(def_k_Dropout, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; }
我们将短期特征的加权向量,与串联层中的长期特征相结合。
//--- Attention and Features if(!cAttAndFeature.FeedForward(cAttentionOut.AsObject(), cFeatureExtraction.getOutput())) return false;
然后,我们将准备好的数据馈送到 LSTM 模块之中。
//--- LSTM if(!CNeuronLSTMOCL::feedForward(cAttAndFeature.AsObject())) return false; //--- return true; }
我们验证操作的逻辑结果,并将其返回给调用者。
接下来,我们按惯例转到构造反向传播方法。不过,我相信您已留意到编码器和解码器的前馈方法之间的相似之处。当然,也有一些细微差别。反向传播方法中也存在类似的细微差别。尽管如此,算法总体上非常相似。故此,我鼓励您在提供的附件中自行探索它们。
2.3可训练模型的架构
我们已经实证了使用 MQL5 实现 TPM 方法。开发这种方法是为了预测股票价格趋势。当然,我们会将其集成到环境状态编码器之中,其架构在 CreateEncoderDescriptions 方法中进行了讲述。
在参数中,该方法接收一个指向动态数组的指针,我们将在其中保存嵌入式模型架构。
bool CreateEncoderDescriptions(CArrayObj *encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
在方法主体中,我们检查所接收指针的相关性,并在必要时创建动态数组对象的新实例。
如常,我们往模型投喂描述环境状态的原生数据。为了记录初始数据,我们用到了一个基础全连接层,其大小应足以写入所分析张量。
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
获得的初始数据在批量归一化层中加以预处理。
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
预处理后的数据随即传递到我们的 TPM 模块。
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTPM; descr.count = LatentCount; descr.window = BarDescr; descr.window_out = HistoryBars; descr.step = int(false); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
从 TPM 模块获得的数据经由一个 3-层 MLP 传播,我们希望在其输出中获得所分析时间序列的预测值。
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.optimization = ADAM; descr.activation = SIGMOID; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = BarDescr * NForecast; descr.optimization = ADAM; descr.activation = TANH; if(!encoder.Add(descr)) { delete descr; return false; }
对于预测值,我们添加了之前在批量归一化层中删除的原始时间序列的统计变量。
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = BarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; }
然后,我们将获得的预测输出、与频域表示对齐。
//--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast; descr.step = int(true); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
参与者和评价者模型是从以前的成品中复制而来的,未有变化。您可在附件中找到它们。
2.4模型训练 EA
在训练模型时,我们应当注意训练递归模型的规范。如您所知,递归模型的主要特点是它们对输入数据序列的敏感性。因此,在模型训练过程中,我们需要按照历史顺序使用训练数据集中的数据。另一方面,这种方式降低了大多数模型的训练效率,因为它促进了小时间间隔内的过渡拟合,故无法推广到整个训练周期。
为了最大限度地减少上述因素的负面影响,在训练过程中,我们将根据历史序列从经验回放缓冲区中随机提取小型子集。然后,我们将针对新的训练包进行抽样。我们以环境状态编码器训练方式为例,研究所提议方法的实现。EA 文件 “...\Experts\TPM\StudyEncoder.mq5” 也附在下面。
void Train(void) { //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9);
在方法主体中,我们首先生成一个从训练集中选择通验的概率向量,按通验的盈利能力排序。之后,我们声明必要的局部变量。
vector<float> result, target, state; bool Stop = false;
接下来,我们添加一个变量,指示一个子集训练批次的大小。
int Batch = 100;
然后我们创建一个嵌套循环系统。在外循环中,我们从训练集中采样一条轨迹,并在该轨迹上采样训练子集的起始状态。
uint ticks = GetTickCount(); //--- for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter += Batch) { int tr = SampleTrajectory(probability); int st = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - NForecast)); if(st <= 0) { iter -= Batch; continue; }
我们清除 LSTM 模块的隐藏状态和上下文缓冲区。
Encoder.Clear();
之后,我们运行一个嵌套循环,从所选环境的状态开始,按顺序迭代其历史序列中的状态。
for(int i = st; (i < MathMin(st + Batch, Buffer[tr].Total - NForecast) && !IsStopped() && !Stop); i++) { state.Assign(Buffer[tr].States[i].state); if(MathAbs(state).Sum() == 0) { iter += i - st - Batch; break; } bState.AssignArray(state);
在嵌套循环的主体中,我们将环境的所分析状态传输到数据缓冲区。基于获得的数据,我们预测下一个价格走势轨迹。
//--- State Encoder if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
然后,我们从经验回放缓冲区加载下一条轨迹的目标值。
//--- Collect target data if(!Result.AssignArray(Buffer[tr].States[i + NForecast].state)) continue; if(!Result.Resize(BarDescr * NForecast)) continue;
接下来,我们检查预测的准确性。在反向传播过程中,我们调整模型参数,朝向下一个走势的预测误差最小化。
if(!Encoder.backProp(Result, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
告知用户学习过程的进度,并转到循环系统的下一次迭代。
if(GetTickCount() - ticks > 500) { double percent = double(iter + i - st) * 100.0 / (Iterations); string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Encoder", percent, Encoder.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } } }
循环系统的所有迭代成功完成之后,我们清除品种图表上的注释字段。我们将训练结果输出到终端日志,并初始化智能系统关闭。
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Encoder", Encoder.getRecentAverageError()); ExpertRemove(); //--- }
对参与者和评价者训练 EA 进行了类似的编辑。尽管这些模型没有添加递归模块,但进行这些编辑对于确保环境状态编码器的正确操作是必要的。这是因为参与者和评价者均将其当作输入数据。
您可在附件中找到模型训练 EA 的完整代码。附件还包含本文中用到的所有程序、类和方法的完整代码。
3. 测试
在本文中,我们探索了一种使用 TPM 预测即将到来的股票轨迹的方法,并实现了我们对所提议方法的解释。现在是时候依据真实数据来测试我们的工作成果了。如常,我们依据 EURUSD 的 2023 年 H1 时间帧历史数据,训练所展示的模型。
我们首先训练环境编码器模型,该模型分析历史价格走势数据,且不评估参与者的动作。这种方式令我们能够在初始数据集上完全训练模型,而无需频繁更新。训练过程相对较迅速,并展现出良好的效果。下图比较了预测和实际价格走势轨迹。
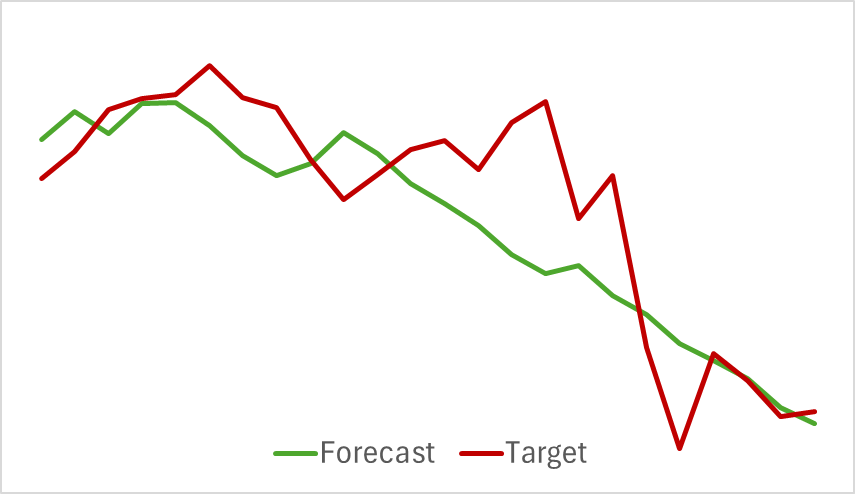
该图表显示了两条线的紧密重叠,预测的轨迹看起来更平滑。这种平滑效果有可能增强参与者训练的稳定性。
如您所知,我们的主要意图是优化参与者的政策。训练环境编码器之后,我们转到训练过程的第二阶段 — 参与者政策训练。该过程本质上是迭代的。由于参与者的动作会有所变化,且可能会超出之前收集的训练数据的边界,因此我们需要定期更新经验回放缓冲区,方法是在其中填充更接近参与者当前政策动作的状态和奖励。
在针对参与者和评价者模型进行多次交替迭代训练,并更新训练数据集之后,我们开发出一项能够在历史训练数据上产生盈利的政策。
为了评估模型在训练数据集之外的性能,我们采用 2024 年 1 月的历史数据对其进行了测试,同时保持其它条件不变。
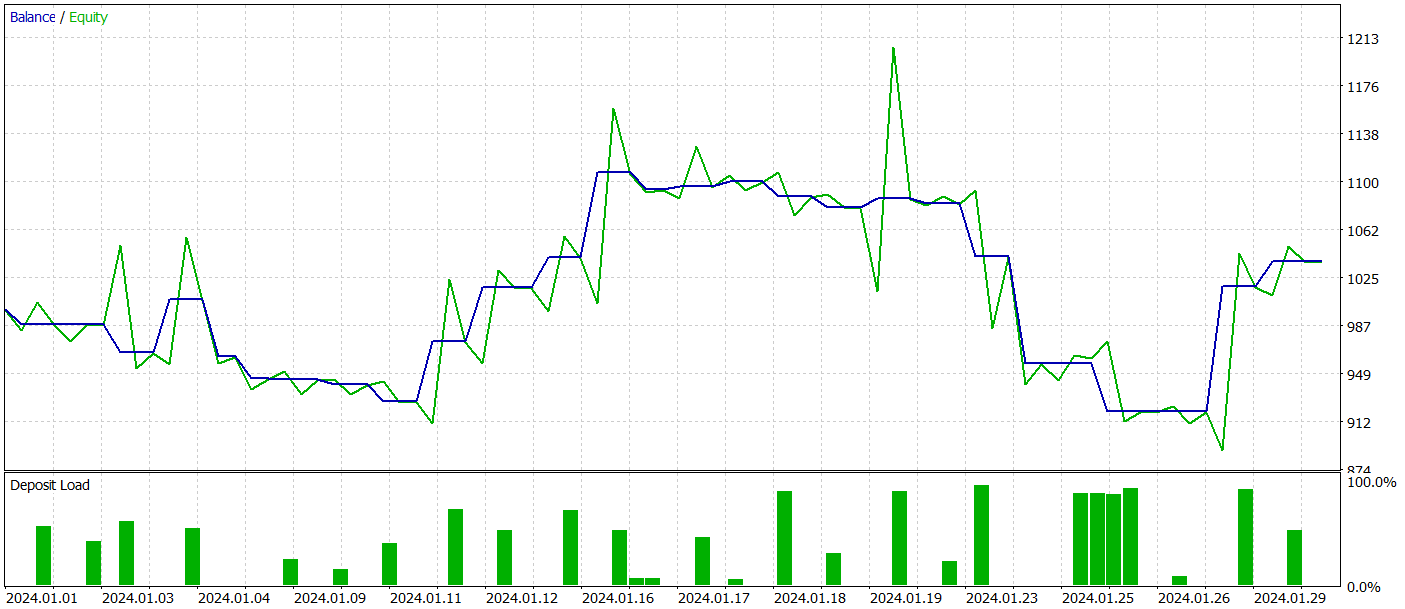
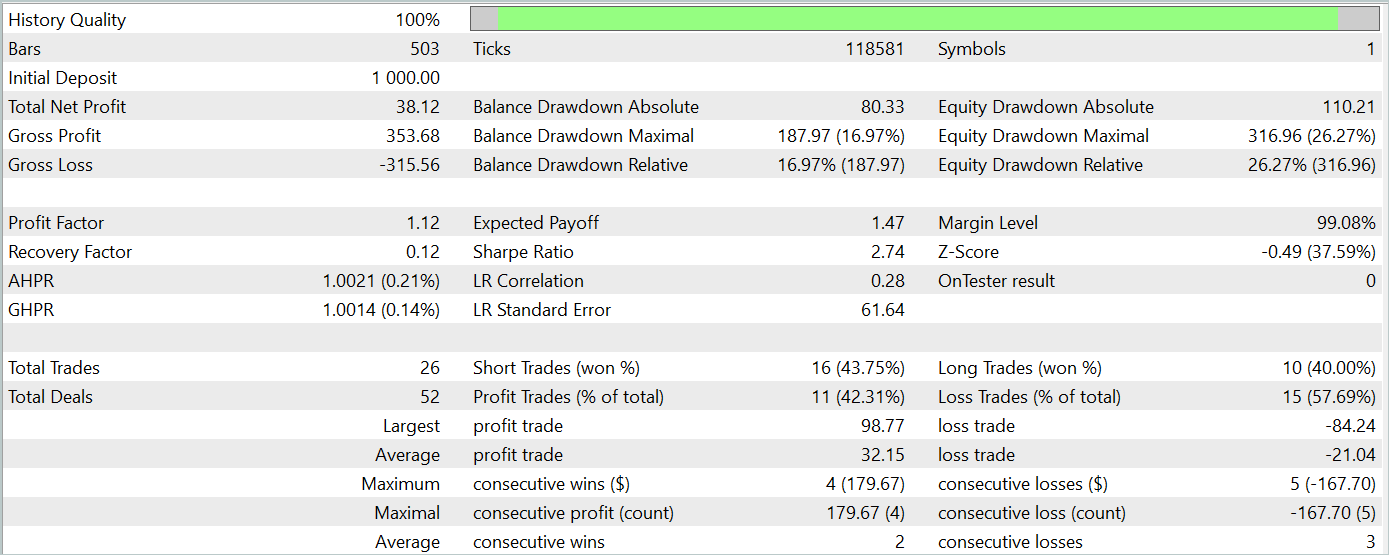
在测试期间,该模型执行了 26 笔交易,其中只有 11 笔是盈利的,即略高于 42%。然而,每笔交易的最大和平均盈利都超过了相应的亏损计量值,成果就是测试期间的整体盈利。测试期间的盈利因子为 1.12。
尽管如此,在本月第三旬的早期部分,余额图表显示出大幅回撤。这引发了担忧。尽管产生了盈利,但该模型仍需要进一步优调。
结束语
在本文中,我们探索了一种使用 TPM 预测价格走势趋势的有趣方法。这种方法有效地把分析短期依赖关系的卷积模型,及识别长期趋势的 PLR 的优势相结合。
在本文的实践部分,我们利用 MQL5 实现了对提议方式的解释,训练了模型,并进行了测试。结果表明,经过训练的模型能够在训练数据集之外的数据上产生盈利。然而,余额图表并未展现出所期待的持续上升趋势,并且有回撤。
总体来说,虽然所提议方法展现出潜力,但我们开发的模型仍需进一步优调。
参考
文章中所用程序
| # | 名称 | 类型 | 说明 |
|---|---|---|---|
| 1 | Research.mq5 | EA | 样本收集 EA |
| 2 | ResearchRealORL.mq5 | EA | 利用 Real ORL方法收集样本的 EA |
| 3 | Study.mq5 | EA | 模型训练 EA |
| 4 | StudyEncoder.mq5 | EA | 编码器训练 EA |
| 5 | Test.mq5 | EA | 模型测试 EA |
| 6 | Trajectory.mqh | 类库 | 系统状态描述结构 |
| 7 | NeuroNet.mqh | 类库 | 创建神经网络的类库 |
| 8 | NeuroNet.cl | 代码库 | OpenCL 程序代码库 |
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/15255
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 创建 MQL5-Telegram 集成 EA 交易 (第一部分):从 MQL5 发送消息到 Telegram
创建 MQL5-Telegram 集成 EA 交易 (第一部分):从 MQL5 发送消息到 Telegram
 交易中的神经网络:时空神经网络(STNN)
交易中的神经网络:时空神经网络(STNN)

