ニューラルネットワークが簡単に（第22部）：回帰モデルの教師なし学習
553
0
内容
はじめに
前々回、前回とオートエンコーダを取り上げましました。そのアーキテクチャにより、バックプロパゲーションアルゴリズムを用いてラベルのないデータに対して様々なニューラルネットワークモデルを訓練することが可能です。このモデルは、主要な特徴を選択しながら、初期データを圧縮することを学習します。実験により、オートエンコーダモデルの有効性が確認されましました。オートエンコーダの学習には、完全連結ニューラルレイヤーを使用していることに注意してください。このようなモデルは、固定された入力データウィンドウで動作します。今回構築したアルゴリズムは、固定入力データウィンドウで動作する任意のモデルを訓練することができます。しかし、回帰モデルのアーキテクチャは異なります。このようなモデルでは、ニューロンの活性化を判断するために、初期データに加えて、その前の状態も利用します。この特徴は、オートエンコーダを構築する際に考慮する必要があります。
1.回帰モデルの学習の特徴
まず、回帰モデルの構成とその目的について思い出してみましょう。価格チャートを見てみましょう。値動きに関連する過去のデータを表示します。各バーは、銘柄の価格が特定の時間間隔で変動する範囲の境界を記述したものです。これは「過去のデータ」なので、変わることはありません。時間が経つと新しいバーが現れますが、古いバーは変わりません。各時点には、変更されない過去のデータと、完全に形成されておらず、その時間間隔が閉じるまで変化する可能性がある最後の1つのローソク足があります。
過去のデータを分析することで、最も可能性の高い将来の値動きを予測しようとします。分析された履歴の深さは、それぞれの場合で異なります。これは、初期データ量が固定されたニューラルネットワークの使用に関する主要な問題の1つであると思われます。過去のデータウィンドウが小さいため、分析の可能性が制限されます。ウィンドウが大きすぎると、モデルとその学習が複雑になります。したがって、入力データウィンドウの大きさを選択する場合、このようなモデルの設計者は妥協して「黄金平均」を決定しなければなりません。
一方、ここで扱っているのは過去のデータです。どのようなウィンドウサイズを選んでも、モデルの繰り返しで、99%以上の情報を再送信することになります。そして、このデータをモデルが再処理します。資源の有効活用とは言えません。ただし、完全連結型も畳み込み型も、以前に処理した情報については何も覚えていません。
上記の問題は、回帰ネットワークを活用することで解決することができます。考え方は次の通りです。各ニューロンの状態は、原始データの処理結果に依存するため、ニューロンの状態は原始データを圧縮したものであると考えることができます。したがって、前の状態と一緒に原始データをニューロンに送り込むことができます。ニューロンの新しい状態は、解析しているシステムの現在の状態と、ニューロンの以前の状態の両方に依存し、その情報はニューロンの以前の状態に圧縮されています。
この方法によって、モデルはシステムの複数の状態を記憶することができます。活性化関数と絶対値が1以下の重み係数を使用することで、最も古い過去のデータの影響を徐々に軽減することができます。その結果、かなり予測可能なメモリホライズンを持つモデルが出来上がりましました。
このようなメモリを使ったモデルを使うことで、意思決定に使う過去データのウィンドウに制限されることがありません。また、モデルがすでに記憶しているため、再送信される情報量を減らすことができます。このような利点から、回帰モデルは時系列処理問題の解決において優先度の高い分野の一つと見なすことができます。
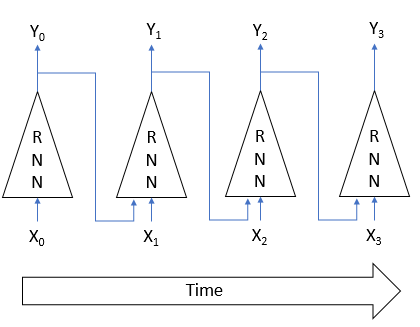
しかし、これらの特徴を利用するためには、特殊な回帰モデルの訓練方法が必要となります。例えば、オートエンコーダのアーキテクチャに話を戻すと、上図のモデルの入力Xiと出力Yiを等しくすると、潜在状態から元のデータを復元するために、前の状態を覚えておく必要はありません。したがって、このモデルでは、学習過程における過去のデータの影響を無効化することができます。現在の状態を評価するだけです。回帰モデルが記憶する能力を失えば、その主な利点は失われることになるので、
モデルアーキテクチャを開発する際には、この事実を考慮する必要があります。学習プロセスは、モデルが以前の反復のデータにアクセスすることを余儀なくされるように組織化されるべきです。
オートエンコーダの構築では、ほとんどの場合、デコーダアーキテクチャはエンコーダアーキテクチャとほぼ同じになります。回帰モデルを扱う際にも、同様の慣行が守られます。奇妙なことに、このようなアーキテクチャの最初の1つは、教師あり学習で使用されましました。「Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation」と題された論文の著者らは、統計的機械翻訳のモデルとしてRNNエンコーダとデコーダを提案しました。このモデルのエンコーダとデコーダは回帰ネットワークです。エンコーダは、原語のフレーズをある潜在的な状態に圧縮し、デコーダはそれをターゲット言語のフレーズに「解きほぐします」。オートエンコーダとよく似ています。
回帰モデルを用いることで、フレーズを1語ずつエンコーダに転送することができ、様々な長さのフレーズでモデルを訓練することが可能になりました。完全なフレーズを受信したエンコーダは、潜在的な状態をデコーダに送信しました。また、デコーダは1語ずつ、そのフレーズの訳語をターゲット言語で伝えました。
英語とフランス語のラベル付きフレーズで訓練した結果、意味的にも構文的にも意味のあるフレーズを返すことができるモデルを得ることができました。
回帰モデルの教師なし学習については、2015年2月に公開された論文「Unsupervised Learning of Video Representations using LSTMs」でよく紹介されています。この論文の著者らは、様々な映像素材に対して回帰オートエンコーダを訓練する一連の実験をおこないました。エンコーダに入力されたデータの復元と、ビデオシーケンスの継続の可能性を予測することの両方が実行されました。
記事では、オートエンコーダの様々なアーキテクチャを紹介されていますが、これらはすべて、信号のエンコードとデコードにLSTMブロックを使用しています。1つのエンコーダと2つのデコーダでモデルを訓練した場合、最良の結果が得られました。1つのデコーダが原始データの復元を担当し、2つ目のデコーダが最も可能性の高い映像シーケンスの続きを予測します。
エンコーダに回帰ブロックを使用することで、元の映像をフレーム単位でモデルに転送することができます。タスクに応じて、回帰デコーダブロックは、フレームごとに再構成または予測されたビデオシーケンスを返します。
さらに、教師なしアルゴリズムで事前訓練した回帰モデルは、教師ありアルゴリズムで追加訓練した後、比較的少量のラベル付きデータでも、ビデオの動き認識に関するタスクで非常に良い結果をもたらすことを論文の著者は示しています。
この2つの論文で紹介された資料は、このようなアプローチが私たちの問題解決に成功することを示唆していますが、
私の実装では、提案されたモデルから若干の逸脱をすることになります。いずれも復号器に回帰ブロックを使用し、フレーム単位で復号したデータを返していました。これは、翻訳と映像解析のタスクに完全に対応するものでした。次のバーを予測するのに良い結果をもたらすかもしれませんが、私はまだそのような実験をしていません。一般に、市場の状況を分析する場合、かなり長い時間間隔をカバーする全体像として評価しますため、市場の状況の変化を少しずつモデルに移していくことになります。そうすると、モデルは現在と過去に受け取ったデータを考慮して状況を評価する必要があります。つまり、潜在的な状態には、可能な限り広い時間間隔に関する情報が含まれている必要があるということです。
この効果を得るために、エンコーダにのみ回帰ブロックを使用することにします。デコーダでも、全結合のニューラルレイヤーを用いながら、エンコーダに転送されたデータを数回の反復で復元していきます。
2.実装
次に、この記事の実践部分に移ります。先に説明したLSTMブロックを基礎に回帰エンコーダを構築していきますが、その構造は下図の通りです。ブロックは4つの完全連結ニューラルレイヤーで構成されています。そのうち3つは、情報の流れを規制するゲートの機能を果たしています。4つ目は原始データを変換します。
LSTMブロックは、メモリと隠れ状態の2つの回帰情報の流れを使用します。
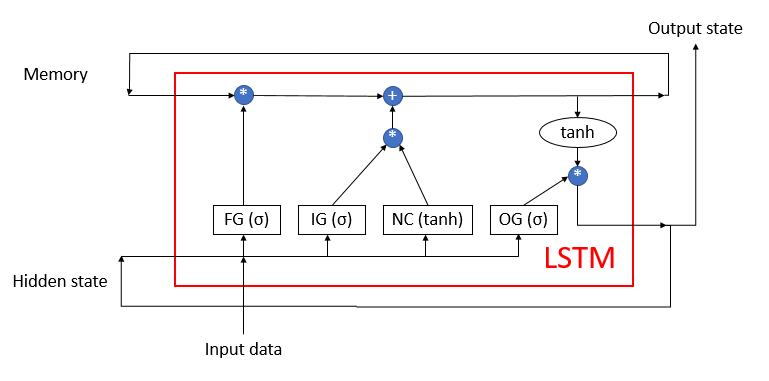
以前、MQL5を用いてLSTMブロックアルゴリズムを再現したことがあります。今度はOpenCLの技術を使って、それを繰り返してみます。このアルゴリズムを実装するために、新しいクラスCNeuronLSTMOCLを作成します。親クラスとなるCNeuronBaseOCLから、バッファとメソッドの主要なセットを継承します。
以下に、メソッドとクラス変数の構造を示します。クラスメソッドは非常にわかりやすいです。これらは、新しいクラスごとにオーバーライドするフィードフォワードおよびバックワードメソッドです。変数の目的について説明する必要があります。
class CNeuronLSTMOCL : public CNeuronBaseOCL { protected: CBufferFloat m_cWeightsLSTM; CBufferFloat m_cFirstMomentumLSTM; CBufferFloat m_cSecondMomentumLSTM; int m_iMemory; int m_iHiddenState; int m_iConcatenated; int m_iConcatenatedGradient; int m_iInputs; int m_iWeightsGradient; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronLSTMOCL(void); ~CNeuronLSTMOCL(void); //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons, ENUM_OPTIMIZATION optimization_type, uint batch) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual int Type(void) override const { return defNeuronLSTMOCL; } };
まず、ここに3つのデータバッファがあることがわかります。
- m_cWeightsLSTM - LSTMブロックの重み係数の行列
- m_cFirstMomentumLSTM - 重みを更新するための最初の運動量の行列
- m_cSecondMomentumLSTM - 重みを更新するための第二運動量の行列
以下にご注目ください。前述の通り、LSTMブロックには4つの完全連結ニューラルレイヤーが含まれています。同時に、重み行列のためのバッファを1つだけ宣言します。m_cWeightsLSTMです。このバッファには、4つのニューラルレイヤーすべての重みが格納されます。連結バッファを使うことで、4つのニューラルレイヤーすべてを同時に並列化することができるようになります。並列整理の仕組みについては、もう少し後で各方式の実装を考える際に詳しく検討することにしましょう。
運動量バッファm_cFirstMomentumLSTMとm_cSecondMomentumLSTMについても同様です。
最新のターミナルビルドでメタクォーツ社は多くの改良を実装しました。また、ここで使用しているOpenCLの技術にも影響を与えました。特に、OpenCLのオブジェクトの最大数を増やし、doubleサポートのないビデオカードでも利用できるようになりました。これにより、各カーネルを呼び出す前にCPUのメモリからデータをロードしたり、実行後にデータをアンロードして戻す必要がなくなるため、モデルの訓練に要する総時間を短縮することができます。訓練処理を開始する前に、すべての初期データを一旦OpenCLのコンテキストメモリにロードし、訓練終了後に結果をコピーすれば十分です。
さらに、デバイスのメインメモリにミラーバッファを作成することなく、OpenCLのコンテキストだけでいくつかのバッファを宣言できるようになります。これは一時的な情報を保存するためのバッファのことです。したがって、多数のバッファに対して、OpenCLコンテキストにバッファへのポインタを格納する変数を作成するのみです。
- m_iMemory - メモリバッファへのポインタ
- m_iHiddenState - 非表示状態バッファへのポインタ
- m_iConcatenated - 4つの内部ニューラルレイヤーを連結した結果バッファへのポインタ
- m_iConcatenatedGradient - 4つの内部ニューラルレイヤーの結果のレベルで誤差勾配を連結したバッファへのポインタ
- m_iWeightsGradient - 4つの内部ニューラルレイヤーの重み行列レベルの誤差勾配のバッファへのポインタ
クラスのコンストラクタで、すべての変数に初期値を代入しています。
CNeuronLSTMOCL::CNeuronLSTMOCL(void) : m_iMemory(-1), m_iConcatenated(-1), m_iConcatenatedGradient(-1), m_iHiddenState(-1), m_iInputs(-1) {}
クラスのデストラクタでは，使用中のバッファをすべて解放しています。
CNeuronLSTMOCL::~CNeuronLSTMOCL(void) { if(!OpenCL) return; OpenCL.BufferFree(m_iConcatenated); OpenCL.BufferFree(m_iConcatenatedGradient); OpenCL.BufferFree(m_iHiddenState); OpenCL.BufferFree(m_iMemory); OpenCL.BufferFree(m_iWeightsGradient); m_cFirstMomentumLSTM.BufferFree(); m_cSecondMomentumLSTM.BufferFree(); m_cWeightsLSTM.BufferFree(); }
クラスメソッドの実装の続きとして、LSTMブロックのオブジェクトを初期化するメソッドを作成しましょう。継承の規則に従い、親クラスの類似メソッドのパラメータを保持したままCNeuronLSTMOCL::Initメソッドをオーバーライドします。初期化メソッドは、次の層のニューロン数、ニューロンのインデックス、OpenCLコンテキストオブジェクトへのポインタ、現在の層のニューロン数、パラメータ最適化方法、バッチサイズをパラメータとして受け取ります。
メソッド本体では、まず親クラスの同様のメソッドを呼び出して、親クラスの継承オブジェクトを初期化し、受信した初期データを制御することになります。操作実行結果に確認するのも忘れてはいけません。
次に、上で宣言したデータバッファを初期化する必要があります。この段階では、必要な原始データがないため、すべてのバッファを完全に初期化することはできません。パラメータには、現在の層のニューロン数、次の層のニューロン数を受け取りますが、前の層のニューロン数は分からないため、LSTMブロックの重みを格納するために必要なバッファのサイズはわかりません。そこで、この段階では、現在の層の要素数だけに依存するサイズのデータバッファだけを作成します。
bool CNeuronLSTMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, numNeurons, optimization_type, batch)) return false; //--- m_iMemory = OpenCL.AddBuffer(sizeof(float) * numNeurons * 2, CL_MEM_READ_WRITE); if(m_iMemory < 0) return false; m_iHiddenState = OpenCL.AddBuffer(sizeof(float) * numNeurons, CL_MEM_READ_WRITE); if(m_iHiddenState < 0) return false; m_iConcatenated = OpenCL.AddBuffer(sizeof(float) * numNeurons * 4, CL_MEM_READ_WRITE); if(m_iConcatenated < 0) return false; m_iConcatenatedGradient = OpenCL.AddBuffer(sizeof(float) * numNeurons * 4, CL_MEM_READ_WRITE); if(m_iConcatenatedGradient < 0) return false; //--- return true; }
各ステップで結果を制御することを忘れないでください。
オブジェクトの初期化メソッドを作成した後、LSTMブロックのフィードフォワードパスの編成に移ります。ご存知のように、OpenCL技術を用いると、GPU上のOpenCLコンテキストで直接計算がおこなわれます。メインプログラムのコードでは、必要なプログラムを呼び出すだけです。したがって、クラスのメソッドを書く前に、適切なカーネルでOpenCLプログラムを補う必要があります。
LSTM_FeedForwardカーネルは、OpenCLプログラムの中でフィードフォワードパスの編成を担当することになります。処理を正しく整理するために、5つのデータバッファへのポインタと1つの定数をカーネルに与えます。
- inputs - ソースデータバッファ
- inputs_size - ソースデータバッファの要素数
- weights -重み行列バッファ
- concatenated -すべての内部層の結果を連結したバッファ
- memory - メモリバッファ
- output — 結果バッファ（隠れ状態バッファを兼ねる）
__kernel void LSTM_FeedForward(__global float* inputs, uint inputs_size, __global float* weights, __global float* concatenated, __global float* memory, __global float* output ) { uint id = (uint)get_global_id(0); uint total = (uint)get_global_size(0); uint id2 = (uint) get_local_id(1);
バッファを2次元のタスク空間で実行することにします。1次元目では、現在のLSTMブロックの要素数を示すことにします。2次元目は、内部のニューラルレイヤーの数によって4つのスレッドに等しくなります。なお、LSTMブロックの要素数は、各内部層の要素数だけでなく、メモリや隠れ状態の要素数も決定します。
そこで、カーネル本体では、まず、各次元でのスレッドの序数を決定します。また、1次元のタスク数を決定します。
LSTMブロックのフィードフォワード処理全体は、条件付きで2つのサブプロセスに分けることができます。
- 内部ニューラルレイヤーの値計算
- ニューラルレイヤーからLSTMブロック出力へのデータフローの実装
最初の処理が完全に終了するまで、2番目の処理の実行は不可能です。これは、第2サブプロセスの実行には、少なくとも現在のLSTMブロック要素内で、4つのニューロンすべての値が必要だからです。そのため、2次元に沿ったデータスレッドの同期が必要です。現在のOpenCLの実装では、ローカルグループ内でのスレッド同期が可能なため、2つ目の次元のタスクに従って、ローカルグループを構築していきます。
次に、原始データと隠された状態の加重和の計算を実装します。まず、隠れ状態の加重和を計算します。
float sum = 0; uint shift = (id + id2 * total) * (total + inputs_size + 1); for(uint i = 0; i < total; i += 4) { if(total - i > 4) sum += dot((float4)(output[i], output[i + 1], output[i + 2], output[i + 3]), (float4)(weights[shift + i], weights[shift + i + 1], weights[shift + i + 2], weights[shift + i + 3])); else for(uint k = i; k < total; k++) sum += output[k] + weights[shift + k]; }
そして、初期データの加重和を加算します。
shift += total; for(uint i = 0; i < inputs_size; i += 4) { if(total - i > 4) sum += dot((float4)(inputs[i], inputs[i + 1], inputs[i + 2], inputs[i + 3]), (float4)(weights[shift + i], weights[shift + i + 1], weights[shift + i + 2], weights[shift + i + 3])); else for(uint k = i; k < total; k++) sum += inputs[k] + weights[shift + k]; } sum += weights[shift + inputs_size];
最後に、バイアスニューロンの値を追加します。
加重和を計算した後、活性化関数の値を計算します。ゲートの活性化関数としてシグモイドが使用されています。新しいコンテンツ層には双曲線タンジェントが使用されます。必要な活性化関数は、2次元目のスレッド識別子によって決定されます。
if(id2 < 3) concatenated[id2 * total + id] = 1.0f / (1.0f + exp(sum)); else concatenated[id2 * total + id] = tanh(sum); //--- barrier(CLK_LOCAL_MEM_FENCE);
前述したように、アルゴリズムを正しく実行するためには、タスク空間の2次元に沿ったスレッドの同期が必要です。barrier関数を使用してスレッドを同期させます。
内部層間の情報伝達の処理を実装するためには、LSTMブロックの各要素に対して1つのスレッドがあればよいのです。したがって、スレッドが同期された後は、タスク空間の2次元目でスレッドIDが0のスレッドに対してのみ処理が実行されることになります。
if(id2 == 0) { float mem = memory[id + total] = memory[id]; float fg = concatenated[id]; float ig = concatenated[id + total]; float og = concatenated[id + 2 * total]; float nc = concatenated[id + 3 * total]; //--- memory[id] = mem = mem * fg + ig * nc; output[id] = og * tanh(mem); } //--- }
これでフォワードパスカーネルとの連携は完了です。メインプログラムから呼び出すことができるようになりました。まず、必要な定数を作成します。
#define def_k_LSTM_FeedForward 32 #define def_k_lstmff_inputs 0 #define def_k_lstmff_inputs_size 1 #define def_k_lstmff_weights 2 #define def_k_lstmff_concatenated 3 #define def_k_lstmff_memory 4 #define def_k_lstmff_outputs 5
次に、このクラスのフィードフォワードパスメソッドの作成に取り掛かります。このメソッドも、以前に考えた他のクラスの同じメソッドと同様に、パラメータに前のニューラルレイヤーのオブジェクトへのポインタを受け取りました。メソッド本体で、すぐにポインタを検証する必要があります。
bool CNeuronLSTMOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL || NeuronOCL.Neurons() <= 0 || NeuronOCL.getOutputIndex() < 0 || !OpenCL) return false;
クラスを初期化する際、前の層のニューロン数が分からないため、全てのデータバッファを初期化することができませんでしました。これで、前のニューラルレイヤーへのポインタができたので、この層のニューロン数を要求し、必要なデータバッファを作成することができます。その前に、バッファがまだ先に作成されていないことを確認します。このフィードフォワードのメソッド呼び出しは、最初のものでなくてもかまいません。前の層の要素数を含む変数が、一種のフラグとして機能することになります。
if(m_iInputs <= 0) { m_iInputs = NeuronOCL.Neurons(); int count = (int)((m_iInputs + Neurons() + 1) * Neurons()); if(!m_cWeightsLSTM.Reserve(count)) return false; float k = (float)(1 / sqrt(Neurons() + 1)); for(int i = 0; i < count; i++) { if(!m_cWeightsLSTM.Add((2 * GenerateWeight()*k - k)*WeightsMultiplier)) return false; } if(!m_cWeightsLSTM.BufferCreate(OpenCL)) return false; //--- if(!m_cFirstMomentumLSTM.BufferInit(count, 0)) return false; if(!m_cFirstMomentumLSTM.BufferCreate(OpenCL)) return false; //--- if(!m_cSecondMomentumLSTM.BufferInit(count, 0)) return false; if(!m_cSecondMomentumLSTM.BufferCreate(OpenCL)) return false; if(m_iWeightsGradient >= 0) OpenCL.BufferFree(m_iWeightsGradient); m_iWeightsGradient = OpenCL.AddBuffer(sizeof(float) * count, CL_MEM_READ_WRITE); if(m_iWeightsGradient < 0) return false; } else if(m_iInputs != NeuronOCL.Neurons()) return false;
準備作業が終わったら、データバッファへのポインタと必要な定数の値をフィードフォワードカーネルのパラメータに渡します。操作の実行を制御することを忘れないでください。
if(!OpenCL.SetArgumentBuffer(def_k_LSTM_FeedForward, def_k_lstmff_inputs, NeuronOCL.getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_FeedForward, def_k_lstmff_concatenated, m_iConcatenated)) return false; if(!OpenCL.SetArgument(def_k_LSTM_FeedForward, def_k_lstmff_inputs_size, m_iInputs)) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_FeedForward, def_k_lstmff_memory, m_iMemory)) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_FeedForward, def_k_lstmff_outputs, getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_FeedForward, def_k_lstmff_weights, m_cWeightsLSTM.GetIndex())) return false;
次に、問題空間とその中での1回目の反復までのシフトを定義します。この場合、問題空間を2次元で指定し、組み合わせる局所群の大きさを2次元で指定します。最初のケースでは、1次元の現在の層要素の合計数を指定します。ローカルグループの場合、1次元目の要素は1つだけ指定します。2次元目では、いずれの場合も内部のニューラルレイヤーの数に応じて4つの要素を示しています。これによって、4スレッドずつのローカルグループを作ることができます。このようなローカルグループの数は、現在のニューラルレイヤーの要素数と同じになります。
uint global_work_offset[] = {0, 0}; uint global_work_size[] = {Neurons(), 4}; uint local_work_size[] = {1, 4};
このように、各ローカルグループのスレッドを同期させることで、4つの内部ニューラルレイヤーすべての値の計算を、現在の層の個々の要素の文脈で同期させているのです。これは、LSTMブロック全体のフィードフォワードパスの正しい計算を実装するのに十分なものです。
次に、カーネルを実行キューに入れます。
if(!OpenCL.Execute(def_k_LSTM_FeedForward, 2, global_work_offset, global_work_size, local_work_size)) return false; //--- return true; }
これでLSTMブロックのフィードフォワードパスは終了し、バックプロパゲーションパスの実装に移ることができます。先ほどのケースと同様に、クラスメソッドを作成する前にOpenCLのプログラムを補足する必要があります。フィードフォワードパスでは、フォワードパス全体を1つのカーネルにまとめることに成功したのですが、今回は3つのカーネルが必要です。
最初のカーネルLSTM_ConcatenatedGradientで、内部層の結果に戻って勾配の伝搬を実装します。パラメータでは、カーネルは4つのデータバッファへのポインタを受け取ります。そのうちの3つは、次の層からの勾配のバッファ、メモリの状態、内部ニューラルレイヤーの結果の連結バッファという初期データを格納することになります。4番目のバッファは、カーネル操作の結果を書き込むために使用されます。
カーネルは、LSTMブロックの要素数に応じて、1次元の問題空間で呼び出されることになります。
カーネル本体では、まずスレッド識別子とスレッドの総数を定義します。そして、信号のバックプロパゲーション経路に沿って移動し、出力ゲートの結果レベル、メモリレベル、新コンテンツニューラルレイヤーのレベル、新コンテンツゲートのレベルで、誤差勾配を求めます。そして、その誤差をゲート忘れレベルで判断します。
__kernel void LSTM_ConcatenatedGradient(__global float* gradient, __global float* concatenated_gradient, __global float* memory, __global float* concatenated ) { uint id = get_global_id(0); uint total = get_global_size(0); float t = tanh(memory[id]); concatenated_gradient[id + 2 * total] = gradient[id] * t; //output gate float memory_gradient = gradient[id] * concatenated[id + 2 * total]; memory_gradient *= 1 - pow(t, 2.0f); concatenated_gradient[id + 3 * total] = memory_gradient * concatenated[id + total]; //new content concatenated_gradient[id + total] = memory_gradient * concatenated[id + 3 * total]; //input gate concatenated_gradient[id] = memory_gradient * memory[id + total]; //forget gate }
その後、LSTMブロックの内層を通して、前のニューラルレイヤーに誤差勾配を伝搬させる必要があります。これを実現するためにLSTM_HiddenGradientレベルを作成します。プログラムのOpenCLアーキテクチャを開発する際、このカーネルの中で、前の層のレベルと重み行列のレベルまで勾配分布を結合することにしたのです。つまり、カーネルは6つのデータバッファと2つの定数へのポインタをパラメータで受け取ることになります。カーネルは1次元の問題空間で呼び出されることになっています。
__kernel void LSTM_HiddenGradient(__global float* concatenated_gradient, __global float* inputs_gradient, __global float* weights_gradient, __global float* hidden_state, __global float* inputs, __global float* weights, __global float* output, const uint hidden_size, const uint inputs_size ) { uint id = get_global_id(0); uint total = get_global_size(0);
カーネル本体で、スレッド識別子とスレッドの総数を定義します。また、重み配列の1つのベクトルの大きさを決定します。
uint weights_step = hidden_size + inputs_size + 1;
次に、連結された入力データバッファのすべての要素をループします。このバッファには、隠れ状態と前のニューラルレイヤーから受け取った現在の状態が含まれています。ループの反復は現在のスレッドIDから始まり、反復ステップは実行中のスレッドの総数に等しくなります。この方法では、実行中のスレッドの数に関係なく、連結されたソースデータ層のすべての要素に対して反復処理をおこなうことができます。
for(int i = id; i < (hidden_size + inputs_size); i += total) { float inp = 0;
このステップでは、ループ本体で、解析対象要素に応じた演算スレッドの分割を実装しています。要素が非表示状態に属している場合は、非表示状態をprivate変数に保存します。次の繰り返しでは非表示状態になるため、結果バッファから該当する値をバッファに移す必要があります。
if(i < hidden_size)
{
inp = hidden_state[i];
hidden_state[i] = output[i];
}
現在の要素が前のニューロン層の入力データバッファに属する場合、初期データの値をprivate変数に転送し、前の層の対応するニューロンに対する誤差勾配を計算します。
else { inp = inputs[i - hidden_size]; float grad = 0; for(uint g = 0; g < 3 * hidden_size; g++) { float temp = concatenated_gradient[g]; grad += temp * (1 - temp) * weights[i + g * weights_step]; } for(uint g = 3 * hidden_size; g < 4 * hidden_size; g++) { float temp = concatenated_gradient[g]; grad += temp * (1 - pow(temp, 2.0f)) * weights[i + g * weights_step]; } inputs_gradient[i - hidden_size] = grad; }
誤差勾配を前のニューラルレイヤーに伝搬した後、誤差勾配を適切なLSTMブロックの重みに分配します。
for(uint g = 0; g < 3 * hidden_size; g++) { float temp = concatenated_gradient[g]; weights[i + g * weights_step] = temp * (1 - temp) * inp; } for(uint g = 3 * hidden_size; g < 4 * hidden_size; g++) { float temp = concatenated_gradient[g]; weights[i + g * weights_step] = temp * (1 - pow(temp, 2.0f)) * inp; } }
カーネルの最後に、各重みベクトルのバイアスニューロンへ誤差勾配を伝搬させます。
for(int i = id; i < 4 * hidden_size; i += total) { float temp = concatenated_gradient[(i + 1) * hidden_size]; if(i < 3 * hidden_size) weights[(i + 1) * weights_step] = temp * (1 - temp); else weights[(i + 1) * weights_step] = 1 - pow(temp, 2.0f); } }
誤差勾配を前のニューラルレイヤーレベルと重み行列に伝搬させた後、重みの更新処理を実行する必要があります。パラメータの最適化手法を全面的に実装しないことにしました。その代わり、私が最もよく使うAdam方式を実装することにします。私の実装と類似しているので、モデルパラメータを最適化するための他のメソッドを追加することができます。
モデルパラメータがLSTM_UpdateWeightsAdamカーネルで更新されます。重み行列レベルの誤差勾配は、既に前のレイヤで計算されており、その結果は重み勾配バッファに書き込まれます。そこで、このカーネルでは、モデルのパラメータを更新する処理だけを実装すればよいのです。Adam方式でパラメータ更新処理を実装するためには、第1運動量と第2運動量を記録するための2つのバッファを追加する必要があります。さらに、訓練用ハイパーパラメータが必要になります。このデータはカーネルパラメータで渡されます。
__kernel void LSTM_UpdateWeightsAdam(__global float* weights, __global float* weights_gradient, __global float *matrix_m, __global float *matrix_v, const float l, const float b1, const float b2 ) { const uint id = get_global_id(0); const uint total = get_global_size(0); const uint id1 = get_global_id(1); const uint wi = id1 * total + id;
ご存知のように、重み行列は2次元の行列です。そこで、2次元のタスク空間でカーネルを呼び出すことにします。
カーネル本体で、両次元でのスレッドの序数を決定し、1次元で動作しているスレッドの総数を決定します。これらの定数によって、目的の重さへのバッファのシフトを決定します。次に、アルゴリズムを実行して、重み行列の対応する要素を更新します。
float g = weights_gradient[wi]; float mt = b1 * matrix_m[wi] + (1 - b1) * g; float vt = b2 * matrix_v[wi] + (1 - b2) * pow(g, 2); float delta = l * (mt / (sqrt(vt) + 1.0e-37f) - (l1 * sign(weights[wi]) + l2 * weights[wi] / total)); weights[wi] = clamp(weights[wi] + delta, -MAX_WEIGHT, MAX_WEIGHT); matrix_m[wi] = mt; matrix_v[wi] = vt; };
ここでOpenCLプログラムの変更を終了し、メインプログラムでのメソッドの実装に移ります。
まず、上記で作成したカーネルと連動する定数を作成します。
#define def_k_LSTM_ConcatenatedGradient 33 #define def_k_lstmcg_gradient 0 #define def_k_lstmcg_concatenated_gradient 1 #define def_k_lstmcg_memory 2 #define def_k_lstmcg_concatenated 3 #define def_k_LSTM_HiddenGradient 34 #define def_k_lstmhg_concatenated_gradient 0 #define def_k_lstmhg_inputs_gradient 1 #define def_k_lstmhg_weights_gradient 2 #define def_k_lstmhg_hidden_state 3 #define def_k_lstmhg_inputs 4 #define def_k_lstmhg_weeights 5 #define def_k_lstmhg_output 6 #define def_k_lstmhg_hidden_size 7 #define def_k_lstmhg_inputs_size 8 #define def_k_LSTM_UpdateWeightsAdam 35 #define def_k_lstmuw_weights 0 #define def_k_lstmuw_weights_gradient 1 #define def_k_lstmuw_matrix_m 2 #define def_k_lstmuw_matrix_v 3 #define def_k_lstmuw_l 4 #define def_k_lstmuw_b1 5 #define def_k_lstmuw_b2 6
次に、クラスのメソッドに移ります。まず、誤差勾配バックプロパゲーションメソッドcalcInputGradientsを作成します。このメソッドは、前のニューラルネットワーク層のオブジェクトへのポインタをパラメータで受け取ります。受信したポインタの有効性を即座に確認します。
bool CNeuronLSTMOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL || NeuronOCL.Neurons() <= 0 || NeuronOCL.getGradientIndex() < 0 || NeuronOCL.getOutputIndex() < 0 || !OpenCL) return false;
OpenCLコンテキストに必要なデータバッファがあるかどうかを確認します。
if(m_cWeightsLSTM.GetIndex() < 0 || m_cFirstMomentumLSTM.GetIndex() < 0 || m_cSecondMomentumLSTM.GetIndex() < 0) return false; if(m_iInputs < 0 || m_iConcatenated < 0 || m_iMemory < 0 || m_iConcatenatedGradient < 0 || m_iHiddenState < 0 || m_iInputs != NeuronOCL.Neurons()) return false;
すべてのチェックが成功したら、カーネルコールに進みます。誤差勾配アルゴリズムに従い、最初にLSTM_ConcatenatedGradientカーネルを使用します。
まず、カーネルパラメータに初期データを転送します。
if(!OpenCL.SetArgumentBuffer(def_k_LSTM_ConcatenatedGradient, def_k_lstmcg_concatenated, m_iConcatenated)) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_ConcatenatedGradient, def_k_lstmcg_concatenated_gradient, m_iConcatenatedGradient)) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_ConcatenatedGradient, def_k_lstmcg_gradient, getGradientIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_ConcatenatedGradient, def_k_lstmcg_memory, m_iMemory)) return false;
は、問題空間の次元を定義します。カーネルを実行キューに入れます。
uint global_work_offset[] = {0}; uint global_work_size[] = {Neurons()}; if(!OpenCL.Execute(def_k_LSTM_ConcatenatedGradient, 1, global_work_offset, global_work_size)) return false;
ここでは、誤差勾配伝搬のための第二カーネルの呼び出し(LSTM_HiddenGradient)も実装していますカーネルにパラメータを渡します。
if(!OpenCL.SetArgumentBuffer(def_k_LSTM_HiddenGradient, def_k_lstmhg_concatenated_gradient, m_iConcatenatedGradient)) return false; if(!OpenCL.SetArgument(def_k_LSTM_HiddenGradient, def_k_lstmhg_hidden_size, Neurons())) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_HiddenGradient, def_k_lstmhg_hidden_state, m_iHiddenState)) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_HiddenGradient, def_k_lstmhg_inputs, NeuronOCL.getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_HiddenGradient, def_k_lstmhg_inputs_gradient, NeuronOCL.getGradientIndex())) return false; if(!OpenCL.SetArgument(def_k_LSTM_HiddenGradient, def_k_lstmhg_inputs_size, m_iInputs)) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_HiddenGradient, def_k_lstmhg_output, getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_HiddenGradient, def_k_lstmhg_weeights, m_cWeightsLSTM.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_HiddenGradient, def_k_lstmhg_weights_gradient, m_iWeightsGradient)) return false;
既に作成されている配列を使って問題空間を指定し、カーネルを実行キューに入れます。
if(!OpenCL.Execute(def_k_LSTM_HiddenGradient, 1, global_work_offset, global_work_size)) return false; //--- return true; }
繰り返しになりますが、すべての操作を忘れずに実装してください。これにより、誤差をタイムリーに追跡することができ、最も都合の悪い時にプログラムが終了してしまうことを防ぐことができます。
誤差勾配を伝播させた後、アルゴリズムを完成させるために、モデルパラメータを更新するためのupdateInputWeightsメソッドを実装する必要があります。このメソッドは、前の層のオブジェクトへのポインタをパラメータで受け取ります。しかし、すでに重み行列のレベルで誤差勾配を定義しています。したがって、前の層のオブジェクトへのポインタの存在は、データ転送の必要性よりも、むしろメソッドオーバーライドの実装に関係しています。この場合、受け取ったポインタの状態はメソッドの結果に影響を与えないので、チェックしません。代わりに、OpenCLのコンテキストで必要な内部バッファの可用性をチェックします。
bool CNeuronLSTMOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(!OpenCL || m_cWeightsLSTM.GetIndex() < 0 || m_iWeightsGradient < 0 || m_cFirstMomentumLSTM.GetIndex() < 0 || m_cSecondMomentumLSTM.GetIndex() < 0) return false;
次に、カーネルにパラメータを渡します。
if(!OpenCL.SetArgumentBuffer(def_k_LSTM_UpdateWeightsAdam, def_k_lstmuw_weights, m_cWeightsLSTM.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_UpdateWeightsAdam, def_k_lstmuw_weights_gradient, m_iWeightsGradient)) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_UpdateWeightsAdam, def_k_lstmuw_matrix_m, m_cFirstMomentumLSTM.GetIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_LSTM_UpdateWeightsAdam, def_k_lstmuw_matrix_v, m_cSecondMomentumLSTM.GetIndex())) return false; if(!OpenCL.SetArgument(def_k_LSTM_UpdateWeightsAdam, def_k_lstmuw_l, lr)) return false; if(!OpenCL.SetArgument(def_k_LSTM_UpdateWeightsAdam, def_k_lstmuw_b1, b1)) return false; if(!OpenCL.SetArgument(def_k_LSTM_UpdateWeightsAdam, def_k_lstmuw_b2, b2)) return false;
問題空間を定義し、カーネルを実行キューに入れます。
uint global_work_offset[] = {0, 0}; uint global_work_size[] = {m_iInputs + Neurons() + 1, Neurons()}; if(!OpenCL.Execute(def_k_LSTM_UpdateWeightsAdam, 2, global_work_offset, global_work_size)) return false; //--- return true; }
バックプロパゲーションアルゴリズムの整理に関する作業はこれで終わりです。クラスCNeuronLSTMOCLの最初のテストをする準備ができています。ただし、訓練したモデルを保存し、動作する状態に戻す必要があることが分かっているため、ファイル操作のためのメソッドを追加することにします。
これまでに検討したニューラルレイヤーのアーキテクチャと同様にSaveメソッドを使用してデータを保存します。パラメータに、データを書き込むためのファイルハンドルを受け取ります。
メソッド本体では、まず親クラスの同様のメソッドを呼び出します。そのため、ほぼ1行のコードで必要なすべてのコントロールが実装でき、親クラスから継承したオブジェクトの保存も可能です。親クラスのメソッド実行結果を確認します。
その後、前の層のニューロン数を保存します。また、重量と運動量の行列を保存します。
bool CNeuronLSTMOCL::Save(const int file_handle) { if(!CNeuronBaseOCL::Save(file_handle)) return false; if(FileWriteInteger(file_handle, m_iInputs, INT_VALUE) < sizeof(m_iInputs)) return false; if(!m_cWeightsLSTM.BufferRead() || !m_cWeightsLSTM.Save(file_handle)) return false; if(!m_cFirstMomentumLSTM.BufferRead() || !m_cFirstMomentumLSTM.Save(file_handle)) return false; if(!m_cSecondMomentumLSTM.BufferRead() || !m_cSecondMomentumLSTM.Save(file_handle)) return false; //--- return true; }
データを保存した後、保存したデータからオブジェクトを復元するためのロードメソッドを作成して、保存されたデータからオブジェクトを復元します。すでに述べたように、ファイルからのデータの読み出しは、書き込み順序に厳密に従ったものです。データ保存方式と同様に、ファイルを読み込むためのファイルハンドルをパラメータとして受け取りました。すぐに親クラスの同様のメソッドを呼び出します。
bool CNeuronLSTMOCL::Load(const int file_handle) { if(!CNeuronBaseOCL::Load(file_handle)) return false;
次に、前の層のニューロン数と、先に保存した重みと運動量のバッファを読み込みます。各バッファをロードした後、ミラーデータバッファの作成を開始します。OpenCLコンテキストの作成を開始します。操作の実行を制御することを忘れないでください。
m_iInputs = FileReadInteger(file_handle); //--- m_cWeightsLSTM.BufferFree(); if(!m_cWeightsLSTM.Load(file_handle) || !m_cWeightsLSTM.BufferCreate(OpenCL)) return false; //--- m_cFirstMomentumLSTM.BufferFree(); if(!m_cFirstMomentumLSTM.Load(file_handle) || !m_cFirstMomentumLSTM.BufferCreate(OpenCL)) return false; //--- m_cSecondMomentumLSTM.BufferFree(); if(!m_cSecondMomentumLSTM.Load(file_handle) || !m_cSecondMomentumLSTM.BufferCreate(OpenCL)) return false;
このメソッドは、ファイルからデータを読み込むだけでなく、訓練済みモデルの機能を完全に復元する必要があります。そのため、ファイルからデータを読み込んだ後、ファイルに保存されていない情報の一時的なデータバッファも作成する必要があります。
if(m_iMemory >= 0) OpenCL.BufferFree(m_iMemory); m_iMemory = OpenCL.AddBuffer(sizeof(float) * 2 * Neurons(), CL_MEM_READ_WRITE); if(m_iMemory < 0) return false; //--- if(m_iConcatenated >= 0) OpenCL.BufferFree(m_iConcatenated); m_iConcatenated = OpenCL.AddBuffer(sizeof(float) * 4 * Neurons(), CL_MEM_READ_WRITE); if(m_iConcatenated < 0) return false; //--- if(m_iConcatenatedGradient >= 0) OpenCL.BufferFree(m_iConcatenatedGradient); m_iConcatenatedGradient = OpenCL.AddBuffer(sizeof(float) * 4 * Neurons(), CL_MEM_READ_WRITE); if(m_iConcatenatedGradient < 0) return false; //--- if(m_iHiddenState >= 0) OpenCL.BufferFree(m_iHiddenState); m_iHiddenState = OpenCL.AddBuffer(sizeof(float) * Neurons(), CL_MEM_READ_WRITE); if(m_iHiddenState < 0) return false; //--- if(m_iWeightsGradient >= 0) OpenCL.BufferFree(m_iWeightsGradient); m_iWeightsGradient = OpenCL.AddBuffer(sizeof(float) * m_cWeightsLSTM.Total(), CL_MEM_READ_WRITE); if(m_iWeightsGradient < 0) return false; //--- return true; }
CNeuronLSTMOCLクラスメソッドでの操作は完了です。
次に、OpenCLのコンテキスト接続プロシージャに新しいカーネルを追加し、基盤となるニューラルレイヤーのディスパッチャメソッドに新しいタイプのニューラルレイヤーへのポインタを追加するだけです。
すべてのメソッドとクラスの完全なコードは、以下の添付ファイルにあります。
3.テスト
新しいニューラルレイヤークラスの準備ができたので、テスト訓練用のモデル作成に移ります。前回の変分オートエンコーダモデルを基に、新たに回帰オートエンコーダモデルを構築しました。そのモデルを「rnn_vae.mq5」という名前で新規ファイルに保存しました。エンコーダのアーキテクチャを変更し、そこに回帰LSTMブロックを追加しました。
回帰エンコーダの入力には、直近の10本のローソク足しか入力されないことに注意してください。
int OnInit() { //--- .................. .................. //--- Net = new CNet(NULL); ResetLastError(); float temp1, temp2; if(!Net || !Net.Load(FileName + ".nnw", dError, temp1, temp2, dtStudied, false)) { printf("%s - %d -> Error of read %s prev Net %d", __FUNCTION__, __LINE__, FileName + ".nnw", GetLastError()); HistoryBars = iHistoryBars; CArrayObj *Topology = new CArrayObj(); if(CheckPointer(Topology) == POINTER_INVALID) return INIT_FAILED; //--- 0 CLayerDescription *desc = new CLayerDescription(); if(CheckPointer(desc) == POINTER_INVALID) return INIT_FAILED; int prev = desc.count = 10 * 12; desc.type = defNeuronBaseOCL; desc.optimization = ADAM; desc.activation = None; if(!Topology.Add(desc)) return INIT_FAILED; //--- 1 desc = new CLayerDescription(); if(CheckPointer(desc) == POINTER_INVALID) return INIT_FAILED; desc.count = prev; desc.batch = 1000; desc.type = defNeuronBatchNormOCL; desc.activation = None; desc.optimization = ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 2 desc = new CLayerDescription(); if(CheckPointer(desc) == POINTER_INVALID) return INIT_FAILED; prev = desc.count = 500; desc.type = defNeuronLSTMOCL; desc.activation = None; desc.optimization = ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 3 desc = new CLayerDescription(); if(CheckPointer(desc) == POINTER_INVALID) return INIT_FAILED; prev = desc.count = prev/2; desc.type = defNeuronLSTMOCL; desc.activation = None; desc.optimization = ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 4 desc = new CLayerDescription(); if(CheckPointer(desc) == POINTER_INVALID) return INIT_FAILED; prev = desc.count = 50; desc.type = defNeuronLSTMOCL; desc.activation = None; desc.optimization = ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 5 desc = new CLayerDescription(); if(CheckPointer(desc) == POINTER_INVALID) return INIT_FAILED; desc.count = prev/2; desc.type = defNeuronVAEOCL; if(!Topology.Add(desc)) return INIT_FAILED; //--- 6 desc = new CLayerDescription(); if(CheckPointer(desc) == POINTER_INVALID) return INIT_FAILED; desc.count = (int) HistoryBars; desc.type = defNeuronBaseOCL; desc.activation = TANH; desc.optimization = ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 7 desc = new CLayerDescription(); if(CheckPointer(desc) == POINTER_INVALID) return INIT_FAILED; desc.count = (int) HistoryBars * 2; desc.type = defNeuronBaseOCL; desc.activation = TANH; desc.optimization = ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 8 desc = new CLayerDescription(); if(CheckPointer(desc) == POINTER_INVALID) return INIT_FAILED; desc.count = (int) HistoryBars * 4; desc.type = defNeuronBaseOCL; desc.activation = TANH; desc.optimization = ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- 9 desc = new CLayerDescription(); if(CheckPointer(desc) == POINTER_INVALID) return INIT_FAILED; desc.count = (int) HistoryBars * 12; desc.type = defNeuronBaseOCL; desc.activation = TANH; desc.optimization = ADAM; if(!Topology.Add(desc)) return INIT_FAILED; delete Net; Net = new CNet(Topology); delete Topology; if(CheckPointer(Net) == POINTER_INVALID) return INIT_FAILED; dError = FLT_MAX; } else { CBufferFloat *temp; Net.getResults(temp); HistoryBars = temp.Total() / 12; delete temp; } //--- .................. .................. //--- return(INIT_SUCCEEDED); }
この記事で以前に説明したように、回帰ブロックの訓練を整理するためには、モデルに「記憶」を調べさせるための条件を追加する必要があります。訓練のために、データスタックを作ってみましょう。そして、フィードフォワードパスの各反復の後、スタックから最も古いローソク足に関する情報を削除し、新しいローソク足に関する情報をスタックの最後に追加することになります。
したがって、スタックには常に、解析されたモデルの複数の履歴状態に関する情報が含まれることになります。履歴の深さは、外部パラメータで決定されます。このスタックを目標値としてオートエンコーダに渡すことになります。スタックサイズがエンコーダ入力の初期データの値を超えると、オートエンコーダは過去の状態のメモリを調べなければならなくなります。
.................. .................. Net.feedForward(TempData, 12, true); TempData.Clear(); if(!Net.GetLayerOutput(1, TempData)) break; uint check_total = check_data.Total(); if(check_total >= check_count) { if(!check_data.DeleteRange(0, check_total - check_count + 12)) return; } for(int t = TempData.Total() - 12 - 1; t < TempData.Total(); t++) { if(!check_data.Add(TempData.At(t))) return; } if((total-it)>(int)HistoryBars) Net.backProp(check_data); .................. ..................
モデルテストのパラメータは同じでした（EURUSD、H1、過去15年、指標のデフォルト設定）。エンコーダに過去10回分のローソク足に関するデータを入力します。デコーダは、過去40個のローソク足をデコードするように訓練されます。テスト結果は下のチャートのとおりです。新しいローソク足の形成が完了するたびに、エンコーダにデータが入力されます。
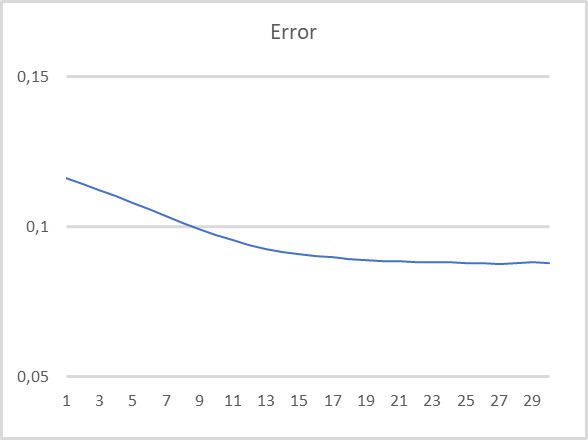
このチャートからわかるように、回帰モデルの教師なし事前学習において、この手法が有効であることが確認されましました。モデルのテスト訓練では、20回の訓練エポックの後、モデルの誤差は9%以下の損失率でほぼ安定しました。また、少なくとも過去30回の繰り返しに関する情報は、モデルの潜在的な状態に保存されます。
結論
今回は、オートエンコーダを用いた回帰モデルの学習について扱いましました。実践編では、回帰オートエンコーダを作成し、そのテスト訓練を実施しました。この実験の結果、オートエンコーダを用いた回帰モデルの教師なし学習に対する提案アプローチが実行可能であると結論付けることができます。このモデルは、テスト時に過去30回分のデータを復元し、かなり良い結果を示しました。
参考文献リスト
- ニューラルネットワークが簡単に（第4部）：回帰ネットワーク
- ニューラルネットワークが簡単に（第14部）：データクラスタリング
- ニューラルネットワークが簡単に（第15部）：MQL5によるデータクラスタリング
- ニューラルネットワークが簡単に（第16部）：クラスタリングの実用化
- ニューラルネットワークが簡単に（第17部）：次元削減
- ニューラルネットワークが簡単に（第18部）：アソシエーションルール
- ニューラルネットワークが簡単に（第19部）：MQL5を使用したアソシエーションルール
- ニューラルネットワークが簡単に（第20部）：オートエンコーダ
- ニューラルネットワークが簡単に（第21部）：バリエーションオートエンコーダ(VAE)
- Unsupervised Learning of Video Representations using LSTMs
- Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation
記事で使用されているプログラム
| # | 名前 | タイプ | 詳細 |
|---|---|---|---|
| 1 | rnn_vae.mq5 | EA | 回帰オートエンコーダの学習EA |
| 2 | VAE.mqh | クラスライブラリ | Variationalautoencoderlatentlayerクラスライブラリ |
| 3 | NeuroNet.mqh | クラスライブラリ | ニューラルネットワークを作成するためのクラスのライブラリ |
| 4 | NeuroNet.cl | コードベース | OpenCLプログラムコードライブラリ |
…
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/11245
チャイキンオシレーター(Chaikin Oscillator)による取引システムの設計方法を学ぶ
データサイエンスと機械学習（第06回）：勾配降下法
一からの取引エキスパートアドバイザーの開発（第25部）：システムの堅牢性の提供(II)
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索