取引におけるニューラルネットワーク：時系列の区分線形表現

MetaTrader 5 — トレーディングシステム | 7 2月 2025, 14:48

451

Dmitriy Gizlyk

はじめに

一般に、時系列データの表現といえば、時間の経過に沿って記録された一連のデータ点を指します。しかし、初期データの量が増えるにつれて、その分析の複雑さも増し、情報を有効に活用する効率が低下します。これは特に金融市場において重要であり、情報分析や意思決定に時間をかけすぎると、利益を逃すリスクや損失の可能性が高まります。こうした状況では、データの次元を削減することで分析の効率と効果を向上させる手法が重要な役割を果たします。その一例が、時系列の区分的線形表現です。

時系列の区分的線形表現とは、小さな区間ごとに線形関数を用いて時系列データを近似する手法です。本記事では、この手法を応用した双方向区分的線形表現(BPLR: Bidirectional Piecewise Linear Representation)のアルゴリズムについて解説します。BPLRは、論文「Bidirectional piecewise linear representation of time series with application to collective anomaly detection」において発表されたもので、時系列データにおける異常検知の課題を解決するために提案された手法です。

時系列データの異常検知は、時系列データマイニングの主要な分野の一つです。その目的は、データセット全体の中で予期しない挙動を特定することにあります。異常はさまざまな要因によって引き起こされるため、特定の検出基準が存在するわけではありません。実際には、予測可能なデータの方が注目されやすく、異常なデータはノイズとして扱われ、無視されることが多いですしかし、異常データには重要な情報が含まれる場合があり、それを検出することは極めて重要です。正確な異常検知は、環境・産業・金融などのさまざまな分野で、不必要な悪影響を軽減するのに役立ちます。

時系列データにおける異常は、以下の3つのカテゴリに分類できます。

点異常：他のデータポイントと比較して異常と見なされるデータポイントのことです。これらの異常は、測定エラー、センサーの故障、データ入力ミス、または突発的なイベントによって引き起こされることが多いです。
文脈異常：あるデータポイントが特定の文脈では異常と見なされるが、その他の状況ではそうではない場合を指します。
集団異常：異常な振る舞いを示す時系列の部分列のことです。この種の異常は、個々に分析すると異常とは見なされませんが、グループ全体の挙動が異常であると判断されます。

集団異常は、分析対象のシステムやプロセスに関する重要な情報を提供する可能性があり、グループレベルでの問題を示唆することがあります。そのため、集団異常の検出は、サイバーセキュリティ、金融、医療などの多くの分野において重要な課題となります。BPLRの提案者は、研究において集団異常の特定に焦点を当てました。

時系列データの高次元性は、生のデータを用いた異常検知において多大な計算リソースを必要とします。しかし、異常検知のパフォーマンスを向上させるためには、典型的なアプローチとして、まず次元削減をおこない、その後、変換された表現空間で距離測定を用いて異常検知を実行する手法が取られます。そこで、BPLRの提案者は、新たな双方向区分的線形表現(BPLR: Bidirectional Piecewise Linear Representation)アルゴリズムを提案しました。この手法によって、入力された時系列データを低次元の表現に変換し、より効率的な分析が可能になります。

さらに、本論文では「区分的積分(PII: Piecewise Integration)」という概念に基づく新たな類似度測定アルゴリズムも提案されています。これにより、比較的低い計算コストで効率的な類似度測定を実現することができます。

1. アルゴリズム

提案されたBPLR法に基づく異常検知は、2つの段階から構成されます。

時系列を表現する
類似性を測定する

BPLRアルゴリズムの説明に入る前に、この手法が異常検知の問題を解決するために開発されたものであることを強調しておきます。分析対象の時系列には一定の周期性があると仮定されており、その周期の長さは実験的に求めるか、または事前の知識から推定することができます。そのため、入力された時系列全体を重複のない部分系列に分割し、それぞれの長さを元データの想定周期と等しくします。得られた部分系列を比較することで、異常領域を特定しようとするのがこの手法の目的です。次に、1つの部分系列を表現するためのアルゴリズムについて説明します。このアルゴリズムは、分析対象の時系列全体に対して繰り返し適用されます。

時系列の表現をおこなうには、各部分系列内で複数の分割点のセットを見つける必要があります。その後、入力された部分系列を線形セグメントの集合に変換します。

まず、部分系列を個別のセグメントに分割するために、最も適切なポイントを特定する必要があります。そのために、すべての可能なトレンド転換点(TTP)を識別します。この手法の提案者は、トレンド転換点を6種類に分類しています。

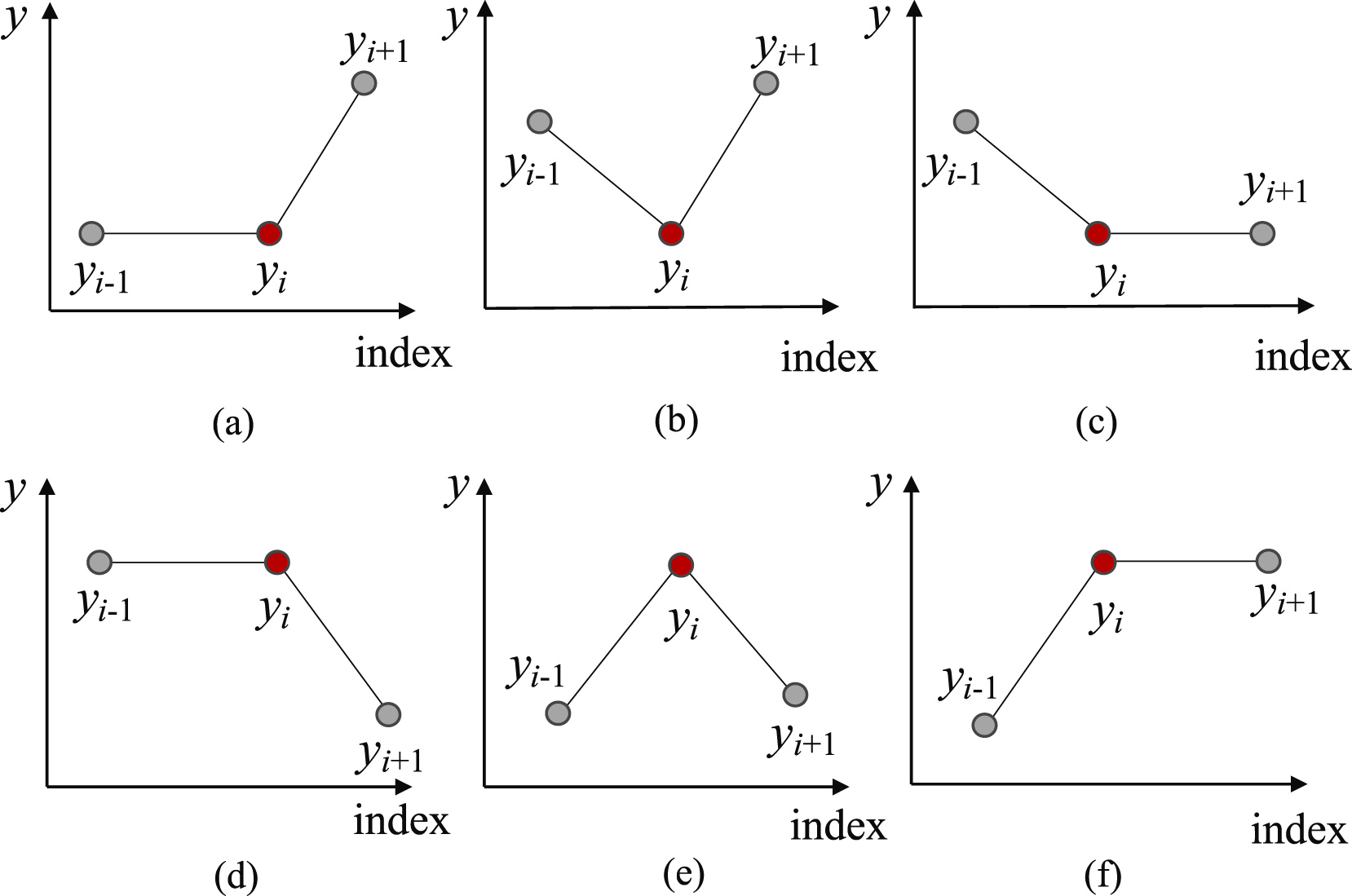
部分配列の最初と最後の要素は自動的にトレンドの転換点とみなされます。

次のステップは、発見された各TPPの重要性を判断することです。TTPの重要性の尺度として、この手法の著者は部分配列の平均値からの偏差を用いることを提案しています。

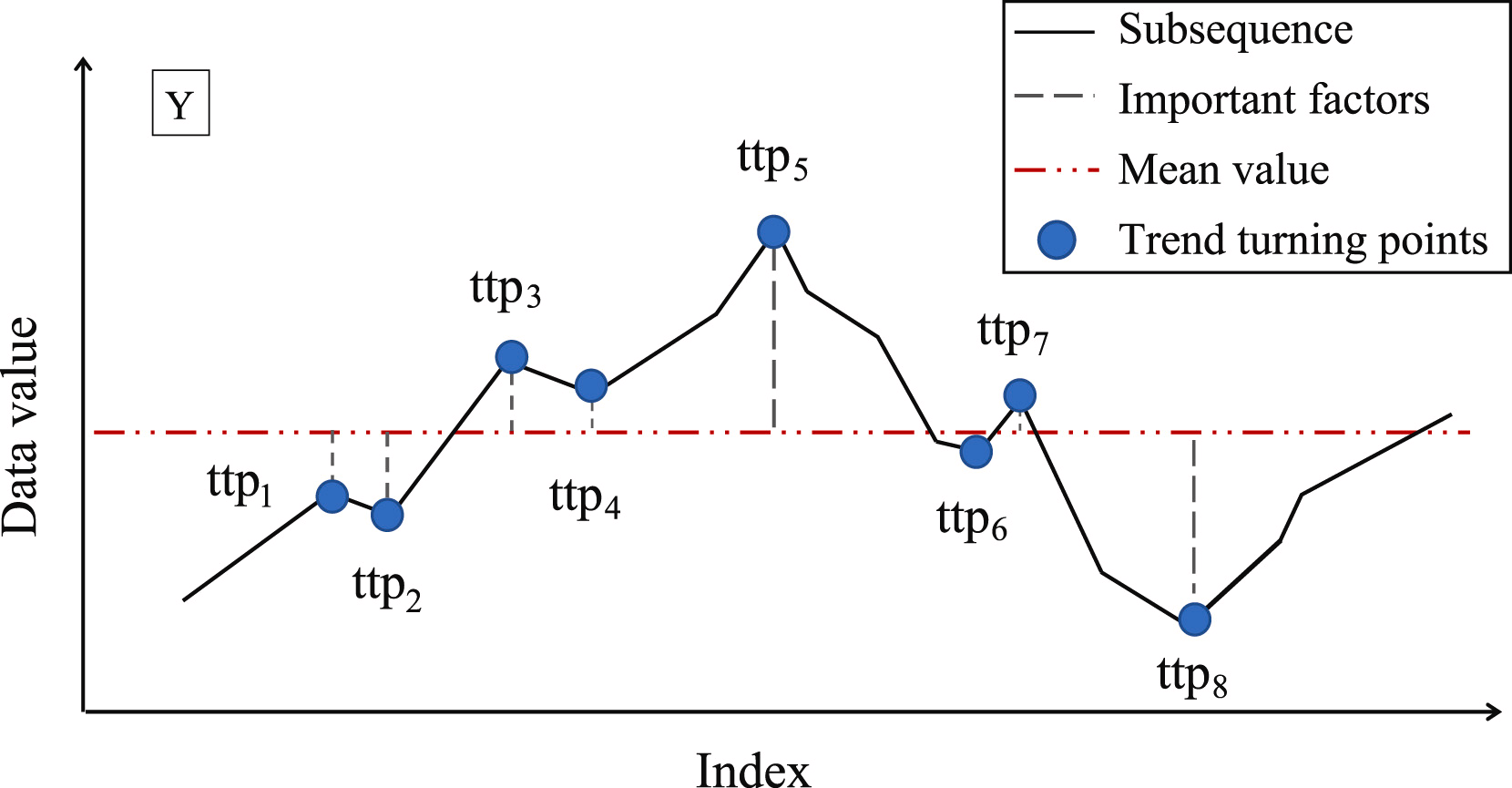
次に、TTPは重要度に応じて並べ替えられます。セグメントは、最も重要度の高いTTP1を起点として、前後2方向に向かって繰り返し決定されます。この際、セグメントの品質を決定するために、追加のハイパーパラメータδßが導入されます。このハイパーパラメータは、セグメント線からのシーケンス点の最大許容偏差を定義します。

前のセグメントの開始点を決定するために、現在解析対象のTTP1から逆順に入力シーケンスの要素をたどります。このとき、TTP1とセグメントの開始候補点の間にあるすべての要素が、δßの範囲内に収まっている必要があります。この閾値を超える点が見つかった時点で検索を停止し、セグメントを確定します。なお、以前に見つかったTTPがそのセグメントの範囲内に含まれる場合、それらは削除されます。

同様に、TTP1以降の方向に向かってセグメントの終点を探索します。極値の前後両方向でセグメントを決定するため、この手法は「双方向」と呼ばれます。

両方のセグメントの端点が決まったら、次に重要度の高い極値を対象に同じ処理を繰り返します。この反復処理は、配列内のすべてのトレンド転換点が処理されるまで続きます。

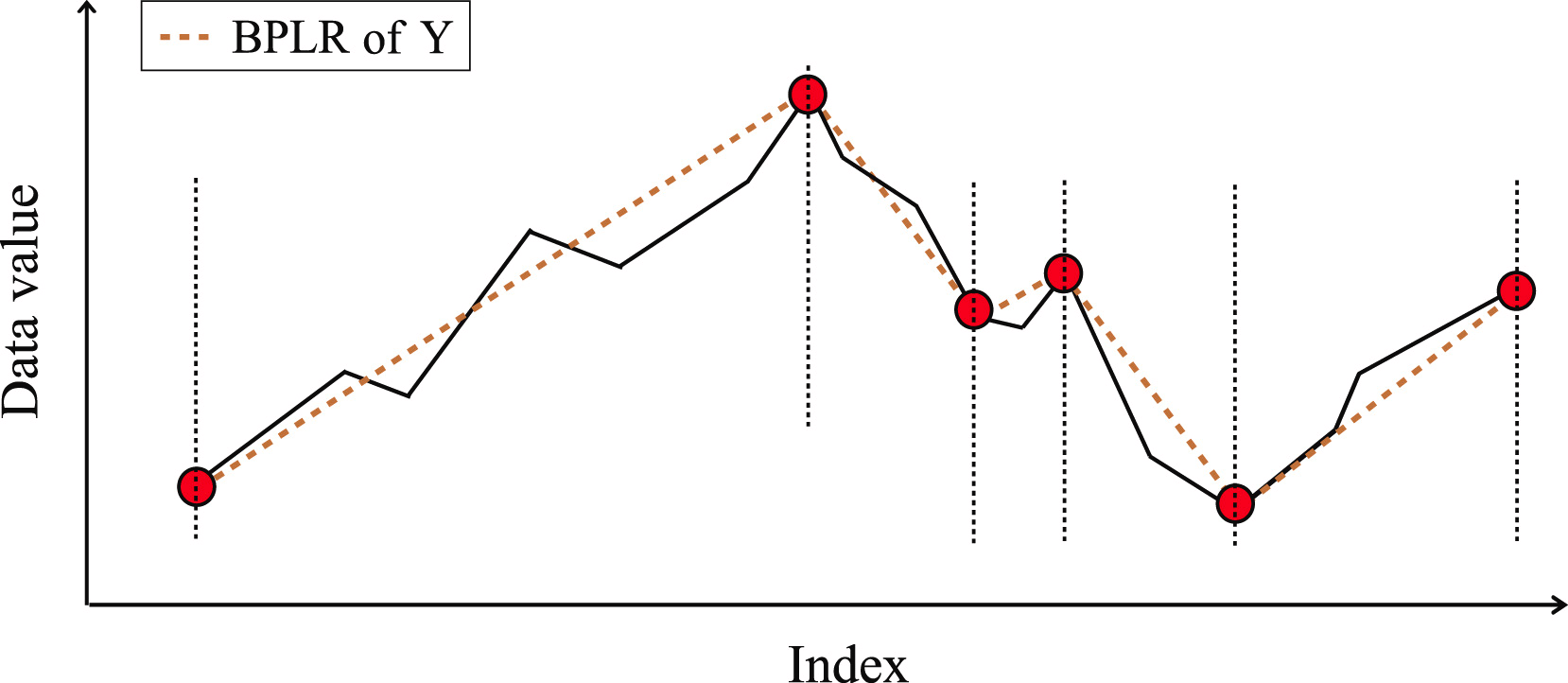
2つの部分配列の類似性は、解析された配列のセグメントが形成する形状の面積に基づいて決定されます。

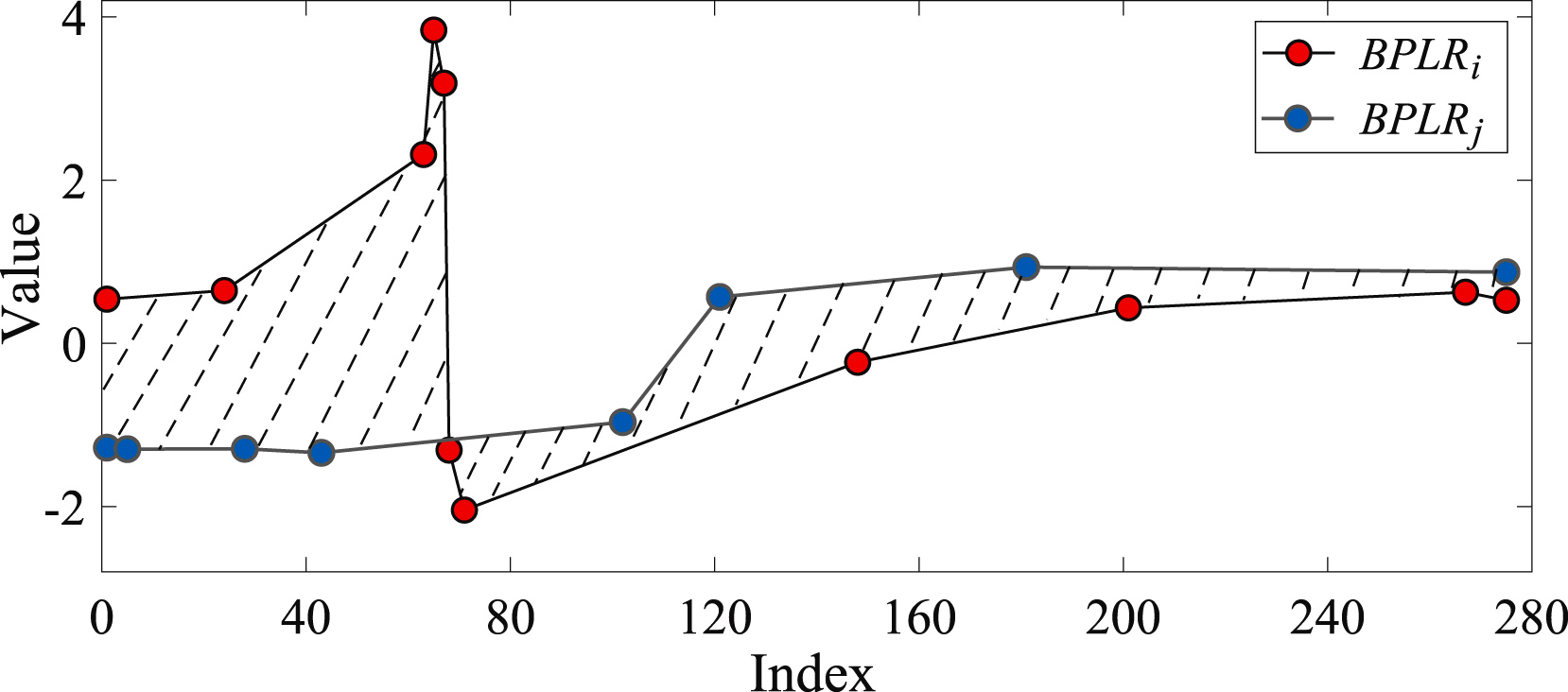
異常検出の問題を解決するために、この手法の著者は距離行列Mdistを作成します。次に、各部分系列について、分析対象の時系列における他の部分系列との総偏差Diを計算します。実際には、Diは行列Mdistのi行目の要素の総和を表します。ある部分系列の総偏差が、他の部分系列の平均値と大きく異なる場合、その部分系列は異常とみなされます。

論文の中で、BPLR法の著者は合成データと実データを用いた実験結果を示し、提案手法の有効性を証明しています。

2. MQL5での実装

これまで、時系列データにおける異常な部分系列を見つけることを目的としたBPLR法の理論的な枠組みについて説明してきました。本記事の実践編では、提案されたアプローチをMQL5に実装します。ただし、提案された手法を完全に使用するのではなく、一部のみを活用する点にご留意ください。

本記事の適用範囲では、時系列の異常検出はおこないません。金融市場は非常にダイナミックで多面的であり、任意の2つの不連続な部分系列の間には、大きな乖離が生じることが予想されるためです。

一方で、時系列データを区分的線形系列として表現する方法には、大きな利点があります。これまでの記事では、データセグメンテーションのメリットについて説明してきましたが、セグメントサイズの決定という課題は依然として重要な問題でした。従来は、セグメントサイズを常に均一に設定していました。しかし、区分的線形表現法を用いることで、入力時系列データに応じた動的なセグメントサイズを使用できるようになり、異なるスケールの時系列データの特徴を抽出する際に役立ちます。また、区分的線形表現はセグメントサイズに関係なく固定サイズで表現されるため、分析の際にも扱いやすいという利点があります。

このアルゴリズムにおいて、もう一つ重要な点はセグメントの表現方法です。「区分的線形表現」という名称自体が、セグメントを線形関数として表現することを示しています。

その結果、各セグメントの時間範囲における主要なトレンドの方向を明示的に示すことができます。さらに、データを圧縮できるという特性も、モデルの複雑さを軽減するという副次的なメリットをもたらします。

また、本実装では、時系列データを部分系列に分割することはおこないません。初期データ全体を区分的線形シーケンスとして表現します。本モデルは、与えられたデータを分析し、結論を導き出した上で、「最適な解決策」を提示することを目的としています。

では、OpenCL側でプログラムの構築を始めましょう。

2.1 OpenCL側での実装

ご存知のとおり、モデルのくン連および運用コストを最適化するために、計算の大部分をOpenCLデバイスのコンテキストへ移行しました。これにより、多次元空間での計算を効率的におこなうことが可能になりました。本実装もこの点において例外ではありません。

分析対象の時系列データをセグメント化するために、PLRカーネルを作成します。

__kernel void PLR(__global const float *inputs,
                  __global float *outputs,
                  __global int *isttp,
                  const int transpose,
                  const float min_step
                 )
  {
   const size_t i = get_global_id(0);
   const size_t lenth = get_global_size(0);
   const size_t v = get_global_id(1);
   const size_t variables = get_global_size(1);

カーネルへのパラメータには、3つのデータバッファへのポインタを渡す予定です。

inputs
outputs
isttp：トレンドの転換点を記録するサービスバッファ

さらに、2つの定数を加えます。

transpose：入出力をトランスポーズする必要性を示すフラグ
min_step：TTPを登録するための、部分配列要素の最小偏差

解析対象のシーケンスの要素数と、多次元時系列における一変量シーケンスの数に応じて、カーネルを2次元タスク空間で呼び出します。したがって、カーネル本体では、まずタスク空間内の現在のスレッドを特定し、次に入力バッファのオフセットを決定するための定数を定義します。

//--- constants
   const int shift_in = ((bool)transpose ? (i * variables + v) : (v * lenth + i));
   const int step_in = ((bool)transpose ? variables : 1);

少しの準備作業をおこなった後、解析対象の要素の位置にTTPが存在するかを判定します。解析対象の時系列における極値は、あらかじめセグメントの極値とみなされるため、自動的にトレンド転換点のステータスを持ちます。

   float value = inputs[shift_in];
   bool bttp = false;
   if(i == 0 || i == lenth - 1)
      bttp = true;

場合によっては、まず解析対象の系列において、現在の要素より前の範囲で最小限必要な値の偏差が最も近い点を探します。同時に、反復区間内の最小値と最大値を記録します。

   else
     {
      float prev = value;
      int prev_pos = i;
      float max_v = value;
      float max_pos = i;
      float min_v = value;
      float min_pos = i;
      while(fmax(fabs(prev - max_v), fabs(prev - min_v)) < min_step && prev_pos > 0)
        {
         prev_pos--;
         prev = inputs[shift_in - (i - prev_pos) * step_in];
         if(prev >= max_v && (prev - min_v) < min_step)
           {
            max_v = prev;
            max_pos = prev_pos;
           }
         if(prev <= min_v && (max_v - prev) < min_step)
           {
            min_v = prev;
            min_pos = prev_pos;
           }
        }

次に同様の方法で、必要な偏差が最小となる次の要素を探します。

      //---
      float next = value;
      int next_pos = i;
      while(fmax(fabs(next - max_v), fabs(next - min_v)) < min_step && next_pos < (lenth - 1))
        {
         next_pos++;
         next = inputs[shift_in + (next_pos - i) * step_in];
         if(next > max_v && (next - min_v) < min_step)
           {
            max_v = next;
            max_pos = next_pos;
           }
         if(next < min_v && (max_v - next) < min_step)
           {
            min_v = next;
            min_pos = next_pos;
           }
        }

現在の値が極値かどうかを確認します。

      if(
         (value >= prev && value > next) ||
         (value > prev && value == next) ||
         (value <= prev && value < next) ||
         (value < prev && value == next)
      )
         if(max_pos == i || min_pos == i)
            bttp = true;
     }

しかし、ここで忘れてはならないのは、最小限必要な偏差を持つ要素を探索する際に、極値のプラトーを形成する複数の要素から値の集合（コリドー）を取得する可能性があることです。したがって、ある要素がTTPフラグを受け取るのは、そのコリドー内で極値となっている場合に限られます。

取得したフラグを保存し、出力バッファをクリアしましょう。また、ここでローカルグループのスレッドを同期させます。

//---
   isttp[shift_in] = (int)bttp;
   outputs[shift_in] = 0;
   barrier(CLK_LOCAL_MEM_FENCE);

さらなる処理を開始する前に、現在の一変量時系列のすべてのスレッドがTTPの存在フラグを記録していることを確実にするため、スレッドを同期させる必要があります。

次の処理は、TTPが定義されたスレッドのみが実行し、その他のスレッドは指定された条件を満たさないため、実質的に処理を終了します。

ここではまず、現在の極値の位置を計算します。そのために、要素の現在の位置に対する正のフラグの数をカウントし、入力バッファ内の前回のTTPの位置をローカル変数に保存します。

//--- calc position
   int pos = -1;
   int prev_in = 0;
   int prev_ttp = 0;
   if(bttp)
     {
      pos = 0;
      for(int p = 0; p < i; p++)
        {
         int current_in = ((bool)transpose ? (p * variables + v) : (v * lenth + p));
         if((bool)isttp[current_in])
           {
            pos++;
            prev_ttp = p;
            prev_in = current_in;
           }
        }
     }

その後、現在のセグメントのトレンドの線形近似のパラメータを決定します。

//--- cacl tendency
   if(pos > 0 && pos < (lenth / 3))
     {
      float sum_x = 0;
      float sum_y = 0;
      float sum_xy = 0;
      float sum_xx = 0;
      int dist = i - prev_ttp;
      for(int p = 0; p < dist; p++)
        {
         float x = (float)(p);
         float y = inputs[prev_in + p * step_in];
         sum_x += x;
         sum_y += y;
         sum_xy += x * y;
         sum_xx += x * x;
        }
      float slope = (dist * sum_xy - sum_x * sum_y) / (dist > 1 ? (dist * sum_xx - sum_x * sum_x) : 1);
      float intercept = (sum_y - slope * sum_x) / dist;

得られた結果を出力バッファに保存します。

      int shift_out = ((bool)transpose ? ((pos - 1) * 3 * variables + v) : (v * lenth + (pos - 1) * 3));
      outputs[shift_out] = slope;
      outputs[shift_out + 1 * step_in] = intercept;
      outputs[shift_out + 2 * step_in] = ((float)dist) / lenth;
     }

ここでは、得られた各セグメントを3つのパラメータで特徴付けます。

slope：トレンドラインの傾き
intercept：入力部分空間での傾向線のシフト
dist：セグメントの長さ

セグメントの持続時間（長さ）の表現について、少し説明しておくべきでしょう。お察しのとおり、この場合、シーケンスの長さを整数値で指定するのは最適な方法ではありません。モデルを効率的に運用するには、正規化されたデータ形式を使用するほうが望ましいためです。そこで、セグメントの長さを、分析対象の一変量時系列の全長に対する割合として表現することにしました。そのため、セグメント内の要素数を、時系列全体の要素数で割ります。また、整数演算による誤差（「罠」）を避けるため、まずセグメントの要素数をint型からfloat 型に変換します。

さらに、最後のセグメントについては特別な処理をおこないます。その理由は、ある時点で形成されるセグメントの数を事前に知ることができないからです。仮に、時系列の変動が大きく、各要素がトレンド転換点(TTP)となるようなケースでは、圧縮をおこなうどころか、データ量が3倍に膨れ上がる可能性もあります。もちろん、そのような極端なケースは稀ですが、不必要なデータの増加は避けるべきです。同時に、データの欠損も防がなければなりません。

そこで、MQL5における時系列データの構造と、その表現方法についての知識を活かします。MQL5では、最新のデータが時系列の先頭（インデックスの小さい部分）に位置し、古いデータは後方（インデックスの大きい部分）に配置されます。このため、より重要な最新データに重点を置く必要があります。分析窓の端にあるデータは、歴史上もっと早い時期に起こったものであり、そのためその後の出来事への影響は少なくなります。とはいえ、そのような影響を完全に無視するわけではありません。

この特性を踏まえ、結果を書き込むためのデータバッファを、入力時系列テンソルとほぼ同じサイズに設定します。これにより、シーケンスの長さの3分の1のサイズでセグメントを格納できます（1つのセグメントを記録するのに3つの要素を使用）。この容量で十分なはずですが、念のため、万が一セグメントが予想以上に多くなった場合には、最後のいくつかのセグメントを統合し、データの損失を回避する仕組みを組み込みます。

   else
     {
      if(pos == (lenth / 3))
        {
         float sum_x = 0;
         float sum_y = 0;
         float sum_xy = 0;
         float sum_xx = 0;
         int dist = lenth - prev_ttp;
         for(int p = 0; p < dist; p++)
           {
            float x = (float)(p);
            float y = inputs[prev_in + p * step_in];
            sum_x += x;
            sum_y += y;
            sum_xy += x * y;
            sum_xx += x * x;
           }
         float slope = (dist * sum_xy - sum_x * sum_y) / (dist > 1 ? (dist * sum_xx - sum_x * sum_x) : 1);
         float intercept = (sum_y - slope * sum_x) / dist;
         int shift_out = ((bool)transpose ? ((pos - 1) * 3 * variables + v) : (v * lenth + (pos - 1) * 3));
         outputs[shift_out] = slope;
         outputs[shift_out + 1 * step_in] = intercept;
         outputs[shift_out + 2 * step_in] = ((float)dist) / lenth;
        }
     }
  }

ほとんどの場合、セグメントの数は少なくなるため、結果バッファの最後の要素はゼロ値で埋められることになります。

ここで重要なのは、上述のアルゴリズムには学習可能なパラメータが含まれていないという点です。そのため、初期データの前処理段階で利用できるものの、バックプロパゲーション（誤差逆伝播）や誤差勾配の分布を直接考慮する設計にはなっていません。しかし、私たちの取り組みでは、このアルゴリズムをニューラルネットワークモデルに組み込むため、後続のニューラル層から前の層へ誤差勾配を伝播させる必要があります。そのためには、バックプロパゲーションアルゴリズムを実装し、誤差勾配を適切に処理する仕組みを追加しなければなりません。なお、学習可能なパラメータが存在しないため、それらを最適化するアルゴリズムは必要ありません。

そこで、バックプロパゲーションアルゴリズムの一環として誤差勾配分布カーネル「PLRGradient」を作成します。

__kernel void PLRGradient(__global float *inputs_gr,
                          __global const float *outputs,
                          __global const float *outputs_gr,
                          const int transpose
                         )
  {
   const size_t i = get_global_id(0);
   const size_t lenth = get_global_size(0);
   const size_t v = get_global_id(1);
   const size_t variables = get_global_size(1);

カーネルのパラメータには、3つのデータバッファへのポインタを渡します。ただし、今回は、2つの誤差勾配バッファ（入力レベルと出力レベル）と、現在の層のフィードフォワード結果のバッファがあります。さらに、カーネルのパラメータとして「データ転置フラグ」も追加します。このフラグはデータバッファ内のオフセットを計算する際に使用されます。

同じ2次元のタスク空間でカーネルを呼び出します。1つ目の次元は時系列シーケンスのサイズによって制限され、2つ目の次元はマルチモーダルソースデータ内の一変量時系列の数によって制約されます。カーネルの本体では、まずタスク空間内の現在のスレッドをすべての次元で特定します。

次に、データバッファのオフセットの定数を定義します。

//--- constants
   const int shift_in = ((bool)transpose ? (i * variables + v) : (v * lenth + i));
   const int step_in = ((bool)transpose ? variables : 1);
   const int shift_out = ((bool)transpose ? v : (v * lenth));
   const int step_out = 3 * step_in;

しかし、まだ準備作業は完了していません。次に、分析対象の入力要素を含むセグメントを特定する必要があります。そのために、ループを実行し、ループ本体でセグメントのサイズを最初のものから順番に確認していきます。目的の入力データ要素を含むセグメントが見つかるまで、ループの繰り返し処理を続けます。

//--- calc position
   int pos = -1;
   int prev_in = 0;
   int dist = 0;
   do
     {
      pos++;
      prev_in += dist;
      dist = (int)fmax(outputs[shift_out + pos * step_out + 2 * step_in] * lenth, 1);
     }
   while(!(prev_in <= i && (prev_in + dist) > i));

すべてのループを繰り返すと、以下が得られます。

pos：入力データの目的の要素を含むセグメントのインデックス
prev_in：最初のセグメント要素への入力データバッファ内のオフセット
dist：セグメントの要素数

フィードフォワード演算の一階微分を計算するには、セグメント要素の位置の合計と、それらの平方値の合計も必要です。

//--- calc constants
   float sum_x = 0;
   float sum_xx = 0;
   for(int p = 0; p < dist; p++)
     {
      float x = (float)(p);
      sum_x += x;
      sum_xx += x * x;
     }

この時点で準備作業は完了し、誤差勾配の計算に移ることができます。まず、傾きとオフセットの誤差勾配を抽出します。

//--- get output gradient
   float grad_slope = outputs_gr[shift_out + pos * step_out];
   float grad_intercept = outputs_gr[shift_out + pos * step_out + step_in];

ここで、トレンドラインの垂直方向のシフトを計算するために、フィードフォワードパスで使用した式を思い出してみましょう。

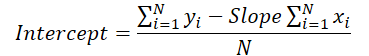
線の傾きの値はシフトの計算に使用されます。そのため、傾きの誤差勾配がシフト調整に与える影響を考慮し、適切に補正する必要があります。この調整をおこなうために、シフト関数を傾きに関して微分し、その導関数を求めます。

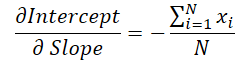
得られた値にシフト誤差勾配を乗じ、その結果を勾配誤差勾配に加えます。

//--- calc gradient
   grad_slope -= sum_x / dist * grad_intercept;

次に、傾きを求める公式を見てみましょう。

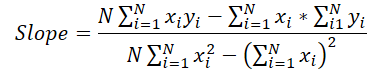
この場合、分母は定数であり、それを使って勾配誤差の勾配を調整することができます。

   grad_slope /= fmax(dist * sum_xx - sum_x * sum_x, 1);

最後に、両計算式における入力データの影響を見てみましょう。

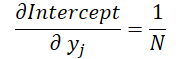
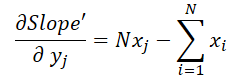
ここで、1≦j≦Nであり

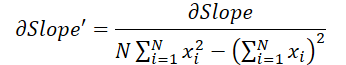
これらの公式を使って、入力データレベルでの誤差勾配を決定してみましょう。

   float grad = grad_intercept / dist;
   grad += (dist * (i - prev_in) - sum_x) * grad_slope;
   if(isnan(grad) || isinf(grad))
      grad = 0;

その結果を、入力データの勾配バッファの対応する要素に保存します。

//--- save result
   inputs_gr[shift_in] = grad;
  }

これで、OpenCLのコンテキスト側に関する研究は終了です。OpenCLの全コードは添付ファイルにあります。

2.2 新しいクラスの実装

OpenCLコンテキスト側での操作が完了したら、メインプログラムコードの操作に移ります。ここでは新しいクラスCNeuronPLROCLを作成し、上記のアルゴリズムを通常のニューラル層の形でモデルに実装できるようにします。

ほとんどの同様のケースでもそうですが、新しいオブジェクトは神経層の基底クラスCNeuronBaseOCLから主要な機能を継承します。以下は新しいクラスの構造体です。

class CNeuronPLROCL  :  public CNeuronBaseOCL
  {
protected:
   bool              bTranspose;
   int               icIsTTP;
   int               iVariables;
   int               iCount;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL)  { return true; }

public:
                     CNeuronPLROCL(void)  : bTranspose(false) {};
                    ~CNeuronPLROCL(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window_in, uint units_count, bool transpose, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronPLROCL;   }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

この構造体には、いくつかの変数が追加された標準的なメソッドセットの再定義が含まれています。新しい変数の目的は、その名前から理解できます。

bTranspose：入出力を転置する必要性を示すフラグ
iCount：解析対象の配列のサイズ（履歴の深さ）
iVariables：マルチモーダル時系列（一変量シーケンス）の分析パラメータ数

フィードフォワードパスのカーネルパラメータには補助データバッファがありますが、メインプログラム側で追加のバッファを作成することはありません。ここでは、そのポインタをローカル変数icIsTTPに保存するだけです。

また、本実装では内部オブジェクトを持たないため、クラスのコンストラクタとデストラクタは空のままにしておくことができます。オブジェクトの初期化はInitメソッド内でおこないます。

bool CNeuronPLROCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                         uint window_in, uint units_count, bool transpose, 
                         ENUM_OPTIMIZATION optimization_type, uint batch
                        )
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_in * units_count, optimization_type, batch))
      return false;

パラメータとして、このメソッドは作成されたオブジェクトのアーキテクチャを定義するための主要な定数を受け取ります。クラス本体では、まず同名の親クラスのメソッドを呼び出します。親クラスのメソッドには、必要なコントロールや継承されたオブジェクト・変数の初期化処理がすでに実装されています。

次に、作成したオブジェクトの構成パラメータを保存します。

   iVariables = (int)window_in;
   iCount = (int)units_count;
   bTranspose = transpose;

メソッドの最後に、OpenCLコンテキスト側に補助データバッファを作成します。

   icIsTTP = OpenCL.AddBuffer(sizeof(int) * Neurons(), CL_MEM_READ_WRITE);
   if(icIsTTP < 0)
      return false;
//---
   return true;
  }

オブジェクトを初期化した後、feedForwardメソッドでフィードフォワードパスのアルゴリズムを構築します。ここでは、上記で作成したフィードフォワードパスのカーネルPLRを呼び出すだけで済みます。しかし、個々の単変量時系列内のスレッドを同期させるためには、ローカルグループを作成する必要があります。

bool CNeuronPLROCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!OpenCL || !NeuronOCL || !NeuronOCL.getOutput())
      return false;
//---
   uint global_work_offset[2] = {0};
   uint global_work_size[2] = {iCount, iVariables};
   uint local_work_size[2] = {iCount, 1};

そのために、2次元のグローバルタスク空間を定義します。最初の次元は、分析されるシーケンスのサイズを示し、2番目の次元は、一変量時系列の数を示します。また、2次元タスク空間におけるローカルグループのサイズも定義します。1つ目の次元のサイズはグローバル値に対応し、2つ目の次元には1を指定します。このように、各ローカルグループは、それぞれ独自の一変量シーケンスを得ます。

次に、必要なパラメータをカーネルに渡すだけです。

   ResetLastError();
   if(!OpenCL.SetArgumentBuffer(def_k_PLR, def_k_plr_inputs, NeuronOCL.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_PLR, def_k_plr_outputs, getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_PLR, def_k_plt_isttp, icIsTTP))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_PLR, def_k_plr_transpose, (int)bTranspose))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_PLR, def_k_plr_step, (float)0.3))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

そしてカーネルを実行キューに入れます。

//---
   if(!OpenCL.Execute(def_k_PLR, 2, global_work_offset, global_work_size, local_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }
//---
   return true;
  }

各段階での作戦統制を忘れてはなりません。メソッドの最後に、メソッドの結果の論理値を呼び出し元に返します。

calcInputGradients誤差勾配分布法のアルゴリズムは、同様の方法で構築されます。ただし、フィードフォワードパスメソッドとは異なり、ここではローカルグループを作らず、各スレッドが独立して処理を実行します。この記事で使用されているすべてのプログラムの完全なコードは、以下の添付ファイルにあります。

前述したように、作成したオブジェクトには学習可能なパラメーターは含まれていません。したがって、updateInputWeightsパラメータ最適化メソッドは、オブジェクトの一般的な構造と実装時の互換性を維持するためにのみ、ここで再定義されます。このメソッドは常にtrueを返します。

これで、新しいクラスのメソッドを実装するためのアルゴリズムの説明は終わりです。この記事で説明していないものも含め、クラスメソッドの完全なコードは添付ファイルにあります。

2.3 モデルアーキテクチャ

時系列の区分線形表現を行うアルゴリズムの一つを実装し、これをモデルのアーキテクチャに組み込めるようになりました。

提案する実装の有効性を検証するため、環境状態エンコーダーのモデル構造に新しいクラスを導入しました。また、時系列の名目分解が個々の線形トレンドに与える影響を評価するため、モデルの構成を大幅に簡素化しました。

前回と同様に、モデルのアーキテクチャはCreateEncoderDescriptionsメソッド内で記述します。

bool CreateEncoderDescriptions(CArrayObj *encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }

パラメータとして、このメソッドはモデルのアーキテクチャを記録するための動的配列オブジェクトへのポインタを受け取ります。メソッド本体では、まず受け取ったポインタの妥当性を確認します。その後、必要に応じて動的配列の新しいインスタンスを作成します。

いつものように、データの前処理を行わず、与えられた履歴の深さにおける環境の状態に関する情報をモデルに入力します。

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

区分線形表現アルゴリズムは、正規化されたデータでも生のデータでも同じように機能しますが、注意しなければならないことがいくつかあります。

まず、本実装では、トレンド転換点を登録するために、時系列データの最小必要偏差をパラメータとして使用しました。当然ながら、このハイパーパラメータは、個々の時系列データごとに慎重に選択する必要があります。特に、一変量系列の値が異なる分布に属するマルチモーダルな時系列を分析する場合、このタスクは大幅に複雑化します。そのため、ほとんどのケースでは、すべての一変量系列に対して単一のハイパーパラメータを適用することは困難です。

次に、PLRの結果は、正規化されたデータを使用したモデルにおいて、より高い性能を発揮します。

もちろん、PLRの出力をモデルに入力する前に正規化をおこなうことも可能ですが、この場合、セグメント数が動的に変化するため、処理がさらに複雑になります。

一方で、区分線形表現層に入力する前にデータを正規化すれば、これらの課題を大幅に簡素化できます。すべての一変量系列を同じ分布に正規化することで、マルチモーダル時系列データの分析に単一のハイパーパラメータを適用できるようになります。さらに、入力データの分布を統一することで、異なる入力シーケンスに対して平均的なハイパーパラメータを用いることも可能になります。

正規化されたデータをレイヤーの入力として受け取った以上、出力も正規化されたシーケンスとなります。したがって、本モデルの次の層には、バッチ正規化層を配置します。

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

次に、一変量シーケンス内で作業するために、入力データを転置します。

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

もちろん、PLRアルゴリズムの本実装では、データ転置レイヤーを使用せず、転置パラメーターを直接活用する方が効率的かもしれません。しかし、本モデルのアーキテクチャをさらに構築するために、本ケースではデータ転置を適用しています。

次に、用意したデータを線状に分割します。

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronPLROCL;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   descr.step = int(false);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

与えられた計画期間における個々の一変量系列を予測するために、3層のMLPを使用します。

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = BarDescr;
   descr.window = HistoryBars;
   descr.step = HistoryBars;
   descr.window_out = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = BarDescr;
   descr.window = LatentCount;
   descr.step = LatentCount;
   descr.window_out = LatentCount;
   descr.optimization = ADAM;
   descr.activation = SIGMOID;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = BarDescr;
   descr.window = LatentCount;
   descr.step = LatentCount;
   descr.window_out = NForecast;
   descr.optimization = ADAM;
   descr.activation = TANH;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

個々の一変量シーケンス値の条件付き独立予測を整理するために、重なりのないウィンドウを持つ畳み込み層を使用している点に注意してください。ここで「条件付き独立予測」という定義を用いているのは、すべての一変量時系列の予測軌跡を構築する際に、同じ重み付け行列が使用されるためです。

次に、予測値を入力データの表現に変換します。

//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = BarDescr;
   descr.window = NForecast;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

元のデータを正規化する際に取り除かれた分布の統計的パラメータを追加します。

//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRevInDenormOCL;
   descr.count = BarDescr*NForecast;
   descr.activation = None;
   descr.optimization = ADAM;
   descr.layers=1;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

モデルの出力では、分析した時系列の予測一変量シーケンスの各ステップを調整するために、FreDFメソッドの成果を活用します。

//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFreDFOCL;
   descr.window = BarDescr;
   descr.count =  NForecast;
   descr.step = int(true);
   descr.probability = 0.7f;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

これで、時系列予測のためにPLRとMLPを統合した環境状態エンコーダーモデルを構築しました。

3.テスト

本稿の実用編では、時系列の区分線形表現(PLR)のアルゴリズムを実装しました。提案するアルゴリズムには学習可能なパラメータが含まれていません。その代わりに、分析対象の時系列データを別の表現に変換する手法を用いています。また、作成したCNeuronPLROCL層を活用し、比較的単純な時系列予測モデルも構築しました。ここでは、これらのアプローチの有効性を評価します。

分析対象の時系列の後続インジケーターを予測する環境状態エンコーダーモデルを訓練するために、前回の記事で収集した訓練データセットを使用します。

モデルの訓練には、2023年を通して収集されたEURUSDのH1時間足の実際の履歴データを使用しました。環境状態エンコーダーモデルの訓練時には、価格変動の履歴データと分析指標のみを使用します。そのため、訓練データセットを更新することなく、望ましい結果が得られるまでモデルを訓練しました。

モデルの訓練プロセスに関しては、その安定性が際立っている点を強調したいです。予測誤差に急激な変動はなく、スムーズに学習が進行しました。

その結果、比較的シンプルなモデルでありながら、良好な成果を得ることができました。例えば、以下に示すのは、実際の価格推移と予測価格推移を比較したチャートです。

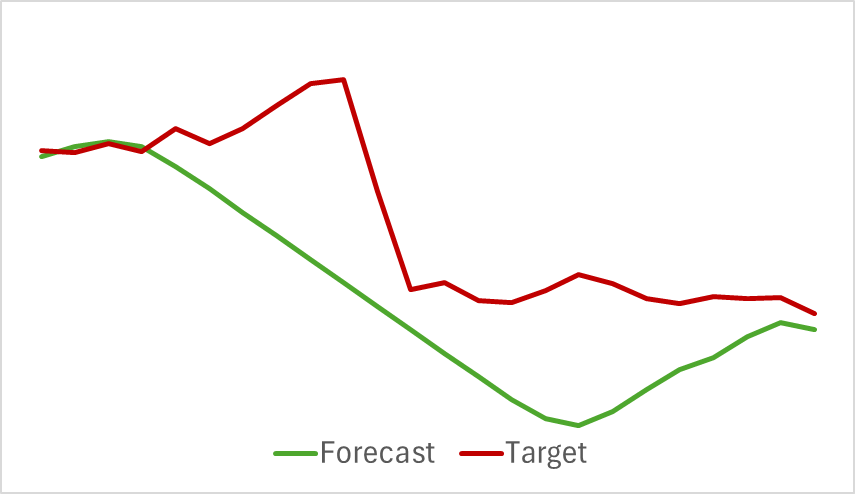
チャートを見ると、モデルが今後の価格変動の主要なトレンドを捉えることに成功していることが分かります。特に、24時間先の予測において、予測軌道の始点と終点が実際の値と比較的近い点は注目に値します。ただし、予測軌道の価格変動の勢いが、実際よりも時間的にやや長く継続する傾向が見られます。

また、分析対象のインジケーターに関する予測軌道も良好な結果を示しています。以下に示すのは、RSI（相対力指数）の予測値のグラフです。

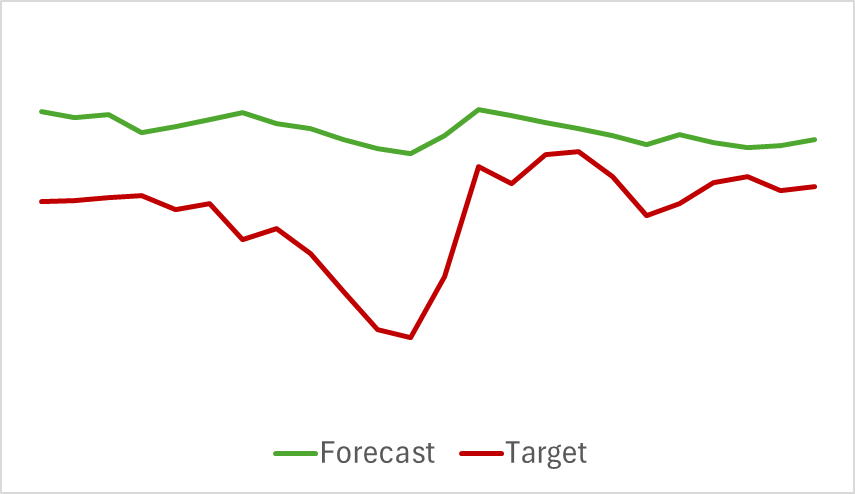
インジケーターの予測値は、実際の値よりもやや高く、振幅も小さめですが、主要なインパルスの発生タイミングや方向は一致しています。

なお、今回提示した価格変動の予測とインジケーターの予測値は、同じ期間に対応している点にご留意ください。2つのグラフを比較すると、インジケーターの予測値と実際の値の主要なモメンタムが、実際の価格変動の主要なモメンタムと時間的に一致していることが確認できます。

結論

本稿では、時系列データを区分的線形分割によって代替的に表現する手法について説明しました。実践編では、提案手法の一つを実装し、検証をおこないました。実験結果から、本手法には十分な可能性があることが示唆されます。

参照文献

Bidirectional piecewise linear representation of time series with application to collective anomaly detection

本連載の他の記事

記事で使用されているプログラム

#	名前	種類	詳細
1	Research.mq5	EA	コレクションEAの例
2	ResearchRealORL.mq5	EA	Real-ORL法による事例収集のためのEA
3	Study.mq5	EA	モデル訓練EA
4	StudyEncoder.mq5	EA	エンコーダー訓練EA
5	Test.mq5	EA	モデルをテストするEA
6	Trajectory.mqh	クラスライブラリ	システム状態記述の構造体
7	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
8	NeuroNet.cl	コードベース	OpenCLプログラムコードライブラリ

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/15217

添付されたファイル |

ZIPをダウンロード

MQL5.zip (1420.3 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

ボラティリティを予測するための計量経済学ツール：GARCHモデル

この記事では、条件付き異分散性(GARCH)という非線形モデルの特性について説明します。また、このモデルを基に、一歩先のボラティリティを予測するためのiGARCHインジケーターを構築しました。モデルのパラメータ推定には、ALGLIB数値解析ライブラリを使用しています。

ニューラルネットワークが簡単に（第97回）：MSFformerによるモデルの訓練

さまざまなモデルアーキテクチャの設計を検討する際、モデルの訓練プロセスには十分な注意が払われないことがよくあります。この記事では、そのギャップを埋めることを目指します。

取引におけるニューラルネットワーク：二重アテンションベースのトレンド予測モデル

前回の記事で取り上げた時系列の区分線形表現の活用について、引き続き議論します。本日は、この手法を他の時系列分析手法と組み合わせることで、価格動向の予測精度を向上させる方法を探ります。

多通貨エキスパートアドバイザーの開発（第14回）：リスクマネージャーにおける適応型ボリューム変更

以前開発されたリスクマネージャーには基本的な機能のみが含まれていました。取引戦略のロジックに干渉することなく取引結果を向上させるために、どのような開発の可能性があるかを検討してみましょう。