ボラティリティを予測するための計量経済学ツール：GARCHモデル

はじめに

ボラティリティは、金融資産の価格変動性を評価するための重要な指標です。価格変動の分析において、大きな値動きはさらなる大きな変動を引き起こしやすいことが、特に金融危機時に顕著に見られます。逆に、小さな変動はその後も小さい変動が続く傾向にあります。このように、相場が落ち着いている期間の後には、不安定な期間が訪れることが一般的です。

この現象を説明しようとした最初のモデルがEngleによって開発されたARCH（自己回帰条件付き異分散性）モデルです。このモデルは、リターンのクラスタリング効果（大きな値と小さな値がまとまって発生する特性）を説明するだけでなく、価格変動の分布に見られる厚い裾（ファットテール）や正の尖度（クルトシス）の発生要因を解明しました。 ARCH条件付きガウスモデルの成功により、さらに多くの一般化モデルが開発されました。それらの目的は、金融時系列データの分析において観察されるさまざまな現象を説明することでした。こうした一般化モデルの中で、最も初期に登場したものの一つが、GARCH（Generalized ARCH：一般化ARCH）モデルです。

GARCHモデルの最大の利点は、ARCHモデルに比べてよりコンパクトであり、サンプルデータに適合させる際に長いラグ構造を必要としないことです。本記事では、GARCHモデルについて説明し、さらに本モデルを活用したボラティリティ予測ツールを紹介します。特に、財務データ分析における主要な目的の一つである「予測」に焦点を当てます。

ボラティリティ推定へのノンパラメトリックアプローチ

ボラティリティを用いたリスク評価は、トレーダーの間で非常に人気のあるトピックです。ボラティリティを測定する最も一般的な方法は、指定された期間の標準偏差を単純に計算することです。

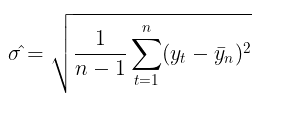
これは、いわゆるノンパラメトリックなボラティリティ推定の手法です。この方法で算出されるボラティリティは、「歴史的ボラティリティ」または「経験的ボラティリティ」と呼ばれます。ガウス型ランダムウォークモデルにおいては、ボラティリティは時間とともに一定であると仮定されるため、これが不確実性や変動性の主要な指標となります。

ボラティリティ推定のパラメトリックアプローチ

一方、GARCHモデルでは、ボラティリティはランダム変数（すなわち、ボラティリティ自体が変動する）であると仮定されます。こちらの方が、より現実に即したアプローチといえます。GARCHプロセスは、以下の式を用いて定義されます。

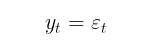
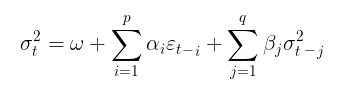
ここで

• Yt：対数価格増分
• εt：モデル残差
• σt²：条件付き分散
• zt = i.i.d.N(0,1)：標準ガウス分布
• zt =iid t-Student(v)：自由度vの標準t分布
• ω、α、β、v：データサンプルから推定されるモデルパラメータ

モデル パラメータには次の制限が課せられます。

• ω>0、分散正条件
• α≥0
• β≥0
• ∑αi + ∑βj <1 、定常条件
• v>2

β = 0の場合、GARCHモデルはARCHモデルになります。

GARCHモデルは通常、条件付きまたは無条件の数学的期待値のモデルによって補完されます。たとえば、一次自己回帰過程AR(1)は、条件付き数学的期待値のモデルとして使用することができます。

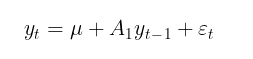
ここで

• u：シフトパラメータ
• A1：自己回帰モデルパラメータ

条件付き平均モデリングの目的は、条件付き分散の検索に使用する一連の二乗残差(εt²)を決定することです。利益系列に自己相関がない場合（通常はそうなります）は、無条件の数学的期待値モデルに進むことができます。

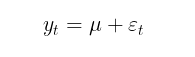
本記事では、計算を簡潔にするため、利益の自己相関を推定しないモデルを使用します。したがって、GARCHモデルにおけるボラティリティ推定の問題は、モデルのパラメータ（μ、ω、α、β、v）を求めるというパラメトリックな問題に帰着されます。

最大尤度法を用いたGARCHモデルパラメータの推定

最大尤度法は、通常、未知のパラメータを推定するために使用されます。残差etがガウス分布に従うと仮定すると、対数尤度関数は次の形になります。

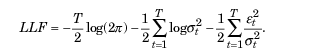
正規性からの逸脱が確認された場合、標準化されたt分布を適切な分布として使用することができます。自由度パラメータvが小さい場合、この分布は正規分布に比べて尖度が高く、裾が重い特性を持ちます。この場合、対数尤度関数は次の形になります。

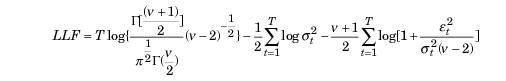
ここで

• Г：ガンマ関数
• T：データサンプルのサイズ

ALGLIB MinBLEICオプティマイザー

GARCHモデルパラメータ値を見つけるには、尤度関数を最大化する必要があります。これには最適化手法が必要です。ALGLIBの数値解析ライブラリを使用すると、この作業を効率的におこなうことができます。目的関数を最大化するために、MinBLEIC (Bound Linear Equality Inequality Constraints)アルゴリズムを選択しました。

//+------------------------------------------------------------------+
//|  Objective Function: Gaussian loglikelihood                      |
//+------------------------------------------------------------------+
void CNDimensional_GaussianFunc::Func(CRowDouble &x,double &func,CObject &obj)
  {
//x[0] - mu;
//x[1] - omega;
//x[2] - alpha;
//x[3] - beta;
   double returns[];
   ArrayResize(returns,N1);
   for(int i=0;i<N1;i++)
     {
      returns[i] = MathLog(close[i+1]/close[i]);
     }

   double residuals[];
   ArrayResize(residuals,N1);
   for(int i = 0; i<N1; i++)
     {
      residuals[i] = (returns[i] - x[0]);
     }

   double condVar[];
   ArrayResize(condVar,N1);
   condVar[0] = x[1]/(1-x[2]-x[3]);  // Unconditional Variance

   for(int i=1; i<N1; i++)
     {
      condVar[i] = x[1] + x[2]*MathPow(residuals[i-1],2) + x[3]*condVar[i-1]; // Conditional Variance
     }

   double LLF[],a[],b[];
   ArrayResize(LLF,N1);
   ArrayResize(a,N1);
   ArrayResize(b,N1);
   for(int i=0; i<N1; i++)
     {

      a[i]= 1/sqrt(2*M_PI*condVar[i]);
      if(!MathIsValidNumber(a[i]))
        {
         break;
        }

      b[i]= MathExp(- MathPow(residuals[i],2)/(2 * condVar[i]));
      if(!MathIsValidNumber(b[i]))
        {
         break;
        }

      LLF[i]=MathLog(a[i]*b[i]);
      if(!MathIsValidNumber(LLF[i]))
        {
         break;
        }
     }

   func = -MathSum(LLF); // Loglikelihood
  }

GARCH関数は目的関数を直接処理し、パラメータの最適値を求めます。そのために、以下の設定が必要となります。

• パラメータの初期値を指定する
• データスケールを設定する（最適化の成功を左右する非常に重要な要素）
• パラメータが変動する範囲（境界）を指定する
• 線形不等式制約を設定する（今回はα + β < 1という定常性の条件のみ）
• 最適化アルゴリズムの停止条件を指定する
• 微分のステップサイズを指定する

//+------------------------------------------------------------------+
//|  Function GARCH  Gaussian                                        |
//+------------------------------------------------------------------+
vector GARCH()
  {
   double              x[],s[];
   int                 ct[];
   CMatrixDouble       c;
   CObject Obj;
   CNDimensional_GaussianFunc ffunc;
   CNDimensional_Rep frep;

   double returns[];
   ArrayResize(returns,N1);
   for(int i=0;i<N1;i++)
     {
      returns[i] = MathLog(close[i+1]/close[i]);
     }
   double returns_mean  = MathMean(returns);
   double returns_var = MathVariance(returns);
   double KurtosisReturns = MathKurtosis(returns);
// Print("KurtosisReturns= ",KurtosisReturns);

// Initial parameters ---------------------------
   ArrayResize(x,4);
   x[0]=returns_mean;  //  Mu
   x[1]=returns_var;  // Omega
   x[2]=0.0;         // alpha
   x[3]=0.0;        // beta
//------------------------------------------------------------
   double mu;
   if(NormalizeDouble(returns_mean,10)==0)
     {
      mu = 0.0000001;
     }
   else
      mu = NormalizeDouble(returns_mean,10);
// Set Scale-----------------------------------------------
   ArrayResize(s,4);
   s[0] = NormalizeDouble(returns_mean,10);  //  Mu
   s[1] = NormalizeDouble(returns_var,10); // omega
   s[2] =1;
   s[3] =1;
//---------------------------------------------------------------
// Linearly inequality constrained: --------------------------------
   c.Resize(1,5);
   c.Set(0,0,0);
   c.Set(0,1,0);
   c.Set(0,2,1);
   c.Set(0,3,1);
   c.Set(0,4,0.999); // alpha + beta <= 0.999
   ArrayResize(ct,1);
   ct[0]=-1; // {-1:<=},{+1:>=},{0:=}
//--------------------------------------------------------------
// Box constraints ------------------------------------------------
   double bndl[4];
   double bndu[4];

   bndl[0] = -0.01;  // mu
   bndl[1] = NormalizeDouble(returns_var/20,10);  // omega
   bndl[2] = 0.0;  // alpha
   bndl[3] = 0.0;  // beta

   bndu[0] = 0.01;  // mu
   bndu[1] = NormalizeDouble(returns_var,10);  // omega
   bndu[2] = 0.999;  // alpha
   bndu[3] = 0.999;  // beta
//--------------------------------------------------------------
   CMinBLEICStateShell state;
   CMinBLEICReportShell rep;
   double epsg=0;
   double epsf=0;
   double epsx=0.00001;
   double diffstep=0.0001;
//--- These variables define stopping conditions for the outer iterations:
//--- * epso controls convergence of outer iterations;algorithm will stop
//---   when difference between solutions of subsequent unconstrained problems
//---   will be less than 0.0001
//--- * epsi controls amount of infeasibility allowed in the final solution
   double epso=0.00001;
   double epsi=0.00001;

   CAlglib::MinBLEICCreateF(x,diffstep,state); //---  create optimizer
   CAlglib::MinBLEICSetBC(state,bndl,bndu);  //--- add boundary constraints
   CAlglib::MinBLEICSetLC(state,c,ct);
   CAlglib::MinBLEICSetScale(state,s);
   CAlglib::MinBLEICSetPrecScale(state); // Preconditioner
   CAlglib::MinBLEICSetInnerCond(state,epsg,epsf,epsx);
   CAlglib::MinBLEICSetOuterCond(state,epso,epsi);
   CAlglib::MinBLEICOptimize(state,ffunc,frep,0,Obj);
   CAlglib::MinBLEICResults(state,x,rep);   // Get parameters
//---------------------------------------------------------

   double residuals[],resSquared[],Realised[];
   ArrayResize(residuals,N1);
   for(int i = 0; i<N1; i++)
     {
      residuals[i] = (returns[i] - x[0]);
     }

   MathPow(residuals,2,resSquared);
   ArrayCopy(resSquared_,resSquared,0,0,WHOLE_ARRAY);
   MathSqrt(resSquared,Realised);

   double condVar[],condStDev[];
   double ForecastCondVar,PriceConf_Upper,PriceConf_Lower;
   ArrayResize(condVar,N1);
   condVar[0] = x[1]/(1-x[2]-x[3]);
   for(int i = 1; i<N1; i++)
     {
      condVar[i] = x[1] + x[2]*MathPow(residuals[i-1],2) + x[3]*condVar[i-1];
     }

   double PlotUncondStDev[];
   ArrayResize(PlotUncondStDev,N1);
   ArrayFill(PlotUncondStDev,0,N1,sqrt(condVar[0])); // for Plot
   ArrayCopy(PlotUncondStDev_,PlotUncondStDev,0,0,WHOLE_ARRAY);
   MathSqrt(condVar,condStDev);
// Print("math expectation of conditional standard deviation = "," ",MathMean(condStDev));

   ArrayCopy(Real,Realised,0,0,WHOLE_ARRAY);
   ArrayCopy(GARCH_,condStDev,0,0,WHOLE_ARRAY);

   vector v_Realised, v_condStDev;
   v_Realised.Assign(Realised);
   v_condStDev.Assign(condStDev);
   double MSE=v_condStDev.Loss(v_Realised,LOSS_MSE); // Mean Squared Error
//-----------------------------------------------------------------------------
//-------- Standardize Residuals--------------------------------------
   double z[];
   ArrayResize(z,N1);
   for(int i = 0; i<N1; i++)
     {
      z[i] = residuals[i]/sqrt(condVar[i]);
     }
   ArrayCopy(Z,z,0,0,WHOLE_ARRAY);
//----------------------------------------------------------------------------------

//-------------- JarqueBeraTest for Normality  ----------------------------------
   double pValueJB;
   int JBTestH;
   CAlglib::JarqueBeraTest(z,N1,pValueJB);
   if(pValueJB <0.05)
      JBTestH =1;
   else
      JBTestH=0; // H=0 - data Normal, H=1 data are not Normal
   double Kurtosis = MathKurtosis(z); // Kurosis = 0 for Normal distribution
//---------------------------------------------------------------------------------

//-------------------------------------------------------------------------------------
//-------- Forecast Conditional Variance for m bars
   double FCV[];
   ArrayResize(FCV,forecast_m);
   for(int i = 0; i<forecast_m; i++)
     {
      FCV[i] = sqrt(x[1]*((1-MathPow(x[2]+x[3],i+1))/(1-x[2]-x[3])) + MathPow(x[2]+x[3],i)*(x[2]*MathPow(residuals[N1-1],2) + x[3]*condVar[N1-1])) ;
     }
   ArrayCopy(FCV_,FCV,0,0,WHOLE_ARRAY);
//-----------------------------------------------------------------------------------
   double LLF[];
   double Loglikelihood;
   ArrayResize(LLF,N1);
   for(int i = 0; i<N1; i++)
     {
      LLF[i] = MathLog(1/sqrt(2*M_PI*condVar[i])*MathExp(- MathPow(residuals[i],2)/(2*condVar[i])));
     }
   Loglikelihood = MathSum(LLF);
//--------------------------------------------------------------------------

   ForecastCondVar= x[1] + x[2]*MathPow(residuals[N1-1],2) + x[3]*condVar[N1-1];
   int err1;
   PriceConf_Lower = close[N1]*MathExp(-MathAbs(MathQuantileNormal((1-pci)/2,0,1,err1))*sqrt(x[1] + x[2]*MathPow(residuals[N1-1],2) + x[3]*condVar[N1-1])); // confidence interval pci%
   PriceConf_Upper = close[N1]*MathExp(MathAbs(MathQuantileNormal((1-pci)/2,0,1,err1))*sqrt(x[1] + x[2]*MathPow(residuals[N1-1],2) + x[3]*condVar[N1-1]));  // confidence interval pci%

//--------------------------------------------------------------------------------------
   vector result= {x[0],x[1],x[2],x[3],rep.GetTerminationType(),ForecastCondVar,PriceConf_Lower,PriceConf_Upper,MSE,Loglikelihood,condVar[0],returns_var,JBTestH,Kurtosis};
   return (result);
  }
//+------------------------------------------------------------------+

GARCH (1,1)モデルを用いたボラティリティ予測

ボラティリティのポイント予測

モデルのパラメータが求まったら、次のステップとして、ボラティリティの予測をおこないます。GARCH (1,1)モデルを用いたmステップ先のボラティリティ予測は、次の式で計算されます。

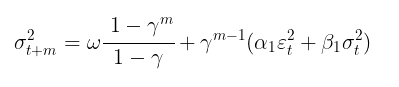
ここで

• γ = α1 + β 1

m →∞の場合、予測は理論的な無条件GARCH分散に収束します（モデルの定常性条件 α₁ + β₁ < 1が満たされている場合）。

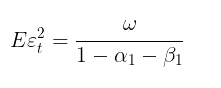
つまり、予測期間が長くなるほど、ボラティリティの予測値は無条件分散の定常値に近づくということです。GARCHスクリプトを用いることで、mステップ先のボラティリティ予測を計算し、それらの値をEεt ²と比較することで、この性質を確認できます。

インターバル予測

ボラティリティのポイント予測は有用ですが、将来の価格変動が収まる範囲を確率的に推定すること、つまり特定の有意水準に基づいた信頼区間を求めることの方が重要です。

ztが独立同分布(i.i.d.)の標準正規分布 N(0,1) に従うと仮定すると、信頼区間は次の式を用いて計算されます。

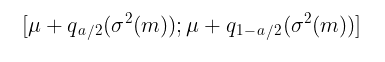
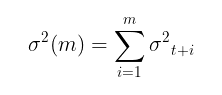
ここで

• q：標準正規分布の分位数

たとえば、信頼性レベルが 90% (a = 1-0,9)の信頼区間の場合、区間は次のようになります。

[ u – 1,65σ ; u + 1,65σ ]

ztが 独立同分布（i.i.d.）のt分布t(v)に従うと仮定すると、状況はさらに複雑になります。この場合、逆分布関数の解析的な式は存在しません。そのため、信頼区間を構築するにはモンテカルロシミュレーションを用いる必要があります。

//+-------------------------------------------------------------------------+
//|Function calculate Forecast Confidence intervals using Monte-Carlo method|
//+-------------------------------------------------------------------------+
bool MCForecastStandardized_t(const double DoF,const double CondStDevForecast,const double prob, double & F_lower[],double & F_upper[])
  {

   double alpha = 1-prob;
   double qlower[1] = {alpha/2};       // q (a/2)
   double qupper[1] = {1-alpha/2};  // q (1-a/2)

   int N = 10000; //number Monte-Carlo simulates
   double h_St[];
   ArrayResize(h_St,N);
   for(int i=0;i<N;i++)
     {
      h_St[i] = CondStDevForecast * Standardized_t(DoF);   // GARCH-Student(1,1)
     }
   MathQuantile(h_St,qlower,F_lower);
   MathQuantile(h_St,qupper,F_upper);
   return(true);
  }

//+--------------------------------------------------------------------------+
//| Function calculate i.i.d. standardized t-distributed variable            |
//+--------------------------------------------------------------------------+
double  Standardized_t(const double DoF)
  {
   double randStandStudent;
   int err;
   randStandStudent = MathRandomNormal(0,1,err) * sqrt(DoF/((MathRandomGamma(DoF/2.0,1)*2.0)));
   randStandStudent = randStandStudent/sqrt(DoF/(DoF-2.0));
   return(randStandStudent);
  }
//+------------------------------------------------------------------+

シミュレーションの回数（デフォルトは10,000）を増やせば増やすほど、予測の精度は向上しますが、その分計算時間も長くなります。最適な回数は100,000と考えられます。この場合、信頼区間はより対称的になります。

条件付きガウスGARCHモデルの妥当性テスト

GARCHモデルがボラティリティの不均一分散性（ヘテロスケダスティシティ）を適切に捉えられているかを確認するためには、標準化残差の自己相関と標準正規分布への適合性をチェックする必要があります。標準化残差は、単に価格の増分から条件付き（または無条件）数学的期待値を引き、GARCHモデルで計算された条件付き標準偏差で割ったものです。

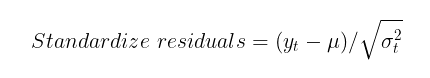
GARCHモデルが実際のデータに適している場合、標準化残差は独立しており、同一に分布する標準正規値となります。

残差分析の例として、過去4年間のEURUSDの日次データを使用し、モデルのパラメータを計算してみましょう。

自己相関の残差の二乗を確認してみましょう。

ご覧のとおり、ラグ20までデータにはわずかな依存関係が見られます。ここで、標準化残差の二乗の自己相関をチェックし、GARCH (1,1)モデルがこの依存関係を適切に説明できたかどうかを確認しましょう。

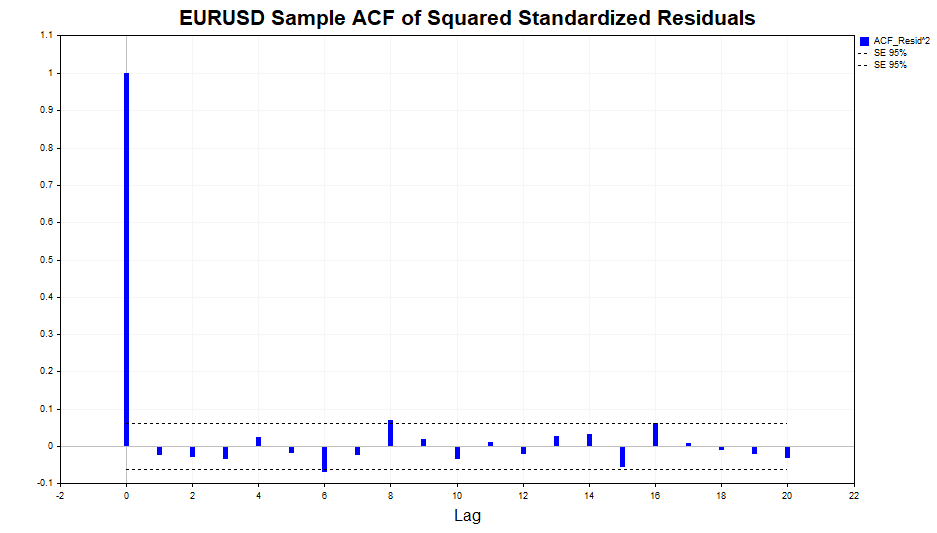
ご覧のとおり、モデルは非常に良い結果を示しました。データには有意な自己相関は見られません。

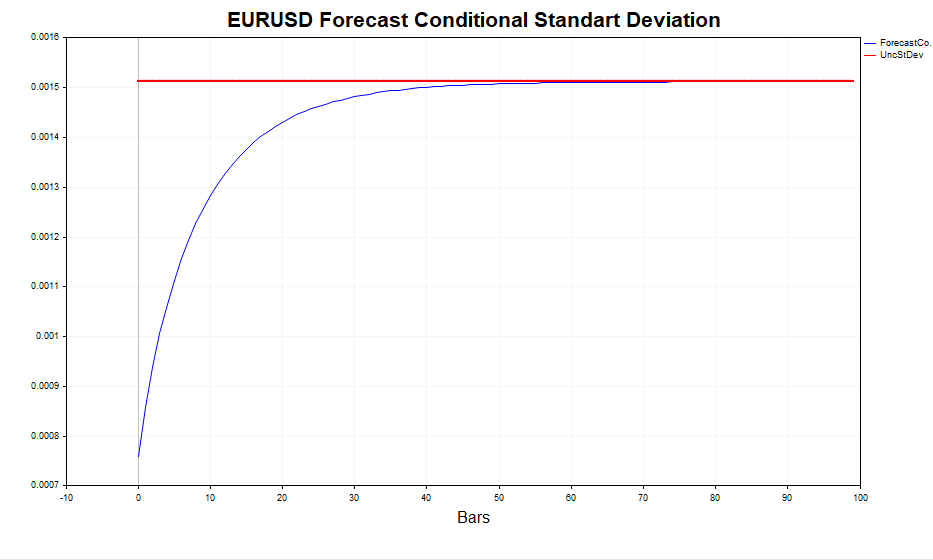
次に、計算された実現ボラティリティ（対数価格増分の2乗）と条件付き標準偏差(GARCH)を見てみましょう。このモデルは、ボラティリティの変化に対して非常に適切に対応しています。また、無条件標準偏差は、GARCHボラティリティが変動する基準となる平均値として機能します。

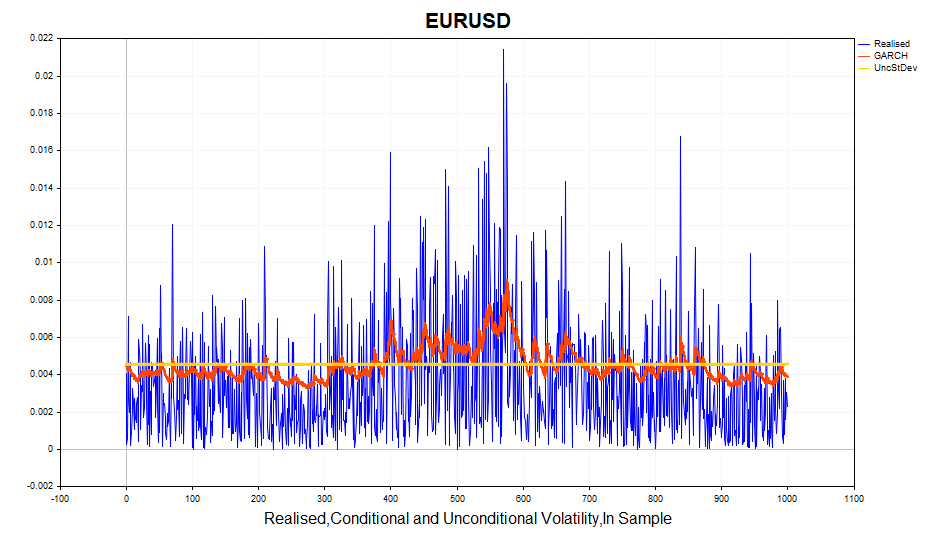
標準化残差の正規性を確認してみましょう。

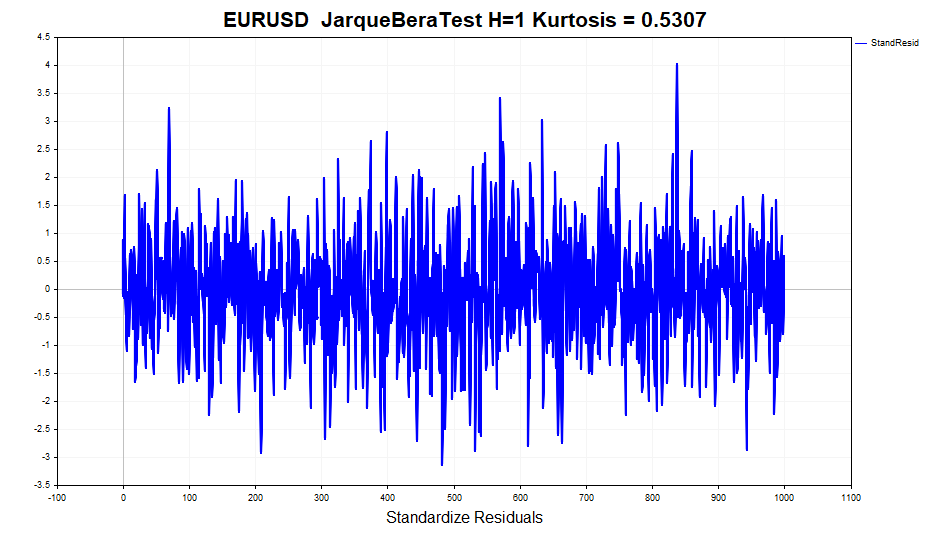
一見すると、データは比較的正規分布に従っているように見えます。はっきりとした重い裾（ヘビーテール）は確認できません。しかし、Jarque-Bera検定 などの正式な正規性検定をおこなうと、帰無仮説は棄却されます。その理由は、超過値(0,5307)が正規分布の値とわずかに異なっているためです。一方で、利益の超過値は1.2904です。つまり、GARCHモデルはピークのある分布の影響を完全には考慮していませんが、一部は捉えています。ご存知のように、無条件GARCHプロセスの分布には厚い裾があります。これは、異なる分散を持つ複数のガウス分布の混合により、厚い裾と正の尖度を持つ分布が形成されるためです。

したがって、標準化残差が条件付き正規分布に従うというGARCHモデルの仮定は破られています。その結果、最大尤度法を使用して得られたモデルパラメータの推定値は、一部の有用な性質を失います。つまり、漸近的に効率的ではなくなります（言い換えれば、より大きなサンプルを用いた場合でも推定精度が低下する可能性があります）。

この場合、正規分布の代わりにt分布を使用することができます。自由度が小さい場合、スチューデント分布は正の超過を持ち、裾が重くなります。この場合、自由度の数は追加の未知パラメータとなり、サンプルを使用して推定する必要があります。

今述べたさまざまな統計情報の視覚的な表示に関連するすべての処理は、分析を容易にするためにGARCHスクリプトに組み込まれています。

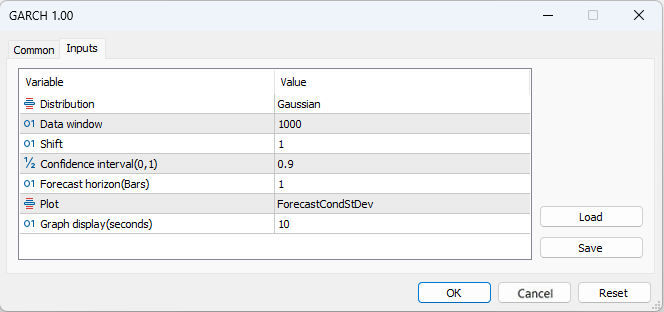
• [Distribution]：標準正規分布または標準スチューデントのt分布
• [Data window]：モデルパラメータを計算するためのデータウィンドウ
• [Shift]：データウィンドウのシフト（1はチャートの最後から2番目のバー）
• [Confidence interval]：信頼区間の有意水準（有意水準が高いほど、信頼区間は広くなる）
• [Forecast horizon]：指定された数のバーの今後のボラティリティ予測
• [Plot]：ボラティリティ予測、標準化残差、実現ボラティリティとGARCHボラティリティの比較、残差の二乗の自己相関関数、および標準化残差の二乗の自己相関関数をチャート上に表示

iGARCHインジケーター

モデルと、このモデルを適用したいデータについての最初の理解を得るためには、GARCHスクリプトで十分です。しかし、ボラティリティをリアルタイムで評価および予測するには、新しいバーごとにモデルパラメータを再計算し、常に変化する市場に素早く適応できるアルゴリズムが必要になります。iGARCH適応インジケーターがこの問題の解決策となります。

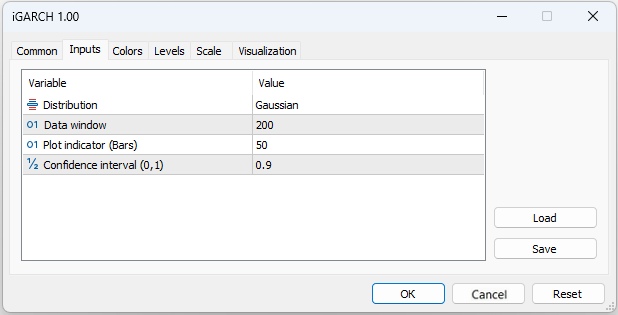
• [Plot indicator]：インジケーターが計算されるバーの数

このインジケーターは、一定の信頼水準で1ステップ先の将来の価格変動に対するボラティリティ（条件付き標準偏差）と信頼区間を予測します。予測はゼロバーに表示され、パラメータ計算に使用するデータ（データウィンドウ）は最初のバーから取得されます。モデルパラメータは各バーごとに最適化されるため、計算に時間がかかる可能性があります（特にt分布を使用したモデルの場合）。そのため、プロットインジケーター（バー）の値を過度に大きく設定することは推奨されません。

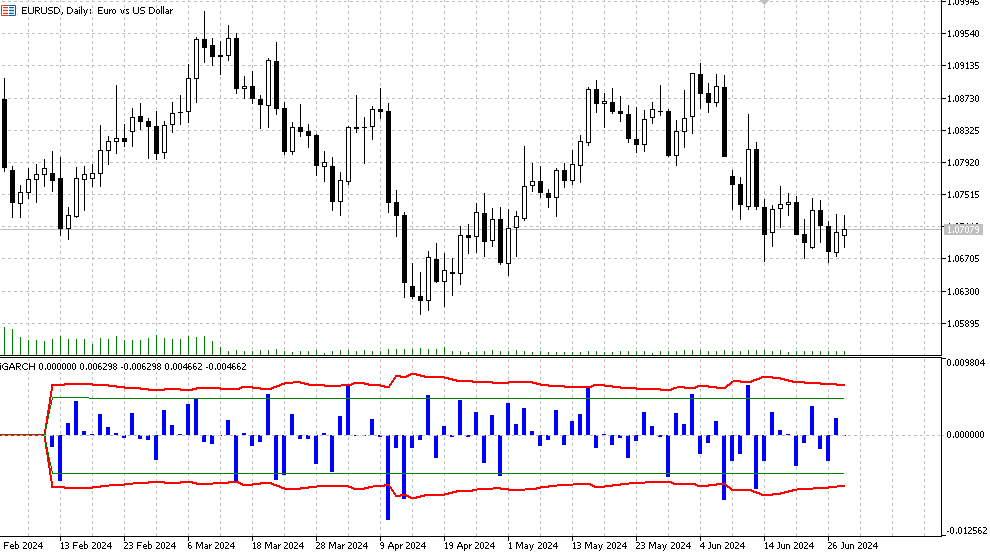
• ヒストグラム：対数利益値LN (Yt/Yt-1)
• 赤い線は、信頼区間の有意水準（デフォルトは 90%）に対して決定された条件付き標準偏差予測の上限と下限です。これは、約90％のケースで対数価格増分がこれらの制限内に収まることを意味します。
• 緑の線はそれぞれ、通常の履歴ボラティリティ、下限値、上限値を表します。

さらに、次の情報が操作ログに表示されます。操作ログは新しいバーごとに更新されます。

• 最適化されたパラメータの最新値（μ、ω、α、β、V）
• 尤度関数（LLF）値
• 選択された有意水準における価格水準の予測
• 最適化の成功報告
• 予測された条件付き標準偏差の値
• GARCH理論無条件標準偏差値
• 過去の標準偏差値

結論

結論として、私は条件付き異分散性を考慮する最も一般的なモデルの一つであるGARCHモデルを検討しました。従来のボラティリティ推定方法は、ボラティリティが時間とともに一定であることを前提としているため、実際の市場環境を十分に反映できていません。それに対し、GARCHモデルはボラティリティの時間変化を考慮できるため、市場の状況をより適切に分析することが可能です。

GARCH (1,1)モデルを用いた例として、対数リターンのボラティリティとその信頼区間を1ステップ先まで予測できる適応型インジケーターを開発しました。これにより、将来の価格変動の確率的な評価が可能となり、ポジションのリスクをより効果的に管理できます。

このインジケーターでは、従来のガウス残差モデルだけでなく、残差がスチューデント分布に従うと仮定するモデルも選択可能です。また、新しいバーごとにモデルのパラメータを最適化することで、現在の市場状況に素早く適応できます。

最大尤度法を用いたモデルパラメータの推定には、ALGLIB数値解析ライブラリのMinBLEIC最適化アルゴリズムを使用しました。GARCHスクリプトは、モデルに関連する必要な統計を計算し、データ内の依存関係を評価するための視覚的なツールも提供します。

したがって、計量経済学研究や金融分析にGARCHモデルを適用することで、より正確なボラティリティ予測が可能となり、リスク管理と投資判断の精度が大幅に向上します。