取引におけるニューラルネットワーク：方向性拡散モデル(DDM)

MetaTrader 5 — トレーディングシステム | YYYY年08月DD日, 08:43

はじめに

拡散モデルを用いた教師なし表現学習は、コンピュータビジョン分野において重要な研究領域となっています。さまざまな研究者による実験結果は、拡散モデルが意味のある視覚表現を学習する上で有効であることを示しています。異なるレベルのノイズによって歪められたデータの再構成は、モデルが複雑な視覚的概念を把握するための適切な基盤を提供します。さらに、トレーニング中に特定のノイズレベルを優先することが、拡散モデルの性能を向上させることが示されています。

論文「Directional Diffusion Models for Graph Representation Learning」の著者たちは、拡散モデルを教師なしのグラフ表現学習に応用することを提案しました。しかし、実際には「バニラ型」（従来型）の拡散モデルには限界があることが判明しました。著者らの実験によると、グラフ構造内のデータは画像データに比べて、より顕著な異方性および方向性のパターンを示すことが多く、従来の等方的な前向き拡散過程に基づくモデルでは、内部の信号対雑音比(SNR)が急速に低下しやすく、異方的構造を適切に捉えることが困難でした。この課題に対応するため、著者らは方向性構造を効率的に捉える新たなアプローチを導入しました。それが方向性拡散モデルであり、SNRの急激な劣化を抑制することができます。本手法では、前向き拡散過程にデータ依存かつ方向性バイアスのかかったノイズを導入します。ノイズ除去モデルが生成する中間的な活性は、下流タスクにおいて重要となる意味的・トポロジー的情報を効果的に捉えることができます。

その結果、方向性拡散モデルはグラフ表現学習における有望な生成的アプローチを提供します。著者らの実験では、本手法がコントラスト学習法や従来の生成的手法を上回る性能を示しました。特に、グラフ分類タスクにおいては、方向性拡散モデルがベースラインの教師あり学習モデルさえも上回る成果を挙げ、拡散ベースの手法がグラフ表現学習において持つ大きな可能性を示しています。

さらに、拡散モデルを取引の文脈で応用することで、市場データの表現と分析を強化する新たな可能性が開かれます。特に方向性拡散モデルは、異方性のあるデータ構造を考慮できる点で有用と考えられます。金融市場は非対称的かつ方向性のある動きに特徴づけられるため、方向性ノイズを取り入れたモデルは、トレンド相場と調整相場の両方において構造的パターンをより効果的に識別できます。この能力により、隠れた依存関係や季節的なトレンドの特定が可能となります。

1. DDMアルゴリズム

グラフと画像に見られるデータには、構造上の大きな違いがあります。バニラ型前向き拡散プロセスでは、等方的なガウスノイズが元のデータに繰り返し加えられ、最終的にはデータが完全にホワイトノイズへと変換されます。このアプローチは、データが等方的な分布に従う場合には適しており、信号対雑音比(SNR)が広範囲にわたって変化する中で、データ点を徐々にノイズへと劣化させながらノイズの混ざったサンプルを生成します。しかし、異方的なデータ分布に対して等方的ノイズを加えると、基盤となる構造が急速に破壊され、SNRが急激にゼロに近づいてしまいます。

この結果として、ノイズ除去モデルは、下流タスクに効果的に利用できるような意味のある判別的特徴表現を学習できなくなります。これに対し、方向性拡散モデルは、データ依存かつ方向性を持つ前向き拡散プロセスを組み込むことで、SNRの低下をより緩やかにします。このようなより穏やかな劣化により、さまざまなSNRレベルにおいて細かい特徴表現を抽出することが可能になり、異方的構造に関する重要な情報が保持されます。抽出された情報は、グラフ分類やノード分類といった下流タスクに活用することができます。

方向性ノイズの生成には、初期の等方的ガウスノイズを2つの追加的な制約によって異方的ノイズに変換する工程が含まれます。これらの制約は、拡散モデルの性能を向上させる上で重要です。

前向き拡散過程のtステップ目における作業状態をG t = ( A, X t )と表し、ここで𝐗t = {xt,1, xt,2, …, xt,N}は観察対象となる特徴量ベクトルを表します。

ここでx0,iはノードiの生の特徴量ベクトルを表し、μ ∈ ℛおよびσ ∈ ℛはそれぞれ全Nノードにわたる特徴の次元dの平均テンソルおよび標準偏差テンソルを示します。⊙は要素ごとの積（アダマール積）を表します。ミニバッチ学習中には、μとσはバッチ内のグラフを用いて計算されます。パラメータɑtは固定の分散スケジュールを表し、これは{β ∈ (0, 1)}という減少する数列によってパラメータ化されています。

バニラ型の拡散プロセスと比較して、方向性拡散モデルは2つの重要な制約を課しています。1つ目の制約では、データに依存しないガウスノイズを、異方的でバッチ固有のノイズへと変換します。この制約のもとでは、ノイズベクトルの各座標が、実データの対応する座標における経験的な平均と標準偏差に一致するように強制されます。その結果、拡散過程全体でデータの本質的な構造が維持され、過剰な発散を防ぎつつ、局所的な一貫性が保たれます。2つ目の制約では、角度的な方向性が導入され、ノイズεを対象x0,iの属する同じ超平面内へ回転させます。これにより、データの方向的な特性が保持され、拡散過程全体を通じてデータの本質的な構造が維持されます。

これら2つの制約は相互に作用しながら、前向き拡散プロセスが元のデータ構造を尊重し、信号の急激な劣化を防ぐように働きます。その結果、SN比（信号対雑音比）の減衰がより緩やかになり、方向性拡散モデルはさまざまなSNRレベルにおいて意味のある特徴表現を抽出できるようになります。これにより、より堅牢で情報豊富な埋め込み表現が得られ、下流タスクの性能が向上します。

この手法の著者らは、バニラ型の拡散モデルと同様のトレーニング戦略に従い、ノイズ除去モデルfθを訓練して逆拡散過程を近似します。しかし、方向性ノイズを用いた前向き拡散の逆過程は閉形式で表現できないため、fθは元の系列そのものを直接予測するように訓練されます。

著者らによる方向性拡散モデルフレームワークの元の可視化図が以下に示されています。

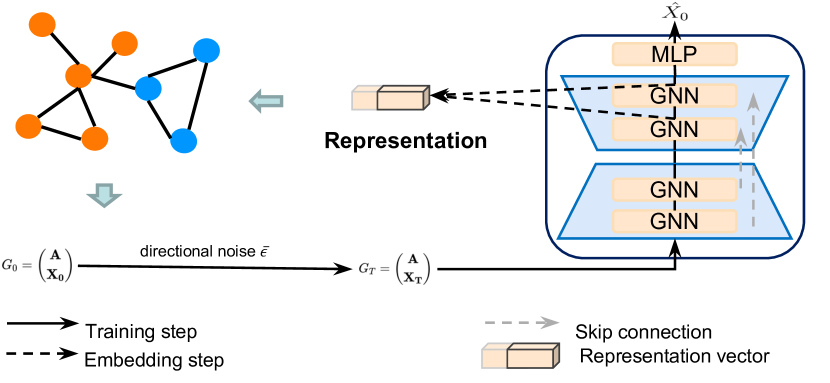
2.MQL5での実装

方向性拡散モデル法の理論的側面を考察した後、本稿の実践的な部分に移り、提案されたアプローチをMQL5で実装します。

実装作業は、次の2つの主要なセクションに分かれます。第1段階では、分析対象データに方向性ノイズを加え、第2段階では、単一のクラス構造内にフレームワークを実装します。

2.1 方向性ノイズの追加

始める前に、方向性ノイズを生成するための一連の処理アルゴリズムについて説明します。まず、正規分布に従うノイズが必要ですが、これは標準のMQL5ライブラリを用いることで簡単に取得できます。

次に、フレームワークの著者が述べている手法に従い、この等方的ノイズを異方的かつデータ依存のノイズへと変換する必要があります。そのためには、各特徴量に対して平均と分散を計算する必要があります。よく見ると、これは以前にCNeuronBatchNormOCLというバッチ正規化層を開発した際に扱ったタスクと似ています。バッチ正規化アルゴリズムは、データを平均0、分散1に標準化します。しかし、スケーリングとシフトの段階でデータの分布が変更されます。理論的には、この統計情報を正規化層自体から取り出すことも可能です。実際、CNeuronRevINDenormOCLという逆正規化クラスを開発した際に、元の分布のパラメータを取得する手順を実装したことがあります。ただし、このアプローチでは、フレームワークの柔軟性と汎用性が制限されてしまいます。

この制約を克服するため、より統合的なアプローチを採用しました。つまり、方向性ノイズの追加とデータの正規化処理を一体化させたのです。ここで、ノイズをどのタイミングで加えるべきという重要な問題が浮かび上がります。

1つ目の選択肢は、正規化前にノイズを加えることです。しかし、これは正規化処理自体を歪めてしまいます。なぜなら、ノイズを加えることでデータの分布が変化し、事前に計算された平均と分散に基づく正規化を適用すると、バイアスのかかった分布になってしまうためです。これは望ましくありません。

2つ目の選択肢は、正規化層の出力にノイズを加えることです。この場合、ガウスノイズをスケーリングおよびシフト係数で調整する必要があります。しかし、元のアルゴリズムの数式を見ると、この調整処理がバイアスを導入し、ノイズが平均オフセット方向へとシフトすることが分かります。結果として、オフセットが大きくなるほど、ノイズは歪み、非対称になります。これもまた望ましくありません。

以上の選択肢の長所と短所を検討した結果、別の戦略を採用することにしました。つまり、正規化処理とスケーリング/オフセットの適用の間にノイズを加えるという方法です。このアプローチでは、正規化されたデータはすでに平均0、分散1の分布になっていることが前提となります。これはまさに私たちがノイズを生成するために使用した分布です。そしてこのノイズを加えたデータを、スケーリングおよびシフトのフェーズに渡すことで、モデルが適切なパラメータを学習できるようになります。

これが私たちの実装戦略となります。ここから実際の実装作業へと進んでいきます。このアルゴリズムはOpenCL側で実装されます。そのため、BatchFeedForwardAddNoiseという新しいカーネルを作成します。このカーネルのロジックは、バッチ正規化層のフィードフォワード処理に大きく依存していますが、それに加えて、ガウスノイズ用のバッファと、偏差のスケーリング係数ɑを追加することで拡張されています。

__kernel void BatchFeedForwardAddNoise(__global const float *inputs, __global float *options,
                                       __global const float *noise, __global float *output,
                                       const int batch, const int optimization, 
                                       const int activation, const float alpha)
  {
   if(batch <= 1)
      return;
   int n = get_global_id(0);
   int shift = n * (optimization == 0 ? 7 : 9);

メソッド本体では、まず正規化バッチのサイズをチェックします。このサイズは「1」より大きい必要があります。次に、現在のスレッドIDに基づいてデータバッファ内のオフセットを決定します。

次に、正規化パラメータバッファに実数が含まれているかどうかを確認します。不正な要素はゼロ値に置き換えられます。

   for(int i = 0; i < (optimization == 0 ? 7 : 9); i++)
     {
      float opt = options[shift + i];
      if(isnan(opt) || isinf(opt))
         options[shift + i] = 0;
     }

次に、ベースカーネルアルゴリズムに従って元のデータを正規化します。

   float inp = inputs[n];
   float mean = (batch > 1 ? (options[shift] * ((float)batch - 1.0f) + inp) / ((float)batch) : inp);
   float delt = inp - mean;
   float variance = options[shift + 1] * ((float)batch - 1.0f) + pow(delt, 2);
   if(batch > 0)
      variance /= (float)batch;
   float nx = (variance > 0 ? delt / sqrt(variance) : 0);

この段階で、平均ゼロ、分散単位の正規化された初期データを取得します。ここでは、事前に方向を調整した上でノイズを追加します。

   float noisex = sqrt(alpha) * nx + sqrt(1-alpha) * fabs(noise[n]) * sign(nx);

その後、スケーリングおよびシフト処理のアルゴリズムを実行し、結果を対応するデータバッファに保存します。これは、ドナーカーネルの実装と同様です。ただし今回は、ノイズが加えられた値に対してスケーリングおよびオフセットを適用します。

   float gamma = options[shift + 3];
   if(gamma == 0 || isinf(gamma) || isnan(gamma))
     {
      options[shift + 3] = 1;
      gamma = 1;
     }
   float betta = options[shift + 4];
   if(isinf(betta) || isnan(betta))
     {
      options[shift + 4] = 0;
      betta = 0;
     }
//---
   options[shift] = mean;
   options[shift + 1] = variance;
   options[shift + 2] = nx;
   output[n] = Activation(gamma * noisex + betta, activation);
  }

フィードフォワードパスアルゴリズムを実装しました。では、バックプロパゲーション処理についてはどうでしょうか。ここで注目すべき点として、バックプロパゲーション操作を実行するために、バッチ正規化層のアルゴリズムを完全に利用することに決めたという点があります。というのも、ノイズ自体は学習対象ではないため、誤差勾配は直接かつ完全に元の入力データへと渡されるからです。先に導入したスケーリング係数ɑは、あくまで元のデータ周辺の領域をわずかにぼかすためのものでしかありません。そのため、この係数は無視でき、誤差勾配は標準的なバッチ正規化アルゴリズムと完全に同じように入力に渡されます。

これにより、OpenCL側の実装作業は完了となります。完全なソースコードは添付ファイルに含まれています。次に、MQL5側の実装へと進みます。ここでは、CNeuronBatchNormWithNoiseという新しいクラスを作成します。クラス名が示す通り、このクラスのコア機能の多くは、バッチ正規化クラスから直接継承されます。唯一オーバーライドが必要なのは、フィードフォワード処理メソッドのみです。新クラスの構造は以下のとおりです。

class CNeuronBatchNormWithNoise  :  public CNeuronBatchNormOCL
  {
protected:
   CBufferFloat      cNoise;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   
public:
                     CNeuronBatchNormWithNoise(void) {};
                    ~CNeuronBatchNormWithNoise(void) {};
   //---
   virtual int       Type(void) const   {  return defNeuronBatchNormWithNoise;    }
  };

お気付きかもしれませんが、新しいクラスCNeuronBatchNormWithNoiseの開発をできるだけシンプルに保つよう努めました。それでも、必要な機能を実現するためには、ノイズを転送するためのバッファが必要です。ノイズはメイン側で生成され、OpenCLコンテキストに渡される形となります。意図的に、オブジェクトの初期化メソッドやファイル関連メソッドをオーバーライドしない方針を取りました。というのも、ランダムに生成されたノイズを保存しておく実用的な理由は存在しないためです。その代わり、ノイズに関連するすべての処理はfeedForwardメソッド内に実装されています。このメソッドは、入力データオブジェクトへのポインタをパラメータとして受け取る仕様となっています。

bool CNeuronBatchNormWithNoise::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!bTrain)
      return CNeuronBatchNormOCL::feedForward(NeuronOCL);

注意していただきたいのは、ノイズが加えられるのはトレーニングフェーズ中のみであるという点です。これは、モデルが入力データ中の意味のある構造を学習できるようにするためです。一方で、実運用（ライブ使用）時には、モデルが現実世界のデータから意味のあるパターンを抽出するフィルターとして機能することを望んでいます。現実のデータには元々ある程度のノイズや不整合が含まれている可能性があるため、この段階では人工的なノイズは加えません。その代わりに、親クラスの機能を用いて通常の正規化処理をおこないます。

以下のコードは、モデルのトレーニング中にのみ実行されます。まず、受け取ったソースデータオブジェクトへのポインタが有効であるかどうかを確認します。

if(!OpenCL || !NeuronOCL)
   return false;

そしてそれを内部変数に保存します。

PrevLayer = NeuronOCL;

その後、正規化パッケージのサイズを確認します。もしそのサイズが1以下であれば、活性化関数を同期させたうえで、メソッドを正の結果（成功）として終了します。というのも、この場合、正規化アルゴリズムの結果は元のデータと等しくなるためです。不要な演算を省くため、受け取った初期データをそのまま次の層へ渡すことにします。

if(iBatchSize <= 1)
  {
   activation = (ENUM_ACTIVATION)NeuronOCL.Activation();
   return true;
  }

上記のすべてのチェックポイントを無事に通過した場合、最初に正規分布に従うノイズを生成します。

double random[];
if(!Math::MathRandomNormal(0, 1, Neurons(), random))
   return false;

その後、生成したノイズをOpenCLコンテキストに渡す必要があります。しかし、オブジェクトの初期化メソッドはオーバーライドしていないため、まずはデータバッファを確認し、要素数が十分であること、および既に作成されたバッファがコンテキスト内に存在していることをチェックします。

if(cNoise.Total() != Neurons() ||
   cNoise.GetOpenCL() != OpenCL)
  {
   cNoise.BufferFree();
   if(!cNoise.AssignArray(random))
      return false;
   if(!cNoise.BufferCreate(OpenCL))
      return false;
  }

いずれかのチェックポイントで負の結果が得られた場合、バッファサイズを変更し、OpenCLコンテキスト内に新しいポインタを作成します。

それ以外の場合は、データをバッファにコピーし、そのままOpenCLコンテキストのメモリへ転送します。

else
  {
   if(!cNoise.AssignArray(random))
      return false;
   if(!cNoise.BufferWrite())
      return false;
  }

次に、実際のバッチサイズを調整し、元データへのノイズレベルをランダムに決定します。

iBatchCount = MathMin(iBatchCount, iBatchSize);
float noise_alpha = float(1.0 - MathRand() / 32767.0 * 0.01);

必要なデータがすべて準備できたので、それを先ほど作成したカーネルのパラメータに渡します。

uint global_work_offset[1] = {0};
uint global_work_size[1];
global_work_size[0] = Neurons();
int kernel = def_k_BatchFeedForwardAddNoise;
ResetLastError();
if(!OpenCL.SetArgumentBuffer(kernel, def_k_normwithnoise_inputs, NeuronOCL.getOutputIndex()))
  {
   printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
   return false;
  }
if(!OpenCL.SetArgumentBuffer(kernel, def_k_normwithnoise_noise, cNoise.GetIndex()))
  {
   printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
   return false;
  }
if(!OpenCL.SetArgumentBuffer(kernel, def_k_normwithnoise_options, BatchOptions.GetIndex()))
  {
   printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
   return false;
  }
if(!OpenCL.SetArgumentBuffer(kernel, def_k_normwithnoise_output, Output.GetIndex()))
  {
   printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
   return false;
  }
if(!OpenCL.SetArgument(kernel, def_k_normwithnoise_activation, int(activation)))
  {
   printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
   return false;
  }
if(!OpenCL.SetArgument(kernel, def_k_normwithnoise_alpha, noise_alpha))
  {
   printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
   return false;
  }
if(!OpenCL.SetArgument(kernel, def_k_normwithnoise_batch, iBatchCount))
  {
   printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
   return false;
  }
if(!OpenCL.SetArgument(kernel, def_k_normwithnoise_optimization, int(optimization)))
  {
   printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
   return false;
  }
//---
if(!OpenCL.Execute(kernel, 1, global_work_offset, global_work_size))
  {
   printf("Error of execution kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                GetLastError(), __LINE__);
   return false;
  }
   iBatchCount++;
//---
   return true;
  }

そしてカーネルを実行キューに入れます。あらゆるステップで操作も管理します。メソッドの最後に、操作の論理結果を呼び出し元に返します。

これで新しいクラスCNeuronBatchNormWithNoiseは完成です。完全なコードは添付ファイルに記載されています。

2.2 DDMフレームワーククラス

元の入力データに方向性ノイズを加えるためのオブジェクトを実装しました。ここからは、方向性拡散モデルフレームワークに対する私たちの解釈の構築へと進みます。

私たちは、フレームワークの著者が提案したアプローチの構造を基本的に踏襲しています。ただし、特定の課題に対応するために、いくつかの点で独自の変更を加えています。本実装では、著者が提案したU字型アーキテクチャを採用していますが、グラフニューラルネットワーク(GNN)をTransformerエンコーダブロックに置き換えています。さらに、著者の実装ではあらかじめノイズが加えられた入力をモデルに与えるのに対し、私たちのアプローチでは、モデル内部でノイズを加える設計にしています。しかし、まずは基本的な部分から順を追って説明していきましょう。

ソリューションを実装するために、CNeuronDiffusionという新しいクラスを作成します。親オブジェクトには、U字型Transformerアーキテクチャを使用します。新クラスの構造は以下のとおりです。

class CNeuronDiffusion  : public CNeuronUShapeAttention
  {
protected:
   CNeuronBatchNormWithNoise  cAddNoise;
   CNeuronBaseOCL             cResidual;
   CNeuronRevINDenormOCL      cRevIn;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronDiffusion(void) {};
                    ~CNeuronDiffusion(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint window_key, uint heads, uint units_count, 
                          uint layers, uint inside_bloks, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronDiffusion;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

提示されたクラス構造では、3つの新しい静的オブジェクトを宣言しています。これらの目的については、クラスメソッドの実装を進める中で明らかになります。ノイズ除去モデルの基本的なアーキテクチャを構築するためには、継承されたオブジェクトを利用します。

すべてのオブジェクトはstaticとして宣言されており、そのためクラスのコンストラクタおよびデストラクタは空のままで問題ありません。オブジェクトの初期化はInitメソッドで実行されます。

メソッドのパラメータでは、生成されるオブジェクトのアーキテクチャを決定する主要な定数を受け取ります。この点について補足すると、今回は親クラスのメソッドからパラメータ構造を完全にそのまま引き継いでおり、変更は行っていません。

bool CNeuronDiffusion::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                            uint window, uint window_key, uint heads, 
                            uint units_count, uint layers, uint inside_bloks, 
                            ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

しかし、新しいアルゴリズムを構築するにあたり、継承されたオブジェクトの使用順序をわずかに変更します。そのため、メソッド本体では、基本インターフェイスのみを初期化するベースクラスの対応メソッドを呼び出します。

その後、元の入力データにノイズを加える正規化オブジェクトを初期化します。このオブジェクトは、入力データの初期処理に使用される予定です。

if(!cAddNoise.Init(0, 0, OpenCL, window * units_count, iBatch, optimization))
   return false;

次に、U字型Transformerの構造を構築します。ここでは、まずMulti-headed Attentionブロックを使用します。

if(!cAttention[0].Init(0, 1, OpenCL, window, window_key, heads, units_count, layers, optimization, iBatch))
   return false;

続いて次元削減のための畳み込み層が続きます。

if(!cMergeSplit[0].Init(0, 2, OpenCL, 2 * window, 2 * window, window, (units_count + 1) / 2, optimization, 
                                                                                                  iBatch))
   return false;

次に、ネックオブジェクトを繰り返し形成します。

 if(inside_bloks > 0)
   {
    CNeuronDiffusion *temp = new CNeuronDiffusion();
    if(!temp)
       return false;
    if(!temp.Init(0, 3, OpenCL, window, window_key, heads, (units_count + 1) / 2, layers, inside_bloks - 1, 
                                                                                     optimization, iBatch))
      {
       delete temp;
       return false;
      }
    cNeck = temp;
   }
 else
   {
   CNeuronConvOCL *temp = new CNeuronConvOCL();
   if(!temp)
      return false;
   if(!temp.Init(0, 3, OpenCL, window, window, window, (units_count + 1) / 2, optimization, iBatch))
     {
      delete temp;
         return false;
     }
   cNeck = temp;
     }

ここで注意していただきたいのは、モデルのアーキテクチャをやや複雑化しているという点です。それに伴い、モデルが解くべき課題も複雑化しています。ポイントとなるのは、ネック部分（中間層）において、類似した方向性拡散オブジェクトを再帰的に追加しているという点です。これはつまり、各新しい層が元の入力データに対してノイズを追加することを意味します。したがって、モデルは非常に多くのノイズを含むデータから情報を復元する方法を学習するようになります。

このアプローチは、拡散モデルの基本的な考え方と矛盾しません。拡散モデルは本質的に生成モデルであり、ノイズからデータを段階的に生成するように設計されているためです。もっとも、この部分では親クラスのオブジェクトをネックに使用することも可能です。

次に、ノイズ除去モデルに第2のAttentionブロックを追加します。

if(!cAttention[1].Init(0, 4, OpenCL, window, window_key, heads, (units_count + 1) / 2, layers, optimization,
                                                                                                     iBatch))
   return false;

また、入力データレベルの次元を復元するために畳み込み層も追加します。

if(!cMergeSplit[1].Init(0, 5, OpenCL, window, window, 2 * window, (units_count + 1) / 2, optimization, iBatch))
   return false;

U字型Transformerのアーキテクチャに従って、得られた結果を残差接続で補足します。これらを書き込むには、基本的なニューラル層を作成します。

if(!cResidual.Init(0, 6, OpenCL, Neurons(), optimization, iBatch))
   return false;
if(!cResidual.SetGradient(cMergeSplit[1].getGradient(), true))
   return false;

その後、残差接続層と次元復元層の勾配バッファを同期します。

次に、フレームワークの著者らによって言及されていないが、メソッドのロジックに従う逆正規化層を追加します。

if(!cRevIn.Init(0, 7, OpenCL, Neurons(), 0, cAddNoise.AsObject()))
   return false;

実際のところ、フレームワークの元のバージョンではデータの正規化は使用されていません。このアルゴリズムは、グラフネットワークによって処理された事前整形済みのグラフデータを使用することが前提となっています。そのため、モデルの出力では元のノイズ除去済みデータが得られることが期待され、トレーニング中にはデータ復元誤差の最小化がおこなわれます。一方、私たちの実装ではデータの正規化を用いているため、結果を正しい値と比較するには、データを元の表現に戻す必要があります。この処理は、逆正規化層によっておこなわれます。

次に、不要なコピー操作を避けるためにデータバッファを差し替え、メソッドの処理結果を論理的な戻り値として呼び出し元プログラムに返す必要があります。

   if(!SetOutput(cRevIn.getOutput(), true))
      return false;
//---
   return true;
  }

ただし、この場合に差し替えるのは出力バッファのポインタのみであることに注意してください。誤差勾配用のバッファには影響を与えません。この決定の理由については、バックプロパゲーションアルゴリズムを検討する際に改めて説明します。

その前に、まずはfeedForwardメソッドを見ていきましょう。

bool CNeuronDiffusion::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cAddNoise.FeedForward(NeuronOCL))
      return false;

メソッドのパラメータとして、入力データオブジェクトへのポインタを受け取ります。このポインタは、内部のノイズ追加層の同名メソッドにそのまま渡されます。

ノイズが加えられた入力データは、最初のAttentionブロックに渡されます。

if(!cAttention[0].FeedForward(cAddNoise.AsObject()))
   return false;

その後、データの次元を変更し、それをネックオブジェクトに渡します。

if(!cMergeSplit[0].FeedForward(cAttention[0].AsObject()))
   return false;
if(!cNeck.FeedForward(cMergeSplit[0].AsObject()))
   return false;

ネックから得られた結果は、2番目のAttentionブロックに送られます。

if(!cAttention[1].FeedForward(cNeck))
   return false;

その後、データの次元を元のレベルまで復元し、ノイズが追加されたデータと合計します。

if(!cMergeSplit[1].FeedForward(cAttention[1].AsObject()))
   return false;
if(!SumAndNormilize(cAddNoise.getOutput(), cMergeSplit[1].getOutput(), cResidual.getOutput(),
                                                                        1, true, 0, 0, 0, 1))
   return false;

メソッドの最後で、データを元の分布空間に戻します。

   if(!cRevIn.FeedForward(cResidual.AsObject()))
      return false;
//---
   return true;
  }

この後は、処理の実行結果を論理値として呼び出し元の関数に返すだけです。

feedForwardメソッドのロジックは比較的単純だと思います。しかし、勾配伝播メソッドcalcInputGradientsでは、話がより複雑になります。ここで重要なのは、私たちが拡散モデルを扱っているという点を思い出すことです。

bool CNeuronDiffusion::calcInputGradients(CNeuronBaseOCL *prevLayer)
  {
   if(!prevLayer)
      return false;

順伝播時と同様に、このメソッドもソースデータオブジェクトへのポインタを受け取ります。しかし今回は、入力データがモデルの出力に与えた影響に応じて、誤差勾配を逆伝播させる必要があります。まず最初に、受け取ったポインタの妥当性を検証します。そうしないと、それ以降の処理が無意味になるからです。

またここで、初期化時にあえて勾配バッファのポインタを差し替えなかったことを思い出してください。この時点で、次の層からの誤差勾配は、対応するインターフェイスバッファ内にのみ存在しています。この設計は、拡散モデルのトレーニングという2つ目の重要な目的を達成するためのものです。理論セクションでも述べたように、拡散モデルは、ノイズから入力データを復元するように訓練されます。したがって、順伝播の出力と元の（ノイズなしの）入力データとの偏差を計算します。

float error = 1;
if(!cRevIn.calcOutputGradients(prevLayer.getOutput(), error) ||
   !SumAndNormilize(cRevIn.getGradient(), Gradient, cRevIn.getGradient(), 1, false, 0, 0, 0, 1))
   return false;

しかし、私たちが目指しているのは、主タスクの文脈において意味のある構造を抽出できるフィルターを構築することです。そのため、再構成誤差の勾配に、メインの経路から受け取った誤差勾配（モデルの予測誤差を示すもの）を加算します。

次に、結合された誤差勾配を残差接続層へと伝播させます。

if(!cResidual.calcHiddenGradients(cRevIn.AsObject()))
   return false;

この段階では、バッファ置換を使用し、2番目のAttentionブロックを通じて勾配をバックプロパゲートします。

if(!cAttention[1].calcHiddenGradients(cMergeSplit[1].AsObject()))
   return false;

そこから、誤差勾配はネットワークの残りの部分へと伝播されます。具体的には、ネック層、次元削減層、第一のAttentoinブロック、そして最後にノイズ注入層を通って流れていきます。

if(!cNeck.calcHiddenGradients(cAttention[1].AsObject()))
   return false;
if(!cMergeSplit[0].calcHiddenGradients(cNeck.AsObject()))
   return false;
if(!cAttention[0].calcHiddenGradients(cMergeSplit[0].AsObject()))
   return false;
if(!cAddNoise.calcHiddenGradients(cAttention[0].AsObject()))
   return false;

ここで停止して、残差接続の誤差勾配を追加する必要があります。

if(!SumAndNormilize(cAddNoise.getGradient(), cResidual.getGradient(), cAddNoise.getGradient(), 1, 
                                                                             false, 0, 0, 0, 1))
   return false;

最後に、勾配を入力層に伝播し、操作の結果を呼び出し関数に返します。

   if(!prevLayer.calcHiddenGradients(cAddNoise.AsObject()))
      return false;
//---
   return true;
  }

これで、Directional Diffusion Frameworkクラス内のメソッドのアルゴリズム実装に関する解説は終了です。すべてのメソッドの完全なソースコードは添付ファイルに含まれています。また、前回の研究からそのまま引き継いだ、トレーニングおよび環境とのインタラクション用プログラムも同様に含まれています。

モデルのアーキテクチャ自体も前回の記事から借用したものです。唯一の変更点は、環境エンコーダ内の適応型グラフ表現層が、学習可能な方向性拡散層に置き換えられたことです。

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronDiffusion;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   descr.window_out = BarDescr;
   descr.layers=2;
   descr.step=3;
   {
      int temp[] = {4};                                  // Heads
      if(ArrayCopy(descr.heads, temp) < (int)temp.Size())
         return false;
   }
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

モデルの完全なアーキテクチャについては、添付ファイルをご覧ください。

それでは、作業の最終段階、つまり実際のデータを使用して実装されたアプローチの有効性を評価する段階に進みましょう。

3.テスト

方向性拡散モデルをMQL5で実装するために多大な努力を注ぎました。次は、これらの手法を実際の取引シナリオで評価する段階です。そのために、2023年の実際のEURUSDデータを用いて提案手法によるモデルの学習をおこないました。トレーニングにはH1（1時間）時間足の過去データを使用しています。

前回の研究と同様に、オフライントレーニング戦略を採用し、Actorの現在のポリシーに合わせてトレーニングデータセットを定期的に更新しました。

先に述べたように、新しい状態エンコーダのアーキテクチャは前回の記事で紹介したモデルを大きく踏襲しています。公正な性能比較を行うために、新モデルのテストパラメータはベースラインで用いたものと同一に保ちました。2024年の最初の3か月間の評価結果を以下に示します。

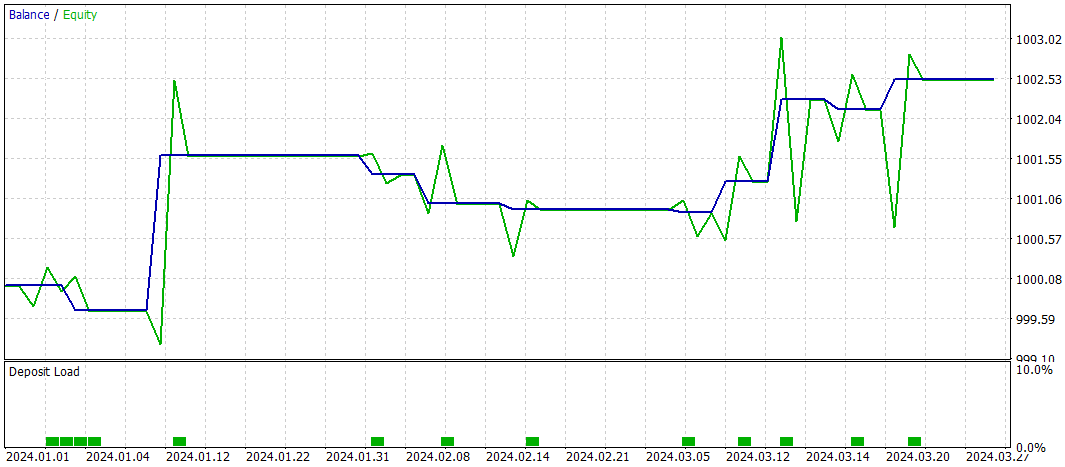
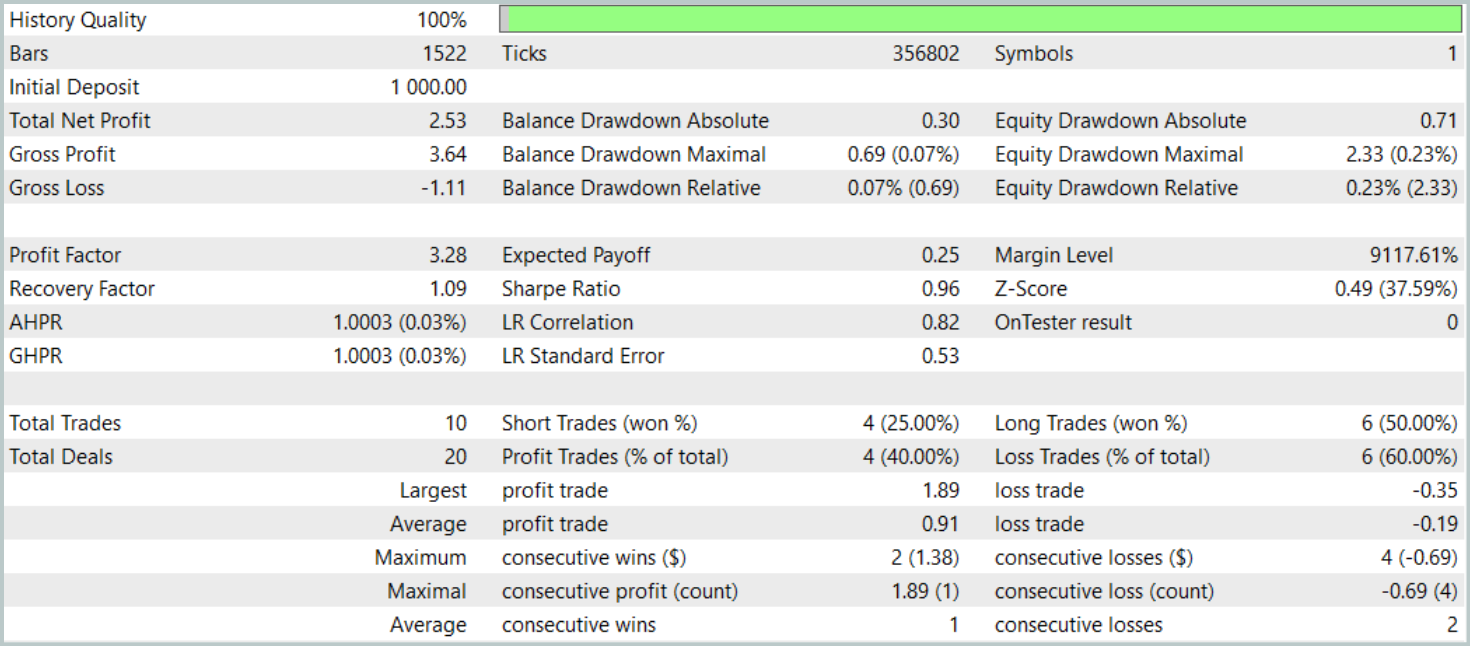
テスト期間中、モデルはわずか10回の取引しかおこないませんでした。これは非常に低い頻度です。さらに、そのうち利益を出した取引は4回のみで、印象的な結果とは言えません。しかしながら、利益を出した取引1回あたりの平均利益および最大利益は、損失を出した取引の約5倍に達しました。その結果、モデルのプロフィットファクターは3.28となりました。

全体として、モデルは良好な利益対損失比を示しましたが、取引回数が限られているため、取引頻度の増加が必要だと考えられます。理想的には、取引の質を損なうことなく頻度を上げることが望まれます。

結論

方向性拡散モデル (DDM: Directional Diffusion Models)は、取引アプリケーションにおける市場データの分析および表現に有望な手法を提供します。金融市場は複雑な構造的関係やマクロ経済要因の影響を受け、しばしば異方的かつ方向性のあるパターンを示します。従来の等方的拡散モデルは、こうした微妙な特徴を十分に捉えられないことがあります。一方、DDMsは方向性ノイズを用いてデータの方向性に適応するため、高ノイズ・高ボラティリティ環境でも主要なパターンやトレンドをより良く識別することが可能です。

実用的な部分では、MQL5を使用して提案された方法のビジョンを実装しました。実際の歴史的市場データでモデルをトレーニングし、未使用のデータで性能評価をおこないました。実験結果に基づき、DDMsは強い可能性を示していると結論づけられます。ただし、現時点の実装はさらなる最適化が必要です。

参照文献

記事で使用されているプログラム

#	名前	種類	詳細
1	Research.mq5	EA	事例収集のためのEA
2	ResearchRealORL.mq5	EA	Real-ORL法による事例収集のためのEA
3	Study.mq5	EA	モデル訓練EA
4	Test.mq5	EA	モデルテストEA
5	Trajectory.mqh	クラスライブラリ	システム状態記述の構造体
6	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
7	NeuroNet.cl	ライブラリ	OpenCLプログラムコードライブラリ

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/16269

添付されたファイル |

ZIPをダウンロード

MQL5.zip (2075.11 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

EAのサンプル

一般的なMACDを使ったEAを例として、MQL4開発の原則を紹介します。

初級から中級まで：配列(IV)

この記事では、C、C++、Javaなどの言語で実装されていることと非常によく似たことを実現する方法について見ていきます。つまり、関数や手続きにほぼ無限の数のパラメータを渡す方法についてです。これは一見すると高度なトピックに思えるかもしれませんが、前回までの内容をきちんと理解していれば、実装は決して難しくありません。もちろん、それらの内容を本当に理解していることが前提です。

エラー 146 (「トレードコンテキストビジー」) と、その対処方法

この記事では、MT4において複数のEAの衝突をさける方法を扱います。ターミナルの操作、MQL4の基本的な使い方がわかる人にとって、役に立つでしょう。

リプレイシステムの開発（第72回）：異例のコミュニケーション(I)

私たちが本日作成する内容は、理解が難しいものになるでしょう。したがって本稿では、初期段階についてのみ説明します。この段階は次のステップに進むための重要な前提条件となるため、ぜひ注意深く読んでください。この資料の目的はあくまで学習にあります。提示された概念を実際に応用するのではなく、あくまで理解・習得することが目的です。