
取引におけるニューラルネットワーク:NAFSによるノード依存型グラフ表現
はじめに
近年、グラフ表現学習は、ノードクラスタリング、リンク予測、ノード分類、グラフ分類など、さまざまな応用分野で広く利用されています。グラフ表現学習の目的は、グラフの情報をノードの埋め込みとしてエンコードすることです。従来のグラフ表現学習手法は、主にグラフ構造の情報を保持することに焦点を当ててきました。しかし、これらの手法には以下の2つの大きな課題があります。
- 浅いアーキテクチャ:グラフ畳み込みネットワーク(GCN: Graph Convolutional Network)は、構造情報をより深く捉えるために複数の層を用いますが、層を増やしすぎると「オーバースムージング」が発生し、ノードの埋め込みが区別できなくなるという問題があります。
- 低スケーラビリティ:GNNベースのグラフ表現学習手法は、計算コストやメモリ消費が大きいため、大規模なグラフへの適用が困難な場合があります。
論文「NAFS:A Simple yet Tough-to-beat Baseline for Graph Representation Learning」の著者らは、これらの問題を解決するために、シンプルな特徴量平滑化と適応的統合に基づく新しいグラフ表現手法を提案しました。ノード依存型特徴量平滑化(NAFS: Node-Adaptive Feature Smoothing)手法は、グラフ構造情報とノード特徴量の両方を活用して、優れたノード埋め込みを生成します。著者らは、ノードごとに「平滑化速度」が大きく異なることに着目し、各ノードに対して平滑化を適応的に調整します。これは、低次数および高次数の近傍情報の両方を活用して実現されます。さらに、異なる平滑化手法によって得られた特徴量をアンサンブル(集合)することで、より表現力の高い特徴を生成します。NAFSは学習を必要としないため、学習コストを大幅に削減し、大規模グラフにも効率的にスケーリング可能です。
1. NAFSアルゴリズム
多くの研究者は、各GCN層において特徴量の平滑化処理と変換処理を分離することによって、大規模なノード分類にスケーラビリティを持たせようと提案してきました。具体的には、まず特徴量の平滑化操作を前処理としておこない、その後、処理済みの特徴量を単純なMLP(多層パーセプトロン)に入力して最終的なノードのラベル予測をおこないます。
このような分離型のGNNは、主に、特徴量平滑化とMLPによる学習の2つの部分で構成されます。平滑化段階では、グラフ構造情報とノード特徴量を統合して、MLPの入力としてより情報量の多い特徴量を生成します。学習時には、MLPはこのスムージングされた特徴量のみに基づいて訓練されます。
一方、別のGNN系統も平滑化と変換の分離をおこないますが、アプローチは異なります。具体的には、生のノード特徴量をまずMLPに通して中間的な埋め込みを生成し、その後で個別化された伝播操作を適用して最終予測を得ます。しかしこの手法では、各エポックごとに再帰的な伝播処理が必要となるため、大規模グラフには不向きです。
構造情報を豊かに捉える最も単純な方法は、GNN層を多層にスタックすることです。しかし、GNNモデルにおける繰り返しの平滑化は、ノード埋め込みが区別できなくなる「オーバースムージング問題」を引き起こします。
定量的な分析によって、ノードの次数が最適な平滑化回数に大きく影響することが実証されています。直感的には、高次数のノードは、低次数のノードよりも少ない平滑化回数で十分だと考えられます。
分離型GNNにおいて特徴量平滑化を用いることで、大規模グラフへのスケーラブルな学習が可能になりますが、すべてのノードに一律に平滑化を適用してしまうと、非最適な埋め込みが生成されます。異なる構造的性質を持つノードには、それぞれに適した平滑化率が必要です。したがって、ノード依存型の特徴量平滑化が求められます。
スムージング処理を逐次的に適用するとき、𝐗 l = Â𝐗 l−1となり、スムージングステップlが進むにつれて、埋め込み行列𝐗l−1はより深い構造情報を蓄積します。このように得られる複数のスケールのノード埋め込み行列{𝐗0, 𝐗1, …, 𝐗K}(KK は最大平滑化ステップ)は、局所および大域的な近傍情報を統合した統一表現Ẋへと統合されます。
NAFSの著者による分析では、各ノードが「定常状態」に到達する速度が大きく異なることが明らかになっています。したがって、ノードごとの個別分析が必要になります。この目的のために、NAFS平滑化重み という概念を導入します。これは、あるノードの局所特徴量ベクトルと平滑化された特徴量ベクトルの距離に基づいて算出されます。この重みにより、各ノードに最適化された平滑化処理が可能になります。
より効果的な代替手法として、平滑化に使われる行列Âをコサイン類似度で置き換える方法もあります。あるノードの局所特徴量ベクトルとスムージング特徴量ベクトルのコサイン類似度が高いということは、そのノードviがまだ定常状態に達しておらず、そのノードに対するスムージング結果[Âk𝐗]iがより新しい情報を含んでいることを示します。したがって、ノードviにとって、コサイン類似度の高いスムージング特徴量は、最終的な埋め込みへの貢献度が高くなるべきです。
異なる平滑化演算子は、それぞれ異なる知識抽出器として機能します。これにより、さまざまなスケールや次元でのグラフ構造の把握が可能になります。この目的のため、NAFSでは特徴量アンサンブルを用い、複数の平滑化演算子によって生成された多様な特徴量を統合します。
NAFSはパラメータの学習を必要とせず、非常に効率的かつスケーラブルにノード埋め込みを生成できます。さらに、ノード依存型の特徴量平滑化戦略により、深い構造情報の捉え方を強化しています。
著者によるNAFS手法の視覚図を以下に示します。
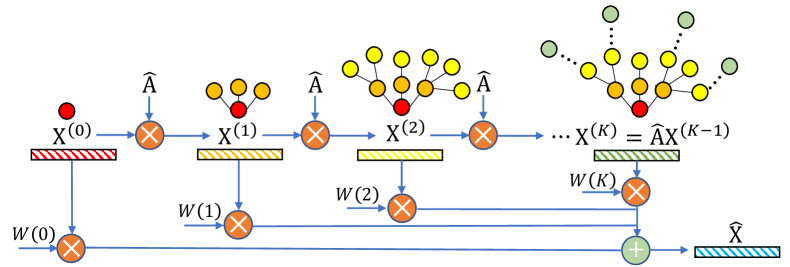
2. MQL5での実装
NAFSフレームワークの理論的側面を解説したところで、ここからはMQL5を用いた実装に移ります。本格的な実装に進む前に、まずフレームワークの主要なステージを明確に整理しておきましょう。
- マルチスケールなノード表現行列の構築
- ノードの特徴量と平滑化された表現とのコサイン類似度に基づく平滑化重みの計算
- 重み付き平均による最終的な埋め込みの算出
注目すべき点として、これらの処理の一部は、既存のライブラリ機能を活用することで実装が可能であるということです。たとえば、コサイン類似度の計算は、行列積を用いることで効率的に実現できます。同様に、重み付き平均の計算も同じく行列演算を通じて処理可能です。さらに、平滑化係数の決定には、Softmax層を用いることで適切な正規化をおこなうことができます。
残された課題は、マルチスケールなノード表現行列をどのように構築するかという点です。
2.1 マルチスケールノード表現行列
マルチスケールなノード表現行列を構築するために、各ノードの特徴量とその直近の隣接ノードの特徴量を単純に平均する手法を用います。異なるサイズの平均ウィンドウを適用することで、マルチスケール的な挙動を実現します。
本プロジェクトにおいては、主要な計算処理をOpenCLコンテキスト内で実装しています。したがって、この行列構築処理も並列計算に委ねられることになります。そのために、OpenCLプログラムFeatureSmoothing内に、新しいカーネルを作成します。
__kernel void FeatureSmoothing(__global const float *feature, __global float *outputs, const int smoothing ) { const size_t pos = get_global_id(0); const size_t d = get_global_id(1); const size_t total = get_global_size(0); const size_t dimension = get_global_size(1);
カーネルのパラメータとしては、2つのデータバッファ(元のデータと結果)へのポインタと、平滑化スケールの数を指定する定数を受け取ります。この実装では、特定の平滑化スケールのステップサイズは定義しておらず、ステップサイズは「1」と仮定します。スムージング対象となる平均ウィンドウは、前後にそれぞれ1要素ずつ拡張されるため、合計で2要素分広がることになります。
ここで重要なのは、平滑化スケールの数は負の値にはできないという点です。この値がゼロの場合は、スムージング処理は行わず、元のデータをそのまま通過させます。
このカーネルは、ローカルワークグループを作成せずに、完全に独立したスレッドで構成される2次元のタスク空間において実行する予定です。第1次元は、分析対象となる元のシーケンスのサイズに対応し、第2次元は、各シーケンス要素を記述するベクトル内の特徴量の数に対応します。
カーネル本体では、タスク空間のすべての次元において、現在のスレッドを特定し、それぞれの次元に対応する全体のサイズを把握します。
これらの情報をもとにして、データバッファ内でのオフセットを算出します。
const int shift_input = pos * dimension + d; const int shift_output = dimension * pos * smoothing + d;
この時点で準備段階は完了し、いよいよマルチスケール表現の生成に入ります。最初のステップは、元のデータをコピーすることです。これは、スムージングをおこなっていない(ゼロレベル)状態の表現に相当します。
float value = feature[shift_input]; if(isinf(value) || isnan(value)) value = 0; outputs[shift_output] = value;
次に、平均ウィンドウ内で各特徴量の平均値を計算するためのループを構成します。想像できる通り、これはウィンドウ内のすべての値を合計し、その合計を含まれる要素数で割ることで求められます。
ここで重要なのは、異なるスケールにおけるすべての平均ウィンドウが、同じ解析対象要素を中心として配置されているという点です。そのため、各スケールは前のスケールで使用した要素をすべて含み、さらに新たな要素を加える形になります。この性質を活かすことで、コストの高いグローバルメモリへのアクセスを最小限に抑えることが可能です。具体的には、各反復において、新たに追加される要素の値のみをこれまでの累積和に加算し、現在のウィンドウに含まれる要素数で割ることで、平均を算出します。
for(int s = 1; s <= smoothing; s++) { if((pos - s) >= 0) { float temp = feature[shift_input - s * dimension]; if(isnan(temp) || isinf(temp)) temp = 0; value += temp; } if((pos + s) < total) { float temp = feature[shift_input + s * dimension]; if(isnan(temp) || isinf(temp)) temp = 0; value += temp; } float factor = 1.0f / (min((int)total, (int)(pos + s)) - max((int)(pos - s), 0) + 1); if(isinf(value) || isnan(value)) value = 0; float out = value * factor; if(isinf(out) || isnan(out)) out = 0; outputs[shift_output + s * dimension] = out; } }
なお、やや直感に反するように聞こえるかもしれませんが、同じスケール内であっても、すべての平均ウィンドウが同じサイズになるとは限らない点にも言及しておくべきでしょう。これは、シーケンスの端に位置する要素に対して、平均ウィンドウがシーケンスの範囲外にはみ出してしまうためです。そのため、各反復において、実際に平均に含まれる要素数を都度計算する必要があります。
同様の考え方に基づいて、誤差勾配の伝播アルゴリズムも構築されており、これも先に説明した処理と同様の手法で実装されています。この処理はFeatureSmoothingGradientカーネル内に実装されており、詳細は読者自身で確認されることを推奨します。OpenCLプログラムの完全なコードは、添付ファイルに含まれています。
2.2 NAFSクラスの構築
OpenCLプログラムに必要な追加を行った後、メインアプリケーションに進み、適応型ノード埋め込み形成のための新しいクラスCNeuronNAFSを作成します。新クラスの構造は以下のとおりです。
class CNeuronNAFS : public CNeuronBaseOCL { protected: uint iDimension; uint iSmoothing; uint iUnits; //--- CNeuronBaseOCL cFeatureSmoothing; CNeuronTransposeOCL cTranspose; CNeuronBaseOCL cDistance; CNeuronSoftMaxOCL cAdaptation; //--- virtual bool FeatureSmoothing(const CNeuronBaseOCL *neuron, const CNeuronBaseOCL *smoothing); virtual bool FeatureSmoothingGradient(const CNeuronBaseOCL *neuron, const CNeuronBaseOCL *smoothing); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return true; } public: CNeuronNAFS(void) {}; ~CNeuronNAFS(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint step, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronNAFS; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
ご覧のように、新しいクラスの構造では、3つの変数と4つの内部層が宣言されています。これらの機能については、オーバーライドされた仮想メソッド内でアルゴリズムを実装する際に詳しく見ていきます。
また、先に説明したOpenCLプログラム内の同名カーネルに対応する2つのラッパーメソッドも用意しています。これらは標準的なカーネル呼び出しのアルゴリズムを用いて構築されています。コードは添付ファイルでご自身でご確認いただけます。
新しいクラスのすべての内部オブジェクトは静的に宣言されているため、クラスのコンストラクタとデストラクタは「空」のままにしておけます。これらの宣言済みおよび継承されたオブジェクトの初期化は、Initメソッド内でおこなわれます。
bool CNeuronNAFS::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint dimension, uint smoothing, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, dimension * units_count, optimization_type, batch)) return false;
このメソッドのパラメータには、作成されるオブジェクトのアーキテクチャを一意に決定するための主な定数が渡されます。これらには次のものが含まれます。
- dimension:単一のシーケンス要素を表す特徴量ベクトルのサイズ
- smoothing:平滑化スケールの数(ゼロに設定した場合、元データが直接コピーされます);
- unit_count:分析対象のシーケンスのサイズ
なお、すべてのパラメータは符号なし整数型であるため、負の値が渡される可能性は排除されています。
メソッド内では、いつものように、まず同名の親クラスのメソッドを呼び出します。親クラスのメソッドはすでにパラメータの検証や継承されたオブジェクトの初期化をおこなっています。結果のテンソルのサイズは、入力テンソルのサイズと一致すると想定され、解析対象シーケンスの要素数と単一要素の特徴量ベクトルサイズの積で計算されます。
親クラスのメソッドが正常に実行された後、外部から渡されたパラメータを対応する名前の内部変数に保存します。
iDimension = dimension; iSmoothing = smoothing; iUnits = units_count;
次に、宣言されたオブジェクトの初期化に進みます。まず、マルチスケールノード表現行列を格納するための内部層を宣言します。そのサイズは完全な行列を格納できる十分な大きさでなければなりません。したがって、元データのサイズのiSmoothing + 1倍となります。
if(!cFeatureSmoothing.Init(0, 0, OpenCL, (iSmoothing + 1) * iUnits * iDimension, optimization, iBatch)) return false; cFeatureSmoothing.SetActivationFunction(None);
マルチスケールノード表現(ここでは様々なスケールのローソク足パターンを表します)を構築した後、これらの表現と解析対象のバーの特徴量ベクトルとの間のコサイン類似度を計算する必要があります。そのために、入力テンソルとマルチスケールノード表現テンソルを掛け合わせます。ただし、この乗算をおこなう前に、マルチスケール表現テンソルを転置する必要があります。
if(!cTranspose.Init(0, 1, OpenCL, (iSmoothing + 1)*iUnits, iDimension, optimization, iBatch)) return false; cTranspose.SetActivationFunction(None);
行列の乗算処理はすでに基底ニューラルレイヤークラスで実装されており、親クラスから継承されています。この演算の結果を保存するために、内部オブジェクトであるcDistanceを初期化します。
if(!cDistance.Init(0, 2, OpenCL, (iSmoothing + 1)*iUnits, optimization, iBatch)) return false; cDistance.SetActivationFunction(None);
念のためお伝えしますが、同じ方向を向く2つのベクトルを掛け合わせると正の値が得られ、逆方向の場合は負の値になります。解析対象のバーが全体のトレンドと一致している場合、バーの特徴量ベクトルと平滑化された値との掛け算の結果は正の値になります。逆に、バーが全体のトレンドに反している場合は、結果は負の値となります。レンジ相場(横ばい)では、平滑化された値のベクトルはゼロに近くなるため、乗算の結果もゼロに近づきます。これらの結果を正規化し、各スケールに対する適応的な影響係数を計算するために、Softmax関数を用います。
if(!cAdaptation.Init(0, 3, OpenCL, cDistance.Neurons(), optimization, iBatch)) return false; cAdaptation.SetActivationFunction(None); cAdaptation.SetHeads(iUnits);
次に、解析対象のノード(バー)の最終的な埋め込みを計算するために、各ノードの適応係数ベクトルと対応するマルチスケール表現行列を掛け合わせます。この演算結果は、親クラスから継承した次の層とのデータ交換用インターフェイスのバッファに書き込まれます。そのため、追加の内部オブジェクトは作成せず、単に活性化関数を無効化して初期化メソッドを完了し、演算の論理結果を呼び出し元に返します。
SetActivationFunction(None); //--- return true; }
新しいオブジェクトの初期化作業が完了したら、feedForwardメソッドでフィードフォワードパスアルゴリズムの構築に進みます。メソッドパラメータでは、ソースデータオブジェクトへのポインタを受け取ります。
bool CNeuronNAFS::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!FeatureSmoothing(NeuronOCL, cFeatureSmoothing.AsObject())) return false;
このデータから、まず先に説明したFeatureSmoothingカーネル用のラッパーメソッドを呼び出して、マルチスケール表現テンソルを構築します。
if(!FeatureSmoothing(NeuronOCL, cFeatureSmoothing.AsObject())) return false;
初期化アルゴリズムの説明で述べたように、次に得られたマルチスケールノード表現行列を転置します。
if(!cTranspose.FeedForward(cFeatureSmoothing.AsObject())) return false;
次に、それを入力テンソルと掛け合わせてコサイン類似度係数を取得します。
if(!MatMul(NeuronOCL.getOutput(), cTranspose.getOutput(), cDistance.getOutput(), 1, iDimension, iSmoothing + 1, iUnits)) return false;
これらの係数は、Softmax関数を使用して正規化されます。
if(!cAdaptation.FeedForward(cDistance.AsObject())) return false;
最後に、得られた適応係数のテンソルを先に形成したマルチスケール表現行列と掛け合わせます。
if(!MatMul(cAdaptation.getOutput(), cFeatureSmoothing.getOutput(), Output, 1, iSmoothing + 1, iDimension, iUnits)) return false; //--- return true; }
この操作の結果、最終的なノード埋め込みが得られ、モデル内のニューラル層インターフェイスのバッファに格納されます。メソッドは処理の論理結果を呼び出し元に返して終了します。
次の開発段階では、新しいNAFSフレームワーククラスの逆伝播アルゴリズムを実装します。ここで考慮すべき重要な点が2つあります。まず、理論セクションで述べたように、新しいオブジェクトには学習可能なパラメータが含まれていません。そのため、updateInputWeights、メソッドは常に成功を返すスタブとしてオーバーライドします。
virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return true; }
ただし、calcInputGradientsメソッドには特に注意が必要です。順伝播処理は単純であるものの、入力データとマルチスケール表現行列の両方が2回使用されます。そのため、誤差勾配を入力データレベルへ正しく逆伝播させるには、構築したアルゴリズムのすべての情報経路を慎重に通過させる必要があります。
bool CNeuronNAFS::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
このメソッドは、誤差勾配を受け取るべき前段階の層オブジェクトへのポインタをパラメータとして受け取ります。そして、各データ要素がモデルの最終出力に与えた影響の大きさに応じて、勾配を適切に分配しなければなりません。メソッド内では、まず受け取ったポインタの有効性を確認します。無効な参照のまま処理を続けると、その後のすべての操作が無意味になるためです。
最初に、後続層から受け取った誤差勾配を適応係数とマルチスケール表現行列の間で分配する必要があります。ただし、適応係数の情報経路を通じて勾配をマルチスケール表現行列に逆伝播させる計画もあるため、この段階ではマルチスケール表現テンソルの勾配を一時的なバッファに保存します。
if(!MatMulGrad(cAdaptation.getOutput(), cAdaptation.getGradient(), cFeatureSmoothing.getOutput(), cFeatureSmoothing.getPrevOutput(), Gradient, 1, iSmoothing + 1, iDimension, iUnits)) return false;
次に、適応係数の情報フローを処理します。ここでは、対応するオブジェクトの勾配分配メソッドを呼び出して、誤差勾配をコサイン類似度テンソルへ逆伝播させます。
if(!cDistance.calcHiddenGradients(cAdaptation.AsObject())) return false;
次のステップでは、誤差勾配を入力データと転置されたマルチスケール表現テンソルの間で分配します。ここでも、2つ目の情報経路を通じて勾配が入力データレベルへさらに伝播することを見越して、対応する勾配を一時的なバッファに保存します。
if(!MatMulGrad(NeuronOCL.getOutput(), PrevOutput, cTranspose.getOutput(), cTranspose.getGradient(), cDistance.getGradient(), 1, iDimension, iSmoothing + 1, iUnits)) return false;
次に、マルチスケール表現の勾配テンソルを転置し、以前に保存したデータと合算します。
if(!cFeatureSmoothing.calcHiddenGradients(cTranspose.AsObject()) || !SumAndNormilize(cFeatureSmoothing.getGradient(), cFeatureSmoothing.getPrevOutput(), cFeatureSmoothing.getGradient(), iDimension, false, 0, 0, 0, 1) ) return false;
最後に、蓄積された誤差勾配を入力データレベルへ伝播させます。まず、マルチスケール表現行列から誤差勾配を渡します。
if(!FeatureSmoothingGradient(NeuronOCL, cFeatureSmoothing.AsObject()) || !SumAndNormilize(NeuronOCL.getGradient(), cFeatureSmoothing.getPrevOutput(), NeuronOCL.getGradient(), iDimension, false, 0, 0, 0, 1) || !DeActivation(NeuronOCL.getOutput(), NeuronOCL.getGradient(), NeuronOCL.getGradient(), (ENUM_ACTIVATION)NeuronOCL.Activation()) ) return false; //--- return true; }
次に、先に保存したデータを加算し、入力層の勾配を調整するために活性化関数の微分を適用します。メソッドは処理の論理結果を呼び出し元に返して終了します。
以上で、CNeuronNAFSクラスのメソッドの説明は完了です。このクラスとそのすべてのメソッドの完全なソースコードは、添付ファイルに含まれています。
2.3 モデルアーキテクチャ
学習可能なモデルのアーキテクチャについて、少し説明しておきます。新しい適応型特徴量平滑化オブジェクトは、環境状態エンコーダモデルに統合されています。このモデル自体は、AMCTフレームワークに関する前回の記事から継承されたものです。したがって、新しいモデルは両フレームワークのアプローチを取り入れています。モデルのアーキテクチャはCreateEncoderDescriptionsメソッド内で実装されています。
一般的なモデル設計の原則に則り、まず全結合層を作成し、ソースデータをモデルに入力します。
bool CreateEncoderDescriptions(CArrayObj *&encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; } //--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
なお、NAFSNAFSアルゴリズムは生の入力データに対して直接適応的な平滑化を適用できることに注意が必要です。しかし、私たちのモデルは取引端末から未処理の生データを直接受け取るため、解析対象の特徴量は非常に異なる値の分布を持つ可能性があります。この影響を最小限に抑えるために、常に正規化層を使用してきました。ここでも同様のアプローチを適用しています。
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
正規化の後に、適応型特徴量平滑化層を適用します。この順序は、ご自身の実験においても推奨されます。というのも、個々の特徴量の分布に大きな違いがある場合、この順序を守らないと、振幅の大きい特徴量が平滑化スケールの適応的注意係数の計算時に支配的になってしまう恐れがあるためです。
新しいオブジェクトのパラメータのほとんどは、すでに馴染みのあるニューラル層記述構造に収まっています。
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronNAFS; descr.count = HistoryBars; descr.window = BarDescr; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM;
この場合、5つの平均化スケールを使用しており、これはウィンドウ{1, 3, 5, 7, 9, 11}の形成に対応しています。
descr.window_out = 5; if(!encoder.Add(descr)) { delete descr; return false; }
エンコーダの残りのアーキテクチャは変更されず、AMCT層が含まれています。
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronAMCT; descr.window = BarDescr; // Window (Indicators to bar) { int temp[] = {HistoryBars, 50}; // Bars, Properties if(ArrayCopy(descr.units, temp) < (int)temp.Size()) return false; } descr.window_out = EmbeddingSize / 2; // Key Dimension descr.layers = 5; // Layers descr.step = 4; // Heads descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
その後に、全結合の次元削減層が続きます。
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
ActorモデルとCriticモデルのアーキテクチャも変更されていません。これらとともに、環境とのインタラクションおよびモデルの学習をおこなうプログラムも前回の研究から引き継いでいます。すべてのコードは添付ファイルにあります。添付ファイルには、記事の作成中に使用されたすべてのプログラムの完全なコードも含まれています。
3.テスト
前のセクションまでで、NAFSフレームワークの提案手法をMQL5で実装するための大幅な作業をおこないました。ここからは、それらの手法が私たちの具体的な課題に対してどの程度有効であるかを評価する段階に入ります。評価のために、2023年の1年間分の実際のEURUSDデータを用いて、これらのアプローチを適用したモデルの学習をおこないます。取引には、H1時間軸の過去データを使用します。
これまで通り、オフラインでのモデル学習をおこない、Actorの現在の方策から生成される値の範囲に適合するよう、学習データセットを定期的に更新しながら進めます。
前述したように、新しい環境状態エンコーダモデルは、対照学習を用いたパターンTransformerを基盤として構築されています。結果比較の明確化を目的に、新モデルではベースラインモデルのテストパラメータを完全に保持した状態でテストを実施しました。2024年の最初の3か月間のテスト結果を以下に示します。
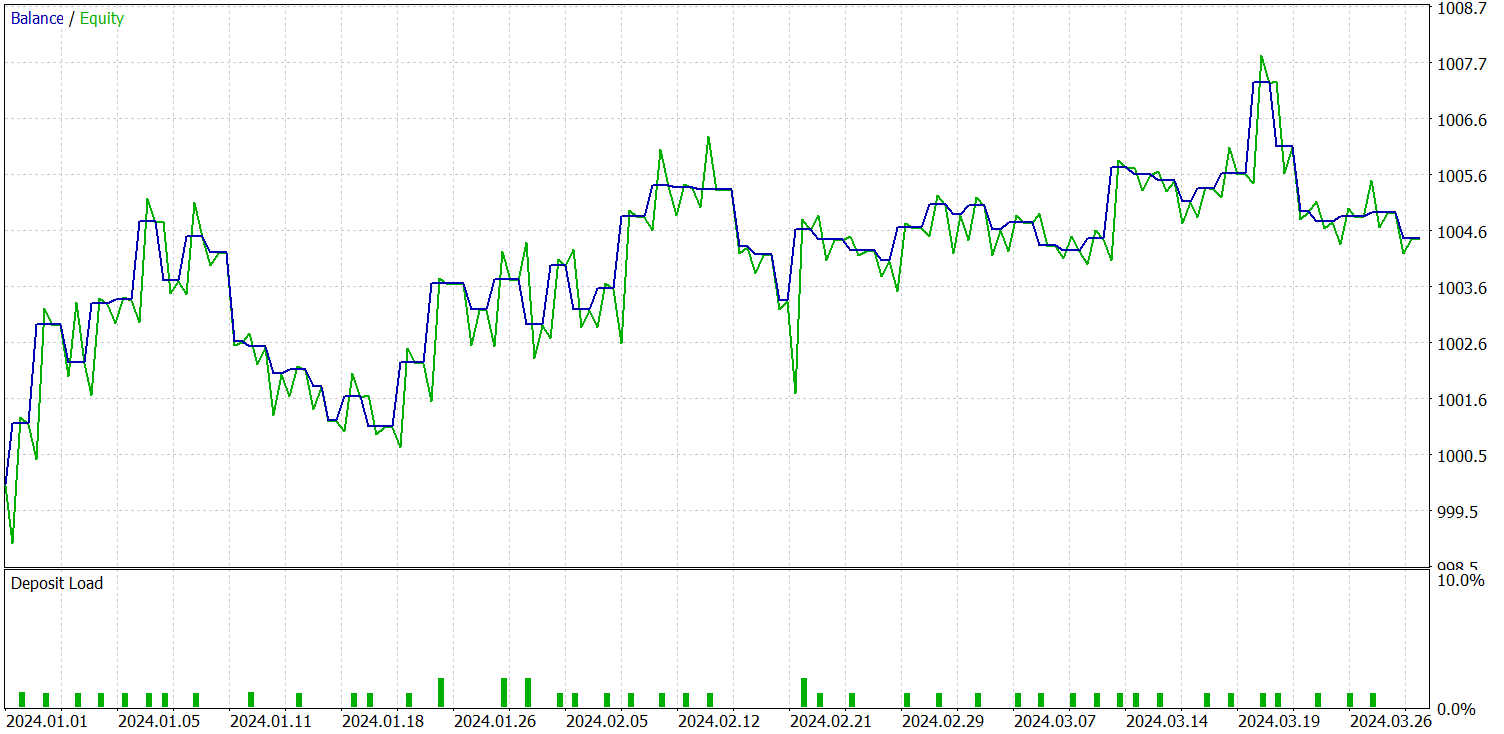
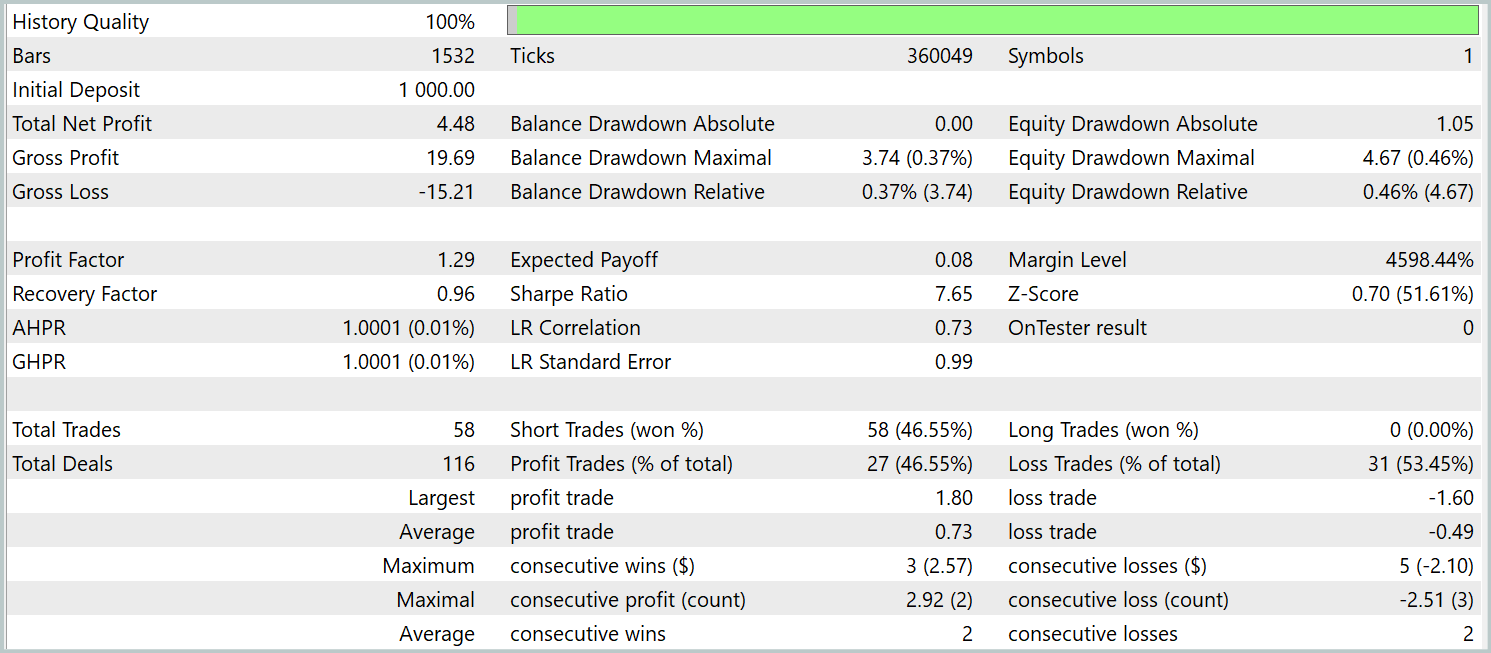
一見すると、今回のモデルとベースラインモデルのテスト結果を比較した際には、評価が分かれる印象を受けます。一方では、プロフィットファクターが1.4から1.29へと低下します。その一方で、取引回数が約2.5倍に増加したことにより、同じテスト期間における総利益は比例して増加しています。
さらに、ベースラインモデルとは異なり、新モデルではテスト期間全体を通じて一貫した右肩上がりのバランス推移が確認されました。ただし、実行されたのはショートポジションのみでした。これは、おそらく平滑化された値におけるグローバルトレンドへのフォーカスが強くなったためであり、その結果として、一部のローカルトレンドがノイズとして除外されてしまった可能性があります。
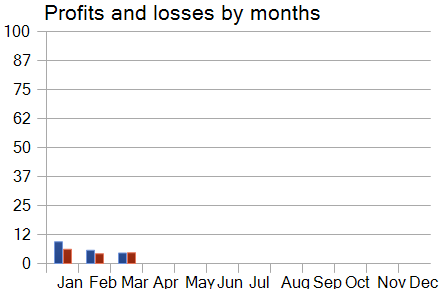
それにもかかわらず、モデルの月次パフォーマンスカーブを分析すると、時間の経過とともに収益性が徐々に低下していることが確認されます。この観察結果は、前回の記事で立てた仮説──テスト期間が長くなるにつれて、学習データセットの代表性が低下する──を裏付けるものとなっています。
結論
本記事では、NAFS (Node-Adaptive Feature Smoothing)手法を取り上げました。これは、パラメータの学習を必要とせずに、グラフ上のノード表現を構築するための、シンプルでありながら効果的なノンパラメトリックアプローチです。本手法は、近傍ノードの特徴を平滑化し、それぞれ異なるスケールでの平滑化戦略をアンサンブル的に組み合わせることで、堅牢かつ情報豊富な最終的な埋め込みを生成します。
実装面では、提案手法をMQL5上で独自に解釈・実装し、実際の過去データを用いてモデルを学習させ、アウトオブサンプルのデータセットで検証をおこないました。これらの実験結果に基づき、提案手法は十分な可能性を示していると結論づけられます。他のフレームワークとの併用も可能であり、ベースラインモデルの効率性を向上させる統合手段として有望です。
参照文献
記事で使用されているプログラム
| # | 名前 | 種類 | 詳細 |
|---|---|---|---|
| 1 | Research.mq5 | EA | 事例収集のためのEA |
| 2 | ResearchRealORL.mq5 | EA | Real-ORL法による事例収集のためのEA |
| 3 | Study.mq5 | EA | モデル訓練EA |
| 4 | Test.mq5 | EA | モデルテストEA |
| 5 | Trajectory.mqh | クラスライブラリ | システム状態記述の構造体 |
| 6 | NeuroNet.mqh | クラスライブラリ | ニューラルネットワークを作成するためのクラスのライブラリ |
| 7 | NeuroNet.cl | ライブラリ | OpenCLプログラムコードライブラリ |
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/16243
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 高度なICT取引システムの開発:インジケーターへのオーダーブロックの実装
高度なICT取引システムの開発:インジケーターへのオーダーブロックの実装
 取引におけるニューラルネットワーク:対照パターンTransformer(最終回)
取引におけるニューラルネットワーク:対照パターンTransformer(最終回)
 MQL5におけるSQLiteの機能:銘柄とマジックナンバー別の取引統計を表示するダッシュボード
MQL5におけるSQLiteの機能:銘柄とマジックナンバー別の取引統計を表示するダッシュボード
 ALGLIBライブラリの最適化手法(第2回):
ALGLIBライブラリの最適化手法(第2回):
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索