Redes neuronales en el trading: Modelo de doble atención para la previsión de tendencias
Introducción
El precio de un instrumento financiero supone una serie temporal muy volátil. En él influyen muchos factores, como los tipos de interés, la inflación, la política monetaria y la confianza de los inversores. Modelar la relación entre el precio de un instrumento financiero y estos factores, además de prever su dinámica, es una tarea difícil para investigadores e inversores.
Existen numerosos estudios sobre la previsión y el análisis de series temporales financieras. Los métodos estadísticos de análisis suelen suponer que las series temporales se generan mediante procesos lineales, lo cual hace que su rendimiento en la previsión no lineal resulte deficiente. Los métodos de aprendizaje automático y aprendizaje profundo han demostrado tener más éxito en la modelación de series temporales financieras gracias a su capacidad de representación no lineal. Ya han sido muchas las investigaciones realizadas para extraer características en momentos concretos y utilizarlas para modelar y predecir resultados. Sin embargo, estos enfoques ignoran las interacciones entre los datos y la continuidad a corto plazo de las fluctuaciones.
Para rellenar estas lagunas, en el artículo "A Dual-Attention-Based Stock Price Trend Prediction Model With Dual Features" se propuso un método de extracción de datos dual. Dicho método se basa tanto en puntos temporales únicos como en puntos temporales múltiples, y combina características de mercado a corto plazo con características temporales a largo plazo para mejorar la precisión de las previsiones. El modelo propuesto se basa en la arquitectura "Codificador-Decodificador" y utiliza un mecanismo de atención en las etapas de codificación y decodificación para identificar las características más relevantes en series temporales largas.
En este artículo veremos un nuevo modelo de predicción de tendencias bursátiles, el Trend Prediction Model, o TPM, que utiliza mecanismos de extracción dual de características y atención dual. El objetivo del modelo TPM será predecir la dirección y la duración de los movimientos de las cotizaciones bursátiles. Los autores del método destacan las siguientes aportaciones principales de los planteamientos propuestos:
- Un nuevo método dual de extracción de características basado en distintos rangos temporales que extrae eficazmente información importante del mercado y optimiza los resultados de las previsiones. El TPM usa el método de regresión lineal por partes y la red neuronal convolucional para extraer las características de mercado a largo y corto plazo de las series temporales financieras, respectivamente. La descripción de la información de mercado con ayuda de características duales mejora el rendimiento del modelo de previsión.
- Un modelo de predicción de tendencias bursátiles (TPM) que utiliza el marco "Codificador-Decodificador" y un mecanismo de atención dual. La adición de mecanismos de atención en las etapas de codificación y descodificación permite al modelo TPM seleccionar de forma adaptativa las características de mercado a corto plazo más relevantes y combinarlas con características temporales a largo plazo para hacer las previsiones más precisas.
1. Algoritmo TPM
Tras analizar los métodos de previsión de series temporales existentes, los autores del algoritmo TPM llegaron a las siguientes conclusiones:
- Una serie temporal financiera unidimensional no contiene información suficiente para prever el próximo movimiento de precios con el grado de certeza necesario.
- Los métodos tradicionales de extracción de características tiene limitaciones en el estudio del comportamiento del mercado.
- El estudio de una serie temporal usando una sola red neuronal resulta incompleto.
En el método TPM, los problemas mencionados se resuelven utilizando mecanismos duales de extracción de características y atención. El algoritmo propuesto incluye 2 fases. En primer lugar, se usa un método de regresión lineal por partes para segmentar las series temporales financieras y extraer características temporales históricas a largo plazo basadas en subsecuencias con distintos intervalos de tiempo, mientras que las características espaciales de mercado a corto plazo basadas en cada punto temporal se generan usando una red neuronal convolucional.
A continuación, en la segunda fase del TPM, las características duales previamente extraídas son analizadas por un modelo de predicción de tendencias basado en el mecanismo de atención dual. El modelo propuesto se basa en la arquitectura Codificador-Decodificador.
El Codificador se basa en un bloque LSTM recurrente al que se añade un mecanismo de atención que se utiliza para extraer de forma adaptativa las características más relevantes del mercado a corto plazo.
El Decodificador se construye de forma similar usando un bloque LSTM y un mecanismo de atención que selecciona y descodifica las características combinadas más relevantes para predecir la tendencia de los precios de las acciones.
Como la información proporcionada por las series temporales financieras univariantes es insuficiente, resulta difícil modelar y predecir la tendencia de los precios de las acciones basándose en esos datos. Los autores del método TPM usan para el análisis datos básicos del mercado, como los precios de apertura y cierre de la barra, los precios máximos y mínimos y el volumen. Y luego los convierten en una serie de indicadores técnicos.
Dada la continuidad de los cambios en los datos, el TPM extrae características temporales a largo plazo usando un método de regresión lineal por partes (PLR). El método PLR suaviza el ruido de las fluctuaciones a corto plazo, reduce la dimensionalidad de los datos y mejora el rendimiento computacional.
Obviamente, el resultado de la segmentación de las series temporales dependerá del umbral de error máximo δ. Tomando como ejemplo los datos del CSI 300, los autores del método utilizan el método PLR para segmentar su precio de cierre histórico. Con un valor umbral δ igual a 2,0, la serie temporal puede dividirse en 16 subsecuencias. No obstante, cuando el valor umbral δ es 4,0, la misma serie temporal solo puede segmentarse en 4 subsecuencias. Como consecuencia de ello, a medida que aumenta el valor del umbral, se ignoran más variaciones de datos y se generan menos subsecuencias. El valor del umbral afecta a la fiabilidad de las características de las series temporales históricas. Cada subsecuencia representa una fluctuación de los datos a lo largo de un periodo temporal. La inclinación sm y la duración dm de cada subsecuencia se generan como características temporales a largo plazo para predecir la tendencia de los precios de las acciones.
Dada la interacción de distintos datos en un mismo momento, las características espaciales de mercado a corto plazo de cada paso temporal se extraen con la ayuda de una red neuronal convolucional (CNN). Para las series temporales financieras analizadas, se construye una matriz de mercado para describir el mercado bursátil. En la matriz de mercado, cada fila representa una dimensión de los datos analizados, y el número de filas será n. Cada columna representa un punto temporal. Como la CNN conserva la relación de vecindad y la localización espacial de los datos de origen, esta puede captar una relación no lineal entre la matriz de mercado y la tendencia de las acciones. y luego obtener las características espaciales de una serie temporal histórica a corto plazo.
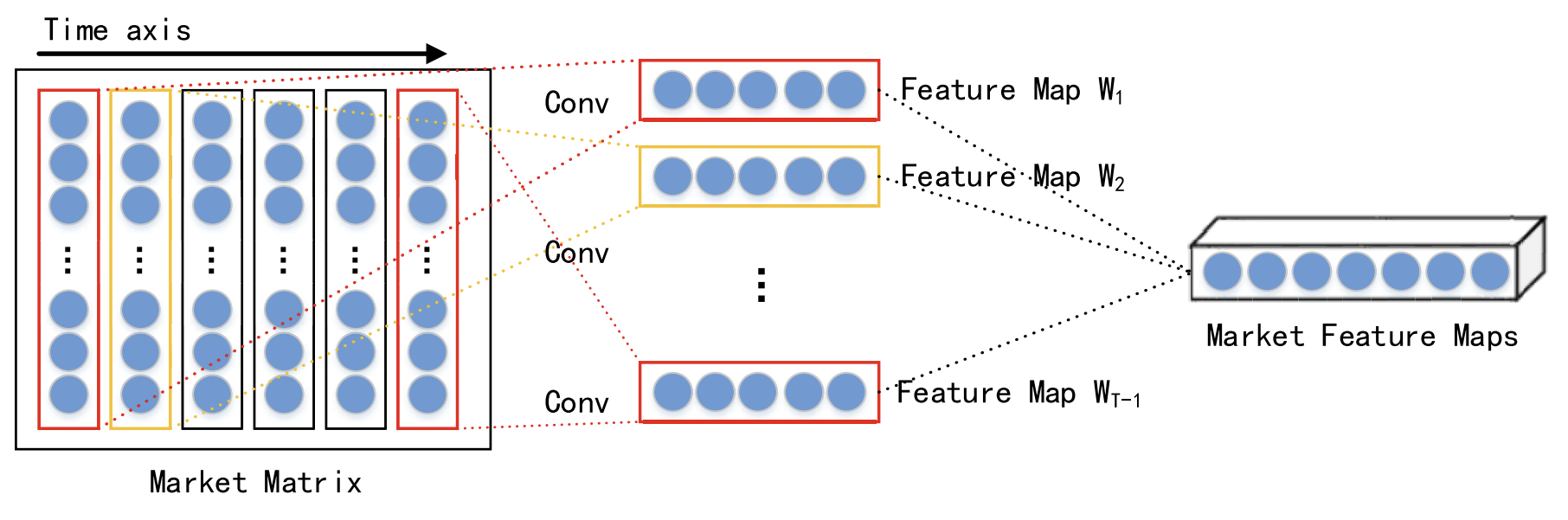
En su trabajo, los autores del método eligen convoluciones de distintos tamaños, como 1 × 3 y 1 × 5, para extraer características espaciales abstractas de mercado multinivel. Una función de activación no lineal seleccionada como función ReLU.
Las capas de convolución van seguidas de una capa de agrupación máxima (max pooling) que reduce el tamaño de los mapas de características y evita el sobreentrenamiento.
Los resultados de varias capas de convolución y agrupación máxima se transfieren a la capa de proyección.
Como ya hemos mencionado, el modelo procesa las características a corto y largo plazo extraídas mediante el marco Codificador-Decodificador. En esta estructura, el Codificador comprime la información original en un vector de tamaño fijo, mientras que el Decodificador procesa estos vectores para producir el resultado final. Sin embargo, cuando hay demasiada información original, el Codificador no puede identificar eficazmente toda la información relevante, lo cual provoca la degradación del rendimiento del modelo. El mecanismo de atención puede optimizar este problema descodificando el estado oculto de las neuronas relevantes.
Obviamente, el Decodificador con mecanismo de atención tiene un problema: no puede seleccionar explícitamente datos de origen relevantes, por lo que los autores del método TPM han añadido un mecanismo de atención tanto en la etapa de codificación como en la de decodificación.
La segunda fase del algoritmo TPM se basa en el mecanismo de atención dual. La estructura Codificador-Decodificador se divide en dos etapas. En el primer paso, las características a corto plazo del mercado espacial extraídas con ayuda de CNN se analizan en un Codificador basado en LSTM con un mecanismo de atención. Las características a corto plazo correspondientes a cada punto temporal se seleccionan de forma adaptativa y se codifican en vectores.
En el segundo paso, los vectores codificados y las características temporales a largo plazo extraídas mediante PLR se introducen en el Decodificador basado en LSTM, que decodifica los vectores y características correspondientes basándose en el mecanismo de atención para predecir la tendencia del mercado bursátil. Gracias a su doble mecanismo de atención, el TPM puede seleccionar de forma adaptativa las características espaciales y temporales más relevantes del mercado para la modelación y previsión de tendencias.
En cada punto temporal t, el Codificador aprende la relación entre la característica original Wt y el estado oculto Ht:
![]()
donde Ht es el estado oculto del Codificador en el tiempo t, fen(•) es una función no lineal, y ʘen denota los parámetros del Codificador.
Los autores del método usan LSTM como una función fen no lineal para capturar las dependencias temporales y formar un Codificador de características a corto plazo. El LSTM es capaz de modelar eficazmente el comportamiento temporal dinámico de las series temporales y evitar los problemas de atenuación o explosión de gradientes de las RNN.
Los autores del método introducen un mecanismo de atención en la etapa de codificación y dividen las características originales de WMarket según la dimensionalidad m de las características. El estado oculto Ht-1 y el estado de la célula (contexto) Ct-1 calculados en el tiempo t-1, correspondientes a las dimensionalidades originales de las características, se identifican y se utilizan para actualizar las características originales en el siguiente tiempo t.
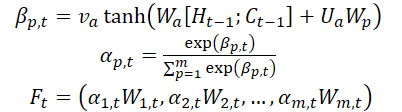
donde va, Wa y Ua son parámetros; la función SoftMax se utiliza para calcular la importancia αm,t de cada dimensionalidad de la característica.
Todas las dimensionalidades Wt se actualizan a Ft y se introducen en el Codificador. A continuación, se actualiza el estado oculto del punto temporal t.
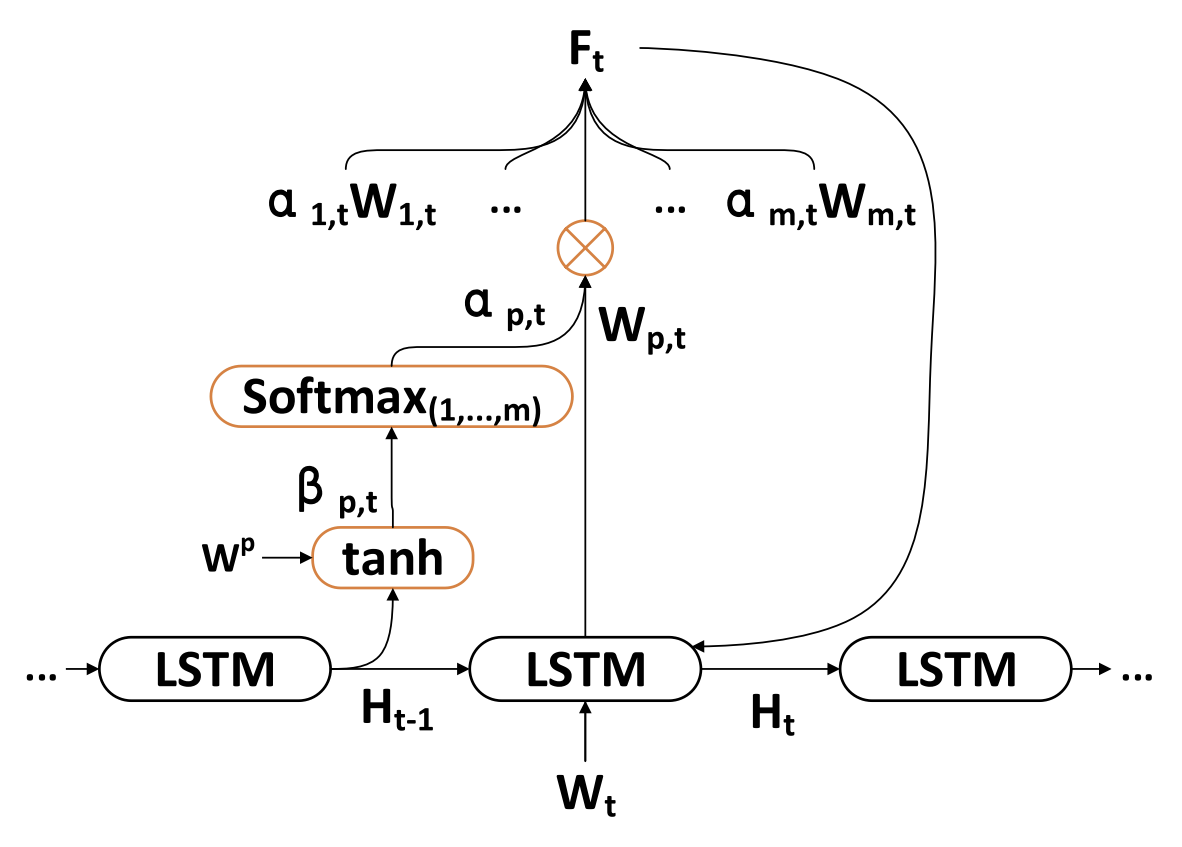
Así, en cada instante de tiempo t, podemos elegir las dimensionalidades relevantes de las características espaciales del mercado, actualizar sistemáticamente las características de origen y el estado oculto del Codificador, y generar el vector de codificación más relevante de las características a corto plazo.
El Decodificador es un bloque LSTM para la predecir la tendencia del mercado de valores. Las características temporales a largo plazo de ZT-1 extraídas mediante el método PLR.
En cada instante temporal t, el Decodificador aprende la relación entre el vector de codificación Wt, la característica a largo plazo Lt y el estado oculto Ht:
![]()
donde H't es el estado oculto del Decodificador en el tiempo t, fde(•) es una función no lineal, y ʘde denota los parámetros del Decodificador.
Los autores del TPM utilizan LSTM como función fde no lineal para capturar las dependencias temporales y formar un Decodificador de características a largo plazo. El procedimiento de cálculo es similar a la etapa del Codificador.
Los autores del TPM introducen un mecanismo de atención en la etapa del Decodificador para obtener los estados ocultos asociados del Codificador de todos los puntos temporales.
El vector de contexto suministrado al Decodificador se obtiene a través de todos los estados ocultos del Codificador.
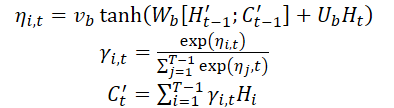
Una vez obtenido el vector de contexto C't, se combina con las características temporales a largo plazo Lt para generar la característica mixta yt:
![]()
Usando las fórmulas anteriores, en cada instante de tiempo t, se seleccionan los estados del Codificador oculto más relevantes de todos los puntos temporales y las características temporales a largo plazo para generar vectores de características mixtos.
A continuación, estudiamos la función de asignación no lineal F(•) entre la tendencia bursátil y los signos duales. En resumen, utilizamos una función lineal para obtener una predicción de la tendencia bursátil en el momento T.
Para entrenar el modelo hemos usado el método de descenso de gradiente estocástico y un optimizador de impulso, con un tamaño de paquete de entrenamiento de 64 y una tasa de aprendizaje de 0,001.
Como función de pérdida se usa la función de error cuadrática con términos de regularización.
A continuación le presentamos la visualización del método TPM realizada por el autor.
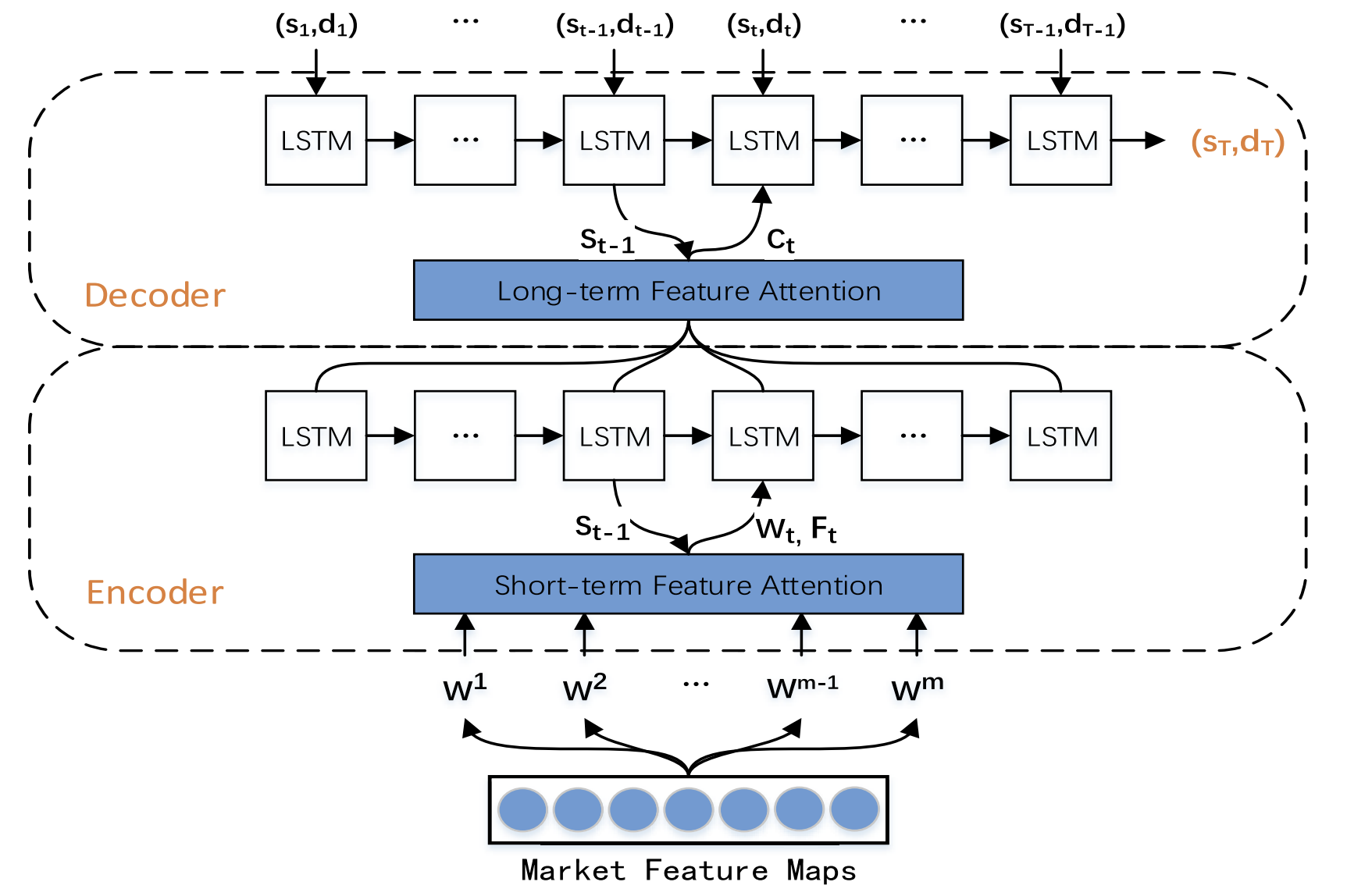
2. Implementación con MQL5
Tras repasar los aspectos teóricos del método TPM propuesto, comenzaremos con la parte práctica de nuestro trabajo, donde haremos realidad nuestra visión de los enfoques propuestos. Como viene siendo habitual, en nuestra aplicación mantendremos el concepto general del enfoque propuesto, pero permitiremos algunas desviaciones en los detalles de la aplicación. Obviamente, esto puede afectar en mayor o menor medida a los resultados finales del modelo.
Bien, comenzaremos nuestro trabajo construyendo el Codificador.
2.1 Codificador TPM
Implementamos el Codificador de nuestro modelo en la clase CNeuronTPMEncoder, que hereda la funcionalidad básica del bloque LSTM CNeuronLSTMOCL creado anteriormente. La elección de la clase de padres no es aleatoria. Después de todo, como recordará, el Codificador del método TPM se basa en el bloque LSTM con la adición de mecanismos de atención.
Además, en nuestra aplicación hemos decidido incluir la extracción de características a corto plazo directamente en el Codificador. Las características las extraeremos utilizando el bloque creado anteriormente para la creación de la estructura de datos piramidal CSCM. Pero hay un matiz a considerar: antes extrajimos las características de series temporales unitarias utilizando el bloque CSCM. Ahora tendremos que modificar ligeramente el flujo de datos para extraer con la característica los puntos temporales individuales.
En general, la estructura del Codificador será la siguiente.
class CNeuronTPMEncoder : public CNeuronLSTMOCL { protected: bool bTSinRow; //--- CNeuronCSCMOCL cFeatureExtraction; CNeuronBaseOCL cMemAndHidden; CNeuronConcatenate cConcatenated; CNeuronSoftMaxOCL cSoftMax; CNeuronBaseOCL cAttentionOut; CNeuronTransposeOCL cTranspose; CBufferFloat cTemp; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronTPMEncoder(void){}; ~CNeuronTPMEncoder(void){}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint variables, uint lenth, uint hidden_size, bool ts_in_row, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual int Type(void) override const { return defNeuronTPMEncoder; } virtual void SetOpenCL(COpenCLMy *obj); };
Aquí vemos el conjunto habitual de métodos redefinidos y varios objetos anidados cuyo propósito conoceremos durante la implementación.
Al igual que antes, declararemos todos los objetos anidados como estáticos, lo cual nos permitirá dejar el constructor y el destructor de la clase "vacíos". La instancia de nuestra nueva clase se inicializará directamente en el método Init.
bool CNeuronTPMEncoder::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint variables, uint lenth, uint hidden_size, bool ts_in_row, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronLSTMOCL::Init(numOutputs, myIndex, open_cl, hidden_size, optimization_type, batch)) return false; if(!SetInputs(variables * lenth)) return false;
En los parámetros, este método obtendrá los parámetros básicos del objeto que se está creando. En este caso, son 3:
- variables — número de secuencias unitarias en las series temporales multimodales analizadas;
- lenth — tamaño de la secuencia analizada (profundidad de la historia);
- hidden_size — tamaño del espacio oculto del bloque LSTM.
Asimismo, añadiremos la bandera ts_in_row, que indicará la ubicación de secuencias unitarias individuales en las filas del tensor de datos de origen.
En el cuerpo del método llamaremos al método homónimo de la clase padre, en el que se implementará el bloque mínimo necesario para el control de los parámetros de la capa creada y la inicialización de los objetos heredados.
Aquí transmitiremos el tamaño del tensor de datos de origen de la clase padre, que será igual al producto del tamaño de la secuencia unitaria por el número de tales secuencias en los datos de origen.
Cabe señalar aquí que dentro del bloque LSTM hemos usado capas totalmente conectadas, y el tensor de datos de origen resulta irrelevante en este caso.
A continuación, inicializaremos el bloque de extracción de características a corto plazo.
uint windows[] = {variables, 6, 5, 4}; if(!cFeatureExtraction.Init(0, 0, OpenCL, windows, lenth, variables, ts_in_row, optimization, batch)) return false;
Para ello, primero estableceremos el tamaño de la ventana de convolución de las capas de extracción de características y llamaremos al método de inicialización del bloque CSCM.
Nótese que al llamar al método de inicialización del bloque CSCM, hemos reordenado los parámetros de tamaño de las secuencias unitarias y su número. Esto se debe a tenemos que extraer características de pasos (barras) temporales individuales en lugar de secuencias unitarias, como se presupone en el método del MSFformer.
El siguiente paso consistirá en inicializar los objetos anidados del bloque de atención. Aquí, primero crearemos una capa en cuyos búferes concatenaremos el estado oculto y el contexto del bloque LSTM en el paso anterior.
if(!cMemAndHidden.Init(0, 1, OpenCL, hidden_size * 2, optimization, batch)) return false;
Para calcular los coeficientes de importancia de las características individuales, utilizaremos la capa de concatenación cuyos resultados normalizamos con la función SoftMax.
if(!cConcatenated.Init(0, 2, OpenCL, variables * lenth, variables * lenth, hidden_size * 2, optimization, batch)) return false; cConcatenated.SetActivationFunction(TANH); if(!cSoftMax.Init(0, 3, OpenCL, variables * lenth, optimization, batch)) return false; cSoftMax.SetHeads(variables);
Observe que, en esta fase, la normalización de los datos se realizará dentro de secuencias unitarias.
Y añadiremos una capa para registrar los resultados de la atención.
if(!cAttentionOut.Init(0, 4, OpenCL, variables * lenth, optimization, batch)) return false;
De ser necesario, inicializaremos la capa de transposición de datos.
bTSinRow = ts_in_row; if(!bTSinRow) { if(!cTranspose.Init(0, 5, OpenCL, variables, lenth, optimization, iBatch)) return false; }
Y añadiremos un búfer auxiliar para registrar los valores intermedios.
//--- if(!cTemp.BufferInit(variables * lenth, 0) || !cTemp.BufferCreate(OpenCL)) return false; //--- return true; }
Una vez inicializados correctamente todos los objetos anidados, transmitiremos el resultado lógico de las operaciones realizadas al programa que realiza la llamada y finalizaremos el método.
Una vez finalizado el trabajo de inicialización del objeto, procederemos a construir el algoritmo de pasada directa para la nueva clase, que implementaremos en el método feedForward.
bool CNeuronTPMEncoder::feedForward(CNeuronBaseOCL *NeuronOCL) { //--- FEATURE EXTRACTION if(!cFeatureExtraction.FeedForward(NeuronOCL)) return false;
Como es habitual, en los parámetros de este método obtendremos el puntero al objeto de la capa neuronal precedente. Pero en este caso, no comprobaremos el puntero obtenido, sino que lo transmitiremos al método de pasada directa de la capa interna de extracción de características a corto plazo. El en cuerpo del método llamado ya se ha implementado el control del puntero recibido.
En el siguiente paso, combinaremos el estado oculto y el contexto de nuestro objeto que se conservó tras la pasada anterior.
//--- Memory and Hidden if(!Concat(m_iHiddenState, m_iMemory, m_iHiddenState, m_iMemory, cMemAndHidden.getOutputIndex(), 1, 1, 0, 0, Neurons())) return false;
Con esto damos por concluido el trabajo preparatorio, así que podemos pasar al bloque de atención, en el que calcularemos los coeficientes de importancia de las características individuales.
if(!cConcatenated.FeedForward(cFeatureExtraction.AsObject(), cMemAndHidden.getOutput())) return false; if(!cSoftMax.FeedForward(cConcatenated.AsObject())) return false; int map = cSoftMax.getOutputIndex();
Si es necesario, transpondremos el tensor de coeficientes de importancia.
if(!bTSinRow) { if(!cTranspose.FeedForward(cSoftMax.AsObject())) return false; map = cTranspose.getOutputIndex(); }
Y ejecutaremos la multiplicación elemento a elemento de los coeficientes obtenidos por las correspondientes características a corto plazo. Para la multiplicación elemento a elemento de 2 tensores, utilizaremos el kernel de pasada directa de la capa Dropout.
Recordemos que creamos este kernel para multiplicar los datos de origen por la máscara de exclusión de neuronas. En este caso, usaremos los coeficientes de importancia como máscara.
Después definiremos la dimensionalidad del espacio de tareas.
uint global_work_offset[1] = {0}; uint global_work_size[1]; global_work_size[0] = int(cSoftMax.Neurons() + 3) / 4;
A continuación, transmitiremos los parámetros al kernel.
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_input, cFeatureExtraction.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_map, map)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_out, cAttentionOut.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_Dropout, def_k_dout_dimension, cSoftMax.Neurons())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Y pondremos este en la cola de ejecución.
if(!OpenCL.Execute(def_k_Dropout, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; }
Tras ejecutar el kernel en el búfer de la capa cAttentionOut, obtendremos las características a corto plazo dado su factor de importancia. Ahora podremos utilizar la funcionalidad básica del bloque LSTM para representar el tensor de características a la salida de nuestro Codificador.
//--- LSTM if(!CNeuronLSTMOCL::feedForward(cAttentionOut.AsObject())) return false; //--- return true; }
No se olvide de supervisar las operaciones en cada fase. Cuando estas se hayan ejecutado con éxito, transmitiremos el resultado lógico de su ejecución al programa que realiza la llamada y finalizaremos el método.
Una vez implementados los algoritmos de pasada directa, normalmente pasamos a construir los métodos de pasada inversa. Y esta clase no será una excepción. En la siguiente etapa, aplicaremos un método para distribuir el gradiente de error entre todos los objetos anidados y el tensor de datos de entrada según su influencia en el resultado final del modelo. Implementaremos esta funcionalidad en el método calcInputGradients.
En los parámetros de este método, de forma similar a como hemos hecho en el método analizado antes, obtendremos el puntero al objeto de la capa neuronal anterior.
bool CNeuronTPMEncoder::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
En el cuerpo del método comprobaremos directamente la relevancia del puntero recibido.
A continuación, usando la funcionalidad heredada, ejecutaremos el gradiente de error a través del algoritmo del bloque LSTM hasta el nivel de los resultados de nuestro bloque de atención.
if(!CNeuronLSTMOCL::calcInputGradients(cAttentionOut.AsObject())) return false;
Luego distribuiremos el gradiente de error en 2 direcciones: los coeficientes de importancia de las características y las propias características. El algoritmo para poner el kernel en la cola será similar al comentado anteriormente.
//--- uint global_work_offset[1] = {0}; uint global_work_size[1]; global_work_size[0] = cSoftMax.Neurons(); ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_f, cFeatureExtraction.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_fg, cTemp.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_s, (bTSinRow ? cSoftMax.getOutputIndex() : cTranspose.getOutputIndex()))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_sg, (bTSinRow ? cSoftMax.getGradientIndex() : cTranspose.getGradientIndex()))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_g, cAttentionOut.getGradientIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_CGConv_HiddenGradient, def_k_cgc_activationf, NeuronOCL.Activation())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_CGConv_HiddenGradient, def_k_cgc_activations, int(None))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.Execute(def_k_CGConv_HiddenGradient, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; }
Pero deberemos considerar dos puntos. En primer lugar, el búfer de distribución del gradiente de error del coeficiente de atención dependerá de la necesidad de usar una capa de transposición del coeficiente de importancia. Y en segundo lugar, utilizaremos las propias características a corto plazo tanto para multiplicarlas por los coeficientes de importancia como para calcular estos coeficientes. Por ello, en esta fase, mantendremos por ahora el gradiente de error de las características a corto plazo en el búfer de datos temporales.
En el siguiente paso, transpondremos el gradiente de error de los coeficientes de importancia de las características individuales, si es necesario.
if(bTSinRow) { if(!cSoftMax.calcHiddenGradients(cTranspose.AsObject())) return false; }
A continuación, transmitiremos el gradiente de error por el algoritmo de bloque de atención hasta el nivel de las características a corto plazo.
if(!cConcatenated.calcHiddenGradients((CObject*)cSoftMax.AsObject(),(CBufferFloat *)NULL,(CBufferFloat *)NULL) || !DeActivation(cConcatenated.getOutput(), cConcatenated.getGradient(), cConcatenated.getGradient(), cConcatenated.Activation())) return false; if(!cFeatureExtraction.calcHiddenGradients(cConcatenated.AsObject(), cMemAndHidden.getOutput(), cMemAndHidden.getGradient())) return false;
Y sumaremos el gradiente de error a nivel de características a corto plazo a partir de los 2 flujos de información.
if(!DeActivation(cFeatureExtraction.getOutput(), GetPointer(cTemp), GetPointer(cTemp), NeuronOCL.Activation()) || !SumAndNormilize(cFeatureExtraction.getGradient(), GetPointer(cTemp), cFeatureExtraction.getGradient(), 1, false)) return false;
Al final del método, bajaremos el gradiente de error al nivel de la capa anterior y transmitiremos el resultado lógico de las operaciones al programa que realiza la llamada.
if(!NeuronOCL.calcHiddenGradients(cFeatureExtraction.AsObject())) return false; //--- return true; }
Una vez distribuido el gradiente de error, solo nos quedará optimizar los parámetros del modelo para minimizar el error global. Realizaremos esta funcionalidad en el método updateInputWeights, llamando a los métodos homónimos de los objetos anidados que contienen los parámetros a entrenar.
bool CNeuronTPMEncoder::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(!CNeuronLSTMOCL::updateInputWeights(cAttentionOut.AsObject())) return false; if(!cFeatureExtraction.UpdateInputWeights(NeuronOCL)) return false; if(!cConcatenated.UpdateInputWeights(cFeatureExtraction.AsObject(), cMemAndHidden.getOutput())) return false; //--- return true; }
Con esto concluirá nuestro análisis de los algoritmos para implementar la funcionalidad principal de nuestra clase de Codificador. Podrá ver el código completo de todos los métodos de esta clase en el archivo adjunto. Allí encontrará también el código completo de todos los programas usados en la elaboración de este artículo.
2.2 Decodificador TPM
Tras implementar los algoritmos del Codificador TPM, abordaremos la segunda etapa, que es la construcción del Decodificador. Supongo que el lector, al familiarizarse con los aspectos teóricos del método TPM, habrá notado una gran similitud en la construcción de los algoritmos del Codificador y el Decodificador. No obstante, la presencia de diferencias, incluso mínimas, requiere la construcción de una nueva clase.
De forma similar a como sucede en el Codificador, heredaremos nuestra nueva clase de Decodificador CNeuronTPM de la clase del bloque LSTM. A continuación, mostraremos la estructura de la nueva clase.
class CNeuronTPM : public CNeuronLSTMOCL { protected: CNeuronTPMEncoder cEncoder; CNeuronPLROCL cFeatureExtraction; CNeuronBaseOCL cMemAndHidden; CNeuronConcatenate cConcatenated; CNeuronSoftMaxOCL cSoftMax; CNeuronBaseOCL cAttentionOut; CNeuronConcatenate cAttAndFeature; CBufferFloat cTemp; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronTPM(void){}; ~CNeuronTPM(void){}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint variables, uint lenth, uint hidden_size, bool ts_in_row, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual int Type(void) override const { return defNeuronTPM; } virtual void SetOpenCL(COpenCLMy *obj); };
Aquí se notan a simple vista las semejanzas con la clase de Codificador discutida anteriormente. Solo hemos añadido 2 objetos anidados. Y puede que haya notado un cambio en el tipo de capa de extracción de características: en el Decodificador utilizamos PLR para extraer las características a largo plazo.
Creo que se habrá dado cuenta de que la clase de Codificador contiene una indicación de pertenencia, pero esto no está presente en el Decodificador. Hay un motivo para ello. El Codificador y el Decodificador usan los datos de origen para extraer distintos niveles de características. Y para no complicar la estructura del modelo en el nivel superior, hemos decidido combinar el Codificador y el Decodificador en un solo bloque. Más arriba, hemos añadido la clase de Codificador construida como una capa interna a la nueva clase, combinando así el algoritmo TPM dentro de la clase actual, como demuestra su nombre, CNeuronTPM.
Los parámetros del nuevo método de inicialización de la clase resultan completamente idénticos a los del método de inicialización del Codificador descrito anteriormente.
bool CNeuronTPM::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint variables, uint lenth, uint hidden_size, bool ts_in_row, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronLSTMOCL::Init(numOutputs, myIndex, open_cl, hidden_size, optimization_type, batch)) return false; if(!SetInputs(hidden_size)) return false;
En el cuerpo del método llamaremos del mismo modo al método de inicialización de la clase padre, solo que el tamaño del tensor de sus datos de origen ya se corresponderá con el tamaño del estado oculto del Codificador. Al fin y al cabo, estamos suministrando a la entrada del Decodificador el vector ponderado de la características recibidas del Codificador.
Aquí mismo inicializaremos el objeto de Codificador.
if(!cEncoder.Init(0, 0, OpenCL, variables, lenth, hidden_size, ts_in_row, optimization, iBatch)) return false;
Y la capa de extracción de características.
if(!cFeatureExtraction.Init(0, 1, OpenCL, variables, lenth, !ts_in_row, optimization, iBatch)) return false;
El algoritmo de inicialización de los objetos del bloque de atención recordará las operaciones similares a la inicialización del Codificador, pero existen diferencias en los tamaños de los tensores de datos de origen.
if(!cMemAndHidden.Init(0, 2, OpenCL, hidden_size * 2, optimization, iBatch)) return false; if(!cConcatenated.Init(0, 3, OpenCL, hidden_size, hidden_size, hidden_size * 2, optimization, iBatch)) return false; cConcatenated.SetActivationFunction(TANH); if(!cSoftMax.Init(0, 4, OpenCL, hidden_size, optimization, iBatch)) return false; cSoftMax.SetHeads(1); if(!cAttentionOut.Init(0, 5, OpenCL, hidden_size, optimization, iBatch)) return false;
Como ya hemos mencionado, en el bloque LSTMutilizaremos capas totalmente conectadas. Por ello, el tensor de características a corto plazo obtenido del Codificador podrá considerarse "impersonal" en el contexto de las secuencias unitarias de las series temporales multimodales originales analizadas. Esto nos permitirá llevar a cabo la normalización de los coeficientes de importancia en general en todo el tensor. Y en esta etapa no nos importará la orientación del tensor de datos de origen.
Luego añadiremos una capa de proyección de características ponderadas a corto y largo plazo de las series temporales analizadas que suministraremos a la entrada del bloque LSTM.
if(!cAttAndFeature.Init(0, 6, OpenCL, hidden_size, hidden_size, variables * lenth, optimization, iBatch)) return false;
Al final de las operaciones de inicialización de la clase, añadiremos un búfer temporal de almacenamiento de datos.
if(!cTemp.BufferInit(variables * lenth, 0) || !cTemp.BufferCreate(OpenCL)) return false; //--- return true; }
Y retornaremos al programa que realiza la llamada el resultado lógico de la inicialización de los objetos anidados.
Después de inicializar los objetos anidados, procederemos a implementar el algoritmo de pasada directa en el método feedForward. De forma similar a otros métodos homónimos, obtendremos en los parámetros el puntero al objeto de la capa neuronal precedente.
bool CNeuronTPM::feedForward(CNeuronBaseOCL *NeuronOCL) { //--- Encoder if(!cEncoder.FeedForward(NeuronOCL)) return false;
Y transmitiremos directamente el puntero obtenido al método de pasada directa de nuestro Codificador.
A continuación, transmitiremos el mismo puntero para extraer las características a largo plazo de la serie temporal analizada.
//--- FEATURE EXTRACTION if(!cFeatureExtraction.FeedForward(NeuronOCL)) return false;
El funcionamiento del bloque de atención es similar al del mismo bloque del Codificador comentado anteriormente.
//--- Memory and Hidden if(!Concat(m_iHiddenState, m_iMemory, m_iHiddenState, m_iMemory, cMemAndHidden.getOutputIndex(), 1, 1, 0, 0, Neurons())) return false; //--- Attention if(!cConcatenated.FeedForward(cEncoder.AsObject(), cMemAndHidden.getOutput())) return false; if(!cSoftMax.FeedForward(cConcatenated.AsObject())) return false;
Ahora multiplicaremos los coeficientes de importancia por el vector de características a corto plazo del Codificador.
uint global_work_offset[1] = {0}; uint global_work_size[1]; global_work_size[0] = int(cSoftMax.Neurons() + 3) / 4; ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_input, cEncoder.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_map, cSoftMax.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_out, cAttentionOut.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_Dropout, def_k_dout_dimension, cSoftMax.Neurons())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.Execute(def_k_Dropout, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; }
Luego combinaremos el vector ponderado de características a corto plazo con las características a largo plazo en una capa de concatenación.
//--- Attention and Features if(!cAttAndFeature.FeedForward(cAttentionOut.AsObject(), cFeatureExtraction.getOutput())) return false;
Y suministraremos los datos así preparados a la entrada del bloque LSTM.
//--- LSTM if(!CNeuronLSTMOCL::feedForward(cAttAndFeature.AsObject())) return false; //--- return true; }
Después comprobaremos el resultado lógico de las operaciones y lo retornaremos al programa que realiza la llamada.
Por lo común, ahora solemos construir los métodos de pasada inversa. Pero creo que se habrá dado cuenta de las similitudes entre los métodos de pasada directa del Codificador y el Decodificador. Obviamente, existen matices a considerar. Existen matices similares en los métodos de pasada inversa. Sin embargo, en general, los algoritmos son bastante similares. Le invitamos a familiarizarse con ellos en el anexo.
2.3 Arquitectura de los modelos entrenados
Ya hemos considerado los algoritmos de implementación del método TPM usando MQL5. Este método se ha desarrollado para predecir las tendencias de movimiento de los precios de las acciones, y es natural que lo implementemos en nuestro Codificador de estado del entorno, cuya arquitectura se presenta en el método CreateEncoderDescriptions.
En los parámetros, el método obtendrá el puntero al array dinámico donde almacenaremos la arquitectura anidada del modelo.
bool CreateEncoderDescriptions(CArrayObj *encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
En el cuerpo del método, obtendremos la relevancia del puntero recibido y, de ser necesario, crearemos una nueva instancia del objeto de array dinámico.
Como de costumbre, suministraremos los datos brutos de la descripción del entorno a la entrada del modelo. Para registrar los datos de origen, utilizaremos una capa básica completamente conectada cuyo tamaño debería ser suficiente para registrar el tensor analizado.
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Los datos de origen recibidos se someterán a un procesamiento primario en la capa de normalización por lotes.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Luego transferiremos los datos preparados a nuestro módulo TPM.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTPM; descr.count = LatentCount; descr.window = BarDescr; descr.window_out = HistoryBars; descr.step = int(false); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Los datos recibidos del módulo TPM pasarán por un MLP de 3 capas, a cuya salida esperamos obtener los valores de previsión de las series temporales analizadas.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.optimization = ADAM; descr.activation = SIGMOID; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = BarDescr * NForecast; descr.optimization = ADAM; descr.activation = TANH; if(!encoder.Add(descr)) { delete descr; return false; }
A los valores predichos, les añadiremos las métricas estadísticas de las serie temporal de origen que se eliminaron previamente en la capa de normalización por lotes.
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = BarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; }
Y coordinaremos los resultados predictivos obtenidos en la representación frecuencial.
//--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast; descr.step = int(true); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
Los modelos del Actor y el Crítico los hemos tomado de artículos anteriores sin modificaciones. Podrá leerlos usted mismo en el archivo adjunto.
2.4 Asesores para el entrenamiento de modelos
A la hora de entrenar modelos, deberemos prestar atención a las características del entrenamiento de modelos recurrentes. Como ya sabemos, la principal característica de los modelos recurrentes es la sensibilidad a la secuencia de datos de entrada. Por consiguiente, al entrenar el modelo necesitamos usar los datos de la muestra de entrenamiento de forma históricamente coherente. Por otro lado, este enfoque reducirá el rendimiento del entrenamiento de la mayoría de los modelos, ya que fomenta el sobreentrenamiento en periodos de tiempo pequeños con una incapacidad para generalizar a todo el periodo de entrenamiento.
Para minimizar el impacto negativo de los factores mencionados, extraeremos aleatoriamente pequeñas submuestras del búfer de reproducción de experiencias durante el entrenamiento, respetando la secuencia histórica para entrenar el modelo. Después, muestrearemos un nuevo paquete de entrenamiento. Después analizaremos la implementación del enfoque propuesto usando como ejemplo el método de entrenamiento del Codificador del entorno (asesor experto "...\Experts\TPM\StudyEncoder.mq5").
void Train(void) { //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9);
En el cuerpo del método, primero generaremos un vector de probabilidades de selección de pasadas partiendo de la muestra de entrenamiento, clasificadas según el rendimiento de las pasadas. A continuación, declararemos las variables locales necesarias.
vector<float> result, target, state; bool Stop = false;
Aquí también añadiremos una variable que especificará el tamaño del paquete de entrenamiento de una submuestra.
int Batch = 100;
Luego organizaremos un sistema de ciclos anidados. En el ciclo externo, muestrearemos una trayectoria de la muestra de entrenamiento y el estado inicial de la submuestra de entrenamiento en la trayectoria seleccionada.
uint ticks = GetTickCount(); //--- for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter += Batch) { int tr = SampleTrajectory(probability); int st = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - NForecast)); if(st <= 0) { iter -= Batch; continue; }
Después borraremos el estado oculto y los búferes de contexto del bloque LSTM.
Encoder.Clear();
A continuación, organizaremos un ciclo anidado de iteración secuencial de estados en su secuencia histórica a partir del estado del entorno seleccionado.
for(int i = st; (i < MathMin(st + Batch, Buffer[tr].Total - NForecast) && !IsStopped() && !Stop); i++) { state.Assign(Buffer[tr].States[i].state); if(MathAbs(state).Sum() == 0) { iter += i - st - Batch; break; } bState.AssignArray(state);
En el cuerpo del ciclo anidado, transferiremos el estado del entorno analizado al búfer de datos. A partir de los datos obtenidos, pronosticaremos la trayectoria posterior del movimiento de los precios.
//--- State Encoder if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
A continuación, cargaremos los valores objetivo de la trayectoria posterior desde el búfer de repetición de experiencias.
//--- Collect target data if(!Result.AssignArray(Buffer[tr].States[i + NForecast].state)) continue; if(!Result.Resize(BarDescr * NForecast)) continue;
Y comprobaremos la exactitud de nuestras predicciones. Como parte de la pasada inversa, ajustaremos los parámetros del modelo para minimizar el error de previsión del movimiento posterior.
if(!Encoder.backProp(Result, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Luego informaremos al usuario del progreso del proceso de aprendizaje y pasaremos a la siguiente iteración del sistema de ciclos.
if(GetTickCount() - ticks > 500) { double percent = double(iter + i - st) * 100.0 / (Iterations); string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Encoder", percent, Encoder.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } } }
Una vez ejecutadas con éxito todas las iteraciones del sistema de ciclos, borraremos el campo de comentarios del gráfico del instrumento. Después enviaremos los resultados del entrenamiento al registro del terminal e inicializaremos la finalización del asesor experto.
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Encoder", Encoder.getRecentAverageError()); ExpertRemove(); //--- }
En el entrenamiento de los modelos del Actor y el Crítico hemos introducido modificaciones similares. Aunque no hemos añadido bloques de recurrencia a los modelos anteriores, realizar estas ediciones era algo necesario para organizar el correcto funcionamiento del Codificador del estado del entorno. Al fin y al cabo, tanto el Actor como el Crítico los utilizan como datos de origen.
Podrá leer el código completo de los asesores de entrenamiento de modelos en el archivo adjunto. Ahí también encontrará el código completo de todos los programas y clases, así como los métodos utilizados en la preparación del presente artículo.
3. Simulación
En este artículo, nos hemos familiarizado con un método que sirve para predecir las próximas trayectorias de las acciones de TPM y hemos implementado nuestra propia visión de los enfoques propuestos. Ahora es el momento de probar nuestros resultados con datos reales. Como siempre, hemos entrenado los modelos presentados con los datos históricos reales del marco temporal EURUSD H1 para 2023.
En primer lugar, hemos entrenado un modelo del Codificador del estado del entorno. Este modelo solo analiza los datos históricos del movimiento de los precios, sin evaluar las acciones del Actor. Esto nos permite entrenar el modelo al completo usando la muestra de entrenamiento inicial sin tener que actualizarla. Y aquí podemos decir que el modelo aprende bastante rápido y no ha mostrado malos resultados. A continuación le mostramos un gráfico en el que se comparan las previsiones y la trayectoria real del movimiento de los precios.
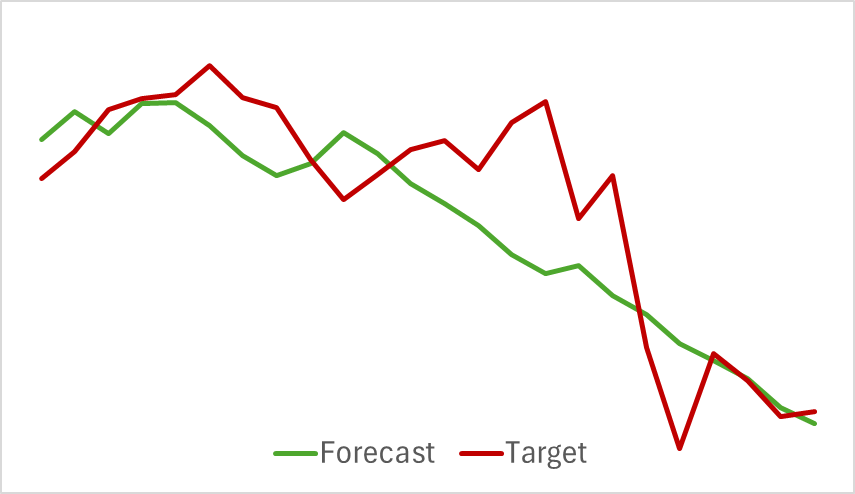
El gráfico muestra un estrecho entrelazamiento de las 2 líneas. Podemos observar que la trayectoria prevista tiene un aspecto más suave. Esto podría contribuir a una entrenamiento más estable para el Actor.
Pero, como ya sabrá, nuestra tarea principal consiste en encontrar la política óptima del Actor. Y después de entrenar el Codificador del estado del entorno, pasaremos a la segunda etapa del proceso de entrenamiento: el entrenamiento de la política del Actor. Este proceso será iterativo por naturaleza. Como las acciones del Actor cambian durante el proceso de entrenamiento, y pueden extenderse más allá del espacio de la muestra de entrenamiento previamente recopilado, necesitaremos actualizar periódicamente el búfer de repetición de experiencias con estados y recompensas próximos a las acciones de la actual política del Actor.
Tras varias iteraciones alternas de entrenamiento de los modelos del Actor y el Crítico con actualizaciones de la muestra de entrenamiento, hemos logrado obtener una política capaz de generar beneficios a lo largo del periodo histórico de la muestra de entrenamiento.
Para verificar la eficacia del modelo fuera de la muestra de entrenamiento (con datos nuevos), hemos probado el modelo con los datos históricos de enero de 2024 manteniendo otras entradas.
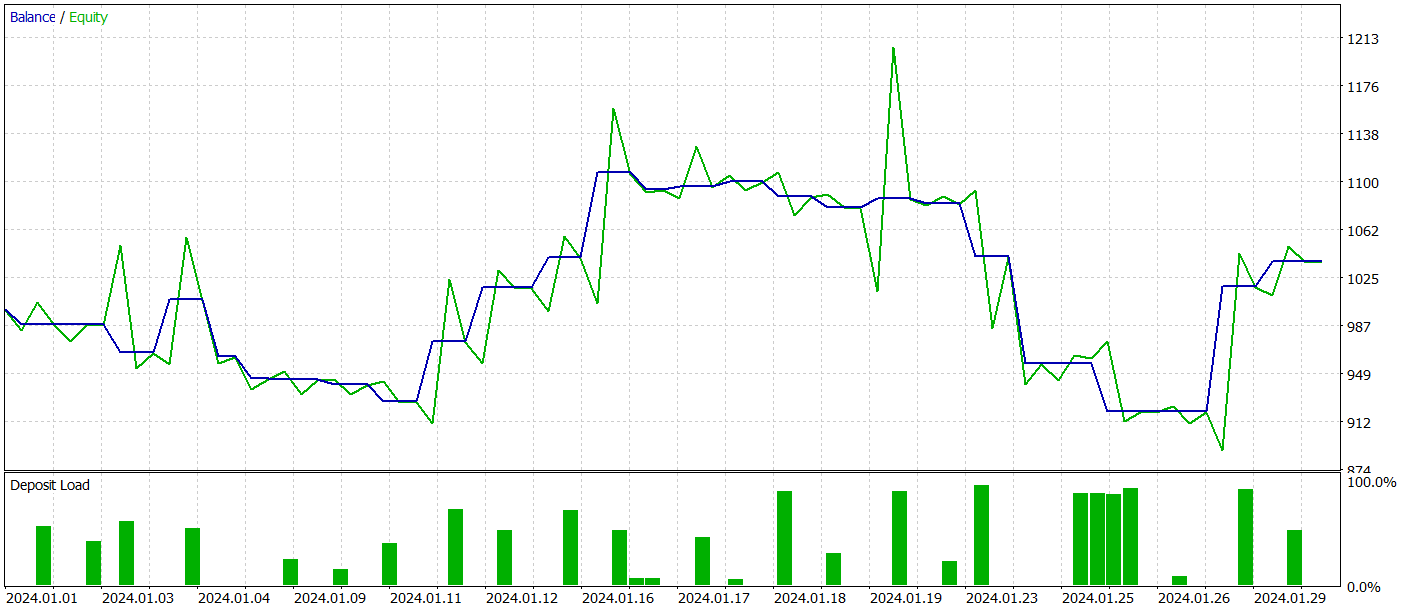
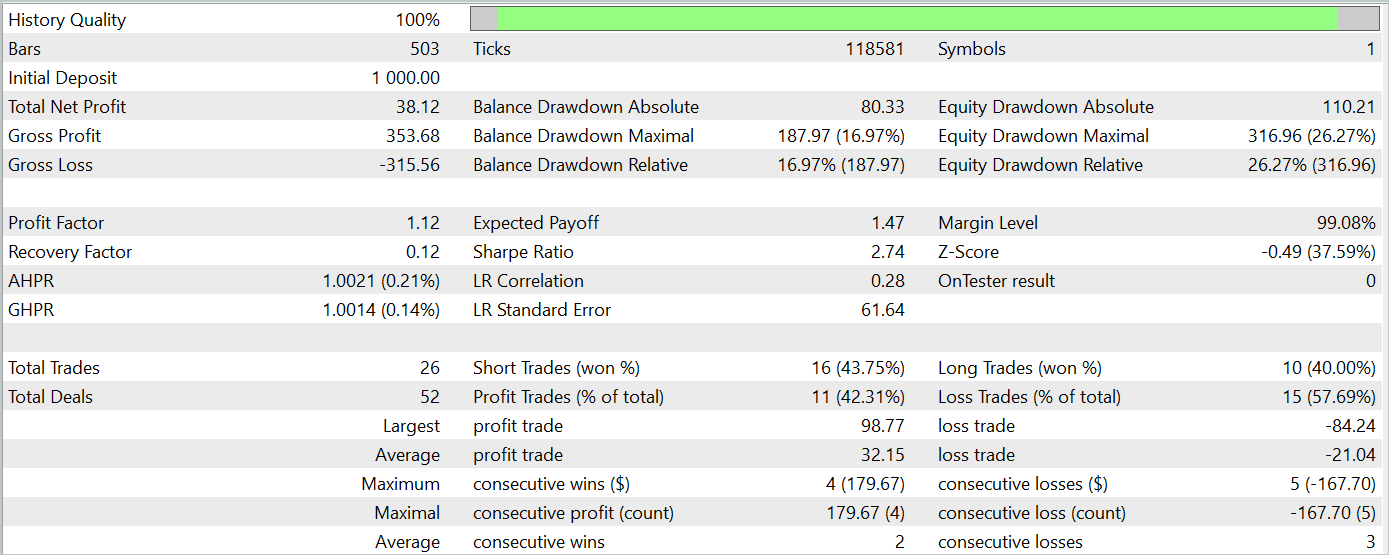
Durante el periodo de prueba, el modelo ha realizado 26 transacciones y solo 11 de ellas se han cerrado con beneficio, lo cual supone algo más del 42%. Sin embargo, tanto la transacción rentable máxima como la media superan a la transacción perdedora análoga. Como resultado, el periodo de pruebas ha obtenido un beneficio global. Según los resultados de la prueba, el factor de beneficio ha sido de 1,12.
No obstante, si observamos el gráfico de balance, podemos apreciar una reducción significativa al principio de la 3ª década del mes. Y esto es muy alarmante. A pesar de los beneficios obtenidos, el modelo aún debe perfeccionarse.
Conclusión
En este artículo, nos hemos familiarizado con un interesante método para predecir las tendencias de movimiento de precios, el TPM. Este método combina con éxito las ventajas de los modelos de convolución para analizar las dependencias a corto plazo y el PLR para identificar las tendencias a largo plazo.
En la parte práctica de nuestro artículo, hemos implementado nuestra propia visión de los enfoques propuestos usando MQL5. Asimismo, hemos entrenado y probado los modelos propuestos. Según los resultados de las pruebas, podemos ver que el modelo entrenado ha sido capaz de obtener beneficios con datos ajenos a la muestra de entrenamiento. Sin embargo, el gráfico de balance no ha mostrado el movimiento unidireccional deseado y muestra ciertas reducciones.
En general, el método propuesto tiene potencial, pero el modelo que hemos entrenado aún necesita perfeccionarse.
Enlaces
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Asesor | Asesor de recopilación de datos |
| 2 | ResearchRealORL.mq5 | Asesor | Asesor de recopilación de ejemplos con el método Real-ORL |
| 3 | Study.mq5 | Asesor | Asesor de entrenamiento de Modelos |
| 4 | StudyEncoder.mq5 | Asesor | Asesor de entrenamiento del Codificador |
| 5 | Test.mq5 | Asesor | Asesor para la prueba de modelos |
| 6 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema. |
| 7 | NeuroNet.mqh | Biblioteca de clases | Biblioteca de clases para crear una red neuronal |
| 8 | NeuroNet.cl | Biblioteca | Biblioteca de código de programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/15255
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Características del Wizard MQL5 que debe conocer (Parte 28): Revisión de las GAN con una introducción a las tasas de aprendizaje
Características del Wizard MQL5 que debe conocer (Parte 28): Revisión de las GAN con una introducción a las tasas de aprendizaje
 Del básico al intermedio: Comando SWITCH
Del básico al intermedio: Comando SWITCH
 Algoritmo de campo eléctrico artificial (AEFA) — Artificial Electric Field Algorithm (AEFA)
Algoritmo de campo eléctrico artificial (AEFA) — Artificial Electric Field Algorithm (AEFA)
 Desarrollo de un sistema comercial basado en el libro de órdenes (Parte I): el indicador
Desarrollo de un sistema comercial basado en el libro de órdenes (Parte I): el indicador
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso