ニューラルネットワークが簡単に（第16部）：クラスタリングの実用化

MetaTrader 5 — トレーディングシステム | 24 8月 2022, 08:34

424

Dmitriy Gizlyk

内容

はじめに

前2回は、データのクラスタリングについて述べましたが、私たちの主な目的は、具体的な実用問題を解決するために、検討されたすべての手法の使いこなし方を学ぶことです。特に、取引関連の場合です。教師なし学習の手法を検討し始めたとき、得られた結果を単独で利用することまたは他のモデルの入力データとして利用することが可能だという話がありました。今回は、クラスタリングの結果に対して考えられる使用例を考えてみます。

1.クラスタリング結果活用の理論的側面

クラスタリング結果の利用に関連した例の実用化に移る前に、これらのアプローチの理論的側面について少し触れておきます。

データクラスタリング結果の活用方法としては、まず、追加的な資金をかけずに実用に供することを試みるという選択肢があります。つまり、クラスタリングの結果は独立して、取引の意思決定に使用することができます。念のため、教師なし学習法は回帰課題を解決するために使われるのではないことをお伝えしておきます。直近の値動きを予測することは、まさに回帰の作業でありますが。一見すると、何かしらの矛盾があるように見えます。

でも、反対側から見てください。クラスタリングの理論的側面から考えると、すでにクラスタリングと図形パターンの定義を比較しています。チャートパターンと同様に、特定のクラスタの要素がチャート上に現れた後の価格の動きについて統計を取ることはできますが、それでは因果関係はわかりません。ただし、ニューラルネットワークを使って構築された数学的モデルには、そのような関係は存在しません。確率的なモデルだけを構築していますが因果関係を深く掘り下げることはありません。

統計情報を収集するためには、すでに訓練済みのクラスタリングモデルとラベル付けされたデータが必要です。クラスタリングモデルはすでに訓練されているので、ラベル付きデータセットは訓練サンプルよりもはるかに小さくても大丈夫ですが、十分かつ代表的なものであることが必要です。

このアプローチは一見すると教師あり学習と似ていますが、大きく異なる点が2つあります。

過剰適合のリスクがないため、ラベル付けされたサンプルサイズを小さくすることができる
教師あり学習では、最適な重み係数を選択するプロセスを繰り返しおこなうため、リソースと時間のコストがかかる数回の訓練エポックが必要になります。最初のパスは、統計情報を収集するのに十分で、この場合、モデル調整はおこなわない

考え方が明確であることを願っています。このようなモデルの実装については、もう少し後で考えることにします。

このオプションの欠点は、クラスタの中心までの距離が無視されることです。つまり、クラスタの中心に近い要素（「理想的なパターン」）と、クラスタの境界にある要素では、結果が同じになります。中心からの要素の最大距離を短くするために、クラスタの数を増やそうとするかもしれませんが、損失関数グラフに従ってクラスタ数を正しく選択できていれば、この方法の効果はわずかなものになります。

クラスタリング結果の2つ目の用途である、別のモデルの元データとして使用することでこの問題の解決を試みることもできますが、クラスタ番号を数値やベクトルの形で2つ目のモデルに入力しても、得られるのはせいぜい上で検討した統計手法の結果に匹敵するデータであることにはご注意ください。同じ結果を得るために追加のコストをかけるのは意味がありません。

クラスタ番号の代わりに、クラスタ中心までの距離をモデルに入力することができます。忘れてはならないのは、ニューラルネットワークは正規化されたデータを好むということです。距離ベクトルのデータをソフトマックス関数で正規化します。

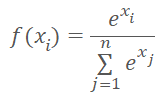
ただし、ソフトマックスは指数に基づいており、そのグラフは下図のようになります。

指数チャート

ここで、クラスタの中心までの距離をソフトマックス関数で正規化した結果、どのようなベクトルになるかを考えてみましょう。すべての距離が正であることは明らかです。距離が大きいほど指数が大きくなり、引数を同じように変化させても関数値がより大きく変化します。そのため、最大距離の方がより大きな重みを占めることになります。距離が短くなると、値の差は小さくなります。したがって、この単純な正規化を使用すると、要素が属していないクラスタを表すベクトルが得られるため、要素が属しているクラスタを特定することがより困難になります。その逆が必要です。

この状況は距離の値の符号を変えるだけで修正できそうですが、負の引数の領域では、指数関数の値は0に近づきます。引数が減少すると、関数値の偏差も0になる傾向があります。

上記の問題を解決する方法として、まず、距離を0から1の範囲で正規化する方法があります。そして、「1-X」にソフトマックス関数を適用します。

正規化した値を入力するモデルの選択は問題によって異なるので、この記事の範囲外です。

ここまではクラスタリング結果の利用に関する主な理論的アプローチについて述べてきましたが、ここからは実践編に移ります。

2.独立したソリューションとしてのクラスタリングの使用

OpenCLプログラム（ファイルunsupervised.cl ）に別のカーネルKmeansStatisticのコードを記述し、各クラスタシグナル処理に関連する統計量を計算することから、統計手法の実装を開始します。このプロセスの構成は、教師あり学習と似ています。実は、ラベル付きデータは必要です。ただし、この処理には、これまでのバックプロパゲーション方式とは根本的に異なる点があります。以前は、モデル関数を最適化することで、参照値に非常に近い結果を得ることができましたが、今回はモデルを一切変えません。その代わり、特定のパターンが出現したときのシステムの反応を統計的に収集します。

カーネルへのパラメータとして、3つのデータバッファへのポインタと、訓練セットの総要素数を渡すことにしますが、このカーネルパラメータには訓練サンプルを渡しません。この機能を実行するために、システム状態記述ベクトルの内容を知る必要はありません。この段階では、分析したシステムの状態がどのクラスに属するかが分かれば十分です。そこで、カーネルパラメータに訓練サンプルを渡す代わりに、訓練セットから各システム状態のクラスタ識別子を含むクラスタベクトルへのポインタを渡すことにします。

2番目の入力データバッファtargetには、特定のバッファが出現した後のシステムの反応を記述するテンソルが含まれます。このテンソルは、パターン出現後のシグナルを表す3つの論理フラグ（買い、売り、未定義）を持つことになります。フラグを利用することで、シグナル統計の計算をより簡単かつより直感的におこなえるようになりますが、同時に、可能なシグナルの変動幅を制限することにもなります。したがって、この手法の使用は、タスクの技術的要件に準拠する必要があります。この連載では、すべての検討されたアルゴリズムを最後のローソク足の形成が始まる前にフラクタル形成を識別する能力の観点から評価しました。ご存知のように、チャート上のフラクタルを特定するには、3本のローソク足が必要です。したがって、実際には、パターンの3本目のローソク足が形成された後にしか特定できないのですが、将来のパターンのローソク足が2本しか形成されていないときに、もちろん、ある程度の確率で、パターン形成を特定する方法を見つけたいのです。この問題を解決するには、各パターンに対して3つのフラグのターゲットシグナルを使用するので十分です。

また、様々な訓練サンプルを使って、パターン出現後のシグナル統計量を収集し、モデルを訓練することも可能です。例えば、十分に長い履歴区間でモデルを訓練することで、分析対象システムの状態の特徴を可能な限り学習させることができます。一方、より短い履歴期間は、データのラベル付けや統計の収集に使用することができます。もちろん、統計を取る前に、対応するクラスタリングをおこなう必要がありました。なぜなら、正しく統計を収集するためには、データが比較可能でなければならないからです。

アルゴリズムの話に戻りましょう。カーネル実行は1次元のタスク空間で実行されます。並列スレッドの数は、作成されたクラスタの数と同じになります。

カーネルの冒頭で、解析されたクラスタのシーケンス番号を決定する現在のスレッドのIDを定義します。また、確率的な結果のテンソルのシフトを即座に決定します。各シグナルの発生回数をカウントするprivate変数を用意します。買い、売り、スキップです。各変数に初期値0を代入します。

次に、訓練サンプルの要素数に等しい反復回数のループを実装します。ループ本体では、まずシステム状態が解析されたクラスタに属するかどうかを確認します。属する場合は、ターゲットフラグテンソルの内容を関連するprivate変数に追加します。

目標値には、0か1しかないフラグを使用します。相互排他的なシグナルを使用することになります。つまり、ある瞬間に、システムの個々の状態に対して、1つのフラグだけが存在することが可能です。この特性のおかげで、パターンの出現回数に別のカウンタを使用する必要はありません。その代わり、ループを抜けた後、3個のprivate変数をすべて合計して、パターンの出現回数の合計を得ることができます。

次に、シグナルの自然和を確率数学の分野に翻訳する必要があります。そのためには、各private変数の値をパターンの総発生数で徐算します。ただし、注意すべき瞬間もいくつかあります。まず、致命的なゼロ除算エラーが発生する可能性を排除する必要があります。第二に、信頼できる本当の確率が必要です。説明します。例えば、あるパラメータが1回だけ発生した場合、そのシグナルが発生する確率は100％となります。しかし、そのようなシグナルは信頼できるのでしょうか。もちろんできません。おそらく、その出現は偶発的なものでしょう。したがって、発生回数が10回未満のパターンについては、すべてのシグナルがゼロの確率で割り当てられることになります。

__kernel void KmeansStatistic(__global double *clusters,
                              __global double *target,
                              __global double *probability,
                              int total_m
                             )
  {
   int c = get_global_id(0);
   int shift_c = c * 3;
   double buy = 0;
   double sell = 0;
   double skip = 0;
   for(int i = 0; i < total_m; i++)
     {
      if(clusters[i] != c)
         continue;
      int shift = i * 3;
      buy += target[shift];
      sell += target[shift + 1];
      skip += target[shift + 2];
     }
//---
   int total = buy + sell + skip;
   if(total < 10)
     {
      probability[shift_c] = 0;
      probability[shift_c + 1] = 0;
      probability[shift_c + 2] = 0;
     }
   else
     {
      probability[shift_c] = buy / total;
      probability[shift_c + 1] = sell / total;
      probability[shift_c + 2] = skip / total;
     }
  }

OpenCLのプログラムでカーネルを作成した後、メインプログラムの側の作業に進みます。まず、先に作成したカーネルと連携するための定数を追加します。もちろん、定数の命名は命名ポリシーに従わなければなりません。

#define def_k_kmeans_statistic   4
#define def_k_kms_clusters       0
#define def_k_kms_targers        1
#define def_k_kms_probability    2
#define def_k_kms_total_m        3

定数の作成後、OpenCLCreate関数に移り、使用カーネル数の合計を変更します。また、新しいカーネルの作成も追加する予定です。

COpenCLMy *OpenCLCreate(string programm)
  {
   ...............
//---
   if(!result.SetKernelsCount(5))
     {
      delete result;
      .return NULL;
     }
//---
   ...............
//---
   if(!result.KernelCreate(def_k_kmeans_statistic, "KmeansStatistic"))
     {
      delete result;
      .return NULL;
     }
//---
   return result;
  }

あとは、このカーネルの呼び出しをメインプログラム側で実装する必要があります。

この呼び出しを可能にするために、CKmeansクラスに Statisticメソッドを作成しましょう。新しいメソッドは、2つのデータバッファ（訓練サンプルと参照値）へのポインタをパラメータとして受け取ります。このデータセットは教師あり学習と似ていますがアプローチには根本的な違いがあります。教師あり学習では、最適な結果が得られるようにモデルを最適化し、それを繰り返しおこなっています。今は単純に1パスで統計を取っています。

メソッド本体では、目標値バッファへのポインタの関連性を確認し、訓練サンプルのクラスタリングメソッドを呼び出しています。この場合の訓練サンプルは、モデルの訓練に使用したものと異なっていても良いですが、目標値に対応している必要があることを忘れてはなりません。

bool CKmeans::Statistic(CBufferDouble *data, CBufferDouble *targets)
  {
   if(CheckPointer(targets) == POINTER_INVALID ||
      !Clustering(data))
      return false;

次に、予測されるシステムの動作の確率的な値を書き込むためのバッファを初期化します。因果関係を分析するわけではないので、あえて「パターンへの対応」という表現はしていません。それは直接的にも間接的にもなりえます。全く関係がありません。過去のデータを使って統計を取るのみです。

   if(CheckPointer(c_aProbability) == POINTER_INVALID)
     {
      c_aProbability = new CBufferDouble();
      if(CheckPointer(c_aProbability) == POINTER_INVALID)
         return false;
     }
   if(!c_aProbability.BufferInit(3 * m_iClusters, 0))
      return false;
//---
   int total = c_aClasters.Total();
   if(!targets.BufferCreate(c_OpenCL) ||
      !c_aProbability.BufferCreate(c_OpenCL))
      return false;

バッファを作成した後、必要なデータをOpenCLのコンテキストメモリにロードし、カーネルを呼び出すプロシージャを実装します。まずカーネルパラメータを渡し、タスク空間の次元と各次元でのオフセットを決定します。その後、カーネルを実行キューに入れ、演算結果を読み出します。操作の実行時には、各手順でのプロセスを必ず制御します。

   if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_statistic, def_k_kms_probability, c_aProbability.GetIndex()))
      return false;
   if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_statistic, def_k_kms_targers, targets.GetIndex()))
      return false;
   if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_statistic, def_k_kms_clusters, c_aClasters.GetIndex()))
      return false;
   if(!c_OpenCL.SetArgument(def_k_kmeans_statistic, def_k_kms_total_m, total))
      return false;
   uint global_work_offset[1] = {0};
   uint global_work_size[1];
   global_work_size[0] = m_iClusters;
   if(!c_OpenCL.Execute(def_k_kmeans_statistic, 1, global_work_offset, global_work_size))
      return false;
   if(!c_aProbability.BufferRead())
      return false;
//---
   data.BufferFree();
   targets.BufferFree();
//---
   return true;
  }

カーネルが正常に実行されると、c_aProbabilityバッファに、各パターンの発生確率が格納されます。あとは、メモリをクリアしてメソッドを完成させるだけです。

しかし、検討された手順は、モデルの訓練に起因するものである可能性があります。実用化のためには、リアルタイムシステムの動作確率を求める必要があります。このため、別のメソッドGetProbabilityを作成します。メソッドのパラメータでは、クラスタリング用のサンプルのみを渡します。このメソッドを呼び出す前に、c_aProbability 確率行列を形成しておくことが非常に重要です。そのため、メソッド本体で最初に確認するのはこの点です。その後、受信データのクラスタリングを開始します。再度、操作実行結果を確認します。

CBufferDouble *CKmeans::GetProbability(CBufferDouble *data)
  {
   if(CheckPointer(c_aProbability) == POINTER_INVALID ||
      !Clustering(data))
      .return NULL;

このメソッドの具体的な特徴は、操作の結果として、ブーリアン値ではなく、データバッファへのポインタを返すことです。そこで、次の手順では、データを収集するための新しいバッファを作成します。

   CBufferDouble *result = new CBufferDouble();
   if(CheckPointer(result) == POINTER_INVALID)
      return result;

リアルタイムに、少数のレコードの確率的なデータを受け取ることを想定しています。ほとんどの場合、レコードは現在のシステム状態の1つだけです。そのため、これ以上の並列計算機への対応はおこなわない予定です。調査したデータクラスタの識別子のバッファに対して反復処理をおこなうループを実装します。ループ本体では、対応するクラスタの確率を結果バッファに転送します。

   int total = c_aClasters.Total();
   if(!result.Reserve(total * 3))
     {
      delete result;
      return result;
     }
   for(int i = 0; i < total; i++)
     {
      int k = (int)c_aClasters.At(i) * 3;
      if(!result.Add(c_aProbability.At(k)) ||
         !result.Add(c_aProbability.At(k + 1)) ||
         !result.Add(c_aProbability.At(k + 2))
        )
        {
         delete result;
         return result;
        }
     }
//---
   return result;
  }

結果バッファでは、確率は分析されたサンプルのシステム状態と同じ順序で配置されています。サンプルに1つのクラスタに属するデータが含まれていた場合、システム動作確率は繰り返されます。

この手法をテストするために、「kmeans_stat.mq5」というエキスパートアドバイザー(EA)を作成しました。そのコードは添付ファイルにあります。ファイル名から理解できるように、各パターンの後にフラクタルが出現する確率を統計したものです。

前回の記事では訓練した500クラスタモデルを用いて実験をおこないました。結果は以下のスクリーンショットのようになります。

パターン形成後のフラクタル形成の統計量

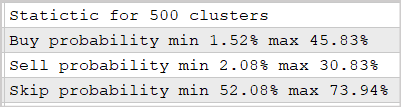
提供されたデータは、この手法を用いることで、フラクタル出現後の市場の反応を30～45％の確率で予測できることを証明しています。特に、多層ニューラルネットを使わなかったことを考慮すると、これはなかなか良い結果です。

3.入力としてのクラスタリング結果の使用

それでは、クラスタリング結果を利用する2つ目のバリエーションの実装に移りましょう。このアプローチでは、クラスタリングの結果を別のモデルに入力することになります。実際には、教師あり学習アルゴリズムを用いたニューラルネットワークなど、問題に適した任意のモデルを選択することができます。

この手法を導入する場合、クラスタリング結果は、クラスタの中心までの距離を正規化したベクトルで表示することはあらかじめ決めています。この機能を実装するために、OpenCLプログラムunsupervised.clで別のカーネルKmeansSoftMaxを作成する必要があります。

この関数はKmeansCulcDistanceカーネルで既に実行されているので、新しいカーネルでは各クラスタの中心までの距離を再計算しません。KmeansSoftMaxでは、利用可能なデータのみを正規化します。

カーネルのパラメータには、2つのデータバッファへのポインタと、使用するクラスタの総数を渡します。データバッファのうち、ソースデータバッファのdistanceと結果バッファのsoftmaxが1つずつ存在することになります。どちらのバッファも同じ大きさで、行列のベクトル表現です。行列の行はシーケンスの個々の要素を表し、列はクラスタを表します。

カーネルはクラスタ化されたサンプルの要素数に応じて、1次元のタスク空間に起動されます。カーネルは2つ目のモデルを訓練するときにも、結果の演算にも使えるので、あえて「訓練サンプル」とは呼ばないことにしました。この2つのバリエーションで入力されるデータが異なることは明らかです。

カーネルコードの実装に進む前に、正規化関数を少し変更して以下のようになったことを思い出してください。

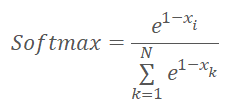
ここで、xは0から1の範囲で正規化されたクラスタ中心までの距離です。

次に上記の式の実装を見てみましょう。カーネル本体では、まず、シーケンスの解析対象要素を示すスレッド識別子を決定します。また、解析済みベクトルの先頭までのバッファの移動量も求めます。初期データと結果のテンソルは同じサイズであるため、2つのバッファのオフセットも同じになります。

次に、0から1の範囲の距離を正規化するために、クラスタ中心からの最大偏差を求める必要があります。距離を計算するとき、偏差の二乗を使ったことを思い出してください。距離ベクトルの値がすべて正になることを意味します。これで少しは楽になります。最大距離を書き込むためにprivate変数mを宣言し、ベクトルの最初の要素の値で初期化します。次に、ベクトルの全要素を反復処理するループを作成します。ベクトル本体では、要素の値を保存した値と比較し、最大値を変数に書き込みます。

最高値が決まったら、各要素の指数値の算出に移ります。また、ベクトル全体の指数値の和もすぐに計算できます。合計を求めるために、private変数sumを0値で初期化します。関連する算術演算は次のループで実行されます。ループの反復回数は、モデルのクラスタ数と同じです。ループ本体では、まず、クラスタ中心までの距離を正規化し「反転」させた指数値をprivate変数に保存します。結果の値をsumに加算し、結果バッファに移動します。バッファに値を書き込む前にprivate変数を使用することで、低速なグローバルメモリアクセスの回数を最小にすることができます。

ループの反復が完了したら、得られた指数値を総和で除算してデータを正規化する必要があります。これらの操作を実行するために、クラスタ数と同じ反復回数のループをもう1つ作成しましょう。ループ終了後、カーネルを終了させます。

__kernel void KmeansSoftMax(__global double *distance,
                            __global double *softmax,
                            inсt total_k
                           )
  {
   int i = get_global_id(0);
   int shift = i * total_k;
   double m=distance[shift];
   for(int k = 1; k < total_k; k++)
      m =  max(distance[shift + k],m);
   double sum = 0;
   for(int k = 0; k < total_k; k++)
     {
      double value =  exp(1-distance[shift + k]/m);
      sum += value;
      softmax[shift + k] = value;
     }
   for(int k = 0; k < total_k; k++)
      softmax[shift + k] /= sum;
  }

OpenCLプログラムの機能を拡張しました。あとはCKmeansクラスからカーネルの呼び出しを追加するだけです。前のカーネル呼び出しコードを追加するために使用した上記の同じスキームにこだわります。

まず、命名規則に従って定数を追加します。

#define def_k_kmeans_softmax     5
#define def_k_kmsm_distance      0
#define def_k_kmsm_softmax       1
#define def_k_kmsm_total_k       2

次に、OpenCLコンテキスト初期化関数OpenCLCreateにカーネル宣言を追加します。

COpenCLMy *OpenCLCreate(string programm)
  {
   ...............
//---
   if(!result.SetKernelsCount(6))
     {
      delete result;
      .return NULL;
     }
//---
   ...............
//---
   if(!result.KernelCreate(def_k_kmeans_softmax, "KmeansSoftMax"))
     {
      delete result;
      .return NULL;
     }
//---
   return result;
  }

そして、もちろん、クラスCKmeans::SoftMaxの新しいメソッドが必要です。このメソッドは、パラメータとして、初期データバッファへのポインタを受け取ります。操作の結果、このメソッドは同じ大きさの結果バッファを返します。

メソッド本体では、まずクラスタリングクラスが以前に訓練したものかどうかを確認します。必要に応じて、モデルの訓練処理を初期化します。ここで、モデル訓練法において、訓練サンプルの最大サイズに制限を設けたことを思い出してください。したがって、モデルを事前に訓練していない場合は、十分な大きさのサンプルをメソッドにパラメータとして渡す必要があります。そうでなければ、このメソッドは結果バッファへの無効なポインタを返します。データクラスタリングモデルがすでに訓練されている場合は、サンプルサイズの制限が解除されます。

CBufferDouble *CKmeans::SoftMax(CBufferDouble *data)
  {
   if(!m_bTrained && !Study(data, (c_aMeans.Maximum() == 0)))
      .return NULL;

次の手順では、使用するオブジェクトへのポインタの有効性を確認します。まず学習メソッドを呼び出してから、オブジェクトのポインタを確認するのは不思議に思われるかもしれません。実は、この学習メソッド自体にも、同様の制御ブロックがあるのです。もし、操作を続ける前に必ずモデルの訓練メソッドを呼び出すのであれば、これらの制御は訓練メソッド内の制御を繰り返すことになり、不要になります。しかし、事前に訓練したモデルを使用する場合、訓練メソッドを呼び出さないため、その制御をおこなうことができません。一方、無効なポインタで操作をさらに実行すると、重大なエラーが発生します。そのため、ポインタを再確認する必要があります。

   if(CheckPointer(data) == POINTER_INVALID || CheckPointer(c_OpenCL) == POINTER_INVALID)
      .return NULL;

ポインタを確認した後、ソースデータバッファのサイズを確認しましょう。少なくとも、システムの第1状態を記述したベクトルを含んでいなければなりません。また、バッファのデータ量は、システム状態記述ベクトルの倍数である必要があります。

   int total = data.Total();
   if(total <= 0 || m_iClusters < 2 || (total % m_iVectorSize) != 0)
      .return NULL;

そして、クラスタに分散させるべきシステム状態の数を決定します。

   int rows = total / m_iVectorSize;
   if(rows < 1)
      .return NULL;

次に、距離の計算と正規化のためのバッファを初期化する必要があります。初期化アルゴリズムは非常にシンプルです。まず、バッファポインタの有効性を確認し、必要であれば新しいオブジェクトを作成します。そして、バッファをゼロ値で埋めます。

   if(CheckPointer(c_aDistance) == POINTER_INVALID)
     {
      c_aDistance = new CBufferDouble();
      if(CheckPointer(c_aDistance) == POINTER_INVALID)
         .return NULL;
     }
   c_aDistance.BufferFree();
   if(!c_aDistance.BufferInit(rows * m_iClusters, 0))
      .return NULL;

   if(CheckPointer(c_aSoftMax) == POINTER_INVALID)
     {
      c_aSoftMax = new CBufferDouble();
      if(CheckPointer(c_aSoftMax) == POINTER_INVALID)
         .return NULL;
     }
   c_aSoftMax.BufferFree();
   if(!c_aSoftMax.BufferInit(rows * m_iClusters, 0))
      .return NULL;

準備作業を完了させるために、OpenCLコンテキストで必要なデータバッファを作成します。

   if(!data.BufferCreate(c_OpenCL) ||
      !c_aMeans.BufferCreate(c_OpenCL) ||
      !c_aDistance.BufferCreate(c_OpenCL) ||
      !c_aSoftMax.BufferCreate(c_OpenCL))
      .return NULL;

これで準備作業は終了です。ここで、必要なカーネルの呼び出しに移ります。このメソッドの全機能を実装するためには、次の2つのカーネルの順次呼び出しを作成する必要があります。

クラスタ中心への距離を決定するKmeansCulcDistance
距離を正規化するKmeansSoftMax

カーネル呼び出しのアルゴリズムは非常にシンプルで、先に述べたクラスタリング結果の統計的利用の方法と同様のものです。まず、カーネルにパラメータを渡す必要があります。

   if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_distance, def_k_kmd_data, data.GetIndex()))
      .return NULL;
   if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_distance, def_k_kmd_means, c_aMeans.GetIndex()))
      .return NULL;
   if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_distance, def_k_kmd_distance, c_aDistance.GetIndex()))
      .return NULL;
   if(!c_OpenCL.SetArgument(def_k_kmeans_distance, def_k_kmd_vector_size, m_iVectorSize))
      .return NULL;

次に、問題空間の次元と各次元でのオフセットを指定します。

   uint global_work_offset[2] = {0, 0};
   uint global_work_size[2];
   global_work_size[0] = rows;
   global_work_size[1] = m_iClusters;

その後、カーネルを実行キューに入れ、演算実行結果を読み出す。

   if(!c_OpenCL.Execute(def_k_kmeans_distance, 2, global_work_offset, global_work_size))
      .return NULL;
   if(!c_aDistance.BufferRead())
      .return NULL;

2番目のカーネルについても同様の操作をおこないます。

   if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_softmax, def_k_kmsm_distance, c_aDistance.GetIndex()))
      .return NULL;
   if(!c_OpenCL.SetArgumentBuffer(def_k_kmeans_softmax, def_k_kmsm_softmax, c_aSoftMax.GetIndex()))
      .return NULL;
   if(!c_OpenCL.SetArgument(def_k_kmeans_softmax, def_k_kmsm_total_k, m_iClusters))
      .return NULL;
   uint global_work_offset1[1] = {0};
   uint global_work_size1[1];
   global_work_size1[0] = rows;
   if(!c_OpenCL.Execute(def_k_kmeans_softmax, 1, global_work_offset1, global_work_size1))
      .return NULL;
   if(!c_aSoftMax.BufferRead())
      .return NULL;

最後にOpenCLコンテキストのメモリをクリアし、結果バッファへのポインタを返してメソッドを終了します。

   data.BufferFree();
   c_aDistance.BufferFree();
//---
   return c_aSoftMax;
  }

以上でk-meansクラスタリングクラスCKmeansにおける修正に関する操作は完了です。次に、アプローチのテストに移ることができます。この目的で、教師あり学習アルゴリズムの記事にあるEArを模してkmeans_net.mq5というEAを作成してみます。実装をテストするために、クラスタリング結果を3つの隠れ層を持つ完全連結パーセプトロンに入力します。EAの全コードは添付ファイルにあります。「Train」学習関数に注目してください。

関数の冒頭で、クラスタリングクラス内のOpenCLコンテキストで動作するオブジェクトインスタンスを初期化して、作成したオブジェクトへのポインタをクラスタリングクラスに渡します。操作実行結果の確認も忘れてはいけません。

void Train(datetime StartTrainBar = 0)
  {
   COpenCLMy *opencl = OpenCLCreate(cl_unsupervised);
   if(CheckPointer(opencl) == POINTER_INVALID)
     {
      ExpertRemove();
      return;
     }
   if(!Kmeans.SetOpenCL(opencl))
     {
      delete opencl;
      ExpertRemove();
      return;
     }

オブジェクトの初期化が成功したら、訓練期間の境界を決定します。

   MqlDateTime start_time;
   TimeCurrent(start_time);
   start_time.year -= StudyPeriod;
   if(start_time.year <= 0)
      start_time.year = 1900;
   datetime st_time = StructToTime(start_time);

履歴データを読み込みます。バッファに読み込まれる指標データは、相場と異なり時系列で表現されることにご注意ください。配列の要素が逆に並んでいるため、これは重要なことです。したがって、データの比較可能性を確保するために、相場の配列を時系列に反転させる必要があります。

   int bars = CopyRates(Symb.Name(), TimeFrame, st_time, TimeCurrent(), Rates);
   if(!RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars))
     {
      ExpertRemove();
      return;
     }
   if(!ArraySetAsSeries(Rates, true))
     {
      ExpertRemove();
      return;
     }

   RSI.Refresh();
   CCI.Refresh();
   ATR.Refresh();
   MACD.Refresh();

履歴データの読み込みに成功したら、事前訓練済みのクラスタリングモデルを読み込みます。

   int handl = FileOpen(StringFormat("kmeans_%d.net", Clusters), FILE_READ | FILE_BIN);
   if(handl == INVALID_HANDLE)
     {
      ExpertRemove();
      return;
     }
   if(FileReadInteger(handl) != Kmeans.Type())
     {
      ExpertRemove();
      return;
     }
   bool result = Kmeans.Load(handl);
   FileClose(handl);
   if(!result)
     {
      ExpertRemove();
      return;
     }

訓練サンプルと目標値の形成に進みます。

   int total = bars - (int)HistoryBars - 1;
   double data[], fractals[];
   if(ArrayResize(data, total * 8 * HistoryBars) <= 0 ||
      ArrayResize(fractals, total * 3) <= 0)
     {
      ExpertRemove();
      return;
     }
//---
   for(int i = 0; (i < total && !IsStopped()); i++)
     {
      Comment(StringFormat("Create data: %d of %d", i, total));
      for(int b = 0; b < (int)HistoryBars; b++)
        {
         int bar = i + b;
         int shift = (i * (int)HistoryBars + b) * 8;
         double open = Rates[bar].open;
         data[shift] = open - Rates[bar].low;
         data[shift + 1] = Rates[bar].high - open;
         data[shift + 2] = Rates[bar].close - open;
         data[shift + 3] = RSI.GetData(MAIN_LINE, bar);
         data[shift + 4] = CCI.GetData(MAIN_LINE, bar);
         data[shift + 5] = ATR.GetData(MAIN_LINE, bar);
         data[shift + 6] = MACD.GetData(MAIN_LINE, bar);
         data[shift + 7] = MACD.GetData(SIGNAL_LINE, bar);
        }
      int shift = i * 3;
      int bar = i + 1;
      fractals[shift] = (int)(Rates[bar - 1].high <= Rates[bar].high && Rates[bar + 1].high < Rates[bar].high);
      fractals[shift + 1] = (int)(Rates[bar - 1].low >= Rates[bar].low && Rates[bar + 1].low > Rates[bar].low);
      fractals[shift + 2] = (int)((fractals[shift] + fractals[shift]) == 0);
     }
   if(IsStopped())
     {
      ExpertRemove();
      return;
     }
   CBufferDouble *Data = new CBufferDouble();
   if(CheckPointer(Data) == POINTER_INVALID ||
      !Data.AssignArray(data))
      return;
   CBufferDouble *Fractals = new CBufferDouble();
   if(CheckPointer(Fractals) == POINTER_INVALID ||
      !Fractals.AssignArray(fractals))
      return;

我々のクラスタリング手法は、初期データ配列を扱うことができるので、訓練サンプル全体を一度にクラスタリングすることができます。

   ResetLastError();
   CBufferDouble *softmax = Kmeans.SoftMax(Data);
   if(CheckPointer(softmax) == POINTER_INVALID)
     {
      printf("Runtime error %d", GetLastError());
      ExpertRemove();
      return;
     }

これらの処理がすべて正常に終了すると、ソフトマックスバッファにパーセプトロンの訓練サンプルが格納されます。目標値もあらかじめ用意しています。そこで、2回目のモデル訓練サイクルに移ることができます。

教師あり学習アルゴリズムのテストと同様に、モデルの訓練は2つのネストされたループを用いて実装される予定です。外側のループは、訓練エポックをカウントします。ある事象が発生したときにループを抜けます。

まず、ちょっとした準備作業をおこないます。必要なローカル変数を初期化する必要があります。

  if(CheckPointer(TempData) == POINTER_INVALID)
     {
      TempData = new CArrayDouble();
      if(CheckPointer(TempData) == POINTER_INVALID)
        {
         ExpertRemove();
         return;
        }
     }
   delete opencl;
   double prev_un, prev_for, prev_er;
   dUndefine = 0;
   dForecast = 0;
   dError = -1;
   dPrevSignal = 0;
   bool stop = false;
   int count = 0;
   do
     {
      prev_un = dUndefine;
      prev_for = dForecast;
      prev_er = dError;
      ENUM_SIGNAL bar = Undefine;
      //---
      stop = IsStopped();

そして、初めてネストされたループに移行します。ネストされたループの反復回数は、訓練サンプルのサイズから検証ゾーンの小さな「テール」を除いたものに等しくなります。

反復回数がサンプルサイズと同じでも、毎回ランダムな要素を選んで学習していくことになります。これをネストされたループの先頭で定義します。訓練サンプルからのランダムなベクトルを使用することで、モデルの均一な訓練を実現します。

      for(int it = 0; (it < total - 300 && !IsStopped()); it++)
        {
         int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (total - 300)) + 300;

ランダムに選んだ要素のインデックスにより、初期データバッファ内のオフセットを決定し、必要なベクトルを一時バッファにコピーします。

         TempData.Clear();
         int shift = i * Clusters;
         if(!TempData.Reserve(Clusters))
           {
            if(CheckPointer(Data) == POINTER_DYNAMIC)
               delete Data;
            if(CheckPointer(Fractals) == POINTER_DYNAMIC)
               delete Fractals;
            if(CheckPointer(softmax) == POINTER_DYNAMIC)
               delete softmax;
            if(CheckPointer(opencl) == POINTER_DYNAMIC)
               delete opencl;
            Comment("");
            //---
            ExpertRemove();
            return;
           }
         for(int c = 0; c < Clusters; c++)
            if(!TempData.Add(softmax.At(shift + c)))
              {
               if(CheckPointer(Data) == POINTER_DYNAMIC)
                  delete Data;
               if(CheckPointer(Fractals) == POINTER_DYNAMIC)
                  delete Fractals;
               if(CheckPointer(softmax) == POINTER_DYNAMIC)
                  delete softmax;
               if(CheckPointer(opencl) == POINTER_DYNAMIC)
                  delete opencl;
               Comment("");
               //---
               ExpertRemove();
               return;
              }

初期データベクトルを生成した後、それをニューラルネットワークの順方向に入力します。フォワードパスが成功すると、その結果を得ることができます。

         if(!Net.feedForward(TempData))
           {
            if(CheckPointer(Data) == POINTER_DYNAMIC)
               delete Data;
            if(CheckPointer(Fractals) == POINTER_DYNAMIC)
               delete Fractals;
            if(CheckPointer(softmax) == POINTER_DYNAMIC)
               delete softmax;
            if(CheckPointer(opencl) == POINTER_DYNAMIC)
               delete opencl;
            Comment("");
            //---
            ExpertRemove();
            return;
           }
         Net.getResults(TempData);

ソフトマックス関数で結果を正規化します。

         double sum = 0;
         for(int res = 0; res < 3; res++)
           {
            double temp = exp(TempData.At(res));
            sum += temp;
            TempData.Update(res, temp);
           }
         for(int res = 0; (res < 3 && sum > 0); res++)
            TempData.Update(res, TempData.At(res) / sum);

モデルの学習過程を視覚的に追うために、現在の状態をチャート上に表示してみましょう。

         switch(TempData.Maximum(0, 3))
           {
            case 1:
               dPrevSignal = (TempData[1] != TempData[2] ? TempData[1] : 0);
               break;
            case 2:
               dPrevSignal = -TempData[2];
               break;
            default:
               dPrevSignal = 0;
               break;
           }
         string s = StringFormat("Study -> Era %d -> %.2f -> Undefine %.2f%% foracast %.2f%%\n %d of %d -> %.2f%%
                                 \nError %.2f\n%s -> %.2f ->> Buy %.5f - Sell %.5f - Undef %.5f",
                                 count, dError, dUndefine, dForecast, it + 1, total - 300,
                                 (double)(it + 1.0) / (total - 300) * 100, Net.getRecentAverageError(), 
                                 EnumToString(DoubleToSignal(dPrevSignal)), dPrevSignal, TempData[1], TempData[2],
                                 TempData[0]);
         Comment(s);
         stop = IsStopped();

ループの繰り返しの最後に、逆伝播メソッドを呼び出し、モデルの重みの行列を更新します。

         if(!stop)
           {
            shift = i * 3;
            TempData.Clear();
            TempData.Add(Fractals.At(shift + 2));
            TempData.Add(Fractals.At(shift));
            TempData.Add(Fractals.At(shift + 1));
            Net.backProp(TempData);
            ENUM_SIGNAL signal = DoubleToSignal(dPrevSignal);
            if(signal != Undefine)
              {
               if((signal == Sell && Fractals.At(shift + 1) == 1) || (signal == Buy && Fractals.At(shift) == 1))
                  dForecast += (100 - dForecast) / Net.recentAverageSmoothingFactor;
               else
                  dForecast -= dForecast / Net.recentAverageSmoothingFactor;
               dUndefine -= dUndefine / Net.recentAverageSmoothingFactor;
              }
            else
              {
               if(Fractals.At(shift + 2) == 1)
                  dUndefine += (100 - dUndefine) / Net.recentAverageSmoothingFactor;
              }
           }
        }

各訓練エポックの後、検証プロットにグラフィックラベルを表示します。この機能を実現するために、もう1つネストしたループを作ってみましょう。ループ本体での操作は先に説明したループとほぼ同じですが、大きく異なる点が2つだけあります。

ランダムな選択ではなく、要素を順番に取る
逆伝播はおこなわない

検証サンプルでは、パラメータを過剰適合させることなく、新しいデータに対してモデルがどのように機能するかを確認するため、逆伝播は存在しません。そのため、モデルの演算結果はデータの供給順序に依存しません（リカレントモデルの場合は例外）。そのため、乱数を発生させるためのリソースを費やさずに、システムの全状態を順次取得します。

      count++;
      for(int i = 0; i < 300; i++)
        {
         TempData.Clear();
         int shift = i * Clusters;
         if(!TempData.Reserve(Clusters))
           {
            if(CheckPointer(Data) == POINTER_DYNAMIC)
               delete Data;
            if(CheckPointer(Fractals) == POINTER_DYNAMIC)
               delete Fractals;
            if(CheckPointer(softmax) == POINTER_DYNAMIC)
               delete softmax;
            if(CheckPointer(opencl) == POINTER_DYNAMIC)
               delete opencl;
            Comment("");
            //---
            ExpertRemove();
            return;
           }

         for(int c = 0; c < Clusters; c++)
            if(!TempData.Add(softmax.At(shift + c)))
              {
               if(CheckPointer(Data) == POINTER_DYNAMIC)
                  delete Data;
               if(CheckPointer(Fractals) == POINTER_DYNAMIC)
                  delete Fractals;
               if(CheckPointer(softmax) == POINTER_DYNAMIC)
                  delete softmax;
               if(CheckPointer(opencl) == POINTER_DYNAMIC)
                  delete opencl;
               Comment("");
               //---
               ExpertRemove();
               return;
              }
         if(!Net.feedForward(TempData))
           {
            if(CheckPointer(Data) == POINTER_DYNAMIC)
               delete Data;
            if(CheckPointer(Fractals) == POINTER_DYNAMIC)
               delete Fractals;
            if(CheckPointer(softmax) == POINTER_DYNAMIC)
               delete softmax;
            if(CheckPointer(opencl) == POINTER_DYNAMIC)
               delete opencl;
            Comment("");
            //---
            ExpertRemove();
            return;
           }
         Net.getResults(TempData);

         double sum = 0;
         for(int res = 0; res < 3; res++)
           {
            double temp = exp(TempData.At(res));
            sum += temp;
            TempData.Update(res, temp);
           }
         for(int res = 0; (res < 3 && sum > 0); res++)
            TempData.Update(res, TempData.At(res) / sum);
         //---
         switch(TempData.Maximum(0, 3))
           {
            case 1:
               dPrevSignal = (TempData[1] != TempData[2] ? TempData[1] : 0);
               break;
            case 2:
               dPrevSignal = -TempData[2];
               break;
            default:
               dPrevSignal = 0;
               break;
           }

チャート上にオブジェクトの表示を追加し、検証サイクルを終了します。

         if(DoubleToSignal(dPrevSignal) == Undefine)
            DeleteObject(Rates[i + 2].time);
         else
            DrawObject(Rates[i + 2].time, dPrevSignal, Rates[i + 2].high, Rates[i + 2].low);
        }

外側ループの反復を終了する前に、現在のモデルの状態を保存し、誤差の値を訓練ダイナミクスファイルに追加します。

      if(!stop)
        {
         dError = Net.getRecentAverageError();
         Net.Save(FileName + ".nnw", dError, dUndefine, dForecast, Rates[0].time, false);
         printf("Era %d -> error %.2f %% forecast %.2f", count, dError, dForecast);
         ChartScreenShot(0, FileName + IntegerToString(count) + ".png", 750, 400);
         int h = FileOpen(FileName + ".csv", FILE_READ | FILE_WRITE | FILE_CSV);
         if(h != INVALID_HANDLE)
           {
            FileSeek(h, 0, SEEK_END);
            FileWrite(h, eta, count, dError, dUndefine, dForecast);
            FileFlush(h);
            FileClose(h);
           }
        }
     }
   while((!(DoubleToSignal(dPrevSignal) != Undefine || dForecast > 70) || 
          !(dError < 0.1 && MathAbs(dError - prev_er) < 0.01 && 
          MathAbs(dUndefine - prev_un) < 0.1 && 
          MathAbs(dForecast - prev_for) < 0.1)) && !stop);

一定の指標に従って、学習サイクルを終了します。これらは、教師あり学習のEAで使用したものと同じ指標です。

そして、訓練メソッドを終了する前に、モデルの訓練メソッドの本体で作成したオブジェクトを削除する必要があります。

   if(CheckPointer(Data) == POINTER_DYNAMIC)
      delete Data;
   if(CheckPointer(Fractals) == POINTER_DYNAMIC)
      delete Fractals;
   if(CheckPointer(softmax) == POINTER_DYNAMIC)
      delete softmax;
   if(CheckPointer(TempData) == POINTER_DYNAMIC)
      delete TempData;
   if(CheckPointer(opencl) == POINTER_DYNAMIC)
      delete opencl;
   Comment("");
//---
   ExpertRemove();
  }

EAの完全なコードは、添付ファイルに記載されています。

EAの性能を評価するために、前回の記事で訓練して、前回のテストで使用した500クラスタのクラスタリングモデルを使ってテストをおこないました。訓練グラフは以下の通りです。

学習過程の損失関数の値のグラフ

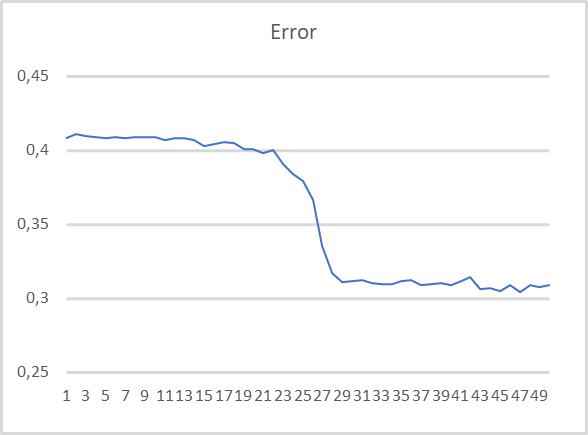
ご覧の通り、訓練グラフは非常に滑らかです。モデルの訓練には、Adamのパラメータ最適化手法を用いました。最初の20エポックは、損失関数が徐々に減少していることを示しており、これはモーメントの蓄積に関連しています。そして、損失関数の値がある最小値まで急激に減少するのが目に見えています。これまで得られた教師ありモデルの訓練グラフでは、損失関数の折れ線が目立っていました。例えば、以下はより複雑なAttentionモデルの訓練グラフです。

Attentionモデル訓練グラフ

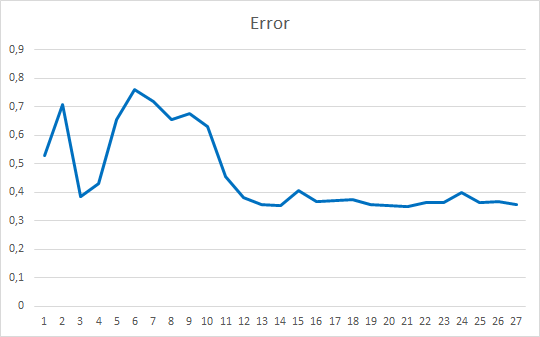
提示された2つのグラフを比較すると、シンプルなモデルでも事前のデータクラスタリングによって、どれだけ効率が上がるかが分かります。

結論

今回は、クラスタリング結果を実用的なケースで解決するために、2つの選択肢を考えて実行しました。テスト結果は、両方の手法を使用することの効率性を示しています。最初のケースには非常に透明で理解しやすい結果を持つシンプルなモデルがあります。2番目の手法を用いることで、モデルの訓練がより滑らかになって高速化され、モデルの性能も向上させることができます。

参考文献リスト

記事で使用されているプログラム

#	ファイル名	タイプ	詳細
1	kmeans.mq5	EA	モデルを訓練するEA
2	kmeans_net.mq5	EA	2つ目のモデルにデータを渡すテストをおこなうEA
3	kmeans_stat.mq5	EA	統計的手法をテストするEA
4	kmeans.mqh	クラスライブラリ	k-means法を実装するためのライブラリ
5	unsupervised.cl	コードベース	k-means法を実装するためのOpenCLプログラムコードライブラリ
6	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
7	NeuroNet.cl	コードベース	OpenCLプログラムコードライブラリ