
Neural networks made easy (Part 10): Multi-Head Attention
Table of Contents
- Introduction
- 1. Multi-Head Attention
- 2. A Bit of Math
- 3. Positional Encoding
- 4. Implementation
- 4.1. Eliminating Keys Tensor
- 4.2. Multi-Head Attention Class
- 4.3. Feed-forward
- 4.4. Feed-backward
- 4.5. Changes in the Neural Network Base Classes
- 5. Testing
- Conclusion
- References
- Programs Used in the Article
Introduction
In the article "Neural networks made easy (Part 8): Attention mechanisms", we have considered the self-attention mechanism and a variant of its implementation. In practice, modern neural network architectures use Multi-Head Attention. This mechanism implies the launch of multiple parallel self-attention threads with different weights. Such a solution should better reveal connections between various elements of the sequence. Let us try to implement a similar architecture and compare the results of these two methods.
1. Multi-Head Attention
The Self-Attention algorithm uses three trained weight matrices (Wq, Wk and Wv). Matrix data is used to get 3 entities: Query, Key and Value. The first two entities define the pairwise relationship between the elements of the sequence, and the last one defines the context of the analyzed element.
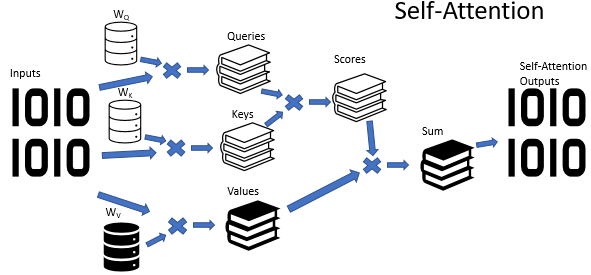
It's no secret that situations are not always clear-cut. On the contrary, it seems that in most cases a situation can be interpreted from different points of view. So, conclusions can be completely opposite, depending on the selected point of view. It is important to consider all possible variants in such situations and to make a decision only after careful analysis. The Multi-Head Attention mechanism has been proposed for solving such problems. Each "head" has its own opinion, while the decision is made by a balanced vote.
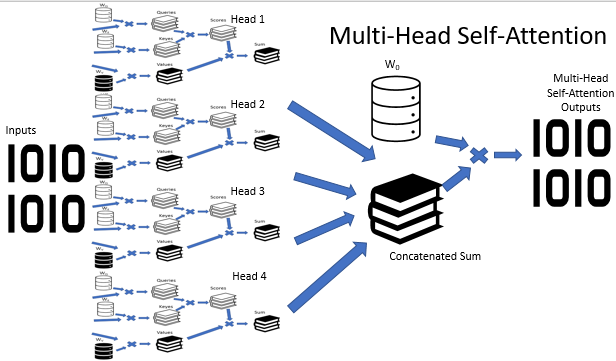
The Multi-Head Attention architecture implies the parallel use of multiple self-attention threads having different weight, which imitates a versatile analysis of a situation. The results of operation of self-attention threads are concatenated into a single tensor. The final result of the algorithm is found by multiplying the tensor by the W0 matrix, the parameters of which are selected during the neural network training process. The whole architecture replaces the Self-Attention block in the encoder and decoder of the transformer architecture.
2. A Bit of Math
The following formula can provide a mathematical description of the Self-Attention algorithm:
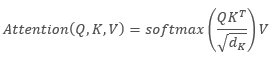 ,
,
where 'Q' is the Query tensor, 'K' is the Key tensor, 'V' is the Values tensor, 'd' is the dimension of one key vector.
In turn
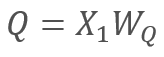 and
and 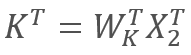 ,
,
where X1 and X2 are the elements of the sequence; Wq and Wk are matrices of weights of Queries and keys, respectively. Thus, we get the following:
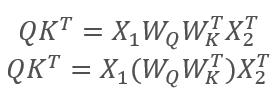
By the matrices associativity property, we can first multiply the weight matrices Wq and Wk. As you can see, the product of the wight matrices does not depend on the input sequence and is the same for all iterations of a particular Self-Attention block (of course, this is true until the next update of the matrix parameters). So, in order to reduce computational operations, we can calculate an intermediate matrix once for a specific approach, and then use it for other calculations.
We can go even further and train one matrix instead of two. However, curiously enough, it is not always possible to reduce the number of operations by training only one matrix. For example, for large dimensions of the input sequence vector, the dimension can be reduced by the matrices Wq and Wk. In this case, if the length of input vectors X1 and X2 is 100 elements, the single matrix will contain 10K elements (100*100). If the dimension is reduced by matrices Wq and Wk by a factor of 10, we will have two matrices each having 1K elements (100*10). Therefore, you should carefully select a solution, taking into account the network performance and the quality of its operation results.
3. Positional Encoding
Also, when working with time series, pay attention to the distance between elements in the sequence. The attention algorithm performs pairwise verification of dependencies between the elements of the sequence, using the same matrices for all elements of the sequence. At the same time, the mutual influence of time series elements strongly depends on the time interval between them. Therefore, another acute question is the addition of a positional coding algorithm.
An ideal position coding algorithm should satisfy several criteria:
- Each element of the sequence must receive a unique code
- The step between any two consecutive elements must be constant
- The model should be easy to adjust and to generalize for sequences of any length
- The model must be deterministic
The authors of the Transformer architecture suggested using not a separate element for encoding a sequence, but a whole vector with a dimension equal to the dimension of an input sequence element. Here, sine is used to describe even elements of the vector, and cosine is used for odd elements. Please note that the sequence element is not a specific array element, but is a vector describing the state of a separate position. In our case, it is a vector describing one candlestick.
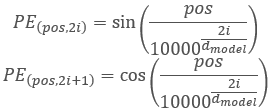 ,
,
where 'pos' is the position of a sequence element, 'i' is the position of the element in the vector of one position element, 'd' is the dimension of the vector of one sequence element.
This solution allows to set positions for each element of the sequence, as well as to determine the distance between them.
Directly in the Transformer architecture, positional coding is outside its scope. It is performed by adding the positional coding tensor to the input sequence tensor before inputting data to the first encoder. Two questions arise:
- Why addition instead of vector concatenation?
- How much will the addition of tensors distort the original data?
Concatenation would increase data dimension and therefore the number of iterations. This would reduce the overall performance of the system. The second aspect of such a solution is that the addition of vectors allows positioning not only the vector of an individual sequence element, but also each element of the vector. Hypothetically, this enables the analysis of dependencies not only between the elements of a sequence, but also between their individual components.
As for data distortion, the neural network knows nothing about the meaning of each element and is trained on data with added encoding, i.e. it does not analyze each element and its position separately. For example, if we see the same doji in the 2nd and 20th position, then we would probably give preference to the closest one. For a neural network with positional coding, these will be completely different signals and will be processed according to the data accumulated during training.
4. Implementation
Let us consider the implementation of the above solutions. In the previous implementation of the Self-Attention algorithm, the dimension used for Queries and Keys vectors was similar to the input sequence. Therefore, I first of all rebuilt the algorithm to train one matrix.
4.1. Eliminating Keys Tensor
The practical solution is quite simple. In the CNeuronAttentionOCL::feedForward method, I have commented out the call of the similar method of the Key convolutional layer. I have also replaced the Key convolutional layer with the previous neural layer in the Score calculation kernel call. Changes in the method code are highlighted below.
bool CNeuronAttentionOCL::feedForward(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=1; OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,prevLayer.getOutputIndex()); OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,prevLayer.Neurons()); if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size)) { printf("Error of execution kernel Normalize: %d",GetLastError()); return false; } if(!prevLayer.Output.BufferRead()) return false; } //--- if(CheckPointer(Querys)==POINTER_INVALID || !Querys.FeedForward(prevLayer)) return false; //if(CheckPointer(Keys)==POINTER_INVALID || !Keys.FeedForward(prevLayer)) // return false; if(CheckPointer(Values)==POINTER_INVALID || !Values.FeedForward(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_querys,Querys.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_keys,prevLayer.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_score,Scores.GetIndex()); OpenCL.SetArgument(def_k_AttentionScore,def_k_as_dimension,iWindow); if(!OpenCL.Execute(def_k_AttentionScore,1,global_work_offset,global_work_size)) { printf("Error of execution kernel AttentionScore: %d",GetLastError()); return false; } if(!Scores.BufferRead()) return false; } //--- Further code has no changes
Similar changes have been implemented in the back propagation method CNeuronAttentionOCL::calcInputGradients. Pay attention that since the first portion of error gradients is written to the previous layer buffer earlier, then the gradient accumulation process starts earlier. Changes are highlighted in the below code.
bool CNeuronAttentionOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false; //--- if(!FF2.calcInputGradients(FF1)) return false; if(!FF1.calcInputGradients(AttentionOut)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,Gradient.GetIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,0.5); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(AttentionOut.getGradient(temp)<=0) return false; } //--- { uint global_work_offset[2]={0,0}; uint global_work_size[2]; global_work_size[0]=iUnits; global_work_size[1]=iWindow; OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_gradient,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_keys,prevLayer.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_keys_g,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_querys,Querys.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_querys_g,Querys.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_values,Values.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_values_g,Values.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_scores,Scores.GetIndex()); if(!OpenCL.Execute(def_k_AttentionGradients,2,global_work_offset,global_work_size)) { printf("Error of execution kernel AttentionGradients: %d",GetLastError()); return false; } double temp[]; if(Querys.getGradient(temp)<=0) return false; } //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,1.0); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(AttentionOut.getGradient(temp)<=0) return false; } //--- if(!Querys.calcInputGradients(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,1.0); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(AttentionOut.getGradient(temp)<=0) return false; } ////--- // if(!Keys.calcInputGradients(prevLayer)) // return false; ////--- // { // uint global_work_offset[1]={0}; // uint global_work_size[1]; // global_work_size[0]=iUnits; // OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); // OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); // OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex()); // OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); // OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,1.0); // if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) // { // printf("Error of execution kernel MatrixSum: %d",GetLastError()); // return false; // } // double temp[]; // if(AttentionOut.getGradient(temp)<=0) // return false; // } //--- Further code has no changes
I have also commented out the update of weights of the Key convolutional layer in the CNeuronAttentionOCL::updateInputWeights method, as well as the declaration of this object in general.
The full code of all methods and functions is available in the attachment.
4.2. Multi-Head Attention Class
Construction of Multi-Head Attention is implemented in a separate class CNeuronMHAttentionOCL, based on the CNeuronAttentionOCL parent class. In the protected block, declare additional instances of convolutional layers Querys and Values, in accordance with the number of attention heads. Four heads are used in the example. Also, add the Scores buffer and the fully connected AttentionOut layer for each attention head. In addition, we need a fully connected layer to concatenate data from attention heads - AttentionConcatenate - and a convolutional layer Weights0, which would allow to imitate weighted voting and to reduce the dimension of the results tensor.
class CNeuronMHAttentionOCL : public CNeuronAttentionOCL { protected: CNeuronConvOCL *Querys2; ///< Convolution layer for Querys Head 2 CNeuronConvOCL *Querys3; ///< Convolution layer for Querys Head 3 CNeuronConvOCL *Querys4; ///< Convolution layer for Querys Head 4 CNeuronConvOCL *Values2; ///< Convolution layer for Values Head 2 CNeuronConvOCL *Values3; ///< Convolution layer for Values Head 3 CNeuronConvOCL *Values4; ///< Convolution layer for Values Head 4 CBufferDouble *Scores2; ///< Buffer for Scores matrix Head 2 CBufferDouble *Scores3; ///< Buffer for Scores matrix Head 3 CBufferDouble *Scores4; ///< Buffer for Scores matrix Head 4 CNeuronBaseOCL *AttentionOut2; ///< Layer of Self-Attention Out CNeuronBaseOCL *AttentionOut3; ///< Layer of Self-Attention Out CNeuronBaseOCL *AttentionOut4; ///< Layer of Self-Attention Out CNeuronBaseOCL *AttentionConcatenate;///< Layer of Concatenate Self-Attention Out CNeuronConvOCL *Weights0; ///< Convolution layer for Weights0 //--- virtual bool feedForward(CNeuronBaseOCL *prevLayer); ///< Feed Forward method.@param prevLayer Pointer to previous layer. virtual bool updateInputWeights(CNeuronBaseOCL *prevLayer); ///< Method for updating weights.@param prevLayer Pointer to previous layer. /// Method to transfer gradients inside Head Self-Attention virtual bool calcHeadGradient(CNeuronConvOCL *query, CNeuronConvOCL *value, CBufferDouble *score, CNeuronBaseOCL *attention, CNeuronBaseOCL *prevLayer); public: /** Constructor */CNeuronMHAttentionOCL(void){}; /** Destructor */~CNeuronMHAttentionOCL(void); virtual bool Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl, uint window, uint units_count, ENUM_OPTIMIZATION optimization_type); ///< Method of initialization class.@param[in] numOutputs Number of connections to next layer.@param[in] myIndex Index of neuron in layer.@param[in] open_cl Pointer to #COpenCLMy object.@param[in] window Size of in/out window and step.@param[in] units_countNumber of neurons.@param[in] optimization_type Optimization type (#ENUM_OPTIMIZATION)@return Boolean result of operations. virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); ///< Method to transfer gradients to previous layer @param[in] prevLayer Pointer to previous layer. //--- virtual int Type(void) const { return defNeuronMHAttentionOCL; }///< Identificator of class.@return Type of class //--- methods for working with files virtual bool Save(int const file_handle); ///< Save method @param[in] file_handle handle of file @return logical result of operation virtual bool Load(int const file_handle); ///< Load method @param[in] file_handle handle of file @return logical result of operation };
The set of class methods rewrites the virtual methods of the parent class. Probably, it can already be called standard. The only exception is the calcHeadGradient method describing error gradient propagation iterations, which are repeated for each head.
Leave the class constructor empty and move the initialization of new objects to the Init initialization method. In the class destructor, implement the deletion of object instances that have been created by this class and declared in the "protected" block.
CNeuronMHAttentionOCL::~CNeuronMHAttentionOCL(void) { if(CheckPointer(Querys2)!=POINTER_INVALID) delete Querys2; if(CheckPointer(Querys3)!=POINTER_INVALID) delete Querys3; if(CheckPointer(Querys4)!=POINTER_INVALID) delete Querys4; if(CheckPointer(Values2)!=POINTER_INVALID) delete Values2; if(CheckPointer(Values3)!=POINTER_INVALID) delete Values3; if(CheckPointer(Values4)!=POINTER_INVALID) delete Values4; if(CheckPointer(Scores2)!=POINTER_INVALID) delete Scores2; if(CheckPointer(Scores3)!=POINTER_INVALID) delete Scores3; if(CheckPointer(Scores4)!=POINTER_INVALID) delete Scores4; if(CheckPointer(Weights0)!=POINTER_INVALID) delete Weights0; if(CheckPointer(AttentionOut2)!=POINTER_INVALID) delete AttentionOut2; if(CheckPointer(AttentionOut3)!=POINTER_INVALID) delete AttentionOut3; if(CheckPointer(AttentionOut4)!=POINTER_INVALID) delete AttentionOut4; if(CheckPointer(AttentionConcatenate)!=POINTER_INVALID) delete AttentionConcatenate; }
The Init method is built by analogy with the parent class method. At the beginning of the method, call the relevant method of the parent class.
bool CNeuronMHAttentionOCL::Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint window,uint units_count,ENUM_OPTIMIZATION optimization_type) { if(!CNeuronAttentionOCL::Init(numOutputs,myIndex,open_cl,window,units_count,optimization_type)) return false;
Then, initialize instances of Querys convolution layer instances. Please note that we initialize objects starting from the second head, since instances of all objects for the first head are initialized in the parent class.
if(CheckPointer(Querys2)==POINTER_INVALID) { Querys2=new CNeuronConvOCL(); if(CheckPointer(Querys2)==POINTER_INVALID) return false; if(!Querys2.Init(0,6,open_cl,window,window,window,units_count,optimization_type)) return false; Querys2.SetActivationFunction(None); } //--- if(CheckPointer(Querys3)==POINTER_INVALID) { Querys3=new CNeuronConvOCL(); if(CheckPointer(Querys3)==POINTER_INVALID) return false; if(!Querys3.Init(0,7,open_cl,window,window,window,units_count,optimization_type)) return false; Querys3.SetActivationFunction(None); } //--- if(CheckPointer(Querys4)==POINTER_INVALID) { Querys4=new CNeuronConvOCL(); if(CheckPointer(Querys4)==POINTER_INVALID) return false; if(!Querys4.Init(0,8,open_cl,window,window,window,units_count,optimization_type)) return false; Querys4.SetActivationFunction(None); }
Similarly initialize class instances for Values, Scores for AttentionOut.
if(CheckPointer(Values2)==POINTER_INVALID) { Values2=new CNeuronConvOCL(); if(CheckPointer(Values2)==POINTER_INVALID) return false; if(!Values2.Init(0,9,open_cl,window,window,window,units_count,optimization_type)) return false; Values2.SetActivationFunction(None); } //--- if(CheckPointer(Values3)==POINTER_INVALID) { Values3=new CNeuronConvOCL(); if(CheckPointer(Values3)==POINTER_INVALID) return false; if(!Values3.Init(0,10,open_cl,window,window,window,units_count,optimization_type)) return false; Values3.SetActivationFunction(None); } //--- if(CheckPointer(Values4)==POINTER_INVALID) { Values4=new CNeuronConvOCL(); if(CheckPointer(Values4)==POINTER_INVALID) return false; if(!Values4.Init(0,11,open_cl,window,window,window,units_count,optimization_type)) return false; Values4.SetActivationFunction(None); } //--- if(CheckPointer(Scores2)==POINTER_INVALID) { Scores2=new CBufferDouble(); if(CheckPointer(Scores2)==POINTER_INVALID) return false; } if(!Scores2.BufferInit(units_count*units_count,0.0)) return false; if(!Scores2.BufferCreate(OpenCL)) return false; //--- if(CheckPointer(Scores3)==POINTER_INVALID) { Scores3=new CBufferDouble(); if(CheckPointer(Scores3)==POINTER_INVALID) return false; } if(!Scores3.BufferInit(units_count*units_count,0.0)) return false; if(!Scores3.BufferCreate(OpenCL)) return false; //--- if(CheckPointer(Scores4)==POINTER_INVALID) { Scores4=new CBufferDouble(); if(CheckPointer(Scores4)==POINTER_INVALID) return false; } if(!Scores4.BufferInit(units_count*units_count,0.0)) return false; if(!Scores4.BufferCreate(OpenCL)) return false; //--- if(CheckPointer(AttentionOut2)==POINTER_INVALID) { AttentionOut2=new CNeuronBaseOCL(); if(CheckPointer(AttentionOut2)==POINTER_INVALID) return false; if(!AttentionOut2.Init(0,12,open_cl,window*units_count,optimization_type)) return false; AttentionOut2.SetActivationFunction(None); } //--- if(CheckPointer(AttentionOut3)==POINTER_INVALID) { AttentionOut3=new CNeuronBaseOCL(); if(CheckPointer(AttentionOut3)==POINTER_INVALID) return false; if(!AttentionOut3.Init(0,13,open_cl,window*units_count,optimization_type)) return false; AttentionOut3.SetActivationFunction(None); } //--- if(CheckPointer(AttentionOut4)==POINTER_INVALID) { AttentionOut4=new CNeuronBaseOCL(); if(CheckPointer(AttentionOut4)==POINTER_INVALID) return false; if(!AttentionOut4.Init(0,14,open_cl,window*units_count,optimization_type)) return false; AttentionOut4.SetActivationFunction(None); }
Initialize the layer for data concatenation AttentionConcatenate. This is a fully connected layer which will only be used for data transmission. Therefore, the number of outgoing connections is equal to "0". The layer size must be enough to store output data of all four attention heads. Indicate the number of neurons in the layer equal to the product of four windows of the output layer of one head by the number of elements in the sequence.
if(CheckPointer(AttentionConcatenate)==POINTER_INVALID) { AttentionConcatenate=new CNeuronBaseOCL(); if(CheckPointer(AttentionConcatenate)==POINTER_INVALID) return false; if(!AttentionConcatenate.Init(0,15,open_cl,4*window*units_count,optimization_type)) return false; AttentionConcatenate.SetActivationFunction(None); }
At the end of the method, initialize the Weights0 convolutional layer. The purpose of the layer is to select an optimal strategy based on the data received from all attention heads. The dimension of the output data will be reduced to the dimension of the original data which are input to the Multi-Head Attention block. When initializing a layer, indicate the size of the input window and step equal to four data windows of the previous layer, and the size of the output window equal to the data window of the previous layer.
if(CheckPointer(Weights0)==POINTER_INVALID) { Weights0=new CNeuronConvOCL(); if(CheckPointer(Weights0)==POINTER_INVALID) return false; if(!Weights0.Init(0,16,open_cl,4*window,4*window,window,units_count,optimization_type)) return false; Weights0.SetActivationFunction(None); } //--- return true; }
The full code of all methods and functions is available in the attachment.
4.3. Feed-forward
The feed-forward algorithm has been mainly constructed using the earlier created OpenCL program. The only exception is the creation of a kernel concatenating the data of 4 tensors from each attention head into a single tensor. The kernel receives in parameters the following: pointers to data buffers and each buffer window sizes, as well as a pointer to the results tensor. The detailed window sizes by input data buffers have been added to allow concatenation of tensors of different sizes with different window sizes.
__kernel void ConcatenateBuffers(__global double *input1, int window1, __global double *input2, int window2, __global double *input3, int window3, __global double *input4, int window4, __global double *output)
In the kernel body, data is copied from input arrays to the output array element by element. The algorithm is quite simple, so I think the attached code is easy to understand.
In the CNeuronMHAttentionOCL class, the feed forward is implemented in the feedForward method. At the beginning of the method, check the validity of the received link to the previous layer and normalize the input data.
bool CNeuronMHAttentionOCL::feedForward(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=1; OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,prevLayer.getOutputIndex()); OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,prevLayer.Neurons()); if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size)) { printf("Error of execution kernel Normalize: %d",GetLastError()); return false; } if(!prevLayer.Output.BufferRead()) return false; }
Then call appropriate convolutional layer methods and recalculate the values of the Querys and Values tensors for all attention heads.
if(CheckPointer(Querys)==POINTER_INVALID || !Querys.FeedForward(prevLayer)) return false; if(CheckPointer(Querys2)==POINTER_INVALID || !Querys2.FeedForward(prevLayer)) return false; if(CheckPointer(Querys3)==POINTER_INVALID || !Querys3.FeedForward(prevLayer)) return false; if(CheckPointer(Querys4)==POINTER_INVALID || !Querys4.FeedForward(prevLayer)) return false; if(CheckPointer(Values)==POINTER_INVALID || !Values.FeedForward(prevLayer)) return false; if(CheckPointer(Values2)==POINTER_INVALID || !Values2.FeedForward(prevLayer)) return false; if(CheckPointer(Values3)==POINTER_INVALID || !Values3.FeedForward(prevLayer)) return false; if(CheckPointer(Values4)==POINTER_INVALID || !Values4.FeedForward(prevLayer)) return false;
Next, recalculate the attention for each head. The algorithm is similar to the parent class described in the article 8. Below is the code for one attention head. Code for other heads is similar, only pointers to the objects of the appropriate attention head are similar.
//--- Scores Head 1 { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_querys,Querys.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_keys,prevLayer.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_score,Scores.GetIndex()); OpenCL.SetArgument(def_k_AttentionScore,def_k_as_dimension,iWindow); if(!OpenCL.Execute(def_k_AttentionScore,1,global_work_offset,global_work_size)) { printf("Error of execution kernel AttentionScore: %d",GetLastError()); return false; } if(!Scores.BufferRead()) return false; } //--- { uint global_work_offset[2]={0,0}; uint global_work_size[2]; global_work_size[0]=iUnits; global_work_size[1]=iWindow; OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_scores,Scores.GetIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_inputs,prevLayer.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_values,Values.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_out,AttentionOut.getOutputIndex()); if(!OpenCL.Execute(def_k_AttentionOut,2,global_work_offset,global_work_size)) { printf("Error of execution kernel Attention Out: %d",GetLastError()); return false; } double temp[]; if(!AttentionOut.getOutputVal(temp)) return false; }
After calculating attention for each head, concatenate the results into a single tensor using the previously written kernel.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_ConcatenateMatrix,def_k_conc_input1,AttentionOut.getOutputIndex());
OpenCL.SetArgument(def_k_ConcatenateMatrix,def_k_conc_window1,iWindow);
OpenCL.SetArgumentBuffer(def_k_ConcatenateMatrix,def_k_conc_input2,AttentionOut2.getOutputIndex());
OpenCL.SetArgument(def_k_ConcatenateMatrix,def_k_conc_window2,iWindow);
OpenCL.SetArgumentBuffer(def_k_ConcatenateMatrix,def_k_conc_input3,AttentionOut3.getOutputIndex());
OpenCL.SetArgument(def_k_ConcatenateMatrix,def_k_conc_window3,iWindow);
OpenCL.SetArgumentBuffer(def_k_ConcatenateMatrix,def_k_conc_input4,AttentionOut4.getOutputIndex());
OpenCL.SetArgument(def_k_ConcatenateMatrix,def_k_conc_window4,iWindow);
OpenCL.SetArgumentBuffer(def_k_ConcatenateMatrix,def_k_conc_out,AttentionConcatenate.getOutputIndex());
if(!OpenCL.Execute(def_k_ConcatenateMatrix,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel Concatenate Matrix: %d",GetLastError());
return false;
}
double temp[];
if(!AttentionConcatenate.getOutputVal(temp))
return false;
}
Pass the tensor concatenation result through the Weights0 convolutional layer to reduce the Multi-Head Attention work result size.
if(CheckPointer(Weights0)==POINTER_INVALID || !Weights0.FeedForward(AttentionConcatenate)) return false;
Then, average the obtained result with the data of the previous layer and normalize the result.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,Weights0.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,Weights0.getOutputIndex());
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow);
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,0.5);
if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel MatrixSum: %d",GetLastError());
return false;
}
if(!Output.BufferRead())
return false;
}
//---
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=1;
OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,Weights0.getOutputIndex());
OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,Weights0.Neurons());
if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel Normalize: %d",GetLastError());
return false;
}
double temp[];
if(!Weights0.getOutputVal(temp))
return false;
}
Then, similarly to the parent class, pass the result through the FeedForward block.
if(!FF1.FeedForward(Weights0)) return false; if(!FF2.FeedForward(FF1)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,Weights0.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,FF2.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,Output.GetIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,0.5); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } if(!Output.BufferRead()) return false; } //--- return true; }
The full code of all methods and functions is available in the attachment.
4.4. Feed-backward
The feed-backward process contains two sub-processes: passing the error gradient down one level and updating the weight matrices. Weights are updated using the previously created OpenCL kernels, while for the error back propagation process we need to make some changes.
First of all, we need to propagate the error gradient by attention heads. To execute this function, create the DeconcatenateBuffers kernel. Input to the kernel pointers to buffers for gradient propagation, window sizes for each buffer and a pointer to the buffer of gradients received from the previous iteration.
__kernel void DeconcatenateBuffers(__global double *output1, int window1, __global double *output2, int window2, __global double *output3, int window3, __global double *output4, int window4, __global double *inputs)
At the kernel beginning, define the ordinal number of the sequence element and the first position shift for the original tensor and the first attention head tensor.
{
int n=get_global_id(0);
int shift=n*(window1+window2+window3+window4);
int shift_out=n*window1;
Next, in a loop, move the vector of error gradients for the first attention head.
for(int i=0;i<window1;i++) output1[shift_out+i]=inputs[shift+i];
Once the cycle ends, adjust the position of the pointer in the original tensor and determine the first position shift in the buffer of the second attention head. Then run a data copying cycle for the second attention head. The operations are repeated for each attention head.
//--- Head 2 shift+=window1; shift_out=n*window2; for(int i=0;i<window2;i++) output2[shift_out+i]=inputs[shift+i]; //--- Head 3 shift+=window2; shift_out=n*window3; for(int i=0;i<window3;i++) output3[shift_out+i]=inputs[shift+i]; //--- Head 4 shift+=window3; shift_out=n*window4; for(int i=0;i<window4;i++) output4[shift_out+i]=inputs[shift+i]; }
Later, after calculating the error gradients for each attention head, it is necessary to combine the gradients into a single data buffer on the previous layer of the neural network. Technically, we could use the SumMatrix kernel by adding the gradients of all the attention heads in pairs. But this solution is not optimal in terms of performance. So, let us create another kernel - Sum5Matrix. In kernel parameters, pass pointers to data buffers (5 input and 1 output), the size of the data window and a multiplier (the sum correction factor). Perhaps, I need to explain why there are 5 incoming buffers with 4 attention heads. The fifth buffer is used to pass-through the error gradient to minimize the risk of gradient fading.
__kernel void Sum5Matrix(__global double *matrix1, ///<[in] First matrix __global double *matrix2, ///<[in] Second matrix __global double *matrix3, ///<[in] Third matrix __global double *matrix4, ///<[in] Fourth matrix __global double *matrix5, ///<[in] Fifth matrix __global double *matrix_out, ///<[out] Output matrix int dimension, ///< Dimension of matrix double multiplyer ///< Multiplyer for output )
In the kernel body, define the shift of the first element of the processed vectors in the sequences and start the cycle for summing gradients. The multiplication of the sum of the error gradients by 0.2 allows the values of the transmitted error to be averaged over the previous layer of the neural network. In turn, the multiplier is implemented in parameters intentionally, to enable the selection of its value while tuning the algorithm.
{
const int i=get_global_id(0)*dimension;
for(int k=0;k<dimension;k++)
matrix_out[i+k]=(matrix1[i+k]+matrix2[i+k]+matrix3[i+k]+matrix4[i+k]+matrix5[i+k])*multiplyer;
}
In the CNeuronMHAttentionOCL class, each subprocess receives its method. Error gradient propagation is performed by the calcInputGradients method. The method receives in parameters a pointer to the object of the previous neural network layer. Check the pointer validity at the method beginning.
bool CNeuronMHAttentionOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false;
Then calculate error gradients through the FeedForward block, using appropriate methods of the convolutional layers FF1 and FF2.
if(!FF2.calcInputGradients(FF1)) return false; if(!FF1.calcInputGradients(Weights0)) return false;
Pass the error gradient around the FeedForward block. Save the average error value in the Weights0 layer gradient buffer.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,Weights0.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,Gradient.GetIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,Weights0.getGradientIndex());
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow);
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,0.5);
if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel MatrixSum: %d",GetLastError());
return false;
}
double temp[];
if(Weights0.getGradient(temp)<=0)
return false;
}
Now, it is time for error propagation by attention heads. We need to increase the size of the gradient tensor to the size of the concatenated attention buffer. To do this, pass the error gradient through the Weights0 convolutional layer, by calling the appropriate method of the convolutional layer.
if(!Weights0.calcInputGradients(AttentionConcatenate)) return false;
After receiving a large enough tensor of error gradients, we can distribute the error by the buffers of the attention heads. Use the deconcatenation kernel created above.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_DeconcatenateMatrix,def_k_dconc_output1,AttentionOut.getGradientIndex());
OpenCL.SetArgument(def_k_DeconcatenateMatrix,def_k_dconc_window1,iWindow);
OpenCL.SetArgumentBuffer(def_k_DeconcatenateMatrix,def_k_dconc_output2,AttentionOut2.getGradientIndex());
OpenCL.SetArgument(def_k_DeconcatenateMatrix,def_k_dconc_window2,iWindow);
OpenCL.SetArgumentBuffer(def_k_DeconcatenateMatrix,def_k_dconc_output3,AttentionOut3.getGradientIndex());
OpenCL.SetArgument(def_k_DeconcatenateMatrix,def_k_dconc_window3,iWindow);
OpenCL.SetArgumentBuffer(def_k_DeconcatenateMatrix,def_k_dconc_output4,AttentionOut4.getGradientIndex());
OpenCL.SetArgument(def_k_DeconcatenateMatrix,def_k_dconc_window4,iWindow);
OpenCL.SetArgumentBuffer(def_k_DeconcatenateMatrix,def_k_dconc_inputs,AttentionConcatenate.getGradientIndex());
if(!OpenCL.Execute(def_k_DeconcatenateMatrix,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel Deconcatenate Matrix: %d",GetLastError());
return false;
}
double temp[];
if(AttentionConcatenate.getGradient(temp)<=0)
return false;
}
The calculation of the error gradient inside an attention head is implemented in a separate method calcHeadGradient. Here we call this method for each attention thread.
if(!calcHeadGradient(Querys,Values,Scores,AttentionOut,prevLayer)) return false; if(!calcHeadGradient(Querys2,Values2,Scores2,AttentionOut2,prevLayer)) return false; if(!calcHeadGradient(Querys3,Values3,Scores3,AttentionOut3,prevLayer)) return false; if(!calcHeadGradient(Querys4,Values4,Scores4,AttentionOut4,prevLayer)) return false;
At the end of the method, sum up the error gradients from all attention heads and pass the result to the previous layer of the neural network.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_Matrix5Sum,def_k_sum5_matrix1,AttentionOut.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_Matrix5Sum,def_k_sum5_matrix2,AttentionOut2.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_Matrix5Sum,def_k_sum5_matrix3,AttentionOut3.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_Matrix5Sum,def_k_sum5_matrix4,AttentionOut4.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_Matrix5Sum,def_k_sum5_matrix5,Weights0.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_Matrix5Sum,def_k_sum5_matrix_out,prevLayer.getGradientIndex());
OpenCL.SetArgument(def_k_Matrix5Sum,def_k_sum5_dimension,iWindow);
OpenCL.SetArgument(def_k_Matrix5Sum,def_k_sum5_multiplyer,0.2);
if(!OpenCL.Execute(def_k_Matrix5Sum,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel Matrix5Sum: %d",GetLastError());
return false;
}
double temp[];
if(prevLayer.getGradient(temp)<=0)
return false;
}
//---
return true;
}
Let's have a look at the calcHeadGradient method. The method receives in parameters pointers to inner neural layers 'query', 'value', 'score', 'attention', related to the attention head under consideration, and a pointer to the previous neural layer.
bool CNeuronMHAttentionOCL::calcHeadGradient(CNeuronConvOCL *query,CNeuronConvOCL *value,CBufferDouble *score,CNeuronBaseOCL *attention,CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false;
The method body begins by checking the validity of the pointer to the previous neural layer. To distribute the error gradient over inner layers, call the AttentionInsideGradients kernel, which was discussed in the article 8.
{
uint global_work_offset[2]={0,0};
uint global_work_size[2];
global_work_size[0]=iUnits;
global_work_size[1]=iWindow;
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_gradient,attention.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_keys,prevLayer.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_keys_g,prevLayer.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_querys,query.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_querys_g,query.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_values,value.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_values_g,value.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_scores,score.GetIndex());
if(!OpenCL.Execute(def_k_AttentionGradients,2,global_work_offset,global_work_size))
{
printf("Error of execution kernel AttentionGradients: %d",GetLastError());
return false;
}
double temp[];
if(query.getGradient(temp)<=0)
return false;
}
This example shows training of one matrix, without dividing into 'query' and 'key'. Therefore, previous layer buffers are specified instead of the key layer buffers. In order not to overwrite the error gradient, obtained on the previous layer, when calculating on other inner layers, transfer the data to the AttentionOut tensor of the current attention head. I have not provided a separate tensor for copying data between buffers. This operation was performed using the two matrices addition kernel SumMatrix. Since we have only one matrix, indicate the previous layer in the pointers of both tensors. To avoid duplication of values, use a multiplier of 0.5.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,prevLayer.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,attention.getGradientIndex());
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow);
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,0.5);
if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel MatrixSum: %d",GetLastError());
return false;
}
double temp[];
if(attention.getGradient(temp)<=0)
return false;
}
Next, calculate the error gradient passing through the query layer by calling the corresponding 'query' layer method. The result is summed up with the gradient obtained at the previous iteration. Multiplier equal to 1 is used at this step. The increased gradient will be averaged at the next step.
if(!query.calcInputGradients(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,attention.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,attention.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,1.0); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(attention.getGradient(temp)<=0) return false; }
Again, at the end of the method, calculate the gradient through the 'value' layer and sum up with the previously obtained gradients. The gradient over the attention head as a whole can be averaged by using the multiplier of 0.33.
if(!value.calcInputGradients(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,attention.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,attention.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow+1); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_multiplyer,0.33); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(prevLayer.getGradient(temp)<=0) return false; } //--- return true; }
After recalculating the error gradients, update the weights of all inner layers. In the updateInputWeights method, write a sequential call of the relevant methods of all inner neural layers.
bool CNeuronMHAttentionOCL::updateInputWeights(CNeuronBaseOCL *prevLayer) { if(!Querys.UpdateInputWeights(prevLayer) || !Querys2.UpdateInputWeights(prevLayer) || !Querys3.UpdateInputWeights(prevLayer) || !Querys4.UpdateInputWeights(prevLayer)) return false; //--- if(!Values.UpdateInputWeights(prevLayer) || !Values2.UpdateInputWeights(prevLayer) || !Values3.UpdateInputWeights(prevLayer) || !Values4.UpdateInputWeights(prevLayer)) return false; if(!Weights0.UpdateInputWeights(AttentionConcatenate)) return false; if(!FF1.UpdateInputWeights(Weights0)) return false; if(!FF2.UpdateInputWeights(FF1)) return false; //--- return true; }
The full code of all methods and functions is available in the attachment.
4.5. Changes in the Neural Network Base Classes
After implementing the Multi-Head Attention algorithm, we need to implement Positional Encoder. This process is included in the CNet::feedForward method of the neural network class. Two parameters have been added to the method for its implementation: window and tem. The first one specifies the data window size and the second one is responsible for the need to enable/disable the function.
bool CNet::feedForward(CArrayDouble *inputVals,int window=1,bool tem=true)
The process itself is implemented in the block for feeding input data to the network. First, declare 2 internal variables, pos (position in the sequence) and dim (the ordinal number of the element inside the data window). Determine the ordinal number of the element inside the data window. To do this, use the remainder of dividing the element ordinal number in the source data tensor by the window size. The position in the sequence is determined by the integer result of dividing the element ordinal number in the source data tensor by the window size. Then, when saving the initial data into the tensor of the neural network input done, add the result of the calculation using the formulas indicated in section 3 of this article.
CNeuronBaseOCL *neuron_ocl=current.At(0); double array[]; int total_data=inputVals.Total(); if(ArrayResize(array,total_data)<0) return false; for(int d=0;d<total_data;d++) { int pos=d; int dim=0; if(window>1) { dim=d%window; pos=(d-dim)/window; } array[d]=inputVals.At(d)+(tem ? (dim%2==0 ? sin(pos/pow(10000,(2*dim+1)/(window+1))) : cos(pos/pow(10000,(2*dim+1)/(window+1)))) : 0); } if(!opencl.BufferWrite(neuron_ocl.getOutputIndex(),array,0,0,total_data)) return false;
Now, it is necessary to make some additional changes for the normal functioning of the neural network. Add constants for working with new kernels to the define block.
#define def_k_ConcatenateMatrix 17 ///< Index of the Multi Head Attention Neuron Concatenate Output kernel (#ConcatenateBuffers) #define def_k_conc_input1 0 ///< Matrix of Buffer 1 #define def_k_conc_window1 1 ///< Window of Buffer 1 #define def_k_conc_input2 2 ///< Matrix of Buffer 2 #define def_k_conc_window2 3 ///< Window of Buffer 2 #define def_k_conc_input3 4 ///< Matrix of Buffer 3 #define def_k_conc_window3 5 ///< Window of Buffer 3 #define def_k_conc_input4 6 ///< Matrix of Buffer 4 #define def_k_conc_window4 7 ///< Window of Buffer 4 #define def_k_conc_out 8 ///< Output tensor //--- #define def_k_DeconcatenateMatrix 18 ///< Index of the Multi Head Attention Neuron Deconcatenate Output kernel (#DeconcatenateBuffers) #define def_k_dconc_output1 0 ///< Matrix of Buffer 1 #define def_k_dconc_window1 1 ///< Window of Buffer 1 #define def_k_dconc_output2 2 ///< Matrix of Buffer 2 #define def_k_dconc_window2 3 ///< Window of Buffer 2 #define def_k_dconc_output3 4 ///< Matrix of Buffer 3 #define def_k_dconc_window3 5 ///< Window of Buffer 3 #define def_k_dconc_output4 6 ///< Matrix of Buffer 4 #define def_k_dconc_window4 7 ///< Window of Buffer 4 #define def_k_dconc_inputs 8 ///< Input tensor //--- #define def_k_Matrix5Sum 19 ///< Index of the kernel for calculation Sum of 2 matrix with multiplyer (#SumMatrix) #define def_k_sum5_matrix1 0 ///< First matrix #define def_k_sum5_matrix2 1 ///< Second matrix #define def_k_sum5_matrix3 2 ///< Third matrix #define def_k_sum5_matrix4 3 ///< Fourth matrix #define def_k_sum5_matrix5 4 ///< Fifth matrix #define def_k_sum5_matrix_out 5 ///< Output matrix #define def_k_sum5_dimension 6 ///< Dimension of matrix #define def_k_sum5_multiplyer 7 ///< Multiplyer for output
Add a constant for identifying the new class.
#define defNeuronMHAttentionOCL 0x7888 ///<Multi-Head Attention neuron OpenCL \details Identified class #CNeuronAttentionOCL
In the neural network class constructor, add a new class to the OpenCL class initialization block.
next=Description.At(1); if(next.type==defNeuron || next.type==defNeuronBaseOCL || next.type==defNeuronConvOCL || next.type==defNeuronAttentionOCL || next.type==defNeuronMHAttentionOCL) { opencl=new COpenCLMy(); if(CheckPointer(opencl)!=POINTER_INVALID && !opencl.Initialize(cl_program,true)) delete opencl; }
Add a new type of neurons in the block initializing neurons in the network.
case defNeuronMHAttentionOCL: neuron_attention_ocl=new CNeuronMHAttentionOCL(); if(CheckPointer(neuron_attention_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_attention_ocl.Init(outputs,0,opencl,desc.window,desc.count,desc.optimization)) { delete neuron_attention_ocl; delete temp; return; } neuron_attention_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_attention_ocl)) { delete neuron_attention_ocl; delete temp; return; } neuron_attention_ocl=NULL; break;
Add the declaration of new kernels.
if(CheckPointer(opencl)==POINTER_INVALID) return; //--- create kernels opencl.SetKernelsCount(20); opencl.KernelCreate(def_k_FeedForward,"FeedForward"); opencl.KernelCreate(def_k_CalcOutputGradient,"CalcOutputGradient"); opencl.KernelCreate(def_k_CalcHiddenGradient,"CalcHiddenGradient"); opencl.KernelCreate(def_k_UpdateWeightsMomentum,"UpdateWeightsMomentum"); opencl.KernelCreate(def_k_UpdateWeightsAdam,"UpdateWeightsAdam"); opencl.KernelCreate(def_k_AttentionGradients,"AttentionInsideGradients"); opencl.KernelCreate(def_k_AttentionOut,"AttentionOut"); opencl.KernelCreate(def_k_AttentionScore,"AttentionScore"); opencl.KernelCreate(def_k_CalcHiddenGradientConv,"CalcHiddenGradientConv"); opencl.KernelCreate(def_k_CalcInputGradientProof,"CalcInputGradientProof"); opencl.KernelCreate(def_k_FeedForwardConv,"FeedForwardConv"); opencl.KernelCreate(def_k_FeedForwardProof,"FeedForwardProof"); opencl.KernelCreate(def_k_MatrixSum,"SumMatrix"); opencl.KernelCreate(def_k_Matrix5Sum,"Sum5Matrix"); opencl.KernelCreate(def_k_UpdateWeightsConvAdam,"UpdateWeightsConvAdam"); opencl.KernelCreate(def_k_UpdateWeightsConvMomentum,"UpdateWeightsConvMomentum"); opencl.KernelCreate(def_k_Normilize,"Normalize"); opencl.KernelCreate(def_k_NormilizeWeights,"NormalizeWeights"); opencl.KernelCreate(def_k_ConcatenateMatrix,"ConcatenateBuffers"); opencl.KernelCreate(def_k_DeconcatenateMatrix,"DeconcatenateBuffers");
Add a new class to the dispatcher methods of the CNeuronBaseOCL class. Changes are highlighted in the below code.
bool CNeuronBaseOCL::FeedForward(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: temp=SourceObject; return feedForward(temp); break; } //--- return false; } bool CNeuronBaseOCL::calcHiddenGradients(CObject *TargetObject) { if(CheckPointer(TargetObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; CNeuronAttentionOCL *at=NULL; CNeuronConvOCL *conv=NULL; switch(TargetObject.Type()) { case defNeuronBaseOCL: temp=TargetObject; return calcHiddenGradients(temp); break; case defNeuronConvOCL: conv=TargetObject; temp=GetPointer(this); return conv.calcInputGradients(temp); break; case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: at=TargetObject; temp=GetPointer(this); return at.calcInputGradients(temp); break; } //--- return false; } bool CNeuronBaseOCL::UpdateInputWeights(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: case defNeuronMHAttentionOCL: temp=SourceObject; return updateInputWeights(temp); break; } //--- return false; }
The full code of all methods and functions is available in the attachment.
5. Testing
The Fractal_OCL_AttentionMHTE Expert Advisor has been created for testing the new architecture. This Expert Advisor has been created on the basis of the Fractal_OCL_Attention Expert Advisor from article 8. It differs from the parent EA only in the attention neurons class type and in the use of the mechanism for encoding the position of input data elements.
CArrayObj *Topology=new CArrayObj(); if(CheckPointer(Topology)==POINTER_INVALID) return INIT_FAILED; //--- CLayerDescription *desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuronBaseOCL; desc.optimization=ADAM; desc.activation=TANH; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronConvOCL; desc.window=12; desc.step=12; desc.window_out=36; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- bool result=true; for(int i=0; (i<2 && result); i++) { desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronMHAttentionOCL; desc.window=36; desc.optimization=ADAM; desc.activation=None; result=Topology.Add(desc); } if(!result) { delete Topology; return INIT_FAILED; } //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=TANH; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=TANH; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=3; desc.type=defNeuron; desc.activation=SIGMOID; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; delete Net; Net=new CNet(Topology); delete Topology;
For the purity of the experiment, I tested in parallel two Expert Advisors (Self-Attention and Multi-Head Attention). The testing was performed in the same conditions: EURUSD, H1 timeframe, data of 20 consecutive candlesticks are fed into the network, and training is performed using the history for the last two years, with parameters being updated by the Adam method.
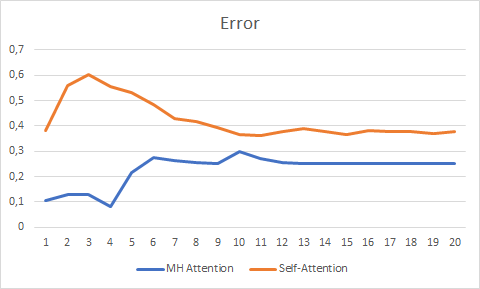
Testing over 20 epochs showed the advantage of Multi-Head Attention which had a smoother error change graph and stabilized with the error of 0.25 against 0.37 for Self-Attention.
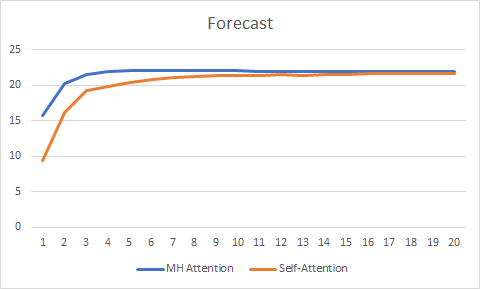
The forecast graph has also shown the better performance of the Multi-Head Attention technology, albeit not so significant.
The full code of all classes and Expert Advisors is available in the attachment.
Conclusion
In this article, we have considered the implementation of the Multi-Head Attention algorithm and have conducted comparative testing against the Single-Head Self-Attention architecture. With equal testing conditions, Multi-Head Attention has generated better results. It should be noted though, that the improvement of the network quality requires extra computational costs.
References
- Neural networks made easy
- Neural networks made easy (Part 2): Network training and testing
- Neural networks made easy (Part 3): Convolutional networks
- Neural networks made easy (Part 4): Recurrent networks
- Neural networks made easy (Part 5): Multithreaded calculations in OpenCL
- Neural networks made easy (Part 6): Experimenting with the neural network learning rate
- Neural networks made easy (Part 7): Adaptive optimization methods
- Neural networks made easy (Part 8): Attention mechanisms
- Neural networks made easy (Part 9): Documenting the work
- Attention Is All You Need
- Multi-Head Attention: Collaborate Instead of Concatenate
Programs Used in the Article
| # | Name | Type | Description |
|---|---|---|---|
| 1 | Fractal_OCL_Attention.mq5 | Expert Advisor | An Expert Advisor with the classification neural network (3 neurons in the output layer) using the Self-Attention mechanism |
| 2 | Fractal_OCL_AttentionMHTE.mq5 | Expert Advisor | An Expert Advisor with the classification neural network (3 neurons in the output layer) using the Multi-Head Attention mechanism |
| 3 | NeuroNet.mqh | Class library | A library of classes for creating a neural network |
| 4 | NeuroNet.cl | Code Base | OpenCL program code library |
| 5 | NN.chm | HTML Help | The converted HTML help file. |
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/8909
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Practical application of neural networks in trading (Part 2). Computer vision
Practical application of neural networks in trading (Part 2). Computer vision
 Developing a self-adapting algorithm (Part II): Improving efficiency
Developing a self-adapting algorithm (Part II): Improving efficiency
 Self-adapting algorithm (Part III): Abandoning optimization
Self-adapting algorithm (Part III): Abandoning optimization
 Brute force approach to pattern search (Part III): New horizons
Brute force approach to pattern search (Part III): New horizons
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Committee of the most advanced GPU-based NS architectures, does Python even have this? )
it's a pity I haven't completely figured out the usual transformers from article 8 yet ))