MetaTrader 5 / 例
English Русский 中文 Español Deutsch Português
preview
ニューラルネットワークが簡単に(第8回): アテンションメカニズム

ニューラルネットワークが簡単に(第8回): アテンションメカニズム

MetaTrader 5 — 例 | 8 2月 2021, 11:51
1 183 0
Dmitriy Gizlyk
Dmitriy Gizlyk

目次

イントロダクション

以前の記事では、ニューラルネットワークを整理するための様々な選択肢を既に検証しました. これには、画像処理アルゴリズムとして使用する畳み込みネットワーク [ 3 ] や，リカレントニューラルネットワーク [4] が含まれており，値だけでなく，ソースデータセット内でのポジションも重要なシーケンスの処理に使用されています．

完全に接続された畳み込み型ニューラルネットワークは、インプットシーケンスサイズが固定されています. リカレントニューラルネットワークは、以前の繰り返しから隠れた状態を転送することで、解析されたシーケンスのわずかな拡張を可能にします. しかし、これらの効果はまた、シーケンスの増加に伴って減少します. 2014年には、機械翻訳を目的とした初の注目メカニズムが発表されました. この仕組みの目的は、原文（文脈）の中で、目的の翻訳語に最も関連性の高いブロックを決定し、強調表示することにありました. このような直感的なアプローチにより、ニューラルネットワークで翻訳されたテキストの品質が大幅に向上しました.


1. アテンションメカニズム

ローソク足のシンボルチャートを分析する際には、トレンドや傾向を定義し、その取引レンジを決定します. それは、全体像からいくつかのオブジェクトを選択し、それらに注意を集中させることを意味します. 我々はオブジェクトが未来の価格行動に影響を与えることを理解しています. このようなアプローチを実装するため、2014年に開発者は、インプットシーケンスと出力シーケンス[ 8 ]の要素間の依存関係を分析して強調する最初のアルゴリズムを提案しました. 提案されたアルゴリズムは「一般化されたアテンションメカニズム」と呼ばれています. 当初、長文翻訳における長期記憶の問題を解決するために、リカレントネットワークを用いた機械翻訳モデルでの利用が提案されました. このアプローチは、以前に検討されたLSTMブロック[4]に基づくリカレントニューラルネットワークの結果を大幅に改善したものです.

リカレントネットワークを用いた古典的な機械翻訳モデルは、エンコーダとデコーダの2つのブロックで構成されています. 第１のブロックは、ソース言語のインプットシーケンスをコンテキストベクトルにエンコードし、第２のブロックは、結果として得られたコンテキストをターゲット言語の単語シーケンスにデコードします. インプットシーケンスの長さが長くなると、文末文の文脈に対する最初の単語の影響力が低下します. その結果、翻訳の質が低下します. LSTMブロックを使用することで、モデルの能力はわずかに向上しましたが、しかし制限されたままでした. 


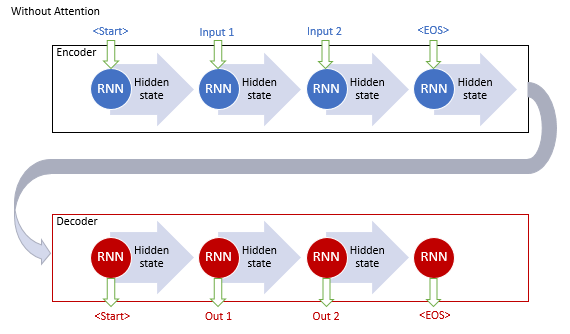
一般的なアテンションメカニズムの支持者は、インプットシーケンスのすべてのリカレントブロックの隠れた状態を蓄積するために、追加のレイヤーを使用することを提案しています. さらに、シーケンス復号化の間、メカニズムは、インプットシーケンスの各要素が出力シーケンスの現在のワードに及ぼす影響を評価し、文脈の最も関連性の高い部分を復号化器に提案しています.


このメカニズム動作アルゴリズムには、以下の繰り返しがあります.

1. エンコーダの隠れた状態を作成し、注目ブロックに蓄積します.

2. 各エンコーダ要素の隠れた状態とデコーダの直近の隠れた状態との間のペアワイズ依存関係を評価します.

3. 得られたスコアを1つのベクトルに結合し，Softmax関数を用いて正規化します．

4. エンコーダのすべての隠れた状態に対応するアライメントスコアを乗算してコンテキストベクトルを計算します.

5. コンテキストベクトルをデコードし、その結果の値をデコーダの前の状態に結合します.

すべての繰り返しは、文末シグナルを受信するまで繰り返されます.

提案されたメカニズムは、限られたインプットシーケンスの長さで問題を解決することを可能にし、リカレントニューラルネットワークを用いた機械翻訳の品質向上を実現しました. このメソッドが人気となり、さらにそのバリエーションが作成されました. 2012年には、彼の論文[ 9 ]の中でMinh-Thang Luongは、注意法の新しいバリエーションを提案しました. 新しいアプローチとの主な差は、依存度計算に3つの関数を使用していることと、デコーダで注目メカニズムを使用している点です.

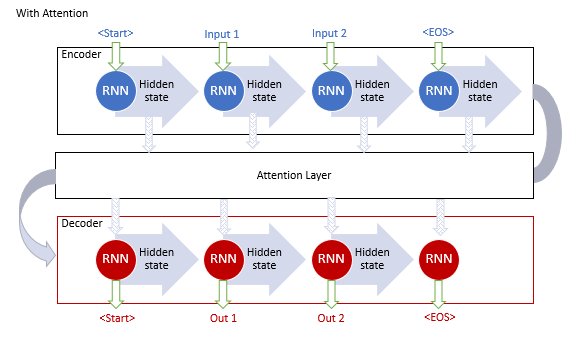
上述のモデルはリカレントブロックを使用していますが，トレーニングに計算コストがかかります． 2017年6月には、記事[ 10 ]で別のバリエーションが提案されています. トランスフォーマー・ニューラルネットワークの新しいアーキテクチャで、リカレント・ブロックを使用せず、新しいセルフ・アテンション・アルゴリズムを使用していました. 前述のアルゴリズムとは異なり、セルフアテンションは1つのシーケンス内のペアワイズ依存性を分析します. トランスフォーマーは、より良い結果のテストを示しました. 現在、このモデルとその派生モデルは、GPT-2やGPT-3など多くのモデルで使用されています. ここでは、セルフアテンションのアルゴリズムをもう少し詳しく考えてみましょう. 

2. セルフアテンションアルゴリズム

トランスのアーキテクチャは、同様のアーキテクチャを持つシーケンシャル・エンコーダーとデコーダー・ブロックをベースにします. 各ブロックは、異なる加重行列を有する複数の同一の層を含みます.

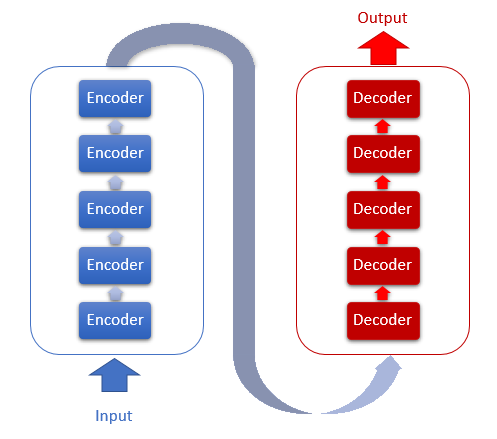
各エンコーダ層には、2つの内部層があります.セルフアテンションとフィードフォワードです. フィードフォワード層は、内層にReLU活性化関数を有するニューロンの完全に接続された2つの層を含みます. 各レイヤはシーケンスのすべての要素に同じ加重で適用され、並列スレッドでシーケンスのすべての要素について同時に独立した計算を行うことができます.

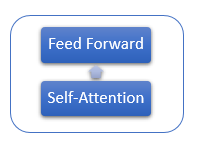
デコーダ層は似たような構造がありますが、インプットシーケンスと出力シーケンス間の依存性を分析するセルフアテンションを追加します.


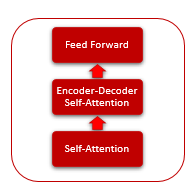
セルフアテンションメカニズム自体は、シーケンスの各要素に対して適用される繰り返し動作を含みます.

1. まず、クエリ、キー、値のベクトルを計算します. ベクトルは、シーケンスの各要素に対応する行列ＷＱ、ＷＫ、ＷＶを乗算することによって得られます.

2. 次に、シーケンスの要素間のペアワイズ依存性を決定します. これを行うには、Query ベクトルにシーケンスの全要素の Key ベクトルを乗算します. この繰り返しは、シーケンス内の各要素のクエリーベクトルに対して繰り返されます. この繰り返しの結果、N*NサイズのScore行列が得られます.

3. 次のステップは、結果の値をKeyベクトル次元の平方根で除算し、各QueryのコンテキストでSoftmax関数で正規化することです. このようにして、配列の要素間のペアワイズ相互依存性の係数が得られます.

4. 各値ベクトルに対応する相互依存係数を乗算して、調整された要素値を得ます. この繰り返しの目的は、関連する要素に焦点を当て、無関係な値の影響を減らすことです.

5. 次に、各要素の調整済みの値ベクトルをすべて合計します. この操作の結果は、自己注目層の出力値のベクトルとなります.

各レイヤの繰り返しの結果はインプットシーケンスに加えられ，式を用いて正規化されます．


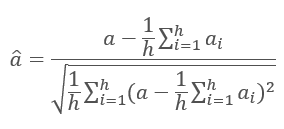
ニューラルネットワーク層の正規化については、記事[ 11 ]でより詳細に考察されています. 

3. 実装

実装では、セルフアテンションのメカニズムを使用することをお勧めします. 実装の選択肢を考えてみましょう.

3.1. コンボリューション層のアップグレード

セルフアテンションアルゴリズムの最初の動作である、クエリ、キー、値のベクトルを計算することから始めます. 解析された配列の各バーの特徴を含むデータマトリックスを入力します. 1つのローソク足の特徴を1つずつ取り、加重行列を掛け合わせてベクトルを求めます. これは[3]の記事で考えた畳み込みレイヤーに似ています. ただし、この場合の出力は数値ではなく、固定サイズのベクトルです. この問題を解決するために、ニューラルネットワークの畳み込み層の動作を担当するCNeuronConvOCLクラスをアップグレードしてみましょう. 出力ベクトルのサイズを格納する変数 iWindowOut を追加します. クラスメソッドの適切な変更を実装します.

class CNeuronConvOCL    :  public CNeuronProofOCL
  {
protected:
   uint              iWindowOut;
//---
   CBufferDouble     *WeightsConv;
   CBufferDouble     *DeltaWeightsConv;
   CBufferDouble     *FirstMomentumConv;
   CBufferDouble     *SecondMomentumConv;
//---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronConvOCL(void) :   iWindowOut(1) {  activation=LReLU;   }
                    ~CNeuronConvOCL(void);
   virtual bool      Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint window, uint step, uint window_out, uint units_count, ENUM_OPTIMIZATION optimization_type);
//---
   virtual bool      SetGradientIndex(int index)   {  return Gradient.BufferSet(index);   }
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);
   virtual int       Type(void)   const   {  return defNeuronConvOCL;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
  };

OpenCL カーネル FeedForwardConv では、出力ベクトルのサイズを取得するためのパラメータを追加します. また、畳み込みレイヤの出力において、一般ベクトルの出力ベクトルの処理済みセグメントのオフセットの計算を追加し、出力レイヤの要素を介して追加のループを実装します.

__kernel void FeedForwardConv(__global double *matrix_w,
                              __global double *matrix_i,
                              __global double *matrix_o,
                              int inputs, int step,
                              int window_in, int window_out,
                              uint activation)
  {
   int i=get_global_id(0);
   int w_in=window_in;
   int w_out=window_out;
   double sum=0.0;
   double4 inp, weight;
   int shift_out=w_out*i;
   int shift_in=step*i;
   for(int out=0;out<w_out;out++)
     {
      int shift=(w_in+1)*out;
      int stop=(w_in<=(inputs-shift_in) ? w_in : (inputs-shift_in));
      for(int k=0; k<=stop; k=k+4)
        {
         switch(stop-k)
           {
            case 0:
              inp=(double4)(1,0,0,0);
              weight=(double4)(matrix_w[shift+k],0,0,0);
              break;
            case 1:
              inp=(double4)(matrix_i[shift_in+k],1,0,0);
              weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],0,0);
              break;
            case 2:
              inp=(double4)(matrix_i[shift_in+k],matrix_i[shift_in+k+1],1,0);
              weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],matrix_w[shift+k+2],0);
              break;
            case 3:
              inp=(double4)(matrix_i[shift_in+k],matrix_i[shift_in+k+1],matrix_i[shift_in+k+2],1);
              weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],matrix_w[shift+k+2],matrix_w[shift+k+3]);
              break;
            default:
              inp=(double4)(matrix_i[shift_in+k],matrix_i[shift_in+k+1],matrix_i[shift_in+k+2],matrix_i[shift_in+k+3]);
              weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],matrix_w[shift+k+2],matrix_w[shift+k+3]);
              break;
           }
         sum+=dot(inp,weight);
        }
      switch(activation)
        {
         case 0:
           sum=tanh(sum);
           break;
         case 1:
           sum=1/(1+exp(-clamp(sum,-50.0,50.0)));
           break;
         case 2:
           if(sum<0)
              sum*=0.01;
           break;
         default:
           break;
        }
      matrix_o[out+shift_out]=sum;
     }
  }

このカーネルを呼び出す際には、追加のパラメータを渡すことを有効にすることを忘れないでください.

bool CNeuronConvOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID)
      return false;
   uint global_work_offset[1]={0};
   uint global_work_size[1];
   global_work_size[0]=Output.Total()/iWindowOut;
   OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_w,WeightsConv.GetIndex());
   OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_i,NeuronOCL.getOutputIndex());
   OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_o,Output.GetIndex());
   OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_inputs,NeuronOCL.Neurons());
   OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_step,iStep);
   OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_window_in,iWindow);
   OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffс_window_out,iWindowOut);
   OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_activation,(int)activation);
   if(!OpenCL.Execute(def_k_FeedForwardConv,1,global_work_offset,global_work_size))
     {
      printf("Error of execution kernel FeedForwardProof: %d",GetLastError());
      return false;
     }
//---
   return Output.BufferRead();
  }

同様の変更がカーネルおよびスロープの再計算 (calcInputGradients) および加重行列の更新 (updateInputWeights) のメソッドに実装されました. すべてのメソッドと関数のフルコードは添付ファイルにあります.

3.2. セルフアテンションブロッククラス

では、セルフアテンションメソッド自体の実装に移りましょう. 記述するために、CNeuronAttentionOCLクラスを作成します. すべての操作は各要素に対して繰り返され、独立して実行されるので、操作を現代化された畳み込みレイヤーに移動させてみましょう. アテンション・ブロック内に、畳み込みレイヤー クエリー、キー、値 を作成し、適切なベクトルを作成するとともに、グラデーションを渡して加重行列を更新します. また、FeedForwardブロックは、畳み込み層FF1とFF2を使用して実装されます. Score行列の値はScoresバッファに保存され、注意法の結果は基底クラスAttentionOutの内部ニューロン層に保存されます.

ここでは、注目アルゴリズムの出力と自己注目クラス全体の出力の差に注目してください. 前者は、値ベクトルの値を調整して自己注意アルゴリズムを実行した後に発生し、AttentionOutに保存されます. 2番目のものはFeedForwardの処理後に取得され、基底クラスのOutputバッファに保存されます.

class CNeuronAttentionOCL : public CNeuronBaseOCL
  {
protected:
   CNeuronConvOCL    *Querys;
   CNeuronConvOCL    *Keys;
   CNeuronConvOCL    *Values;
   CBufferDouble     *Scores;
   CNeuronBaseOCL    *AttentionOut;     
   CNeuronConvOCL    *FF1;
   CNeuronConvOCL    *FF2;
//---
   uint              iWindow;
   uint              iUnits;  
//---
   virtual bool      feedForward(CNeuronBaseOCL *prevLayer);
   virtual bool      updateInputWeights(CNeuronBaseOCL *prevLayer);

public:
                     CNeuronAttentionOCL(void) : iWindow(1), iUnits(0) {};
                    ~CNeuronAttentionOCL(void);
   virtual bool      Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl, uint window, uint units_count, ENUM_OPTIMIZATION optimization_type);
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer);
   //---
   virtual int       Type(void)   const   {  return defNeuronAttentionOCL;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
  };

変数iWindowsとiUnitsでは、出力ウィンドウのサイズと出力シーケンスの要素数をそれぞれ保存します.

このクラスはInitメソッドで初期化されます. このメソッドは，パラメータとして，要素の序数，COpenCL オブジェクトへのポインタ，ウィンドウサイズ，要素の数，最適化方法を受け取ります． メソッドの先頭で、親クラスの該当するメソッドを呼び出します.

bool CNeuronAttentionOCL::Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint window,uint units_count,ENUM_OPTIMIZATION optimization_type)
  {
   if(!CNeuronBaseOCL::Init(numOutputs,myIndex,open_cl,units_count*window,optimization_type))
      return false;

次に、クエリー、キー、値のベクトルを計算するための畳み込みネットワーク・クラスのインスタンスを宣言し、初期化します.

//---
   if(CheckPointer(Querys)==POINTER_INVALID)
     {
      Querys=new CNeuronConvOCL();
      if(CheckPointer(Querys)==POINTER_INVALID)
         return false;
      if(!Querys.Init(0,0,open_cl,window,window,window,units_count,optimization_type))
         return false;
      Querys.SetActivationFunction(TANH);
     }
//---
   if(CheckPointer(Keys)==POINTER_INVALID)
     {
      Keys=new CNeuronConvOCL();
      if(CheckPointer(Keys)==POINTER_INVALID)
         return false;
      if(!Keys.Init(0,1,open_cl,window,window,window,units_count,optimization_type))
         return false;
      Keys.SetActivationFunction(TANH);
     }
//---
   if(CheckPointer(Values)==POINTER_INVALID)
     {
      Values=new CNeuronConvOCL();
      if(CheckPointer(Values)==POINTER_INVALID)
         return false;
      if(!Values.Init(0,2,open_cl,window,window,window,units_count,optimization_type))
         return false;
      Values.SetActivationFunction(None);
     }

さらにアルゴリズムの中で、スコアバッファを宣言します. バッファのサイズに注意してください - シーケンス内の要素数と等しい辺を持つ正方行列を格納するのに十分なメモリがある必要があります.

   if(CheckPointer(Scores)==POINTER_INVALID)
     {
      Scores=new CBufferDouble();
      if(CheckPointer(Scores)==POINTER_INVALID)
         return false;
     }
   if(!Scores.BufferInit(units_count*units_count,0.0))
      return false;
   if(!Scores.BufferCreate(OpenCL))
      return false;

また、ニューロンのAttentionOut層を宣言します. このレイヤーは、セルフアテンションの結果を保存するためのバッファとして機能します. 同時に、FeedForwardブロックのインプットレイヤーとして使用します. そのサイズは、ウィンドウの幅と要素数の積です.

   if(CheckPointer(AttentionOut)==POINTER_INVALID)
     {
      AttentionOut=new CNeuronBaseOCL();
      if(CheckPointer(AttentionOut)==POINTER_INVALID)
         return false;
      if(!AttentionOut.Init(0,3,open_cl,window*units_count,optimization_type))
         return false;
      AttentionOut.SetActivationFunction(None);
     }

FeedForwardブロックを実装するために、畳み込みレイヤーの2つのインスタンスを初期化します. 第１のインスタンス（隠れ層）は、２倍幅のウィンドウを出力し、LReLU活性化関数（"漏れ "のあるReLU）を有することに注意してください. 2層目（FF2）の場合は、SetGradientIndexメソッドを使って親クラスのグラデーションバッファに置き換えます. バッファをコピーすることで、データをコピーする必要がなくなります.

   if(CheckPointer(FF1)==POINTER_INVALID)
     {
      FF1=new CNeuronConvOCL();
      if(CheckPointer(FF1)==POINTER_INVALID)
         return false;
      if(!FF1.Init(0,4,open_cl,window,window,window*2,units_count,optimization_type))
         return false;
      FF1.SetActivationFunction(LReLU);
     }
//---
   if(CheckPointer(FF2)==POINTER_INVALID)
     {
      FF2=new CNeuronConvOCL();
      if(CheckPointer(FF2)==POINTER_INVALID)
         return false;
      if(!FF2.Init(0,5,open_cl,window*2,window*2,window,units_count,optimization_type))
         return false;
      FF2.SetActivationFunction(None);
      FF2.SetGradientIndex(Gradient.GetIndex());
     }

メソッドの最後にキーパラメータを保存します.

   iWindow=window;
   iUnits=units_count;
   activation=FF2.Activation();
//---
   return true;
  }

3.3. セルフアテンションフィードフォワード

次に、CNeuronAttentionOCL クラスの feedForward メソッドを考えてみましょう. この方法は、ニューラルネットワークの前の層へのポインタをパラメータとして受け取ります. そこで、まず、受信したポインタの有効性を確認します.

bool CNeuronAttentionOCL::feedForward(CNeuronBaseOCL *prevLayer)
  {
   if(CheckPointer(prevLayer)==POINTER_INVALID)
      return false;

データをさらに処理する前に、インプットデータを正規化します. このステップは、本著者のセルフアテンションメカニズムでは提供されていません. ただし、スコアマトリクスの正規化段階でオーバーフローしないように、テスト結果に基づいて追加しました. データを正規化するために特別なカーネルが作成されました. feedForwardメソッドで呼び出します.

  {
   uint global_work_offset[1]={0};
   uint global_work_size[1];
   global_work_size[0]=1;
   OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,prevLayer.getOutputIndex());
   OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,prevLayer.Neurons());
   if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size))
     {
      printf("Error of execution kernel Normalize: %d",GetLastError());
      return false;
     }
   if(!prevLayer.Output.BufferRead())
      return false;
  }

正規化カーネルの内部を見てみましょう. カーネルの先頭で，正規化されたシーケンスの最初の要素へのオフセットを計算します． そして、正規化された配列の平均値と標準偏差を算出します. カーネルの最後に、バッファ内のデータを更新します. 

__kernel void Normalize(__global double *buffer,
                        int dimension)
  {
   int n=get_global_id(0);
   int shift=n*dimension;
   double mean=0;
   for(int i=0;i<dimension;i++)
      mean+=buffer[shift+i];
   mean/=dimension;
   double variance=0;
   for(int i=0;i<dimension;i++)
      variance+=pow(buffer[shift+i]-mean,2);
   variance=sqrt(variance/dimension);
   for(int i=0;i<dimension;i++)
      buffer[shift+i]=(buffer[shift+i]-mean)/(variance==0 ? 1 : variance);
  }

ソース・データを正規化した後、クエリ、キー、および値のベクトルを計算します. これを行うには，畳み込みレイヤクラスの適切なインスタンスの FeedForward メソッドを呼び出します（このメソッドについては以前に検討しました）．

   if(CheckPointer(Querys)==POINTER_INVALID || !Querys.FeedForward(prevLayer))
      return false;
   if(CheckPointer(Keys)==POINTER_INVALID || !Keys.FeedForward(prevLayer))
      return false;
   if(CheckPointer(Values)==POINTER_INVALID || !Values.FeedForward(prevLayer))
      return false;

Self-Attention アルゴリズムに沿ってさらに進んで、Score マトリクスを計算します. 計算はOpenCLを使ってGPU上で行います. メインプログラムメソッドにカーネルコールを実装します. 呼び出されたスレッドの数は、クラスの単位数と同じです. 各スレッドはそのウィンドウサイズで動作します. 言い換えれば、各スレッドは、1つの要素の自身のクエリベクトルを取り、シーケンスの全要素のキーベクトルと一致させます.

  {
   uint global_work_offset[1]={0};
   uint global_work_size[1];
   global_work_size[0]=iUnits;
   OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_querys,Querys.getOutputIndex());
   OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_keys,Keys.getOutputIndex());
   OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_score,Scores.GetIndex());
   OpenCL.SetArgument(def_k_AttentionScore,def_k_as_dimension,iWindow);
   if(!OpenCL.Execute(def_k_AttentionScore,1,global_work_offset,global_work_size))
     {
      printf("Error of execution kernel AttentionScore: %d",GetLastError());
      return false;
     }
   if(!Scores.BufferRead())
      return false;
  }

カーネルの最初に、'querys' と 'score' 配列を使って初期要素のオフセットを決定します. 得られた値を小さくするための係数を計算します. 値を正規化するときに必要な量を計算するための変数をゼロアウトします. 次に，対応する依存関係を計算しながら，キー行列のすべての要素の上にループを実装します． 検討しているカーネルは、スコア行列の計算と正規化の段階を組み合わせたものであることに注意してください. したがって、クエリベクトルとキーベクトルの積を計算した後、得られた値を係数で割って、得られた値の指数を計算します. 結果として得られた指数は行列に保存され、合計に加算されます. ループの最後に、前のサイクルで保存されたすべての値を計算された指数の和で割る2番目のループを実装します. カーネルの出力には，計算された正規化されたScore行列が含まれます．  

__kernel void AttentionScore(__global double *querys,
                             __global double *keys,
                             __global double *score,
                             int dimension)
  {
   int q=get_global_id(0);
   int shift_q=q*dimension;
   int units=get_global_size(0);
   int shift_s=q*units;
   double koef=sqrt((double)(units*dimension));
   if(koef<1)
      koef=1;
   double sum=0;
   for(int k=0;k<units;k++)
     {
      double result=0;
      int shift_k=k*dimension;
      for(int i=0;i<dimension;i++)
         result+=(querys[shift_q+i]*keys[shift_k+i]);
      result=exp(result/koef);
      score[shift_s+k]=result;
      sum+=result;   
     }
   for(int k=0;k<units;k++)
      score[shift_s+k]/=sum;
  }

引き続き、セルフアテンションアルゴリズムについて考えてみましょう. Score行列を正規化した後，得られた値のValueベクトルを補正し，インプットシーケンス要素の文脈で得られたベクトルを合計する必要があります． 自己注目ブロックの出力では、得られた値がインプットシーケンスに加算されます. 繰り返しはすべて、次のAttentionOutカーネルで結合されます. カーネルコールは、メインプログラムのコードに実装されています. このカーネルは、シーケンスの要素（iUnits）によるものと、各要素の特徴量（iWindow）によるもの2つの方法で、スレッドのセットで実行されることに注意してください. 結果の値は、AttentionOut層の出力バッファに保存されます.

  {
   uint global_work_offset[2]={0,0};
   uint global_work_size[2];
   global_work_size[0]=iUnits;
   global_work_size[1]=iWindow;
   OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_scores,Scores.GetIndex());
   OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_inputs,prevLayer.getOutputIndex());
   OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_values,Values.getOutputIndex());
   OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_out,AttentionOut.getOutputIndex());
   if(!OpenCL.Execute(def_k_AttentionOut,2,global_work_offset,global_work_size))
     {
      printf("Error of execution kernel Attention Out: %d",GetLastError());
      return false;
     }
   double temp[];
   if(!AttentionOut.getOutputVal(temp))
      return false;
  }

カーネル本体では、インプットシーケンスと出力シーケンスのベクトル内の処理された要素のオフセットを決定します. そして、Scoreの積を対応するValueの値で合計するサイクルを整理します. 周期的な繰り返しが完了するとすぐに、ニューラルネットワークの前の層から受信したインプットベクトルに結果の和を追加します. 結果を送信バッファに書き込みます.

__kernel void AttentionOut(__global double *scores,
                         __global double *values,
                         __global double *inputs,
                         __global double *out)
  {
   int units=get_global_size(0);
   int u=get_global_id(0);
   int d=get_global_id(1);
   int dimension=get_global_size(1);
   int shift=u*dimension+d;
   double result=0;
   for(int i=0;i<units;i++)
      result+=scores[u*units+i]*values[i*dimension+d];
   out[shift]=result+inputs[shift];
  }

この時点で、セルフアテンションアルゴリズムは完成したと考えることができます. あとは、上記の方法で結果のデータを正規化するだけです. 違うのは正規化バッファだけです.

  {
   uint global_work_offset[1]={0};
   uint global_work_size[1];
   global_work_size[0]=1;
   OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,AttentionOut.getOutputIndex());
   OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,AttentionOut.Neurons());
   if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size))
     {
      printf("Error of execution kernel Normalize: %d",GetLastError());
      return false;
     }
   double temp[];
   if(!AttentionOut.getOutputVal(temp))
      return false;
  }

さらに、トランスフォーマーエンコーダアルゴリズムに従って、シーケンスの各要素を、１つの隠れ層を有する完全に接続されたニューラルネットワークに渡す. この処理では、シーケンスのすべての要素に同じ加重行列が適用されます. この処理を現代化した畳み込みレイヤークラスを使って実装してみました. メソッドコードでは、畳み込みクラスの対応するインスタンスの FeedForward メソッドを順次呼び出します.

   if(!FF1.FeedForward(AttentionOut))
      return false;
   if(!FF2.FeedForward(FF1))
      return false;

フィードフォワード処理を完了するためには、完全に接続されたネットワークパスの結果と自己注目メカニズムの結果を合計する必要があります. そのために、フィードフォワードメソッドの最後に呼び出される2つのベクトルの加算のカーネルを作成しました.

  {
   uint global_work_offset[1]={0};
   uint global_work_size[1];
   global_work_size[0]=iUnits;
   OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getOutputIndex());
   OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,FF2.getOutputIndex());
   OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,Output.GetIndex());
   OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow);
   if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size))
     {
      printf("Error of execution kernel MatrixSum: %d",GetLastError());
      return false;
     }
   if(!Output.BufferRead())
      return false;
  }
//---
   return true;
  }

シンプルなサイクルはカーネルの内部で編成され、インプットベクトル値の要素ごとの合計で構成されます.

__kernel void SumMatrix(__global double *matrix1,
                        __global double *matrix2,
                        __global double *matrix_out,
                        int dimension)
  {
   const int i=get_global_id(0)*dimension;
   for(int k=0;k<dimension;k++)
      matrix_out[i+k]=matrix1[i+k]+matrix2[i+k];
  }

すべてのメソッドと関数のフルコードは添付ファイルにあります.

3.4. セルフアテンションフィードバックワード

フィードフォワードパスに続いてフィードバックワードが行われ、その間に誤差がニューラルネットワークの下位レベルに供給され、最適な結果を選択するために重み行列が調整されます. このクラスは、記事5に記載の親クラスメソッドを使用して、ニューラルネットワークの上部完全接続層から誤差勾配を受信します. 誤差スロープを供給するための更なるメカニズムは、内部アーキテクチャの複雑さに起因する大幅な改善を必要とします.

誤差スロープを内部の畳み込み層とネットワークの前のニューラル層に渡すために、calcInputGradientsメソッドを作成してみましょう. このメソッドは、ニューロンの前の層へのポインタをパラメータとして受け取ります. いつものように、最初に受信したポインタの有効性を確認してください. そして、逆順で、フィードフォワードFF2、FF1ブロックの畳み込み層のメソッドを順次呼び出します. バッファ置換を使っているので、内側のFF2層は親クラスのメソッドを使って次のニューラルネットワーク層から直接誤差スロープを受け取ります.

bool CNeuronAttentionOCL::calcInputGradients(CNeuronBaseOCL *prevLayer)
  {
   if(CheckPointer(prevLayer)==POINTER_INVALID)
      return false;
//---
   if(!FF2.calcInputGradients(FF1))
      return false;
   if(!FF1.calcInputGradients(AttentionOut))
      return false;

フィードフォワードパスの出力では、フィードフォワードと自己注意の結果を合計していますので、誤差スロープも2つの枝に分かれています. したがって、FF1から得られた誤差スロープは、ニューラルネットワークの次の層から得られた誤差スロープと合計されます. ベクトル和算カーネルについては上述したとおりです. そこで、その呼び出しを追加してみましょう.

  {
   uint global_work_offset[1]={0};
   uint global_work_size[1];
   global_work_size[0]=iUnits;
   OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex());
   OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,Gradient.GetIndex());
   OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex());
   OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow);
   if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size))
     {
      printf("Error of execution kernel MatrixSum: %d",GetLastError());
      return false;
     }
   double temp[];
   if(AttentionOut.getGradient(temp)<=0)
      return false;
  }

次のステップでは、エラースロープをクエリ、キー、値に伝搬させます. 誤差スロープはAttentionIsideGradientsカーネル内のベクトルに渡されます. 以下のメソッドでは、2次元のスレッドの集合で呼び出します. 

  {
   uint global_work_offset[2]={0,0};
   uint global_work_size[2];
   global_work_size[0]=iUnits;
   global_work_size[1]=iWindow;
   OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_gradient,AttentionOut.getGradientIndex());
   OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_keys,Keys.getOutputIndex());
   OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_keys_g,Keys.getGradientIndex());
   OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_querys,Querys.getOutputIndex());
   OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_querys_g,Querys.getGradientIndex());
   OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_values,Values.getOutputIndex());
   OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_values_g,Values.getGradientIndex());
   OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_scores,Scores.GetIndex());
   if(!OpenCL.Execute(def_k_AttentionGradients,2,global_work_offset,global_work_size))
     {
      printf("Error of execution kernel AttentionGradients: %d",GetLastError());
      return false;
     }
   double temp[];
   if(Keys.getGradient(temp)<=0)
      return false;
  }

カーネルはパラメータでデータバッファへのポインタを受け取ります. ディメンションはカーネルの開始時に、スレッドの数や実行中のスレッドによって決定されます. そして、補正係数を計算し、シーケンスのすべての要素をループさせます. ループ内では、まず、スロープベクトルに対応するスコアベクトルを乗算することで、値ベクトルの誤差スロープを計算します. 誤差スロープを2で割っていることに注意してください. これは前のステップでまとめてしまったため、誤差が2倍になってしまったからです. これを2で割ると平均値が出てきます.

__kernel void AttentionIsideGradients(__global double *querys,__global double *querys_g,
                                      __global double *keys,__global double *keys_g,
                                      __global double *values,__global double *values_g,
                                      __global double *scores,
                                      __global double *gradient)
  {
   int u=get_global_id(0);
   int d=get_global_id(1);
   int units=get_global_size(0);
   int dimension=get_global_size(1);
   double koef=sqrt((double)(units*dimension));
   if(koef<1)
      koef=1;
//---
   double vg=0;
   double qg=0;
   double kg=0;
   for(int iu=0;iu<units;iu++)
     {
      double g=gradient[iu*dimension+d]/2;
      double sc=scores[iu*units+u];
      vg+=sc*g;

次に、ネストになったループを整理して、Score行列の要素に対するグラデーションを定義します. その後、クエリとキーのベクトルの要素のスロープを計算します. 外部ループの最後に、計算されたグラデーションを対応するグローバルバッファに割り当てます.

//---
      double sqg=0;
      double skg=0;
      for(int id=0;id<dimension;id++)
        {
         sqg+=values[iu*dimension+id]*gradient[u*dimension+id]/2;
         skg+=values[u*dimension+id]*gradient[iu*dimension+id]/2;
        }
      qg+=(scores[u*units+iu]==0 || scores[u*units+iu]==1 ? 0.0001 : scores[u*units+iu]*(1-scores[u*units+iu]))*sqg*keys[iu*dimension+d]/koef;
//---
      kg+=(scores[iu*units+u]==0 || scores[iu*units+u]==1 ? 0.0001 : scores[iu*units+u]*(1-scores[iu*units+u]))*skg*querys[iu*dimension+d]/koef;
     }
   int shift=u*dimension+d;
   values_g[shift]=vg;
   querys_g[shift]=qg;
   keys_g[shift]=kg;
  }

次に、クエリ、キー、値ベクトルからエラースロープを渡さなければなりません. すべてのベクトルは、同じ初期データに異なる行列を掛け合わせて得られるので、誤差スロープも合計しなければならないことに注意してください. エラーグラデーションを蓄積するためのバッファを別途確保していませんでした. しかし、グラデーションを計算する際に値を合計するには、バッファのゼロ化を追跡するなど、コードをさらに複雑にする必要があります. 誤差スロープの計算には既存のメソッドを使い、さらにAttentionOutレイヤーのスロープバッファに値を蓄積していくことにしました.

   if(!Querys.calcInputGradients(prevLayer))
      return false;
//---
  {
   uint global_work_offset[1]={0};
   uint global_work_size[1];
   global_work_size[0]=iUnits;
   OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex());
   OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex());
   OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex());
   OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow);
   if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size))
     {
      printf("Error of execution kernel MatrixSum: %d",GetLastError());
      return false;
     }
   double temp[];
   if(AttentionOut.getGradient(temp)<=0)
      return false;
  }
//---
   if(!Keys.calcInputGradients(prevLayer))
      return false;
//---
  {
   uint global_work_offset[1]={0};
   uint global_work_size[1];
   global_work_size[0]=iUnits;
   OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex());
   OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex());
   OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex());
   OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow);
   if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size))
     {
      printf("Error of execution kernel MatrixSum: %d",GetLastError());
      return false;
     }
   double temp[];
   if(AttentionOut.getGradient(temp)<=0)
      return false;
  }
//---
   if(!Values.calcInputGradients(prevLayer))
      return false;
//---
  {
   uint global_work_offset[1]={0};
   uint global_work_size[1];
   global_work_size[0]=iUnits;
   OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex());
   OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex());
   OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,prevLayer.getGradientIndex());
   OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow+1);
   if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size))
     {
      printf("Error of execution kernel MatrixSum: %d",GetLastError());
      return false;
     }
   double temp[];
   if(prevLayer.getGradient(temp)<=0)
      return false;
  }
//---
  {
   uint global_work_offset[1]={0};
   uint global_work_size[1];
   global_work_size[0]=1;
   OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,prevLayer.getGradientIndex());
   OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,prevLayer.Neurons());
   if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size))
     {
      printf("Error of execution kernel Normalize: %d",GetLastError());
      return false;
     }
   double temp[];
   if(prevLayer.getGradient(temp)<=0)
      return false;
  }
//---
   return true;
  }

誤差スロープを前のレイヤーレベルにフィードした後、updateInputWeightsメソッドで加重行列を修正します. このメソッドはいたってシンプルです. ネストされた畳み込みレイヤーの適切なメソッドを呼び出します.

bool CNeuronAttentionOCL::updateInputWeights(CNeuronBaseOCL *prevLayer)
  {
   if(!Querys.UpdateInputWeights(prevLayer))
      return false;
   if(!Keys.UpdateInputWeights(prevLayer))
      return false;
   if(!Values.UpdateInputWeights(prevLayer))
      return false;
   if(!FF1.UpdateInputWeights(AttentionOut))
      return false;
   if(!FF2.UpdateInputWeights(FF1))
      return false;
//---
   return true;
  }

3.5. ニューラルネットワーク基底クラスの変更

注意すべきブロックを終えました. さて、ニューラルネットワークの基底クラスに追加をしてみましょう. まず最初に、新しいカーネルを扱うための定数を定義ブロックに追加します.

#define def_k_FeedForwardConv    7
#define def_k_ffc_matrix_w       0
#define def_k_ffc_matrix_i       1
#define def_k_ffc_matrix_o       2
#define def_k_ffc_inputs         3
#define def_k_ffc_step           4
#define def_k_ffc_window_in      5
#define def_k_ffс_window_out     6
#define def_k_ffc_activation     7
//---
#define def_k_CalcHiddenGradientConv 8
#define def_k_chgc_matrix_w      0
#define def_k_chgc_matrix_g      1
#define def_k_chgc_matrix_o      2
#define def_k_chgc_matrix_ig     3
#define def_k_chgc_outputs       4
#define def_k_chgc_step          5
#define def_k_chgc_window_in     6
#define def_k_chgc_window_out    7
#define def_k_chgc_activation    8
//---
#define def_k_UpdateWeightsConvMomentum      9
#define def_k_uwcm_matrix_w       0
#define def_k_uwcm_matrix_g       1
#define def_k_uwcm_matrix_i       2
#define def_k_uwcm_matrix_dw      3
#define def_k_uwcm_inputs         4
#define def_k_uwcm_learning_rates 5
#define def_k_uwcm_momentum       6
#define def_k_uwcm_window_in      7
#define def_k_uwcm_window_out     8
#define def_k_uwcm_step           9
//---
#define def_k_UpdateWeightsConvAdam   10
#define def_k_uwca_matrix_w      0
#define def_k_uwca_matrix_g      1
#define def_k_uwca_matrix_i      2
#define def_k_uwca_matrix_m      3
#define def_k_uwca_matrix_v      4
#define def_k_uwca_inputs        5
#define def_k_uwca_l             6
#define def_k_uwca_b1            7
#define def_k_uwca_b2            8
#define def_k_uwca_window_in     9
#define def_k_uwca_window_out    10
#define def_k_uwca_step          11
//---
#define def_k_AttentionScore     11
#define def_k_as_querys          0
#define def_k_as_keys            1
#define def_k_as_score           2
#define def_k_as_dimension       3
//---
#define def_k_AttentionOut       12
#define def_k_aout_scores        0
#define def_k_aout_values        1
#define def_k_aout_inputs        2
#define def_k_aout_out           3
//---
#define def_k_MatrixSum          13
#define def_k_sum_matrix1        0
#define def_k_sum_matrix2        1
#define def_k_sum_matrix_out     2
#define def_k_sum_dimension      3
//---
#define def_k_AttentionGradients 14
#define def_k_ag_querys          0
#define def_k_ag_querys_g        1
#define def_k_ag_keys            2
#define def_k_ag_keys_g          3
#define def_k_ag_values          4
#define def_k_ag_values_g        5
#define def_k_ag_scores          6
#define def_k_ag_gradient        7
//---
#define def_k_Normilize          15
#define def_k_norm_buffer        0
#define def_k_norm_dimension     1

また、ニューロの新しいクラスの定数を追加します.

#define defNeuronAttentionOCL 0x7887

ニューラルネットワークのレイヤーを記述する CLayerDescription クラスに、送信ベクトルウィンドウのニューロンの数を指定するフィールドを追加します.

class CLayerDescription    :  public CObject
  {
public:
                     CLayerDescription(void);
                    ~CLayerDescription(void) {};
   //---
   int               type;
   int               count;
   int               window;
   int               window_out;
   int               step;
   ENUM_ACTIVATION   activation;
   ENUM_OPTIMIZATION optimization;
  };

CNetニューラルネットワーククラスのコンストラクタでは、OpenCLで動作するクラスのインスタンスを初期化するために新しいクラスを追加します.

CNet::CNet(CArrayObj *Description)
  {
   if(CheckPointer(Description)==POINTER_INVALID)
      return;
//---
..........
..........
..........
//---
   next=Description.At(1);
   if(next.type==defNeuron || next.type==defNeuronBaseOCL || next.type==defNeuronConvOCL  || next.type==defNeuronAttentionOCL)
     {
      opencl=new COpenCLMy();
      if(CheckPointer(opencl)!=POINTER_INVALID && !opencl.Initialize(cl_program,true))
         delete opencl;
     }
   else
     {
      if(CheckPointer(opencl)!=POINTER_INVALID)
         delete opencl;
     }

さらにコンストラクタ本体に、注目ニューロンの新しいクラスを初期化するコードを追加します.

      if(CheckPointer(opencl)!=POINTER_INVALID)
        {
         CNeuronBaseOCL *neuron_ocl=NULL;
         CNeuronConvOCL *neuron_conv_ocl=NULL;
         CNeuronAttentionOCL *neuron_attention_ocl=NULL;
         switch(desc.type)
           {
            case defNeuron:
            case defNeuronBaseOCL:
              neuron_ocl=new CNeuronBaseOCL();
              if(CheckPointer(neuron_ocl)==POINTER_INVALID)
                {
                 delete temp;
                 return;
                }
              if(!neuron_ocl.Init(outputs,0,opencl,desc.count,desc.optimization))
                {
                 delete neuron_ocl;
                 delete temp;
                 return;
                }
              neuron_ocl.SetActivationFunction(desc.activation);
              if(!temp.Add(neuron_ocl))
                {
                 delete neuron_ocl;
                 delete temp;
                 return;
                }
              neuron_ocl=NULL;
              break;
            case defNeuronConvOCL:
              neuron_conv_ocl=new CNeuronConvOCL();
              if(CheckPointer(neuron_conv_ocl)==POINTER_INVALID)
                {
                 delete temp;
                 return;
                }
              if(!neuron_conv_ocl.Init(outputs,0,opencl,desc.window,desc.step,desc.window_out,desc.count,desc.optimization))
                {
                 delete neuron_conv_ocl;
                 delete temp;
                 return;
                }
              neuron_conv_ocl.SetActivationFunction(desc.activation);
              if(!temp.Add(neuron_conv_ocl))
                {
                 delete neuron_conv_ocl;
                 delete temp;
                 return;
                }
              neuron_conv_ocl=NULL;
              break;
            case defNeuronAttentionOCL:
              neuron_attention_ocl=new CNeuronAttentionOCL();
              if(CheckPointer(neuron_attention_ocl)==POINTER_INVALID)
                {
                 delete temp;
                 return;
                }
              if(!neuron_attention_ocl.Init(outputs,0,opencl,desc.window,desc.count,desc.optimization))
                {
                 delete neuron_attention_ocl;
                 delete temp;
                 return;
                }
              neuron_attention_ocl.SetActivationFunction(desc.activation);
              if(!temp.Add(neuron_attention_ocl))
                {
                 delete neuron_attention_ocl;
                 delete temp;
                 return;
                }
              neuron_attention_ocl=NULL;
              break;
            default:
              return;
              break;
           }
        }

コンストラクタの最後に新しいカーネルの初期化を追加します.

   if(CheckPointer(opencl)==POINTER_INVALID)
      return;
//--- create kernels
   opencl.SetKernelsCount(16);
   opencl.KernelCreate(def_k_FeedForward,"FeedForward");
   opencl.KernelCreate(def_k_CalcOutputGradient,"CalcOutputGradient");
   opencl.KernelCreate(def_k_CalcHiddenGradient,"CalcHiddenGradient");
   opencl.KernelCreate(def_k_UpdateWeightsMomentum,"UpdateWeightsMomentum");
   opencl.KernelCreate(def_k_UpdateWeightsAdam,"UpdateWeightsAdam");
   opencl.KernelCreate(def_k_AttentionGradients,"AttentionIsideGradients");
   opencl.KernelCreate(def_k_AttentionOut,"AttentionOut");
   opencl.KernelCreate(def_k_AttentionScore,"AttentionScore");
   opencl.KernelCreate(def_k_CalcHiddenGradientConv,"CalcHiddenGradientConv");
   opencl.KernelCreate(def_k_CalcInputGradientProof,"CalcInputGradientProof");
   opencl.KernelCreate(def_k_FeedForwardConv,"FeedForwardConv");
   opencl.KernelCreate(def_k_FeedForwardProof,"FeedForwardProof");
   opencl.KernelCreate(def_k_MatrixSum,"SumMatrix");
   opencl.KernelCreate(def_k_UpdateWeightsConvAdam,"UpdateWeightsConvAdam");
   opencl.KernelCreate(def_k_UpdateWeightsConvMomentum,"UpdateWeightsConvMomentum");
   opencl.KernelCreate(def_k_Normilize,"Normalize");
//---
   return;
  }

CNeuronBaseクラスのディスパッチャメソッドに新しいクラスのニューロンの処理を追加します.

bool CNeuronBaseOCL::FeedForward(CObject *SourceObject)
  {
   if(CheckPointer(SourceObject)==POINTER_INVALID)
      return false;
//---
   CNeuronBaseOCL *temp=NULL;
   switch(SourceObject.Type())
     {
      case defNeuronBaseOCL:
      case defNeuronConvOCL:
      case defNeuronAttentionOCL:
        temp=SourceObject;
        return feedForward(temp);
        break;
     }
//---
   return false;
  }

bool CNeuronBaseOCL::calcHiddenGradients(CObject *TargetObject)
  {
   if(CheckPointer(TargetObject)==POINTER_INVALID)
      return false;
//---
   CNeuronBaseOCL *temp=NULL;
   CNeuronAttentionOCL *at=NULL;
   CNeuronConvOCL *conv=NULL;
   switch(TargetObject.Type())
     {
      case defNeuronBaseOCL:
        temp=TargetObject;
        return calcHiddenGradients(temp);
        break;
      case defNeuronConvOCL:
         conv=TargetObject;
         temp=GetPointer(this);
         return conv.calcInputGradients(temp);
         break;
      case defNeuronAttentionOCL:
         at=TargetObject;
         temp=GetPointer(this);
         return at.calcInputGradients(temp);
         break;
     }
//---
   return false;
  }

すべてのメソッドと関数のフルコードは添付ファイルにあります.

4. テスト

上記のすべての変更が終わったら、ニューラルネットワークに新しいクラスのニューロンを追加して、新しいアーキテクチャをテストすることができます. ニューラルネットワークのアーキテクチャだけが以前のEAとは異なる、テスト用EAFractal_OCL_Attentionを作成しました. 繰り返しになりますが、第１層は、初期データを書き込むための基本的なニューロンで構成されており、各ヒストリー足には12個の特徴量があります. 第2の層は、シグモイド活性化関数と36個のニューロンのアウトゴーイングウィンドウを有する修正畳み込み層として宣言されています. このレイヤは、元のデータの埋め込みと正規化の関数を実行します. 続いて、セルフアテンションメカニズムを備えたエンコーダの2層構造です. ニューロンの3つの完全に接続された層がニューラルネットワークを完成させます.

      CLayerDescription *desc=new CLayerDescription();
      if(CheckPointer(desc)==POINTER_INVALID)
         return INIT_FAILED;
      desc.count=(int)HistoryBars*12;
      desc.type=defNeuronBaseOCL;
      desc.optimization=ADAM;
      desc.activation=TANH;
      if(!Topology.Add(desc))
         return INIT_FAILED;
      //---
      desc=new CLayerDescription();
      if(CheckPointer(desc)==POINTER_INVALID)
         return INIT_FAILED;
      desc.count=(int)HistoryBars;
      desc.type=defNeuronConvOCL;
      desc.window=12;
      desc.step=12;
      desc.window_out=36;
      desc.optimization=ADAM;
      desc.activation=SIGMOID;
      if(!Topology.Add(desc))
         return INIT_FAILED;
      //---
      bool result=true;
      for(int i=0; (i<2 && result); i++)
        {
         desc=new CLayerDescription();
         if(CheckPointer(desc)==POINTER_INVALID)
            return INIT_FAILED;
         desc.count=(int)HistoryBars;
         desc.type=defNeuronAttentionOCL;
         desc.window=36;
         desc.optimization=ADAM;
         desc.activation=None;
         result=Topology.Add(desc);
        }
      if(!result)
        {
         delete Topology;
         return INIT_FAILED;
        }
      //---
      desc=new CLayerDescription();
      if(CheckPointer(desc)==POINTER_INVALID)
         return INIT_FAILED;
      desc.count=200;
      desc.type=defNeuron;
      desc.activation=TANH;
      desc.optimization=ADAM;
      if(!Topology.Add(desc))
         return INIT_FAILED;
      //---
      desc=new CLayerDescription();
      if(CheckPointer(desc)==POINTER_INVALID)
         return INIT_FAILED;
      desc.count=200;
      desc.type=defNeuron;
      desc.activation=TANH;
      desc.optimization=ADAM;
      if(!Topology.Add(desc))
         return INIT_FAILED;
      //---
      desc=new CLayerDescription();
      if(CheckPointer(desc)==POINTER_INVALID)
         return INIT_FAILED;
      desc.count=3;
      desc.type=defNeuron;
      desc.activation=SIGMOID;
      desc.optimization=ADAM;
      if(!Topology.Add(desc))
         return INIT_FAILED;

EAのコード全体は添付ファイルに記載されています.

EAテストは同条件でi=実行しました.EURUSD、H1時間枠、20著書の連続ローソク足のデータをネットワークに投入し、過去2年間のヒストリーを用いてトレーニングを行い、パラメータはアダムメソッドで更新します.

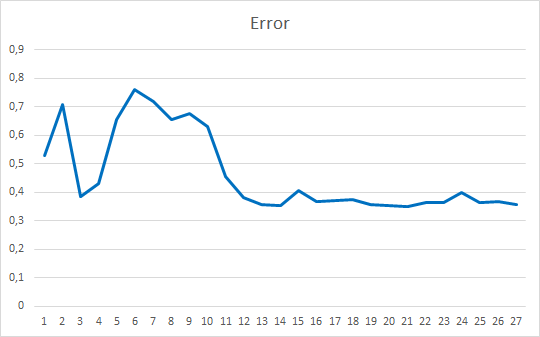
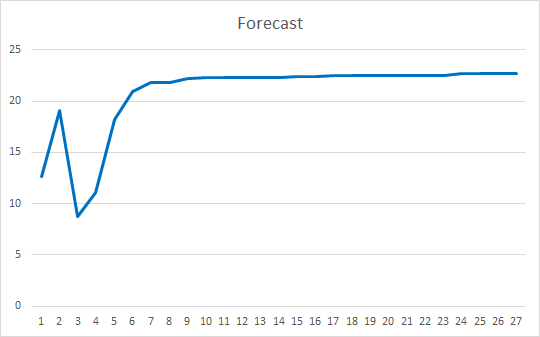
このEAは、ゼロ値を除いて-1から1までのランダムな加重で初期化されました. 25エポックでテストした結果、EAの誤差は35～36%で、ヒット率は22～23%でしました.



結論

今回は、注目のメカニズムについて考えてみました. Self-Attntionブロックを作成し、ヒストリーデータ上での動作をテストしました. 結果として得られたエキスパートアドバイザは、ニューラルネットワーク操作の誤差を減らし、予測結果の "ヒット "という点でスムーズな結果を示しました. 得られた結果から、このアプローチを用いることが可能であることが示されています. しかし、結果を改善するためには追加のタスクが必要です. さらなる開発オプションとして、加重の異なる複数の注目スレッドを並列に使用することを検討することができます. 記事10では、このアプローチを「マルチは注意を払っていた」としています.


レファレンス

  1. ニューラルネットワークが簡単に
  2. ニューラルネットワークが簡単に(パート2): ネットワークトレーニングとテスト
  3. ニューラルネットワークが簡単に（その3）. 畳み込みネットワーク
  4. ニューラルネットワークが簡単に(その4）.リカレントネットワーク
  5. ニューラルネットワークが簡単に (その5). OpenCLでのマルチスレッド計算
  6. ニューラルネットワークが簡単に(その６）.ニューラルネットワークの学習率の実験
  7. ニューラルネットワークが簡単に（その７）．適応的最適化法
  8. 揃えて翻訳する共同学習によるニューラル機械翻訳
  9. アテンションベースのニューラル機械翻訳への効果的なアプローチ
  10. Attention Is All You Need
  11. レイヤの正規化

記事中で使用したプログラム

# 名前 タイプ 詳細
1 Fractal_OCL_Attention.mq5  EA 自己アテンションメカニズムを利用した分類ニューラルネットワーク（出力層に3つのニューロン）を持つEA
2 NeuroNet.mqh クラスライブラリ ニューラルネットワークを作成するためのクラスのライブラリ
3 NeuroNet.cl コードベース OpenCL プログラムコードライブラリ

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/8765

添付されたファイル |
ZIPをダウンロード
MQL5.zip (489.86 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
ニューラルネットワークが簡単に(第9部)：作業の文書化 ニューラルネットワークが簡単に(第9部)：作業の文書化
長い道のりでした。ライブラリ内のコードはどんどん増えてきており、すべてのリンクと依存関係を追跡することが困難になっています。したがって、以前に作成したコードのドキュメントを作成し、新しい手順ごとに更新し続けることをお勧めします。適切に準備された文書化は、作業の整合性を確認するのに役立ちます。
DoEasyライブラリの時系列(第59部): 単一ティックのデータを格納するオブジェクト DoEasyライブラリの時系列(第59部): 単一ティックのデータを格納するオブジェクト
本稿からは、価格データを処理するライブラリ機能を作成します。今日、さらに別のティックで到着したすべての価格データを格納するオブジェクトクラスを作成します。
自己適応アルゴリズムの開発(第I部)：基本的なパターンの検索 自己適応アルゴリズムの開発(第I部)：基本的なパターンの検索
この連載では、ほとんどの市場要因を考慮した自己適応アルゴリズムの開発を示すとともに、これらの状況を体系化してロジックで説明し、取引活動で考慮に入れる方法を示します。非常に単純なアルゴリズムから始めて、徐々に理論を習得し、非常に複雑なプロジェクトに進化していきます。
DoEasyライブラリの時系列(第58部): 指標バッファデータの時系列 DoEasyライブラリの時系列(第58部): 指標バッファデータの時系列
時系列の操作に関するトピックのしめくくりとして、指標バッファに格納されているストレージ、検索、およびデータの並べ替えを整理します。これにより、プログラムでライブラリベースで作成される指標の値に基づいて分析をさらに実行できます。ライブラリのすべてのコレクションクラスの一般的な概念により、対応するコレクションで必要なデータを簡単に見つけることができます。それぞれ、今日作成されたクラスでも同じことが可能です。