取引におけるニューラルネットワーク：シャープネス低減によるTransformerの効率向上(SAMformer)

はじめに

多変量時系列予測は、過去のパターンに基づいて将来の動向を予測するために時系列データを分析する、古典的な機械学習タスクです。特徴量間の相関や長期的な時間依存性のため、特に難易度の高い問題です。この学習課題は、観測値が逐次的に収集される現実世界の応用（例：医療データ、電力消費、株価）でよく見られます。

近年、Transformerベースのアーキテクチャは、自然言語処理やコンピュータビジョンの分野で画期的な性能を達成しています。Transformerは特に系列データの処理に優れており、時系列予測に自然に適合します。しかし、最先端の多変量時系列予測は、依然としてより単純なMLPベースのモデルで達成されることが多いのが現状です。

近年、Transformerを時系列データに適用する研究では、主に二次的な計算コストを削減するためのAttention機構の最適化や、時系列を分解して基礎的なパターンを捉えやすくする方法に焦点が当てられてきました。しかし、論文「SAMformer:Unlocking the Potential of Transformers in Time Series Forecasting with Sharpness-Aware Minimization and Channel-Wise Attention」の著者らは、重要な課題を指摘しています。それは、大規模データが存在しない場合におけるTransformersの学習不安定性です。

コンピュータビジョンや自然言語処理の分野では、Attention行列がエントロピー崩壊やランク崩壊に陥ることが観察されています。これらの問題を緩和するため、いくつかの手法が提案されてきました。しかし、時系列予測においては、Transformerアーキテクチャを過学習させずに効果的に学習させる方法は依然として未解決の問題です。著者らは、学習の不安定性に対処することで、長期の多変量予測においてTransformerの性能を大幅に向上させられることを示そうとしています。これは、従来のTransformerの限界に関する通説に反するものです。

1. SAMformerアルゴリズム

本研究では、多変量システムにおける長期予測に焦点を当てています。長さL（ルックバックウィンドウ）のD次元時系列が与えられたとき、入力データは行列𝐗 ∈ R D×Lとして表されます。目的は、予測区間Hにおける次の値を予測することであり、これを𝐘∈R D×Hと表します。N個の観測からなる学習データセットがあると仮定し、パラメータωを持つ予測モデルf𝝎:RD×L→RD×Lを学習させ、学習データにおける平均二乗誤差(MSE)を最小化することが目標です。

最近の研究では、Transformerは、入力データを直接予測値に射影する単純な線形ニューラルネットワークと同等の性能を示すことが分かっています。この現象を調査するため、SAMformerフレームワークでは、時系列予測の設定を模倣する合成回帰タスクを生成する生成モデルを採用しています。著者らは、ランダムな入力データから時系列の継続部分を生成する線形モデルを用い、出力に少量のノイズを加えています。このプロセスにより、15,000組の入出力ペアが作成され、10,000組を学習用、5,000組を検証用に分割しています。

この生成的アプローチを活用し、SAMformerの著者らは、予測タスクを効率的かつ不要な複雑性なしで処理できるTransformerアーキテクチャを設計しています。そのために、従来のTransformerエンコーダを簡略化し、Self-Attentionブロックとその後の残差接続のみを残しました。FeedForwardブロックの代わりに、次の値を直接予測するための線形層を使用しています。

重要なのは、SAMformerフレームワークではチャネル単位のAttentionを採用している点です。これにより、L>DであるためAttention行列が大幅に小さくなり、過剰パラメータ化のリスクが低減されます。また、データ生成が識別プロセスに従っているため、チャネル単位のAttentionの方が適しています。

このタスクにおけるAttentionの役割を理解するため、著者らは「Random Transformer」というモデルを提案しています。このモデルでは、予測層のみを最適化し、Self-Attentionブロックのパラメータは学習中もランダム初期化のまま固定します。これにより、Transformerは事実上線形モデルとして振る舞うことになります。著者らは、このモデルと、Adam法で最適化したSAMformerモデル、さらに最小二乗解に対応するOracleモデルとの局所最小値を比較し、その結果を（論文中の図として）示しています。

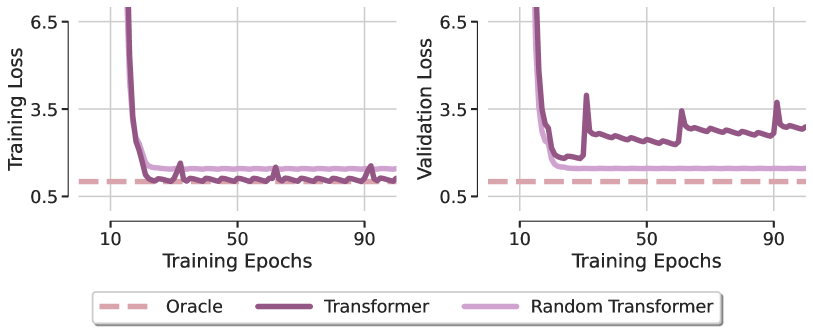
最初の驚くべき発見は、どちらのTransformerモデルも合成回帰タスクの線形依存性を再現できなかったという点です。これは、好条件の設計を持つ単純なアーキテクチャであっても、最適化の過程で明らかな汎化能力の欠如が見られることを示しています。この傾向は、異なるオプティマイザや学習率の設定においても一貫して確認されました。このことから、SAMformerの著者らは、Transformerの限られた汎化能力は主にAttentionモジュール内の学習困難さに起因すると結論づけています。

この現象をより深く理解するために、SAMformerの著者らは学習のさまざまなエポックにおけるAttention行列を可視化しました。その結果、Attention行列は最初のエポック直後にほぼ単位行列と同じ形状を示し、その後ほとんど変化しないことが分かりました。特に、Softmax関数がAttention値間の差を増幅させるため、この傾向が顕著になっていました。この振る舞いはAttentionにおけるエントロピー崩壊の兆候を示しており、結果としてフルランクのAttention行列が生じます。著者らは、これがTransformerの学習硬直性の原因の一つであると指摘しています。

さらに、SAMformerの著者らは、エントロピー崩壊とTransformerの損失ランドスケープの鋭さとの間に関係があることも観察しました。Random Transformerと比較すると、標準のTransformerはより鋭い最小値に収束し、エントロピーも大幅に低くなります（Random TransformerではAttention重みが初期化時に固定されるため、学習中もエントロピーが一定に保たれます）。これらの病理的なパターンは、Transformerが学習中にエントロピー崩壊と鋭い損失ランドスケープという二重の影響を受けることで性能が低下することを示唆しています。

近年の研究では、Transformerの損失ランドスケープが他のアーキテクチャよりも鋭いことが確認されています。これは、特に小規模データセットで学習する際に見られる学習の不安定性や性能の低下を説明する一因となる可能性があります。

これらの課題に対処し、汎化性能と学習の安定性を向上させるために、SAMformerの著者らは2つのアプローチを検討しています。1つ目は、Sharpness-Aware Minimization (SAM)であり、これは次のように学習目的を修正します。

ここで、ρ(>0)はハイパーパラメータを表し、ωはモデルパラメータを表します。

2つ目のアプローチでは、すべての重み行列に対してスペクトル正規化を用いた再パラメータ化を導入し、さらにσReparamと呼ばれる追加の学習可能なスカラーを組み合わせます。

実験結果は、提案手法が目標とする成果を達成する上で有効であることを示しています。特筆すべきは、これはSAM単独で達成されているという点です。というのも、σReparam 手法はAttention行列のエントロピーを増加させたにもかかわらず、最適性能に近づくことができなかったためです。さらに、SAMによって得られたシャープネスは標準的なTransformerと比べて数桁も低くなっており、一方でSAMにおけるAttentionのエントロピーはベースラインのTransformerとほぼ同等で、学習後半にわずかに増加する程度にとどまりました。これは、このシナリオではエントロピー崩壊が無害であることを示しています。

SAMformerフレームワークはさらに、Reversible Instance Normalization(RevIN)を取り入れています。この手法は、時系列データにおける学習時とテスト時の分布変化に対処するうえで有効であることが確認されています。上述の研究が示すように、このモデルはSAMを用いて最適化され、より平坦な局所最小値に誘導されます。結果として、全体としては、著者らの図（原論文の可視化）に示されているように、エンコーダブロックを1つだけ持つシンプルなTransformerモデルとなります。

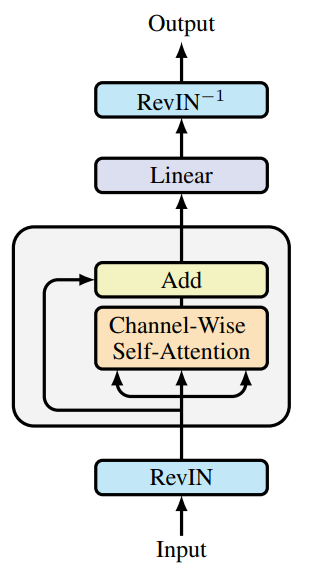
SAMformerは、他のモデルで一般的な空間（または時間）AttentionがL×Lの行列を用いるのとは異なり、D×D行列で表されるチャネル単位のAttentionを保持している点が重要です。この設計には2つの大きな利点があります。

• 特徴量の順列不変性が保たれるため、通常Attention層の前に適用される位置エンコーディングが不要になります。
• 多くの実世界データセットではD≤Lであるため、計算時間とメモリの複雑性が削減されます。

チャネル単位のAttentionは、すべての時系列ステップにおいて各特徴量が他の特徴量に与える平均的な影響を学習します。

2. MQL5での実装

SAMformerフレームワークの理論的側面をカバーした後は、その実際のMQL5による実装に移ります。この段階で重要なのは、モデルで何をどのように実装するのかを明確に定義することです。SAMformerの著者らが提案したコンポーネントを改めて見ていきます。

• Transformerエンコーダを自己注意Self-Attentionブロックと残差接続のみに削減すること
• チャネル単位Attention
• 可逆正規化(RevIN)
• SAM最適化

エンコーダの削減は興味深い点ですが、実際には学習可能パラメータ数の削減が主な価値です。機能的には、元のフレームワークのように、ニューラル層をエンコーダのFeedForwardブロックの一部と呼ぶか、Attentionの後に置かれた予測層と呼ぶかによって、モデルの振る舞いは変わりません。

チャネル単位のAttentionを実装するには、入力データをAttentionブロックに渡す前に転置するだけで十分です。この工程にはモデルの構造的変更は不要です。

Reversible Instance Normalization (RevIN)はすでに馴染みがあります。残る課題は、SAM最適化の実装です。SAMは、損失値が一様に低い領域内にあるパラメータ集合を探索することで動作します。

SAM最適化アルゴリズムはいくつかのステップからなります。まず、順伝播をおこない、モデルパラメータに対する損失の勾配を計算します。次に、この勾配を正規化し、シャープネス係数でスケーリングした上で現在のパラメータに加えます。その後、この摂動を加えたパラメータで再び順伝播をおこない、新しい勾配を計算します。そして、先ほど加えた摂動を引いて元の重みに戻し、最後にSGDまたはAdamといった標準的なオプティマイザでパラメータを更新します。SAMformerの著者らは後者を推奨しています。

重要な点として、SAMformerの著者らはモデル全体で勾配を正規化しています。これは計算負荷が高くなる可能性があります。そのため、モデルパラメータ数を減らすことの意義が高まり、内部層の削減やAttentionヘッド数の削減が実用的な必須要件となります。SAMformerの著者らもこれを実際におこなっています。

一方、私たちの実装では若干異なるアプローチを取ります。具体的には、個々のニューラル層レベルで勾配正規化をおこない、さらに1つのニューロンの出力に寄与する各パラメータグループごとに勾配を別々に正規化します。この実装は、まずプログラムのOpenCL側で新しいカーネルを開発するところから始めます。

2.1 OpenCLプログラムの拡張

これまでの作業からも分かるように、私たちは主に全結合層と畳み込み層という2種類のニューラル層に依存しています。すべてのAttentionモジュールは畳み込み層を用いて構築されており、シーケンス中の個々の要素を重複なく分析・変換するために適用されています。したがって、この2種類の層をSAM最適化で強化することを選びました。OpenCL側では、勾配正規化用と摂動重みω+ε生成用の2つのカーネルを開発します。

まず、全結合層用のカーネルCalcEpsilonWeightsを作成します。このカーネルは4つのデータバッファへのポインタと、シャープネス分散係数を受け取ります。3つのバッファは入力データを保持し、4つ目のバッファは出力結果を格納するために使われます。 

__kernel void CalcEpsilonWeights(__global const float *matrix_w,
                                 __global const float *matrix_g,
                                 __global const float *matrix_i,
                                 __global float *matrix_epsw,
                                 const float rho
                                )
  {
   const size_t inp = get_local_id(0);
   const size_t inputs = get_local_size(0) - 1;
   const size_t out = get_global_id(1);

私たちは、このカーネルを2次元のタスク空間で呼び出し、スレッドを第1次元ごとにグループ化する予定です。カーネル本体内では、まずタスク空間内の全次元における現在の実行スレッドを即座に特定します。

次に、同じワークグループ内のスレッド間でデータをやり取りするため、デバイス上にローカルメモリ配列を宣言します。

   __local float temp[LOCAL_ARRAY_SIZE];
   const int ls = min((int)inputs, (int)LOCAL_ARRAY_SIZE);

次のステップでは、入力および出力の勾配バッファにおける対応する要素同士の積として、各解析対象要素の誤差の勾配を計算します。その後、この結果を対応するパラメータの絶対値でスケーリングします。これにより、層の出力により大きく寄与するパラメータの影響が増幅されます。

   const int shift_w = out * (inputs + 1) + inp;
   const float w =IsNaNOrInf(matrix_w[shift_w],0);
   float grad = fabs(w) * IsNaNOrInf(matrix_g[out],0) * (inputs == inp ? 1.0f : IsNaNOrInf(matrix_i[inp],0));

最後に、結果として得られた勾配のL2ノルムを計算します。これは、ローカルメモリ配列と2回のリダクションループを用いて、ワークグループ内の計算値の二乗和を合計することで行います。これは、以前の実装で用いた手法に従ったものです。

   const int local_shift = inp % ls;
   for(int i = 0; i <= inputs; i += ls)
     {
      if(i <= inp && inp < (i + ls))
         temp[local_shift] = (i == 0 ? 0 : temp[local_shift]) + IsNaNOrInf(grad * grad,0);
      barrier(CLK_LOCAL_MEM_FENCE);
     }
//---
   int count = ls;
   do
     {
      count = (count + 1) / 2;
      if(inp < count)
         temp[inp] += ((inp + count) < inputs ? IsNaNOrInf(temp[inp + count],0) : 0);
      if(inp + count < inputs)
         temp[inp + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

蓄積された合計の平方根が、勾配のL2ノルムを表します。この値を用いて、調整されたパラメータ値を計算します。

   float norm = sqrt(IsNaNOrInf(temp[0],0));
   float epsw = IsNaNOrInf(w * w * grad * rho / (norm + 1.2e-7), w);
//---
   matrix_epsw[shift_w] = epsw;
  }

次に、得られた値を対応するグローバル結果バッファの要素に保存します。

同様の手法で、畳み込み層の初期パラメータ調整をおこなうCalcEpsilonWeightsConvカーネルも構築しています。ただしご存じの通り、畳み込み層には独自の特性があります。一般にパラメータ数は少ないものの、各パラメータは入力データ層の複数の要素と相互作用し、結果バッファの複数の要素の値に寄与します。そのため、各パラメータの勾配は、出力バッファの複数の要素にわたる影響を集約して計算されます。

この畳み込み特有の振る舞いはカーネルのパラメータにも影響します。ここでは、入力シーケンスのサイズと入力ウィンドウのストライドを定義する2つの追加定数が現れます。

__kernel void CalcEpsilonWeightsConv(__global const float *matrix_w,
                                     __global const float *matrix_g,
                                     __global const float *matrix_i,
                                     __global float *matrix_epsw,
                                     const int inputs,
                                     const float rho,
                                     const int step
                                    )
  {
//---
   const size_t inp = get_local_id(0);
   const size_t window_in = get_local_size(0) - 1;
   const size_t out = get_global_id(1);
   const size_t window_out = get_global_size(1);
   const size_t v = get_global_id(2);
   const size_t variables = get_global_size(2);

タスク空間も3次元に拡張します。第1次元は入力データウィンドウに対応し、オフセットで拡張されています。第2次元は畳み込みフィルターの数を表し、第3次元は独立した入力シーケンスの数を示します。これまでと同様に、操作スレッドは第1次元ごとにワークグループにまとめます。

カーネル内では、タスク空間の全次元にわたって現在の実行スレッドを特定します。その後、OpenCLコンテキスト内にローカルメモリ配列を初期化し、ワークグループ内のスレッド間通信を可能にします。

   __local float temp[LOCAL_ARRAY_SIZE];
   const int ls = min((int)(window_in + 1), (int)LOCAL_ARRAY_SIZE);

次に、出力バッファにおけるフィルターごとの要素数を計算し、データバッファ内の対応するオフセットを決定します。

   const int shift_w = (out + v * window_out) * (window_in + 1) + inp;
   const int total = (inputs - window_in + step - 1) / step;
   const int shift_out = v * total * window_out + out;
   const int shift_in = v * inputs + inp;
   const float w = IsNaNOrInf(matrix_w[shift_w], 0);

この時点で、解析対象のパラメータの現在の値をローカル変数に格納します。この最適化により、後続のステップでグローバルメモリへのアクセス回数を減らすことができます。

次の段階では、解析中のパラメータによって影響を受けた出力バッファのすべての要素から、勾配の寄与を集約します。

   float grad = 0;
   for(int t = 0; t < total; t++)
     {
      if(inp != window_in && (inp + t * step) >= inputs)
         break;
      float g = IsNaNOrInf(matrix_g[t * window_out + shift_out],0);
      float i = IsNaNOrInf(inp == window_in ? 1.0f : matrix_i[t * step + shift_in],0);
      grad += IsNaNOrInf(g * i,0);
     }

次に、収集した勾配をパラメータの絶対値でスケーリングします。

   grad *= fabs(w);

その後、先に説明した2段階のリダクションアルゴリズムを適用し、ワークグループ内で勾配の二乗和を合計します。

   const int local_shift = inp % ls;
   for(int i = 0; i <= inputs; i += ls)
     {
      if(i <= inp && inp < (i + ls))
         temp[local_shift] = (i == 0 ? 0 : temp[local_shift]) + IsNaNOrInf(grad * grad,0);
      barrier(CLK_LOCAL_MEM_FENCE);
     }
//---
   int count = ls;
   do
     {
      count = (count + 1) / 2;
      if(inp < count)
         temp[inp] += ((inp + count) < inputs ? IsNaNOrInf(temp[inp + count],0) : 0);
      if(inp + count < inputs)
         temp[inp + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

得られた合計の平方根を取ることで、誤差勾配の目的とするL2ノルムが得られます。

   float norm = sqrt(IsNaNOrInf(temp[0],0));
   float epsw = IsNaNOrInf(w * w * grad * rho / (norm + 1.2e-7),w);
//---
   matrix_epsw[shift_w] = epsw;
  }

その後、調整後のパラメータ値を計算し、結果バッファの対応する要素に格納します。

これで、OpenCL側の実装作業は完了です。完全なコードは添付ファイルにあります。

2.2 SAM最適化による全結合層

OpenCL側の作業が完了した後は、ライブラリ実装に移ります。ここでは、SAM最適化が統合された全結合層用オブジェクトCNeuronBaseSAMOCLを作成します。新しいクラスの構造体は以下のとおりです。

class CNeuronBaseSAMOCL  :  public CNeuronBaseOCL
  {
protected:
   float             fRho;
   CBufferFloat      cWeightsSAM;
   //---
   virtual bool      calcEpsilonWeights(CNeuronBaseSAMOCL *NeuronOCL);
   virtual bool      feedForwardSAM(CNeuronBaseSAMOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronBaseSAMOCL(void) {};
                    ~CNeuronBaseSAMOCL(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint numNeurons, float rho, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual int       Type(void)        const    {  return defNeuronBaseSAMOCL;      }
   virtual int       Activation(void)  const    {  return (fRho == 0 ? (int)None : (int)activation);   }
   virtual int       getWeightsSAMIndex(void)   {  return cWeightsSAM.GetIndex();   }
   //---
   virtual CLayerDescription* GetLayerInfo(void);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

構造体からも分かるように、主な機能はベースとなる全結合層から継承しています。基本的に、このクラスはベース層のコピーであり、パラメータ更新メソッドのみをオーバーライドしてSAM最適化のロジックを組み込んでいます。

加えて、先に説明したカーネルと連携するためのラッパーメソッドcalcEpsilonWeightsを追加し、変更された重みバッファfeedForwardSAMを使用する順伝播メソッドの修正版も作成しました。

なお、元のSAMformerフレームワークでは、モデルパラメータにεを適用した後、元の状態に戻すために再度減算をおこなっていました。私たちはこれとは異なる方法を取り、摂動されたパラメータを別のバッファに格納しています。これにより、εの減算ステップを省略でき、全体の実行時間を短縮することが可能になりました。ただし、まずは基本から説明します。

摂動されたモデルパラメータ用のバッファは静的に宣言されており、コンストラクタとデストラクタは空のままにできます。宣言済みおよび継承されたすべてのオブジェクトの初期化は、Initメソッド内で行います。

bool CNeuronBaseSAMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons, 
                             float rho, ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, numNeurons, optimization_type, batch))
      return false;

メソッドのパラメータとして、作成されるオブジェクトのアーキテクチャを決定する主要な定数を受け取ります。メソッド内では、まず親クラスのInitメソッドを呼び出し、継承されたコンポーネントの検証と初期化を実行します。

親メソッドが正常に完了したら、シャープネス半径係数を内部変数に保存します。

   fRho = fabs(rho);
   if(fRho == 0 || !Weights)
      return true;

次に、シャープネス係数の値とパラメータ行列の有無を確認します。係数が「0」の場合、またはパラメータ行列が存在しない場合（つまり、その層に出力接続がない場合）、メソッドは正常終了します。そうでない場合は、代替パラメータ用のバッファを作成する必要があります。構造的にはメインの重みバッファと同一ですが、この段階ではゼロ値で初期化されます。

   if(!cWeightsSAM.BufferInit(Weights.Total(), 0) ||
      !cWeightsSAM.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

これでメソッドが修了します。

OpenCLカーネルをキューに投入するためのラッパーメソッドについては、各自で確認されることをお勧めします。コードは添付ファイルに記載されています。パラメータ更新メソッドupdateInputWeightsに移りましょう。

bool CNeuronBaseSAMOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;
   if(NeuronOCL.Type() != Type() || fRho == 0)
      return CNeuronBaseOCL::updateInputWeights(NeuronOCL);

このメソッドは、通常どおり入力データオブジェクトへのポインタを受け取ります。まず最初に、このポインタが無効であれば以降の操作で重大なエラーが発生するため、ポインタの検証をおこないます。

次に、このコンテキストでは重要となる入力データオブジェクトの型を確認します。また、シャープネス係数は「0」より大きくなければなりません。そうでない場合、SAMのロジックは通常の最適化処理と同等になってしまいます。これらの条件を満たすと、親クラスの該当メソッドを呼び出します。

これらのチェックが通過したら、SAM手法の処理を実行します。SAMアルゴリズムでは、パラメータにεを加えて摂動した後に、完全な順伝播と逆伝播を行い、誤差勾配を分配します。ただし、先に述べたように、今回のSAM実装は単一層単位で動作します。ここで疑問になるのは、「各層の目標値はどこから取得するのか」という点です。

一見すると、解決策は単純で、最後の順伝播結果と誤差勾配を単純に加算すればよいように思えます。しかし、注意点があります。後続層から勾配が渡される際には、通常、活性化関数の導関数によって調整されています。したがって、単純な加算では結果が歪んでしまいます。そこで一案として、活性化関数の導関数に基づいて勾配補正を逆算する仕組みを実装する方法も考えられます。しかし、私たちはより簡潔で効率的な方法を採用しました。それは、活性化関数の戻り値を返すメソッドをオーバーライドし、シャープネス係数がゼロの場合はNoneを返すようにする方法です。これにより、次の層から活性化関数の導関数で修正されていない生の誤差勾配を受け取ることができます。したがって、この生の誤差勾配と順伝播の結果を加算すればよく、この2つの和が解析対象となるレイヤーの実質的な目標値となります。

   if(!SumAndNormilize(Gradient, Output, Gradient, 1, false, 0, 0, 0, 1))
      return false;

次に、ラッパーメソッドを呼び出して、調整されたモデルパラメータを取得します。

   if(!calcEpsilonWeights(NeuronOCL))
      return false;

そして、摂動を加えたパラメータを用いて順伝播処理を実行します。

   if(!feedForwardSAM(NeuronOCL))
      return false;

この時点で、誤差勾配バッファには目標値が格納されており、結果バッファには摂動を加えたパラメータによって生成された出力が格納されています。これらの値の差異を求めるために、目標出力との差分を計算する親クラスのメソッドを呼び出すだけで済みます。

   float error = 1;
   if(!calcOutputGradients(Gradient, error))
      return false;

あとは、更新された誤差勾配に基づいてモデルのパラメータを更新するだけです。これは、親クラスの対応するメソッドを呼び出すことで実行します。

   return CNeuronBaseOCL::updateInputWeights(NeuronOCL);
  }

ファイル操作メソッドについても少し触れておきます。ディスク容量を節約するために、摂動を加えた重みバッファcWeightsSAMは保存しないことにしました。このバッファはパラメータ更新時にのみ使用され、各呼び出しごとに上書きされるため、そのデータを保持しても実用的な価値はありません。したがって、保存データのサイズ増加は、浮動小数点数要素1つ分（係数）のみとなります。

bool CNeuronBaseSAMOCL::Save(const int file_handle)
  {
   if(!CNeuronBaseOCL::Save(file_handle))
      return false;
   if(FileWriteFloat(file_handle, fRho) < INT_VALUE)
      return false;
//---
   return true;
  }

一方で、cWeightsSAMバッファは必要な機能を実行するために依然として欠かせません。そのサイズは重要であり、現在の層のすべてのパラメータを格納できるだけの容量が必要です。したがって、以前に保存したモデルを読み込む際には、このバッファを再作成する必要があります。データ読み込みメソッドでは、まず基底クラスの同等メソッドを呼び出します。

bool CNeuronBaseSAMOCL::Load(const int file_handle)
  {
   if(!CNeuronBaseOCL::Load(file_handle))
      return false;

次に、基本構造を超えるファイルの内容を確認し、存在する場合はシャープネス係数を読み取ります。

   if(FileIsEnding(file_handle))
      return false;
   fRho = FileReadFloat(file_handle);

その後、シャープネス係数がゼロでないことを確認し、有効なパラメータ行列が存在することを確かめます（注意：出力接続を持たないレイヤーの場合、ポインタが無効である可能性があります）。

   if(fRho == 0 || !Weights)
      return true;

どちらかの確認で条件を満たさない場合、パラメータの最適化は基本的な手法に劣化し、調整後のパラメータ用バッファを再作成する必要はありません。したがって、このメソッドは正常終了します。

この確認に失敗することは、SAM最適化にとっては重大ですが、モデル全体の動作にとっては致命的ではありません。そのため、プログラムは基本的な最適化手法を用いて処理を続行します。

バッファの作成が必要な場合、まず既存のバッファをクリアします。このとき、あえてクリア操作の結果は確認しません。これは、読み込み時点でバッファがまだ存在しない可能性があるためです。 

   cWeightsSAM.BufferFree();

次に、適切なサイズの新しいバッファをゼロ値で初期化し、そのOpenCLコピーを作成します。

   if(!cWeightsSAM.BufferInit(Weights.Total(), 0) ||
      !cWeightsSAM.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

今回は、これらの操作の実行を検証します。これらの操作の成功はモデルの今後の動作にとって重要であるためです。完了後は、操作のステータスを呼び出し元の関数に返します。

これで、SAM最適化対応の全結合層(CNeuronBaseSAMOCL)の実装についての説明は終了です。このクラスとそのメソッドのフルソースコードは、添付ファイルに記載されています。

残念ながら、この記事では文字数の制限に達してしまいましたが、作業はまだ完了していません。次回の記事では、実装を続け、SAM機能を組み込んだ畳み込み層の解説に移ります。また、提案した技術のTransformerアーキテクチャへの応用や、実際の過去データに対する提案手法の性能テストも行います。

結論

SAMformerは、多変量時系列の長期予測におけるTransformerモデルの主要な欠点、たとえば学習の複雑さや小規模データセットでの汎化性能の低さに対する効果的な解決策を提供します。浅いアーキテクチャとシャープネス認識最適化を用いることで、SAMformerは不良な局所最小値を回避するだけでなく、最先端の手法を上回る性能を示します。さらに、使用するパラメータ数も少なくて済みます。著者らによる結果は、時系列タスクの汎用ツールとしての潜在能力を示しています。

本記事の実践的な部分では、MQL5を用いて提案手法の私たちなりの実装を構築しました。しかし、作業はまだ進行中です。次回の記事では、提案手法が実際の課題解決にどれほど有用かを評価します。

参照文献

SAMformer:Unlocking the Potential of Transformers in Time Series Forecasting with Sharpness-Aware Minimization and Channel-Wise Attention

Sharpness-Aware Minimization for Efficiently Improving Generalization

この連載の他の記事記事

記事で使用されているプログラム

#	名前	種類	詳細
1	Research.mq5	EA	事例収集用EA
2	ResearchRealORL.mq5	EA	Real-ORL法を用いた例収集用のEA
3	Study.mq5	EA	モデル学習用EA
4	StudyEncoder.mq5	EA	エンコード訓練用EA
5	Test.mq5	EA	モデルテスト用EA
6	Trajectory.mqh	クラスライブラリ	システム状態記述の構造体
7	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
8	NeuroNet.cl	ライブラリ	OpenCLプログラムコードライブラリ