
Neural networks made easy (Part 8): Attention mechanisms
Contents
- Introduction
- 1. Attention Mechanisms
- 2. Self-Attention Algorithm
- 3. Implementation
- 3.1. Upgrading the Convolutional Layer
- 3.2. Self-Attention Block Class
- 3.3. Self-Attention Feed-Forward
- 3.4. Self-Attention Feed-Backward
- 3.5. Changes in the Neural Network Base Classes
- 4. Testing
- Conclusions
- References
- Programs Used in the Article
Introduction
In previous articles, we have already tested various options for organizing neural networks. These included convolutional networks [3] used image processing algorithms, as well as recurrent neural networks [4], used for working with sequences in which not only the values are important, but also their position in the source data set.
Fully connected and convolutional neural networks have a fixed input sequence size. Recurrent neural networks enable a slight expansion of the analyzed sequence by transferring hidden states from previous iterations. But their effectiveness also decreases along with sequence increase. In 2014, the first attention mechanism was presented for machine translation purposes. The purpose of the mechanism was to determine and highlight the blocks of the source sentence (context) which are most relevant for the target translation word. Such an intuitive approach has significantly improved the quality of texts translated by neural networks.
1. Attention Mechanisms
When analyzing a candlestick symbol chart, we define trends and tendencies, as well as determine their trading ranges. It means, we select some objects from the general picture and focus our attention on them. We understand that objects affect the future price behavior. To implement such an approach, back in 2014 developers proposed the first algorithm which analyzes and highlights dependencies between the elements of the input and output sequences [8]. The proposed algorithm is called "Generalized Attention Mechanism". It was initially proposed for use in machine translation models using recurrent networks as a solution to the problem of long-term memory in the translation of long sentences. This approach significantly improved the results of the previously considered recurrent neural networks based on LSTM blocks [4].
The classical machine translation model using recurrent networks consists of two blocks, Encoder and Decoder. The first block encodes the input sequence in the source language into a context vector, and the second block decodes the resulting context into a sequence of words in the target language. When the length of the input sequence increases, the influence of the first words on the final sentence context decreases. As a consequence, the quality of translation decreases. The use of LSTM blocks slightly increased the capabilities of the model, but still they remained limited.
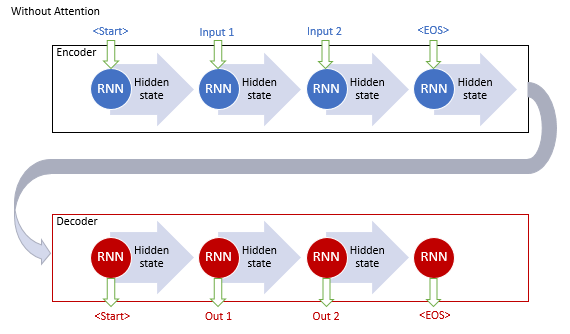
The authors of the general attention mechanism proposed using an additional layer to accumulate the hidden states of all recurrent blocks of the input sequence. Further, during sequence decoding, the mechanism should evaluate the influence of each element of the input sequence on the current word of the output sequence and suggest the most relevant part of the context to the decoder.
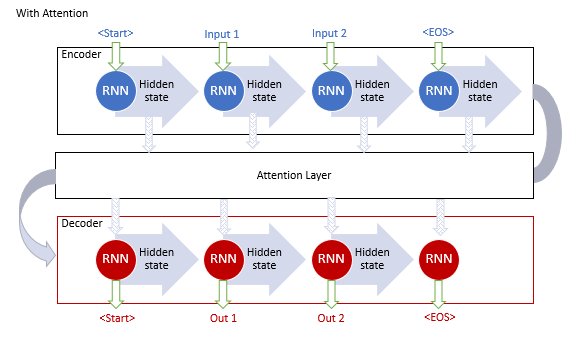
This mechanism operating algorithm included the following iterations:
1. Creating hidden states of the Encoder and accumulating them in the attention block.
2. Evaluating pairwise dependencies between the hidden states of each Encoder element and the last hidden state of the Decoder.
3. Combining the resulting scores into a single vector and normalizing them using the Softmax function.
4. Computing the context vector by multiplying all the hidden states of the Encoder by their corresponding alignment scores.
5. Decoding the context vector and combining the resulting value with the previous state of the Decoder.
All iterations are repeated until the end-of-sentence signal is received.
The proposed mechanism enabled the solution of the problem with a limited length of the input sequence and provided the improvement of the quality of machine translation using recurrent neural networks. The method become popular and further its variations were created. In 2012, Minh-Thang Luong in his article [9] suggested a new variation of the attention method. The main differences of the new approach were the use of three functions for calculating the degree of dependencies and the point of using the attention mechanism in Decoder.
The above-described models use recurrent blocks, which are computationally expensive to train. In June 2017, another variation was proposed in article [10]. This was a new architecture of the Transformer neural network, which did not use recurrent blocks, but used a new Self-Attention algorithm. Unlike the previously described algorithm, Self-Attention analyzes pairwise dependencies within one sequence. Transformer showed better results testing. Today, this model and its derivatives are used in many models, including GPT-2 and GPT-3. Let us consider the Self-Attention algorithm in more detail.
2. Self-Attention Algorithm
The Transformer architecture is based on sequential Encoder and Decoder blocks with a similar architecture. Each of the blocks includes several identical layers with different weight matrices.
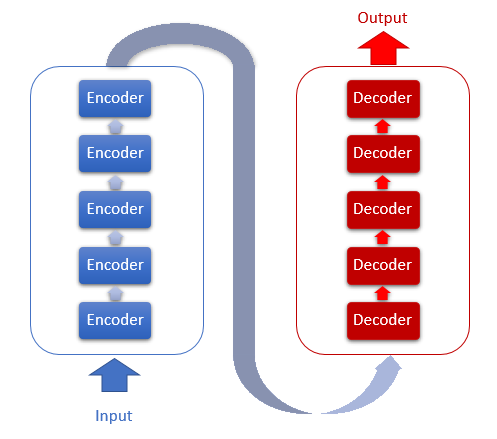
Each Encoder layer contains 2 inner layers: Self-Attention and Feed Forward. The Feed Forward layer includes two fully connected layers of neurons with the ReLU activation function on the inner layer. Each layer is applied to all elements of the sequence with the same weights, which allows simultaneous independent computations for all elements of the sequence in parallel threads.
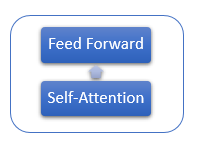
The Decoder layer has a similar structure, but it has an additional Self-Attention which analyzes the dependencies between the input and output sequences.
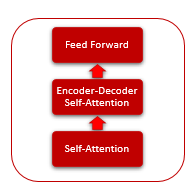
The Self-Attention mechanism itself includes several iterative actions which are applied for each element of the sequence.
1. First, we calculate the Query, Key and Value vectors. These vectors are obtained by multiplying each element of the sequence by the corresponding matrix WQ, WK and WV.
2. Next, determine pairwise dependencies between the elements of the sequence. To do this, multiply the Query vector by the Key vectors of all elements of the sequence. This iteration is repeated for the Query vector of each element in the sequence. As a result of this iteration we obtain a Score matrix sized N*N, where N is the size of the sequence.
3. The next step is to divide the resulting value by the square root of the Key vector dimension and to normalize it by the Softmax function in the context of each Query. Thus, we obtain the coefficients of pairwise interdependence between the elements of the sequence.
4. Multiply each Value vector by the corresponding interdependence coefficient to obtain the adjusted element value. The purpose of this iteration is to focus on relevant elements and to reduce the impact of irrelevant values.
5. Next, sum up all the adjusted Value vectors for each element. The result of this operation will be the vector of the output values of the Self-Attention layer.
Results of iterations of each layer are added to the input sequence and are normalized using the formula.
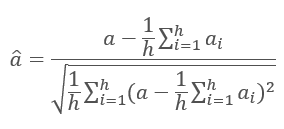
Normalization of neural network layers is discussed in more detail in the article [11].
3. Implementation
I suggest using the Self-Attention mechanism in our implementation. Let us consider implementation options.
3.1. Upgrading the Convolutional Layer
We start with the first action of the Self-Attention algorithm — calculating the Query, Key and Value vectors. Input a data matrix containing features for each bar of the analyzed sequence. Take features of one candlestick one by one and multiply them by the weight matrix to obtain a vector. This resembles to me a convolution layer considered in article [3]. However, in this case the output is not a number, but a fixed sized vector. To solve this problem, let us upgrade the CNeuronConvOCL class which is responsible for the operation of a convolutional layer of the neural network. Add the iWindowOut variable which will store the size of the output vectors. Implement appropriate changes in the class methods.
class CNeuronConvOCL : public CNeuronProofOCL { protected: uint iWindowOut; //--- CBufferDouble *WeightsConv; CBufferDouble *DeltaWeightsConv; CBufferDouble *FirstMomentumConv; CBufferDouble *SecondMomentumConv; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronConvOCL(void) : iWindowOut(1) { activation=LReLU; } ~CNeuronConvOCL(void); virtual bool Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint window, uint step, uint window_out, uint units_count, ENUM_OPTIMIZATION optimization_type); //--- virtual bool SetGradientIndex(int index) { return Gradient.BufferSet(index); } //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); virtual int Type(void) const { return defNeuronConvOCL; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); };
In the OpenCL kernel FeedForwardConv, add a parameter for obtaining the size of the output vector. Also, add the calculation of the offset of the processed segment of the output vector in the general vector, at the convolutional layer output, and implement an additional loop through elements of the output layer.
__kernel void FeedForwardConv(__global double *matrix_w, __global double *matrix_i, __global double *matrix_o, int inputs, int step, int window_in, int window_out, uint activation) { int i=get_global_id(0); int w_in=window_in; int w_out=window_out; double sum=0.0; double4 inp, weight; int shift_out=w_out*i; int shift_in=step*i; for(int out=0;out<w_out;out++) { int shift=(w_in+1)*out; int stop=(w_in<=(inputs-shift_in) ? w_in : (inputs-shift_in)); for(int k=0; k<=stop; k=k+4) { switch(stop-k) { case 0: inp=(double4)(1,0,0,0); weight=(double4)(matrix_w[shift+k],0,0,0); break; case 1: inp=(double4)(matrix_i[shift_in+k],1,0,0); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],0,0); break; case 2: inp=(double4)(matrix_i[shift_in+k],matrix_i[shift_in+k+1],1,0); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],matrix_w[shift+k+2],0); break; case 3: inp=(double4)(matrix_i[shift_in+k],matrix_i[shift_in+k+1],matrix_i[shift_in+k+2],1); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],matrix_w[shift+k+2],matrix_w[shift+k+3]); break; default: inp=(double4)(matrix_i[shift_in+k],matrix_i[shift_in+k+1],matrix_i[shift_in+k+2],matrix_i[shift_in+k+3]); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],matrix_w[shift+k+2],matrix_w[shift+k+3]); break; } sum+=dot(inp,weight); } switch(activation) { case 0: sum=tanh(sum); break; case 1: sum=1/(1+exp(-clamp(sum,-50.0,50.0))); break; case 2: if(sum<0) sum*=0.01; break; default: break; } matrix_o[out+shift_out]=sum; } }
Do not forget to enable the passing of an additional parameter when calling this kernel.
bool CNeuronConvOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=Output.Total()/iWindowOut; OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_w,WeightsConv.GetIndex()); OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_i,NeuronOCL.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_o,Output.GetIndex()); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_inputs,NeuronOCL.Neurons()); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_step,iStep); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_window_in,iWindow); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffс_window_out,iWindowOut); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_activation,(int)activation); if(!OpenCL.Execute(def_k_FeedForwardConv,1,global_work_offset,global_work_size)) { printf("Error of execution kernel FeedForwardProof: %d",GetLastError()); return false; } //--- return Output.BufferRead(); }
Similar changes have been implemented in kernels and in methods recalculating gradients (calcInputGradients) and updating the weight matrix (updateInputWeights). The full code of all methods and functions is available in the attachment.
3.2. Self-Attention Block Class
Now, let us move on to implementing the Self-Attention method itself. To describe it, create the CNeuronAttentionOCL class. Since all our operations are repeated for each element and are performed independently, let is move some of the operations into the modernized convolutional layers. Inside our attention block, create convolutional layers Querys, Keys, Values, which will be responsible for creating appropriate vectors, as well as for passing gradients and updating the weight matrix. The FeedForward block will also be implemented using convolutional layers FF1 and FF2. The values of the Score matrix will be saved into the Scores buffer; the results of the attention method will be saved into the inner neuron layer of the base class AttentionOut.
Here, pay attention to the difference between the output of the attention algorithm and the output of the entire Self-Attention class. The former one occurs after executing the Self-Attention algorithm by adjusting the values of the Value vectors; it is saved in AttentionOut. The second one is obtained after processing FeedForward - it is saved in the Output buffer of the base class.
class CNeuronAttentionOCL : public CNeuronBaseOCL { protected: CNeuronConvOCL *Querys; CNeuronConvOCL *Keys; CNeuronConvOCL *Values; CBufferDouble *Scores; CNeuronBaseOCL *AttentionOut; CNeuronConvOCL *FF1; CNeuronConvOCL *FF2; //--- uint iWindow; uint iUnits; //--- virtual bool feedForward(CNeuronBaseOCL *prevLayer); virtual bool updateInputWeights(CNeuronBaseOCL *prevLayer); public: CNeuronAttentionOCL(void) : iWindow(1), iUnits(0) {}; ~CNeuronAttentionOCL(void); virtual bool Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl, uint window, uint units_count, ENUM_OPTIMIZATION optimization_type); virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); //--- virtual int Type(void) const { return defNeuronAttentionOCL; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); };
In variables iWindows and iUnits, we will save the size of the output window and the number of elements in the output sequence, respectively.
The class will be initialized in the Init method. The method will receive in parameters the ordinal number of the element, a pointer to the COpenCL object, window size, the number of elements and the optimization method. At the beginning of the method, call the relevant method of the parent class.
bool CNeuronAttentionOCL::Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint window,uint units_count,ENUM_OPTIMIZATION optimization_type) { if(!CNeuronBaseOCL::Init(numOutputs,myIndex,open_cl,units_count*window,optimization_type)) return false;
Then, declare and initialize the instances of the convolutional network class for calculating the Querys, Keys and Values vectors.
//--- if(CheckPointer(Querys)==POINTER_INVALID) { Querys=new CNeuronConvOCL(); if(CheckPointer(Querys)==POINTER_INVALID) return false; if(!Querys.Init(0,0,open_cl,window,window,window,units_count,optimization_type)) return false; Querys.SetActivationFunction(TANH); } //--- if(CheckPointer(Keys)==POINTER_INVALID) { Keys=new CNeuronConvOCL(); if(CheckPointer(Keys)==POINTER_INVALID) return false; if(!Keys.Init(0,1,open_cl,window,window,window,units_count,optimization_type)) return false; Keys.SetActivationFunction(TANH); } //--- if(CheckPointer(Values)==POINTER_INVALID) { Values=new CNeuronConvOCL(); if(CheckPointer(Values)==POINTER_INVALID) return false; if(!Values.Init(0,2,open_cl,window,window,window,units_count,optimization_type)) return false; Values.SetActivationFunction(None); }
Further in the algorithm, declare the Scores buffer. Pay attention to the size of the buffer - it must have enough memory to store a square matrix with sides equal to the number of elements in the sequence.
if(CheckPointer(Scores)==POINTER_INVALID) { Scores=new CBufferDouble(); if(CheckPointer(Scores)==POINTER_INVALID) return false; } if(!Scores.BufferInit(units_count*units_count,0.0)) return false; if(!Scores.BufferCreate(OpenCL)) return false;
Also, declare the AttentionOut layer of neurons. This layer will serve as a buffer for storing the Self-Attention results. At the same time, it will be used as an input layer for the FeedForward block. Its size is equal to the product of the window width by the number of elements.
if(CheckPointer(AttentionOut)==POINTER_INVALID) { AttentionOut=new CNeuronBaseOCL(); if(CheckPointer(AttentionOut)==POINTER_INVALID) return false; if(!AttentionOut.Init(0,3,open_cl,window*units_count,optimization_type)) return false; AttentionOut.SetActivationFunction(None); }
Initialize two instances of the convolutional layer to implement the FeedForward block. Note that the first instance (hidden layer) outputs a window 2 times wider and has an LReLU activation function (ReLU with "leakage"). For the second layer (FF2), replace the gradient buffer with the gradient buffer of the parent class using the SetGradientIndex method. By copying the buffer, we eliminate the need to copy data.
if(CheckPointer(FF1)==POINTER_INVALID) { FF1=new CNeuronConvOCL(); if(CheckPointer(FF1)==POINTER_INVALID) return false; if(!FF1.Init(0,4,open_cl,window,window,window*2,units_count,optimization_type)) return false; FF1.SetActivationFunction(LReLU); } //--- if(CheckPointer(FF2)==POINTER_INVALID) { FF2=new CNeuronConvOCL(); if(CheckPointer(FF2)==POINTER_INVALID) return false; if(!FF2.Init(0,5,open_cl,window*2,window*2,window,units_count,optimization_type)) return false; FF2.SetActivationFunction(None); FF2.SetGradientIndex(Gradient.GetIndex()); }
Save the key parameters at the end of the method.
iWindow=window; iUnits=units_count; activation=FF2.Activation(); //--- return true; }
3.3. Self-Attention Feed-Forward
Next, let us consider the feedForward method of the CNeuronAttentionOCL class. The method receives in parameters a pointer to the previous layer of the neural network. So, first of all, check the validity of the received pointer.
bool CNeuronAttentionOCL::feedForward(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false;
Before further processing the data, normalize the input data. This step is not provided by the author's Self-Attention mechanism. However, I have added it based on testing results, in order to prevent overflow during the Score matrix normalization stage. A special kernel has been created to normalize the data. Call it in the feedForward method.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=1;
OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,prevLayer.getOutputIndex());
OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,prevLayer.Neurons());
if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel Normalize: %d",GetLastError());
return false;
}
if(!prevLayer.Output.BufferRead())
return false;
}
Let us have a look inside the normalization kernel. At the beginning of the kernel, calculate the offset to the first element of the normalized sequence. Then we calculate the average value for the normalized sequence and the standard deviation. At the end of the kernel, update data in the buffer.
__kernel void Normalize(__global double *buffer, int dimension) { int n=get_global_id(0); int shift=n*dimension; double mean=0; for(int i=0;i<dimension;i++) mean+=buffer[shift+i]; mean/=dimension; double variance=0; for(int i=0;i<dimension;i++) variance+=pow(buffer[shift+i]-mean,2); variance=sqrt(variance/dimension); for(int i=0;i<dimension;i++) buffer[shift+i]=(buffer[shift+i]-mean)/(variance==0 ? 1 : variance); }
After normalizing the source data, calculate the Querys, Keys and Values vectors. To do this, call the FeedForward method of the appropriate instance of the convolutional layer class (this method has been considered earlier).
if(CheckPointer(Querys)==POINTER_INVALID || !Querys.FeedForward(prevLayer)) return false; if(CheckPointer(Keys)==POINTER_INVALID || !Keys.FeedForward(prevLayer)) return false; if(CheckPointer(Values)==POINTER_INVALID || !Values.FeedForward(prevLayer)) return false;
Moving further along the Self-Attention algorithm, calculate the Score matrix. Calculations will be performed on a GPU using OpenCL. Implement kernel call in the main program method. The number of threads called is equal to the number of units in the class. Each thread will work in its window size. In other words, each thread will take its own Query vector of one element and will match it with the Key vectors of all elements of the sequence.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_querys,Querys.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_keys,Keys.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_score,Scores.GetIndex());
OpenCL.SetArgument(def_k_AttentionScore,def_k_as_dimension,iWindow);
if(!OpenCL.Execute(def_k_AttentionScore,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel AttentionScore: %d",GetLastError());
return false;
}
if(!Scores.BufferRead())
return false;
}
At the beginning of the kernel, determine the offsets of the initial element using the 'querys' and 'score' arrays. Calculate the coefficient to reduce the obtained values. Zero out the variable for calculating the amount that we need when normalizing the values. Next, implement a loop over all the elements of the key matrix, while calculating the corresponding dependencies. Please note that the kernel we are considering combines score matrix calculating and normalizing stages. Therefore, after calculating the products of the Query and Key vectors, divide the resulting value by a coefficient and calculate the exponent of the obtained value. The resulting exponent should be saved in a matrix and added to the sum. At the end of the loop, implement the second loop, in which all the values saved in the previous cycle are divided by the calculated sum of exponents. The kernel output will contain the calculated and normalized Score matrix.
__kernel void AttentionScore(__global double *querys, __global double *keys, __global double *score, int dimension) { int q=get_global_id(0); int shift_q=q*dimension; int units=get_global_size(0); int shift_s=q*units; double koef=sqrt((double)(units*dimension)); if(koef<1) koef=1; double sum=0; for(int k=0;k<units;k++) { double result=0; int shift_k=k*dimension; for(int i=0;i<dimension;i++) result+=(querys[shift_q+i]*keys[shift_k+i]); result=exp(result/koef); score[shift_s+k]=result; sum+=result; } for(int k=0;k<units;k++) score[shift_s+k]/=sum; }
Let us continue considering the Self-Attention algorithm. After normalizing the Score matrix, it is necessary to correct the Values vectors for the obtained values and to sum the obtained vectors in the context of input sequence elements . At the output of the Self-Attention block, the obtained values are summed added to the input sequence. All these iterations are combined in the next AttentionOut kernel. The kernel call is implemented in the main program code. Please note that this kernel will be run with a set of threads in two ways: by elements of the sequence (iUnits) and by the number of features for each element (iWindow). The resulting values will be saved to the output buffer of the AttentionOut layer.
{
uint global_work_offset[2]={0,0};
uint global_work_size[2];
global_work_size[0]=iUnits;
global_work_size[1]=iWindow;
OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_scores,Scores.GetIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_inputs,prevLayer.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_values,Values.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_out,AttentionOut.getOutputIndex());
if(!OpenCL.Execute(def_k_AttentionOut,2,global_work_offset,global_work_size))
{
printf("Error of execution kernel Attention Out: %d",GetLastError());
return false;
}
double temp[];
if(!AttentionOut.getOutputVal(temp))
return false;
}
In the kernel body, determine the offset for the processed element in the vectors of the input and output sequences. Then, organize a cycle to sum up the products of Scores by the corresponding Value values. As soon as the cyclic iterations have completed, add the resulting sum to the input vector received from the previous layer of the neural network. Write the result to the outgoing buffer.
__kernel void AttentionOut(__global double *scores, __global double *values, __global double *inputs, __global double *out) { int units=get_global_size(0); int u=get_global_id(0); int d=get_global_id(1); int dimension=get_global_size(1); int shift=u*dimension+d; double result=0; for(int i=0;i<units;i++) result+=scores[u*units+i]*values[i*dimension+d]; out[shift]=result+inputs[shift]; }
At this point, the Self-Attention algorithm can be considered completed. Now, we only need to normalize the resulting data using the above-described method. The only difference is in the normalization buffer.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=1;
OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,AttentionOut.getOutputIndex());
OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,AttentionOut.Neurons());
if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel Normalize: %d",GetLastError());
return false;
}
double temp[];
if(!AttentionOut.getOutputVal(temp))
return false;
}
Further, according to the Transformer encoder algorithm, we pass each element of the sequence through a fully connected neural network with one hidden layer. In this process, the same weight matrix is applied to all elements of the sequence. I have implemented this process by using a modernized convolutional layer class. In the method code, I sequentially call the FeedForward methods of the corresponding instances of the convolutional class.
if(!FF1.FeedForward(AttentionOut)) return false; if(!FF2.FeedForward(FF1)) return false;
To complete the feed-forward process, it is necessary to sum the results of the fully connected network pass with the results of the Self-Attention mechanism. For this purpose, I have created a kernel of addition of two vectors, which is called at the end of the feed-forward method.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,FF2.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,Output.GetIndex());
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow);
if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel MatrixSum: %d",GetLastError());
return false;
}
if(!Output.BufferRead())
return false;
}
//---
return true;
}
A simple cycle is organized inside the kernel, with element-wise summing of the incoming vector values.
__kernel void SumMatrix(__global double *matrix1, __global double *matrix2, __global double *matrix_out, int dimension) { const int i=get_global_id(0)*dimension; for(int k=0;k<dimension;k++) matrix_out[i+k]=matrix1[i+k]+matrix2[i+k]; }
The full code of all methods and functions is available in the attachment.
3.4. Self-Attention Feed-Backward
The feed-forward pass is followed by feed-backward, during which the error is fed to lower levels of the neural network and the weight matrix is adjusted to select optimal results. The class receives the error gradient from the upper fully connected layer of the neural network, using the parent class method described in article 5. Further mechanism for feeding the error gradient requires significant improvement, which is due to the complexity of the internal architecture.
To pass the error gradient to the inner convolutional layers and to the previous neural layer of the network, let us create the calcInputGradients method. The method receives in parameters a pointer to the previous layer of neurons. As always, check the validity of the received pointer first. Then, in reverse order, sequentially call the methods of the convolutional layers of the Feed Forward FF2 and FF1 block. We use buffer substitution, so the inner FF2 layer receives the error gradient directly from the next neural network layer using the methods of the parent class.
bool CNeuronAttentionOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false; //--- if(!FF2.calcInputGradients(FF1)) return false; if(!FF1.calcInputGradients(AttentionOut)) return false;
Since at the output of the feed-forward pass we summed up the results of Feed Forward and Self-Attention, the error gradient also comes in two branches. Therefore, the error gradient obtained from FF1 is summed up with the error gradient obtained from the next layer of the neural network. The vector summation kernel is described above. So, let us add its call.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,Gradient.GetIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex());
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow);
if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel MatrixSum: %d",GetLastError());
return false;
}
double temp[];
if(AttentionOut.getGradient(temp)<=0)
return false;
}
In the next step, propagate the error gradient to Querys, Keys and Values. The error gradient will be passed to the vectors in the AttentionIsideGradients kernel. In the below method, call it with a set of threads in two dimensions.
{
uint global_work_offset[2]={0,0};
uint global_work_size[2];
global_work_size[0]=iUnits;
global_work_size[1]=iWindow;
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_gradient,AttentionOut.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_keys,Keys.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_keys_g,Keys.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_querys,Querys.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_querys_g,Querys.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_values,Values.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_values_g,Values.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_scores,Scores.GetIndex());
if(!OpenCL.Execute(def_k_AttentionGradients,2,global_work_offset,global_work_size))
{
printf("Error of execution kernel AttentionGradients: %d",GetLastError());
return false;
}
double temp[];
if(Keys.getGradient(temp)<=0)
return false;
}
The kernel receives pointers to data buffers in parameters. The dimensions are determined at the kernel beginning, by the number or running threads. Then we calculate the correction factor and loop over all the elements of the sequence. Inside the loop, we first calculate the error gradient on the Value vector by multiplying the gradient vector by the corresponding Score vector. Note that the error gradient is divided by 2. This is because we summed it up in the previous step and thus doubled the error. Now we divide it by two to have an average value.
__kernel void AttentionIsideGradients(__global double *querys,__global double *querys_g, __global double *keys,__global double *keys_g, __global double *values,__global double *values_g, __global double *scores, __global double *gradient) { int u=get_global_id(0); int d=get_global_id(1); int units=get_global_size(0); int dimension=get_global_size(1); double koef=sqrt((double)(units*dimension)); if(koef<1) koef=1; //--- double vg=0; double qg=0; double kg=0; for(int iu=0;iu<units;iu++) { double g=gradient[iu*dimension+d]/2; double sc=scores[iu*units+u]; vg+=sc*g;
Next, organize a nested loop to define the gradient on the elements of the Score matrix. After that calculate the gradient of the elements of the Querys and Keys vectors. At the end of the external loop, assign the calculated gradients to the corresponding global buffers.
//--- double sqg=0; double skg=0; for(int id=0;id<dimension;id++) { sqg+=values[iu*dimension+id]*gradient[u*dimension+id]/2; skg+=values[u*dimension+id]*gradient[iu*dimension+id]/2; } qg+=(scores[u*units+iu]==0 || scores[u*units+iu]==1 ? 0.0001 : scores[u*units+iu]*(1-scores[u*units+iu]))*sqg*keys[iu*dimension+d]/koef; //--- kg+=(scores[iu*units+u]==0 || scores[iu*units+u]==1 ? 0.0001 : scores[iu*units+u]*(1-scores[iu*units+u]))*skg*querys[iu*dimension+d]/koef; } int shift=u*dimension+d; values_g[shift]=vg; querys_g[shift]=qg; keys_g[shift]=kg; }
Next, we have to pass the error gradients from the Querys, Keys and Values vectors. Pay attention, that since all vectors are obtained by multiplying the same initial data by different matrices, the error gradients also should be summed up. I did not allocate a separate buffer to accumulate error gradients. However, summing values when calculating gradients requires additional complication of the code, with the tracking of buffer zeroing. I decided to use existing methods for calculating error gradients and further accumulate the values in the gradient buffer of the AttentionOut layer.
if(!Querys.calcInputGradients(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(AttentionOut.getGradient(temp)<=0) return false; } //--- if(!Keys.calcInputGradients(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(AttentionOut.getGradient(temp)<=0) return false; } //--- if(!Values.calcInputGradients(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,prevLayer.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow+1); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(prevLayer.getGradient(temp)<=0) return false; } //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=1; OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,prevLayer.getGradientIndex()); OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,prevLayer.Neurons()); if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size)) { printf("Error of execution kernel Normalize: %d",GetLastError()); return false; } double temp[]; if(prevLayer.getGradient(temp)<=0) return false; } //--- return true; }
After feeding the error gradient to the previous layer level, correct the weight matrices in the updateInputWeights method. The method is quite simple. It calls appropriate methods of nested convolutional layers.
bool CNeuronAttentionOCL::updateInputWeights(CNeuronBaseOCL *prevLayer) { if(!Querys.UpdateInputWeights(prevLayer)) return false; if(!Keys.UpdateInputWeights(prevLayer)) return false; if(!Values.UpdateInputWeights(prevLayer)) return false; if(!FF1.UpdateInputWeights(AttentionOut)) return false; if(!FF2.UpdateInputWeights(FF1)) return false; //--- return true; }
3.5. Changes in the Neural Network Base Classes
We have finished working with the class of our attention block. Now, let us make some additions to the base classes of our neural network. First of all, add constants to the define block for working with new kernels.
#define def_k_FeedForwardConv 7 #define def_k_ffc_matrix_w 0 #define def_k_ffc_matrix_i 1 #define def_k_ffc_matrix_o 2 #define def_k_ffc_inputs 3 #define def_k_ffc_step 4 #define def_k_ffc_window_in 5 #define def_k_ffс_window_out 6 #define def_k_ffc_activation 7 //--- #define def_k_CalcHiddenGradientConv 8 #define def_k_chgc_matrix_w 0 #define def_k_chgc_matrix_g 1 #define def_k_chgc_matrix_o 2 #define def_k_chgc_matrix_ig 3 #define def_k_chgc_outputs 4 #define def_k_chgc_step 5 #define def_k_chgc_window_in 6 #define def_k_chgc_window_out 7 #define def_k_chgc_activation 8 //--- #define def_k_UpdateWeightsConvMomentum 9 #define def_k_uwcm_matrix_w 0 #define def_k_uwcm_matrix_g 1 #define def_k_uwcm_matrix_i 2 #define def_k_uwcm_matrix_dw 3 #define def_k_uwcm_inputs 4 #define def_k_uwcm_learning_rates 5 #define def_k_uwcm_momentum 6 #define def_k_uwcm_window_in 7 #define def_k_uwcm_window_out 8 #define def_k_uwcm_step 9 //--- #define def_k_UpdateWeightsConvAdam 10 #define def_k_uwca_matrix_w 0 #define def_k_uwca_matrix_g 1 #define def_k_uwca_matrix_i 2 #define def_k_uwca_matrix_m 3 #define def_k_uwca_matrix_v 4 #define def_k_uwca_inputs 5 #define def_k_uwca_l 6 #define def_k_uwca_b1 7 #define def_k_uwca_b2 8 #define def_k_uwca_window_in 9 #define def_k_uwca_window_out 10 #define def_k_uwca_step 11 //--- #define def_k_AttentionScore 11 #define def_k_as_querys 0 #define def_k_as_keys 1 #define def_k_as_score 2 #define def_k_as_dimension 3 //--- #define def_k_AttentionOut 12 #define def_k_aout_scores 0 #define def_k_aout_values 1 #define def_k_aout_inputs 2 #define def_k_aout_out 3 //--- #define def_k_MatrixSum 13 #define def_k_sum_matrix1 0 #define def_k_sum_matrix2 1 #define def_k_sum_matrix_out 2 #define def_k_sum_dimension 3 //--- #define def_k_AttentionGradients 14 #define def_k_ag_querys 0 #define def_k_ag_querys_g 1 #define def_k_ag_keys 2 #define def_k_ag_keys_g 3 #define def_k_ag_values 4 #define def_k_ag_values_g 5 #define def_k_ag_scores 6 #define def_k_ag_gradient 7 //--- #define def_k_Normilize 15 #define def_k_norm_buffer 0 #define def_k_norm_dimension 1
Also, add a constant of the new class of neuros.
#define defNeuronAttentionOCL 0x7887
In the CLayerDescription class describing the layers of the neural network, add a field for specifying the number of neurons in the outgoing vector window.
class CLayerDescription : public CObject { public: CLayerDescription(void); ~CLayerDescription(void) {}; //--- int type; int count; int window; int window_out; int step; ENUM_ACTIVATION activation; ENUM_OPTIMIZATION optimization; };
In the CNet neural network class constructor, add new classes to initialize an instance of the class working with OpenCL.
CNet::CNet(CArrayObj *Description)
{
if(CheckPointer(Description)==POINTER_INVALID)
return;
//---
..........
..........
..........
//---
next=Description.At(1);
if(next.type==defNeuron || next.type==defNeuronBaseOCL || next.type==defNeuronConvOCL || next.type==defNeuronAttentionOCL)
{
opencl=new COpenCLMy();
if(CheckPointer(opencl)!=POINTER_INVALID && !opencl.Initialize(cl_program,true))
delete opencl;
}
else
{
if(CheckPointer(opencl)!=POINTER_INVALID)
delete opencl;
}
Further in the constructor body, add code to initialize the new class of the attention neuron.
if(CheckPointer(opencl)!=POINTER_INVALID) { CNeuronBaseOCL *neuron_ocl=NULL; CNeuronConvOCL *neuron_conv_ocl=NULL; CNeuronAttentionOCL *neuron_attention_ocl=NULL; switch(desc.type) { case defNeuron: case defNeuronBaseOCL: neuron_ocl=new CNeuronBaseOCL(); if(CheckPointer(neuron_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_ocl.Init(outputs,0,opencl,desc.count,desc.optimization)) { delete neuron_ocl; delete temp; return; } neuron_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_ocl)) { delete neuron_ocl; delete temp; return; } neuron_ocl=NULL; break; case defNeuronConvOCL: neuron_conv_ocl=new CNeuronConvOCL(); if(CheckPointer(neuron_conv_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_conv_ocl.Init(outputs,0,opencl,desc.window,desc.step,desc.window_out,desc.count,desc.optimization)) { delete neuron_conv_ocl; delete temp; return; } neuron_conv_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_conv_ocl)) { delete neuron_conv_ocl; delete temp; return; } neuron_conv_ocl=NULL; break; case defNeuronAttentionOCL: neuron_attention_ocl=new CNeuronAttentionOCL(); if(CheckPointer(neuron_attention_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_attention_ocl.Init(outputs,0,opencl,desc.window,desc.count,desc.optimization)) { delete neuron_attention_ocl; delete temp; return; } neuron_attention_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_attention_ocl)) { delete neuron_attention_ocl; delete temp; return; } neuron_attention_ocl=NULL; break; default: return; break; } }
Add initialization of new kernels at the end of the constructor.
if(CheckPointer(opencl)==POINTER_INVALID) return; //--- create kernels opencl.SetKernelsCount(16); opencl.KernelCreate(def_k_FeedForward,"FeedForward"); opencl.KernelCreate(def_k_CalcOutputGradient,"CalcOutputGradient"); opencl.KernelCreate(def_k_CalcHiddenGradient,"CalcHiddenGradient"); opencl.KernelCreate(def_k_UpdateWeightsMomentum,"UpdateWeightsMomentum"); opencl.KernelCreate(def_k_UpdateWeightsAdam,"UpdateWeightsAdam"); opencl.KernelCreate(def_k_AttentionGradients,"AttentionIsideGradients"); opencl.KernelCreate(def_k_AttentionOut,"AttentionOut"); opencl.KernelCreate(def_k_AttentionScore,"AttentionScore"); opencl.KernelCreate(def_k_CalcHiddenGradientConv,"CalcHiddenGradientConv"); opencl.KernelCreate(def_k_CalcInputGradientProof,"CalcInputGradientProof"); opencl.KernelCreate(def_k_FeedForwardConv,"FeedForwardConv"); opencl.KernelCreate(def_k_FeedForwardProof,"FeedForwardProof"); opencl.KernelCreate(def_k_MatrixSum,"SumMatrix"); opencl.KernelCreate(def_k_UpdateWeightsConvAdam,"UpdateWeightsConvAdam"); opencl.KernelCreate(def_k_UpdateWeightsConvMomentum,"UpdateWeightsConvMomentum"); opencl.KernelCreate(def_k_Normilize,"Normalize"); //--- return; }
Add processing of the new class of neurons in the dispatcher methods of the CNeuronBase class.
bool CNeuronBaseOCL::FeedForward(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: temp=SourceObject; return feedForward(temp); break; } //--- return false; } bool CNeuronBaseOCL::calcHiddenGradients(CObject *TargetObject) { if(CheckPointer(TargetObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; CNeuronAttentionOCL *at=NULL; CNeuronConvOCL *conv=NULL; switch(TargetObject.Type()) { case defNeuronBaseOCL: temp=TargetObject; return calcHiddenGradients(temp); break; case defNeuronConvOCL: conv=TargetObject; temp=GetPointer(this); return conv.calcInputGradients(temp); break; case defNeuronAttentionOCL: at=TargetObject; temp=GetPointer(this); return at.calcInputGradients(temp); break; } //--- return false; }
The full code of all methods and functions is available in the attachment.
4. Testing
After all the above changes, we can add the new class of neurons to the neural network and test the new architecture. I have created a testing EA Fractal_OCL_Attention, which differs from previous EAs only in the architecture of the neural network. Again, the first layer consists of basic neurons for writing initial data and contains 12 features for each history bar. The second layer is declared as a modified convolutional layer with a sigmoidal activation function and an outgoing window of 36 neurons. This layer performs the function of embedding and normalization of the original data. This is followed by two layers of an encoder with a Self-Attention mechanism. Three fully connected layers of neurons complete the neural network.
CLayerDescription *desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuronBaseOCL; desc.optimization=ADAM; desc.activation=TANH; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronConvOCL; desc.window=12; desc.step=12; desc.window_out=36; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- bool result=true; for(int i=0; (i<2 && result); i++) { desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronAttentionOCL; desc.window=36; desc.optimization=ADAM; desc.activation=None; result=Topology.Add(desc); } if(!result) { delete Topology; return INIT_FAILED; } //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=TANH; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=TANH; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=3; desc.type=defNeuron; desc.activation=SIGMOID; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED;
The full EA code can be found in the attachment.
EA testing was i=performed in the same conditions: EURUSD, H1 timeframe, data of 20 consecutive candlesticks are fed into the network, and training is performed using the history for the last two years, with parameters being updated by the Adam method.
The Expert Advisor was initialized with random weights ranging from -1 to 1, excluding zero values. After testing on 25 epochs, the EA showed an error of 35-36% with a hit of 22-23%
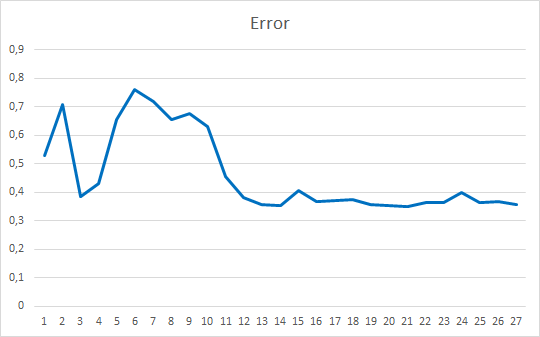
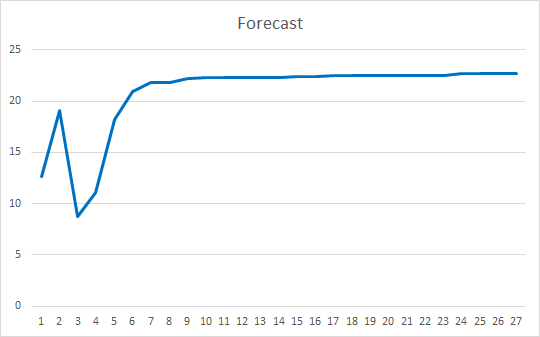
Conclusions
In this article, we have considered attention mechanisms. We have created a Self-Attntion block and tested its operation on historical data. The resulting Expert Advisor showed quite smooth results in terms reducing the error in the neural network operation and in terms of "hitting" of the predicted results. The results obtained indicate that it is possible to use this approach. However, additional work is required to improve the results. As a further development option, you can consider the use of several parallel threads of attention with different weights. In article 10, this approach is called "Multi had attention".
References
- Neural networks made easy
- Neural networks made easy (Part 2): Network training and testing
- Neural networks made easy (Part 3): Convolutional networks
- Neural networks made easy (Part 4): Recurrent networks
- Neural networks made easy (Part 5): Multithreaded calculations in OpenCL
- Neural networks made easy (Part 6): Experimenting with the neural network learning rate
- Neural networks made easy (Part 7): Adaptive optimization methods
- Neural Machine Translation by Jointly Learning to Align and Translate
- Effective Approaches to Attention-based Neural Machine Translation
- Attention Is All You Need
- Layer Normalization
Programs Used in the Article
| # | Name | Type | Description |
|---|---|---|---|
| 1 | Fractal_OCL_Attention.mq5 | Expert Advisor | An Expert Advisor with the classification neural network (3 neurons in the output layer) using the Self-Attention mechanism |
| 2 | NeuroNet.mqh | Class library | A library of classes for creating a neural network |
| 3 | NeuroNet.cl | Code Base | OpenCL program code library |
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/8765
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Developing a self-adapting algorithm (Part I): Finding a basic pattern
Developing a self-adapting algorithm (Part I): Finding a basic pattern
 Neural networks made easy (Part 9): Documenting the work
Neural networks made easy (Part 9): Documenting the work
 Using spreadsheets to build trading strategies
Using spreadsheets to build trading strategies
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
I have also seen this machine translation, but still it is somewhat incorrect.
If to rephrase it into human language, the meaning is as follows: "the SA mechanism is a development of a fully-connected neural network, and the key difference from PNN is that the elementary element that PNN analyses is the output of a single neuron, while the elementary element that SA analyses is a certain vector of context"? Am I right, or are there some other key differences?
The vector is from recurrent networks, because a sequence of letters is fed to translate the text. BUT SA has an encoder that translates the original vector into a shorter length vector that carries as much information about the original vector as possible. Then these vectors are decoded and superimposed on each other at each iteration of training. That is, it is a kind of information compression (context selection), i.e. all the most important things remain in the algorithm's opinion, and this main thing is given more weight.
In fact, it is just an architecture, don't look for sacred meaning there, because it does not work much better on time series than the usual NN or LSTM.
Vector is from recurrence networks, because to translate the text, a sequence of letters is fed in. But SA has an encoder that translates the original vector into a shorter vector that carries as much information about the original vector as possible. Then these vectors are decoded and superimposed on each other at each iteration of training. That is, it is a kind of information compression (context selection), i.e. all the most important things remain in the algorithm's opinion, and this main thing is given more weight.
In fact, it is just an architecture, don't look for sacred meaning there, because it does not work much better on time series than the usual NN or LSTM.
Looking for sacral meaning is the most important thing if you need to design something unusual. And the problem of market analysis is not in the models themselves, but in the fact that these (market) time series are too noisy and whatever model is used, it will pull out exactly as much information as it is embedded. And, alas, it is not enough. To increase the amount of information to be "pulled out", it is necessary to increase the initial amount of information. And it is precisely when the amount of information increases that the most important features of EO - scalability and adaptability - come to the fore.
A vector is simply a sequential set of numbers. This term is not tied to recurrent HH, or even to machine learning in general. This term can be used in absolutely any mathematical problem in which the order of numbers is required: even in school arithmetic problems.
Searching for sacral meaning is the most important thing if you need to design something unusual. And the problem of market analysis is not in the models themselves, but in the fact that these (market) time series are too noisy and whatever model is used, it will pull out exactly as much information as it is embedded. And, alas, it is not enough. To increase the amount of information to be "pulled out", it is necessary to increase the initial amount of information. And it is precisely when the amount of information increases that the most important features of EO - scalability and adaptability - come to the fore.
This term is attached to recurrent networks that work with sequences. It just uses an additive in the form of an attention mechanism, instead of gates like in lstm. You can come up with roughly the same thing on your own if you smoke MO theory for a long time.
That the problem is not in the models - 100% agree. But still any algorithm of TC construction can be formalised in one way or another in the form of NS architecture :) it's a two-way street.Some conceptual questions are interesting:
How does this Self-attention system differ from a simple fully connected layer, because in it too the next neuron has access to all previous ones? What is its key advantage? I can't understand it, although I have read quite a lot of lectures on this topic .
There is a big "ideological" difference here. In brief, a full-link layer analyses the whole set of source data as a single whole. And even an insignificant change of one of the parameters is evaluated by the model as something radically new. Therefore, any operation with the source data (compression/stretching, rotation, adding noise) requires retraining of the model.
Attention mechanisms, as you have correctly noticed, work with vectors (blocks of data), which in this case it is more correct to call Embeddings - an encoded representation of a separate object in the analysed array of source data. In Self-Attention each such Embedding is transformed into 3 entities: Query, Key and Value. In essence, each of the entities is a projection of the object into some N-dimensional space. Note that a different matrix is trained for each entity, so the projections are made into different spaces. Query and Key are used to evaluate the influence of one entity on another in the context of the original data. Dot product Query of object A and Key of object B show the magnitude of dependency of object A on object B. And since Query and Key of one object are different vectors, the coefficient of influence of object A on B will be different from the coefficient of influence of object B on A. The dependency (influence) coefficients are used to form the Score matrix, which is normalised by the SoftMax function in terms of Query objects. The normalised matrix is multiplied by the Value entity matrix. The result of the operation is added to the original data. This can be evaluated as adding a sequence context to each individual entity. Here we should note that each entity gets an individual representation of the context.
The data is then normalised so that the representation of all objects in the sequence have a comparable appearance.
Typically, several consecutive Self-Attention layers are used. Therefore, the data contents at the input and output of the block will be very different in content, but similar in size.
Transformer was proposed for language models. And was the first model that learnt not only to translate the source text verbatim, but also to rearrange words in the context of the target target target language.
In addition, Transformer models are able to ignore out-of-context data (objects) due to context-aware data analysis.
There is a big "ideological" difference here. In brief, the full-link layer analyses the entire set of input data as a whole. And even an insignificant change of one of the parameters is evaluated by the model as something radically new. Therefore, any operation with the source data (compression/stretching, rotation, adding noise) requires retraining of the model.
Attention mechanisms, as you have correctly noticed, work with vectors (blocks of data), which in this case it is more correct to call Embeddings - an encoded representation of a separate object in the analysed array of source data. In Self-Attention each such Embedding is transformed into 3 entities: Query, Key and Value. In essence, each of the entities is a projection of the object into some N-dimensional space. Note that a different matrix is trained for each entity, so the projections are made into different spaces. Query and Key are used to evaluate the influence of one entity on another in the context of the original data. Dot product Query of object A and Key of object B show the magnitude of dependency of object A on object B. And since Query and Key of one object are different vectors, the coefficient of influence of object A on B will be different from the coefficient of influence of object B on A. The dependency (influence) coefficients are used to form the Score matrix, which is normalised by the SoftMax function in terms of Query objects. The normalised matrix is multiplied by the Value entity matrix. The result of the operation is added to the original data. This can be evaluated as adding a sequence context to each individual entity. Here we should note that each object gets an individual representation of the context.
The data is then normalised so that the representation of all objects in the sequence has a comparable appearance.
Typically, several consecutive Self-Attention layers are used. Therefore, the data contents at the input and output of the block will be very different in content, but similar in size.
Transformer was proposed for language models. And was the first model that learnt not only to translate the source text verbatim, but also to rearrange words in the context of the target target target language.
In addition, Transformer models are able to ignore out-of-context data (objects) due to context-aware data analysis.
Thank you very much! Your articles have helped a lot to understand such a complex and complex topic.
The depth of your knowledge is just amazing really.