Redes neuronales en el trading: Transformador vectorial jerárquico (HiVT)

Introducción

Los retos a los que se enfrenta la conducción autónoma coinciden en gran medida con los que afrontan los tráders. La navegación por entornos dinámicos maniobrando con seguridad es una tarea de importancia crítica para los vehículos autónomos. Para lograr dicho objetivo, estos vehículos necesitan comprender su entorno y predecir futuros acontecimientos en la carretera. Sin embargo, predecir con exactitud las maniobras de los usuarios próximos en la carretera, como coches, bicicletas y peatones, supone todo un reto, sobre todo cuando se desconocen sus objetivos o intenciones. En las escenas de tráfico multiusuario, el comportamiento de un agente viene determinado por complejas interacciones con otros agentes, complicadas aún más por las normas de tráfico dependientes del mapa, que hacen extremadamente difícil comprender los diversos comportamientos de múltiples agentes en una escena.

Estudios recientes usan un enfoque vectorizado para representar las escenas de forma más compacta extrayendo un conjunto de vectores o puntos de las trayectorias y las características de los mapas. No obstante, los enfoques vectoriales existentes tropiezan con problemas cuando se les exige que realicen previsiones de tráfico en tiempo real ante la rápida evolución del tráfico de carretera, ya que estos métodos suelen ser inestables ante los cambios de posición y orientación del sistema de coordenadas. Para mitigar dicho problema, las escenas se normalizan de forma que estén centrados en el agente objetivo y alineados con su dirección de movimiento. Este enfoque resulta problemático cuando hay que predecir el movimiento de un gran número de agentes en una escena, debido al elevado coste computacional que supone volver a normalizar la escena y recalcular las características para cada agente objetivo. Además, los trabajos existentes modelan las interrelaciones de todos los elementos en todas las dimensiones del espacio y el tiempo para captar las interacciones detalladas entre los elementos vectorizados, lo cual inevitablemente conlleva un coste computacional excesivo a medida que aumenta el número de elementos. Dado que una predicción precisa en tiempo real resulta fundamental para la seguridad de la conducción autónoma, muchos investigadores pretenden llevar este proceso al siguiente nivel desarrollando un nuevo marco que permita predecir el movimiento de múltiples agentes con mayor rapidez y precisión.

Uno de estos enfoques se presenta en el artículo "HiVT: Hierarchical Vector Transformer for Multi-Agent Motion Prediction". Este explota las simetrías y la estructura jerárquica del problema de la predicción del movimiento de un conjunto de agentes. Los autores del HiVT consideran el problema de la predicción del movimiento en varios pasos y modelan jerárquicamente las relaciones entre elementos utilizando un Transformer.

En el primer paso, el modelo evita la costosa modelización de las interacciones de todos los elementos entre sí, extrayendo en su lugar las características contextuales de manera local. La escena completa se divide en un conjunto de regiones locales, cada una centrada en un agente simulado. Para cada área local centrada en el agente, se extraen características contextuales de elementos locales vectorizados que contienen información rica relacionada con el agente central.

En la segunda fase, se realiza una transferencia de información global entre las regiones locales centradas en el agente para compensar las limitaciones de los campos de visión locales y captar las dependencias de largo alcance en la escena. Para ello, los autores del método utilizan un Transformer equipado con enlaces geométricos entre los marcos de referencia locales.

Las representaciones locales y globales resultantes permiten al descodificador predecir las futuras trayectorias de todos los agentes en una única pasada directa del modelo. Y para explotar de forma adicional la simetría del problema, los autores del método introducen una representación de la escena independiente del desplazamiento del sistema global de coordenadas, en la que las posiciones relativas se utilizan para caracterizar todos los elementos vectorizados. Basándose en esta representación de la escena, se introducen módulos de atención cruzada invariantes de rotación para el aprendizaje espacial que pueden aprender representaciones locales y globales independientes de la rotación de la escena.

1. Algoritmo HiVT

El algoritmo del método HiVT comienza representando la escena de la carretera como un conjunto de elementos vectorizados. Partiendo de esta representación de la escena, el modelo agrega jerárquicamente información espacio-temporal sobre la escena. La escena de la carretera está formado por los agentes y la información cartográfica. Para obtener una representación estructurada de la escena, primero extraemos elementos vectorizados que incluyen segmentos de trayectoria de los agentes de la carretera y segmentos del carril en los datos cartográficos.

Un elemento vectorizado se asocia con atributos semánticos y geométricos. A diferencia de los métodos vectorizados anteriores, en los que los atributos geométricos de los agentes o los carriles incluyen las posiciones absolutas de los puntos, los autores del método evitan el uso de posiciones absolutas y proponen describir los atributos geométricos utilizando posiciones relativas. Esto convierte la escena al completo en un conjunto de vectores. En concreto, la trayectoria del agente i se presenta como "pt,i — pt-1,i", donde pt,i es la ubicación del agente i en el paso temporal t.

Para un segmento de carril xi el atributo geométrico se establece como p1,xi — p0,xi, donde p0,xi y p1,xi son las coordenadas iniciales y finales xi Transformando un conjunto de puntos en un conjunto de vectores, dicha representación garantiza de forma natural la invarianza a la traslación. No obstante, también se perderá información sobre las posiciones relativas entre elementos. Para preservar las relaciones espaciales, introduciremos vectores de posición relativa para los pares agente-agente y agente-carril. Por ejemplo, el vector de posición del agente j respecto al agente i en el paso temporal t es igual a ptj — pti, que describe al completo la relación espacial entre los dos agentes y también es invariante a la traslación. Sin pérdida de información, tal representación de la escena garantiza que cualquier función de aprendizaje aplicada respetará la invarianza de traslación.

Para predecir con exactitud las futuras trayectorias de los agentes en un entorno altamente dinámico, el modelo debe aprender de forma eficaz las dependencias espaciotemporales entre un gran número de elementos vectorizados. El Transformer ya ha demostrado su potencial en la captación de dependencias a largo plazo entre elementos en una amplia variedad de tareas. Sin embargo, la aplicación directa de transformadores a elementos espaciotemporales se enfrenta a una complejidad de O((NT + L)^2), donde N, T y L son los números de los agentes, los pasos temporales históricos y los segmentos de carril, respectivamente. Para extraer eficazmente la información de un gran número de elementos, los autores del HiVT proponen factorizar los tamaños espaciales y temporales entrenando las relaciones espaciales solo de forma local en cada paso temporal. En concreto, dividen el espacio en N regiones locales, cada una centrada en torno a un único agente de la escena. Dentro de cada región local hay segmentos de la trayectoria y el entorno local del agente central, donde la información del entorno incluye segmentos de trayectoria de agentes vecinos y segmentos de carriles locales que rodean al agente central. Para cada región local, añadimos la información local en un único vector de características, modelando secuencialmente las interacciones agente-agente en cada paso temporal, las dependencias temporales para cada agente y las interacciones agente-carril en el paso temporal actual. Tras la adición, el vector de características contendrá abundante información relacionada con el agente central. La complejidad computacional se reduce de O((NT + L)^2) hasta O(NT^2 + TN^2 + NL) gracias a la factorización de los tamaños espaciales y temporales y se reduce de forma adicional hasta O(NT^2 + TNk + Nl) gracias a la limitación del radio de las regiones locales, donde k < N y l < L

Aunque un codificador local puede extraer representaciones ricas, la cantidad de información se limitará a la gama de regiones locales. Para evitar pérdidas en la calidad de las predicciones, los autores del método usan además un módulo de interacción global para compensar los limitados campos receptivos locales y captar la dinámica al nivel de la escena en el que se realiza el intercambio de mensajes entre regiones locales. El módulo de interacción global mejora enormemente la expresividad del modelo con un coste de complejidad de O(N^2), que resulta relativamente ligero en comparación con el codificador local.

El problema de la predicción del movimiento de varios agentes presenta simetrías de traslación y rotación. Los métodos existentes renormalizan todos los elementos vectorizados respecto a cada agente y realizan predicciones para un único agente varias veces para lograr la invarianza. Este paradigma se escala de manera lineal con respecto al número de agentes. En comparación, el modelo HiVT puede realizar predicciones para todos los agentes en una única pasada directa sin perder invarianza, utilizando una representación invariante de la escena y módulos de aprendizaje espacial resistentes a la rotación.

El módulo de interacción Agente-Agente está diseñado para explorar la relación entre el agente central y los agentes vecinos en cada región local y en cada paso temporal. Para explotar las simetrías del problema, los autores del método proponen un bloque de atención cruzada resistente a la rotación que permite añadir información espacial. En concreto, toman el último segmento de la trayectoria del agente central pT,i — pT-1,i como vector de referencia de la región local y rotan todos los vectores locales según la orientación del vector de referencia ʘi. Los vectores rotados y sus atributos semánticos asociados son procesados por un perceptrón multicapa (MLP) para obtener la incorporación del agente central zti y la incorporación de cualquier agente vecino ztij en cualquier paso temporal t.

Como todos los atributos geométricos se normalizan con respecto al agente central antes de introducirlos en el MLP, estas incorporaciones serán independientes de la rotación del sistema de coordenadas global. Además de los segmentos de trayectoria, los datos iniciales de la función фnbr(•) también contienen vectores de posiciones de los agentes vecinos en relación con el agente central, lo cual hace que las incorporaciones de los vecinos sean espacialmente conscientes. La incorporación del agente central se convierte en un vector Query, mientras que las incorporaciones de los agentes vecinos se utilizan para calcular las entidades Key y Value. Las entidades resultantes se usan en el bloque de atención.

A diferencia del Transformer clásico, los autores del HiVT proponen utilizar la función de control de combinación de las características del entorno con las características del agente central zti. Esto permite al bloque de atención controlar mejor la actualización de las características. Al igual que sucede en la arquitectura Transformer original, la unidad de atención propuesta puede ampliarse a múltiples cabezas de atención. Los resultados del bloque de atención multicabeza se pasan por un bloque MLP para obtener la incorporación espacial sti del agente i en el paso temporal t.

Además, los autores del método usan la normalización de los datos de las capas antes de cada bloque y las conexiones residuales después de cada bloque. En la práctica, este módulo puede implementarse usando operaciones eficientes de paralelismo de entrenamiento sobre todas las regiones locales y pasos temporales.

La captura adicional de la información temporal de cada región local se realiza mediante el codificador del Transformer temporal que sigue al módulo de interacción Agente-Agente. Para cualquier agente central i, la secuencia inicial de este módulo constará de incorporaciones sti obtenidas del módulo de interacción Agente-Agente en diferentes pasos temporales. Los autores del método añaden un token entrenado adicional sT+1 al final de la secuencia original. Después, añaden la codificación posicional aprendida a todos los tokens y apilan estos en una matriz Si que se suministra como entrada a la unidad de atención temporal.

El módulo de aprendizaje temporal también consta de bloques alternos de atención multicabeza y bloques MLP.

La estructura local del mapa puede indicar las futuras intenciones del agente central. Por consiguiente, la información del mapa local se añade a la incorporación del agente central. Para ello, primero rotamos los segmentos de carretera locales y los vectores de posición relativa agente-carretera en el paso temporal T actual. A continuación, los vectores rotados se codifican con la ayuda de un MLP. Utilizando las características espacio-temporales del agente central como Query y las características del segmento de carretera codificadas utilizando un MLP como vectores Key-Value, la atención cruzada agente-carretera se realiza de forma similar a los enfoques descritos anteriormente.

Los autores del método aplican además un bloque MLP para obtener la incorporación local final hi del agente central i. Tras el modelado secuencial de las interacciones Agente-Agente, las dependencias temporales y las interacciones Agente-Carretera, las incorporaciones contienen información enriquecida relacionada con los agentes centrales de las regiones locales.

En el siguiente paso del algoritmo HiVT, las incorporaciones locales se procesan en el módulo de interacción global para captar las dependencias a largo plazo en la escena. Como las características locales se extraen en sistemas de coordenadas centrados en el agente, el módulo de interacción global deberá tener en cuenta las relaciones geométricas entre cuadros individuales cuando las regiones locales intercambian información. Para ello, los autores del método amplían el codificador del Transformer para tener en cuenta las diferencias entre los sistemas de coordenadas locales. Cuando se transmite un mensaje del agente j al agente i, los autores del método usan un MLP para obtener una incorporación por pares, que luego se incluye en la transformación vectorial.

Para captar de forma global las interacciones por pares, se utiliza el mismo mecanismo de atención espacial que en el codificador local, seguido de un bloque MLP y dando como salida una representación global para cualquier agente.

Los movimientos predictivos de los agentes de transporte son intrínsecamente multimodales. Por lo tanto, los autores del método proponen parametrizar la distribución de las futuras trayectorias como una mezcla de modelos donde cada componente es una distribución de Laplace. Las predicciones se realizan para todos los agentes en una sola pasada. Y para cada agente i de cada componente f, el MLP obtiene representaciones locales y globales como entradas. Y retorna la localización y su incertidumbre asociada del agente en cada paso temporal futuro en el sistema de coordenadas local. El tensor de resultados de la cabeza de regresión tiene una dimensionalidad [F, N, H, 4], donde F es el número de componentes de la mezcla, N es el número de agentes en la escena, y H es el horizonte de predicción de los futuros pasos temporales. Aquí también se usa un MLP. A continuación, la función SoftMax ofrece los coeficientes de mezcla del modelo para cada agente.

Ahora presentaremos la visualización de autor del método HiVT.

2. Implementación con MQL5

Más arriba hemos analizado una descripción bastante extensa del complejo algoritmo propuesto por los autores del método HiVT. Ahora es el momento de pasar a la parte práctica de nuestro trabajo, en la que implementaremos nuestra visión de los enfoques propuestos utilizando herramientas MQL5.

Y aquí debemos señalar que los enfoques propuestos por los autores del método son muy diferentes de los mecanismos que hemos utilizado anteriormente. Así que tenemos mucho trabajo por delante.

2.1 Vectorización del estado inicial

Comenzaremos organizando el proceso de vectorización del estado. Obviamente, ya hemos analizado antes varios algoritmos para la vectorización del estado inicial. Entre ellos se encuentran la representación lineal a trozos de series temporales, la segmentación de datos y diversos enfoques de incorporación. Pero en este caso, los autores del método ofrecen un enfoque radicalmente distinto. Y lo implementamos en el lado OpenCL en el kernel HiVTPrepare.

__kernel void HiVTPrepare(__global const float *data,
                          __global float2 *output
                         )
  {
   const size_t t = get_global_id(0);
   const size_t v = get_global_id(1);
   const size_t total_v = get_global_size(1);

En los parámetros del kernel, utilizamos solo los dos punteros a los búferes de datos globales: los valores iniciales y los resultados de operaciones.

Nótese aquí que, a diferencia de los datos de origen, usaremos el tipo de vector float2 para el búfer de resultados. Ya lo hemos utilizado anteriormente para magnitudes complejas. Pero en este caso no usaremos las matemáticas de los números complejos. El uso del tipo de datos especificado estará relacionado con la rotación de la escena en el espacio bidimensional. Y en un vector de 2 elementos nos resultará más cómodo almacenar coordenadas y desplazamiento en el plano.

Como ya habrá notado, en los parámetros del kernel no trasmitimos constantes que definan la dimensionalidad de los tensores de los datos de origen y los resultados. Planeamos obtener esta información a partir de un espacio de tareas bidimensional. En la primera dimensión indicaremos la profundidad de la historia analizada, mientras que en la segunda indicaremos el número de series temporales unitarias en la secuencia multimodal analizada.

Aquí estamos asumiendo que nuestra secuencia multimodal será un conjunto de series temporales unitarias univariantes.

En el cuerpo del kernel, identificamos el flujo actual en todas las dimensiones del espacio de tareas. A continuación, definimos las constantes de desplazamiento en los búferes de datos globales.

   const int shift_data = t * total_v;
   const int shift_out = shift_data * total_v;

Para aclarar el desplazamiento en el búfer de resultados, vale la pena hablar un poco sobre el algoritmo que planeamos implementar en este kernel.

Como hemos mencionado en la parte teórica, los autores del método HiVT proponen sustituir los valores absolutos por valores relativos con la rotación de la escena alrededor del agente central.

Siguiendo esta lógica, primero determinamos el desplazamiento de cada agente en un paso de tiempo individual.

   float value = data[shift_data + v + total_v] - data[shift_data + v];

A continuación, encontramos el ángulo de inclinación del desplazamiento resultante. Obviamente, necesitamos 2 coordenadas de desplazamiento para obtener el ángulo de inclinación en el plano. Pero solo hay 1 indicador en los datos de origen. No obstante, se trata de una serie temporal. Por ello, podemos tomar "1" para el desplazamiento en el segundo eje como un desplazamiento en el eje temporal de 1 paso.

   const float theta = atan(value);

Y ahora podemos determinar el seno y el coseno del ángulo para construir la matriz de rotación.

   const float cos_theta = cos(theta);
   const float sin_theta = sin(theta);

A continuación, podemos realizar la rotación del vector de movimiento del agente central.

   const float2 main = Rotate(value, cos_theta, sin_theta);

Como debemos realizar la rotación para todos los agentes, hemos hecho de esta operación una función separada.

Observe que, como resultado de la rotación, obtenemos un desplazamiento a lo largo de 2 ejes de coordenadas. Y para almacenar los datos, utilizamos la variable vectorial float2.

A continuación, organizamos un ciclo para iterar todos los agentes presentes en un determinado paso temporal.

   for(int a = 0; a < total_v; a++)
     {
      float2 o = main;
      if(a != v)
         o -= Rotate(data[shift_data + a + total_v] - data[shift_data + a], cos_theta, sin_theta);
      output[shift_out + a] = o;
     }
  }

En el cuerpo del ciclo mantendremos el desplazamiento para el agente central, mientras que para los otros agentes contaremos su desplazamiento relativo al central. Para ello, primero determinamos el desplazamiento de cada agente. Lo rotamos según la matriz de rotación del agente central. Y restar el desplazamiento resultante del vector de movimiento del agente central.

Así, para cada agente en cada paso temporal, obtenemos un tensor de descripción de la escena de 2 columnas (coordenadas en el plano) con un número de filas igual al número de series unitarias analizadas.

Aquí debemos decir que los autores del método limitan el número de agentes al radio del segmento local. Nosotros no lo hemos hecho, ya que la divergencia de los valores de los indicadores suele dar señales comerciales bastante buenas.

2.2 La atención dentro de un solo paso temporal

La siguiente cuestión a la que nos enfrentamos durante la aplicación de los enfoques propuestos es la organización de los mecanismos de atención entre agentes dentro de un mismo paso temporal.

Ya hemos implementado antes mecanismos de atención dentro de variables individuales. Pero se trata de un análisis, por así decirlo, "vertical". Y en este caso tendremos que analizar de forma "horizontal". Obviamente, podríamos resolver este problema creando una nueva clase de "atención horizontal", pero se trata de un planteamiento bastante laborioso.

Sin embargo, existe una solución más rápida. Podríamos transponer los datos de origen y aprovechar las soluciones de "atención vertical" disponibles. Sin embargo, deberemos considerar un pequeño detalle: En este caso, el algoritmo disponible de transposición de matrices bidimensionales no es el adecuado. Por ello, crearemos un algoritmo de transposición de tensores tridimensionales. En este proceso de transposición, intercambiaremos las dimensiones 1 y 2, mientras que la 3 permanecerá inalterada.

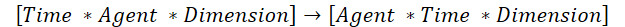
Esto es lo que necesitamos para utilizar los algoritmos de "atención vertical" disponibles.

Para organizar este proceso, crearemos el kernel TransposeRCD.

__kernel void TransposeRCD(__global const float *matrix_in, ///<[in] Input matrix
                           __global float *matrix_out ///<[out] Output matrix
                          )
  {
   const int r = get_global_id(0);
   const int c = get_global_id(1);
   const int d = get_global_id(2);
   const int rows = get_global_size(0);
   const int cols = get_global_size(1);
   const int dimension = get_global_size(2);
//---
   matrix_out[(c * rows + r)*dimension + d] = matrix_in[(r * cols + c) * dimension + d];
  }

Debemos decir que el algoritmo del kernel es casi exactamente el mismo que el del kernel análogo de transposición de una matriz bidimensional. Solo se añade 1 dimensión más del espacio de tareas. Y, en consecuencia, el desplazamiento en los búferes de datos se ajustará para tener en cuenta la medición añadida.

Lo mismo puede decirse de la estructura de clase CNeuronTransposeRCDOCL. Aquí hemos usado deliberadamente la clase de transporte matricial bidimensional CNeuronTransposeOCL como clase padre. 

class CNeuronTransposeRCDOCL  :  public CNeuronTransposeOCL
  {
protected:
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronTransposeRCDOCL(void){};
                    ~CNeuronTransposeRCDOCL(void){};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint count, uint window, uint dimension, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) const { return defNeuronTransposeRCDOCL; }
  };

Observe que no estamos declarando ninguna variable u objeto adicional en el cuerpo de la clase. Las heredadas nos bastan para organizar el proceso. Y esto nos permite redefinir solo los métodos de llamada al kernel, mientras que el resto de la funcionalidad está cubierta por los métodos de la clase padre. Por consiguiente, no nos detendremos ahora en el análisis sintáctico de los algoritmos de los métodos de esta clase. Le sugiero que los analice por su cuenta. Encontrará el código completo de esta clase y todos sus métodos en el archivo adjunto.

2.3 Bloque de atención Agente-Agente

Ahora vamos a pasar a la implementación del bloque de atención Agente-Agente. Recordemos que este bloque asume la construcción de la atención entre las incorporaciones locales de los agentes dentro de un único paso temporal. La clase de transposición tensorial tridimensional creada anteriormente nos ha facilitado mucho el trabajo. Sin embargo, el uso del método de mecanismo de control de combinación de características propuesto por los autores requiere ajustes en el algoritmo.

Para organizar los procesos del bloque de atención indicado, crearemos una nueva clase CNeuronHiVTAAEncoder. Como clase padre en este caso usaremos la capa de atención de variables independientes CNeuronMVMHAttentionMLKV.

class CNeuronHiVTAAEncoder : public CNeuronMVMHAttentionMLKV
  {
protected:
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronHiVTAAEncoder(void){};
                    ~CNeuronHiVTAAEncoder(void){};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint window_key, uint heads, uint heads_kv, 
                          uint units_count, uint layers, uint layers_to_one_kv, uint variables, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronMVMHAttentionMLKV;   }
  };

Como puede ver, tampoco declaramos ninguna variable u objeto adicional en la estructura de esta clase. Esta vez nos favorece la estructura de la clase padre. Recordemos que la clase CNeuronMVMHAttentionMLKV usa colecciones dinámicas de búferes de datos, que a su vez son manejados por los métodos de la clase. Y podemos añadir a las colecciones existentes el número necesario de búferes de datos.

La inicialización de una nueva instancia de un objeto de nuestra clase se realiza en el método Init.

bool CNeuronHiVTAAEncoder::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                                uint window, uint window_key, uint heads, uint heads_kv, 
                                uint units_count, uint layers, uint layers_to_one_kv, uint variables, 
                                ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count * variables, 
                                                                   optimization_type, batch))
      return false;

En los parámetros del método, obtenemos las constantes básicas que nos permiten definir de forma inequívoca la arquitectura del objeto especificado por el usuario. En el cuerpo del método, como siempre, llamamos al método homónimo de la clase básica de la capa neuronal.

Observe que no estamos llamando al método de la clase padre directa, sino de la clase básica, ya que posteriormente todavía tenemos algunos búferes de datos para redefinir.

Una vez ejecutado con éxito el método de la clase padre, guardamos en variables internas las constantes de definición de la arquitectura del objeto obtenidas del programa externo.

   iWindow = fmax(window, 1);
   iWindowKey = fmax(window_key, 1);
   iUnits = fmax(units_count, 1);
   iHeads = fmax(heads, 1);
   iLayers = fmax(layers, 1);
   iHeadsKV = fmax(heads_kv, 1);
   iLayersToOneKV = fmax(layers_to_one_kv, 1);
   iVariables = variables;

Y calculamos directamente las constantes que definen los tamaños de los objetos internos.

   uint num_q = iWindowKey * iHeads * iUnits * iVariables;      //Size of Q tensor
   uint num_kv = iWindowKey * iHeadsKV * iUnits * iVariables;   //Size of KV tensor
   uint q_weights = (iWindow * iHeads + 1) * iWindowKey;        //Size of weights' matrix of Q tenzor
   uint kv_weights = (iWindow * iHeadsKV + 1) * iWindowKey;     //Size of weights' matrix of KV tenzor
   uint scores = iUnits * iUnits * iHeads * iVariables;         //Size of Score tensor
   uint mh_out = iWindowKey * iHeads * iUnits * iVariables;     //Size of multi-heads self-attention
   uint out = iWindow * iUnits * iVariables;                    //Size of attention out tensore
   uint w0 = (iWindowKey * iHeads + 1) * iWindow;               //Size W0 weights matrix
   uint gate = (2 * iWindow + 1) * iWindow;                     //Size of weights' matrix gate layer
   uint self = (iWindow + 1) * iWindow;                         //Size of weights' matrix self layer

El algoritmo en su conjunto se hereda de la clase padre, solo se introducen algunas modificaciones puntuales.

Tras completar el trabajo preparatorio, organizamos un ciclo con un número de iteraciones igual al número determinado de capas anidadas. En el cuerpo de este ciclo, en cada iteración crearemos los objetos necesarios para cumplir la funcionalidad de cada capa anidada aparte.

   for(uint i = 0; i < iLayers; i++)
     {
      CBufferFloat *temp = NULL;
      for(int d = 0; d < 2; d++)
        {
         //--- Initilize Q tensor
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(num_q, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!QKV_Tensors.Add(temp))
            return false;

Aquí crearemos primero los búferes para los datos intermedios y los resultados de los bloques individuales, y también para registrar los gradientes de error correspondientes.

Tenga en cuenta que el búfer de datos y los gradientes de error correspondientes tendrán el mismo tamaño. Por consiguiente, para reducir el trabajo manual, crearemos un ciclo anidado de 2 iteraciones. La primera iteración del ciclo creará los búferes de datos, mientras que la segunda iteración creará los correspondientes búferes de gradiente de error.

Lo primero que haremos es crear un búfer para escribir las entidades Query. A esto le seguirá una cola de búferes para Key y Value.

         //--- Initilize KV tensor
         if(i % iLayersToOneKV == 0)
           {
            temp = new CBufferFloat();
            if(CheckPointer(temp) == POINTER_INVALID)
               return false;
            if(!temp.BufferInit(num_kv, 0))
               return false;
            if(!temp.BufferCreate(OpenCL))
               return false;
            if(!K_Tensors.Add(temp))
               return false;
            temp = new CBufferFloat();
            if(CheckPointer(temp) == POINTER_INVALID)
               return false;
            if(!temp.BufferInit(num_kv, 0))
               return false;
            if(!temp.BufferCreate(OpenCL))
               return false;
            if(!V_Tensors.Add(temp))
               return false;
            temp = new CBufferFloat();
            if(CheckPointer(temp) == POINTER_INVALID)
               return false;
            if(!temp.BufferInit(2 * num_kv, 0))
               return false;
            if(!temp.BufferCreate(OpenCL))
               return false;
            if(!KV_Tensors.Add(temp))
               return false;
           }

Los algoritmos de creación e inicialización de los búferes de datos son completamente idénticos. Solo nuestro algoritmo ofrece la posibilidad de usar un único tensor Key-Value para múltiples capas anidadas. Por lo tanto, antes de crear los búferes, comprobaremos si esta acción es necesaria en la capa actual.

A continuación, inicializaremos el búfer de coeficientes de dependencia entre objetos.

         //--- Initialize scores
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(scores, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!S_Tensors.Add(temp))
            return false;

Y el búfer de resultados de la atención multicabeza.

         //--- Initialize multi-heads attention out
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(mh_out, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!AO_Tensors.Add(temp))
            return false;

Según el algoritmo Multi-Haed Self-Attention, los resultados de la atención multicabeza se comprimen en los datos de origen mediante una capa de proyección. Así que crearemos un búfer para guardar la proyección obtenida.

         //--- Initialize attention out
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(out, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Tensors.Add(temp))
            return false;

El algoritmo descrito hasta ahora sigue casi exactamente el método de la clase padre. Pero también están los cambios introducidos para organizar el mecanismo de gestión de las combinaciones de características. Aquí, según el algoritmo propuesto, primero deberemos concatenar los datos de origen con los resultados del bloque de atención.

         //--- Initialize Concatenate
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(2 * out, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Tensors.Add(temp))
            return false;

Y los coeficientes de control se calcularán sobre su base.

         //--- Initialize Gate
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(out, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Tensors.Add(temp))
            return false;

Después, realizaremos una proyección de los datos de origen.

         //--- Initialize Self
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(out, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Tensors.Add(temp))
            return false;

Y al final del ciclo anidado, crearemos un búfer de resultados de la capa anidada actual.

         //--- Initialize Out
         if(i == iLayers - 1)
           {
            if(!FF_Tensors.Add(d == 0 ? Output : Gradient))
               return false;
            continue;
           }
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit(out, 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Tensors.Add(temp))
            return false;
        }

Observe aquí que solo estamos creando los búferes de resultados y de gradientes para las capas interiores intermedias. Para la última capa anidada, simplemente copiaremos los punteros a los búferes correspondientes de nuestra clase.

Tras crear los búferes de resultados intermedios y los gradientes de error correspondientes, inicializaremos las matrices de parámetros de entrenamiento. Tendremos varias. En primer lugar, hablamos de la matriz de generación de entidades de Query.

      //--- Initilize Q weights
      temp = new CBufferFloat();
      if(CheckPointer(temp) == POINTER_INVALID)
         return false;
      if(!temp.Reserve(q_weights))
         return false;
      float k = (float)(1 / sqrt(iWindow + 1));
      for(uint w = 0; w < q_weights; w++)
        {
         if(!temp.Add(GenerateWeight() * 2 * k - k))
            return false;
        }
      if(!temp.BufferCreate(OpenCL))
         return false;
      if(!QKV_Weights.Add(temp))
         return false;

Aquí primero crearemos un búfer y luego lo llenaremos con parámetros aleatorios. Estos parámetros se optimizarán durante el entrenamiento del modelo.

Del mismo modo, creamos los parámetros para generar las entidades Key y Value. Sin embargo, no generaremos estas matrices para cada capa anidada.

      //--- Initilize K weights
      if(i % iLayersToOneKV == 0)
        {
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.Reserve(kv_weights))
            return false;
         for(uint w = 0; w < kv_weights; w++)
           {
            if(!temp.Add(GenerateWeight() * 2 * k - k))
               return false;
           }
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!K_Weights.Add(temp))
            return false;
         //---
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.Reserve(kv_weights))
            return false;
         for(uint w = 0; w < kv_weights; w++)
           {
            if(!temp.Add(GenerateWeight() * 2 * k - k))
               return false;
           }
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!V_Weights.Add(temp))
            return false;
        }

Además, necesitaremos una matriz para proyectar los resultados de la atención multicabeza.

      //--- Initilize Weights0
      temp = new CBufferFloat();
      if(CheckPointer(temp) == POINTER_INVALID)
         return false;
      if(!temp.Reserve(w0))
         return false;
      for(uint w = 0; w < w0; w++)
        {
         if(!temp.Add(GenerateWeight() * 2 * k - k))
            return false;
        }
      if(!temp.BufferCreate(OpenCL))
         return false;
      if(!FF_Weights.Add(temp))
         return false;

Aquí también añadiremos parámetros para el bloque de control de combinación de características.

      //--- Initilize Gate Weights
      temp = new CBufferFloat();
      if(CheckPointer(temp) == POINTER_INVALID)
         return false;
      if(!temp.Reserve(gate))
         return false;
      k = (float)(1 / sqrt(2 * iWindow + 1));
      for(uint w = 0; w < gate; w++)
        {
         if(!temp.Add(GenerateWeight() * 2 * k - k))
            return false;
        }
      if(!temp.BufferCreate(OpenCL))
         return false;
      if(!FF_Weights.Add(temp))
         return false;

Y las proyecciones de los datos de origen.

      //--- Self
      temp = new CBufferFloat();
      if(CheckPointer(temp) == POINTER_INVALID)
         return false;
      if(!temp.Reserve(self))
         return false;
      k = (float)(1 / sqrt(iWindow + 1));
      for(uint w = 0; w < self; w++)
        {
         if(!temp.Add(GenerateWeight() * 2 * k - k))
            return false;
        }
      if(!temp.BufferCreate(OpenCL))
         return false;
      if(!FF_Weights.Add(temp))
         return false;

A continuación, solo nos quedará añadir los búferes de datos para registrar los momentos a nivel de la matriz de pesos que se utilizarán en el proceso de optimización de los parámetros.

      //---
      for(int d = 0; d < (optimization == SGD ? 1 : 2); d++)
        {
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit((d == 0 || optimization == ADAM ? q_weights : iWindowKey * iHeads), 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!QKV_Weights.Add(temp))
            return false;
         if(i % iLayersToOneKV == 0)
           {
            temp = new CBufferFloat();
            if(CheckPointer(temp) == POINTER_INVALID)
               return false;
            if(!temp.BufferInit((d == 0 || optimization == ADAM ? kv_weights : iWindowKey * iHeadsKV), 0))
               return false;
            if(!temp.BufferCreate(OpenCL))
               return false;
            if(!K_Weights.Add(temp))
               return false;
            //---
            temp = new CBufferFloat();
            if(CheckPointer(temp) == POINTER_INVALID)
               return false;
            if(!temp.BufferInit((d == 0 || optimization == ADAM ? kv_weights : iWindowKey * iHeadsKV), 0))
               return false;
            if(!temp.BufferCreate(OpenCL))
               return false;
            if(!V_Weights.Add(temp))
               return false;
           }
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit((d == 0 || optimization == ADAM ? w0 : iWindow), 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Weights.Add(temp))
            return false;
         //--- Initilize Gate Momentum
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit((d == 0 || optimization == ADAM ? gate : 2 * iWindow), 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Weights.Add(temp))
            return false;
         //--- Initilize Self Momentum
         temp = new CBufferFloat();
         if(CheckPointer(temp) == POINTER_INVALID)
            return false;
         if(!temp.BufferInit((d == 0 || optimization == ADAM ? self : iWindow), 0))
            return false;
         if(!temp.BufferCreate(OpenCL))
            return false;
         if(!FF_Weights.Add(temp))
            return false;
        }
     }

Una vez que los objetos de capa anidados se hayan inicializado correctamente, crearemos un búfer adicional que se usará para registrar temporalmente los resultados intermedios.

   if(!Temp.BufferInit(MathMax(2 * num_kv, out), 0))
      return false;
   if(!Temp.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

Luego finalizaremos el método. Al hacerlo, retornaremos el resultado lógico de las operaciones del método al programa que realiza la llamada.

El siguiente paso, después de inicializar el objeto, consistirá en construir el algoritmo de pasada hacia adelante, que se implementará en el método feedForward.

bool CNeuronHiVTAAEncoder::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(CheckPointer(NeuronOCL) == POINTER_INVALID)
      return false;

En los parámetros de este método obtendremos el puntero al objeto con los datos de origen y comprobaremos inmediatamente la relevancia del puntero recibido. Y si este control tiene éxito, crearemos un ciclo en el que organizaremos la ejecución secuencial de las operaciones de cada capa anidada.

   CBufferFloat *kv = NULL;
   for(uint i = 0; (i < iLayers && !IsStopped()); i++)
     {
      //--- Calculate Queries, Keys, Values
      CBufferFloat *inputs = (i == 0 ? NeuronOCL.getOutput() : FF_Tensors.At(10 * i - 6));
      CBufferFloat *q = QKV_Tensors.At(i * 2);
      if(IsStopped() || 
         !ConvolutionForward(QKV_Weights.At(i * (optimization == SGD ? 2 : 3)), inputs, q, 
                                                       iWindow, iWindowKey * iHeads, None))
         return false;

En primer lugar, generaremos las entidades Query. Y luego, si es necesario, formamos un tensor Key-Value.

      if((i % iLayersToOneKV) == 0)
        {
         uint i_kv = i / iLayersToOneKV;
         kv = KV_Tensors.At(i_kv * 2);
         CBufferFloat *k = K_Tensors.At(i_kv * 2);
         CBufferFloat *v = V_Tensors.At(i_kv * 2);
         if(IsStopped() || 
           !ConvolutionForward(K_Weights.At(i_kv * (optimization == SGD ? 2 : 3)), inputs, k, 
                                                        iWindow, iWindowKey * iHeadsKV, None))
            return false;
         if(IsStopped() || 
            !ConvolutionForward(V_Weights.At(i_kv * (optimization == SGD ? 2 : 3)), inputs, v, 
                                                         iWindow, iWindowKey * iHeadsKV, None))
            return false;
         if(IsStopped() || 
            !Concat(k, v, kv, iWindowKey * iHeadsKV * iVariables, iWindowKey * iHeadsKV * iVariables, iUnits))
            return false;
        }

Una vez formados los tensores de las entidades requeridas, podremos calcular los resultados de la atención multicabeza.

      //--- Score calculation and Multi-heads attention calculation
      CBufferFloat *temp = S_Tensors.At(i * 2);
      CBufferFloat *out = AO_Tensors.At(i * 2);
      if(IsStopped() || !AttentionOut(q, kv, temp, out))
         return false;

Y los comprimiremos hasta la dimensionalidad de los datos de origen.

      //--- Attention out calculation
      temp = FF_Tensors.At(i * 10);
      if(IsStopped() || 
         !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9)), out, temp, 
                                                       iWindowKey * iHeads, iWindow, None))
         return false;

Para calcular los coeficientes de control, primero concatenaremos los resultados del bloque de atención y los datos de origen.

      //--- Concat
      out = FF_Tensors.At(i * 10 + 1);
      if(IsStopped() || !Concat(temp, inputs, out, iWindow, iWindow, iUnits))
         return false;

Y luego calcularemos los coeficientes de control.

      //--- Gate
      if(IsStopped() || 
         !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 1), out, 
                                 FF_Tensors.At(i * 10 + 2), 2 * iWindow, iWindow, SIGMOID))
         return false;

Nos quedará hacer una proyección de los datos de origen.

      //--- Self
      if(IsStopped() || 
         !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 2), inputs, 
                                         FF_Tensors.At(i * 10 + 3), iWindow, iWindow, None))
         return false;

A continuación, combinaremos la proyección obtenida con los resultados del bloque de atención considerando los coeficientes de control.

      //--- Out
      if(IsStopped() || 
        !GateElementMult(FF_Tensors.At(i * 10 + 3), temp, FF_Tensors.At(i * 10 + 2), 
                                                          FF_Tensors.At(i * 10 + 4)))
         return false; 
     }
//---
   return true;
  }

Y procederemos a trabajar con la siguiente capa anidada en una nueva iteración del ciclo.

Una vez que las operaciones de todas las capas anidadas se hayan ejecutado con éxito, finalizaremos el método y retornaremos el resultado lógico de las operaciones del método al programa que realiza la llamada.

Con esto concluiremos nuestro trabajo sobre los métodos de pasada directa. Le sugiero que se familiarice con los algoritmos de los métodos de pasada inversa. Permítame recordarle que el código completo de esta clase y sus métodos, así como todos los programas utilizados en la preparación de este artículo, se pueden encontrar en el archivo adjunto.

Conclusión

En este artículo hemos introducido un método bastante interesante y prometedor, el Transformador vectorial jerárquico (HiVT), propuesto para la predicción de movimientos multiagente. Este método ofrece un enfoque eficaz para resolver el problema de la predicción descomponiendo el problema en etapas de extracción del contexto local y modelización global de las interacciones.

Los autores del método abordan el problema de forma exhaustiva y proponen una serie de enfoques para mejorar la eficacia del modelo propuesto. Por desgracia, el volumen del trabajo sobre la aplicación de los enfoques propuestos excede el formato del artículo. Y en esta ocasión solo hemos podido hacer algunos trabajos preparatorios. Finalizaremos el trabajo iniciado en el próximo artículo. También presentaremos los resultados de las pruebas de los enfoques propuestos con datos históricos reales.

Enlaces

HiVT: Hierarchical Vector Transformer for Multi-Agent Motion Prediction

Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor de recopilación de ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de Modelos
4	StudyEncoder.mq5	Asesor	Asesor de entrenamiento del Codificador
5	Test.mq5	Asesor	Asesor para la prueba de modelos
6	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema.
7	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
8	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL