
Нейросети — это просто (Часть 8): Механизмы внимания
Содержание
- Введение
- 1. Механизмы внимания
- 2. Алгоритм Self-Attention
- 3. Реализация
- 3.1. Модернизируем сверточный слой
- 3.2. Класс блока Self-Attention
- 3.3. Прямой проход Self-Attention
- 3.4. Обратный проход Self-Attention
- 3.5. Точечные изменения в базовых классах нейронной сети
- 4. Тестирование
- Заключение
- Ссылки
- Программы, используемые в статье
Введение
В предыдущих статьях мы уже протестировали различные варианты организации нейронных сетей. В том числе сверточные сети,[3] заимствованные из алгоритмов обработки изображений, и рекуррентные нейронные сети [4], используемые для работы с последовательностями, в которых важны как сами значения, так и их место в исходном наборе данных.
Полносвязные и сверточные нейронные сети имеют фиксированные размер входной последовательности. Рекуррентные нейронные сети позволяют немного расширить анализируемую последовательность за счет передачи скрытых состояний с предыдущих итераций. Но и их эффективность снижается с ростом последовательности. В 2014 году в области программного перевода было предложено использование первого механизма внимания, который был призван программным путем определять и выделять блоки исходного предложения (контекст), наиболее релевантные для целевого слова перевода. Такой интуитивно понятный людям подход, позволил значительно повысить качество перевода текстов нейронными сетями.
1. Механизмы внимания
Анализируя свечной график движения инструмента, мы выделяем тренды и тенденции, определяем зоны "проторговки". Т.е. из общей картины мы выделяем некоторые объекты, концентрируя свое внимание именно на них. Для нас интуитивно понятно, что объекты в разной степени влияют на будущее поведение цены. Для реализации именно такого подхода и был предложен в сентябре 2014 года первый алгоритм, анализирующий и выделяющий зависимости между элементами входной и выходной последовательностей [8]. Предложенный алгоритм называют "обобщенный механизм внимания". И изначально он был предложен для использования в моделях машинного перевода с использованием рекуррентных сетей и решал задачу долгосрочной памяти в переводе длинных предложений. Такой подход значительно превысил результаты, ранее рассмотренных нами рекуррентных нейронных сетей на основе LSTM блоков [4].
Классическая модель машинного перевода с использованием рекуррентных сетей состоит из двух блоков Encoder и Decoder. Первый кодирует входную последовательность на исходном языке в вектор контекста, а второй декодирует полученный контекст в последовательность слов на целевом языке. С увеличением длины входной последовательности влияние первых слов на итоговый контекст предложения снижается, и, как следствие, снижается качество перевода. Использование LSTM блоков немного увеличивало возможности модели, но все равно они оставались ограниченными.
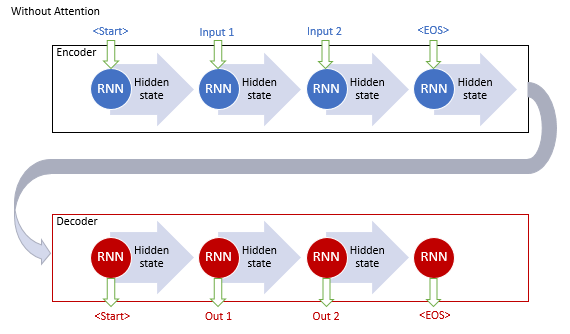
Авторы базового механизма внимания предложили использовать дополнительный слой, который бы аккумулировал скрытые состояния всех рекуррентных блоков входной последовательности. И далее, в процессе декодирования последовательности, оценивал бы влияние каждого элемента входной последовательности на текущее слово выходной последовательности и предлагал декодеру наиболее релевантную часть контекста.
Алгоритм работы такого механизма включал следующие итерации:
1. Создание скрытых состояний Encoder и аккумулирование их в блоке внимания.
2. Оценка парных зависимостей между скрытыми состояниями каждого элемента Encoder и последнего срытого состояния Decoder.
3. Полученные оценки объединяются в единый вектор и нормализуются путем использования функции Softmax.
4. Вычисления вектора контекста, путем умножения всех скрытых состояний Encoder на соответствующее им оценки выравнивания.
5. Декодирование вектора контекста и объединение полученного значения с предыдущим состоянием Decoder.
Все итерации повторяются до получения сигнала конца предложения.
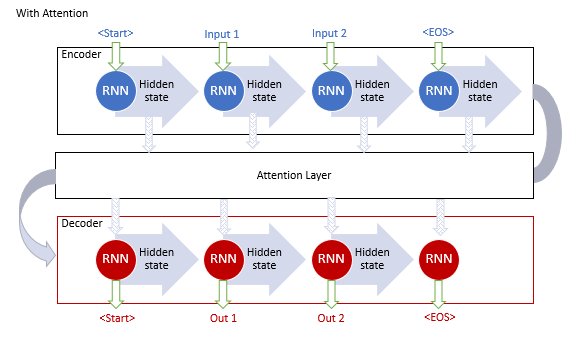
Предложенный механизм позволил решить проблему с ограничением длины входной последовательности и повысить качество машинного перевода с использованием рекуррентных нейронных сетей. И как следствие, получил широкое распространение и различные вариации реализации. В частности, в августе 2015 год Minh-Thang Luong в статье [9] предложил свою вариацию метода внимания. Основными отличиями нового подхода стали использование трех функций для вычисления степени зависимостей и точка использования механизма внимания в Decoder.
Описанные выше модели используют рекуррентные блоки, обучение которых требует много затрат. В июне 2017 года в статье [10] была предложена новая архитектура нейронной сети Трансформер, в которой отказались от использования рекуррентных блоков и предложили новый алгоритм внимания Self-Attention. В отличии от описанного выше алгоритм Self-Attention анализирует парные зависимости внутри одной последовательности. На тестах Трансформер показал лучшие результаты и на сегодняшний день данная модель и ее производные используется во многих моделях, в том числе GPT-2 и GPT-3. Рассмотрим алгоритм Self-Attention подробнее.
2. Алгоритм Self-Attention
В основе архитектуры Трансформера лежат последовательные блоки Encoder и Decoder со схожей архитектурой. Каждый из блоков включает несколько одинаковых слоев с разными весовыми матрицами.
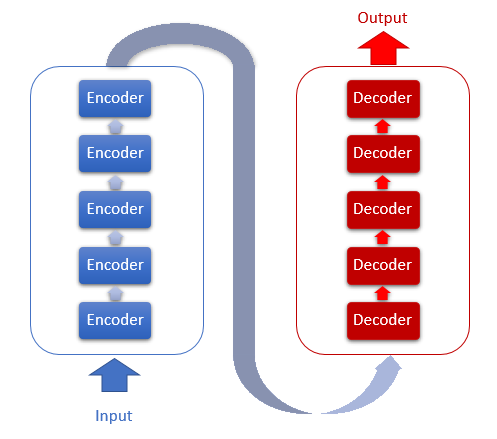
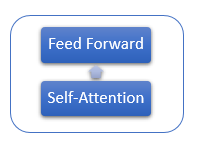
Каждый слой Encoder содержит 2 внутренних слоя: Self-Attention и Feed Forward. Слой Feed Forward включает 2 полносвязных слоя нейронов с функцией активации ReLU на внутреннем слое. Каждый слой применяется для всех элементов последовательности с одинаковыми весовыми коэффициентами, что позволяет одновременно проводить независимые вычисления для всех элементов последовательности в параллельных потоках.
Слой Decoder имеет схожую структуру, но добавляется еще один слой Self-Attention, анализирующий зависимости между входными и выходными последовательностями.
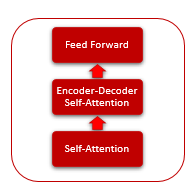
Сам же механизм Self-Attention включается в себя несколько итерационных действий, применяемых для каждого элемента последовательности.
1. Вначале вычисляем векторы Query (запрос), Key (ключ) и Value (значение). Указанные векторы получаются путем умножения каждого элемента последовательности на соответствующую матрицу WQ, WK и WV.
2. Далее определяем парные зависимости между элементами последовательности. Для этого перемножим вектор Query с векторами Key всех элементов последовательности. Данная итерация повторяется для вектора Query каждого элемента последовательности. В результате данной итерации получаем матрицу Score размером N*N, где N — размер последовательности.
3. Следующим этапом разделим полученные значение на квадратный корень из размерности вектора Key и нормализуем функцией Softmax в разрезе каждого Query. Таким образом, получаем коэффициенты попарной взаимозависимости между элементами последовательности.
4. Умножением каждого вектора Value на соответствующий коэффициент взаимозависимости получаем скорректированное значение элемента. Цель данной итерации — акцентировать внимание на релевантных элементах и снизить влияние нерелевантных значений.
5. Далее суммируем все скорректированные вектора Value для каждого элемента. Результат данной операции и будет вектор выходных значений слоя Self-Attention.
Результаты итераций каждого слоя складываются с входной последовательностью и нормализуются по формуле.
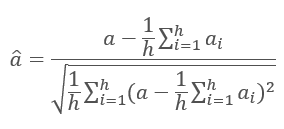
Подробнее о нормализации слоев нейронной сети рассказывается в статье [11].
3. Реализация
В нашей разработке предлагаю реализовать механизм Self-Attention. Давайте проработаем варианты реализации.
3.1. Модернизируем сверточный слой
Рассмотрим первое действие алгоритма Self-Attention — вычисление векторов Qeury, Key и Value. На входе мы получаем матрицу данных, содержащую признаки по каждому бару анализируемой последовательности. Поочередно мы берем признаки одной свечи и, перемножая их с матрицей весов, получаем вектор. На мой взгляд это очень напоминает рассмотренный в статье [3] сверточный слой. Только на выходе должно быть не одно число, а вектор фиксированной длины. Для решения этой задачи модернизируем класс CNeuronConvOCL, отвечающий за работу сверточного слоя нейронной сети. Добавим переменную iWindowOut, в которой будем хранить размер выходного вектора, и внесем соответствующие корректировки в методы класса.
class CNeuronConvOCL : public CNeuronProofOCL { protected: uint iWindowOut; //--- CBufferDouble *WeightsConv; CBufferDouble *DeltaWeightsConv; CBufferDouble *FirstMomentumConv; CBufferDouble *SecondMomentumConv; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronConvOCL(void) : iWindowOut(1) { activation=LReLU; } ~CNeuronConvOCL(void); virtual bool Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint window, uint step, uint window_out, uint units_count, ENUM_OPTIMIZATION optimization_type); //--- virtual bool SetGradientIndex(int index) { return Gradient.BufferSet(index); } //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); virtual int Type(void) const { return defNeuronConvOCL; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); };
В OpenCL кернеле FeedForwardConv добавим параметр для получения размера выходного вектора, добавим вычисление смещения обрабатываемого участка выходного вектора в общем векторе на выходе сверточного слоя и организуем дополнительный цикл по перебору элементов выходного вектора.
__kernel void FeedForwardConv(__global double *matrix_w, __global double *matrix_i, __global double *matrix_o, int inputs, int step, int window_in, int window_out, uint activation) { int i=get_global_id(0); int w_in=window_in; int w_out=window_out; double sum=0.0; double4 inp, weight; int shift_out=w_out*i; int shift_in=step*i; for(int out=0;out<w_out;out++) { int shift=(w_in+1)*out; int stop=(w_in<=(inputs-shift_in) ? w_in : (inputs-shift_in)); for(int k=0; k<=stop; k=k+4) { switch(stop-k) { case 0: inp=(double4)(1,0,0,0); weight=(double4)(matrix_w[shift+k],0,0,0); break; case 1: inp=(double4)(matrix_i[shift_in+k],1,0,0); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],0,0); break; case 2: inp=(double4)(matrix_i[shift_in+k],matrix_i[shift_in+k+1],1,0); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],matrix_w[shift+k+2],0); break; case 3: inp=(double4)(matrix_i[shift_in+k],matrix_i[shift_in+k+1],matrix_i[shift_in+k+2],1); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],matrix_w[shift+k+2],matrix_w[shift+k+3]); break; default: inp=(double4)(matrix_i[shift_in+k],matrix_i[shift_in+k+1],matrix_i[shift_in+k+2],matrix_i[shift_in+k+3]); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],matrix_w[shift+k+2],matrix_w[shift+k+3]); break; } sum+=dot(inp,weight); } switch(activation) { case 0: sum=tanh(sum); break; case 1: sum=1/(1+exp(-clamp(sum,-50.0,50.0))); break; case 2: if(sum<0) sum*=0.01; break; default: break; } matrix_o[out+shift_out]=sum; } }
И не забываем добавить передачу дополнительного параметра при вызове данного кернела.
bool CNeuronConvOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=Output.Total()/iWindowOut; OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_w,WeightsConv.GetIndex()); OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_i,NeuronOCL.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_o,Output.GetIndex()); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_inputs,NeuronOCL.Neurons()); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_step,iStep); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_window_in,iWindow); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffс_window_out,iWindowOut); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_activation,(int)activation); if(!OpenCL.Execute(def_k_FeedForwardConv,1,global_work_offset,global_work_size)) { printf("Error of execution kernel FeedForwardProof: %d",GetLastError()); return false; } //--- return Output.BufferRead(); }
Аналогичные изменения были внесены в кернелы и методы пересчета градиентов (calcInputGradients) и обновления матрицы весовых коэффициентов (updateInputWeights). С полным кодом всех методов и функций можно ознакомиться во вложении.
3.2. Класс блока Self-Attention
Далее приступим к реализации непосредственно самого метода Self-Attention. Для его описания создадим класс CNeuronAttentionOCL. Так как все операции у нас повторяются для каждого элемента и выполняются независимо, то мы вынесем часть операций в модернизированные сверточные слои. Создадим внутри нашего блока внимания сверточные слои Querys, Keys, Values, которые будут отвечать за созданием соответствующих векторов, а также за передачу градиентов и обновление матрицы весов. Блок FeedForward также организуем с использованием сверточных слоев FF1 и FF2. Значения матрицы Score будем сохранять в буфере Scores, а результаты метода внимания во внутренний слой нейронов базового класса AttentionOut.
Здесь следует обратить внимание на отличие выхода алгоритма внимания от выхода всего нашего класса Self-Attention. Первый получаем после выполнения алгоритма Self-Attention корректировкой значений векторов Value и сохраняем в AttentionOut, а второй после отработки FeedForward и сохраняем в буфере Output базового класса.
class CNeuronAttentionOCL : public CNeuronBaseOCL { protected: CNeuronConvOCL *Querys; CNeuronConvOCL *Keys; CNeuronConvOCL *Values; CBufferDouble *Scores; CNeuronBaseOCL *AttentionOut; CNeuronConvOCL *FF1; CNeuronConvOCL *FF2; //--- uint iWindow; uint iUnits; //--- virtual bool feedForward(CNeuronBaseOCL *prevLayer); virtual bool updateInputWeights(CNeuronBaseOCL *prevLayer); public: CNeuronAttentionOCL(void) : iWindow(1), iUnits(0) {}; ~CNeuronAttentionOCL(void); virtual bool Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl, uint window, uint units_count, ENUM_OPTIMIZATION optimization_type); virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); //--- virtual int Type(void) const { return defNeuronAttentionOCL; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); };
В переменных iWindows и iUnits будем сохранять размер выходного окна и количество элементов входной последовательности, соответственно.
Инициализацию класса будем осуществлять в методе Init. В параметрах методу будем передавать порядковый номер элемента, указатель на объект COpenCL, размер окна, количество элементов и метод оптимизации. В начале метода вызовем аналогичный метод родительского класса.
bool CNeuronAttentionOCL::Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint window,uint units_count,ENUM_OPTIMIZATION optimization_type) { if(!CNeuronBaseOCL::Init(numOutputs,myIndex,open_cl,units_count*window,optimization_type)) return false;
Затем объявим и инициализируем экземпляры класса сверточной сети для вычисления векторов Querys, Keys и Values.
//--- if(CheckPointer(Querys)==POINTER_INVALID) { Querys=new CNeuronConvOCL(); if(CheckPointer(Querys)==POINTER_INVALID) return false; if(!Querys.Init(0,0,open_cl,window,window,window,units_count,optimization_type)) return false; Querys.SetActivationFunction(TANH); } //--- if(CheckPointer(Keys)==POINTER_INVALID) { Keys=new CNeuronConvOCL(); if(CheckPointer(Keys)==POINTER_INVALID) return false; if(!Keys.Init(0,1,open_cl,window,window,window,units_count,optimization_type)) return false; Keys.SetActivationFunction(TANH); } //--- if(CheckPointer(Values)==POINTER_INVALID) { Values=new CNeuronConvOCL(); if(CheckPointer(Values)==POINTER_INVALID) return false; if(!Values.Init(0,2,open_cl,window,window,window,units_count,optimization_type)) return false; Values.SetActivationFunction(None); }
Двигаясь далее по алгоритму, объявим буфер Scores. Обратите внимание на размер буфера, в нем должно быть достаточно памяти для хранения квадратной матрицы со стороной равной количеству элементов в последовательности.
if(CheckPointer(Scores)==POINTER_INVALID) { Scores=new CBufferDouble(); if(CheckPointer(Scores)==POINTER_INVALID) return false; } if(!Scores.BufferInit(units_count*units_count,0.0)) return false; if(!Scores.BufferCreate(OpenCL)) return false;
Также объявим слой нейронов AttentionOut. Данный слой будет служить буфером для сохранения результатов работы Self-Attention и одновременно входным слоем блока FeedForward. Его размер равен произведению ширины окна на количество элементов.
if(CheckPointer(AttentionOut)==POINTER_INVALID) { AttentionOut=new CNeuronBaseOCL(); if(CheckPointer(AttentionOut)==POINTER_INVALID) return false; if(!AttentionOut.Init(0,3,open_cl,window*units_count,optimization_type)) return false; AttentionOut.SetActivationFunction(None); }
И инициализируем два экземпляра сверточного слоя для реализации блока FeedForward. Обратите внимание, что первый (скрытый слой) на выходе возвращает окно в 2 раза шире и имеет функцию активации LReLU (ReLU c "утечкой"). А у второго слоя (FF2) методом SetGradientIndex подменяем буфер градиента на буфер градиента родительского класса. Подмена буфера поможет нам исключить операцию копирования данных.
if(CheckPointer(FF1)==POINTER_INVALID) { FF1=new CNeuronConvOCL(); if(CheckPointer(FF1)==POINTER_INVALID) return false; if(!FF1.Init(0,4,open_cl,window,window,window*2,units_count,optimization_type)) return false; FF1.SetActivationFunction(LReLU); } //--- if(CheckPointer(FF2)==POINTER_INVALID) { FF2=new CNeuronConvOCL(); if(CheckPointer(FF2)==POINTER_INVALID) return false; if(!FF2.Init(0,5,open_cl,window*2,window*2,window,units_count,optimization_type)) return false; FF2.SetActivationFunction(None); FF2.SetGradientIndex(Gradient.GetIndex()); }
И в заключении метода сохраняем ключевые параметры.
iWindow=window; iUnits=units_count; activation=FF2.Activation(); //--- return true; }
3.3. Прямой проход Self-Attention
Следующим этапом рассмотрим метод feedForward класса CNeuronAttentionOCL. В параметрах метод получает указатель на предыдущий слой нейронной сети и, первым делом, проверяем действительность полученного указателя.
bool CNeuronAttentionOCL::feedForward(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false;
Перед дальнейшей обработкой данных проведем нормализацию входных данных. Данный шаг не предусмотрен авторским механизмом Self-Attention, но был добавлен по результатам тестирования для предотвращения переполнения на этапе нормализации матрицы Score. Для нормализации данных был создан специальный кернел, а в методе feedForward осуществим его вызов.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=1;
OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,prevLayer.getOutputIndex());
OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,prevLayer.Neurons());
if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel Normalize: %d",GetLastError());
return false;
}
if(!prevLayer.Output.BufferRead())
return false;
}
Посмотрим внутрь кернела нормализации. В начале кернела вычислим смещение до первого элемента нормализуемой последовательности. Затем вычислим среднее значение для нормализуемой последовательности и среднеквадратичное отклонение. И в заключении кернела обновим данные в буфере.
__kernel void Normalize(__global double *buffer, int dimension) { int n=get_global_id(0); int shift=n*dimension; double mean=0; for(int i=0;i<dimension;i++) mean+=buffer[shift+i]; mean/=dimension; double variance=0; for(int i=0;i<dimension;i++) variance+=pow(buffer[shift+i]-mean,2); variance=sqrt(variance/dimension); for(int i=0;i<dimension;i++) buffer[shift+i]=(buffer[shift+i]-mean)/(variance==0 ? 1 : variance); }
После нормализации исходных данных вычислим вектора Querys, Keys и Values. Для этого вызовем метод FeedForward соответствующего экземпляра класса сверточного слоя (данный метод рассмотрен выше).
if(CheckPointer(Querys)==POINTER_INVALID || !Querys.FeedForward(prevLayer)) return false; if(CheckPointer(Keys)==POINTER_INVALID || !Keys.FeedForward(prevLayer)) return false; if(CheckPointer(Values)==POINTER_INVALID || !Values.FeedForward(prevLayer)) return false;
Двигаясь далее по алгоритму Self-Attention, вычислим матрицу Score. Вычисления также будем производить на GPU с использование OpenCL. В методе основной программы организуем вызов кернела. Количество вызываемых потоков равно количеству юнитов в классе, при этом каждый поток будет работать в размере своего окна. Иными словами, каждый поток возьмет свой Query вектор одного элемента и сопоставит его с векторами Key всех элементов последовательности.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_querys,Querys.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_keys,Keys.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_score,Scores.GetIndex());
OpenCL.SetArgument(def_k_AttentionScore,def_k_as_dimension,iWindow);
if(!OpenCL.Execute(def_k_AttentionScore,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel AttentionScore: %d",GetLastError());
return false;
}
if(!Scores.BufferRead())
return false;
}
В начале кернела определяем смещения начального элемента по массивам querys и score. Вычислим коэффициент для уменьшения полученных значений. И обнулим переменную для подсчета суммы, которая нам потребуется при нормализации значений. Далее организуем цикл по перебору всех элементов матрицы ключей с вычислением соответствующих зависимостей. Следует заметить, что рассматриваемый кернел объединил этапы вычисления и нормализации матрицы score. Поэтому, после вычисления произведений векторов Query и Key, полученное значение разделим на коэффициент и вычислим экспоненту полученного значения. Полученную экспоненту сохраним в матрицу и прибавим к сумме. По завершении цикла, организуем второй цикл, в котором все значения, сохраненные в предыдущем цикле, разделим на посчитанную сумму экспонент. На выходе из кернела получаем пересчитанную и нормализованную матрицу Score.
__kernel void AttentionScore(__global double *querys, __global double *keys, __global double *score, int dimension) { int q=get_global_id(0); int shift_q=q*dimension; int units=get_global_size(0); int shift_s=q*units; double koef=sqrt((double)(units*dimension)); if(koef<1) koef=1; double sum=0; for(int k=0;k<units;k++) { double result=0; int shift_k=k*dimension; for(int i=0;i<dimension;i++) result+=(querys[shift_q+i]*keys[shift_k+i]); result=exp(result/koef); score[shift_s+k]=result; sum+=result; } for(int k=0;k<units;k++) score[shift_s+k]/=sum; }
Двигаемся дальше по алгоритму Self-Attention. После нормализации матрицы Score нам остается скорректировать вектора Values на полученные значения и просуммировать полученные вектора в разрезе элементов входной последовательности. На выходе из блока Self-Attention полученные значения складываются с входной последовательностью. Все эти итерации объединены в следующем кернеле AttentionOut. В коде основной программы организуем вызов данного кернела. Обратите внимание, что этот кернел мы будем запускать с набором потоков в двух изменениях: по элементам последовательности (iUnits) и по количеству признаков для каждого элемента (iWindow). Сохранять полученные значения будем в выходной буфер слоя AttentionOut.
{
uint global_work_offset[2]={0,0};
uint global_work_size[2];
global_work_size[0]=iUnits;
global_work_size[1]=iWindow;
OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_scores,Scores.GetIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_inputs,prevLayer.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_values,Values.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_out,AttentionOut.getOutputIndex());
if(!OpenCL.Execute(def_k_AttentionOut,2,global_work_offset,global_work_size))
{
printf("Error of execution kernel Attention Out: %d",GetLastError());
return false;
}
double temp[];
if(!AttentionOut.getOutputVal(temp))
return false;
}
В теле кернела определим смещение для обрабатываемого элемента в векторах входной и выходной последовательностей. Затем организуем цикл по суммированию произведений коэффициентов Score на соответствующие значения Value. По завершении циклических итераций полученную сумму складываем с входным вектором, полученным от предыдущего слоя нашей нейронной сети. Результат записываем в исходящий буфер.
__kernel void AttentionOut(__global double *scores, __global double *values, __global double *inputs, __global double *out) { int units=get_global_size(0); int u=get_global_id(0); int d=get_global_id(1); int dimension=get_global_size(1); int shift=u*dimension+d; double result=0; for(int i=0;i<units;i++) result+=scores[u*units+i]*values[i*dimension+d]; out[shift]=result+inputs[shift]; }
На этом алгоритм Self-Attention можно считать выполненным. Остается нормализовать полученные данные методом, описанным выше. Разница только в буфере для нормализации.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=1;
OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,AttentionOut.getOutputIndex());
OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,AttentionOut.Neurons());
if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel Normalize: %d",GetLastError());
return false;
}
double temp[];
if(!AttentionOut.getOutputVal(temp))
return false;
}
Далее, по алгоритму энкодера Трансформера, пропускаем каждый элемент последовательности через полносвязную нейронную сеть с одним скрытым слоем. При этом для всех элементов последовательности применяется одна и та же матрица весовых коэффициентов. Я реализовал данный процесс путем использования модернизированного класса сверточного слоя. И в коде метода последовательно вызываю методы FeedForward соответствующих экземпляров сверточного класса.
if(!FF1.FeedForward(AttentionOut)) return false; if(!FF2.FeedForward(FF1)) return false;
Для завершения процесса прямого прохода нам остается сложить результаты прохода полносвязной сети с результатами работы механизма Self-Attention. Для этого был создан kernel сложения двух векторов, который мы вызываем в завершении нашего метода прямого прохода.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,FF2.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,Output.GetIndex());
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow);
if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel MatrixSum: %d",GetLastError());
return false;
}
if(!Output.BufferRead())
return false;
}
//---
return true;
}
Внутри кернела организован простой цикл с поэлементным суммированием значений входящих векторов.
__kernel void SumMatrix(__global double *matrix1, __global double *matrix2, __global double *matrix_out, int dimension) { const int i=get_global_id(0)*dimension; for(int k=0;k<dimension;k++) matrix_out[i+k]=matrix1[i+k]+matrix2[i+k]; }
С полным кодом всех методов и функций можно ознакомиться во вложении.
3.4. Обратный проход Self-Attention
За прямым проходом следует обратный проход, в ходе которого передается ошибка на нижние слои нейронной сети и корректируются матрицы весов для подбора оптимальных результатов. От верхнего полносвязного слоя нейронной сети наш класс получает градиент ошибки методом родительского класса, описанном в статье [5]. Дальнейший механизм передачи градиента ошибки требует значительной доработки, что обусловлено сложностью внутренней архитектуры.
Для передачи градиента ошибки во внутренние сверточные слои и на предыдущий нейронный слой нашей сети создадим метод calcInputGradients. В параметрах метод получает указатель на предыдущий слой нейронов и, как всегда, сразу проверяем действительность полученной ссылки. И затем в обратном порядке последовательно вызываем одноименные методы сверточных слоев блока Feed Forward FF2 и FF1. Напомню, что благодаря подмене буфера наш внутренний слой FF2 получает градиент ошибки напрямую от последующего слоя нейронной сети методами родительского класса.
bool CNeuronAttentionOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false; //--- if(!FF2.calcInputGradients(FF1)) return false; if(!FF1.calcInputGradients(AttentionOut)) return false;
Так как на выходе прямого прохода мы складывали результаты Feed Forward и Self-Attention, то и градиент ошибки к нам приходит по двум веткам. Следовательно, градиент ошибки, полученный от FF1 суммируем с градиентом ошибки, полученным от последующего слоя нейронной сети. Кернел суммирования векторов описан выше, а здесь мы добавим его вызов.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,Gradient.GetIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex());
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow);
if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel MatrixSum: %d",GetLastError());
return false;
}
double temp[];
if(AttentionOut.getGradient(temp)<=0)
return false;
}
Следующим шагом распространим градиент ошибки на Querys, Keys и Values. Работу по передаче градиента ошибки на вектора организуем в кернеле AttentionIsideGradients, а данном методе организуем его вызов с набором потоков в двух измерениях.
{
uint global_work_offset[2]={0,0};
uint global_work_size[2];
global_work_size[0]=iUnits;
global_work_size[1]=iWindow;
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_gradient,AttentionOut.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_keys,Keys.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_keys_g,Keys.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_querys,Querys.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_querys_g,Querys.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_values,Values.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_values_g,Values.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_scores,Scores.GetIndex());
if(!OpenCL.Execute(def_k_AttentionGradients,2,global_work_offset,global_work_size))
{
printf("Error of execution kernel AttentionGradients: %d",GetLastError());
return false;
}
double temp[];
if(Keys.getGradient(temp)<=0)
return false;
}
В параметрах кернел получает указатели на буфера данных, а размерности измерений определим вначале кернела по количеству запущенных потоков. Затем вычислим корректирующий коэффициент и организуем цикл по перебору всех элементов последовательности. Внутри цикла сначала посчитаем градиент ошибки на векторе Value, перемножив вектор градиента на соответствующий вектор Score. Обратите внимание, что градиент ошибки мы делим на 2. Это связано с тем, что, просуммировав его на предыдущем шаге, мы задваиваем ошибку, а поделив на два, в расчет берем среднее значение.
__kernel void AttentionIsideGradients(__global double *querys,__global double *querys_g, __global double *keys,__global double *keys_g, __global double *values,__global double *values_g, __global double *scores, __global double *gradient) { int u=get_global_id(0); int d=get_global_id(1); int units=get_global_size(0); int dimension=get_global_size(1); double koef=sqrt((double)(units*dimension)); if(koef<1) koef=1; //--- double vg=0; double qg=0; double kg=0; for(int iu=0;iu<units;iu++) { double g=gradient[iu*dimension+d]/2; double sc=scores[iu*units+u]; vg+=sc*g;
Далее организуем вложенный цикл по определению градиента на элементах матрицы Score. После чего вычислим градиент элементов векторов Querys и Keys. По завершении внешнего цикла присваиваем посчитанные градиенты соответствующим глобальным буферам.
//--- double sqg=0; double skg=0; for(int id=0;id<dimension;id++) { sqg+=values[iu*dimension+id]*gradient[u*dimension+id]/2; skg+=values[u*dimension+id]*gradient[iu*dimension+id]/2; } qg+=(scores[u*units+iu]==0 || scores[u*units+iu]==1 ? 0.0001 : scores[u*units+iu]*(1-scores[u*units+iu]))*sqg*keys[iu*dimension+d]/koef; //--- kg+=(scores[iu*units+u]==0 || scores[iu*units+u]==1 ? 0.0001 : scores[iu*units+u]*(1-scores[iu*units+u]))*skg*querys[iu*dimension+d]/koef; } int shift=u*dimension+d; values_g[shift]=vg; querys_g[shift]=qg; keys_g[shift]=kg; }
Далее нам предстоит передать градиенты ошибок с векторов Querys, Keys и Values. Здесь следует обратить внимание, что, так как все вектора получаются путем умножения одних и тех же исходных данных на разные матрицы, то и градиенты ошибок нам предстоит сложить. Для аккумулирования градиентов ошибок я не выделял отдельный буфер, а суммирование значений при вычислении градиентов требует дополнительного усложнение кода с отслеживанием моментов обнуления буфера. Было принято решение использовать существующие методы для вычисления градиентов ошибок с последующим аккумулированием значений в буфере градиента слоя AttentionOut.
if(!Querys.calcInputGradients(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(AttentionOut.getGradient(temp)<=0) return false; } //--- if(!Keys.calcInputGradients(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(AttentionOut.getGradient(temp)<=0) return false; } //--- if(!Values.calcInputGradients(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,prevLayer.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow+1); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(prevLayer.getGradient(temp)<=0) return false; } //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=1; OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,prevLayer.getGradientIndex()); OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,prevLayer.Neurons()); if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size)) { printf("Error of execution kernel Normalize: %d",GetLastError()); return false; } double temp[]; if(prevLayer.getGradient(temp)<=0) return false; } //--- return true; }
После передачи градиента ошибки на уровень предыдущего слоя скорректируем матрицы весовых коэффициентов в методе updateInputWeights. Построение данного метода на мой взгляд не представляет сложностей. В нем лишь осуществляется вызов одноименных методов вложенных сверточных слоев.
bool CNeuronAttentionOCL::updateInputWeights(CNeuronBaseOCL *prevLayer) { if(!Querys.UpdateInputWeights(prevLayer)) return false; if(!Keys.UpdateInputWeights(prevLayer)) return false; if(!Values.UpdateInputWeights(prevLayer)) return false; if(!FF1.UpdateInputWeights(AttentionOut)) return false; if(!FF2.UpdateInputWeights(FF1)) return false; //--- return true; }
3.5. Точечные изменения в базовых классах нейронной сети
Завершив работу с классом нашего блока внимания внесем точечные дополнения в базовые классы нашей нейронной сети. Прежде всего добавим константы в блок define для работы с новыми кернелами.
#define def_k_FeedForwardConv 7 #define def_k_ffc_matrix_w 0 #define def_k_ffc_matrix_i 1 #define def_k_ffc_matrix_o 2 #define def_k_ffc_inputs 3 #define def_k_ffc_step 4 #define def_k_ffc_window_in 5 #define def_k_ffс_window_out 6 #define def_k_ffc_activation 7 //--- #define def_k_CalcHiddenGradientConv 8 #define def_k_chgc_matrix_w 0 #define def_k_chgc_matrix_g 1 #define def_k_chgc_matrix_o 2 #define def_k_chgc_matrix_ig 3 #define def_k_chgc_outputs 4 #define def_k_chgc_step 5 #define def_k_chgc_window_in 6 #define def_k_chgc_window_out 7 #define def_k_chgc_activation 8 //--- #define def_k_UpdateWeightsConvMomentum 9 #define def_k_uwcm_matrix_w 0 #define def_k_uwcm_matrix_g 1 #define def_k_uwcm_matrix_i 2 #define def_k_uwcm_matrix_dw 3 #define def_k_uwcm_inputs 4 #define def_k_uwcm_learning_rates 5 #define def_k_uwcm_momentum 6 #define def_k_uwcm_window_in 7 #define def_k_uwcm_window_out 8 #define def_k_uwcm_step 9 //--- #define def_k_UpdateWeightsConvAdam 10 #define def_k_uwca_matrix_w 0 #define def_k_uwca_matrix_g 1 #define def_k_uwca_matrix_i 2 #define def_k_uwca_matrix_m 3 #define def_k_uwca_matrix_v 4 #define def_k_uwca_inputs 5 #define def_k_uwca_l 6 #define def_k_uwca_b1 7 #define def_k_uwca_b2 8 #define def_k_uwca_window_in 9 #define def_k_uwca_window_out 10 #define def_k_uwca_step 11 //--- #define def_k_AttentionScore 11 #define def_k_as_querys 0 #define def_k_as_keys 1 #define def_k_as_score 2 #define def_k_as_dimension 3 //--- #define def_k_AttentionOut 12 #define def_k_aout_scores 0 #define def_k_aout_values 1 #define def_k_aout_inputs 2 #define def_k_aout_out 3 //--- #define def_k_MatrixSum 13 #define def_k_sum_matrix1 0 #define def_k_sum_matrix2 1 #define def_k_sum_matrix_out 2 #define def_k_sum_dimension 3 //--- #define def_k_AttentionGradients 14 #define def_k_ag_querys 0 #define def_k_ag_querys_g 1 #define def_k_ag_keys 2 #define def_k_ag_keys_g 3 #define def_k_ag_values 4 #define def_k_ag_values_g 5 #define def_k_ag_scores 6 #define def_k_ag_gradient 7 //--- #define def_k_Normilize 15 #define def_k_norm_buffer 0 #define def_k_norm_dimension 1
И, конечно, добавим константу нового класса нейронов.
#define defNeuronAttentionOCL 0x7887
В класс описания слоев нейронной сети CLayerDescription добавим поле для указания количества нейронов в окне исходящего вектора.
class CLayerDescription : public CObject { public: CLayerDescription(void); ~CLayerDescription(void) {}; //--- int type; int count; int window; int window_out; int step; ENUM_ACTIVATION activation; ENUM_OPTIMIZATION optimization; };
В конструкторе класса нейронной сети CNet добавим новые классы для инициализации экземпляра класса работы с OpenCL.
CNet::CNet(CArrayObj *Description)
{
if(CheckPointer(Description)==POINTER_INVALID)
return;
//---
..........
..........
..........
//---
next=Description.At(1);
if(next.type==defNeuron || next.type==defNeuronBaseOCL || next.type==defNeuronConvOCL || next.type==defNeuronAttentionOCL)
{
opencl=new COpenCLMy();
if(CheckPointer(opencl)!=POINTER_INVALID && !opencl.Initialize(cl_program,true))
delete opencl;
}
else
{
if(CheckPointer(opencl)!=POINTER_INVALID)
delete opencl;
}
Далее по телу конструктора добавим код для инициализации нового класса нейрона внимания.
if(CheckPointer(opencl)!=POINTER_INVALID) { CNeuronBaseOCL *neuron_ocl=NULL; CNeuronConvOCL *neuron_conv_ocl=NULL; CNeuronAttentionOCL *neuron_attention_ocl=NULL; switch(desc.type) { case defNeuron: case defNeuronBaseOCL: neuron_ocl=new CNeuronBaseOCL(); if(CheckPointer(neuron_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_ocl.Init(outputs,0,opencl,desc.count,desc.optimization)) { delete neuron_ocl; delete temp; return; } neuron_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_ocl)) { delete neuron_ocl; delete temp; return; } neuron_ocl=NULL; break; case defNeuronConvOCL: neuron_conv_ocl=new CNeuronConvOCL(); if(CheckPointer(neuron_conv_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_conv_ocl.Init(outputs,0,opencl,desc.window,desc.step,desc.window_out,desc.count,desc.optimization)) { delete neuron_conv_ocl; delete temp; return; } neuron_conv_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_conv_ocl)) { delete neuron_conv_ocl; delete temp; return; } neuron_conv_ocl=NULL; break; case defNeuronAttentionOCL: neuron_attention_ocl=new CNeuronAttentionOCL(); if(CheckPointer(neuron_attention_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_attention_ocl.Init(outputs,0,opencl,desc.window,desc.count,desc.optimization)) { delete neuron_attention_ocl; delete temp; return; } neuron_attention_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_attention_ocl)) { delete neuron_attention_ocl; delete temp; return; } neuron_attention_ocl=NULL; break; default: return; break; } }
И в конце конструктора добавим инициализацию новых кернелов.
if(CheckPointer(opencl)==POINTER_INVALID) return; //--- create kernels opencl.SetKernelsCount(16); opencl.KernelCreate(def_k_FeedForward,"FeedForward"); opencl.KernelCreate(def_k_CalcOutputGradient,"CalcOutputGradient"); opencl.KernelCreate(def_k_CalcHiddenGradient,"CalcHiddenGradient"); opencl.KernelCreate(def_k_UpdateWeightsMomentum,"UpdateWeightsMomentum"); opencl.KernelCreate(def_k_UpdateWeightsAdam,"UpdateWeightsAdam"); opencl.KernelCreate(def_k_AttentionGradients,"AttentionIsideGradients"); opencl.KernelCreate(def_k_AttentionOut,"AttentionOut"); opencl.KernelCreate(def_k_AttentionScore,"AttentionScore"); opencl.KernelCreate(def_k_CalcHiddenGradientConv,"CalcHiddenGradientConv"); opencl.KernelCreate(def_k_CalcInputGradientProof,"CalcInputGradientProof"); opencl.KernelCreate(def_k_FeedForwardConv,"FeedForwardConv"); opencl.KernelCreate(def_k_FeedForwardProof,"FeedForwardProof"); opencl.KernelCreate(def_k_MatrixSum,"SumMatrix"); opencl.KernelCreate(def_k_UpdateWeightsConvAdam,"UpdateWeightsConvAdam"); opencl.KernelCreate(def_k_UpdateWeightsConvMomentum,"UpdateWeightsConvMomentum"); opencl.KernelCreate(def_k_Normilize,"Normalize"); //--- return; }
В диспетчерские методы класса CNeuronBase добавим обработку нового класса нейронов.
bool CNeuronBaseOCL::FeedForward(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: temp=SourceObject; return feedForward(temp); break; } //--- return false; }
bool CNeuronBaseOCL::calcHiddenGradients(CObject *TargetObject) { if(CheckPointer(TargetObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; CNeuronAttentionOCL *at=NULL; CNeuronConvOCL *conv=NULL; switch(TargetObject.Type()) { case defNeuronBaseOCL: temp=TargetObject; return calcHiddenGradients(temp); break; case defNeuronConvOCL: conv=TargetObject; temp=GetPointer(this); return conv.calcInputGradients(temp); break; case defNeuronAttentionOCL: at=TargetObject; temp=GetPointer(this); return at.calcInputGradients(temp); break; } //--- return false; }
С полным кодом всех методов и функций можно ознакомиться во вложении.
4. Тестирование
После внесения всех изменений в методы класса можно добавить новый класс нейронов в нейронную сеть и протестировать новую архитектуру. Для тестирования был создан советник Fractal_OCL_Attention, который отличается от советников предыдущих статей только архитектурой нейронной сети. Как и ранее, первый слой состоит из базовых нейронов для записи исходных данных и содержит по 12 признаков для каждого бара истории. Второй слой объявлен как модифицированный сверточный с сигмоидальной функцией активации и исходящим окном в 36 нейронов. Этот слой выполняет функцию эмбединга и нормализации исходных данных. Далее следует 2 слоя энкодера с механизмом Self-Attention. И закрывают нейронную сеть 3 полносвязных слоя нейронов.
CLayerDescription *desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuronBaseOCL; desc.optimization=ADAM; desc.activation=TANH; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronConvOCL; desc.window=12; desc.step=12; desc.window_out=36; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- bool result=true; for(int i=0; (i<2 && result); i++) { desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronAttentionOCL; desc.window=36; desc.optimization=ADAM; desc.activation=None; result=Topology.Add(desc); } if(!result) { delete Topology; return INIT_FAILED; } //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=TANH; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=TANH; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=3; desc.type=defNeuron; desc.activation=SIGMOID; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED;
С полным кодом советника можно ознакомиться во вложении.
Тестирование советника осуществлялось при тех же условиях, что и в предыдущих статьях этого цикла: инструмент EURUSD, таймфрейм H1, на вход подаются данные за 20 последовательных свечей, обучение проводится на истории за 2 последних года с обновлением параметров методом Adam.
Советник был инициализирован случайными весами в диапазоне от -1 до 1, исключая нулевые значения. По результатам тестирования 25 эпох советник показал ошибку в 35-36% с попаданием 22-23%
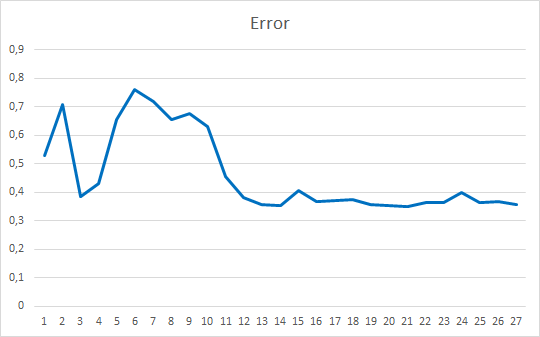
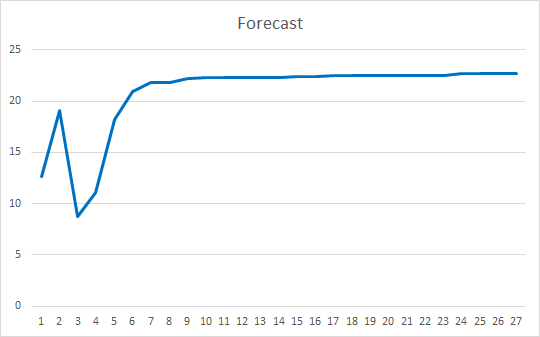
Заключение
В данной статье мы рассмотрели механизмы внимания, создали блок Self-Atttntion и протестировали его работу на исторических данных. Построенный советник показал довольно гладкие результаты по снижению ошибки работы нейронной сети и уровню "попадания" предсказанных результатов. Полученные результаты говорят о возможности использования подхода, но для улучшения результатов требуется дополнительная проработка. Как вариант на развитие можно рассмотреть использование нескольких параллельных потоков внимания с различными весовыми коэффициентами. В статье [10] такой подход назван как Multi had attention.
Ссылки
- Нейросети — это просто
- Нейросети — это просто (Часть 2): обучение и тестирование сети
- Нейросети — это просто (Часть 3): сверточные сети
- Нейросети — это просто (Часть 4): рекуррентные сети
- Нейросети — это просто (Часть 5): многопоточные вычисления в OpenCL
- Нейросети — это просто (Часть 6): эксперименты с коэффициентом обучения нейронной сети
- Нейросети — это просто (Часть 7): Адаптивные методы оптимизации
- Neural Machine Translation by Jointly Learning to Align and Translate
- Effective Approaches to Attention-based Neural Machine Translation
- Attention Is All You Need
- Layer Normalization
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Fractal_OCL_Attention.mq5 | Советник | Советник с нейронной сетью классификации (3 нейрона в выходном слое) с использованием механизма Self-Attention |
| 2 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 3 | NeuroNet.cl | Библиотека | Библиотека кода программы OpenCL |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Разработка самоадаптирующегося алгоритма (Часть I): Поиск базовой закономерности
Разработка самоадаптирующегося алгоритма (Часть I): Поиск базовой закономерности
 Градиентный бустинг в задачах трансдуктивного и активного машинного обучения
Градиентный бустинг в задачах трансдуктивного и активного машинного обучения
 Использование электронных таблиц для построения торговых стратегий
Использование электронных таблиц для построения торговых стратегий
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Я тоже видел этот машинный перевод, но все таки он несколько некорректен.
Если переформулировать на человеческий язык то смысл в следующем: "механизм SA является развитием полносвязной нейронной сети, и ключевое отличие от ПНС заключается в том, что элементарный элемент, которые анализирует ПНС - это выход одного нейрона, в тоже время элементарные элемент, который анализирует SA - это определенный вектор контекста"? Я прав, или есть еще какие то ключевые различия?
Вектор - это из рекуррентных сетей, потому что для перевода текста подается последвательность буков. НО в SA есть энкодер, который переводит исходный вектор в вектор меньшей длины, который несет как бы максимум информации об исходном векторе. Потом эти вектора декодируются и накладываются друг на друга на каждой итерации обучения. То есть это как бы сжатие информации (выделение контекста), то есть остается все самое главное по мнению алгоритма, и этому главному придается бОльший вес.
На самом деле это просто архитектура, не надо там искать сакральный смысл, потому что на временных рядах она работает не сильно лучше обычной NN или LSTM.
Вектор - это из рекуррентных сетей, потому что для перевода текста подается последвательность буков. НО в SA есть энкодер, который переводит исходный вектор в вектор меньшей длины, который несет как бы максимум информации об исходном векторе. Потом эти вектора декодируются и накладываются друг на друга на каждой итерации обучения. То есть это как бы сжатие информации (выделение контекста), то есть остается все самое главное по мнению алгоритма, и этому главному придается бОльший вес.
На самом деле это просто архитектура, не надо там искать сакральный смысл, потому что на временных рядах она работает не сильно лучше обычной NN или LSTM.
Искать сакральный смысл - как раз самое важное, если требуется спроектировать что то необычное. Да и проблема анализа рынка не в самих моделях, а в том что эти(рыночные) временные ряды слишком зашумлены и какую бы модель не применяли, она вытащит ровно столько информации, сколько заложено. А заложено, увы, тут маловато. Чтобы увеличить количество "вытаскиваемой" информации, надо увеличить исходное количество информации. И вот как раз при увеличении количестве информации и выходят вперед самые важные особенности НН - масштабируемость и адаптируемость.
Вектор - это просто последовательный набор чисел. Этот термин не привязан ни то, что к рекуррентным НН, а даже к машинному обучению вообще. Этот термин может применяться абсолютно в любой математической задаче, в которой требуется порядок чисел: хоть в школьных задачах по арифметике.
Искать сакральный смысл - как раз самое важное, если требуется спроектировать что то необычное. Да и проблема анализа рынка не в самих моделях, а в том что эти(рыночные) временные ряды слишком зашумлены и какую бы модель не применяли, она вытащит ровно столько информации, сколько заложено. А заложено, увы, тут маловато. Чтобы увеличить количество "вытаскиваемой" информации, надо увеличить исходное количество информации. И вот как раз при увеличении количестве информации и выходят вперед самые важные особенности НН - масштабируемость и адаптируемость.
Этот термин привязан к рекуррентным сетям, которые работают с последовательностями. Просто используется добавка в виде механизма внимания, вместо гейтов по типу как в lstm. Примерно такое же можно придумать самостоятельно, если долго курить теорию МО.
То, что проблема не в моделях - 100% согласен. Но все равно любой алгоритм построения ТС можно так или иначе потом оформить в виде архитектуры НС :) палка о 2-х концах.Наконец-то статья с реализацией механизма внимания на низком уровне без всяких высокоуровневых либ с реализацией в 3 строчки.
Интересны некоторые концептуальные вопросы:
Чем отличается данная система Self-attention от простого полносвязного слоя, ведь в нем тоже последующий нейрон имеет доступ ко всем предыдущим? В чем её ключевое преимущество? Никак не могу понять этого, хотя прочел достаточно много лекций по этой теме.
Здесь большая "идеологическая" разница. Если кратко, то полносвязный слой анализирует всю совокупность исходных данных, как единое целое. И даже незначительное изменение одного из параметров оценивается моделью как что-то кардинально новое. Поэтому любая операция с исходными данными (сжатие/растяжение, вращение, добавление шума) требует переобучение модели.
Механизмы внимания, как Вы правильно заметили, работают с векторами (блоками данных), которые в данном случае корректней называть Эмбедингами - закодированное представление отдельного объекта в анализируемом массиве исходных данных. В Self-Attention каждый такой эмбединг трансформируется в 3 сущности: Query, Key и Value. По существу, каждая из сущностей является проекцией объекта в некое N-мерное пространство. Замечу, что для каждой сущности обучается своя матрица, поэтому и проекции осуществляются в разные пространства. Query и Key используются для оценки влияния одного объекта на другой в контексте исходных данных. Dot product Query объекта A и Key объекта B показывают величину зависимости объекта A от объекта В. А поскольку Query и Key одного объекта являются разными векторами, то коэффициент влияния объекта А на B будет отличаться от коэффициента влияния объекта B на A. Из коэффициентов зависимости (влияния) формируется матрица Score, которая нормализуется функцией SoftMax в разрезе Query объектов. Нормализованная матрица умножается на матрицу сущностей Value. Результат операции прибавляется к исходным данным. Это можно оценивать как добавление контекста последовательности к каждому отдельному объекту. Здесь надо обратить внимание, что каждый объект получает индивидуальное представление контекста.
Далее данные нормализуются, чтобы представление всех объектов последовательности имели сопоставимый вид.
Как правило, используется несколько подряд слоев Self-Attention. Поэтому содержимое данных на входе и выходе блока будут сильно отличаться по содержанию, но аналогичные по размеру.
Transformer был предложен для языковых моделей. И был первый моделью, которая научилась не только дословно переводить исходный текст, но и переставлять слова в контексте целевого языка перевода.
Кроме того, модели Transformer благодаря анализу данных с учетом контекста способны игнорировать данные (объекты), выпадающие из контекста.
Здесь большая "идеологическая" разница. Если кратко, то полносвязный слой анализирует всю совокупность исходных данных, как единое целое. И даже незначительное изменение одного из параметров оценивается моделью как что-то кардинально новое. Поэтому любая операция с исходными данными (сжатие/растяжение, вращение, добавление шума) требует переобучение модели.
Механизмы внимания, как Вы правильно заметили, работают с векторами (блоками данных), которые в данном случае корректней называть Эмбедингами - закодированное представление отдельного объекта в анализируемом массиве исходных данных. В Self-Attention каждый такой эмбединг трансформируется в 3 сущности: Query, Key и Value. По существу, каждая из сущностей является проекцией объекта в некое N-мерное пространство. Замечу, что для каждой сущности обучается своя матрица, поэтому и проекции осуществляются в разные пространства. Query и Key используются для оценки влияния одного объекта на другой в контексте исходных данных. Dot product Query объекта A и Key объекта B показывают величину зависимости объекта A от объекта В. А поскольку Query и Key одного объекта являются разными векторами, то коэффициент влияния объекта А на B будет отличаться от коэффициента влияния объекта B на A. Из коэффициентов зависимости (влияния) формируется матрица Score, которая нормализуется функцией SoftMax в разрезе Query объектов. Нормализованная матрица умножается на матрицу сущностей Value. Результат операции прибавляется к исходным данным. Это можно оценивать как добавление контекста последовательности к каждому отдельному объекту. Здесь надо обратить внимание, что каждый объект получает индивидуальное представление контекста.
Далее данные нормализуются, чтобы представление всех объектов последовательности имели сопоставимый вид.
Как правило, используется несколько подряд слоев Self-Attention. Поэтому содержимое данных на входе и выходе блока будут сильно отличаться по содержанию, но аналогичные по размеру.
Transformer был предложен для языковых моделей. И был первый моделью, которая научилась не только дословно переводить исходный текст, но и переставлять слова в контексте целевого языка перевода.
Кроме того, модели Transformer благодаря анализу данных с учетом контекста способны игнорировать данные (объекты), выпадающие из контекста.
Спасибо большое! Ваши статьи сильно помогли разобраться в столь сложной и комплексной теме.
Глубина ваших знаний просто поражает на самом деле.