Redes Neurais de Maneira Fácil (Parte 8): Mecanismos de Atenção
1 285
0
Conteúdo
- Introdução
- 1. Mecanismos de Atenção
- 2. Algoritmo Self-Attention
- 3. Implementação
- 3.1. Atualizando a camada convolucional
- 3.2. Classe de Bloco Self-Attention
- 3.3. Propagação Direta do Self-Attention
- 3.4. Retropropagação do Self-Attention
- 3.5. Alterações nas Classes Base da Rede Neural
- 4. Teste
- Conclusões
- Referências
- Programas Utilizados no Artigo
Introdução
Nos artigos anteriores, nós já testamos várias opções para organizar as redes neurais. Estes incluem as redes convolucionais [3] usadas nos algoritmos de processamento de imagem, bem como as redes neurais recorrentes [4], usadas para trabalhar com sequências nas quais não apenas os valores são importantes, mas também sua posição no conjunto de dados de origem.
As redes neurais totalmente conectadas e convolucionais têm um tamanho de sequência de entrada fixo. As redes neurais recorrentes permitem uma ligeira expansão da sequência analisada, transferindo seus estados ocultos das iterações anteriores. Mas sua eficácia também diminui com o aumento da sequência. Em 2014, foi apresentado o primeiro mecanismo de atenção para fins de tradução automática. O objetivo do mecanismo era determinar e destacar os blocos da frase de origem (contexto) que são mais relevantes para a palavra de destino da tradução. Essa abordagem intuitiva melhorou significativamente a qualidade dos textos traduzidos pelas redes neurais.
1. Mecanismos de Atenção
Ao analisar um gráfico de vela do símbolo, nós definimos as tendências, bem como determinamos suas faixas de negociação. Isso significa que nós selecionamos alguns objetos da imagem geral e focamos nossa atenção neles. Nós entendemos que os objetos afetam o comportamento do preço futuro. Para implementar tal abordagem, em 2014 os desenvolvedores propuseram o primeiro algoritmo que analisa e destaca as dependências entre os elementos das sequências de entrada e saída [8]. O algoritmo proposto é denominado "Mecanismo de Atenção Generalizado". Ele foi inicialmente proposto para o uso em modelos de tradução automática utilizando as redes recorrentes como solução para o problema de memória de longo prazo na tradução de frases longas. Esta abordagem melhorou significativamente os resultados das redes neurais recorrentes anteriormente consideradas com base nos blocos LSTM [4].
O modelo clássico de tradução automática usando as redes recorrentes consiste em dois blocos, o Encoder e o Decoder. O primeiro bloco codifica a sequência de entrada no idioma de origem em um vetor de contexto e o segundo bloco decodifica o contexto resultante em uma sequência de palavras no idioma de destino. Quando o comprimento da sequência de entrada aumenta, a influência das primeiras palavras no contexto da frase final diminui. Como consequência, a qualidade da tradução diminui. O uso dos blocos LSTM aumentou ligeiramente a capacidade do modelo, mas ainda assim permaneceram limitados.
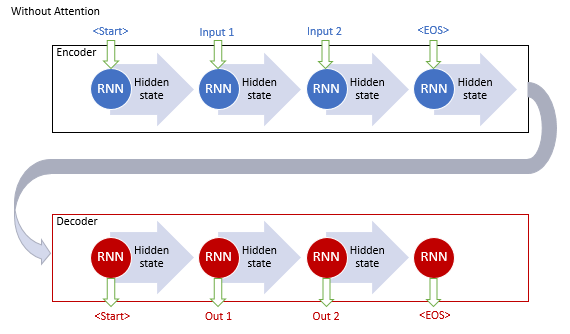
Os autores do mecanismo de atenção generalizado propuseram o uso de uma camada adicional para acumular os estados ocultos de todos os blocos recorrentes da sequência de entrada. Além disso, durante a decodificação da sequência, o mecanismo deve avaliar a influência de cada elemento da sequência de entrada na palavra atual da sequência de saída e sugerir a parte mais relevante do contexto para o decodificador.
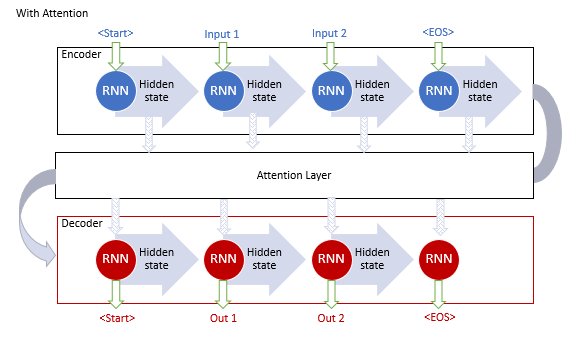
Este algoritmo incluiu as seguintes iterações:
1. Criação dos estados ocultos do Encoder e a acumulação deles no bloco de atenção.
2. Avaliação das dependências dos pares entre os estados ocultos de cada elemento do Encoder e o último estado oculto do Decoder.
3. Combinação das pontuações resultantes em um único vetor e a normalização dela usando a função Softmax.
4. Cálculo do vetor de contexto multiplicando todos os estados ocultos do Encoder por suas pontuações de alinhamento correspondentes.
5. Decodificação do vetor de contexto e a combinação do valor resultante com o estado anterior do Decoder.
Todas as iterações são repetidas até que o sinal de fim da linha seja recebido.
O mecanismo proposto possibilitou a solução do problema com um comprimento limitado da sequência de entrada e proporcionou a melhoria da qualidade da tradução automática utilizando as redes neurais recorrentes. O método se popularizou e, posteriormente, foram criadas suas variações. Em 2012, Minh-Thang Luong, em seu artigo [9], sugeriu uma nova variação do método de atenção. As principais diferenças da nova abordagem foram o uso de três funções para calcular o grau de dependências e o ponto de uso do mecanismo de atenção no Decoder.
Os modelos descritos acima usam blocos recorrentes, que são computacionalmente caros para treinar. Em junho de 2017, outra variação foi proposta no artigo [10]. Essa era uma nova arquitetura da rede neural Transformer, que não usava blocos recorrentes, mas usava um novo algoritmo de atenção (Self-Attention). Ao contrário do algoritmo descrito anteriormente, o Self-Attention analisa as dependências dos pares dentro de uma sequência. O Transformer mostrou melhores resultados no teste. Hoje, este modelo e seus derivados são usados em muitos modelos, incluindo o GPT-2 e o GPT-3. Vamos considerar o algoritmo Self-Attention com mais detalhes.
2. Algoritmo Self-Attention
A arquitetura do Transformer é baseada em blocos de Encoder e Decoder sequenciais com uma arquitetura semelhante. Cada um dos blocos inclui várias camadas idênticas com diferentes matrizes de peso.
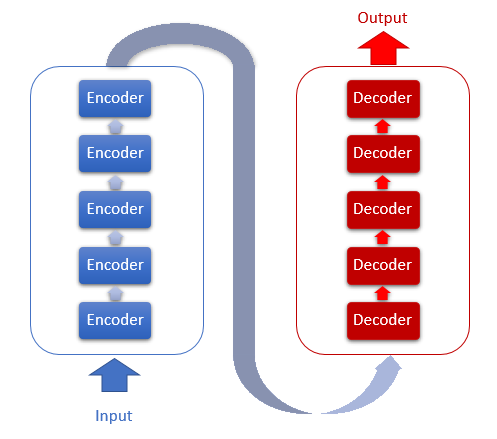
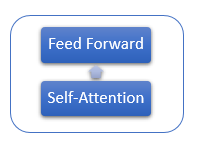
Cada camada do Encoder contém 2 camadas internas: Self-Attention e Feed-Forward. A camada Feed Forward inclui duas camadas de neurônios totalmente conectadas com a função de ativação ReLU na camada interna. Cada camada é aplicada a todos os elementos da sequência com os mesmos pesos, o que permite cálculos independentes simultâneos para todos os elementos da sequência em threads paralelos.
A camada do Decoder tem uma estrutura semelhante, mas possui um Self-Attention adicional que analisa as dependências entre as sequências de entrada e saída.
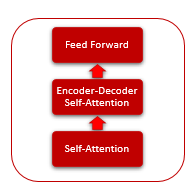
O próprio mecanismo de Self-Attention inclui várias ações iterativas que são aplicadas a cada elemento da sequência.
1. Primeiro, nós calculamos os vetores Query, Key e Value. Esses vetores são obtidos multiplicando-se cada elemento da sequência pela matriz correspondente WQ, WK e WV.
2. Em seguida, determinamos as dependências dos pares entre os elementos da sequência. Para fazer isso, multiplique o vetor Query pelos vetores Key de todos os elementos da sequência. Essa iteração é repetida para o vetor Query de cada elemento na sequência. Como resultado dessa iteração, nós obtemos uma matriz Score de tamanho N*N, onde N é o tamanho da sequência.
3. A próxima etapa é dividir o valor resultante pela raiz quadrada da dimensão do vetor Key e normalizá-lo pela função Softmax no contexto de cada Query. Assim, nós obtemos os coeficientes de interdependência pareada entre os elementos da sequência.
4. Multiplicamos cada vetor Value pelo coeficiente de interdependência correspondente para obter o valor do elemento ajustado. O objetivo desta iteração é focar em elementos relevantes e reduzir o impacto de valores irrelevantes.
5. Em seguida, somamos todos os vetores Value ajustados para cada elemento. O resultado desta operação será o vetor dos valores de saída da camada Self-Attention.
Os resultados das iterações de cada camada são adicionados à sequência de entrada e normalizados usando a fórmula.
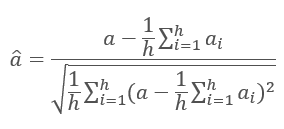
A normalização das camadas da rede neural é discutida em mais detalhes no artigo [11].
3. Implementação
Eu recomendo usar o mecanismo de Self-Attention em nossa implementação. Vamos considerar as opções de implementação.
3.1. Atualizando a camada convolucional
Nós começamos com a primeira ação do algoritmo Self-Attention - calculando os vetores Query, Key e Value. Inserimos uma matriz de dados contendo recursos para cada barra da sequência analisada. Obtemos os recursos de uma vela, um por um, e multiplicamos pela matriz de peso para obter um vetor. Isso se assemelha a uma camada de convolução considerada no artigo [3]. No entanto, neste caso, a saída não é um número, mas um vetor de tamanho fixo. Para resolver este problema, vamos atualizar a classe CNeuronConvOCL que é responsável pelo funcionamento de uma camada convolucional da rede neural. Adicionamos a variável iWindowOut que irá armazenar o tamanho dos vetores de saída. Implementamos as mudanças apropriadas nos métodos de classe.
class CNeuronConvOCL : public CNeuronProofOCL { protected: uint iWindowOut; //--- CBufferDouble *WeightsConv; CBufferDouble *DeltaWeightsConv; CBufferDouble *FirstMomentumConv; CBufferDouble *SecondMomentumConv; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronConvOCL(void) : iWindowOut(1) { activation=LReLU; } ~CNeuronConvOCL(void); virtual bool Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint window, uint step, uint window_out, uint units_count, ENUM_OPTIMIZATION optimization_type); //--- virtual bool SetGradientIndex(int index) { return Gradient.BufferSet(index); } //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); virtual int Type(void) const { return defNeuronConvOCL; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); };
No kernel OpenCL FeedForwardConv, adicionamos um parâmetro para obter o tamanho do vetor de saída. Além disso, adicionamos o cálculo do deslocamento do segmento processado do vetor de saída no vetor geral, na saída da camada convolucional, e implementamos um loop adicional através dos elementos da camada de saída.
__kernel void FeedForwardConv(__global double *matrix_w, __global double *matrix_i, __global double *matrix_o, int inputs, int step, int window_in, int window_out, uint activation) { int i=get_global_id(0); int w_in=window_in; int w_out=window_out; double sum=0.0; double4 inp, weight; int shift_out=w_out*i; int shift_in=step*i; for(int out=0;out<w_out;out++) { int shift=(w_in+1)*out; int stop=(w_in<=(inputs-shift_in) ? w_in : (inputs-shift_in)); for(int k=0; k<=stop; k=k+4) { switch(stop-k) { case 0: inp=(double4)(1,0,0,0); weight=(double4)(matrix_w[shift+k],0,0,0); break; case 1: inp=(double4)(matrix_i[shift_in+k],1,0,0); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],0,0); break; case 2: inp=(double4)(matrix_i[shift_in+k],matrix_i[shift_in+k+1],1,0); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],matrix_w[shift+k+2],0); break; case 3: inp=(double4)(matrix_i[shift_in+k],matrix_i[shift_in+k+1],matrix_i[shift_in+k+2],1); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],matrix_w[shift+k+2],matrix_w[shift+k+3]); break; default: inp=(double4)(matrix_i[shift_in+k],matrix_i[shift_in+k+1],matrix_i[shift_in+k+2],matrix_i[shift_in+k+3]); weight=(double4)(matrix_w[shift+k],matrix_w[shift+k+1],matrix_w[shift+k+2],matrix_w[shift+k+3]); break; } sum+=dot(inp,weight); } switch(activation) { case 0: sum=tanh(sum); break; case 1: sum=1/(1+exp(-clamp(sum,-50.0,50.0))); break; case 2: if(sum<0) sum*=0.01; break; default: break; } matrix_o[out+shift_out]=sum; } }
Não se esqueça de habilitar a passagem de um parâmetro adicional ao chamar este kernel.
bool CNeuronConvOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=Output.Total()/iWindowOut; OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_w,WeightsConv.GetIndex()); OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_i,NeuronOCL.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_FeedForwardConv,def_k_ffc_matrix_o,Output.GetIndex()); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_inputs,NeuronOCL.Neurons()); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_step,iStep); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_window_in,iWindow); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffс_window_out,iWindowOut); OpenCL.SetArgument(def_k_FeedForwardConv,def_k_ffc_activation,(int)activation); if(!OpenCL.Execute(def_k_FeedForwardConv,1,global_work_offset,global_work_size)) { printf("Error of execution kernel FeedForwardProof: %d",GetLastError()); return false; } //--- return Output.BufferRead(); }
Mudanças semelhantes foram implementadas nos kernels e nos métodos de recálculo dos gradientes (calcInputGradients) e na atualização da matriz de peso (updateInputWeights) O código completo de todos os métodos e funções está disponível em anexo.
3.2. Classe de Bloco Self-Attention
Agora, vamos prosseguir com a implementação do próprio método de Self-Attention. Para descrevê-lo, criamos a classe CNeuronAttentionOCL. Como todas as nossas operações são repetidas para cada elemento e realizadas independentemente, vamos mover algumas das operações para as camadas convolucionais modernizadas. Dentro do nosso bloco de atenção, criamos as camadas convolucionais Querys, Keys, Values, que será responsável por criar os vetores apropriados, bem como por passar os gradientes e atualizar a matriz de peso. O bloco FeedForward também será implementado usando as camadas convolucionais FF1 e FF2. Os valores da matriz Score serão salvos no buffer Scores; os resultados do método de atenção serão salvos na camada interna dos neurônios da classe base AttentionOut.
Aqui, preste atenção à diferença entre a saída do algoritmo de atenção e a saída de toda a classe Self-Attention. A primeira ocorre após a execução do algoritmo Self-Attention ajustando os valores dos vetores Value; ele é salvo em AttentionOut. O segundo é obtido após o processamento do FeedForward - ele é salvo no buffer Output da classe base.
class CNeuronAttentionOCL : public CNeuronBaseOCL { protected: CNeuronConvOCL *Querys; CNeuronConvOCL *Keys; CNeuronConvOCL *Values; CBufferDouble *Scores; CNeuronBaseOCL *AttentionOut; CNeuronConvOCL *FF1; CNeuronConvOCL *FF2; //--- uint iWindow; uint iUnits; //--- virtual bool feedForward(CNeuronBaseOCL *prevLayer); virtual bool updateInputWeights(CNeuronBaseOCL *prevLayer); public: CNeuronAttentionOCL(void) : iWindow(1), iUnits(0) {}; ~CNeuronAttentionOCL(void); virtual bool Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl, uint window, uint units_count, ENUM_OPTIMIZATION optimization_type); virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); //--- virtual int Type(void) const { return defNeuronAttentionOCL; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); };
Nas variáveis iWindows e iUnits, nós salvaremos o tamanho da janela de saída e o número de elementos na sequência de saída, respectivamente.
A classe será inicializada no método Init. O método receberá nos parâmetros o número ordinal do elemento, um ponteiro para o objeto COpenCL, o tamanho da janela, o número de elementos e o método de otimização. No início do método, chamamos o método relevante da classe pai.
bool CNeuronAttentionOCL::Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint window,uint units_count,ENUM_OPTIMIZATION optimization_type) { if(!CNeuronBaseOCL::Init(numOutputs,myIndex,open_cl,units_count*window,optimization_type)) return false;
Em seguida, declaramos e inicializamos as instâncias da classe da rede convolucional para o cálculo dos vetores Querys, Keys e Values.
//--- if(CheckPointer(Querys)==POINTER_INVALID) { Querys=new CNeuronConvOCL(); if(CheckPointer(Querys)==POINTER_INVALID) return false; if(!Querys.Init(0,0,open_cl,window,window,window,units_count,optimization_type)) return false; Querys.SetActivationFunction(TANH); } //--- if(CheckPointer(Keys)==POINTER_INVALID) { Keys=new CNeuronConvOCL(); if(CheckPointer(Keys)==POINTER_INVALID) return false; if(!Keys.Init(0,1,open_cl,window,window,window,units_count,optimization_type)) return false; Keys.SetActivationFunction(TANH); } //--- if(CheckPointer(Values)==POINTER_INVALID) { Values=new CNeuronConvOCL(); if(CheckPointer(Values)==POINTER_INVALID) return false; if(!Values.Init(0,2,open_cl,window,window,window,units_count,optimization_type)) return false; Values.SetActivationFunction(None); }
Mais adiante no algoritmo, nós declaramos o buffer de Scores. Preste atenção ao tamanho do buffer - ele deve ter memória suficiente para armazenar uma matriz quadrada com os lados iguais ao número de elementos na sequência.
if(CheckPointer(Scores)==POINTER_INVALID) { Scores=new CBufferDouble(); if(CheckPointer(Scores)==POINTER_INVALID) return false; } if(!Scores.BufferInit(units_count*units_count,0.0)) return false; if(!Scores.BufferCreate(OpenCL)) return false;
Além disso, declaramos a camada AttentionOut de neurônios. Essa camada servirá como um buffer para armazenar os resultados do Self-Attention. Ao mesmo tempo, ele será usado como uma camada de entrada para o bloco FeedForward. Seu tamanho é igual ao produto da largura da janela pelo número de elementos.
if(CheckPointer(AttentionOut)==POINTER_INVALID) { AttentionOut=new CNeuronBaseOCL(); if(CheckPointer(AttentionOut)==POINTER_INVALID) return false; if(!AttentionOut.Init(0,3,open_cl,window*units_count,optimization_type)) return false; AttentionOut.SetActivationFunction(None); }
Inicializamos as duas instâncias da camada convolucional para implementar o bloco FeedForward. Observe que a primeira instância (camada oculta) gera uma janela 2 vezes mais larga e tem uma função de ativação LReLU (ReLU com "vazamento"). Para a segunda camada (FF2), substituímos o buffer do gradiente pelo buffer de gradiente da classe pai usando o método SetGradientIndex. Ao copiar o buffer, nós eliminamos a necessidade de copiar os dados.
if(CheckPointer(FF1)==POINTER_INVALID) { FF1=new CNeuronConvOCL(); if(CheckPointer(FF1)==POINTER_INVALID) return false; if(!FF1.Init(0,4,open_cl,window,window,window*2,units_count,optimization_type)) return false; FF1.SetActivationFunction(LReLU); } //--- if(CheckPointer(FF2)==POINTER_INVALID) { FF2=new CNeuronConvOCL(); if(CheckPointer(FF2)==POINTER_INVALID) return false; if(!FF2.Init(0,5,open_cl,window*2,window*2,window,units_count,optimization_type)) return false; FF2.SetActivationFunction(None); FF2.SetGradientIndex(Gradient.GetIndex()); }
Salvamos os parâmetros-chave no final do método.
iWindow=window; iUnits=units_count; activation=FF2.Activation(); //--- return true; }
3.3. Propagação Direta do Self-Attention
A seguir, vamos considerar o método feedForward da classe CNeuronAttentionOCL. O método recebe em parâmetros um ponteiro para a camada anterior da rede neural. Portanto, em primeiro lugar, verificamos a validade do ponteiro recebido.
bool CNeuronAttentionOCL::feedForward(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false;
Antes de continuar a processar os dados, normalizamos os dados de entrada. Esta etapa não é fornecida pelo mecanismo Self-Attention do autor. No entanto, eu o adicionei com base nos resultados do teste, a fim de evitar o estouro durante o estágio de normalização da matriz Score. Um kernel especial foi criado para normalizar os dados. Chamamos ele no método feedForward.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=1;
OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,prevLayer.getOutputIndex());
OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,prevLayer.Neurons());
if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel Normalize: %d",GetLastError());
return false;
}
if(!prevLayer.Output.BufferRead())
return false;
}
Vamos dar uma olhada dentro do kernel de normalização. No início do kernel, calculamos o deslocamento para o primeiro elemento da sequência normalizada. Em seguida, nós calculamos o valor médio para a sequência normalizada e o desvio padrão. No final do kernel, atualizamos os dados no buffer.
__kernel void Normalize(__global double *buffer, int dimension) { int n=get_global_id(0); int shift=n*dimension; double mean=0; for(int i=0;i<dimension;i++) mean+=buffer[shift+i]; mean/=dimension; double variance=0; for(int i=0;i<dimension;i++) variance+=pow(buffer[shift+i]-mean,2); variance=sqrt(variance/dimension); for(int i=0;i<dimension;i++) buffer[shift+i]=(buffer[shift+i]-mean)/(variance==0 ? 1 : variance); }
Após normalizar os dados de origem, calculamos os vetores Querys, Keys e Values. Para fazer isso, chamamos o método FeedForward da instância apropriada da classe da camada convolucional (este método foi considerado anteriormente).
if(CheckPointer(Querys)==POINTER_INVALID || !Querys.FeedForward(prevLayer)) return false; if(CheckPointer(Keys)==POINTER_INVALID || !Keys.FeedForward(prevLayer)) return false; if(CheckPointer(Values)==POINTER_INVALID || !Values.FeedForward(prevLayer)) return false;
Avançando ao longo do algoritmo Self-Attention, calculamos a matriz Score. Os cálculos serão realizados em uma GPU usando OpenCL. Implementamos a chamada do kernel no método do programa principal. O número de threads chamados é igual ao número de unidades da classe. Cada thread funcionará em seu tamanho de janela. Em outras palavras, cada thread pegará seu próprio vetor Query de um elemento e o combinará com os vetores Key de todos os elementos da sequência.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_querys,Querys.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_keys,Keys.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionScore,def_k_as_score,Scores.GetIndex());
OpenCL.SetArgument(def_k_AttentionScore,def_k_as_dimension,iWindow);
if(!OpenCL.Execute(def_k_AttentionScore,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel AttentionScore: %d",GetLastError());
return false;
}
if(!Scores.BufferRead())
return false;
}
No início do kernel, determinamos os deslocamentos do elemento inicial usando os arrays 'querys' e 'score'. Calculamos o coeficiente para reduzir os valores obtidos. Zeramos a variável para calcular a quantidade de que nós precisamos ao normalizar os valores. Em seguida, implementamos um loop sobre todos os elementos da matriz principal, enquanto calculamos as dependências correspondentes. Observe que o kernel que nós estamos considerando combina os estágios de cálculo e normalização da matriz Score. Portanto, após calcular os produtos dos vetores Query e Key, dividimos o valor resultante por um coeficiente e calculamos o expoente do valor obtido. O expoente resultante deve ser salvo em uma matriz e adicionado à soma. No final do loop, implementamos o segundo loop, no qual todos os valores salvos no ciclo anterior são divididos pela soma calculada dos expoentes. A saída do kernel conterá a matriz Score calculada e normalizada.
__kernel void AttentionScore(__global double *querys, __global double *keys, __global double *score, int dimension) { int q=get_global_id(0); int shift_q=q*dimension; int units=get_global_size(0); int shift_s=q*units; double koef=sqrt((double)(units*dimension)); if(koef<1) koef=1; double sum=0; for(int k=0;k<units;k++) { double result=0; int shift_k=k*dimension; for(int i=0;i<dimension;i++) result+=(querys[shift_q+i]*keys[shift_k+i]); result=exp(result/koef); score[shift_s+k]=result; sum+=result; } for(int k=0;k<units;k++) score[shift_s+k]/=sum; }
Vamos continuar considerando o algoritmo Self-Attention. Após normalizar a matriz Score, é necessário corrigir os vetores Values para os valores obtidos e somar os vetores obtidos no contexto dos elementos da sequência de entrada. Na saída do bloco Self-Attention, os valores obtidos são somados à sequência de entrada. Todas essas iterações são combinadas no próximo kernel AttentionOut. A chamada do kernel é implementada no código do programa principal. Observe que este kernel será executado com um conjunto de threads de duas maneiras: por elementos da sequência (iUnits) e pelo número de recursos para cada elemento (iWindow). Os valores resultantes serão salvos no buffer de saída da camada AttentionOut.
{
uint global_work_offset[2]={0,0};
uint global_work_size[2];
global_work_size[0]=iUnits;
global_work_size[1]=iWindow;
OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_scores,Scores.GetIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_inputs,prevLayer.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_values,Values.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionOut,def_k_aout_out,AttentionOut.getOutputIndex());
if(!OpenCL.Execute(def_k_AttentionOut,2,global_work_offset,global_work_size))
{
printf("Error of execution kernel Attention Out: %d",GetLastError());
return false;
}
double temp[];
if(!AttentionOut.getOutputVal(temp))
return false;
}
No corpo do kernel, determinamos o deslocamento para o elemento processado nos vetores das sequências de entrada e saída. Em seguida, organizamos um ciclo para somar os produtos de Scores pelos valores correspondentes de Value. Assim que as iterações cíclicas forem concluídas, adicionamos a soma resultante ao vetor de entrada recebido da camada anterior da rede neural. Gravamos o resultado no buffer de saída.
__kernel void AttentionOut(__global double *scores, __global double *values, __global double *inputs, __global double *out) { int units=get_global_size(0); int u=get_global_id(0); int d=get_global_id(1); int dimension=get_global_size(1); int shift=u*dimension+d; double result=0; for(int i=0;i<units;i++) result+=scores[u*units+i]*values[i*dimension+d]; out[shift]=result+inputs[shift]; }
Nesse ponto, o algoritmo Self-Attention pode ser considerado concluído. Agora, nós precisamos apenas normalizar os dados resultantes usando o método descrito acima. A única diferença está no buffer de normalização.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=1;
OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,AttentionOut.getOutputIndex());
OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,AttentionOut.Neurons());
if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel Normalize: %d",GetLastError());
return false;
}
double temp[];
if(!AttentionOut.getOutputVal(temp))
return false;
}
Além disso, de acordo com o algoritmo codificador Transformer, nós passamos cada elemento da sequência por uma rede neural totalmente conectada com uma camada oculta. Nesse processo, a mesma matriz de peso é aplicada a todos os elementos da sequência. Eu implementei esse processo usando uma classe da camada convolucional modernizada. No código do método, eu chamo sequencialmente os métodos FeedForward das instâncias correspondentes da classe convolucional.
if(!FF1.FeedForward(AttentionOut)) return false; if(!FF2.FeedForward(FF1)) return false;
Para concluir o processo de feed-forward, é necessário somar os resultados da passagem de rede totalmente conectada com os resultados do mecanismo Self-Attention. Para isso, eu criei um kernel de adição de dois vetores, que é chamado no final do método feed-forward.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,FF2.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,Output.GetIndex());
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow);
if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel MatrixSum: %d",GetLastError());
return false;
}
if(!Output.BufferRead())
return false;
}
//---
return true;
}
Um ciclo simples é organizado dentro do kernel, com a soma dos elementos do vetor de entrada.
__kernel void SumMatrix(__global double *matrix1, __global double *matrix2, __global double *matrix_out, int dimension) { const int i=get_global_id(0)*dimension; for(int k=0;k<dimension;k++) matrix_out[i+k]=matrix1[i+k]+matrix2[i+k]; }
O código completo de todos os métodos e funções está disponível em anexo.
3.4. Retropropagação do Self-Attention
A passagem feed-forward é seguida pela feed-backward, durante o qual o erro é alimentado para níveis mais baixos da rede neural e a matriz de peso é ajustada para selecionar os resultados ideais. A classe recebe o gradiente de erro da camada superior totalmente conectada da rede neural, usando o método da classe pai descrito no artigo 5. Outro mecanismo para alimentar o gradiente de erro requer uma melhoria significativa, que se deve à complexidade da arquitetura interna.
Para passar o gradiente de erro para as camadas convolucionais internas e para a camada neural anterior da rede, vamos criar o método calcInputGradients. O método recebe nos parâmetros um ponteiro para a camada anterior de neurônios. Como sempre, verificamos primeiro a validade do ponteiro recebido. Então, em ordem reversa, chamamos sequencialmente os métodos das camadas convolucionais do bloco Feed Forward FF2 e FF1. Nós usamos a substituição de buffer, então a camada FF2 interna recebe o gradiente de erro diretamente da próxima camada de rede neural usando os métodos da classe pai.
bool CNeuronAttentionOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false; //--- if(!FF2.calcInputGradients(FF1)) return false; if(!FF1.calcInputGradients(AttentionOut)) return false;
Como na saída da passagem de feed-forward, nós somamos os resultados de Feed Forward e Self-Attention, o gradiente de erro também vem em duas ramificações. Portanto, o gradiente de erro obtido de FF1 é somado ao gradiente de erro obtido da próxima camada da rede neural. O kernel da soma do vetor é descrito acima. Então, vamos adicionar sua chamada.
{
uint global_work_offset[1]={0};
uint global_work_size[1];
global_work_size[0]=iUnits;
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,Gradient.GetIndex());
OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex());
OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow);
if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size))
{
printf("Error of execution kernel MatrixSum: %d",GetLastError());
return false;
}
double temp[];
if(AttentionOut.getGradient(temp)<=0)
return false;
}
Na próxima etapa, propagamos o gradiente de erro para Querys, Keys e Values. O gradiente de erro será passado para os vetores no kernel AttentionIsideGradients. No método abaixo, chamamos com um conjunto de threads em duas dimensões.
{
uint global_work_offset[2]={0,0};
uint global_work_size[2];
global_work_size[0]=iUnits;
global_work_size[1]=iWindow;
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_gradient,AttentionOut.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_keys,Keys.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_keys_g,Keys.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_querys,Querys.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_querys_g,Querys.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_values,Values.getOutputIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_values_g,Values.getGradientIndex());
OpenCL.SetArgumentBuffer(def_k_AttentionGradients,def_k_ag_scores,Scores.GetIndex());
if(!OpenCL.Execute(def_k_AttentionGradients,2,global_work_offset,global_work_size))
{
printf("Error of execution kernel AttentionGradients: %d",GetLastError());
return false;
}
double temp[];
if(Keys.getGradient(temp)<=0)
return false;
}
O kernel recebe ponteiros para os buffers de dados nos parâmetros. As dimensões são determinadas no início do kernel, pelo número ou pelas threads em execução. Em seguida, nós calculamos o fator de correção e fazemos um loop sobre todos os elementos da sequência. Dentro do loop, nós primeiro calculamos o gradiente de erro no vetor Value multiplicando o vetor gradiente pelo vetor Score correspondente. Observe que o gradiente de erro é dividido por 2. Isso ocorre porque nós resumimos na etapa anterior e, portanto, duplicamos o erro. Agora nós dividimos por dois para ter um valor médio.
__kernel void AttentionIsideGradients(__global double *querys,__global double *querys_g, __global double *keys,__global double *keys_g, __global double *values,__global double *values_g, __global double *scores, __global double *gradient) { int u=get_global_id(0); int d=get_global_id(1); int units=get_global_size(0); int dimension=get_global_size(1); double koef=sqrt((double)(units*dimension)); if(koef<1) koef=1; //--- double vg=0; double qg=0; double kg=0; for(int iu=0;iu<units;iu++) { double g=gradient[iu*dimension+d]/2; double sc=scores[iu*units+u]; vg+=sc*g;
Em seguida, organizamos um loop aninhado para definir o gradiente nos elementos da matriz Score. Depois calculamos o gradiente dos elementos dos vetores Querys e Keys. No final do loop externo, atribuímos os gradientes calculados aos buffers globais correspondentes.
//--- double sqg=0; double skg=0; for(int id=0;id<dimension;id++) { sqg+=values[iu*dimension+id]*gradient[u*dimension+id]/2; skg+=values[u*dimension+id]*gradient[iu*dimension+id]/2; } qg+=(scores[u*units+iu]==0 || scores[u*units+iu]==1 ? 0.0001 : scores[u*units+iu]*(1-scores[u*units+iu]))*sqg*keys[iu*dimension+d]/koef; //--- kg+=(scores[iu*units+u]==0 || scores[iu*units+u]==1 ? 0.0001 : scores[iu*units+u]*(1-scores[iu*units+u]))*skg*querys[iu*dimension+d]/koef; } int shift=u*dimension+d; values_g[shift]=vg; querys_g[shift]=qg; keys_g[shift]=kg; }
Em seguida, nós temos que passar os gradientes de erro dos vetores Querys, Keys e Values. Preste atenção que, uma vez que todos os vetores são obtidos pela multiplicação dos mesmos dados iniciais por matrizes diferentes, os gradientes de erro também devem ser somados. Eu não aloquei um buffer separado para acumular o gradiente de erro. No entanto, somar valores ao calcular gradientes requer uma complicação adicional do código, com o monitoramento da zeragem do buffer. Eu decidi usar os métodos existentes para calcular o gradiente de erro e posteriormente acumular seus valores no buffer de gradiente da camada AttentionOut.
if(!Querys.calcInputGradients(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(AttentionOut.getGradient(temp)<=0) return false; } //--- if(!Keys.calcInputGradients(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,AttentionOut.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(AttentionOut.getGradient(temp)<=0) return false; } //--- if(!Values.calcInputGradients(prevLayer)) return false; //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=iUnits; OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix1,AttentionOut.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix2,prevLayer.getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_MatrixSum,def_k_sum_matrix_out,prevLayer.getGradientIndex()); OpenCL.SetArgument(def_k_MatrixSum,def_k_sum_dimension,iWindow+1); if(!OpenCL.Execute(def_k_MatrixSum,1,global_work_offset,global_work_size)) { printf("Error of execution kernel MatrixSum: %d",GetLastError()); return false; } double temp[]; if(prevLayer.getGradient(temp)<=0) return false; } //--- { uint global_work_offset[1]={0}; uint global_work_size[1]; global_work_size[0]=1; OpenCL.SetArgumentBuffer(def_k_Normilize,def_k_norm_buffer,prevLayer.getGradientIndex()); OpenCL.SetArgument(def_k_Normilize,def_k_norm_dimension,prevLayer.Neurons()); if(!OpenCL.Execute(def_k_Normilize,1,global_work_offset,global_work_size)) { printf("Error of execution kernel Normalize: %d",GetLastError()); return false; } double temp[]; if(prevLayer.getGradient(temp)<=0) return false; } //--- return true; }
Depois de alimentar o gradiente de erro para o nível da camada anterior, corrigimos as matrizes de peso no método updateInputWeights. O método é bastante simples. Ele chama os métodos apropriados de camadas convolucionais aninhadas.
bool CNeuronAttentionOCL::updateInputWeights(CNeuronBaseOCL *prevLayer) { if(!Querys.UpdateInputWeights(prevLayer)) return false; if(!Keys.UpdateInputWeights(prevLayer)) return false; if(!Values.UpdateInputWeights(prevLayer)) return false; if(!FF1.UpdateInputWeights(AttentionOut)) return false; if(!FF2.UpdateInputWeights(FF1)) return false; //--- return true; }
3.5. Alterações nas Classes Base da Rede Neural
Nós terminamos de trabalhar com a classe do nosso bloco de atenção. Agora, vamos fazer algumas adições às classes básicas de nossa rede neural. Em primeiro lugar, adicionamos as constantes ao bloco de definição para trabalhar com novos kernels.
#define def_k_FeedForwardConv 7 #define def_k_ffc_matrix_w 0 #define def_k_ffc_matrix_i 1 #define def_k_ffc_matrix_o 2 #define def_k_ffc_inputs 3 #define def_k_ffc_step 4 #define def_k_ffc_window_in 5 #define def_k_ffс_window_out 6 #define def_k_ffc_activation 7 //--- #define def_k_CalcHiddenGradientConv 8 #define def_k_chgc_matrix_w 0 #define def_k_chgc_matrix_g 1 #define def_k_chgc_matrix_o 2 #define def_k_chgc_matrix_ig 3 #define def_k_chgc_outputs 4 #define def_k_chgc_step 5 #define def_k_chgc_window_in 6 #define def_k_chgc_window_out 7 #define def_k_chgc_activation 8 //--- #define def_k_UpdateWeightsConvMomentum 9 #define def_k_uwcm_matrix_w 0 #define def_k_uwcm_matrix_g 1 #define def_k_uwcm_matrix_i 2 #define def_k_uwcm_matrix_dw 3 #define def_k_uwcm_inputs 4 #define def_k_uwcm_learning_rates 5 #define def_k_uwcm_momentum 6 #define def_k_uwcm_window_in 7 #define def_k_uwcm_window_out 8 #define def_k_uwcm_step 9 //--- #define def_k_UpdateWeightsConvAdam 10 #define def_k_uwca_matrix_w 0 #define def_k_uwca_matrix_g 1 #define def_k_uwca_matrix_i 2 #define def_k_uwca_matrix_m 3 #define def_k_uwca_matrix_v 4 #define def_k_uwca_inputs 5 #define def_k_uwca_l 6 #define def_k_uwca_b1 7 #define def_k_uwca_b2 8 #define def_k_uwca_window_in 9 #define def_k_uwca_window_out 10 #define def_k_uwca_step 11 //--- #define def_k_AttentionScore 11 #define def_k_as_querys 0 #define def_k_as_keys 1 #define def_k_as_score 2 #define def_k_as_dimension 3 //--- #define def_k_AttentionOut 12 #define def_k_aout_scores 0 #define def_k_aout_values 1 #define def_k_aout_inputs 2 #define def_k_aout_out 3 //--- #define def_k_MatrixSum 13 #define def_k_sum_matrix1 0 #define def_k_sum_matrix2 1 #define def_k_sum_matrix_out 2 #define def_k_sum_dimension 3 //--- #define def_k_AttentionGradients 14 #define def_k_ag_querys 0 #define def_k_ag_querys_g 1 #define def_k_ag_keys 2 #define def_k_ag_keys_g 3 #define def_k_ag_values 4 #define def_k_ag_values_g 5 #define def_k_ag_scores 6 #define def_k_ag_gradient 7 //--- #define def_k_Normilize 15 #define def_k_norm_buffer 0 #define def_k_norm_dimension 1
Além disso, adicionamos uma constante da nova classe de neurônios.
#define defNeuronAttentionOCL 0x7887
Na classe CLayerDescription que descreve as camadas da rede neural, adicionamos um campo para especificar o número de neurônios na janela do vetor de saída.
class CLayerDescription : public CObject { public: CLayerDescription(void); ~CLayerDescription(void) {}; //--- int type; int count; int window; int window_out; int step; ENUM_ACTIVATION activation; ENUM_OPTIMIZATION optimization; };
No construtor de classe de rede neural CNet, adicionamos novas classes para inicializar uma instância da classe que trabalha com OpenCL.
CNet::CNet(CArrayObj *Description)
{
if(CheckPointer(Description)==POINTER_INVALID)
return;
//---
..........
..........
..........
//---
next=Description.At(1);
if(next.type==defNeuron || next.type==defNeuronBaseOCL || next.type==defNeuronConvOCL || next.type==defNeuronAttentionOCL)
{
opencl=new COpenCLMy();
if(CheckPointer(opencl)!=POINTER_INVALID && !opencl.Initialize(cl_program,true))
delete opencl;
}
else
{
if(CheckPointer(opencl)!=POINTER_INVALID)
delete opencl;
}
Mais adiante no corpo do construtor, adicionamos o código para inicializar a nova classe do neurônio de atenção.
if(CheckPointer(opencl)!=POINTER_INVALID) { CNeuronBaseOCL *neuron_ocl=NULL; CNeuronConvOCL *neuron_conv_ocl=NULL; CNeuronAttentionOCL *neuron_attention_ocl=NULL; switch(desc.type) { case defNeuron: case defNeuronBaseOCL: neuron_ocl=new CNeuronBaseOCL(); if(CheckPointer(neuron_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_ocl.Init(outputs,0,opencl,desc.count,desc.optimization)) { delete neuron_ocl; delete temp; return; } neuron_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_ocl)) { delete neuron_ocl; delete temp; return; } neuron_ocl=NULL; break; case defNeuronConvOCL: neuron_conv_ocl=new CNeuronConvOCL(); if(CheckPointer(neuron_conv_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_conv_ocl.Init(outputs,0,opencl,desc.window,desc.step,desc.window_out,desc.count,desc.optimization)) { delete neuron_conv_ocl; delete temp; return; } neuron_conv_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_conv_ocl)) { delete neuron_conv_ocl; delete temp; return; } neuron_conv_ocl=NULL; break; case defNeuronAttentionOCL: neuron_attention_ocl=new CNeuronAttentionOCL(); if(CheckPointer(neuron_attention_ocl)==POINTER_INVALID) { delete temp; return; } if(!neuron_attention_ocl.Init(outputs,0,opencl,desc.window,desc.count,desc.optimization)) { delete neuron_attention_ocl; delete temp; return; } neuron_attention_ocl.SetActivationFunction(desc.activation); if(!temp.Add(neuron_attention_ocl)) { delete neuron_attention_ocl; delete temp; return; } neuron_attention_ocl=NULL; break; default: return; break; } }
Adicionamos a inicialização de novos kernels no final do construtor.
if(CheckPointer(opencl)==POINTER_INVALID) return; //--- create kernels opencl.SetKernelsCount(16); opencl.KernelCreate(def_k_FeedForward,"FeedForward"); opencl.KernelCreate(def_k_CalcOutputGradient,"CalcOutputGradient"); opencl.KernelCreate(def_k_CalcHiddenGradient,"CalcHiddenGradient"); opencl.KernelCreate(def_k_UpdateWeightsMomentum,"UpdateWeightsMomentum"); opencl.KernelCreate(def_k_UpdateWeightsAdam,"UpdateWeightsAdam"); opencl.KernelCreate(def_k_AttentionGradients,"AttentionIsideGradients"); opencl.KernelCreate(def_k_AttentionOut,"AttentionOut"); opencl.KernelCreate(def_k_AttentionScore,"AttentionScore"); opencl.KernelCreate(def_k_CalcHiddenGradientConv,"CalcHiddenGradientConv"); opencl.KernelCreate(def_k_CalcInputGradientProof,"CalcInputGradientProof"); opencl.KernelCreate(def_k_FeedForwardConv,"FeedForwardConv"); opencl.KernelCreate(def_k_FeedForwardProof,"FeedForwardProof"); opencl.KernelCreate(def_k_MatrixSum,"SumMatrix"); opencl.KernelCreate(def_k_UpdateWeightsConvAdam,"UpdateWeightsConvAdam"); opencl.KernelCreate(def_k_UpdateWeightsConvMomentum,"UpdateWeightsConvMomentum"); opencl.KernelCreate(def_k_Normilize,"Normalize"); //--- return; }
Adicionamos o processamento da nova classe de neurônios nos métodos dispatcher da classe CNeuronBase.
bool CNeuronBaseOCL::FeedForward(CObject *SourceObject) { if(CheckPointer(SourceObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; switch(SourceObject.Type()) { case defNeuronBaseOCL: case defNeuronConvOCL: case defNeuronAttentionOCL: temp=SourceObject; return feedForward(temp); break; } //--- return false; } bool CNeuronBaseOCL::calcHiddenGradients(CObject *TargetObject) { if(CheckPointer(TargetObject)==POINTER_INVALID) return false; //--- CNeuronBaseOCL *temp=NULL; CNeuronAttentionOCL *at=NULL; CNeuronConvOCL *conv=NULL; switch(TargetObject.Type()) { case defNeuronBaseOCL: temp=TargetObject; return calcHiddenGradients(temp); break; case defNeuronConvOCL: conv=TargetObject; temp=GetPointer(this); return conv.calcInputGradients(temp); break; case defNeuronAttentionOCL: at=TargetObject; temp=GetPointer(this); return at.calcInputGradients(temp); break; } //--- return false; }
O código completo de todos os métodos e funções está disponível em anexo.
4. Teste
Depois de todas as mudanças acima, nós podemos adicionar a nova classe de neurônios à rede neural e testar a nova arquitetura. Eu criei um EA de teste Fractal_OCL_Attention, que difere dos EAs anteriores apenas na arquitetura da rede neural. Novamente, a primeira camada consiste em neurônios básicos para escrever dados iniciais e contém 12 recursos para cada barra do histórico. A segunda camada é declarada como uma camada convolucional modificada com uma função de ativação sigmoidal e uma janela de saída de 36 neurônios. Essa camada desempenha a função de incorporação e normalização dos dados originais. Isso é seguido por duas camadas de um codificador com o mecanismo Self-Attention. Três camadas de neurônios totalmente conectadas completam a rede neural.
CLayerDescription *desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuronBaseOCL; desc.optimization=ADAM; desc.activation=TANH; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronConvOCL; desc.window=12; desc.step=12; desc.window_out=36; desc.optimization=ADAM; desc.activation=SIGMOID; if(!Topology.Add(desc)) return INIT_FAILED; //--- bool result=true; for(int i=0; (i<2 && result); i++) { desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars; desc.type=defNeuronAttentionOCL; desc.window=36; desc.optimization=ADAM; desc.activation=None; result=Topology.Add(desc); } if(!result) { delete Topology; return INIT_FAILED; } //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=TANH; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=200; desc.type=defNeuron; desc.activation=TANH; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=3; desc.type=defNeuron; desc.activation=SIGMOID; desc.optimization=ADAM; if(!Topology.Add(desc)) return INIT_FAILED;
O código completo do EA pode ser encontrado em anexo.
O teste do EA foi realizado nas mesmas condições: símbolo EURUSD, tempo gráfico H1, alimentando a rede com os dados das 20 velas consecutivas e o treinamento é executado usando o histórico dos últimos dois anos, com os parâmetros sendo atualizados pelo método de Adam.
O Expert Advisor foi inicializado com os pesos aleatórios variando de -1 a 1, excluindo os valores iguais a zero. Depois de testar em 25 épocas, o EA mostrou um erro de 35-36% com um acerto de 22-23%
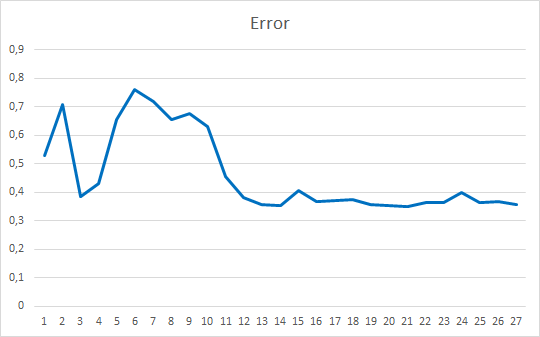
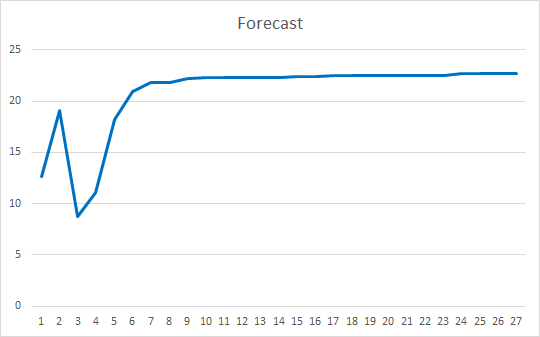
Conclusões
Neste artigo, nós consideramos os mecanismos de atenção. Criamos o bloco Self-Attention e testamos o seu funcionamento nos dados históricos. O Expert Advisor resultante mostrou resultados bastante suaves em termos de redução do erro na operação da rede neural e em termos de "acerto" dos resultados previstos. Os resultados obtidos indicam que é possível utilizar esta abordagem. No entanto, é necessário trabalho adicional para melhorar os resultados. Como uma opção de desenvolvimento adicional, você pode considerar o uso de várias threads paralelas de atenção com pesos diferentes. No artigo 10, essa abordagem é chamada de "Multi-head attention".
Referências
- Redes neurais de maneira fácil
- Redes neurais de maneira fácil (Parte 2): Treinamento e teste da rede
- Redes Neurais de Maneira Fácil (Parte 3): Redes Convolucionais
- Redes Neurais de Maneira Fácil (Parte 4): Redes Recorrentes
- Redes Neurais de Maneira Fácil (Parte 5): Cálculos em Paralelo com o OpenCL
- Redes neurais de Maneira Fácil (Parte 6): Experimentos com a taxa de aprendizado da rede neural
- Redes Neurais de Maneira Fácil(Parte 7): Métodos de otimização adaptativos
- Neural Machine Translation by Jointly Learning to Align and Translate
- Effective Approaches to Attention-based Neural Machine Translation
- Attention Is All You Need
- Layer Normalization
Programas Utilizados no Artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Fractal_OCL_Attention.mq5 | Expert Advisor | Um Expert Advisor com a rede neural de classificação (3 neurônios na camada de saída) usando o mecanismo de Self-Attention |
| 2 | NeuroNet.mqh | Biblioteca de classe | Uma biblioteca de classes para a criação de uma rede neural |
| 3 | NeuroNet.cl | Código Base | Biblioteca do código do programa OpenCL |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/8765
Gradient boosting no aprendizado de máquina transdutivo e ativo
Trabalhando com séries temporais na biblioteca DoEasy (Parte 58): séries temporais de dados de buffers de indicadores
Desenvolvendo um algoritmo auto-adaptável (Parte I): encontrando um padrão básico
WebSocket para MetaTrader 5
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso