Нейросети в трейдинге: Модель адаптивной графовой диффузии (SAGDFN)

Введение

Многомерные временные ряды характеризуются не только привычной временной зависимостью (трендами, сезонностью, внезапными всплесками активности), но и пространственной корреляцией, которая гораздо коварнее. Она описывает то, как изменения в одной последовательности влияют на другие. И эти связи живут своей жизнью: появляются и исчезают, меняются по силе и направлению в зависимости от глобальных новостей, изменений в денежно-кредитной политике государств, политических кризисов или технологических прорывов. Например, курс EURUSD может меняться под влиянием изменения цен на газ в Европе из-за энергетических шоков, а акции производителей микросхем — от ситуации на азиатских заводах.

Традиционные модели вроде ARIMA или VAR неплохо справлялись с отдельными временными рядами, но как только речь заходит о сотнях инструментов, они начинают буксовать. Методы машинного обучения следующего поколения (опорные векторы, гауссовские процессы) расширили горизонты анализа, но их архитектура редко учитывала богатую ткань перекрестных связей. Даже современные рекуррентные нейронные сети (RNN) и трансформеры, продемонстрировавшие впечатляющие результаты в обработке последовательностей, в многомерном контексте оказались ограничены: им не хватало изящества для работы с динамическими сетями корреляций.

На этом фоне появились графовые нейронные сети (GNN), которые изначально были созданы для задач с ярко выраженной структурой графа: транспортные сети, социальные взаимодействия, цепочки поставок. Но в финансовом мире построить такой граф — задача сродни искусству. Две компании из одной отрасли могут вести себя диаметрально противоположно, а два далеких рынка (например, США и Япония) синхронно реагировать на одни и те же макроэкономические стимулы.

Ответом стали адаптивные графовые нейронные сети (adaptive-weight-GNN), которые строят граф прямо из данных, а не из предположений. Они обучают матрицу связей между активами, выявляя не формальные, а реальные корреляции. Классический пример: золото и японская иена, которые часто ведут себя как защитные активы. В обычное время их связь может быть неочевидной, но в периоды глобальных потрясений модель уловит синхронность их движения и скорректирует прогноз.

Тем не менее и эти подходы не свободны от ограничений. Первое — масштабируемость: матрица корреляций N×N для большого количества активов превращается в прожорливого монстра, который может заблокировать даже мощные графические ускорители, загружая их память промежуточными расчетами. Второе — ложные связи. Многие адаптивные алгоритмы предполагают, что все узлы в какой-то мере связаны между собой, но это не так. В финансовых прогнозах малозначительная акция локального рынка не должна оказывать весомого влияния на глобальные прогнозы.

Для решения этих проблем был разработан новый подход, основанный на графовой диффузии и принципе пространственной разреженности. Его суть в том, чтобы не пытаться анализировать все возможные связи, а выделять ключевые узлы — своего рода якоря влияния, которые задают тон всей системе. В финансовом контексте это могут быть доллар США, евро, нефть, золото, фондовые индексы S&P 500 и Nikkei 225.

Среди подобных алгоритмов выделяется фреймворк SAGDFN, представленный в работе "SAGDFN: A Scalable Adaptive Graph Diffusion Forecasting Network for Multivariate Time Series Forecasting". Авторы фреймворка предлагают осуществлять выбор наиболее значимых узлов с помощью алгоритма Significant Nodes Sampling. А дальнейшее уточнение взаимозависимостей проводится модулем Sparse Spatial Multi-Head Attention. В результате формируется компактная матрица N×M, где M во много раз меньше N.

Использование предложенного подхода снижает вычислительную сложность с N² до MN и одновременно уменьшает потребление памяти. Он позволяет строить прогнозы для огромных массивов данных без перегрузки вычислительных мощностей и делает систему более устойчивой к шуму. Особенно важным это становится в периоды рыночной турбулентности, возникающие на неожиданных решениях центробанков и резких колебаниях цен на сырьевые ресурсы.

Практические последствия очевидны. Крупные инвестиционные фонды получают инструмент для более тонкой ребалансировки портфелей. Хедж-фонды — основу для стратегий, которые учитывают не только динамику отдельных активов, но и сложный танец глобальных взаимосвязей. Алгоритмические трейдеры — возможность работать с большим количеством инструментов без критической задержки принятия решений.

Алгоритм SAGDFN

Scalable Adaptive Graph Diffusion Forecasting Network (SAGDFN) — это современный алгоритм, разработанный с целью сделать прогнозирование временных рядов более гибким, масштабируемым и эффективным даже при работе с чрезвычайно большими графами. Основная идея заключается в том, чтобы существенно снизить вычислительную нагрузку и требования к памяти без ущерба для точности прогнозов. Вместо того чтобы механически обрабатывать всю графовую структуру, модель фокусируется на наиболее значимых элементах и связях, которые оказывают реальное влияние на конечный результат. Такой подход не только устраняет избыточный шум, но и позволяет выстраивать прогнозы быстрее, экономнее и точнее.

Важнейшую роль в работе SAGDFN играет функция α-Entmax. Она выступает своеобразным фильтром, который помогает модели выделять действительно важные пространственные корреляции между узлами графа и игнорировать второстепенные связи. Это особенно ценно в условиях, когда данные обладают сложной и динамически изменяющейся структурой, как, например, на финансовых рынках или в системах городского транспорта. На основе отобранных связей формируется компактная матрица смежности, которая не задаётся вручную, а создаётся в процессе обучения. Такой динамический характер построения делает алгоритм более гибким и способным подстраиваться под новые условия без необходимости полной перенастройки.

Архитектура SAGDFN опирается на проверенную временем схему Энкодер-Декодер, но при этом она не требует заранее заданных знаний о пространственных связях. Это обеспечивает универсальность модели и её применимость в самых разных областях: от анализа финансовых колебаний, где важно улавливать взаимосвязи между множеством активов, до прогнозирования потоков энергии, логистических маршрутов и даже производственных цепочек. Модель последовательно выявляет наиболее значимых соседей каждого узла, объединяет их с исходной информацией и формирует плотную матрицу смежности, которая затем используется для пространственно-временного анализа.

Особенность SAGDFN заключается в том, что обучение всех ключевых компонентов происходит синхронно и согласованно. В едином цикле оптимизируются индексы значимых узлов, их встраивания, параметры внимания и итоговая матрица смежности. Для калибровки используется функция потерь L1, которая позволяет достичь баланса между точностью прогноза и устойчивостью к шуму в данных. Такой подход гарантирует, что модель со временем не только повышает качество прогнозов, но и адаптируется к изменениям структуры анализируемой системы.

Следовательно, SAGDFN решает одну из давних проблем графовых нейронных сетей: как сохранить высокую точность прогнозирования, избегая чрезмерной сложности и избыточных вычислительных затрат.

Функционал выбора наиболее значимых узлов авторы фреймворка SAGDFN возложили на модуль Significant Neighbors Sampling (SNS) — это методологический подход, направленный на оптимизацию вычислительных процессов в графовых нейронных сетях (GNN), когда речь идёт о прогнозировании временных рядов с большим количеством взаимосвязанных элементов.

Традиционные реализации графовых моделей строят полную матрицу смежности размером N×N и используют её для последующей графовой свёртки, чтобы выявлять пространственные корреляции между всеми узлами анализируемого графа. Однако подобный подход характеризуется квадратичной вычислительной сложностью, что делает его крайне затратным по ресурсам. Особенно если количество узлов превышает 2'000 — ситуация, которая часто наблюдается в реальных прикладных задачах, будь то финансовые рынки, транспортные сети или промышленные системы мониторинга.

Основная идея SNS заключается в переосмыслении важности связей: далеко не каждый узел оказывает значимое влияние на состояние конкретного элемента графа. Для качественного прогноза достаточно учитывать лишь небольшое наиболее релевантное подмножество соседей, которые вносят ключевой вклад в динамику процесса. Метод предлагает динамически отбирать таких значимых соседей среди всех N узлов, создавая компактную матрицу смежности размером N×M, где M существенно меньше N. Это снижает нагрузку на вычислительные ресурсы и ускоряет обработку данных, сохраняя при этом способность модели адекватно отражать внутренние зависимости системы.

Работа SNS начинается с инициализации матрицы эмбеддингов узлов E ∈ R^N×d, где каждая строка Ei является векторным представлением i-го узла и содержит информацию о его характеристиках и взаимосвязях. Параллельно формируется матрица кандидатов C ∈ {1,…,N}^N×M, где каждая строка задаёт набор потенциально значимых соседей для соответствующего узла. На этом этапе ещё не определено, кто именно окажется наиболее важным — задача отбора решается далее, с учётом пространственных и контекстных особенностей данных.

Далее алгоритм SNS проводит ранжирование M кандидатов для каждого узла по их значимости, используя меру близости между эмбеддингами — чаще всего это евклидово расстояние, хотя возможно применение и других метрик. Чем меньше расстояние между векторными представлениями двух узлов, тем выше вероятность, что их взаимосвязь действительно отражает реальное влияние одного на другой. После этого формируется итоговый набор из K наиболее значимых соседей, которые служат ядром матрицы смежности. Оставшиеся M−K позиций могут быть дополнены случайно выбранными элементами для увеличения разнообразия связей и повышения устойчивости модели к локальным колебаниям данных. Этот комбинированный подход позволяет избежать чрезмерной жёсткости структуры и предотвращает переобучение, которое часто возникает при статичном фиксировании связей.

На выходе метод формирует индексную выборку I значимых узлов, на основе которой строится компактная матрица смежности As размером N×M. Такое решение значительно снижает вычислительную сложность, приближая её к линейной по сравнению с традиционной квадратичной реализацией O(N²). И при этом не жертвует качеством прогноза. В результате, SNS открывает возможность применения графовых нейронных сетей в тех сферах, где ранее подобные подходы считались слишком ресурсоёмкими: в реальном времени можно прогнозировать колебания рыночных цен, распределение транспортных потоков, изменения потребления энергии и другие процессы, где взаимосвязь элементов играет решающую роль.

Таким образом, Significant Neighbors Sampling не просто экономит ресурсы — он позволяет переосмыслить саму концепцию работы с графами большого размера. Отказ от глобальной обработки всех связей в пользу динамического и избирательного анализа создаёт условия для построения более гибких и адаптивных прогнозных моделей, которые учатся фокусироваться на том, что действительно важно, а не тонуть в избыточных данных.

Модуль разреженного пространственного многоголового внимания (Sparse Spatial Multi-Head Attention) в SAGDFN является ядром, которое преобразует отобранные значимые соседние узлы в компактную матрицу связей As размером N×M, определяющую, сколько информации должно перетекать от каждого из M узлов к конкретному узлу i во время графовой свертки. В отличие от подходов, основанных на предварительной информации о топологии, модуль SS-MHA строится полностью на данных. Он не использует внешние структуры и не подвержен ошибочным или устаревшим представлениям о пространственных связях. Это делает модель универсальной и применимой для решения различных задач на финансовых рынках, энергетических сетях или транспортных потоках, где зависимости между компонентами изменяются со временем и не поддаются простой ручной модели.

Технически модуль объединяет две ключевые идеи. Во-первых, внутреннее произведение векторов позволяет эффективно и параллельно оценивать базовую меру схожести между узлами: вектор узла i трансформируется в матрицу размером M×d, повторяя строку и конкатенируя её с эмбеддингами его M значимых соседей. Это формирует матрицу, которая одновременно содержит информацию о локальном контексте узла и его кандидатах-соседях, открывая путь к быстрым матричным операциям на современных платформах автоматического дифференцирования.

Во-вторых, авторы фреймворка SAGDFN отказываются от чисто линейного подхода и обучают нелинейную меру корреляции через небольшие Feed-Forward нейронные блоки (FFN). Для каждого узла и каждой головы внимания эти FFN преобразуют конкатенированные представления в матрицу оценок Y, где две колонки интерпретируются как вероятные и менее вероятные корреляции, соответственно. Многоголовая архитектура здесь напоминает работу группы экспертов, наблюдающих за одним и тем же набором данных под разными углами: одна голова выявляет сезонные связи, другая — реакцию на новости, третья — латентные маркеры риска.

Ключевым этапом является нормализация оценок. Вместо стандартного SoftMax, который размывает веса по всему набору и часто создает множество мелких, незначимых связей, авторы фреймворка предлагают использовать функцию α-Entmax. Она обеспечивает разреженные, но информативные распределения внимания: большие значения усиливаются, слабые — подавляются до нуля. В финансовых приложениях это критично: на рынке лишь немногие инструменты действительно задают направление в данный момент — резервная валюта, крупный индекс или ключевой товар. α-Entmax действует как оптика, фокусирующаяся на ярких объектах и отсекающая фоновый шум. Параметр α обеспечивает гибкость: изменяясь от SoftMax (α=1) до SparseMax (α=2). Подбирается оптимальная степень разреженности для конкретного домена данных.

Практически, для каждой головы внимания формируются нормализованные оценки Z^p, которые объединяются в многомерный тензор Zi для узла i. Затем по всем узлам собирается тензор Z размером N×M×(2P) и с помощью линейного преобразования с весами Wa сворачивается в итоговую матрицу As размером N×M. Эта матрица больше не представляет собой плотныйN×N граф, а аккуратно отбирает для каждого узла лишь те M сигналов, которые реально влияют на последующую графовую свертку.

Такой подход особенно эффективен для финансовых рынков, где инструменты, влияющие на движение цены сегодня, могут не влиять завтра. Например, в период паники ведущими могут быть золото и иена, в фазу экономического роста — индекс S&P 500 и технологические акции, при энергетическом шоке — цены на нефть и валюты энергетических экспортеров. Модуль позволяет выявлять таких явных и скрытых лидеров, исключая случайные корреляции, способные исказить прогноз.

Кроме улучшения точности прогнозов, α-Entmax дает и другие преимущества: разреженные оценки уменьшают количество ненужных операций в графовой свертке, делая модель более интерпретируемой; аналитик может видеть, какие M узлов реально повлияли на прогноз конкретного инструмента. Комбинация случайной подстановки при выборе соседей и разреженной нормализации гарантирует обновление эмбеддингов по всей сети, не упуская важные переменные.

Техническая реализация учитывает эффективное использование GPU и автоматических фреймворков: конкатенация и пакетная обработка, компактные FFN для каждой головы, линейное преобразование последнего тензора Z в As для тонкой параметризации влияния каждой головы и каждого канала.

В совокупности Sparse Spatial Multi-Head Attention обеспечивает практический компромисс между точностью и ресурсной эффективностью: чувствительность к наиболее важным сигналам, адаптацию к изменяющимся условиям и масштабируемость для тысяч временных рядов.

Прогнозирование на основе архитектуры Encoder–Decoder в фреймворке SAGDFN — это кульминация всех предыдущих этапов. Здесь объединяются ранее отобранные значимые соседи, разреженное пространственное многоголовое внимание и эффективная графовая свёртка с мощной последовательной моделью, позволяющей учесть временную динамику. В отличие от простых подходов, которые фокусируются на пространственных зависимостях или временном аспекте, предложенный авторами фреймворка подход позволяет описать и использовать оба измерения совместно. Это дает более точные и устойчивые прогнозы для мультимодальных временных рядов.

Интуитивно работу Encoder–Decoder можно представить следующим образом. Энкодер концентрирует информацию из исторической последовательности, аккумулируя пространственно-временные паттерны в компактном представлении скрытых состояний. Декодер затем, шаг за шагом, генерирует прогнозы, используя полученное представление и поступающие на каждом шаге прогнозные значения.

В данном случае критическим узлом является быстрый механизм графовой диффузии, основанный на компактной матрице смежности As, который обеспечивает передачу релевантной информации между узлами графа на каждой временной итерации.

Многошаговая графовая свёртка, реализующая информационную диффузию по соседям, задаётся выражением:

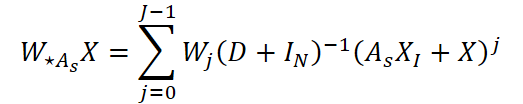
где D — диагональная матрица степеней для As, IN — единичная матрица размера N, а XI — матрица исходных данных, агрегированных по выбранным M соседям (индексация по I).

Такой оператор сохраняет информацию о собственном состоянии узла (термин X) и аккумулирует сигнал от значимых соседей (AsXI), затем нормализует их по сумме степеней и пропускает через линейные фильтры Wj. Практическая выгода — возможность контролировать радиус распространения информации через параметр J: небольшое J фиксирует локальные связи, большое — даёт учёт более удалённых влияний.

Далее авторы фреймворка SAGDFN интегрируют эту графовую операцию внутрь GRU-подобного шага, заменяя стандартное умножение матриц на графовую свёртку. Так возникает OneStepFastGConv, одношаговая итерация, которая сочетает в себе пространственную агрегацию и временную рекуррентность:

Здесь конкатенация ⊕ объединяет текущее наблюдение и предыдущее скрытое состояние, а операции ⊙ и σ имеют привычный смысл. Такой шаг гарантирует, что перед обновлением скрытого состояния каждый узел учитывает собственные признаки и сигнал от своих наиболее значимых партнёров по графу. Это особенно важно для финансов: при формировании прогноза цены акции учитывается не только её собственная история, но и движения ключевых связанных инструментов — валют, сырья, индексов.

Прогнозирование данных осуществляется в два этапа — Encoder и Decoder. В Encoder запускаем OneStepFastGConv на историческом окне длины h, получая в конце представление Ht0-1, которое аккумулирует пространственно-временную информацию всего анализируемого окна данных.

Затем Decoder стартует с начального состояния Ht0-1 и наблюдения на шаге t0, последовательно генерируя заданное количество шагов вперёд.

Обучение происходит сквозным обратным распространением — градиенты по Θ (включая эмбеддинги, параметры FFN в модуле внимания, веса графовой свёртки и параметры GRU) вычисляются и используются для обновления модели. Примечательно, что поскольку эмбеддинги участвуют в отборе соседей и в расчёте As, структура графа также изменяется по ходу обучения: это даёт системе адаптивность, позволяя ей открывать новые значимые связи по мере изменения рынка.

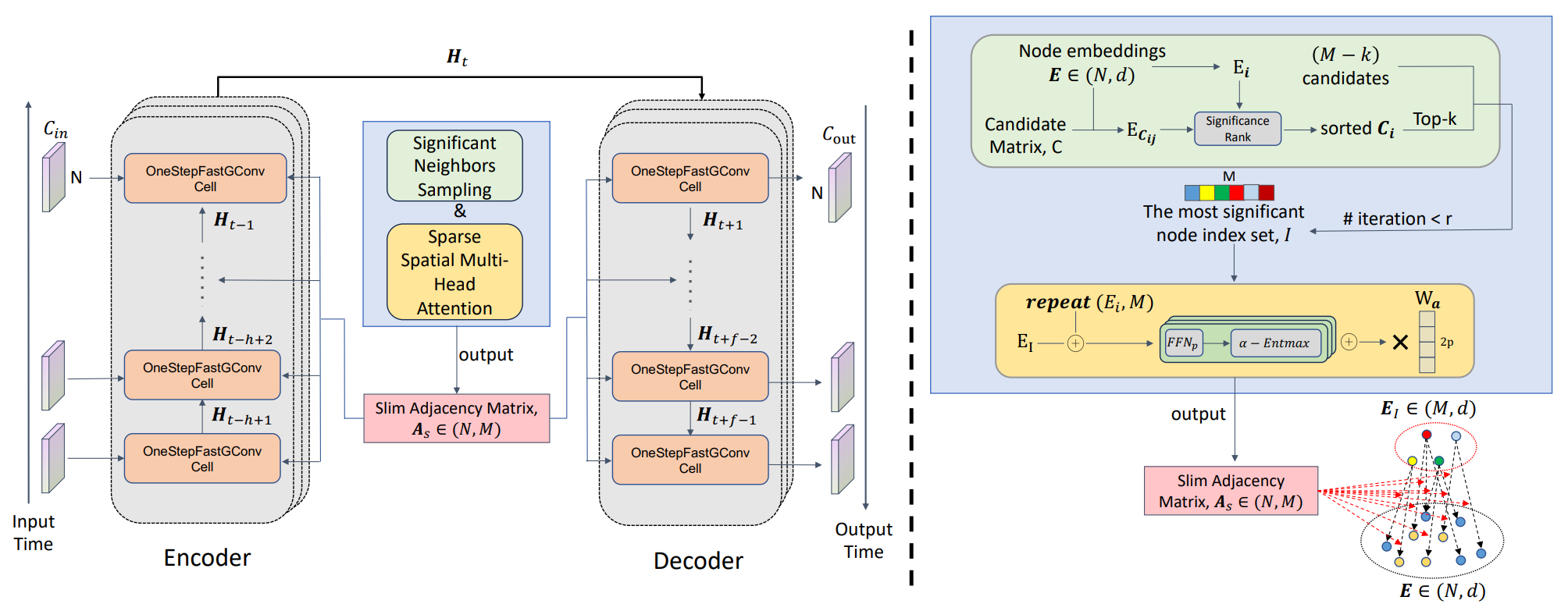
Encoder–Decoder, объединённый с OneStepFastGConv и адаптивной структурой As, создаёт мощную и гибкую платформу для пространственно‑временного прогнозирования. Она сочетает интерпретируемость (через разреженную матрицу связей и визуализацию релевантных соседей), адаптивность (динамическое обновление эмбеддингов и структуры графа) и практическую масштабируемость, что делает её особенно ценным инструментом для анализа и принятия решений на финансовых рынках.

Авторская визуализация фреймворка SAGDFN представлена ниже.

Реализация средствами MQL5

После подробного разбора теоретической части фреймворка SAGDFN, мы переходим к практической реализации предложенных подходов. Здесь мы покажем один из реальных путей переноса идей авторов фреймворка в среду MQL5. В ходе работы рассмотрим следующие моменты:

• подготовка данных;
• хранение и обновление эмбеддингов;
• выборка значимых соседей;
• механизм разреженного внимания;
• встраивание быстрой графовой свертки в рекуррентную логику.

Наша цель — рабочая, воспроизводимая и, главное, практичная реализация, пригодная для реальной роботы.

Модуль Significant Neighbors Sampling занимается одним простым, но крайне важным делом: он отвечает за выбор тех самых лидеров, которые действительно формируют информационный ландшафт сети. Именно от корректного отбора соседей зависит, какие сигналы будут усилены, а какие останутся фоновым шумом.

Здесь надо сказать, что авторы фреймворка SAGDFN предложили ранжировать M наиболее значимых соседей, полученных на предыдущем шаге, формируя набор из K наиболее близких элементов, которые служат ядром матрицы смежности. Оставшиеся M−K позиций дополняются случайно выбранными элементами для увеличения разнообразия связей. В своей реализации мы решили пойти дальше и добавить параллельное ранжирование случайной выборки.

Идея проста и вместе с тем эффективна: вместо того чтобы сначала взять K ближайших кандидатов, а потом дополнить их случайными элементами, мы формируем два пула — заранее отобранных и случайных претендентов. А затем оцениваем их одновременно. В итоговую выборку попадают действительно ближайшие по эмбеддингу узлы из объединённого пула, независимо от того, были они взяты по эвристике или случайно. Это сочетание эксплуатации и эксплорации даёт модели одновременно стабильность и гибкость: она удерживает проверенных лидеров, но не упускает шанс заметить новые центры влияния рынка.

Техническую реализацию этого алгоритма перенесем в OpenCL-контекст. Для этого создадим кернел SignificantNeighborsSampling.

__kernel void SignificantNeighborsSampling(__global const float *data,
                                           __global const float *candidates,
                                           __global const float *random_cands,
                                           __global float *neighbors,
                                           const int dimension
                                          )
  {
   const size_t main = get_global_id(0);
   const size_t slave = get_local_id(1);
   const int total_main = (int)get_global_size(0);
   const int total_slave = (int)get_local_size(1);

Кернел начинается с объявления сигнатуры. Он принимает на вход глобальные массивы data, candidates и random_cands, предназначенные для хранения эмбеддингов рядов и двух пулов кандидатов. Массив служит neighbors для записи результатов. А целочисленная dimension, отвечает за размер эмбеддинга. Сигнатура задаёт рамки работы — один глобальный work-item отвечает за один основной узел (main), а набор локальных work-item'ов внутри группы отвечает за обработку кандидатов.

Далее идёт извлечение идентификаторов исполнительного контекста, объявляются локальные массивы и вычисляется рабочий локальный размер.

   __local int Idx[LOCAL_ARRAY_SIZE];
   __local float Temp[LOCAL_ARRAY_SIZE];
   const int ls = min(total_slave, (int)LOCAL_ARRAY_SIZE);

Локальная память — это сильный инструмент для ускорения: здесь она используется как буфер для временного хранения индексов и расстояний в пределах подгруппы.

В следующем блоке определяем сдвиги в плоских массивах исходных данных до необходимых элементов последовательности.

   const int shift_main = RCtoFlat(main, 0, total_main, dimension, 0);
   int cand = (int)candidates[slave];
   int rand_cand = (int)random_cands[slave];

Далее следует обратить внимание, что для поиска наиболее близких соседей мы используем 2 пула, один из которых сгенерирован случайной выборкой. И в таком случае весьма вероятно наличие одного или более элементов последовательности в обеих выборках. Поэтому следующим блоком идёт простая проверка дубликатов. Это защищает от повторного рассмотрения одного и того же индекса, что логично и экономит вычисления. На первом этапе проверяем дублирование в рамках текущего потока.

//--- duplicate check
   if(rand_cand == cand)
      rand_cand = -1;

Затем проверяем наличие дубликатов среди пула ранее отобранных соседей.

//--- Look in candidates
   for(int l = 0; l < total_slave; l += ls)
     {
      if(slave >= l && slave < (l + ls))
         Idx[slave - l] = cand;
      BarrierLoc;
      for(int i = 0; i < ls; i++)
        {
         if(i >= (slave - l))
            continue;
         if(cand == Idx[i])
            cand = -1;
         if(rand_cand == Idx[i])
            rand_cand = -1;
        }
      BarrierLoc;
     }

Здесь мы порционно записываем индексы кандидатов в локальный массив данных, а затем каждый поток сверяет свои индексы с элементами массива.

Обратите внимание, что для гарантии сохранения одной копии каждого элемента мы проверяем на дублирование только индексы предшествующих потоков. Следовательно, исключаются только элементы последующих потоков, сохраняя элемент первого встраивания.

И далее аналогичным образом проводим проверку в пуле случайной выборки кандидатов.

//--- Look in random candidates
   for(int l = 0; l < total_slave; l += ls)
     {
      if(slave >= l && slave < (l + ls))
         Idx[slave - l] = rand_cand;
      BarrierLoc;
      for(int i = 0; i < ls; i++)
        {
         if(i >= (slave - l))
            continue;
         if(cand == Idx[i])
            cand = -1;
         if(rand_cand == Idx[i])
            rand_cand = -1;
        }
      BarrierLoc;
     }

Когда кандидаты прошли проверку на уникальность в пределах локальной группы, мы рассчитываем плоские смещения shift_cand и shift_rand_cand, чтобы получить начало эмбеддинга каждого кандидата в массиве data.

   const int shift_cand = RCtoFlat(cand, 0, total_main, dimension, 0);
   const int shift_rand_cand = RCtoFlat(rand_cand, 0, total_main, dimension, 0);

Далее начинается вычисление евклидова расстояния. Вначале инициализируются локальные переменные дистанций кандидатов обоих пулов нулевыми значениями.

//--- calc distance
   float dist_cand = 0;
   float dist_rand_cand = 0;
   for(int d = 0; d < dimension; d++)
     {
      float value = IsNaNOrInf(data[shift_main + d], 0);
      if(main != cand && cand >= 0)
         dist_cand += pow(value - IsNaNOrInf(data[shift_cand + d], 0), 2.0f);
      if(main != rand_cand && rand_cand >= 0)
         dist_rand_cand += pow(value - IsNaNOrInf(data[shift_rand_cand + d], 0), 2.0f);
     }

Затем, в цикле по размерности эмбеддингов, извлекается значение целевого эмбеддинга и кандидатов. Для определения дистанции в локальных переменных суммируются квадраты разницы целевого элемента и соответствующего кандидата.

Стоит обратить внимание, что вычисления осуществляются только для неудаленных элементов.

После подсчёта расстояний идёт подготовка к ранжированию позиции. Вначале инициализируем локальные переменные cand_position и rand_position нулевыми значениями, что соответствует первому элементу массива. Однако мы проверяем равенство расстояний элементов из предварительно отобранного и случайного пулов. В случае идентичности расстояний, мы отдаем предпочтение пулу ранее отобранных кандидатов и увеличиваем значение rand_position.

//--- calc position
   int cand_position = 0;
   int rand_position = (int)(dist_cand >= dist_rand_cand);

Затем начинается серия блоков, в которых по кускам локальной памяти Temp коллективно собираются текущие расстояния и считается, сколько элементов локальной выборки имеют расстояние меньше рассматриваемого. Первая серия копирует дистанции пула предварительно отобранных кандидатов (или -1 для отсутствующих).

//--- by candidates
   for(int l = 0; l < total_slave; l += ls)
     {
      if(slave >= l && slave < (l + ls))
         Temp[slave - l] = (cand >= 0 ? IsNaNOrInf(dist_cand, -1) : -1);
      BarrierLoc;
      for(int i = 0; i < ls; i++)
        {
         if(i == (slave - l))
            continue;
         if(Temp[i] < 0)
            continue;
         if(cand >= 0)
           {
            if(Temp[i] < dist_cand)
               cand_position++;
            else
               if(Temp[i] < dist_cand && i < (slave - l))
                  cand_position++;
           }
         if(rand_cand >= 0)
           {
            if(Temp[i] < dist_rand_cand)
               rand_position++;
            else
               if(Temp[i] < dist_rand_cand && i < (slave - l))
                  rand_position++;
           }
        }
      BarrierLoc;
     }

Каждый поток в группе пробегает по элементам Temp, увеличивая cand_position и rand_position в зависимости от того, какие расстояния меньше. Здесь используется тонкая логика tie-breaking: если два расстояния равны, порядок определяется индексом, что обеспечивает детерминированность ранжирования при равных расстояниях. Барьеры гарантируют, что Temp корректно заполнен перед чтением и очищен далее.

Похожая вторая серия делает то же самое, но переносит в Temp расстояния элементов случайной выборки и ещё раз корректирует позиции, учитывая остаток локальной подгруппы.

//--- by random candidates
   for(int l = 0; l < total_slave; l += ls)
     {
      if(slave >= l && slave < (l + ls))
         Temp[slave - l] = (rand_cand >= 0 ? IsNaNOrInf(dist_rand_cand, -1) : -1);
      BarrierLoc;
      for(int i = 0; i < ls; i++)
        {
         if(i == (slave - l))
            continue;
         if(Temp[i] < 0)
            continue;
         if(cand >= 0)
           {
            if(Temp[i] < dist_cand)
               cand_position++;
            else
               if(Temp[i] < dist_cand && i < (slave - l))
                  cand_position++;
           }
         if(rand_cand >= 0)
           {
            if(Temp[i] < dist_rand_cand)
               rand_position++;
            else
               if(Temp[i] < dist_rand_cand && i < (slave - l))
                  rand_position++;
           }
        }
      BarrierLoc;
     }

Понимание этой части важно: алгоритм реализует распределённый подсчёт позиции — каждый slave сам вычисляет, на каком месте в отсортированном по расстоянию списке локальной группы он окажется. Это даёт нам ранжирование без глобальной сортировки, полностью локально, что экономит и память, и время.

Финальный этап — запись результата. Если кандидат существует и его позиция меньше общего количества искомых соседей, то вычисляется индекс смещения и в соответствующую ячейку массива neighbors записывается индекс кандидата.

//--- result
   if(cand >= 0 && cand_position < total_slave)
     {
      const int shift_dist_cand = RCtoFlat(main, cand_position, total_main, total_slave, 0);
      neighbors[shift_dist_cand] = cand;
     }
   if(rand_cand >= 0 && rand_position < total_slave)
     {
      const int shift_dist_cand = RCtoFlat(main, rand_position, total_main, total_slave, 0);
      neighbors[shift_dist_cand] = rand_cand;
     }
  }

Представленный алгоритм делает параллельную оценку детерминированных и случайных кандидатов, устраняет дубликаты локально, вычисляет расстояния и ранжирует кандидатов по месту в локальной подвыборке без глобальной сортировки.

Сегодня мы проделали большую и насыщенную работу, и статья уже получилась весьма основательной. Сейчас самое время сделать паузу, позволить мыслям устаканиться и взглянуть на проделанное со свежей стороны. В следующей статье мы вернёмся к теме с новыми силами и продолжим начатый путь, двигаясь дальше шаг за шагом.

Заключение

В этой статье мы познакомились с фреймворком SAGDFN, который выделяется среди аналогичных решений, благодаря своей масштабируемости, способности эффективно работать с крупными графами и минимизировать вычислительные затраты без потери точности. Его адаптивный подход к выбору значимых связей между узлами позволяет сохранять ключевую информацию и при этом избегать перегрузки модели лишними данными.

В теоретическом блоке мы подробно разобрали ключевые особенности и внутренние механизмы фреймворка. Объяснили принципы работы алгоритма, а затем сделали первый шаг к его практической реализации. Особое внимание было уделено модулю Significant Neighbors Sampling, который играет важную роль в оптимизации вычислений и снижении издержек при работе с большими графами. При этом мы внесли ряд усовершенствований, сделав процесс отбора соседей более гибким и адаптивным.

Эта работа стала важным этапом на пути создания полноценного прогностического инструмента, способного эффективно обрабатывать большие объемы данных и извлекать из них полезные пространственно-временные зависимости. В следующем материале мы продолжим эту линию, дополняя архитектуру новыми компонентами и постепенно приближаясь к комплексному тестированию всей системы на реальных исторических данных.

Ссылки

• SAGDFN: A Scalable Adaptive Graph Diffusion Forecasting Network for Multivariate Time Series Forecasting
• Другие статьи серии

Программы, используемые в статье

#	Имя	Тип	Описание
1	Study.mq5	Советник	Советник офлайн обучения моделей
2	StudyOnline.mq5	Советник	Советник онлайн обучения моделей
3	Test.mq5	Советник	Советник для тестирования модели
4	Trajectory.mqh	Библиотека класса	Структура описания состояния системы и архитектуры моделей
5	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
6	NeuroNet.cl	Библиотека	Библиотека кода OpenCL-программы