Нейросети в трейдинге: Модель темпоральных запросов (TQNet)

Введение

Прогнозирование многомерных временных рядов в финансах — это игра на опережение, где ставка сделана на точность и скорость. Курсы валют, индексы, объемы торгов, процентные ставки, показатели ликвидности — все эти параметры непрерывно взаимодействуют, образуя сложную, постоянно меняющуюся систему. Трейдеры, управляющие активами и аналитики знают: чтобы быть на шаг впереди, нужно понимать, как все переменные влияют друг на друга в реальном времени. Именно в этом умении видеть картину целиком и заключена суть современного прогнозирования на финансовых рынках.

Проблема в том, что финансовые данные — это не лабораторные измерения в стерильных условиях. Рынок живёт своей жизнью: резкие скачки котировок на новостях, периоды высокой и низкой волатильности, неожиданные корреляции, которые появляются и исчезают в считанные часы. Добавьте сюда шумы (ошибки измерений, запаздывания котировок, разрывы в данных), и перед нами вырисовывается классическая задача: как извлечь надёжный сигнал в мире, полном случайностей. Особенно сложной становится ситуация, когда локальные связи между параметрами в одном временном фрагменте противоречат глобальной картине по всей истории наблюдений. Это словно пытаться прогнозировать курс валюты, ориентируясь только на один день, когда весь тренд тянется месяцами в противоположном направлении.

Чтобы преодолеть этот разрыв, в работе "Temporal Query Network for Efficient Multivariate Time Series Forecasting" был предложен новый подход Temporal Query — инструмент, который позволяет объединить локальное и глобальное видение рынка. В его основе лежат обучаемые векторы, которые циклически смещаются во времени, фиксируя устойчивые межрыночные зависимости, проверенные всей историей данных. При этом сами котировки, индикаторы и другие рыночные параметры выступают ключами и значениями в многоголовом механизме внимания, отвечая за уникальные особенности каждого конкретного момента. Это даёт двойной эффект: модель сохраняет способность реагировать на мгновенные изменения и при этом опирается на фундаментальные, более устойчивые рыночные связи.

На базе этого принципа был разработан фреймворк Temporal Query Network (TQNet) — минималистичное, но мощное архитектурное решение, способное прогнозировать динамику множества взаимосвязанных финансовых инструментов. Её структура предельно проста: всего один слой многоголового внимания и неглубокая полносвязная сеть. Но за этой простотой скрывается способность выявлять тонкие зависимости между активами и реагировать на них быстрее, чем большинство традиционных методов. В экспериментах, проведенных авторами фреймворка, TQNet продемонстрировал точность, сопоставимую с самыми сложными архитектурами, но при этом работал с вычислительной скоростью, сравнимой с лёгкими линейными моделями.

Особенность TQNet заключается в способности адаптироваться к разным горизонтам прогнозирования, используя один и тот же принцип балансировки локальных и глобальных зависимостей. Это особенно ценно на финансовых рынках, где ситуация может разворачиваться за минуты, но при этом подчиняться долгосрочным закономерностям, которые нельзя игнорировать.

На современных финансовых рынках выигрывает не тот, кто видит только детали, и не тот, кто полагается лишь на общую картину, а тот, кто умеет объединить эти два уровня восприятия. Temporal Query и TQNet дают именно такую возможность и делают это с элегантной простотой, достойной того, чтобы стать частью арсенала любого серьёзного аналитика.

Алгоритм TQNet

В основе задачи прогнозирования многомерных временных рядов (Multivariate Time Series Forecasting, MTSF) лежит стремление предсказать будущее поведение сразу нескольких взаимосвязанных переменных. Формально, на момент времени t у нас есть наблюдаемая историческая последовательность Xt ∈ R^C*L. Здесь C — количество переменных или каналов (валютные пары, рыночные индексы, объёмы торгов и другие показатели), а L — длина окна наблюдения (сколько прошлых точек мы учитываем). Задача состоит в том, чтобы построить прогноз на горизонте H, получив Yt ∈ R^C*H — последовательность будущих значений тех же переменных.

В терминах финансовых рынков это может означать прогнозирование котировок основных валютных пар на ближайшие часы, дни торгов по ключевым индексам, или динамики процентных ставок на горизонте в несколько недель, опираясь на исторические данные за выбранный период. При этом важно учитывать не только индивидуальные временные паттерны каждой переменной, но и взаимные корреляции между ними — ведь рынок движется как единый организм, и изменения в одном сегменте могут мгновенно отражаться в другом.

Для решения этой задачи был предложен фреймворк Temporal Query Network (TQNet). Несмотря на простоту архитектурного решения, фреймворк сочетает в себе два ключевых механизма: выделение межпеременных зависимостей и моделирование временной структуры.

Работа TQNet начинается с подачи анализируемой последовательности Xt в слой многоголового механизма внимания, усиленного компонентом Temporal Query (TQ-MHA). Этот слой отвечает за выявление и интеграцию межпеременных корреляций — как глобальных, устойчивых во времени, так и локальных, характерных для текущего рыночного контекста. Затем результат обрабатывается неглубокой многослойной полносвязной сетью (MLP), которая уточняет временные зависимости и помогает модели улавливать тренды и ритмику изменений.

Оба этих блока (TQ-MHA и MLP) дополнены остаточными соединениями, что повышает стабильность обучения и снижает риск деградации качества на больших выборках. Завершающим этапом служит линейный слой с Dropout, который проецирует полученные скрытые представления на пространство выходных данных, формируя прогноз Ŷt ∈ R^C*H.

Ключевым элементом архитектуры TQNet является метод Temporal Query (TQ) — особый способ формирования запросов (Query) в механизме внимания. Его идея проста и элегантна: вместо того, чтобы получать запросы напрямую из исходных данных, как это делается в классическом Self-Attention, авторы фреймворка предлагают использовать набор обучаемых векторов, которые периодически смещаются во времени. Такой приём позволяет фиксировать глобальные корреляции между переменными, устойчивые к кратковременным рыночным колебаниям и шумам.

Формально, имея размер периода W в анализируемых данных, мы инициализируем матрицу параметров θTQ ∈ R^C*W. Где C — количество переменных (каналов), а W — длина вектора, определяющая интервал периодического сдвига. Эти параметры изначально заполняются нулями и в процессе обучения адаптивно подстраиваются под внутренние зависимости в данных. Выбор W особенно важен: на финансовых рынках он может соответствовать, например, числу торговых сессий в неделе, повторяющимся циклам ликвидности, или другим устойчивым сезонным паттернам. Определить его можно либо на основе экспертных знаний о рынке, либо с помощью статистических методов.

Принцип работы TQ таков: для каждого анализируемого примера на момент времени t извлекаем фрагмент длины L из матрицы θTQ, начиная с позиции, вычисляемой как t mod W и, если необходимо, закольцовываем выборку по кругу. Таким образом, два момента времени, отстоящие ровно на W шагов, будут иметь идентичные векторы запросов. Это создаёт эффект периодической памяти, позволяя модели повторно использовать выученные глобальные зависимости и снижая влияние случайных рыночных возмущений.

В контексте финансов это можно сравнить с опытным трейдером, который помнит типичные рыночные сценарии в одни и те же дни недели или в определённые часы торгов, и использует это знание при анализе текущей ситуации.

В TQNet этот подход встроен в механизм многоголового внимания (TQ-MHA). Здесь Запросы (Query) формируются не из исходных данных, а из временных TQ-векторов, отражающих глобальные зависимости. При этом Ключи (Key) и Значения (Value) по-прежнему извлекаются из текущей анализируемой последовательности Xt, сохраняя всю локальную, уникальную информацию о рынке в данный момент времени.

Индекс h соответствует номеру головы внимания, а W h ^Q, W h ^K, W h ^V — обучаемые матрицы проекций.

Далее вычисляется внимание для каждой головы.

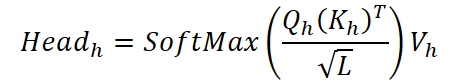
А результаты, аналогично классическому Multi-Head Self-Attention, объединяются и проходят через итоговую проекцию.

Такое сочетание глобальных Запросов и локальных Ключей/Значений создаёт баланс между устойчивостью к шуму и адаптацией к текущему контексту. В реальных рыночных данных, где периоды спокойствия могут резко сменяться фазами высокой турбулентности, этот баланс критичен. Модель не теряет способность реагировать на уникальные события — вроде неожиданной макроэкономической статистики или резких движений на новостях — но при этом опирается на каркас глобальных зависимостей, которые сохраняются сквозь время.

Цель предлагаемой техники Temporal Query (TQ) — органично объединить в механизме внимания как глобальные, так и локальные взаимосвязи временного ряда. Идея проста, но эффективна: Запросы (Query) формируются не напрямую из исходных данных, а из периодически сдвигаемых обучаемых векторов θTQ, тогда как Ключи (Key) по-прежнему извлекаются из исходной последовательности. Такой подход позволяет балансировать между общей картиной рынка и индивидуальными особенностями каждого конкретного фрагмента данных.

Чтобы на практике оценить влияние глобальных и локальных зависимостей, авторы фреймворка сравнили три сценария:

1. Классический вариант, когда Query и Key строятся из сырых данных. В этом случае, внимание фиксирует лишь локальные, выборочные связи между наблюдениями.
2. Смешанный подход — именно он реализован в TQNet. Здесь Query формируется из обучаемых TQ-векторов, а Key — из исходных данных. В результате, при вычислении коэффициентов внимания учитываются и глобальные, и выборочные зависимости, что особенно важно на финансовых рынках, где общие тренды переплетаются с моментными колебаниями.
3. Чисто глобальная схема, когда Query и Key формируются из обучаемых TQ-векторов. Такой метод полностью игнорирует локальные вариации, концентрируясь на общей структуре временного ряда.

Сводные результаты, полученные на крупных мультивариантных датасетах с числом переменных более 100 и усреднённые по четырём прогнозным горизонтам, демонстрируют, что наилучший результат показал именно подход TQNet. В нём сочетаются оба типа корреляций. На втором месте — традиционная схема с чисто выборочными связями, замыкает тройку чисто глобальный вариант. Итог однозначен: гармоничное объединение глобальных и локальных зависимостей повышает точность прогноза и устойчивость модели, что особенно ценно при работе с динамичными финансовыми рядами.

После того, как слой TQ-MHA выделил устойчивые межпеременные связи и интегрировал их с локальной информацией, в дело вступает многослойный перцептрон (MLP). Его задача — проработать уже извлечённые признаки во временной плоскости, уловить тренды, ритмику и задержки во взаимосвязях.

Несмотря на простоту, MLP остаётся удивительно эффективным инструментом для выделения временных закономерностей. В архитектуре TQNet он реализован в лёгком варианте: всего два полносвязных слоя с активацией GeLU, которая обеспечивает более плавную обработку сигналов по сравнению с ReLU, особенно в условиях сложных рыночных колебаний.

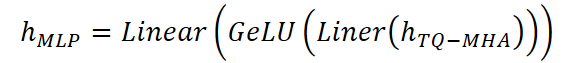
С финансовой точки зрения этот шаг можно сравнить с ситуацией, когда аналитик, получив сводку по ключевым взаимосвязям на рынке, проводит дополнительный разбор: выделяет закономерности внутри дня, оценивает амплитуды колебаний, выявляет точки инерции и разворота.

Далее полученные представления передаются в слой проекции результатов. Здесь применяется линейное преобразование, которое адаптирует внутренние представления под конкретный горизонт планирования H. Дополнительно может использоваться Dropout, чтобы снизить переобучение и повысить устойчивость модели.

Отдельное внимание в TQNet уделено вопросу устойчивости к сдвигам распределения данных — явлению, крайне распространённому в финансовой среде. Курсы валют, цены на сырьё, фондовые индексы — все они могут резко менять статистические характеристики под влиянием новостей, макроэкономических факторов или регуляторных решений. Если модель привязана к старому распределению, её прогнозы быстро теряют актуальность.

Чтобы этого избежать, в фреймворке TQNet используется обратимая нормализация (RevIN) — метод, проверенный в ряде современных архитектур. Его смысл в том, что перед обработкой модель вычитает среднее значение и делит данные на стандартное отклонение, а после построения прогноза возвращает данные в исходный масштаб. В терминах торговли это можно уподобить тому, как опытный аналитик всегда пересматривает свои ориентиры, если меняются условия на рынке. Нормализация убирает кратковременные смещения в масштабе и волатильности, позволяя модели концентрироваться на паттернах, а не на случайных изменениях масштаба котировок.

Таким образом, в TQNetMLP и проекция результатов работают как финишная шлифовка прогноза. TQ-MHA даёт скелет межпеременных зависимостей, MLP прорабатывает их во времени, а нормализация защищает от статистических перекосов. В результате модель выдаёт прогноз, который одновременно учитывает локальные особенности текущего момента и сохраняет глобальную рыночную согласованность.

Авторская визуализация фреймворка TQNet представлена ниже.

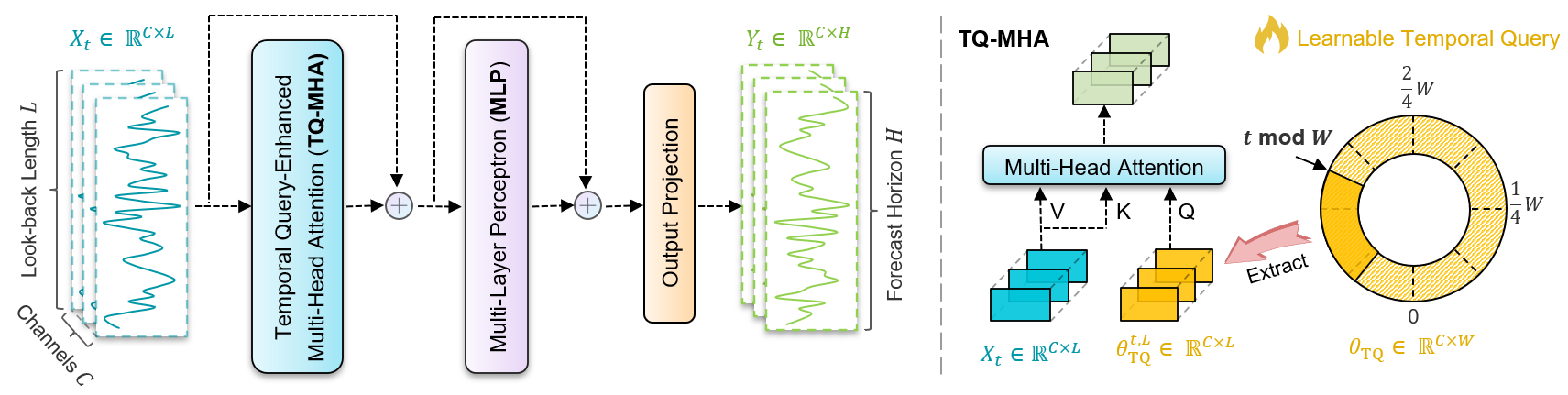
Реализация средствами MQL5

После того как мы разобрали теоретические основы фреймворка TQNet и показали, почему сочетание глобальных и локальных корреляций способно повысить точность прогнозирования, настало время перейти от концепций к практике. Теперь мы сосредоточимся на одном из вариантов реализации этих идей в среде MQL5, адаптируя архитектуру под задачи анализа и прогнозирования временных рядов на финансовых рынках.

Здесь каждый элемент от формирования Запросов и Ключей до нормализации данных и проекции результатов будет воплощён в коде. Это позволит нам продемонстрировать, как теория превращается в инструмент, готовый к реальной торговле. Такой подход позволит проверить эффективность TQNet в условиях живых котировок и оценить его устойчивость на разных рыночных фазах: от спокойных боковиков до стремительных трендов.

Используя накопленный опыт построения различных модулей внимания, можно провести содержательное сравнение TQNet с классическим блоком Cross-Attention. В традиционной схеме кросс-внимание оперирует тензорами Запросов (Queries), Ключей (Keys) и Значений (Values), которые формируются на основе различных источников данных. Такой подход позволяет одной последовательности внимательно обрабатывать информацию, содержащуюся в другой, выявляя взаимосвязи между ними.

В случае TQNet, этот принцип получает более тонкую и целенаправленную адаптацию под задачи прогнозирования временных рядов. Здесь роль источников данных распределяется так, чтобы Запросы могли нести глобальную, обобщённую информацию, заложенную в обучаемых векторах θTQ, а Ключи — сохраняли связь с локальной структурой исходных данных. Это сочетание играет ключевую роль в финансовых рынках, где общие паттерны, например сезонность или повторяющиеся макроэкономические циклы, должны быть интегрированы с локальными изменениями — резкими скачками цен, рыночными шумами и краткосрочными дисбалансами спроса и предложения.

Таким образом, TQNet можно рассматривать как своеобразный гибрид кросс-внимания, в котором глобальная память модели и мгновенные рыночные сигналы соединяются в одном механизме. Это не только расширяет диапазон учитываемых взаимосвязей, но и делает модель более устойчивой к резким режимным переключениям, что особенно ценно в условиях высокой волатильности валютных, фондовых или товарных рынков.

В этой связи перед нами встает ключевая задача — формирование и обучение тензора параметров глобальной корреляции, который будет использоваться в качестве источника данных для генерации Запросов. Именно этот тензор, представляющий собой обучаемые векторы θTQ, несёт в себе информацию о глобальных взаимосвязях между переменными и служит фундаментом для корректного построения механизма внимания.

Процесс его обучения требует аккуратного подхода: тензор должен адаптироваться к структуре данных, улавливая устойчивые корреляции, но при этом оставаться устойчивым к шуму и локальным выбросам. В финансовых рядах это особенно важно, поскольку временные ряды активов подвержены резким колебаниям — от краткосрочных всплесков ликвидности до неожиданных событий на рынке.

Выстроив и обучив такой тензор, мы обеспечиваем модели способность использовать глобальные рыночные шаблоны при обработке каждой новой последовательности. Запросы, формируемые на его основе, действуют как фильтр, который направляет внимание модели на наиболее значимые взаимосвязи между переменными, одновременно интегрируя их с локальными особенностями текущего временного фрагмента. Это позволяет TQNet достигать высокой точности прогнозирования, сочетая стабильность глобальной памяти и адаптивность к конкретным рыночным условиям.

В нашем арсенале уже имеется объект CParams, в котором реализован алгоритм создания и поддержки обучаемых параметров. Теоретически мы могли бы использовать его для формирования тензора глобальных корреляций. Однако возникает вопрос эффективности такого подхода.

Дело в том, что для задач прогнозирования многомерных временных рядов на финансовых рынках требуется достаточно объёмный тензор, способный вместить корреляции на протяжении целого цикла анализируемых данных. С другой стороны, чрезмерно большой тензор приведёт к значительным вычислительным затратам, что негативно скажется на скорости обучения и работе модели в реальном времени.

Тем более, что большая часть этих вычислительных ресурсов будет задействована напрасно. На каждом шаге обучения или прогнозирования мы используем лишь небольшую часть тензора, соответствующую текущему временному окну. Остальная часть остаётся пассивной, а операции над ней — фактически пустые.

При этом, объём тензора и число пустых операций растут пропорционально увеличению длины цикла и количеству анализируемых переменных. Для финансовых данных, где число каналов может достигать сотен, а исторические периоды включают тысячи временных шагов, такая неэффективность быстро превращается в узкое место, замедляя обучение и снижая общую производительность модели.

Поэтому крайне важно искать решения, которые позволят сократить ненужные вычисления, оставляя при этом модель способной захватывать глобальные корреляции без потери точности.

В поисках более эффективного решения, мы решили несколько переосмыслить подход к хранению и обновлению параметров корреляций. Вместо того, чтобы использовать один статичный объект CParams для генерации всего тензора, мы создали реплику этого объекта, в которой реализовали массив внутренних объектов обучаемых параметров.

Каждый элемент массива теперь соответствует отдельному временному шагу, что позволяет использовать только те данные и параметры, которые актуальны для текущего окна прогнозирования. Такой подход существенно сокращает ненужные вычисления, одновременно сохраняя способность модели фиксировать глобальные взаимосвязи между переменными на протяжении всего периода анализа.

Иными словами, мы получили динамический тензор параметров, где каждый элемент отвечает за конкретный момент времени, а ненужные операции над остальными шагами полностью исключены. Это делает нашу реализацию TQNet гораздо более экономичной и масштабируемой для больших финансовых наборов данных.

После того, как мы разобрали концепцию динамического тензора параметров и обосновали необходимость использования массива объектов для каждого временного шага, естественным следующим шагом становится рассмотрение конкретной реализации этого подхода в коде. В нашей архитектуре ключевую роль играет класс CCircleParams, который наследуется базовый функционал от полносвязного нейронного слоя CNeuronBaseOCL.

class CCircleParams  :  public CNeuronBaseOCL
  {
protected:
   CLayer            cOnes;
   CNeuronBaseOCL    *cCurrent;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override          { return FeedForward(); }

   ///\ingroup neuron_base_opt
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override   { return UpdateInputWeights(); }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override   { return true; }

public:
                     CCircleParams(void) : cCurrent(NULL) {};
                    ~CCircleParams(void)  {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint numNeurons, uint period, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   virtual bool      Identity(const int rows, const int cols);
   virtual bool      Zeros(void);
   //---
   virtual bool      FeedForward(void);
   virtual bool      UpdateInputWeights(void);
   virtual bool      SetPosition(int position);
   //---
   virtual bool      Save(const int file_handle) override;
   virtual bool      Load(const int file_handle) override;
   //---
   virtual int       Type(void) override const  {  return defCircleParams; }
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   virtual CBufferFloat   *getWeightsParams(void);
   virtual int       GetPeriod(void) const { return cOnes.Total(); }
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
  };

Этот класс представляет собой специализированный контейнер для хранения и управления обучаемыми параметрами корреляций, обеспечивая их корректное обновление и эффективное взаимодействие с механизмами OpenCL-контекста, что особенно важно при работе с крупными финансовыми массивами данных на GPU.

Внутри класса CCircleParams особое место занимает объект cOnes, который является динамическим массивом обучаемых тензоров, поддерживая периодическую природу объекта. Параметр cCurrent выступает указателем на активный объект в массиве и отражает состояние конкретного временного шага. Это позволяет модели динамически переключать контекст работы, обрабатывая каждый временной фрагмент с максимальной точностью и одновременно сохраняя глобальные зависимости, накопленные за весь период анализа.

Структура объекта CCircleParams формируется и настраивается в методе инициализации Init, который отвечает за подготовку всех необходимых компонентов для корректной работы тензора параметров корреляций.

bool CCircleParams::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                         uint numNeurons, uint period,
                         ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, numNeurons, optimization_type, batch))
      return false;

При вызове метода сначала происходит инициализация унаследованных интерфейсов средствами родительского класса CNeuronBaseOCL, что задаёт фундаментальные параметры объекта. Если на этом этапе возникает ошибка, метод сразу возвращает false, предотвращая дальнейшую некорректную работу.

Далее подготавливаем динамический массив cOnes: очищаем и связываем с контекстом OpenCL, чтобы все последующие операции над тензорами могли выполняться эффективно на GPU.

   cOnes.Clear();
   cOnes.SetOpenCL(OpenCL);
   for(uint i = 0; i < period; i++)
     {
      cCurrent = new CNeuronBaseOCL();
      if(!cCurrent)
         return false;
      if(!cCurrent.Init(Neurons(), i, OpenCL, 1, optimization, iBatch) ||
         !cOnes.Add(cCurrent))
        {
         delete cCurrent;
         return false;
        }
      cCurrent.SetActivationFunction(None);
     }

Основной цикл метода отвечает за формирование массива объектов, каждый из которых соответствует отдельному временному шагу. Для каждого шага создаётся новый экземпляр CNeuronBaseOCL, который инициализируется с идентичными параметрами, специфичными для каждого шага. После успешной инициализации, объект добавляется в контейнер cOnes, который управляет всеми временными шагами. В случае любой ошибки создаваемый объект сразу удаляется, что предотвращает утечки памяти и сохраняет целостность структуры.

Для каждого вновь созданного нейрона также отключается функция активации, что важно для корректной работы тензора корреляций, где на этапе Feed-Forward требуется только передача значений без нелинейного преобразования.

После того, как все объекты временных шагов созданы, метод SetPosition устанавливает активным первый элемент нашего массива, обеспечивая начальное состояние для дальнейших вычислений.

//---
   if(!SetPosition(0))
      return false;
//---
   return true;
  }

Таким образом, метод Init не просто создаёт массив объектов, а формирует структурированное и управляемое хранилище параметров, где каждый элемент отражает конкретный момент времени. Это позволяет модели эффективно использовать глобальные корреляции, избегая лишних вычислений и обеспечивая готовность к обучению и прогнозированию многомерных финансовых временных рядов.

Метод SetPosition играет ключевую роль в управлении динамическим тензором параметров корреляций в CCircleParams. Его задача — переключить активный объект на определённый временной шаг, обеспечивая работу модели с актуальными данными именно для этого момента.

При вызове метода указатель cCurrent перенаправляется на элемент массива cOnes, соответствующий заданной позиции. Если выбранный объект отсутствует или не инициализирован, метод возвращает false, сигнализируя о проблеме и предотвращая некорректные вычисления. В противном случае, когда объект успешно выбран, метод возвращает true, подтверждая готовность модели к дальнейшей обработке данных.

bool CCircleParams::SetPosition(int position)
  {
   cCurrent = cOnes[position];
   if(!cCurrent)
      return false;
//---
   return true;
  }

Простота реализации скрывает важную функциональность: именно через SetPosition модель TQNet может динамически работать с различными временными шагами, активируя соответствующие параметры корреляций без необходимости пересоздавать или перегружать весь тензор. Для финансовых временных рядов это особенно важно, поскольку каждый новый временной фрагмент требует учёта как локальных, так и глобальных зависимостей, а эффективное управление активной позицией позволяет модели оставаться быстрой и адаптивной даже при больших объёмах данных.

Следует подчеркнуть, что при стандартной инициализации в процессе работы метода Init все тензоры глобальных корреляций заполняются случайными значениями. Для большинства сценариев такой подход является вполне приемлемым: случайная инициализация обеспечивает разнообразие начальных условий и позволяет обучаемым параметрам постепенно адаптироваться к структуре данных.

Однако авторы фреймворка TQNet рекомендуют иной подход — инициализацию тензора нулевыми значениями. Такой метод особенно оправдан при работе с финансовыми временными рядами, где важно начать обучение без предварительных предположений о корреляциях между переменными, чтобы модель могла постепенно выявить устойчивые зависимости исключительно на основе исторических данных.

Для реализации этого подхода в CCircleParams создаётся метод Zeros, который последовательно обнуляет параметры всех временных шагов. При вызове этого метода каждый элемент массива cOnes проходит обработку, и все значения тензора глобальных корреляций устанавливаются в ноль. Это позволяет задать чистый лист для обучения, гарантируя, что начальные прогнозы модели не будут смещены случайными начальными значениями, а весь процесс адаптации будет строго определяться анализируемыми данными и структурой TQNet.

bool CCircleParams::Zeros(void)
  {
   matrix<float> zeros = matrix<float>::Zeros(Neurons(), 2);
//---
   CBufferFloat *w = NULL;
   for(int i = 0; i < cOnes.Total(); i++)
     {
      if(!cOnes[i])
         return false;
      w = cOnes[i].getWeights();
      if(!w || !w.AssignArray(zeros))
         return false;
      w.BufferFree();
      if(!w.BufferCreate(OpenCL))
         return false;
     }
//---
   return FeedForward();
  }

Таким образом, метод Zeros обеспечивает удобный и эффективный способ контролировать начальное состояние глобальных корреляций, повышая прозрачность и предсказуемость обучения модели на финансовых данных.

В качестве альтернативы нулевой инициализации мы реализуем метод, позволяющий инициализировать тензор глобальных корреляций диагональной единичной матрицей. Такой подход может быть полезен при необходимости задать изначально независимые переменные, оставляя модели возможность постепенно выявлять реальные зависимости между ними в процессе обучения.

Метод Identity начинает работу с проверки соответствия размеров создаваемой матрицы и количества нейронов в объекте.

bool CCircleParams::Identity(const int rows, const int cols)
  {
   if(rows * cols != Neurons())
      return false;
   matrix<float> ident = matrix<float>::Identity(rows, cols);
   if(!ident.Reshape(rows * cols, 1))
      return false;
   if(!ident.Resize(rows * cols, 2))
      return false;
   if(!ident.Col(vector<float>::Zeros(rows * cols), 1))
      return false;

Затем формируется диагональная единичная матрица заданных размеров, которая последовательно преобразуется и масштабируется под внутренние структуры данных класса. Особое внимание уделяется подготовке и перераспределению памяти через методы Reshape и Resize, а также обнулению дополнительного столбца смещений для обеспечения корректной работы при присвоении значений.

После подготовки матрицы метод проходит по всем временным шагам в контейнере cOnes.

   CBufferFloat *w = NULL;
   for(int i = 0; i < cOnes.Total(); i++)
     {
      if(!cOnes[i])
         return false;
      w = cOnes[i].getWeights();
      if(!w || !w.AssignArray(ident))
         return false;
      w.BufferFree();
      if(!w.BufferCreate(OpenCL))
         return false;
     }
//---
   return FeedForward();
  }

Для каждого шага получаются веса через метод getWeights, и им присваивается содержимое подготовленной диагональной матрицы. После этого буфер в OpenCL-контексте освобождается и создаётся заново c новыми значениями, что обеспечивает корректное взаимодействие с GPU при дальнейшем обучении модели.

Завершается процесс вызовом метода FeedForward, который позволяет сразу проверить корректность распространения значений через слой. Такой способ инициализации обеспечивает, что на старте обучения глобальные корреляции между переменными не смещены и начинаются с нейтрального состояния, но при этом сохраняется структура, позволяющая модели эффективно накапливать и учитывать реальные зависимости в процессе прогнозирования.

В финансовом контексте это особенно важно: единичная диагональная матрица задаёт чистый старт для каждой переменной, исключая любые начальные предубеждения, при этом позволяя модели постепенно выявлять устойчивые рыночные взаимосвязи, такие как корреляции между активами.

После того, как мы подробно рассмотрели алгоритмы инициализации и способы подготовки начальных параметров корреляций, логично перейти к описанию алгоритма прямого прохода — одного из ключевых этапов работы класса CCircleParams.

Метод FeedForward обеспечивает подготовку глобальных параметров корреляции, соответствующих текущему временному шагу, позволяя модели обновлять внутренние состояния.

bool CCircleParams::FeedForward(void)
  {
   if(!cCurrent)
      if(!SetPosition(0))
         return false;
//---
   return CNeuronBaseOCL::feedForward(cCurrent);
  }

Сначала метод проверяет, установлен ли активный шаг в указателе cCurrent. Если текущий объект не задан, вызывается метод SetPosition, чтобы автоматически выбрать первый временной шаг в массиве cOnes, обеспечивая корректное начало вычислений.

После установки активного шага, управление передается одноименному методу родительского класса, что позволяет сформировать необходимые параметры глобальных корреляций.

Таким образом, FeedForward выполняет роль связующего звена между подготовленной структурой тензора глобальных корреляций и механизмом внимания TQNet. Предложенный подход обеспечивает гибкость и точность прогнозов, делая модель способной реагировать как на локальные колебания рынка, так и на долгосрочные тренды.

После того, как мы разобрали механизм прямого прохода и убедились, как FeedForward обеспечивает корректное распространение данных через активный временной шаг, естественным продолжением становится рассмотрение метода UpdateInputWeights, отвечающего за обновление параметров модели.

Этот метод играет ключевую роль в обучении: именно здесь происходят изменения весов и параметров корреляций на основе вычисленных градиентов, что позволяет модели постепенно адаптироваться к структуре данных. В CCircleParams метод реализован через передачу управления одноименному методу родительского класса с указанием активного элемента временного шага.

bool CCircleParams::UpdateInputWeights(void)
  {
   return CNeuronBaseOCL::updateInputWeights(cCurrent);
  }

Передаваемый указатель на текущий объект временного шага обеспечивает, что обновление происходит только для актуального сегмента тензора. Это повышает эффективность и предотвращает ненужные вычисления над остальными временными шагами.

Следует особо подчеркнуть, что на этом этапе мы сознательно не проверяем актуальность указателя в переменной cCurrent. Это сделано намеренно. Крайне важно, чтобы во время прямого и обратного проходов модель работала с одним и тем же объектом временного шага. Любое его переопределение в процессе обновления весов могло бы нарушить согласованность вычислений и привести к ошибкам в адаптации параметров.

При этом заботу о корректности указателя берёт на себя метод родительского класса. В случае возникновения ошибки он просто вернёт false, предотвращая некорректное обновление весов. Такой подход позволяет сосредоточиться на сути процесса обновлении параметров текущего временного шага без лишней нагрузки и риска нарушить структуру тензора глобальных корреляций.

Для финансовых временных рядов это особенно важно. Модель уверенно оперирует актуальными данными каждого шага, одновременно сохраняя глобальные закономерности, что обеспечивает точность прогнозов и стабильность обучения, даже при динамичных и шумных рыночных изменениях.

Думаю вы заметили, что мы пропустили этап распространения градиентов ошибки вниз по модели. Вместо этого метод calcInputGradients переопределяется заглушкой, которая всегда возвращает положительный результат. Такой подход может показаться необычным, но для обновления параметров глобальной корреляции этого вполне достаточно. Модели требуется лишь знать градиенты ошибки на уровне результатов слоя, чтобы скорректировать веса текущего временного шага.

Нижележащие данные при этом не участвуют в вычислениях, так как объект CCircleParams по сути не работает с внешними исходными входами. Распространение градиентов на этот уровень не имеет смысла.

Использование заглушки при этом выполняет важную роль: оно позволяет интегрировать новый объект в общую структуру модели, сохраняя совместимость с другими компонентами сети и обеспечивая возможность корректного обновления весов без лишней нагрузки.

В совокупности эти возможности превращают CCircleParams из абстрактной идеи динамического тензора глобальных корреляций в полноценный управляемый объект, который способен эффективно интегрироваться в TQNet. Модель получает возможность одновременно фиксировать устойчивые глобальные паттерны и учитывать локальные особенности данных на каждом временном шаге. Для финансовых рынков это особенно важно: модель учится распознавать повторяющиеся сезонные циклы, устойчивые корреляции между активами, а также реагировать на краткосрочные колебания, рыночный шум и внезапные события.

Мы проделали значительную работу, и статья уже обрела солидный объём. Всё изложенное требует времени, чтобы информация усвоилась и улеглась в сознании читателя. Пора сделать небольшой перерыв, чтобы осмыслить накопленный материал.

В следующей статье мы продолжим работу, перейдём к построению алгоритмов внимания и полной интеграции компонентов TQNet, демонстрируя, как описанные структуры и методы превращаются в эффективный инструмент прогнозирования финансовых временных рядов.

Заключение

В данной статье мы познакомились с фреймворком TQNet, который сочетает в себе модульность, гибкость и высокую производительность. Это делает его особенно ценным инструментом для задач прогнозирования и анализа финансовых временных рядов. Архитектура фреймворка построена так, чтобы каждый компонент выполнял чётко определённую роль, а замена или модернизация отдельных узлов не требовала переработки всей системы.

Практическая часть была посвящена реализации нового объекта CCircleParams, предназначенного для управления параметрами глобальных корреляций. Мы подробно рассмотрели процесс его инициализации, организацию временных шагов, а также разработали альтернативные алгоритмы задания стартовых значений тензоров. Особое внимание уделили построению прямого прохода, механизму обновления весов и синхронизации вычислений между временными шагами.

Таким образом, мы получили гибкий и надёжный элемент фреймворка, который готов к полноценной работе в составе более сложных моделей. В следующей статье мы сосредоточимся на создании единой вычислительной цепочки и проведём тестирование на исторических данных, чтобы оценить эффективность и устойчивость системы в реальных условиях финансового рынка.

Ссылки

• Temporal Query Network for Efficient Multivariate Time Series Forecasting
• Другие статьи серии

Программы, используемые в статье

#	Имя	Тип	Описание
1	Study.mq5	Советник	Советник офлайн обучения моделей
2	StudyOnline.mq5	Советник	Советник онлайн обучения моделей
3	Test.mq5	Советник	Советник для тестирования модели
4	Trajectory.mqh	Библиотека класса	Структура описания состояния системы и архитектуры моделей
5	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
6	NeuroNet.cl	Библиотека	Библиотека кода OpenCL-программы