Нейросети — это просто (Часть 7): Адаптивные методы оптимизации

MetaTrader 5 — Торговые системы | 6 ноября 2020, 09:15

6 881

Dmitriy Gizlyk

Содержание

2. Реализация

Введение

В предыдущих статьях мы рассмотрели разные типы нейронов, но всегда использовали метод стохастического градиентного спуска для обучения нейронной сети. Данный метод, наверное, можно назвать базовым и различные его вариации очень часто используются на практике. Тем не менее, он не единственный и существует целый ряд других методов для обучения нейронных сетей. Сегодня я предлагаю посмотреть в сторону адаптивных методов обучения. Это семейство методов позволяет изменять скорость обучения нейронов в процессе обучения нейронной сети.

1. Отличительные особенности адаптивных методов оптимизации

Не секрет, что не все признаки, подаваемые на вход нейронной сети имеют одинаковое влияние на конечный результат. Одни параметры могут содержать много шума и меняться чаще других с различной амплитудой. В выборке каких-то параметров могут встречаться редкие значения, которые в процессе обучения с фиксированным коэффициентом обучения нейронной сети будут не замечены. Одним из недостатков рассмотренного ранее метода стохастического градиентного спуска является отсутствие механизмов оптимизации на подобных выборках. И как следствие, процесс обучения может остановиться в локальном минимуме. Для решения подобной проблемы были предложены адаптивные методы обучения нейронных сетей, которые позволяют динамически изменять скорость обучения в процессе обучения нейронной сети. Существует целый ряд подобных методов и их разновидностей. Рассмотрим наиболее часто встречаемые.

1.1. Метод адаптивного градиента (AdaGrad)

Метод адаптивного градиента был предложен в 2011 году и является вариацией к методу стохастического градиентного спуска. Если сравнить математические формулы обоих методов, то легко заметить единственное отличие — в AdaGrad скорость обучение делится на корень квадратный из суммы квадратов градиентов за все предшествующие итерации обучения. Такой подход позволяет снизить скорость обучения часто обновляемых параметров.

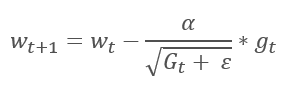
Основной недостаток данного метода следует из его формулы — сумма квадратов градиентов может только расти и, как следствие, скорость обучения стремится к "0". Что в конечном счете, приведет к остановке обучения.

Платой за использование данного метода является необходимость проведения дополнительных расчетов и выделение дополнительной памяти для хранения суммы квадратов градиентов для каждого нейрона.

1.2. Метод RMSProp

Логическим продолжением метода AdaGrad является метод RMSProp. Для исключения сведения скорости обучения к "0" было предложено заменить сумму квадратов градиентов в знаменателе формулы обновления весов на экспоненциальную среднюю квадратов градиентов. Такой подход позволяет исключить постоянный и бесконечный рост значения в знаменателе и в большей степени учитывать последние значения градиента, которые характеризуют текущее состояние модели.

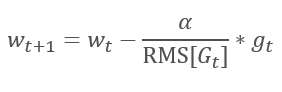
1.3. Метод Adadelta

Практически одновременно с RMSProp был предложен еще один, очень похожий, адаптивный метод обучения Adadelta. В этом методе, также как и RMSProp предлагается использовать экспоненциальную среднюю суммы квадратов градиентов в знаменателе формулы изменения весовых коэффициентов. Но в отличии от RMSProp, в данном методе предложено полностью отказаться от коэффициента обучения в формуле обновления и заменить его на экспоненциальное среднее из суммы квадратов предыдущих изменений анализируемого параметра.

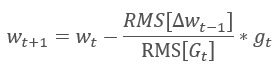
Такой подход позволяет полностью отказаться от коэффициента обучения в формуле обновления весовых коэффициентов и построить максимально адаптивный алгоритм обучения. Но платой за это будут дополнительные итерации вычислений и выделение дополнительной памяти для хранения еще одного значения в каждом нейроне.

1.4. Метод адаптивной оценки моментов (Adam)

В 2014 году Diederik P. Kingma и Jimmy Lei Ba предложили метод адаптивной оценки моментов Adam. По словам авторов, метод объединяет преимущества методов AdaGrad и RMSProp и хорошо работает при on-line обучении. Данный метод показывает стабильно хорошие результаты на разных выборках и в последнее время рекомендуется к применению по умолчанию в различных пакетах.

В основе метода лежит расчет экспоненциальной средней градиента m и экспоненциального среднего квадратов градиента v. Каждая экспоненциальная средняя имеет свой гиперпараметр ß, определяющий период усреднения.

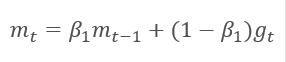
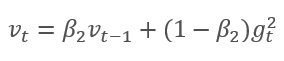
Авторы предлагают использовать по умолчанию ß1 на уровне 0,9 и ß2 на уровне 0,999. При этом m0 и v0 принимают нулевые значения. С такими параметрами формулы, представленные выше, в начале обучения возвращают значения близкие к "0" и, как следствие, получим низкую скорость обучения на начальном этапе. Для ускорения обучения авторы предложили скорректировать полученные моменты.

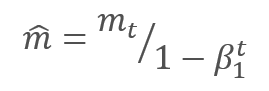
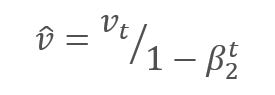
Обновление параметров осуществляется путем корректировки на отношение скорректированного момента градиента m к корню квадратному из скорректированного момента квадрата градиента v. Для исключения деления на ноль в знаменатель добавляют близкую к "0" константу Ɛ. Полученное отношение корректируется на коэффициент обучения α, который в данном случае выступает верхней границей шага обучения. По умолчанию авторы предлагают использовать α на уровне 0,001.

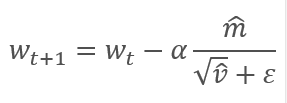
2. Реализация

После рассмотрения теоретических аспектов можно приступить к практической реализации. И реализовать я предлагаю метод Adam с гиперпараметрами, предлагаемыми авторами по умолчанию. Позже все желающие смогут поэкспериментировать с различными вариациями гиперпараметров.

В построенной нами ранее нейронной сети для обучения использовался стохастический градиентный спуск, для которого мы уже реализовали алгоритм обратного распространения ошибки. Следовательно, для реализации метода Adam мы можем воспользоваться существующим функционалом обратного распространения ошибки. Остается реализовать непосредственно алгоритм обновления весовых коэффициентов. За данный функционал у нас отвечает метод updateInputWeights и реализован в каждом классе нейронов. Разумеется, что мы не будем перечеркивать проделанную ранее работу, удаляя построенный ранее алгоритм стохастического градиентного спуска. Создадим альтернативный алгоритм и дадим возможность выбора используемого метода обучения.

2.1. Построение кернела OpenCL

Рассмотрим реализацию метода Adam для класса CNeuronBaseOCL. Сначала создадим кернел UpdateWeightsAdam для реализации метода в OpenCL. В параметрах кернелу будем передавать указатели на матрицы:

весовых коэффициентов — matrix_w,
градиентов ошибки — matrix_g,
входных данных — matrix_i,
экспоненциальных средних градиентов — matrix_m,
экспоненциальных средних квадратов градиентов — matrix_v.

__kernel void UpdateWeightsAdam(__global double *matrix_w,
                                __global double *matrix_g,
                                __global double *matrix_i,
                                __global double *matrix_m,
                                __global double *matrix_v,
                                int inputs, double l, double b1, double b2)

Дополнительно в параметрах кернела передадим размер массива входных данных и гиперпараметры алгоритма Adam.

В начале кернела получим порядковые номера потока в двух измерениях, которые нам укажут номера нейронов текущего и предыдущего слоев, соответственно. По полученным номерам определим начальный номер обрабатываемого элемента в буферах. Обращаю внимание, что полученный номер потока во втором измерении умножается на "4". Это связано с тем, что для снижения числа потоков и общего времени выполнения программы далее мы будем использовать векторные вычисления с 4-х элементными векторами.

  {
   int i=get_global_id(0);
   int j=get_global_id(1);
   int wi=i*(inputs+1)+j*4;

После определения позиции обрабатываемых элементов в буферах данных объявим векторные переменные и заполним их соответствующими значениями. Здесь мы воспользуемся описанным ранее методом и заполним нулями недостающие данные в векторах.

   double4 m, v, weight, inp;
   switch(inputs-j*4)
     {
      case 0:
        inp=(double4)(1,0,0,0);
        weight=(double4)(matrix_w[wi],0,0,0);
        m=(double4)(matrix_m[wi],0,0,0);
        v=(double4)(matrix_v[wi],0,0,0);
        break;
      case 1:
        inp=(double4)(matrix_i[j],1,0,0);
        weight=(double4)(matrix_w[wi],matrix_w[wi+1],0,0);
        m=(double4)(matrix_m[wi],matrix_m[wi+1],0,0);
        v=(double4)(matrix_v[wi],matrix_v[wi+1],0,0);
        break;
      case 2:
        inp=(double4)(matrix_i[j],matrix_i[j+1],1,0);
        weight=(double4)(matrix_w[wi],matrix_w[wi+1],matrix_w[wi+2],0);
        m=(double4)(matrix_m[wi],matrix_m[wi+1],matrix_m[wi+2],0);
        v=(double4)(matrix_v[wi],matrix_v[wi+1],matrix_v[wi+2],0);
        break;
      case 3:
        inp=(double4)(matrix_i[j],matrix_i[j+1],matrix_i[j+2],1);
        weight=(double4)(matrix_w[wi],matrix_w[wi+1],matrix_w[wi+2],matrix_w[wi+3]);
        m=(double4)(matrix_m[wi],matrix_m[wi+1],matrix_m[wi+2],matrix_m[wi+3]);
        v=(double4)(matrix_v[wi],matrix_v[wi+1],matrix_v[wi+2],matrix_v[wi+3]);
        break;
      default:
        inp=(double4)(matrix_i[j],matrix_i[j+1],matrix_i[j+2],matrix_i[j+3]);
        weight=(double4)(matrix_w[wi],matrix_w[wi+1],matrix_w[wi+2],matrix_w[wi+3]);
        m=(double4)(matrix_m[wi],matrix_m[wi+1],matrix_m[wi+2],matrix_m[wi+3]);
        v=(double4)(matrix_v[wi],matrix_v[wi+1],matrix_v[wi+2],matrix_v[wi+3]);
        break;
     }

Вектор градиентов получаем умножением градиента текущего нейрона на вектор входных данных.

   double4 g=matrix_g[i]*inp;

Далее посчитаем экспоненциальные средние градиента и его квадрата.

   double4 mt=b1*m+(1-b1)*g;
   double4 vt=b2*v+(1-b2)*pow(g,2)+0.00000001;

И посчитаем дельты изменения параметров.

   double4 delta=l*mt/sqrt(vt);

Обратите внимание, что в кернеле мы не скорректировали полученные моменты. Данный шаг опущен здесь намеренно. Так как коэффициенты ß1 и ß2 для всех нейронов одинаковы, а t в нашем случае это количество итераций обновления параметров нейрона тоже для всех нейронов одинаково. То и коэффициент корректировки будет для всех нейронов одинаковый. Поэтому, мы не будем пересчитывать коэффициент для каждого нейрона, а посчитаем его один раз в коде основной программы и передадим в кернел скорректированный на данную величину коэффициент обучения.

После вычисления дельт нам только остается скорректировать весовые коэффициенты и обновить в буферах посчитанные моменты. И выходим из кернела.

   switch(inputs-j*4)
     {
      case 2:
        matrix_w[wi+2]+=delta.s2;
        matrix_m[wi+2]=mt.s2;
        matrix_v[wi+2]=vt.s2;
      case 1:
        matrix_w[wi+1]+=delta.s1;
        matrix_m[wi+1]=mt.s1;
        matrix_v[wi+1]=vt.s1;
      case 0:
        matrix_w[wi]+=delta.s0;
        matrix_m[wi]=mt.s0;
        matrix_v[wi]=vt.s0;
        break;
      default:
        matrix_w[wi]+=delta.s0;
        matrix_m[wi]=mt.s0;
        matrix_v[wi]=vt.s0;
        matrix_w[wi+1]+=delta.s1;
        matrix_m[wi+1]=mt.s1;
        matrix_v[wi+1]=vt.s1;
        matrix_w[wi+2]+=delta.s2;
        matrix_m[wi+2]=mt.s2;
        matrix_v[wi+2]=vt.s2;
        matrix_w[wi+3]+=delta.s3;
        matrix_m[wi+3]=mt.s3;
        matrix_v[wi+3]=vt.s3;
        break;
     }
  };

И здесь в коде есть еще одно ухищрение. Обратите внимание на обратный порядок вариантов case в операторе switch. При этом оператор break поставлен только после вариантов case 0 и default. Такой подход дает нам возможность не дублировать повторяющийся код для всех вариантов.

2.2. Изменения в коде класса нейрона основной программы

После построения кернела внесем изменения в код основной программы. Сначала добавим в блок define константы для работы с кернелом.

#define def_k_UpdateWeightsAdam   4
#define def_k_uwa_matrix_w        0
#define def_k_uwa_matrix_g        1
#define def_k_uwa_matrix_i        2
#define def_k_uwa_matrix_m        3
#define def_k_uwa_matrix_v        4
#define def_k_uwa_inputs          5
#define def_k_uwa_l               6
#define def_k_uwa_b1              7
#define def_k_uwa_b2              8

Создадим перечисления для указания способов обучения и добавим в перечисления буфера моментов.

enum ENUM_OPTIMIZATION
  {
   SGD,
   ADAM
  };
//---
enum ENUM_BUFFERS
  {
   WEIGHTS,
   DELTA_WEIGHTS,
   OUTPUT,
   GRADIENT,
   FIRST_MOMENTUM,
   SECOND_MOMENTUM
  };

Затем, непосредственно в теле класса CNeuronBaseOCL добавим буферы для хранения моментов, константы экспоненциальных средних, счетчик для подсчета итераций обучения и переменную для хранения метода обучения.

class CNeuronBaseOCL    :  public CObject
  {
protected:
   .........
   .........
   ..........
   CBufferDouble     *FirstMomentum;
   CBufferDouble     *SecondMomentum;
//---
   .........
   .........
   const double      b1;
   const double      b2;
   int               t;
//---
   .........
   .........
   ENUM_OPTIMIZATION optimization;

В конструкторе класса зададим значения констант и инициализируем буферы.

CNeuronBaseOCL::CNeuronBaseOCL(void)   :  alpha(momentum),
                                          activation(TANH),
                                          optimization(SGD),
                                          b1(0.9),
                                          b2(0.999),
                                          t(1)
  {
   OpenCL=NULL;
   Output=new CBufferDouble();
   PrevOutput=new CBufferDouble();
   Weights=new CBufferDouble();
   DeltaWeights=new CBufferDouble();
   Gradient=new CBufferDouble();   
   FirstMomentum=new CBufferDouble();   
   SecondMomentum=new CBufferDouble();   
  }

И не забываем добавить удаление объектов буферов в деструкторе класса.

CNeuronBaseOCL::~CNeuronBaseOCL(void)
  {
   if(CheckPointer(Output)!=POINTER_INVALID)
      delete Output;
   if(CheckPointer(PrevOutput)!=POINTER_INVALID)
      delete PrevOutput;
   if(CheckPointer(Weights)!=POINTER_INVALID)
      delete Weights;
   if(CheckPointer(DeltaWeights)!=POINTER_INVALID)
      delete DeltaWeights;
   if(CheckPointer(Gradient)!=POINTER_INVALID)
      delete Gradient;
   if(CheckPointer(FirstMomentum)!=POINTER_INVALID)
      delete FirstMomentum;
   if(CheckPointer(SecondMomentum)!=POINTER_INVALID)
      delete SecondMomentum;
   OpenCL=NULL;
  }

В параметрах функции инициализации класса добавим метод обучения и в зависимости от заданного метода обучения проведем инициализацию буферов. При обучении стохастическим градиентным спуском инициализируем буфер дельт, а буфера моментов удалим. При обучении методом Adam наоборот инициализируем буферы моментов и удалим буфер дельт.

bool CNeuronBaseOCL::Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint numNeurons, ENUM_OPTIMIZATION optimization_type)
  {
   if(CheckPointer(open_cl)==POINTER_INVALID || numNeurons<=0)
      return false;
   OpenCL=open_cl;
   optimization=optimization_type;
//---
   ....................
   ....................
   ....................
   ....................
//---
   if(numOutputs>0)
     {
      if(CheckPointer(Weights)==POINTER_INVALID)
        {
         Weights=new CBufferDouble();
         if(CheckPointer(Weights)==POINTER_INVALID)
            return false;
        }
      int count=(int)((numNeurons+1)*numOutputs);
      if(!Weights.Reserve(count))
         return false;
      for(int i=0;i<count;i++)
        {
         double weigh=(MathRand()+1)/32768.0-0.5;
         if(weigh==0)
            weigh=0.001;
         if(!Weights.Add(weigh))
            return false;
        }
      if(!Weights.BufferCreate(OpenCL))
         return false;
   //---
      if(optimization==SGD)
        {
         if(CheckPointer(DeltaWeights)==POINTER_INVALID)
           {
            DeltaWeights=new CBufferDouble();
            if(CheckPointer(DeltaWeights)==POINTER_INVALID)
               return false;
           }
         if(!DeltaWeights.BufferInit(count,0))
            return false;
         if(!DeltaWeights.BufferCreate(OpenCL))
            return false;
         if(CheckPointer(FirstMomentum)==POINTER_INVALID)
            delete FirstMomentum;
         if(CheckPointer(SecondMomentum)==POINTER_INVALID)
            delete SecondMomentum;
        }
      else
        {
         if(CheckPointer(DeltaWeights)==POINTER_INVALID)
            delete DeltaWeights;
//---
         if(CheckPointer(FirstMomentum)==POINTER_INVALID)
           {
            FirstMomentum=new CBufferDouble();
            if(CheckPointer(FirstMomentum)==POINTER_INVALID)
               return false;
           }
         if(!FirstMomentum.BufferInit(count,0))
            return false;
         if(!FirstMomentum.BufferCreate(OpenCL))
            return false;
//---
         if(CheckPointer(SecondMomentum)==POINTER_INVALID)
           {
            SecondMomentum=new CBufferDouble();
            if(CheckPointer(SecondMomentum)==POINTER_INVALID)
               return false;
           }
         if(!SecondMomentum.BufferInit(count,0))
            return false;
         if(!SecondMomentum.BufferCreate(OpenCL))
            return false;
        }
     }
   else
     {
      if(CheckPointer(Weights)!=POINTER_INVALID)
         delete Weights;
      if(CheckPointer(DeltaWeights)!=POINTER_INVALID)
         delete DeltaWeights;
     }
//---
   return true;
  }

И конечно, внесем изменения непосредственно в метод обновления весовых коэффициентов updateInputWeights. Прежде всего создадим разветвление алгоритма в зависимости от метода обучения.

bool CNeuronBaseOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID)
      return false;
   uint global_work_offset[2]={0,0};
   uint global_work_size[2];
   global_work_size[0]=Neurons();
   global_work_size[1]=NeuronOCL.Neurons();
   if(optimization==SGD)
     {

Для стохастического градиентного спуска перенесем весь код без изменений.

      OpenCL.SetArgumentBuffer(def_k_UpdateWeightsMomentum,def_k_uwm_matrix_w,NeuronOCL.getWeightsIndex());
      OpenCL.SetArgumentBuffer(def_k_UpdateWeightsMomentum,def_k_uwm_matrix_g,getGradientIndex());
      OpenCL.SetArgumentBuffer(def_k_UpdateWeightsMomentum,def_k_uwm_matrix_i,NeuronOCL.getOutputIndex());
      OpenCL.SetArgumentBuffer(def_k_UpdateWeightsMomentum,def_k_uwm_matrix_dw,NeuronOCL.getDeltaWeightsIndex());
      OpenCL.SetArgument(def_k_UpdateWeightsMomentum,def_k_uwm_inputs,NeuronOCL.Neurons());
      OpenCL.SetArgument(def_k_UpdateWeightsMomentum,def_k_uwm_learning_rates,eta);
      OpenCL.SetArgument(def_k_UpdateWeightsMomentum,def_k_uwm_momentum,alpha);
      ResetLastError();
      if(!OpenCL.Execute(def_k_UpdateWeightsMomentum,2,global_work_offset,global_work_size))
        {
         printf("Error of execution kernel UpdateWeightsMomentum: %d",GetLastError());
         return false;
        }
     }

Далее в ответвлении метода Adam зададим буферы обмена данными для соответствующего кернела.

   else
     {
      if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_w,NeuronOCL.getWeightsIndex()))
         return false;
      if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_g,getGradientIndex()))
         return false;
      if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_i,NeuronOCL.getOutputIndex()))
         return false;
      if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_m,NeuronOCL.getFirstMomentumIndex()))
         return false;
      if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_v,NeuronOCL.getSecondMomentumIndex()))
         return false;

Затем скорректируем коэффициент обучения для текущей итерации обучения.

      double lt=eta*sqrt(1-pow(b2,t))/(1-pow(b1,t));

И зададим гиперпараметры обучения.

      if(!OpenCL.SetArgument(def_k_UpdateWeightsAdam,def_k_uwa_inputs,NeuronOCL.Neurons()))
         return false;
      if(!OpenCL.SetArgument(def_k_UpdateWeightsAdam,def_k_uwa_l,lt))
         return false;
      if(!OpenCL.SetArgument(def_k_UpdateWeightsAdam,def_k_uwa_b1,b1))
         return false;
      if(!OpenCL.SetArgument(def_k_UpdateWeightsAdam,def_k_uwa_b2,b2))
         return false;

Теперь вспомним, что в кернеле мы использовали векторные величины для вычислений и уменьшим в четыре 4 раза количество потоков во втором измерении.

      uint rest=global_work_size[1]%4;
      global_work_size[1]=(global_work_size[1]-rest)/4 + (rest>0 ? 1 : 0);

После проведения всей подготовительной работы осуществим непосредственно вызов кернела и увеличим счетчик итераций обучения.

      ResetLastError();
      if(!OpenCL.Execute(def_k_UpdateWeightsAdam,2,global_work_offset,global_work_size))
        {
         printf("Error of execution kernel UpdateWeightsAdam: %d",GetLastError());
         return false;
        }
      t++;
     }

И уже после разветвления, не зависимо от метода обучения прочитаем пересчитанные весовые коэффициенты. Как я уже писал в предыдущей статье, считывание буфера нужно осуществлять и для скрытых слоев, т.к. эта операция не только производит считывание данных, но и запускает выполнение кернела.

//---
   return NeuronOCL.Weights.BufferRead();
  }

Помимо дополнений алгоритма расчета метода обучения необходимо внести коррективы в методы сохранения и загрузки информации о предыдущих результатах обучения нейронов. В метод Save добавим сохранение метода обучения и счетчика итераций обучения.

bool CNeuronBaseOCL::Save(const int file_handle)
  {
   if(file_handle==INVALID_HANDLE)
      return false;
   if(FileWriteInteger(file_handle,Type())<INT_VALUE)
      return false;
//---
   if(FileWriteInteger(file_handle,(int)activation,INT_VALUE)<INT_VALUE)
      return false;
   if(FileWriteInteger(file_handle,(int)optimization,INT_VALUE)<INT_VALUE)
      return false;
   if(FileWriteInteger(file_handle,(int)t,INT_VALUE)<INT_VALUE)
      return false;

Дале оставляем без изменения сохранение общих для обоих методов обучения буферов.

   if(CheckPointer(Output)==POINTER_INVALID || !Output.BufferRead() || !Output.Save(file_handle))
      return false;
   if(CheckPointer(PrevOutput)==POINTER_INVALID || !PrevOutput.BufferRead() || !PrevOutput.Save(file_handle))
      return false;
   if(CheckPointer(Gradient)==POINTER_INVALID || !Gradient.BufferRead() || !Gradient.Save(file_handle))
      return false;
//---
   if(CheckPointer(Weights)==POINTER_INVALID)
     {
      FileWriteInteger(file_handle,0);
      return true;
     }
   else
      FileWriteInteger(file_handle,1);
//---
   if(CheckPointer(Weights)==POINTER_INVALID || !Weights.BufferRead() || !Weights.Save(file_handle))
      return false;

После чего создадим разветвление алгоритма для каждого метода обучения с сохранением специфических буферов.

   if(optimization==SGD)
     {
      if(CheckPointer(DeltaWeights)==POINTER_INVALID || !DeltaWeights.BufferRead() || !DeltaWeights.Save(file_handle))
         return false;
     }
   else
     {
      if(CheckPointer(FirstMomentum)==POINTER_INVALID || !FirstMomentum.BufferRead() || !FirstMomentum.Save(file_handle))
         return false;
      if(CheckPointer(SecondMomentum)==POINTER_INVALID || !SecondMomentum.BufferRead() || !SecondMomentum.Save(file_handle))
         return false;
     }
//---
   return true;
  }

Аналогичные изменения в той же последовательности сделаем в методе Load.

С полным кодом всех методов и функций можно ознакомиться во вложении.

2.3. Изменения в коде классов без использования OpenCL

Для поддержания работоспособности всех классов в одинаковых условиях внес аналогичные изменения и в классы работающие в чистом MQL5 без использования OpenCL.

Первым делом добавим переменные для хранения данных моментов в класс CConnection и зададим начальные значения в конструкторе класса.

class CConnection : public CObject
  {
public:
   double            weight;
   double            deltaWeight;
   double            mt;
   double            vt;

                     CConnection(double w) { weight=w; deltaWeight=0; mt=0; vt=0; }

Также необходимо добавить обработку новых переменных в методы сохранения и загрузки данных соединения.

bool CConnection::Save(int file_handle)
  {
   ...........
   ...........
   ...........
   if(FileWriteDouble(file_handle,mt)<=0)
      return false;
   if(FileWriteDouble(file_handle,vt)<=0)
      return false;
//---
   return true;
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CConnection::Load(int file_handle)
  {
   ............
   ............
   ............
   mt=FileReadDouble(file_handle);
   vt=FileReadDouble(file_handle);
//---
   return true;
  }

Далее добавим переменные для хранения метода оптимизации и счетчика итераций обновления весов в класс нейрона CNeuronBase.

class CNeuronBase    :  public CObject
  {
protected:
   .........
   .........
   .........
   ENUM_OPTIMIZATION optimization;

   const double      b1;
   const double      b2;
   int               t;

Затем, внесем дополнения в метод инициализации нейрона. Прежде всего, добавим в параметры метода переменную для указания способа оптимизации и организуем его сохранения в определенной выше переменной.

bool CNeuronBase::Init(uint numOutputs,uint myIndex, ENUM_OPTIMIZATION optimization_type)
  {
   optimization=optimization_type;

После чего создадим разветвление алгоритма по методу оптимизации в метод обновления весовых коэффициентов updateInputWeights. Перед циклом перебора соединений пересчитаем скорректированный коэффициент обучения, а в цикле создадим две ветки пересчета весов.

bool CNeuron::updateInputWeights(CLayer *&prevLayer)
  {
   if(CheckPointer(prevLayer)==POINTER_INVALID)
      return false;
//---
   double lt=eta*sqrt(1-pow(b2,t))/(1-pow(b1,t));
   int total=prevLayer.Total();
   for(int n=0; n<total && !IsStopped(); n++)
     {
      CNeuron *neuron= prevLayer.At(n);
      CConnection *con=neuron.Connections.At(m_myIndex);
      if(CheckPointer(con)==POINTER_INVALID)
         continue;
      if(optimization==SGD)
         con.weight+=con.deltaWeight=(gradient!=0 ? eta*neuron.getOutputVal()*gradient : 0)+(con.deltaWeight!=0 ? alpha*con.deltaWeight : 0);
      else
        {
         con.mt=b1*con.mt+(1-b1)*gradient;
         con.vt=b2*con.vt+(1-b2)*pow(gradient,2)+0.00000001;
         con.weight+=con.deltaWeight=lt*con.mt/sqrt(con.vt);
         t++;
        }
     }
//---
   return true;
  }

И добавим обработку новых переменных в методы сохранения и загрузки.

С полным кодом всех методов можно ознакомиться во вложении.

2.4. Изменения в коде класса нейронной сети основной программы

Помимо изменений в классах нейронов нам нужно внести изменения и в другие объекты нашего кода. Прежде всего, нам нужно будет передать из основной программы в нейрон информацию о методе обучения. За передачу информации из основной программы в класс нейронной сети отвечает класс CLayerDescription. Для передачи информации о методе обучения добавим соответствующую переменную в указанный класс.

class CLayerDescription    :  public CObject
  {
public:
                     CLayerDescription(void);
                    ~CLayerDescription(void) {};
   //---
   int               type;
   int               count;
   int               window;
   int               step;
   ENUM_ACTIVATION   activation;
   ENUM_OPTIMIZATION optimization;
  };

И внесем финальные дополнения в конструктор класса нейронной сети CNet. Здесь добавим указание метода оптимизации при инициализации нейронов сети, увеличим количество используемых кернелов OpenCL и объявим новый кернел оптимизации Adam. Ниже приведен измененный код конструктора, изменения выделены заливкой.

CNet::CNet(CArrayObj *Description)
  {
   if(CheckPointer(Description)==POINTER_INVALID)
      return;
//---
   int total=Description.Total();
   if(total<=0)
      return;
//---
   layers=new CArrayLayer();
   if(CheckPointer(layers)==POINTER_INVALID)
      return;
//---
   CLayer *temp;
   CLayerDescription *desc=NULL, *next=NULL, *prev=NULL;
   CNeuronBase *neuron=NULL;
   CNeuronProof *neuron_p=NULL;
   int output_count=0;
   int temp_count=0;
//---
   next=Description.At(1);
   if(next.type==defNeuron || next.type==defNeuronBaseOCL)
     {
      opencl=new COpenCLMy();
      if(CheckPointer(opencl)!=POINTER_INVALID && !opencl.Initialize(cl_program,true))
         delete opencl;
     }
   else
     {
      if(CheckPointer(opencl)!=POINTER_INVALID)
         delete opencl;
     }
//---
   for(int i=0; i<total; i++)
     {
      prev=desc;
      desc=Description.At(i);
      if((i+1)<total)
        {
         next=Description.At(i+1);
         if(CheckPointer(next)==POINTER_INVALID)
            return;
        }
      else
         next=NULL;
      int outputs=(next==NULL || (next.type!=defNeuron && next.type!=defNeuronBaseOCL) ? 0 : next.count);
      temp=new CLayer(outputs);
      int neurons=(desc.count+(desc.type==defNeuron || desc.type==defNeuronBaseOCL ? 1 : 0));
      if(CheckPointer(opencl)!=POINTER_INVALID)
        {
         CNeuronBaseOCL *neuron_ocl=NULL;
         switch(desc.type)
           {
            case defNeuron:
            case defNeuronBaseOCL:
              neuron_ocl=new CNeuronBaseOCL();
              if(CheckPointer(neuron_ocl)==POINTER_INVALID)
                {
                 delete temp;
                 return;
                }
              if(!neuron_ocl.Init(outputs,0,opencl,desc.count,desc.optimization))
                {
                 delete temp;
                 return;
                }
              neuron_ocl.SetActivationFunction(desc.activation);
              if(!temp.Add(neuron_ocl))
                {
                 delete neuron_ocl;
                 delete temp;
                 return;
                }
              neuron_ocl=NULL;
              break;
            default:
              return;
              break;
           }
        }
      else
      for(int n=0; n<neurons; n++)
        {
         switch(desc.type)
           {
            case defNeuron:
               neuron=new CNeuron();
               if(CheckPointer(neuron)==POINTER_INVALID)
                 {
                  delete temp;
                  delete layers;
                  return;
                 }
               neuron.Init(outputs,n,desc.optimization);
               neuron.SetActivationFunction(desc.activation);
               break;
            case defNeuronConv:
               neuron_p=new CNeuronConv();
               if(CheckPointer(neuron_p)==POINTER_INVALID)
                 {
                  delete temp;
                  delete layers;
                  return;
                 }
               if(CheckPointer(prev)!=POINTER_INVALID)
                 {
                  if(prev.type==defNeuron)
                    {
                     temp_count=(int)((prev.count-desc.window)%desc.step);
                     output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
                    }
                  else
                     if(n==0)
                       {
                        temp_count=(int)((output_count-desc.window)%desc.step);
                        output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
                       }
                 }
               if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count,desc.optimization))
                  neuron=neuron_p;
               break;
            case defNeuronProof:
               neuron_p=new CNeuronProof();
               if(CheckPointer(neuron_p)==POINTER_INVALID)
                 {
                  delete temp;
                  delete layers;
                  return;
                 }
               if(CheckPointer(prev)!=POINTER_INVALID)
                 {
                  if(prev.type==defNeuron)
                    {
                     temp_count=(int)((prev.count-desc.window)%desc.step);
                     output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
                    }
                  else
                     if(n==0)
                       {
                        temp_count=(int)((output_count-desc.window)%desc.step);
                        output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
                       }
                 }
               if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count,desc.optimization))
                  neuron=neuron_p;
               break;
            case defNeuronLSTM:
               neuron_p=new CNeuronLSTM();
               if(CheckPointer(neuron_p)==POINTER_INVALID)
                 {
                  delete temp;
                  delete layers;
                  return;
                 }
               output_count=(next!=NULL ? next.window : desc.step);
               if(neuron_p.Init(outputs,n,desc.window,1,output_count,desc.optimization))
                  neuron=neuron_p;
               break;
           }
         if(!temp.Add(neuron))
           {
            delete temp;
            delete layers;
            return;
           }
         neuron=NULL;
        }
      if(!layers.Add(temp))
        {
         delete temp;
         delete layers;
         return;
        }
     }
//---
   if(CheckPointer(opencl)==POINTER_INVALID)
      return;
//--- create kernels
   opencl.SetKernelsCount(5);
   opencl.KernelCreate(def_k_FeedForward,"FeedForward");
   opencl.KernelCreate(def_k_CaclOutputGradient,"CaclOutputGradient");
   opencl.KernelCreate(def_k_CaclHiddenGradient,"CaclHiddenGradient");
   opencl.KernelCreate(def_k_UpdateWeightsMomentum,"UpdateWeightsMomentum");
   opencl.KernelCreate(def_k_UpdateWeightsAdam,"UpdateWeightsAdam");
//---
   return;
  }

С полным кодом всех классов и их методов можно ознакомиться во вложении.

3. Тестирование

Тестирование оптимизации методом Adam осуществлялось в тех же условиях, что и все предыдущие тестирования: инструмент EURUSD, таймфрейм H1, на вход подаются данные за 20 последовательных свечей, обучение проводится на истории за 2 последних года. Для тестирования был создан советник Fractal_OCL_Adam. Данный советник был создан из советника Fractal_OCL путем указания метода оптимизации Adam при описании нейронной сети в функции OnInit основной программы.

      desc.count=(int)HistoryBars*12;
      desc.type=defNeuron;
      desc.optimization=ADAM;

Количество слоев и нейронов осталось не изменным.

Советник был инициализирован случайными весами в диапазоне от -1 до 1, исключая нулевые значения. В ходе тестирования буквально после 2-й эпохи обучения ошибка нейронной сети стабилизировалась в районе 30%. Напомню, что при обучении методом стохастического градиентного спуска ошибка стабилизировалась в районе 42% после 5-й эпохи обучения.

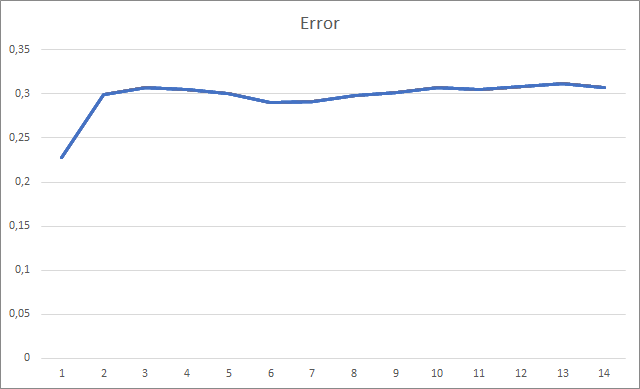
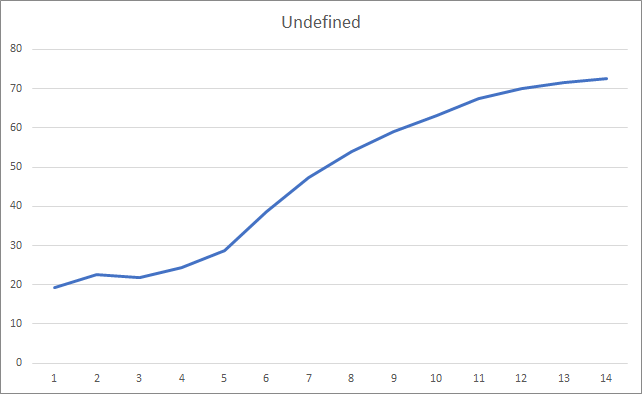
График пропущенных фракталов демонстрирует плавный рост показателя в ходе всего обучения. При этом после 12 эпох обучения наблюдается постепенное снижение темпов роста показателя. После 14-й эпохи обучения значение данного показателя составила 72,5%. Для сравнения, при обучении аналогичной нейронной сети методом стохастического градиентного спуска после 10 эпох обучения доля пропущенных фракталов составляла 97-100% при различных коэффициентах обучения.

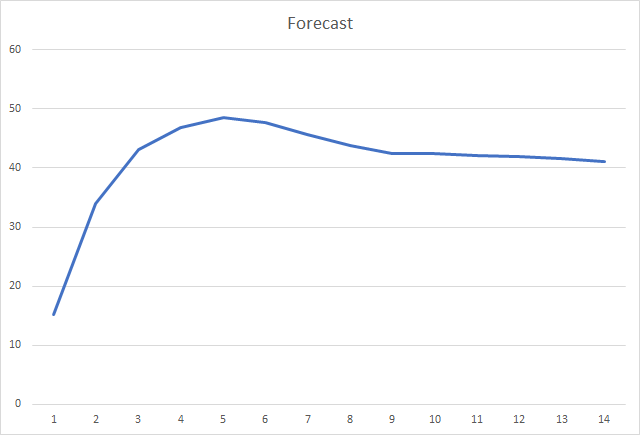
И, наверное, самым важным показателем является доля правильно определенных фракталов. В ходе обучения после 5-й эпохи данный показатель достиг 48,6% и потом постепенно снизился до 41,1%. При обучения методом стохастического градиентного спуска после 90 эпох обучения данный показатель не превышал 10%.

Заключение

В статье были рассмотрены отличительные особенности адаптивных методов оптимизации параметров нейронных сетей и добавлен метод оптимизации Adam в построенную ранее модель нейронной сети. В ходе тестирования проведено обучение нейронной сети методом Adam и полученные результаты превышают полученные ранее показатели при обучении аналогичной нейронной сети методом стохастического градиентного спуска.

Проделанная работа показывает наше поступательное движение к цели.

Ссылки

Программы, используемые в статье

#	Имя	Тип	Описание
1	Fractal_OCL_Adam.mq5	Советник	Советник с нейронной сетью классификации(3 нейрона в выходном слое) с использованием технологии OpenCL и методом обучения Adam
2	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
3	NeuroNet.cl	Библиотека	Библиотека кода программы OpenCL

Прикрепленные файлы |

Загрузить ZIP

MQL5.zip (430.54 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Последние комментарии | Перейти к обсуждению на форуме трейдеров (11)

Borys Ivanov | 7 июл. 2022 в 20:47

Всем привет . кто сталкивался с такой ошибкой при попытке чтения файла ?

OnInit - 198 -> Error of read AUDNZD.......

Dmitriy Gizlyk | 7 июл. 2022 в 22:54

Borys Ivanov #:

Всем привет . кто сталкивался с такой ошибкой при попытке чтения файла ?

OnInit - 198 -> Error of read AUDNZD.......

Данное сообщение лишь информирует, что не была загружена предварительно обученная сеть. Если Вы первый раз запускаете свой советник, то это нормально и не обращайте внимание на сообщение. Если Вы уже обучали нейронную сеть и хотели продолжить её обучение, то тогда надо проверять в каком месте произошла ошибка чтения данных из файла.

К сожалению, вы не указали код ошибки, чтобы можно было сказать больше.

Borys Ivanov | 8 июл. 2022 в 19:14

Dmitriy Gizlyk #:

К сожалению, вы не указали код ошибки, чтобы можно было сказать больше.

Здравствуйте.

Расскажу подробнее.

при запуске эксперта в первый раз. С такими модификациями в коде:

 dError=Net.getRecentAverageError();
         if(add_loop)
           {
            Net.Save(FileName+".nnw",dError,dUndefine,dForecast,dtStudied,false);
            printf("Era %d -> error %.2f %% forecast %.2f",count,dError,dForecast);
           }
         ChartScreenShot(0,FileName+IntegerToString(count)+".png",750,400);
         int h=FileOpen(CSV,FILE_READ|FILE_WRITE|FILE_CSV);
         if(h!=INVALID_HANDLE)
           {
            FileSeek(h,0,SEEK_END);
            FileWrite(h,eta,count,dError,dUndefine,dForecast);
            FileFlush(h);
            FileClose(h);
            Print("Файл должен быть создан ChartScreenShot ");
           }
          else Print("Операция FileOpen ChartScreenShot неудачна, ошибка ",GetLastError()); 
        }
     }

в журнеле пишется это :

KO 0 18:49:15.205 Core 1 NZDUSD: load 27 bytes of history data to synchronize in 0:00:00.001

FI 0 18:49:15.205 Core 1 NZDUSD: history synchronized from 2016.01.04 to 2022.06.28

FF 0 18:49:15.205 Core 1 2019.01.01 00:00:00 OnInit - 202 -> Error of read AUDNZD_PERIOD_D1_ 20Fractal_OCL_Adam 1.nnw prev Net 0

CH 0 18:49:15.205 Core 1 2019.01.01 00:00:00 OpenCL: GPU device 'gfx902' selected

KN 0 18:49:15.205 Core 1 2019.01.01 00:00:00 Era 1 -> error 0.01 % forecast 0.01

QK 0 18:49:15.205 Core 1 2019.01.01 00:00:00 Файл должен быть создан ChartScreenShot

HH 0 18:49:15.205 Core 1 2019.01.01 00:00:00 Era 2 -> error 0.01 % forecast 0.01

CP 0 18:49:15.205 Core 1 2019.01.01 00:00:00 Файл должен быть создан ChartScreenShot

PS 2 18:49:19.829 Core 1 disconnected

OL 0 18:49:19.829 Core 1 connection closed

NF 3 18:49:19.829 Tester stopped by user

И в директории "C:\Users\Borys\AppData\Roaming\MetaQuotes\Tester\BA9DEC643240F2BF3709AAEF5784CBBC\Agent-127.0.0.1-3000\MQL5\Files"

создаеться этот файл :

Fractal_10000000.csv

#define FileName        Symb.Name()+"_"+EnumToString((ENUM_TIMEFRAMES)Period())+"_"+IntegerToString(HistoryBars,3)+StringSubstr(__FILE__,0,StringFind(__FILE__,".",0))
#define CSV             "Fractal_"+StringSubstr(DoubleToString(eta),2)+".csv"

с таким содержимым :

0.1 1 0.006391065067727753 0.30606698779533065 0.009849141883310947

0.1 2 0.01416031275898674 0.320172057079727 0.009671500063084178

0.1 1 0.021322935369592233 0.4824709164481285 0.009510368103745911

0.1 2 0.03047882579179044 0.4736268224037817 0.009336035129387396

0.1 1 0.04096262961921367 0.4747386346906194 0.009164897823757697

0.1 2 0.04745129346676422 0.9935630387598718 0.1983981648307233

и так далее...

При повторном запуске, выводиться таже ошибка и файл .csv перезаписываеться.

Тойсть Эксперет всегда находиться в обучении потому-что не находит файл.

И второй вопрос . подскажите код (для считывания данных из выходного нейрона ) для открытия ордеров buy sell уже при обученной сети .

Спасибо за статью и за ответ.

Dmitriy Gizlyk | 8 июл. 2022 в 19:57