Нейросети — это просто (Часть 3): Сверточные сети
11 034
8
Содержание
- Введение
- 1. Отличительные особенности сверточных нейронных сетей
- 2. Принципы обучения нейронов сверточных слоев
- 3. Построение сверточной нейронной сети
- 3.1. Базовый класс нейронов
- 3.2. Элемент подвыборочного слоя
- 3.3. Элемент сверточного слоя
- 3.4. Создание класса сверточной нейронной сети
- 4. Тестирование
- Заключение
- Ссылки
- Программы, используемые в статье
Введение
Продолжая тему нейронных сетей, предлагаю рассмотреть принципы работы и построения сверточных нейронных сетей (Convolutional Neural Network). Данный вид нейронных сетей широко применяется в задачах распознования объектов на фото и видеоизображениях. Считается, что сверточные нейронные сети устойчивы к изменению масштаба, смене ракурса и прочим пространственным искажениям изображения. Их архитектура позволяет одинаково успешно находить объекты в любом месте сцены. Применительно к трейдингу, с использованием сверточных нейронных сетей хочу улучшить детектирование торговых паттернов на ценовом графике.
1. Отличительные особенности сверточных нейронных сетей
В сверточных сетях, по сравнению с полносвязным перцептроном, добавляются 2 новых вида слоев: сверточный(фильтр) и подвыборочный (субдискретизирующий). Чередуясь, указанные слои призваны выделить основные компоненты и отсеять шумы в исходных данных с параллельным понижением размерности (объема) данных, которые в последующем передаются на вход полносвязного перцептрона для принятия решения. Графически структура сверточной нейронной сети представлена на рисунке ниже. В зависимости от решаемых задач допускается последовательное использование нескольких групп из чередующихся сверточного и подвыборочного слоев.
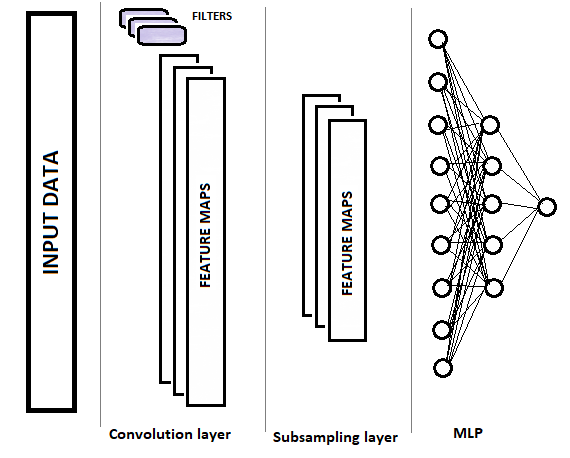
1.1. Сверточный слой
За распознавание объектов в массиве исходных данных отвечает сверточный слой (Convolution layer). В данном слое осуществляются последовательные операции математической свертки исходных данных с небольшим шаблоном (фильтром), выступающими в качестве ядра свертки.
Свёртка — операция в функциональном анализе, которая при применении к двум функциям f и g возвращает третью функцию, соответствующую взаимокорреляционной функции f(x) и g(-x). Операцию свёртки можно интерпретировать как «схожесть» одной функции с отражённой и сдвинутой копией другой.(Wikipedia)
Иными словами, сверточный слой осуществляет поиск шаблонного элемента во всей исходной выборке. При этом на каждой итерации шаблон сдвигается по массиву исходных данных с заданным шагом, который может быть от "1" до размера шаблона. Если величина шага смещения меньше размера шаблона, то такая свертка называется с перекрытием.
В результате операции свертки получаем массив признаков, показывающих "схожесть" исходных данных с искомым шаблоном на каждой итерации. Для нормализации данных используются функции активации. Размер полученного массива будет меньше массива исходных данных, количество таких массивов равно количеству шаблонов (фильтров).
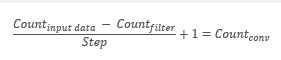
Немаловажен для нас и тот факт, что сами шаблоны не задаются при проектировании нейронной сети, а подбираются в процессе обучения.
1.2. Подвыборочный слой
Следующий, подвыборочный слой используется для снижения размерности массива признаков и фильтрации шумов. Применение данной итерации обусловлено предположением, что наличие сходства исходных данных с шаблоном первично, а точные координаты признака в массиве исходных данных не столь важны. Это позволяет решать проблему масштабирования, т.к. допускает некую вариативность расстояния между искомыми объектами.
На данном этапе происходит уплотнение данных путем сохранения максимального или среднего значения в пределах заданного "окна". Таким образом, сохраняется только одно значение для каждого "окна" данных. Операции осуществляются итерационно со смещением окна на заданный шаг при каждой новой итерации. Уплотнение данных выполняется отдельно для каждого массива признаков.
Довольно часто применяются подвыборочные слои с окном и шагом равным 2, что позволяет вдвое снизить размерность массива признаков. Но в практике допускается и использование большего размера окна, а также итерации уплотнения могут осуществляться как с перекрытием (величина шага меньше размера окна), так и без.
На выходе подвыборочного слоя получаем массивы признаков меньшей размерности.
В зависимости от сложности решаемых задач, после подвыборочного слоя возможно использование еще одну или несколько групп из сверточного и подвыборочного слоя. Принципы их построения и функциональность соответствуют описанным выше. В общем же случае, после одной или нескольких групп свертка + уплотнения массивы полученных признаков по всем фильтрам собираются в единый вектор и подаются на вход многослойного перцептрона для принятия решения нейронной сетью (о построение многослойного перцептрона рассказано в первой части данного цикла статей).
2. Принципы обучения нейронов сверточных слоев
Обучение сверточных нейронных сетей отсуществляется уже известным из предыдущих публикаций методом обратного распространения ошибки. Данный метод относится к методам обучения с учителем и заключается в спуске градиента ошибки от выходного слоя нейронов, через скрытые слои к входному слою нейронов с корректировкой весовых коэффициентов в сторону антиградиента.
Об обучении многослойного перцептрона я уже рассказывал в первой статье этого цикла, поэтому не буду останавливаться. Рассмотрим обучение нейронов подвыборочного и сверточного слоев.
В подвыборочном слое градиент ошибки считается для каждого элемента в массиве признаков по аналогии с градиентами нейронов полносвязного перцепртрона. Алгоритм передачи градиента на предыдущий слой зависит от применяемой операции уплотнения. Если берется только максимальное значение, то и весь градиент передается на нейрон с максимальным значением (для остальных элементов в пределах окна уплотнения устанавливается нулевой градиент). Если же используется операция усреднения в пределах окна, то и градиент равномерно распределяется на все элементы в пределах окна.
Т.к. в операции уплотнения не используются весовые коэффициенты, то и в процессе обучения ничто не корректируется.
Немного сложнее происходят вычисления при обучении нейронов сверточного слоя. Градиент ошибки рассчитывается для каждого элемента массива признаков и спускается к соответствующим нейронам предыдущего слоя. В основе процесса обучения сверточного слоя лежат операции свертки и обратной свертки.
Для передачи градиента ошибки от подвыборочного слоя к сверточному, сначала дополняются края массива градиентов ошибок, полученных от подвыборочного слоя, нулевыми элементами и затем производится свертка полученного массива с ядром свертки, развернутым на 180°. На выходе получаем массив градиентов ошибок размером равным массиву входных данных, в котором индексы градиентов будут соответствовать индексу корреспондирующего нейрона, предшествующего сверточному слою.
Для получения дельт весовых коэффициентов осуществляется свертка матрицы входных значений с матрицей градиентов ошибок данного слоя, развернутой на 180°. На выходе получим массив дельт с размером равным ядру свертки. Полученные дельты нужно скорректировать на производную функции активации сверточного слоя и коэффициент обучения. После чего, весовые коэффициенты ядра свертки изменяются на величину скорректированных дельт.
Наверное, звучит довольно сложно для понимания. Попробуем прояснить данные моменты при подробном рассмотрении кода.
3. Построение сверточной нейронной сети
Как уже было сказана выше, сверточная нейронная сеть будет состоять из 3-х типов нейронных слоев (сверточный, подвыборочный и полносвязный) с отличительными классами нейронов и различными функциями для прямого и обратного прохода. В тоже время, нам нужно объединить все нейроны в единую сеть и организовать вызов именно того метода обработки данных, который соответствует обрабатываемому нейрону. На мой взгляд, наиболее простой способ организовать данный процесс с помощью функционала наследования классов и виртуализации функций.
Вначале построим структуру наследования классов.
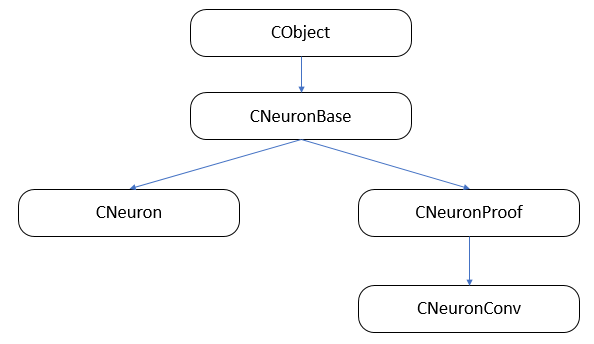
3.1. Базовый класс нейронов.
В первой статье мы создали класс слоя CLayer наследником класса CArrayObj, который является классом динамического массива для хранения ссылок на объекты класса CObject. Следовательно, все нейроны у нас должны унаследоваться от данного класса. На базе класса CObject создадим базовый класс CNeuronBase. В теле класса объявим общие для всех типов нейронов переменные и создадим шаблоны основных методов. Все методы класса объявлены виртуальными для возможности последующего переопределения.
class CNeuronBase : public CObject { protected: double eta; double alpha; double outputVal; uint m_myIndex; double gradient; CArrayCon *Connections; //--- virtual bool feedForward(CLayer *prevLayer) { return false; } virtual bool calcHiddenGradients( CLayer *&nextLayer) { return false; } virtual bool updateInputWeights(CLayer *&prevLayer) { return false; } virtual double activationFunction(double x) { return 1.0; } virtual double activationFunctionDerivative(double x) { return 1.0; } virtual CLayer *getOutputLayer(void) { return NULL; } public: CNeuronBase(void); ~CNeuronBase(void); virtual bool Init(uint numOutputs, uint myIndex); //--- virtual void setOutputVal(double val) { outputVal=val; } virtual double getOutputVal() { return outputVal; } virtual void setGradient(double val) { gradient=val; } virtual double getGradient() { return gradient; } //--- virtual bool feedForward(CObject *&SourceObject); virtual bool calcHiddenGradients( CObject *&TargetObject); virtual bool updateInputWeights(CObject *&SourceObject); //--- virtual bool Save( int const file_handle); virtual bool Load( int const file_handle) { return(Connections.Load(file_handle)); } //--- virtual int Type(void) const { return defNeuronBase; } };
Названия переменных и методов соответствуют описанным ранее. Предлагаю рассмотреть методы feedForward(CObject *&SourceObject), сalcHiddenGradients(CObject *&TargetObject) и updateInputWeights(CObject *&SourceObject), так как в указанных методах осуществляется диспетчеризация по работе с полносвязными и сверточными слоями.
3.1.1. Прямой проход.
Метод feedForward(CObject *&SourceObject) вызывается при прямом проходе для вычисления результирующего значения нейрона. При прямом проходе в полносвязных слоях каждый нейрон берет значения всех нейронов предыдущего слоя и, соответственно, на вход должен получить весь предыдущий слой. В сверточных и подвыборочных слоях на вход нейрона подается только часть данных, относящаяся к данному фильтру. В рассматриваемом методе выбор алгоритма осуществляется на основании типа класса, полученного в параметрах.
В начале проверяем действительность ссылки на объект, полученной в параметрах метода.
bool CNeuronBase::feedForward(CObject *&SourceObject) { bool result=false; //--- if(CheckPointer(SourceObject)==POINTER_INVALID) return result;
Так как внутри оператора выбора нельзя объявлять экземпляры классов, подготовим шаблоны заранее.
CLayer *temp_l; CNeuronProof *temp_n;
Далее в операторе выбора проверим тип полученного в параметрах объекта. Если мы получили ссылку на слой нейронов, то предыдущий слой является полносвязным и, следовательно, вызовем метод для работы с полносвязными слоями (подробно описано в первой статье). Если же мы имеем дело с нейроном сверточного или подвыборочного слоя, то сначала мы получим слой выходных нейронов данного фильтра и затем воспользуемся методом обработки полносвязного слоя, передав ему в параметрах слой нейронов текущего фильтра с сохранением результата отработки в переменную result (подробнее о строении нейронов сверточного и подвыборочного слоев будет рассказано ниже). После отработки выходим из метода с передачей результата работы.
switch(SourceObject.Type()) { case defLayer: temp_l=SourceObject; result=feedForward(temp_l); break; case defNeuronConv: case defNeuronProof: temp_n=SourceObject; result=feedForward(temp_n.getOutputLayer()); break; } //--- return result; }
3.1.2. Расчет градиента ошибки.
По аналогии с прямым проходом создан диспетчер для вызова функции расчета градиента ошибки на скрытых слоях нейронной сети сalcHiddenGradients(CObject *&TargetObject). Структура построения и логика метода аналогична описанному выше. Сначала проверяем действительность полученной ссылки. Затем объявляем переменные для хранения ссылок на соответствующие объекты. И в функции выбора по типу полученного объекта выбираем нужный метод. Отличия начинаются если в параметрах передана ссылка на элемент сверточного или подвыборочного слоя. Расчет градиента ошибки через такие нейроны отличается и распространяется не на все нейроны предыдущего слоя, а только в пределах окна выборки. Поэтому, расчет градиента перенесен в эти нейроны в метод calcInputGradients. При этом есть отличия в методах для расчета по слою или для конкретного нейрона. Следовательно, требуемый метод вызывается в зависимости от типа объекта из которого вызывается.
bool CNeuronBase::calcHiddenGradients(CObject *&TargetObject) { bool result=false; //--- if(CheckPointer(TargetObject)==POINTER_INVALID) return result; //--- CLayer *temp_l; CNeuronProof *temp_n; switch(TargetObject.Type()) { case defLayer: temp_l=TargetObject; result=calcHiddenGradients(temp_l); break; case defNeuronConv: case defNeuronProof: switch(Type()) { case defNeuron: temp_n=TargetObject; result=temp_n.calcInputGradients(GetPointer(this),m_myIndex); break; default: temp_n=GetPointer(this); temp_l=temp_n.getOutputLayer(); temp_n=TargetObject; result=temp_n.calcInputGradients(temp_l); break; } break; } //--- return result; }
Диспетчер updateInputWeights(CObject *&SourceObject) для обновления весовых коэффициентов построен по принципам описанным выше. С подробным кодом метода можно ознакомиться во вложении.
3.2. Элемент подвыборочного слоя.
Основным кирпичиком подвыборочного слоя выступает класс CNeuronProof, который наследуется от ранее описанного базового класса CNeuronBase. При проработке архитектуры было принято решение о создании в подвыборочном слое одного экземпляра такого класса на каждый фильтр. В связи с этим вводятся дополнительные переменные iWindow и iStep для хранения размера окна уплотнения и шага сдвига, соответственно. Также добавляем внутренний слой нейронов для хранения массивов признаков, градиентов ошибок и, при необходимости, весовых коэффициентов для передачи признаков в полносвязный перцептрон. И добавим метод для получения ссылки на внутренний слой нейронов по запросу.
class CNeuronProof : public CNeuronBase { protected: CLayer *OutputLayer; int iWindow; int iStep; virtual bool feedForward(CLayer *prevLayer); virtual bool calcHiddenGradients( CLayer *&nextLayer); public: CNeuronProof(void){}; ~CNeuronProof(void); virtual bool Init(uint numOutputs,uint myIndex,int window, int step, int output_count); //--- virtual CLayer *getOutputLayer(void) { return OutputLayer; } virtual bool calcInputGradients( CLayer *prevLayer) ; virtual bool calcInputGradients( CNeuronBase *prevNeuron, uint index) ; //--- methods for working with files virtual bool Save( int const file_handle) { return(CNeuronBase::Save(file_handle) && OutputLayer.Save(file_handle)); } virtual bool Load( int const file_handle) { return(CNeuronBase::Load(file_handle) && OutputLayer.Load(file_handle)); } virtual int Type(void) const { return defNeuronProof; } };
Не забываем переопределить логику работы для объявленных в базовом классе виртуальных функций.
3.2.1. Прямой проход.
Метод feedForward предназначен для отсеивания шумов и понижения размерности массива признаков. В описываемом решении для уплотнения данных используется функция арифметического среднего. Рассмотрим детальнее код метода. Вначале метода проверим актуальность полученной ссылки на предыдущий слой нейронов.
bool CNeuronProof::feedForward(CLayer *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false;
Затем организуем цикл по перебору всех нейронов полученного в параметрах слоя с заданным шагом.
int total=prevLayer.Total()-iWindow+1; CNeuron *temp; for(int i=0;(i<=total && result);i+=iStep) {
В теле цикла создадим вложенный цикл для подсчета суммы выходных значений нейронов предыдущего слоя в пределах заданного окна уплотнения.
double sum=0; for(int j=0;j<iWindow;j++) { temp=prevLayer.At(i+j); if(CheckPointer(temp)==POINTER_INVALID) continue; sum+=temp.getOutputVal(); }
После подсчета суммы обратимся к соответствующему нейрону внутреннего слоя хранения результирующих данных и запишем в его результирующее значение отношение полученной суммы к размеру окна, что и составит среднее арифметическое для текущего окна уплотнения.
temp=OutputLayer.At(i/iStep); if(CheckPointer(temp)==POINTER_INVALID) return false; temp.setOutputVal(sum/iWindow); } //--- return true; }
По завершении перебора всех нейронов завершаем работу метода.
3.2.2. Расчет градиента ошибки.
Для расчета градиента ошибки в данном классе создана два метода: calcHiddenGradients и calcInputGradients. Первый собирает данные о градиентах ошибки последующего слоя и считает градиент для элементов текущего слоя. Второй на основе данных полученных в первом методе распределяет ошибку по элементам предыдущего слоя.
В начале метода calcHiddenGradients, как обычно, проверим действительность полученной в параметрах ссылки. Дополнительно проверим состояния внутреннего слоя нейронов.
bool CNeuronProof::calcHiddenGradients( CLayer *&nextLayer) { if(CheckPointer(nextLayer)==POINTER_INVALID || CheckPointer(OutputLayer)==POINTER_INVALID || OutputLayer.Total()<=0) return false;
Далее в цикле переберем все нейроны внутреннего слоя и вызовем метод по подсчету градиента ошибки.
gradient=0; int total=OutputLayer.Total(); CNeuron *temp; for(int i=0;i<total;i++) { temp=OutputLayer.At(i); if(CheckPointer(temp)==POINTER_INVALID) return false; temp.setGradient(temp.sumDOW(nextLayer)); } //--- return true; }
Хочу обратить внимание, что данный метод правильно отрабатывает, если далее следует полносвязный слой нейронов. Если далее следует сверточный или подвыборочный слой необходимо использовать метод calcInputGradients нейрона последующего слоя.
В параметрах метод calcInputGradients получает ссылку на предыдущий слой. И мы сразу, в начале метода, проверяем действительность данной ссылки состояние внутреннего слоя нейронов.
bool CNeuronProof::calcInputGradients(CLayer *prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID || CheckPointer(OutputLayer)==POINTER_INVALID) return false;
Затем проверяем тип первого элемента полученного в параметрах слоя. В случае, если полученная ссылка указывает на подвыборочный или сверточный слой, то запросим ссылку на внутренний слой нейронов, соответствующего фильтра.
if(prevLayer.At(0).Type()!=defNeuron) { CNeuronProof *temp=prevLayer.At(m_myIndex); if(CheckPointer(temp)==POINTER_INVALID) return false; prevLayer=temp.getOutputLayer(); if(CheckPointer(prevLayer)==POINTER_INVALID) return false; }
Далее организуем цикл по перебору всех нейронов предыдущего слоя с обязательной проверкой действительность ссылки на обрабатываемый нейрон.
CNeuronBase *prevNeuron, *outputNeuron; int total=prevLayer.Total(); for(int i=0;i<total;i++) { prevNeuron=prevLayer.At(i); if(CheckPointer(prevNeuron)==POINTER_INVALID) continue;
Определим на какие нейроны внутреннего слоя влияет обрабатываемый нейрон.
double prev_gradient=0; int start=i-iWindow+iStep; start=(start-start%iStep)/iStep; double stop=(i-i%iStep)/iStep+1;
В цикле посчитаем градиент ошибки для обрабатываемого нейрона и сохраним полученный результат. После перебора всех нейронов предыдущего слоя завершаем работу метода.
for(int out=(int)fmax(0,start);out<(int)fmin(OutputLayer.Total(),stop);out++) { outputNeuron=OutputLayer.At(out); if(CheckPointer(outputNeuron)==POINTER_INVALID) continue; prev_gradient+=outputNeuron.getGradient()/iWindow; } prevNeuron.setGradient(prev_gradient); } //--- return true; }
Аналогичным образом построен метод с аналогичным названием для подсчета градиента отдельного нейрона. Отличие заключается в исключении внешнего цикла по перебору нейронов. Вместо него идет обращение по порядковому номеру нейрона.
Так как в подвыборочном слое не используются весовые коэффициенты, то и метод их обновления можно опустить. Или, как вариант, для сохранения унификации структуры классов нейронов можно создать пустой метод, который при вызове будет возвращать значение true.
С полным кодом всех методов и функций можно ознакомиться во вложении.
3.3. Элемент сверточного слоя.
Для построения сверточного слоя будем использовать объекты класса CNeuronConv, которые будут наследоваться от класса CNeuronProof. В качестве функции активации для данного типа нейронов я выбрал параметрическую ReLU. Данная функция более легкая для расчета, по сравнению с гиперболическим тангенсом, используемым в нейронах полносвязного перцептрона. Для ее расчета введем дополнительную переменную param.
class CNeuronConv : public CNeuronProof { protected: double param; //PReLU param virtual bool feedForward(CLayer *prevLayer); virtual bool calcHiddenGradients(CLayer *&nextLayer); virtual double activationFunction(double x); virtual bool updateInputWeights(CLayer *&prevLayer); public: CNeuronConv() : param(0.01) { }; ~CNeuronConv(void) { }; //--- virtual bool calcInputGradients(CLayer *prevLayer) ; virtual bool calcInputGradients(CNeuronBase *prevNeuron, uint index) ; virtual double activationFunctionDerivative(double x); virtual int Type(void) const { return defNeuronConv; } };
Методы прямого и обратного прохода построены по алгоритмам аналогичным класса CNeuron Proof. Отличия заключаются только в использовании функции активации и весовых коэффициентов. Поэтому не вижу причин для их детального рассмотрения. Разберем метод корректировки весовых коэффициентов updateInputWeights.
В параметрах метод получает ссылку на предшествующий слой нейронов и мы сразу проверяем действительность полученной ссылки и состояние внутреннего слоя.
bool CNeuronConv::updateInputWeights(CLayer *&prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID || CheckPointer(OutputLayer)==POINTER_INVALID) return false;
Далее, создаем цикл по перебору всех весовых коэффициентов и, разумеется, после получения ссылки на объект очередной связи проверяем ее действительность.
CConnection *con; for(int n=0; n<iWindow && !IsStopped(); n++) { con=Connections.At(n); if(CheckPointer(con)==POINTER_INVALID) continue;
После этого считаем свертку массива входных данных с массивом градиентов ошибок внутреннего слоя, развернутого на 180°. Для этого организовываем цикл по перебору всех элементов внутреннего слоя и умножению на элементы массива входных данных по схеме:
- первый элемент массива входных данных (со сдвигом на количество шагов равных порядковому номеру весового коэффициента) на последний элемент массива градиента ошибок.
- второй элемент массива входных данных (со сдвигом на количество шагов равных порядковому номеру весового коэффициента) на предпоследний элемент массива градиента ошибок.
- и т.д. до элемент с индексом равным количеству элементов в массиве внутреннего слоя со сдвигом на количество шагов равных порядковому номеру весового коэффициента умножается на первый элемент массива градиента ошибок.
Полученные произведения суммируем.
double delta=0; int total_i=OutputLayer.Total(); CNeuron *prev, *out; for(int i=0;i<total_i;i++) { prev=prevLayer.At(n*iStep+i); out=OutputLayer.At(total_i-i-1); if(CheckPointer(prev)==POINTER_INVALID || CheckPointer(out)==POINTER_INVALID) continue; delta+=prev.getOutputVal()*out.getGradient(); }
Рассчитанная сумма произведений и является базой для корректировки весовых коэффициентов. Корректируем весовые коэффициенты с учетом заданной скорости обучения.
con.weight+=con.deltaWeight=(delta!=0 ? eta*delta : 0)+(con.deltaWeight!=0 ? alpha*con.deltaWeight : 0); } //--- return true; }
После корректировки всех весовых коэффициентов выходим из метода.
Класс CNeuron подробно описан в первой статье данного цикла и практически не изменился, поэтому разрешите не останавливаться на нем в этой статье.
3.4. Создание класса сверточной нейронной сети.
Теперь, когда созданы все кирпичики можно приступать к строительству дома — создадим класс сверточной нейронной сети, который объединит все типы нейронов в четкую структуру и организует работу нашей нейронной сети. Первый вопрос, который возникает при создании данного класса — это как мы будем задавать требуемую структуру сети. В полносвязный перцептрон мы передавали массив элементов в котором указывали количество нейронов в каждом слое. Сейчас же нам нужно больше информации для генерации нужного слоя сети. Создадим небольшой класс CLayerDescription для описания построения слоя. Данный класс не содержит никаких методов (кроме конструктора и деструктора), а включает только переменные для указания типа нейронов в слое, количество таких нейронов, размер окна и шага для нейронов сверточного и подвыборочного слоев. В параметрах же конструктора класса сверточной нейронной сети мы будем передавать ссылку на массив классов с описанием слоев.
class CLayerDescription : public CObject { public: CLayerDescription(void); ~CLayerDescription(void){}; //--- int type; int count; int window; int step; }; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ CLayerDescription::CLayerDescription(void) : type(defNeuron), count(0), window(1), step(1) {}
Рассмотрим структуру класса сверточной нейронной сети CNetConvolution. Данный класс содержит:
- layers — массив слоев;
- recentAverageError — текущая ошибка сети;
- recentAverageSmoothingFactor — фактор усреднения ошибки;
- CNetConvolution — конструктор класса;
- ~CNetConvolution — деструктор класса;
- feedForward — метод прямого прохода;
- backProp — метод обратного прохода;
- getResults — метод для получения результатов последнего прямого прохода;
- getRecentAverageError — метод для получения текущей ошибки сети;
- Save и Load — методы для сохранения и загрузки ранее созданной и обученной сети.
class CNetConvolution { public: CNetConvolution(CArrayObj *Description); ~CNetConvolution(void) { delete layers; } bool feedForward( CArrayDouble *inputVals); void backProp( CArrayDouble *targetVals); void getResults(CArrayDouble *&resultVals) ; double getRecentAverageError() { return recentAverageError; } bool Save( string file_name, double error, double undefine, double forecast, datetime time, bool common=true); bool Load( string file_name, double &error, double &undefine, double &forecast, datetime &time, bool common=true); //--- static double recentAverageSmoothingFactor; virtual int Type(void) const { return defNetConv; } private: CArrayLayer *layers; double recentAverageError; };
Наименование методов и алгоритмы построения аналогичны описанным ранее для полносвязного перцептрона в первой статье данного цикла. Остановимся только на основных методах класса.
3.4.1. Конструктор класса сверточной нейронной сети.
Рассмотрим конструктор класса. В параметрах конструктор получает ссылку на массив описаний слоев для построения сети. Соответственно, проверяем действительность полученной ссылки, определяем количество слоев для построения и создаем новый экземпляр массива слоев.
CNetConvolution::CNetConvolution(CArrayObj *Description)
{
if(CheckPointer(Description)==POINTER_INVALID)
return;
//---
int total=Description.Total();
if(total<=0)
return;
//---
layers=new CArrayLayer();
if(CheckPointer(layers)==POINTER_INVALID)
return; Далее объявляем внутренние переменные.
CLayer *temp; CLayerDescription *desc=NULL, *next=NULL, *prev=NULL; CNeuronBase *neuron=NULL; CNeuronProof *neuron_p=NULL; int output_count=0; int temp_count=0;
На этом подготовительный этап закончен и приступаем непосредственно к цикличности генерации слое нейронной сети. В начале цикла считываем информацию о текущем и последующем слоях.
for(int i=0;i<total;i++) { prev=desc; desc=Description.At(i); if((i+1)<total) { next=Description.At(i+1); if(CheckPointer(next)==POINTER_INVALID) return; } else next=NULL;
Подсчитаем количество выходных связей для слоя и создадим новый экземпляр класса нейронного слоя. Обратите внимание, что количество связей на выходе слоя указываем только перед полносвязным слоем, в противном случае указываем нулевое значение. Это связано с тем, что сверточные нейроны сами хранят входные весовые коэффициенты, а подвыборочный слой их вообще не использует.
int outputs=(next==NULL || next.type!=defNeuron ? 0 : next.count); temp=new CLayer(outputs);
Далее в цикле идет генерация нейронов с разделением алгоритма по типу нейронов в создаваемом слое. Для полносвязных слоев осуществляется создание нового экземпляра нейрона и его инициализация. Обратите внимание, что для полносвязных слоев создается на один нейрон больше, чем указано в описании. Данный нейрон будет использоваться в качестве байесовского смещения.
for(int n=0;n<(desc.count+(i>0 && desc.type==defNeuron ? 1 : 0));n++) { switch(desc.type) { case defNeuron: neuron=new CNeuron(); if(CheckPointer(neuron)==POINTER_INVALID) { delete temp; delete layers; return; } neuron.Init(outputs,n); break;
Для сверточного слоя создадим новый экземпляр нейрона. Посчитаем количество выходных элементов на основании информации о предыдущем слое и инициализируем только-что созданный нейрон.
case defNeuronConv: neuron_p=new CNeuronConv(); if(CheckPointer(neuron_p)==POINTER_INVALID) { delete temp; delete layers; return; } if(CheckPointer(prev)!=POINTER_INVALID) { if(prev.type==defNeuron) { temp_count=(int)((prev.count-desc.window)%desc.step); output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2)); } else if(n==0) { temp_count=(int)((output_count-desc.window)%desc.step); output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2)); } } if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count)) neuron=neuron_p; break;
Аналогичный алгоритм применяется для нейронов подвыборочного слоя.
case defNeuronProof: neuron_p=new CNeuronProof(); if(CheckPointer(neuron_p)==POINTER_INVALID) { delete temp; delete layers; return; } if(CheckPointer(prev)!=POINTER_INVALID) { if(prev.type==defNeuron) { temp_count=(int)((prev.count-desc.window)%desc.step); output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2)); } else if(n==0) { temp_count=(int)((output_count-desc.window)%desc.step); output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2)); } } if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count)) neuron=neuron_p; break; }
После объявления и инициализации нейрона добавляем его в нейронный слой.
if(!temp.Add(neuron)) { delete temp; delete layers; return; } neuron=NULL; }
По завершению цикла генерации нейронов очередного слоя добавляем слой в хранилище. После генерации всех слоев выходим из метода.
if(!layers.Add(temp)) { delete temp; delete layers; return; } } //--- return; }
3.4.2. Метод прямого прохода сверточной нейронной сети.
Вся работа нейронной сети организована в методе прямого прохода feedForward. В параметрах данный метод получает исходные данные для анализа (в нашем случае это информация с ценового графика и используемых индикаторов). Первым делом проверяем действительность полученной ссылки на массив данных и состояние инициализации нейронной сети.
bool CNetConvolution::feedForward(CArrayDouble *inputVals) { if(CheckPointer(layers)==POINTER_INVALID || CheckPointer(inputVals)==POINTER_INVALID || layers.Total()<=1) return false;
Затем объявляем вспомогательные переменные и переносим полученные внешние данные на входной слой нейронной сети.
CLayer *previous=NULL; CLayer *current=layers.At(0); int total=MathMin(current.Total(),inputVals.Total()); CNeuronBase *neuron=NULL; for(int i=0;i<total;i++) { neuron=current.At(i); if(CheckPointer(neuron)==POINTER_INVALID) return false; neuron.setOutputVal(inputVals.At(i)); }
После загрузки исходных данных в нейронную сеть запускаем цикл последовательно перебора нейронных слоев от входа нейронной сети к ее выходу.
CObject *temp=NULL; for(int l=1;l<layers.Total();l++) { previous=current; current=layers.At(l); if(CheckPointer(current)==POINTER_INVALID) return false;
Внутри запущенного цикла для каждого слоя запускаем вложенный цикл по перебору всех нейронов слоя с пересчетом их значений. Обратите внимание, что для полносвязных нейронных слоев не пересчитывается значение на последнем нейроне. Как уже говорилось выше, он используется в качестве байесовского смещения, и мы будем использовать только его весовой коэффициент.
total=current.Total(); if(current.At(0).Type()==defNeuron) total--; //--- for(int n=0;n<total;n++) { neuron=current.At(n); if(CheckPointer(neuron)==POINTER_INVALID) return false;
Далее выбор метода зависит от типа нейронов предыдущего слоя. Для полносвязных слоев вызовем метод прямого распространения с указанием в параметрах ссылки на предыдущий слой.
if(previous.At(0).Type()==defNeuron) { temp=previous; if(!neuron.feedForward(temp)) return false; continue; }
Если ранее был сверточный или подвыборочный слой, то посмотрим на тип пересчитываемого нейрона. Для нейрона полносвязного слоя соберем внутренние слои всех нейронов предыдущего слоя в единый слой и затем вызовем метод прямого распространения текущего нейрона с указанием в параметрах ссылки на суммарный слой нейронов.
if(neuron.Type()==defNeuron) { if(n==0) { CLayer *temp_l=new CLayer(total); if(CheckPointer(temp_l)==POINTER_INVALID) return false; CNeuronProof *proof=NULL; for(int p=0;p<previous.Total();p++) { proof=previous.At(p); if(CheckPointer(proof)==POINTER_INVALID) return false; temp_l.AddArray(proof.getOutputLayer()); } temp=temp_l; } if(!neuron.feedForward(temp)) return false; if(n==total-1) { CLayer *temp_l=temp; temp_l.FreeMode(false); temp_l.Shutdown(); delete temp_l; } continue; }
По завершении цикла перебора всех нейронов такого слоя нужно удалить объект суммарного нейрона. При этом нам нужно удалить объект слоя без удаления объектов нейронов, содержащихся в данном слое, т. к. эти же объекты и далее будут использоваться в наших сверточных и подвыборочных слоях. Для этого установим флаг m_free_mode в состояние false и только потом удалим объект.
Если же перед нами элемент сверточного или подвыборочного слоя, то вызовем метод прямого распространения с передачей в параметрах ссылки на предыдущий элемент соответствующего фильтра.
temp=previous.At(n); if(CheckPointer(temp)==POINTER_INVALID) return false; if(!neuron.feedForward(temp)) return false; } } //--- return true; }
После перебора всех нейронов и слоев выходим из метода.
3.4.3. Метод обратного прохода сверточной нейронной сети.
Обучение нейронной сети осуществляется в методе обратного прохода backProp. В нем реализован метод обратного распространения ошибки от выходного слоя нейронной сети к ее входам. Следовательно, в параметрах данный метод получает фактические данные.
В начале метода проверяем действительность ссылки на объект эталонных значений.
void CNetConvolution::backProp(CArrayDouble *targetVals) { if(CheckPointer(targetVals)==POINTER_INVALID) return;
Затем, посчитаем среднеквадратичную ошибку на выходе прямого прохода нейронной сети от фактических данных и рассчитаем градиенты ошибки нейронов выходного слоя.
CLayer *outputLayer=layers.At(layers.Total()-1); if(CheckPointer(outputLayer)==POINTER_INVALID) return; //--- double error=0.0; int total=outputLayer.Total()-1; for(int n=0; n<total && !IsStopped(); n++) { CNeuron *neuron=outputLayer.At(n); double target=targetVals.At(n); double delta=(target>1 ? 1 : target<-1 ? -1 : target)-neuron.getOutputVal(); error+=delta*delta; neuron.calcOutputGradients(targetVals.At(n)); } error/= total; error = sqrt(error); recentAverageError+=(error-recentAverageError)/recentAverageSmoothingFactor;
Следующим шагом организуем цикл с перебором всех слоев нейронной сети в обратном порядке, в котором запустим вложенный цикл с перебором всех нейронов соответствующего слоя для пересчета градиентов ошибок нейронов в скрытых слоях.
CNeuronBase *neuron=NULL; CObject *temp=NULL; for(int layerNum=layers.Total()-2; layerNum>0; layerNum--) { CLayer *hiddenLayer=layers.At(layerNum); CLayer *nextLayer=layers.At(layerNum+1); total=hiddenLayer.Total(); for(int n=0; n<total && !IsStopped(); ++n) {
Как и при прямом проходе, выбор нужного метода обновления градиентов ошибок осуществляется на основании анализа типов текущего нейрона и нейронов последующего слоя. Если далее следует полносвязный слой нейронов, то вызываем метод calcHiddenGradients анализируемого нейрона с передачей в параметрах ссылки на объект последующего слоя нейронной сети.
neuron=hiddenLayer.At(n); if(nextLayer.At(0).Type()==defNeuron) { temp=nextLayer; neuron.calcHiddenGradients(temp); continue; }
Если же далее следует сверточный или подвыборочный слой, то в таком случае проверяем тип текущего нейрона. Для полносвязного нейрона организуем цикл по перебору всех фильтров последующего слоя с запуском пересчета градиента ошибки по каждому фильтру для данного нейрона и суммируем полученные градиенты. В случае, когда текущий слой также является сверточный или подвыборочный, определим градиент ошибки по соответствующему фильтру.
if(neuron.Type()==defNeuron) { double g=0; for(int i=0;i<nextLayer.Total();i++) { temp=nextLayer.At(i); neuron.calcHiddenGradients(temp); g+=neuron.getGradient(); } neuron.setGradient(g); continue; } temp=nextLayer.At(n); neuron.calcHiddenGradients(temp); } }
После обновления всех градиентов запустим аналогичные циклы с той же логикой разветвления для обновления весовых коэффициентов нейронов. После обновления весов выходим из метода.
for(int layerNum=layers.Total()-1; layerNum>0; layerNum--) { CLayer *layer=layers.At(layerNum); CLayer *prevLayer=layers.At(layerNum-1); total=layer.Total()-(layer.At(0).Type()==defNeuron ? 1 : 0); int n_conv=0; for(int n=0; n<total && !IsStopped(); n++) { neuron=layer.At(n); if(CheckPointer(neuron)==POINTER_INVALID) return; if(neuron.Type()==defNeuronProof) continue; switch(prevLayer.At(0).Type()) { case defNeuron: temp=prevLayer; neuron.updateInputWeights(temp); break; case defNeuronConv: case defNeuronProof: if(neuron.Type()==defNeuron) { for(n_conv=0;n_conv<prevLayer.Total();n_conv++) { temp=prevLayer.At(n_conv); neuron.updateInputWeights(temp); } } else { temp=prevLayer.At(n); neuron.updateInputWeights(temp); } break; default: temp=NULL; break; } } } }
С полным кодом всех методов и классов можно ознакомиться во вложении.
4. Тестирование
Для проверки работы сверточной нейронной сети был взят советник классификации из второй статьи данного цикла. Напомню, перед нейронной сетью стоит задача предсказания фрактала на текущей свече. Для этого на вход нейронной сети подается информация о формациях N последних свечей и данные 4-х осцилляторов за тот же период.
В сверточном слое нашей новой нейронной сети мы создадим 4 фильтра, которые будут искать паттерны в совокупности данных о формации свечи и показаниях осцилляторов на анализируемой свече. Окно и шаг фильтров будут соответствовать количеству данных на описание одной свечи. Иными словами, мы сравним всю информацию о каждой свече с неким паттерном и вернем значение сходимости. Такой подход позволит нам при необходимости дополнять исходные данные новой информацией о свечах (включение дополнительных индикаторов для анализа и т. д.) без существенной потери производительности.
В подвыборочном слое мы уменьшим размер массива признаков и сгладим результаты путем усреднения данных.
В самом советнике потребовались минимальные изменения. Это изменение класса нейронной сети при объявлении переменных и создании экземпляра.
CNetConvolution *Net;
Также изменения были внесены в части задании структуры нейронной сети в функции OnInit. Для тестирования была использована сеть с одним сверточным и одним подвыборочным слоем и 4-мя фильтрами в каждом. Структура полносвязных слоев осталась без изменений (сделано намеренно для оценки влияния сверточных слоев на работу всей сети).
Net=new CNetConvolution(NULL); ResetLastError(); if(CheckPointer(Net)==POINTER_INVALID || !Net.Load(FileName+".nnw",dError,dUndefine,dForecast,dtStudied,false)) { printf("%s - %d -> Error of read %s prev Net %d",__FUNCTION__,__LINE__,FileName+".nnw",GetLastError()); CArrayObj *Topology=new CArrayObj(); if(CheckPointer(Topology)==POINTER_INVALID) return INIT_FAILED; //--- CLayerDescription *desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=(int)HistoryBars*12; desc.type=defNeuron; if(!Topology.Add(desc)) return INIT_FAILED; //--- int filters=4; desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=filters; desc.type=defNeuronConv; desc.window=12; desc.step=12; if(!Topology.Add(desc)) return INIT_FAILED; //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=filters; desc.type=defNeuronProof; desc.window=3; desc.step=2; if(!Topology.Add(desc)) return INIT_FAILED; //--- int n=1000; bool result=true; for(int i=0;(i<4 && result);i++) { desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=n; desc.type=defNeuron; result=(Topology.Add(desc) && result); n=(int)MathMax(n*0.3,20); } if(!result) { delete Topology; return INIT_FAILED; } //--- desc=new CLayerDescription(); if(CheckPointer(desc)==POINTER_INVALID) return INIT_FAILED; desc.count=3; desc.type=defNeuron; if(!Topology.Add(desc)) return INIT_FAILED; delete Net; Net=new CNetConvolution(Topology); delete Topology; if(CheckPointer(Net)==POINTER_INVALID) return INIT_FAILED; dError=-1; dUndefine=0; dForecast=0; dtStudied=0; }
В остальном код советника остался без изменений.
Тестирование проводилось на паре EURUSD период H1. В одном терминале на разных графиках одного инструмента одновременно было запущено 2 советника: со сверточной и полносвязной нейронной сетью. Параметры полносвязных слоев сверточной нейронной сети аналогичны полносвязной сети второго советника, т. е. к ранее построенной сети мы только добавили сверточный и подвыборочный слои.
Тестирование показала небольшой прирост производительности в сверточной нейронной сети. Несмотря на добавление двух слоев, по результатам 24 эпох среднее время обучения одной эпохи сверточной нейронной сети составило 2 часа 4 минуты, а полносвязной сети 2 часа 10 минут.
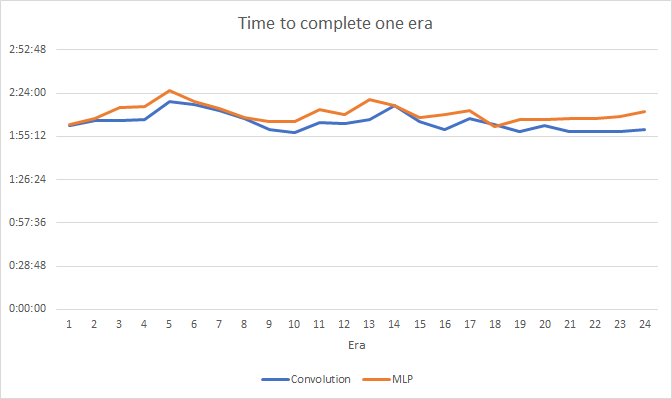
При этом сверточная нейронная сеть показывает немногим лучшие результаты по погрешности предсказания и "попадании в цель".
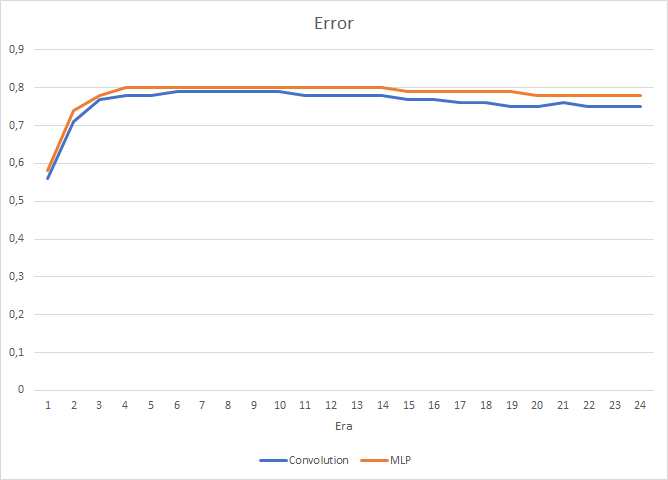
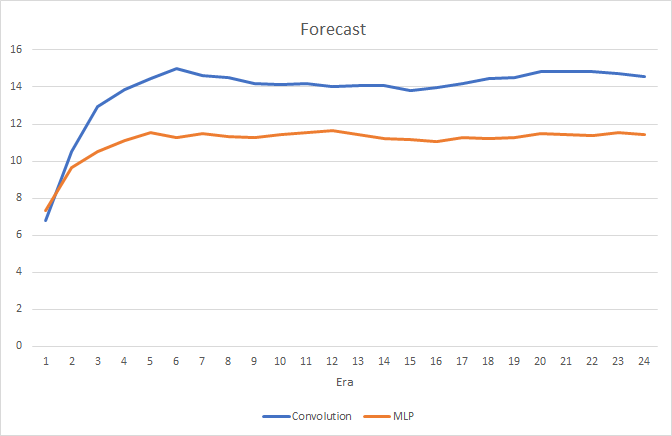
Визуально можно заметить, что на графике сверточной нейронной сети сигналы появляются реже, но ближе к цели.
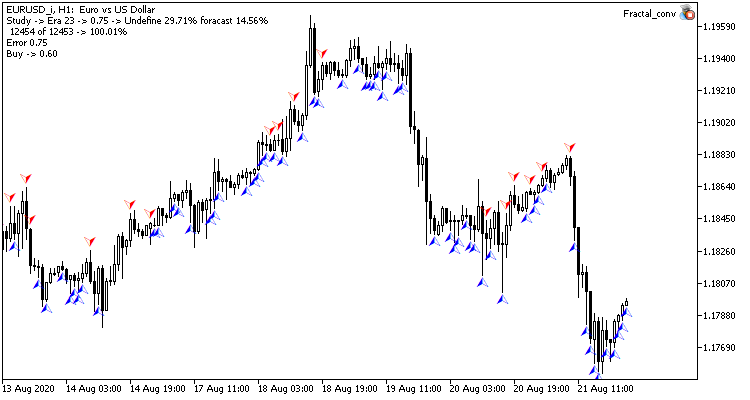
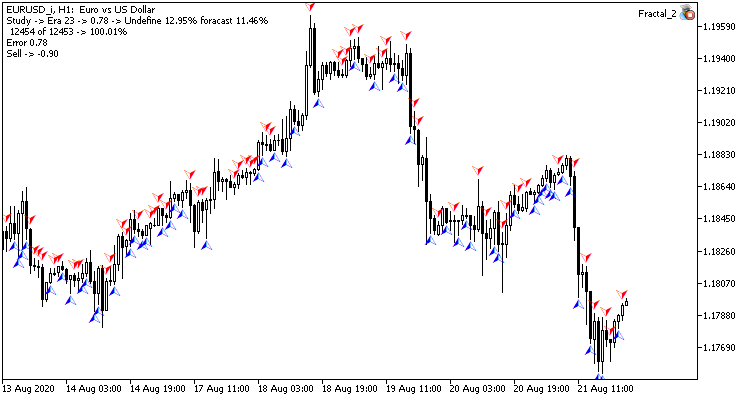
Заключение
В данной статье мы рассмотрели возможность использование сверточных нейронных сетей на финансовых рынках. И тестирование показывает, что их использование позволяет улучшить результаты работы полносвязной нейронной сети. В частности, это может быть связано с предварительной обработкой данных, подаваемых на вход полносвязного перцептрона. В сверточном и подвыборочном слоях осуществляется фильтрация данных от шума, что позволяет повысить качество исходных данных и, как результат, качество работы нейронной сети. А снижение размерности помогает уменьшить количество связей перцептрона с исходными данными, что дает прирост в производительности.
Ссылки
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Fractal.mq5 | Советник | Советник с нейронной сетью регрессии (1 нейрон в выходном слое) |
| 2 | Fractal_2.mq5 | Советник | Советник с нейронной сетью классификации (3 нейрона в выходном слое) |
| 3 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети (перцептрона) |
| 4 | Fractal_conv.mq5 | Советник | Советник со сверточной нейронной сетью классификации (3 нейрона в выходном слое) |
Работа с таймсериями в библиотеке DoEasy (Часть 51): Составные мультипериодные мультисимвольные стандартные индикаторы
Работа с таймсериями в библиотеке DoEasy (Часть 50): Мультипериодные мультисимвольные стандартные индикаторы со смещением
Торговля на форекс и ее базовая математика
Параллельная оптимизация методом роя частиц (Particle Swarm Optimization)
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
там получается не 2 часа, а 2 дня :)
а размер выборки какой? сколько признаков и кол-во сэмплов
Выборка 12453 свечи (H1 за 2 года). На вход сети подается информация за 20 свечей по 12 признаков на свечу. Время обучения одной эпохи 2-2,5 часа.
Hi Dimitriy!
Thanks for this series of articles about Neural Networks! I really enjoy reading these articles (by google translation into English) as I have also implemented Neural Networks with back-propagation and different techniques of optimization (such as Adam, RMSprop, etc.) in MQL5 language. To be honest, the MQL5 language is too slow for training non-toy problems but such implementations are still valuable. Despite the educational aspect of implementing Neural Networks, we notice that we are not limited to MQL5 programming language to train a network. We can use high performance packages to train a network and then transfer the weights (and other hyper-parameters) into our MQL5 programs to test and trade live. Please continue publishing your good work! :)
Best regards, Rasoul
Hi Dimitriy!
Thanks for this series of articles about Neural Networks! I really enjoy reading these articles (by google translation into English) as I have also implemented Neural Networks with back-propagation and different techniques of optimization (such as Adam, RMSprop, etc.) in MQL5 language. To be honest, the MQL5 language is too slow for training non-toy problems but such implementations are still valuable. Despite the educational aspect of implementing Neural Networks, we notice that we are not limited to MQL5 programming language to train a network. We can use high performance packages to train a network and then transfer the weights (and other hyper-parameters) into our MQL5 programs to test and trade live. Please continue publishing your good work! :)
Best regards, Rasoul
Thanks.
Статья безусловно интересная. Особенно, в плане того, что всё реализовано на MQL и не требуется библиотек. Надеюсь, что будет продолжение. К сожалению, тестирование советника, пока не дало положительных результатов.