Нейросети в трейдинге: Обучение метапараметров на основе гетерогенности (HimNet)

Введение

Появление широкого спектра инструментов сбора потоковых данных привело к массовому аккумулированию пространственно–временных рядов в самых разных областях деятельности человека. В торговых системах формируются потоки котировок, заявок и сделок по разным площадкам, тикерам и типам инструментов. По мере роста объёмов данных, точное прогнозирование таких рядов становится инструментом снижения издержек, управления рисками и улучшения исполнения торговых стратегий. Ошибка прогноза локальной ликвидности или волатильности напрямую превращается в проскальзывание, потерянную прибыль и искажение показателей торговой стратегии. Поэтому качественная модель должна видеть не только глобальный тренд, но и локальные, контекстные отличия: где и когда рынок жёсткий, а где — рыхлый.

Ключевая трудность — пространственно-временная неоднородность данных. Пространственная неоднородность на рынке проявляется, когда разные торговые площадки или активы показывают разные паттерны одновременно. Например, одни биржи могут иметь глубокую ликвидность, другие — арбитражные разрывы, особенно в периоды высокой волатильности. В этих условиях попытка усреднить поведение всех площадок приводит к сглаживанию важных локальных эффектов и потере точности.

Временная неоднородность проявляется сильнее, чем кажется на первый взгляд. Поведение одного и того же финансового инструмента в разное время суток и в разные календарные даты меняется кардинально. Открытие и закрытие торговой сессии — два ярких примера: в первые минуты после открытия наблюдается всплеск объёма и волатильности, а поздним вечером, наоборот, — низкая активность. Новости и макроанонсы создают краткосрочные режимы экстремальной волатильности. Праздничные дни и выходные приводят к усыплению активности. В совокупности это значит, что один и тот же шаблон нельзя считать стационарным во времени — его статистика меняется, и модель должна это учитывать.

Ранее предложенные подходы пытались решать проблему разными путями, но каждый из них имеет узкие места с точки зрения применения в торговле. Графовые методы использовали топологию и заранее вычисленные метрики схожести между точками данных — это похоже на трейдера, который строит свою стратегию полностью по карте ликвидности, нарисованной заранее. В реальном мире карта устаревает быстро: меняется состав маркетмейкеров, появляются новые площадки, возникают временные разрывы ликвидности.

Методы метаобучения давали идею хранить несколько наборов параметров для разных режимов, но часто требовали внешней информации. Для финансов это значит, что нужна доступная и корректная метаинформация о каждой площадке и инструменте. Но не всегда её можно получить в реальном времени. Кроме того, многие такие подходы слишком тяжёлые по памяти и по вычислениям.

Подходы на основе представлений (Representation Learning) научились извлекать информативные эмбеддинги из сырых данных. Это мощно, но часто дальше идёт упрощённая обработка эмбеддингов, и ценность хорошего представления теряется на следующем шаге. Self-Supervised обучение добавляет вспомогательные задачи, чтобы эмбеддинги стали богаче — это полезно, но не всегда позволяет оптимально обучать модель целевой задаче прогнозирования в едином цикле.

Именно поэтому авторы работы "Heterogeneity-Informed Meta-Parameter Learning for Spatiotemporal Time Series Forecasting" предложили иной подход — фреймворк HimNet. Их решение сочетает два ключевых компонента. Сначала — неявное выявление неоднородности через обучаемые пространственные и временные эмбеддинги, а затем — использование этой информации для метаобучения параметров модели. Проще говоря, создатели фреймворка не только стремятся определить различия между отдельными участками данных, но и обучают модель подбирать и генерировать уникальные параметры для каждого контекста.

Представьте, что в пуле торговой информации есть:

1. акции крупнейшего эмитента на основной бирже в рабочие часы;
2. те же акции на внебиржевых площадках после локального новостного всплеска;
3. мелкие бумаги с малой ликвидностью;
4. криптовалютные рынки с разной глубиной стаканов.

Пространственные эмбеддинги выделят эти группы в отдельные кластеры. Затем система извлекает из пула метапараметров уникальные наборы параметров для каждого кластера. Для основного рынка — агрессивные параметры с учётом низкого проскальзывания. А для внебиржевых торгов — консервативные параметры, увеличивающие запас прочности исполнения. Малые бумаги получают параметры с более широкой регуляризацией, чтобы не переобучаться на шуме. А крипта — набор, учитывающий высокий уровень шума и частые арбитражные разрывы. Все это обучается в едином цикле, так что модель учится одновременно различать контексты и подбирать для них лучшие параметры.

Временные примеры столь же важны. Утренние часы открытия часто требуют быстрой реакции и краткосрочных прогнозов объёма. Периоды после публикации ключевых макроданных — режим повышенной волатильности. Поздние часы — режим низкой активности. Предложенный авторами фреймворка механизм метапараметров может выделять отдельные наборы параметров для режимов времени. Это похоже на то, как опытный трейдер меняет стиль торговли в зависимости от времени суток и календаря.

Технически, ключевая идея — это кластеризация эмбеддингов и динамическое квантование параметров через небольшой и вычислительно экономный пул метапараметров. Это решает сразу несколько проблем предыдущих подходов. Во-первых, отсутствует жесткая зависимость от внешних вспомогательных признаков — модель сама выявляет релевантные контексты. Во-вторых, пул метапараметров компактный, поэтому затраты памяти и вычислительных ресурсов остаются управляемыми, что важно для систем с низкой латентностью исполнения. В-третьих, авторы фреймворка переходят от пассивного выявления неоднородностей к их активному использованию: кластеры напрямую определяют, какие параметры применяются. Это увеличивает точность прогнозов и улучшает качество исполнения.

Интерпретируемость заслуживает отдельного упоминания. Метапараметры и кластеры можно визуализировать: карта кластеров покажет, какие площадки и какие временные окна принадлежат одному режиму; тепловая диаграмма метапараметров продемонстрирует, как различаются настройки для режимов низкой и высокой волатильности. Для практиков это не только красивый график, но и инструмент контроля: если кластер неожиданно включает в себя разные по сути площадки, это сигнал для дополнительной проверки данных или для пересмотра процедуры предварительной обработки.

Наконец, устойчивость и переносимость. Важное свойство фреймворка HimNet — его гибкость между доменами. Метапараметры и эмбеддинги обучаются так, чтобы быть применимыми и к другим инструментам и площадкам с минимальной донастройкой.

В итоге, фреймворк HimNet предлагает практический и эффективный путь выявления пространственно-временных режимов, формирует компактный пул метапараметров и обучает модель использовать полученную информацию. Это даёт трейдерам и разработчикам систем прогнозирования инструмент, который одновременно улучшает точность, сохраняет вычислительную эффективность и повышает интерпретируемость.

Алгоритм HimNet

Ключевым моментом в моделировании пространственно-временной неоднородности является корректное идентифицирование и разделение контекста исходных данных по времени и пространству. Вместо использования внешних справочных данных, авторы фреймворка HimNet создают обучаемые эмбеддинги, которые назначают каждому пространственно-временному контексту уникальное представление. Это даёт модели гибкость и адаптивность, важные для решения реальных финансовых задач.

Для временного измерения авторы фреймворка создают два словаря эмбедингов:

• словарь времени дняDtod ∈ R^{Nd * dtod};
• словарь дней неделиDdow ∈ R^{Nw * ddow}.

Здесь dtod и ddow — размеры соответствующих векторов, Nd — число шагов внутри торгового дня, Nw — число дней в неделе.

Для мини-батча исходных данных X^b ∈ R^B*T*N с исторической длиной T авторы фреймворка предлагают использовать метку времени последнего шага каждого образца, чтобы выбрать из словарей временные эмбеддинги Etod ∈ R^B*dtod и Edow ∈ R^B*ddow. А затем объединяют их путем конкатенации в общий временной эмбеддинг.

Практический смысл этого разделения прост. Время дня фиксирует периодичность с высокой разрешающей способностью: утренние всплески на открытии, обеденное затишье, вечерняя сессия. День недели захватывает более длинные циклы: поведение в будни и в выходные, а также повторяющиеся шаблоны вокруг отчётных дат и экономических релизов. Вместе эти словари позволяют модели распознавать временные режимы на нескольких шкалах и подбирать под них подходящие параметры прогнозирования.

Для пространственного измерения авторы фреймворка используют матрицу пространственных эмбеддингов Es ∈ R^N*ds, где N — число временных рядов или локаций, а ds — размер вектора для каждой локации. В отличие от временных словарей, здесь каждое пространство напрямую связано со своим обучаемым вектором, инициализируемым случайно. Цель — захватить функциональные различия между площадками, которые влияют на паттерны рядов: глубина стакана, скорость исполнения, профиль участников, тип инструментов и инфраструктурные особенности. Это позволяет учесть пространственную неоднородность без явного использования вспомогательных признаков.

Такое обучение эмбеддингов по сути выполняет динамическую кластеризацию. В процессе обучения представления в матрицах постепенно расходятся и группируются в зависимости от исходных данных. Эмбеддинги, относящиеся к похожим по поведению пространственно-временным контекстам, сближаются в латентном пространстве. А те, что имеют разные динамики — расходятся. В результате формируются естественные кластеры — типичные режимы поведения. Это похоже на языковые модели, где король и королева оказываются близки по смыслу. Только здесь близость отражает сходство рыночных режимов. Важно, что такая кластеризация получается органично, без жёстких внешних ограничений или ручной разметки. Модель сама учится, какие контексты схожи, а какие — нет.

Приведём подробнее финансовые примеры, чтобы конкретнее показать, как это работает на практике. Рассмотрим несколько типичных контекстов:

• Открытие основной фондовой сессии. Высокая активность, большие объёмы, быстрые ценовые колебания. Для таких временных и пространственных сочетаний модель выделит специфический эмбеддинг и подберёт параметры, ориентированные на короткие горизонты и быструю реакцию — это важно для алгоритмов быстрого исполнения и сокращения проскальзывания.
• Внебиржевые торги по тем же бумагам в ночной период. Низкие объёмы, редкие сделки, повышенный риск резких скачков при единичных ордерах. Здесь временные эмбеддинги будут отличаться, и метапараметры обяжут модель быть консервативнее, повышая устойчивость и снижая вероятность переобучения на шум.
• Криптовалютные биржи с разной глубиной стакана. Одна биржа — глубокая ликвидность, другая — тонкая и арбитражная. Пространственные эмбеддинги разделят эти площадки, и модель применит разные стратегии прогнозирования объёмов и цены, что полезно для арбитражных систем.
• Дни крупных макрорелизов или квартальных отчётов. Временные эмибеддиги дня недели совместно с временем дня выделят такие окна; модель переключится на режим с увеличенной чувствительностью к краткосрочным сигналам и более широкими доверительными интервалами.

Ключевая идея простая и вместе с тем рабочая. Наша задача не только фиксировать неоднородность, но и научиться ею управлять. Делать её практически полезной для прогнозов и исполнения на рынках. Вместо того, чтобы пытаться держать отдельный набор параметров для каждой минуты и для каждой биржи, что экономически и технически неприемлемо, авторы фреймворка расширяют пространство параметров модели вдоль временного и пространственного измерений, а затем компактно представляют это расширение в виде небольших пулов метапараметров. Для конкретного пространственно-временного Запроса итоговые параметры генерируются как взвешенная комбинация кандидатов пула: Θ = Q · P. Такая схема позволяет вместо оптимизации огромного множества уникальных параметров работать в рамках компактного набора, что резко снижает требования по памяти и вычислениям. Вместо роста по масштабу всех временных шагов и локаций, мы платим за адаптацию лишь небольшим числом кандидатов.

На практике это означает, что мы держим отдельно небольшой временной пул, из которого извлекаем временной эмбеддинг Et, и получаем временные метапараметры. Аналогично пространственный эмбеддинг Es обращается к пространственному пулу и даёт метапараметры для каждой унитарной последовательности. При этом нельзя забывать и про смешанные пространственно-временные сигнатуры: напрямую строить полный совместный пул было бы неэффективно, поэтому авторы фреймворка кодируют исходные данные Xt в пространственно-временной эмбеддинг Est = Fenc(Xt) и используют его в качестве запроса к относительно небольшому пулу для генерации ST-метапараметров. Благодаря такому разделению, модель получает гибкость — она умеет подбирать параметры под конкретное время, под конкретную площадку и под конкретную одновременную комбинацию событий, не теряя при этом управляемости и скорости работы.

Эта схема даёт и практические преимущества для бизнеса. Малый размер пулов делает генерацию метапараметров дешёвой по времени отклика, что критично в задачах с жёсткими требованиями по латентности. Совместное обучение пулов и основной модели позволяет градиентам проходить через Запросы к пулам, так что эмбеддинги и параметры оптимизируются согласованно. При этом необходимо следить за стабильностью обучения, контролировать распределение весов-запросов через ограничение энтропии или температурное сглаживание, чтобы один кандидат не захватил весь трафик и не привёл к переусложнённой, плохо обобщающейся модели.

Выбор размера пула — компромисс между выраженной адаптивностью и риском переобучения; на практике его подбирают по валидации, ориентируясь на число типичных режимов, наблюдаемых в целевых рынках.

Архитектура фреймворка HimNet опирается на сочетание графовых свёрток и рекуррентных правил: такие блоки умеют одновременно слушать историю исходных данных и учитывать связи между отдельными унитарными последовательностями. Представьте трейдера, который одновременно смотрит ленту сделок и карту взаимосвязей между рынками — и принимает решение, опираясь на обе картины. Именно такую роль играет базовая ячейка модели. Она агрегирует соседние сигналы по графу и обновляет скрытое состояние с учётом времени.

С точки зрения технической реализации, базовый блок — это модифицированная Graph Convolutional Recurrent Unit (GCRU). Внутри — привычные reset и update врата, состояние кандидатов, смешивание старого и нового скрытого представления. Но есть одна важная деталь — параметры графовой свёртки здесь не фиксированы. Они генерируются динамически с помощью метамеханизмов. Это означает, что весовые шаблоны агрегации соседей (как одна последовательность влияет на другую) меняются в зависимости от контекста. Для финансового рынка это критично — взаимосвязи эластичны. В периоде массовых реакций крупной биржи они близки. В другом временном интервале, когда одна площадка временно уходит из торговли, они распадаются.

Модель строится по классической схеме Энкодер-Декодер. Энкодер в фреймворке HimNet работает в двух параллельных потоках, которые затем складываются. Один поток адаптируется по времени. Он получает временные эмбеддинги и на их основе формирует временные метапараметры. Другой поток адаптируется по пространству, используя пространственные эмбеддинги последовательностей, выдаёт метапараметры для каждой точки. Такой двухканальный подход позволяет модели одновременно учитывать, что происходит сейчас и где это происходит. Но авторы фреймворка не останавливаются на этом. Чтобы учесть совместные пространственно-временные эффекты, Декодер получает латентное состояние и проецирует его в пространственно-временной эмбеддинг. Который служит запросом к пулу ST-метапараметров. Результатом становится набор рекуррентных весов, специфичных для текущей комбинации времени, места и динамики.

Адаптивная матрица смежности — ещё одна важная часть. Вместо того, чтобы держать статичную матрицу связей, модель генерирует её из пространственных эмбеддингов: скалярные произведения эмбеддингов проходят через ReLU и SoftMax. В результате получается матрица, отражающая текущие рыночные взаимосвязи. Практическим эффектом этого является то, что когда на одной бирже начинается всплеск, модель автоматически усиливает влияние этой биржи на соседние узлы. Когда ликвидность уходит с какой-то площадки, её влияние ослабляется. Это делает поведение модели чувствительным к реальному состоянию рынка, а не к статичной карте, которая быстро устаревает.

Декодер в HimNet итеративно генерирует прогнозы для следующих шагов. Он берёт начальное скрытое состояние, применяет GCRU-ячейку с ST-метапараметрами и выдаёт прогноз для каждого будущего шага. Такой подход позволяет не просто выдавать усреднённый прогноз для всех последовательностей — он формирует прогнозы, учитывающие локальные режимы и временные окна.

Обучение организовано end-to-end. Авторы фреймворка используют простую, но понятную метрику — MAE по всем шагам и площадкам. Это удобно: потеря измеряется в тех же единицах, что и прогнозируемая величина, и легче интерпретируется бизнесом. При обучении важно контролировать стабильность: полезно вводить L2-регуляризацию для пулов метапараметров, температурное сглаживание при генерации весов и ограничение скорости обновления. Размер пулов выбирают балансом:

• слишком мал — модель не охватит все режимы;
• слишком велик — появится риск излишней специализации и рост вычислительной нагрузки.

С точки зрения практического применения HimNet приносит осязаемую пользу. Точная локальная оценка ликвидности уменьшает проскальзывание при исполнении крупных блоков. Арбитражным системам HimNet даёт контекст для фильтрации ложных разрывов и выявления устойчивых расхождений между биржами.

Наконец, инженерные детали делают систему пригодной для промышленного развертывания. Генерация метапараметров — это умножения маленьких матриц, что не создаёт взрывного роста потребления памяти. Пулы компактны и позволяют держать низкую латентность, необходимую для задач с жёсткими временными требованиями. Все это упрощает интеграцию HimNet в пайплайн исполнения ордеров и в систему риск-контроля.

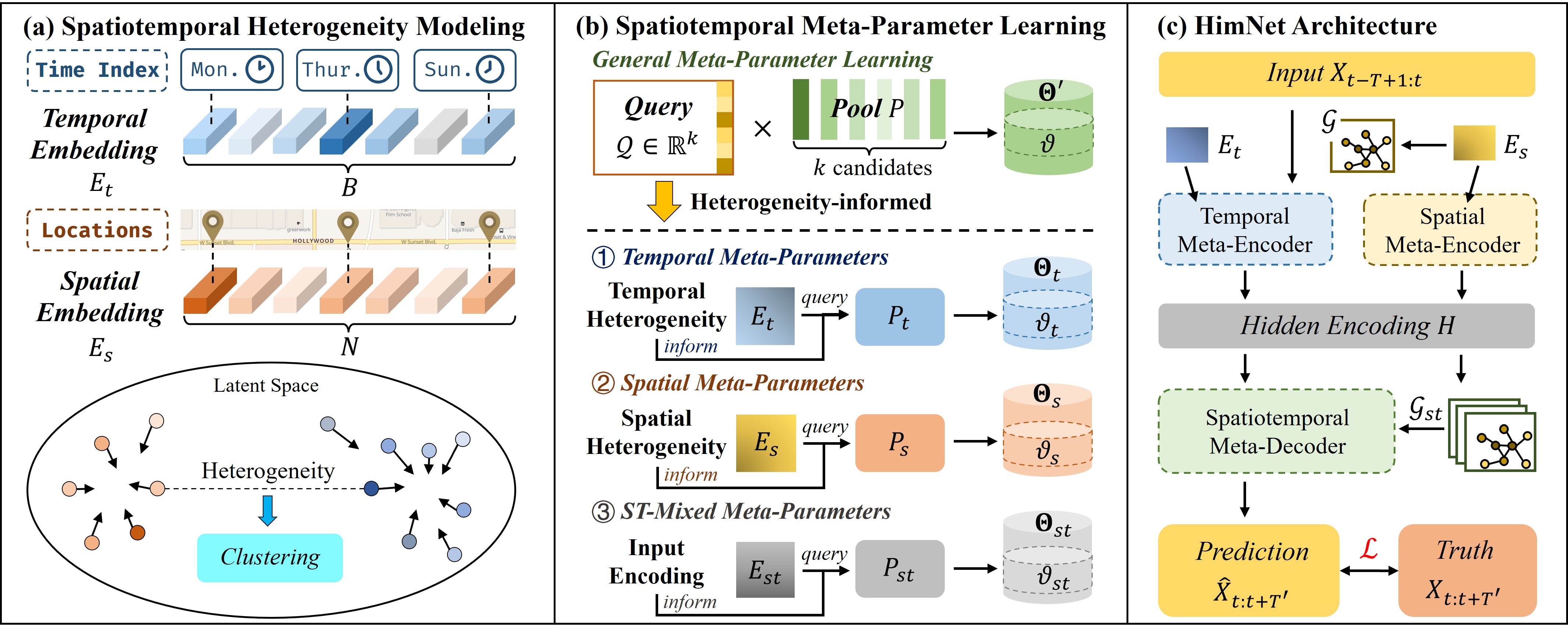
Авторская визуализация фреймворка HimNet представлена ниже.

Реализация средствами MQL5

После детального разбора теоретических основ фреймворка HimNet, логичный шаг — показать, как эти идеи воплотить в рабочем коде MQL5. Практическая реализация — это не сухая транспозиция формул, а перевод архитектуры в ограничения и возможности реальной торговой платформы. Мы поступим системно и аккуратно: разобьём большую архитектуру на независимые, хорошо описанные объекты и будем собирать модель шаг за шагом, как мастер собирает хронометр — детально, предсказуемо и с уважением к каждой шестерёнке. Такой подход облегчает тестирование, ускоряет отладку и позволяет безболезненно масштабировать решение под разные рынки и таймфреймы.

На уровне инфраструктуры MQL5 это означает, что блоки предварительной обработки, эмбедингов, метапараметров и рекуррентных ячеек живут как отдельные компоненты. Потоки свечей и показателей анализируемых индикаторов превращаются в аккуратные окна данных фиксированной длины. Эмбеддинги времени и унитарных последовательностей подают в модули генерации весов. GCRU-ячейка получает на вход графовую структуру рынка и возвращает обновлённое скрытое состояние. Всё звучит стройно, но есть один узел, без которого HimNet теряет остроту — это способ быстро и стабильно слушать соседей по графу на расстоянии нескольких рёбер. В финансовых терминах — ловить не только прямые влияния между последовательностями, но также эффект второго и третьего порядка, когда всплеск ликвидности на одном узле прокатывается по сети и доходит до анализируемого инструмента с задержкой и затуханием.

Именно здесь на сцену выходит полином Чебышева. Он позволяет построить локальный K-hop фильтр поверх графа без тяжёлой спектральной декомпозиции. Вместо вычисления собственных векторов авторы фреймворка используют простую рекурсию, которая по матрице связей генерирует базис из матриц T0, T1, …, TK-1. Каждая такая матрица отвечает за слой соседства: от самого узла до K-ой окрестности. В результате одна операция свёртки превращается в аккуратную линейную комбинацию нескольких заранее подготовленных преобразований. Для торговли это критично: меньше задержек, меньше удар по памяти, стабильная численная работа на длинных сериях и при больших N. Когда рынок шумит, такой фильтр помогает выделить устойчивые связи и не реагировать на случайные всплески.

Чтобы эта идея заработала в продакшене, нам нужен отдельный объект, который по текущей матрице смежности быстро строит матрицы полинома Чебышева нужного порядка. Он станет тихим мотором всего графового слоя: получает на вход адаптивный support, построенный из эмбеддингов, и возвращает компактный набор Tk, готовый к применению в GCRU.

Первый шаг нашей практической работы — внесение изменений в OpenCL-программу. GPU для этой задачи подходит как нельзя лучше: многопоточность и векторные операции позволяют обрабатывать большие матрицы смежности значительно быстрее, чем на CPU. Это особенно критично для финансовых данных, где размер графа может быть достаточно большим с разветвленными связями.

Алгоритм кернела прямого прохода ChebStep — это своего рода сердце механизма генерации полиномов Чебышева, работающего прямо в недрах OpenCL. И он очень похож на слаженную работу биржевого движка, где каждый тик и каждый ордер вплетены в единую логику.

__kernel void ChebStep(__global const float* support,
                       __global float* outputs,
                       const int step
                      )
  {
   const size_t l = get_local_id(0);
   const size_t r = get_global_id(1);
   const size_t c = get_global_id(2);
   const size_t total_l = get_local_size(0);
   const size_t total_r = get_global_size(1);
   const size_t total_c = get_global_size(2);

Программа начинается с получения координат в пространстве задач. Локальные и глобальные идентификаторы потоков — это наши биржевые трейдеры, каждый из которых отвечает за отдельную часть матрицы. Они работают параллельно, чтобы весь массив данных был обработан не последовательно, как в старых ручных торгах, а синхронно, словно в автоматизированной системе высокочастотного трейдинга. Локальный буфер Temp играет роль временного клирингового центра — сюда складываются промежуточные суммы, которые потом синхронизируются и образуют окончательный результат.

   __local float Temp[LOCAL_ARRAY_SIZE];
//---
   if(step <= 0 || total_r != total_c)
      return;

Алгоритм сразу же накладывает важное ограничение: если шаг меньше или равен нулю, либо если матрица не квадратная, смысла продолжать вычисления нет. Это тот самый случай, когда трейдер отказывается от сделки, если условия рынка не соответствуют правилам стратегии.

Дальше начинается последовательная иерархия построения степеней полиномов Чебышева. На первом шаге всё просто: формируется единичная матрица, где диагональ заполняется единицами. Это словно стартовый капитал — база, с которой всё начинается.

if(step <= 3)
  {
   const float diag = (r == c ? 1.0f : 0.0f);
   if(l == 0)
      outputs[RCtoFlat(r, c, total_r, total_c, 0)] = diag;

На втором шаге в игру вступает исходная матрица смежности, та самая карта связей между вершинами графа, отражающая реальную структуру рынка. Она добавляется в выходной массив, и уже здесь начинается приближение к реальному движению котировок.

if(step < 2)
   return;
if(l == 0)
  {
   const float s = IsNaNOrInf(support[RCtoFlat(r, c, total_r, total_c, 0)], 0);
   outputs[RCtoFlat(r, c, total_r, total_c, 1)] = s;
  }

На третьем шаге формируется вторая степень — матричный квадрат. Код в цикле перемножает строки и столбцы, аккуратно суммируя произведения. Это похоже на анализ кросс-корреляций между активами, когда мы ищем не только прямую зависимость, но и косвенные связи через третьи звенья.

Получившаяся матрица отражает более сложные взаимодействия, где влияние не ограничивается прямыми связями, а распространяется по соседям. После суммирования применяется нормировка и корректировка, чтобы убрать избыточность, словно трейдер фильтрует шум из котировок и оставляет только значимые сигналы.

 if(step < 3)
    return;
 float out = 0;
 for(int t = 0; t < total_c; t += total_l)
   {
    const float s1 = IsNaNOrInf(support[RCtoFlat(r, t + l, total_r, total_c, 0)], 0);
    const float s2 = IsNaNOrInf(support[RCtoFlat(t + l, c, total_r, total_c, 0)], 0);
    out += IsNaNOrInf(s1 * s2, 0);
   }
 out = 2 * LocalSum(out, 0, Temp);
 if(l == 0)
   {
    out -= diag;
    outputs[RCtoFlat(r, c, total_r, total_c, 2)] = IsNaNOrInf(out, 0);
   }
 return;
}

Если шаг больше трёх, алгоритм выходит на уровень общей рекуррентной формулы полиномов Чебышева. Здесь каждая новая матрица строится не с нуля, а из комбинации предыдущих степеней. Код берёт матрицу смежности, умножает её на результат предыдущего шага и корректирует, вычитая ещё более раннюю матрицу. Этот процесс напоминает построение сложных торговых индикаторов: например, экспоненциальные скользящие средние учитывают предыдущее состояние, сглаживая резкие колебания, но при этом не забывают историю.

   float out = 0;
   for(int t = 0; t < total_c; t += total_l)
     {
      if((t + l) >= total_c)
         continue;
      const float s1 = IsNaNOrInf(support[RCtoFlat(r, t + l, total_r, total_c, 0)], 0);
      const float s2 = IsNaNOrInf(outputs[RCtoFlat(t + l, c, total_r, total_c, step - 2)], 0);
      out += IsNaNOrInf(s1 * s2, 0);
     }
   out = 2 * LocalSum(out, 0, Temp);
   if(l == 0)
     {
      out -= IsNaNOrInf(outputs[RCtoFlat(r, c, total_r, total_c, step - 3)], 0);
      outputs[RCtoFlat(r, c, total_r, total_c, step - 1)] = IsNaNOrInf(out, 0);
     }
   return;
  }

Таким образом, модель шаг за шагом выстраивает всё более глубокие приближения спектральных свойств графа. 

Каждая итерация в кернеле завершается синхронизацией данных и проверкой на корректность. В коде активно используется функция защиты от NaN и бесконечностей — это напоминание о том, что рынок не прощает ошибок. Подобно тому, как риск-менеджмент контролирует границы убытков, здесь любая аномалия отсекается на раннем этапе, чтобы не исказить общий результат.

В результате такой пошаговой логики мы получаем целую лестницу полиномов Чебышева, которые становятся строительным материалом для спектральных фильтров в графовых нейросетях. На практике это значит, что алгоритм не просто смотрит на рынок через призму текущих связей, а строит многослойную оптику, позволяющую уловить как локальные, так и дальние зависимости между инструментами. Это сродни тому, как опытный аналитик способен увидеть в движении золота косвенный сигнал для валютного рынка, или в динамике облигаций — предвестник изменений в акциях.

После того, как мы разобрались с алгоритмом прямого построения полиномов Чебышева и увидели, как шаг за шагом строится их вычислительная структура, естественно перейти к механизму обратного распространения ошибки. Здесь в игру вступает специальный кернел, который отвечает за аккуратное распределение градиентов по полиномам Чебышева и до матрицы смежности, обеспечивая корректное обучение всей модели.

__kernel void ChebStepGrad(__global const float* support,
                           __global float* support_g,
                           __global const float* outputs,
                           __global float* outputs_g,
                           const int step
                          )
  {
   const size_t l = get_local_id(0);
   const size_t r = get_global_id(1);
   const size_t c = get_global_id(2);
   const size_t total_l = get_local_size(0);
   const size_t total_r = get_global_size(1);
   const size_t total_c = get_global_size(2);
//---
   __local float Temp[LOCAL_ARRAY_SIZE];
//---
   if(step < 1 || total_r!=total_c)
      return;

В начале работы алгоритм также инициализирует локальные и глобальные идентификаторы, которые, словно биржевые котировки, определяют положение каждой вычислительной единицы в огромной сетке параллельных потоков. Локальная память выделяется под временный массив, чтобы ускорить редукции, а первые проверки гарантируют, что шаг корректен, и матрица имеет квадратную форму. Подобно тому, как трейдер никогда не станет анализировать неполный стакан заявок, здесь программа сразу прекращает работу при некорректных условиях.

Когда шаг получения градиентов ошибки больше или равен 2, начинается самое интересное. Сначала берётся градиент последующего шага и напрямую вычитается из предыдущего уровня выходов. Этот момент можно сравнить с коррекцией прогноза: если на последнем такте стратегия дала ошибку, её тень откладывается на предыдущем.

if(step >= 2)
  {
   float grad = IsNaNOrInf(outputs_g[RCtoFlat(r, c, total_r, total_c, step)], 0);
   if(l == 0)
      outputs_g[RCtoFlat(r, c, total_r, total_c, step - 2)] -= grad;

Далее алгоритм вычисляет градиенты по матрице смежности. Каждый поток берёт свой кусок данных и умножает ошибку из выходов на соответствующие значения предыдущего шага, аккуратно суммируя всё это через локальную память. В итоге формируется корректирующий сигнал, который напоминает донастройку весов в портфеле — когда одни активы перегружены, их влияние постепенно перераспределяется.

//--- support grad
grad = 0;
for(int t = 0; t < total_c; t += total_l)
  {
   if((t + l) >= total_c)
      continue;
   const float s2 = IsNaNOrInf(outputs[RCtoFlat(c, t + l, total_r, total_c, step - 2)], 0);
   grad += IsNaNOrInf(outputs_g[RCtoFlat(r, t + l, total_r, total_c, step)] * s2, 0);
  }
grad = LocalSum(grad, 0, Temp);
if(l == 0)
   outputs_g[RCtoFlat(r, c, total_r, total_c, 1)] += grad;
BarrierLoc;

После синхронизации потоков наступает момент для следующей части — вычисления градиента по полиному Tk-1. Здесь всё работает по аналогии: каждый поток берёт часть матрицы смежности, умножает её на ошибки следующего шага и аккуратно добавляет вклад в общую сумму. В результате формируется поправка для градиентов полиномов на уровне k-1. Этот процесс похож на то, как аналитик возвращается на шаг назад в своей модели и проверяет, не было ли там переоценки риска, добавляя соответствующую корректировку.

 //--- T(k-1) grad
 grad = 0;
 for(int t = 0; t < total_c; t += total_l)
   {
    if((t + l) >= total_c)
       continue;
    const float s2 = IsNaNOrInf(support[RCtoFlat(t + l, r, total_r, total_c, 0)], 0);
    grad += IsNaNOrInf(outputs_g[RCtoFlat(t + l, c, total_r, total_c, step)] * s2, 0);
   }
 grad = LocalSum(grad, 0, Temp);
 if(l == 0)
    outputs_g[RCtoFlat(r, c, total_r, total_c, step - 1)] += grad;
}

Обратите внимание: все градиенты ошибки мы аккуратно собираем в тензор, соответствующий полиномам Чебышева. Туда же попадают и промежуточные градиенты матрицы смежности, которые вычисляются на каждом шаге обратного прохода. Важно помнить, что сама матрица смежности хранится внутри полинома первого порядка, а значит, именно этот уровень становится ключевой точкой пересечения потоков данных. И только дойдя до него, мы переносим накопленный градиент ошибки в буфер матрицы смежности, словно фиксируя итоговый баланс после серии промежуточных корректировок.

Таким образом, этот кернел берёт на себя роль своеобразного «ревизора» вычислений, который не даёт ошибке потеряться или размыться по пути назад. Каждое значение проходит через систему локальных сумм, корректируется и направляется туда, где оно способно изменить веса в пользу более точного прогноза. И как на рынке, где каждая лишняя десятая доля процента может сыграть ключевую роль, так и здесь аккуратное распределение градиента по шагам позволяет модели устойчиво обучаться и не сбиваться с курса.

Теперь, когда фундамент (генерация матриц и распределение градиентов) у нас готов, возникает естественный вопрос: кто же будет управлять всем этим процессом на стороне основной программы? Нужен объект, который возьмёт на себя роль своеобразного диспетчера, аккуратно оборачивая низкоуровневые OpenCL-кернелы и предоставляя удобный интерфейс для взаимодействия с другими модулями модели. Так появляется класс CChebPolinom, наследующий базовые интерфейсы от объекта полносвязного слоя CNeuronBaseOCL.

class CChebPolinom   :  public CNeuronBaseOCL
  {
protected:
   uint              iDimension;
   uint              iSteps;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return true; }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CChebPolinom(void)   {};
                    ~CChebPolinom(void)   {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint dimension,
                          uint steps, ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual bool      Save(const int file_handle) override;
   virtual bool      Load(const int file_handle) override;
   //---
   virtual int       Type(void) override const  {  return defChebPolinom; }
   virtual uint      GetDimension(void) const { return iDimension; }
   virtual uint      GetSteps(void) const { return iSteps; }
  };

Внутри он хранит ключевые параметры — размерность пространства и число шагов, необходимых для разложения по полиномам Чебышева. Эти параметры определяют границы вычислений и глубину, которую модель может достичь в работе с графовой структурой.

Инициализация объекта осуществляется в методе Init, который позволяет задать все необходимые параметры.

bool CChebPolinom::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint dimension,
                        uint steps, ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, dimension * dimension * steps,
                                                              optimization_type, batch))
      return false;
//---
   iDimension = dimension;
   iSteps = steps;
//---
   return true;
  }

Алгоритм метода довольно прост. Вначале мы передаем управления одноименному методу родительского класса, указав размерность объекта достаточную для сохранения конкатенированного тензора всех необходимых полиномов Чебышева. А затем объект сохраняет внутри себя два основных параметра: размерность iDimension и число шагов iSteps. Эти значения становятся своеобразной паспортной частью класса, на которую будут ориентироваться все остальные методы. Можно сказать, что здесь мы окончательно формируем рабочее пространство: задаём как ширину полотна, так и количество слоёв, через которые будет проходить информация.

Возврат true в конце метода подтверждает успешную подготовку объекта к работе. И хотя реализация выглядит лаконичной, именно на этом этапе решается принципиальный вопрос: сможет ли наш алгоритм эффективно развернуть полиномиальное приближение на GPU.

Метод прямого прохода feedForward по своей сути играет роль диспетчера, который лишь оборачивает и организует вызов соответствующего кернела OpenCL-программы. Его структура предельно узнаваема: проверка исходных данных, подготовка параметров работы и последовательный вызов ядра. Однако специфика задачи — генерация и применение полиномов Чебышева — вносит сюда свою изюминку.

bool CChebPolinom::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL || NeuronOCL.Neurons() != (iDimension * iDimension))
      return false;

Сначала метод убеждается, что на вход подан корректный объект, и что число нейронов совпадает с размером матрицы смежности iDimension * iDimension. Если это условие не выполняется, дальнейшая работа попросту теряет смысл.

Далее идёт подготовка рабочих диапазонов: глобальные размеры сетки вычислений определяются так, чтобы учесть реальное ограничение GPU по размеру локальной группы, а также отразить матричную структуру задачи — три измерения по сути раскладывают сетку вычислений по осям матрицы.

   uint global_work_offset[3] = { 0 };
   uint global_work_size[3] = { MathMin(iDimension, uint(OpenCL.GetMaxLocalSize(0))),
                                iDimension, iDimension
                              };
   uint local_work_size[3] = { global_work_size[0], 1, 1 };

Ключевым элементом здесь становится цикл по шагам. Именно он отражает рекурсивную природу построения полиномов Чебышева: чтобы получить значение полинома на k-ом уровне, необходимо опереться на предыдущие значения. Начиная с минимального корректного шага (обычно второго, поскольку первые два задаются базовыми условиями), метод последовательно передаёт в кернел номер шага, а затем запускает выполнение. Таким образом, на каждом витке GPU получает новую задачу — построить очередной уровень полиномиального приближения.

//---
   uint kernel = def_k_ChebStep;
   setBuffer(kernel, def_k_cheb_support, NeuronOCL.getOutputIndex())
   setBuffer(kernel, def_k_cheb_outputs, getOutputIndex())
   for(int step =::MathMin(2, MathMax(int(iSteps) - 1, 0)); step < int(iSteps); step++)
     {
      setArgument(kernel, def_k_cheb_step, step + 1)
      kernelExecuteLoc(kernel, global_work_offset, global_work_size, local_work_size)
     }
//---
   return true;
  }

Получается своеобразная матрёшка вычислений: каждый шаг зависит от предыдущего, но при этом вся работа распараллелена по элементам матрицы. На финансовых рынках подобный подход напоминает стратегию построения прогнозов на основе скользящих горизонтов: каждый новый прогноз формируется не с нуля, а как продолжение предыдущего, уточняя и углубляя картину.

Именно в этом скрыта сила данного метода — лаконичный по форме, он соединяет простоту диспетчерской логики с глубокой математической рекурсией.

Метод, отвечающий за распределение градиентов ошибки, построен по схожему принципу. Как и в случае с прямым проходом, здесь основная задача метода — корректно организовать вызовы соответствующего кернела OpenCL-программы, при этом учитывать рекурсивную структуру вычислений полиномов Чебышева. Все накопленные градиенты аккуратно суммируются и распределяются по соответствующим шагам, с особым вниманием к матрице смежности и промежуточным полиномам.

Подробный разбор строк этого метода можно провести самостоятельно. Полный исходный код класса, включая все его методы, представлен во вложении, что позволяет составить целостное представление о работе этой части фреймворка.

Объём материала уже внушителен, и сейчас самое время сделать небольшую паузу, чтобы систематизировать и упорядочить всю полученную информацию. Подробное разложение по полочкам позволит лучше усвоить принципы работы и взаимосвязи компонентов. Продолжение построения алгоритмов фреймворка HimNet, включая практическую интеграцию всех модулей, мы рассмотрим в следующей статье.

Заключение

В этой статье мы познакомились с теоретическими аспектами фреймворка HimNet и перешли к практической реализации предложенных подходов средствами MQL5 и OpenCL. Мы подробно разобрали концепцию пространственно-временных метапараметров. Посмотрели, как графовые свёрточные рекуррентные блоки способны учитывать временные и пространственные зависимости, а также рассмотрели алгоритмы генерации и применения полиномов Чебышева на GPU для ускорения вычислений и повышения устойчивости модели.

В следующей статье мы продолжим работу по построению алгоритмов фреймворка HimNet.

Ссылки

• Heterogeneity-Informed Meta-Parameter Learning for Spatiotemporal Time Series Forecasting
• Другие статьи серии

Программы, используемые в статье

#	Имя	Тип	Описание
1	Study.mq5	Советник	Советник офлайн обучения моделей
2	StudyOnline.mq5	Советник	Советник онлайн обучения моделей
3	Test.mq5	Советник	Советник для тестирования модели
4	Trajectory.mqh	Библиотека класса	Структура описания состояния системы и архитектуры моделей
5	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
6	NeuroNet.cl	Библиотека	Библиотека кода OpenCL-программы