Градиентный бустинг в задачах трансдуктивного и активного машинного обучения

Введение

Полуконтролируемое (semi-supervised), или трансдуктивное обучение, использует неразмеченные данные для того, чтобы модель могла лучше и проще понять общую структуру данных. Это согласуется с нашим мышлением. Человеческий мозг, запоминая всего несколько образов, способен экстраполировать знания об этих образах на новые объекты в общих чертах, не концентрируясь на незначительных деталях. Это приводит к меньшей подгонке и хорошей обобщающей способности. 

Термин трансдукции был введен Владимиром Наумовичем Вапником, изобретателем машины опорных векторов или SVM (support vector machine). По его мнению, метод трансдукции более предпочтителен, чем метод индукции, так как индукция требует решения более общей задачи (восстановления функции) перед решением более конкретной задачи (вычисления результатов на новых данных). 

 «…при решении интересующей задачи не решайте более общую задачу в качестве промежуточного шага. Постарайтесь получить ответ, который вам действительно нужен, но не более общий» 

Данное предположение Владимира Наумовича согласуется с аналогичным наблюдением, сделанным ранее Бертраном Расселом:

«…мы придем к выводу, что Сократ смертен с большим подходом к определённости, если мы сделаем наш аргумент чисто индуктивным, чем если бы мы пошли путем „все люди смертны“ , а затем используем дедукцию»

Ожидается, что обучение без учителя (на неразмеченных данных) станет гораздо более важным в долгосрочной перспективе. Обучение людей и животных, в основном, происходит без учителя: они открывают структуру мира наблюдая за ней, а не узнавая название каждого объекта. 

Таким образом, полуконтролируемое обучение сочетает в себе обучение с учителем и без учителя.  Обучение с учителем происходит на небольшом объеме размеченных данных, после чего модель экстраполирует свои знания на большую неразмеченную область. 

Использование немаркированных данных подразумевает некоторую связь с лежащим в основе распределением данных. Должно выполняться хотя бы одно из следующих предположений:

• Предположение плавности. Точки, расположенные близко друг к другу, с большей вероятностью будут иметь одну и ту же метку. Это также предполагается при обучении с учителем и дает предпочтение геометрически простым границам, разделяющим классы. В случае полуконтролируемого обучения предположение о плавности дополнительно дает преимущество в областях с низкой плотностью точек, где несколько точек находятся рядом друг с другом, но в разных классах.
• Кластерное предположение. Данные, как правило, образуют дискретные кластеры, и точки в одном кластере с большей вероятностью имеют общую метку (хотя данные, которые имеют общую метку, могут распространяться по нескольким кластерам). Это частный случай предположения плавности, который приводит к обучению с помощью алгоритмов кластеризации.
  
• Предположение избыточности данных. Данные лежат приблизительно на коллекторе гораздо меньшей размерности, чем пространство исходной разметки. В этом случае изучение многообразия с использованием как помеченных, так и немаркированных данных может избежать проклятия размерности. Затем обучение может продолжаться с использованием расстояний и плотностей, определенных на многообразии.
  

Более подробно про полуконтролируемое en. обучение.

Основным методом полуконтролируемого обучения является псевдоразметка, которая осуществляется следующим образом:

• Используется некоторая мера близости (например, эвклидово расстояние) для того, чтобы разметить оставшуюся часть данных на основе размеченной (псевдо-метки).
• Объединяются тренировочные метки с псевдометками, а также признаки.
• Модель обучается на всем наборе данных.

Исследователями было обнаружено, что использование маркированных данных совместно с немаркированными, может значительно повысить точность модели. Я уже использовал подобную идею в предыдущей статье путем оценки плотности вероятности распределения размеченных данных и семплинга из этого распределения. Но распределение новых данных может отличаться, поэтому полуконтролируемое обучение может дать некоторые преимущества, что и покажет эксперимент в данной статье.

Активное обучение (active learning) является неким логическим продолжением полуконтролируемого обучения. Это итеративный процесс разметки новых данных таким способом, чтобы границы, разделяющие классы, были расположены оптимально.

Основная гипотеза активного обучения состоит в том, что алгоритм обучения может сам выбирать данные, на которых он хочет учиться. Он может работать лучше традиционных методов при значительно меньшем количестве данных для обучения. Под традиционными методами здесь подразумевается обычное обучение с учителем на размеченных данных (supervised learning). Такое обучение можно, условно, назвать пассивным. Модель просто обучается на размеченных данных, и чем их больше, тем лучше. Одна из наиболее трудоемких задач пассивного обучения — это сбор и маркировка данных. Во многих случаях могут существовать ограничения, связанные со сбором дополнительных данных или, как в нашем случае, с их адекватной разметкой. 

В активном обучении существует три наиболее популярных сценария, в которых учащийся (обучающаяся модель) будет запрашивать новые метки экземпляров классов из неразмеченной области:

• Запрос искусственно синтезированного примера.  В данном случае модель генерирует экземпляр из некоторого распределения, которое является общим для всех примеров. Например, это может быть экземпляр класса с добавленным к нему шумом, либо просто правдоподобная точка рассматриваемого пространства. И эта новая точка отправляется оракулу для тренировки. Оракул — это условное название функции-оценщика, которая оценивает ценность данного экземпляра-признака для модели.
• Выборочное семплирование на основе потока. Данный подход подразумевает перебор точек из немаркированной выборки, после чего Оракул выбирает, хочет ли он запросить метку класса для данной точки или же отклонить ее на основе некоторого информационного критерия. 
• Семплирование на основе пула. Данный сценарий предполагает наличие большого пула немаркированных примеров, как и в предыдущем случае. Экземпляры выбираются из пула на основе некоторой меры информативности. Эта мера применяется ко всем экземплярам пула, а затем выбираются самые информативные экземпляры. Это наиболее распространенный сценарий среди адептов активного обучения. Все неразмеченные примеры будут ранжированы, а затем выбраны наиболее информативные.

Каждый сценарий может основываться на определенной стратегии запроса. Как уже было отмечено выше, основное отличие активного от пассивного обучения заключается в возможности запрашивать экземпляры из неразмеченной области на основе прошлых запросов и ответов модели. Соответственно, все запросы требуют некоторой меры информативности. 

Давайте перечислим наиболее популярные стратегии запросов:

• Наименьшая достоверность (или неопределенность классификации). В данной стратегии выбирается пример, относительно которого модель наименее уверена. Например, вероятность отнесения метки к определенному классу ниже какой-то границы.
• Маржинальное семплирование.  Недостатком первого подхода является то, что он определяет вероятность принадлежности только к одной метке, тогда как вероятности принадлежности к другим не учитываются. Маржинальный подход выбирает наименьшую разницу вероятностей между двумя наиболее вероятными метками.
• Семплирование на основе энтропии. Формула энтропии применяется к каждому экземпляру, и запрашивается экземпляр с наибольшим значением.

Как и в случае полуконтролируемого обучения, процесс активного обучения имеет несколько шагов:

• Обучается модель на размеченных данных.
  
• Используется эта же модель для маркировки неразмеченных данных, чтобы предсказать вероятности (псевдо-метки).
• Выбирается стратегия запроса новых примеров.
• Выбираются n-примеров из пула данных по информационному критерию и добавляются в обучающую выборку. 
• Этот цикл повторяется, пока не будет достигнут некоторый критерий останова. Критерием останова может служить количество итераций или же оценка ошибки обучения, а также иные внешние критерии.

Aктивное обучение

Перейдем сразу к активному обучению и протестируем его эффективность на наших данных.

На текущий момент существует несколько библиотек для активного обучения на языке Python, здесь я приведу три самые распространенные:

• modAL это достаточно легкий в понимании и освоении пакет, который является своего рода оберткой для популярной библиотеки машинного обучения scikit-learn и полностью совместим с ней. В нем представлены наиболее популярные методы активного обучения.
• Libact использует стратегию многорукого бандита поверх существующих стратегий запросов для динамического выбора наилучшего запроса. 
• Alipy представляет собой некую лабораторию от поставщиков пакета, в котором собрано большое количество стратегий запросов.

Мой выбор пал на библиотеку modAL как на более интуитивную, подходящую для знакомства с философией активного обучения. Она дает большую свободу в конструировании моделей и создания своих собственных, используя стандартные блоки или создавая свои новые.

Давайте представим описанный выше процесс обучения на схеме, которая уже не требует детальных пояснений:

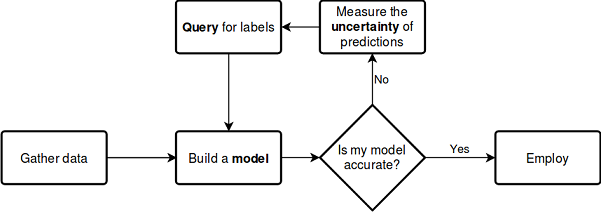
см. документацию

Библиотека хороша тем, что можно использовать любой классификатор из поставки scikit-learn. Следующий пример демонстрирует использование случайного леса в качестве обучающейся модели:

from modAL.models import ActiveLearner
from modAL.uncertainty import entropy_sampling
from sklearn.ensemble import RandomForestClassifier

learner = ActiveLearner(
    estimator=RandomForestClassifier(),
    query_strategy=entropy_sampling,
    X_training=X_training, y_training=y_training
)

Случайный лес здесь выступает в роли обучающейся модели и оценщика, позволяющего выбирать новые семплы из неразмеченных данных в зависимости от стратегии запроса (например, на основе энтропии, как в данном примере). Далее в модель передается датасет, состоящий из небольшого количества размеченных данных. Это необходимо для предварительного обучения. 

Библиотека modAL позволяет легко комбинировать стратегии запросов и делать из них составные взвешенные:

from modAL.utils.combination import make_linear_combination, make_product
from modAL.uncertainty import classifier_uncertainty, classifier_margin

# creating new utility measures by linear combination and product
# linear_combination will return 1.0*classifier_uncertainty + 1.0*classifier_margin
linear_combination = make_linear_combination(
    classifier_uncertainty, classifier_margin,
    weights=[1.0, 1.0]
)
# product will return (classifier_uncertainty**0.5)*(classifier_margin**0.1)
product = make_product(
    classifier_uncertainty, classifier_margin,
    exponents=[0.5, 0.1]
)

После того как запрос сформирован, из неразмеченной области данных выбираются примеры, удовлетворяющие критериям запросов, при помощи селекторов multi_argmax или weighted_randm:

from modAL.utils.selection import multi_argmax

# defining the custom query strategy, which uses the linear combination of
# classifier uncertainty and classifier margin
def custom_query_strategy(classifier, X, n_instances=1):
    utility = linear_combination(classifier, X)
    query_idx = multi_argmax(utility, n_instances=n_instances)
    return query_idx, X[query_idx]

custom_query_learner = ActiveLearner(
    estimator=GaussianProcessClassifier(1.0 * RBF(1.0)),
    query_strategy=custom_query_strategy,
    X_training=X_training, y_training=y_training
)

Стратегии запросов

Было отмечено, что существует три основных стратегии запросов. Все стратегии основаны на неопределенности классификации, поэтому они называются мерами неопределенности. Давайте посмотрим, как они работают под капотом.

Неопределенность классификации, в простом случае, оценивается как U(x)=1−P(x^|x), где x это случай, который необходимо предсказать, а x^ с крышкой — это наиболее вероятный прогноз. Например, если существует три класса и три элемента выборки, то соответствующие неопределенности можно рассчитать как:

[[0.1 , 0.85, 0.05],
 [0.6 , 0.3 , 0.1 ],
 [0.39, 0.61, 0.0 ]]

1 - proba.max(axis=1)

[0.15, 0.4 , 0.39]

Таким образом, будет выбран второй пример как наиболее неопределенный.

Маржинальность классификации это разница вероятностей первого и второго наиболее вероятных запросов, определяющаяся по формуле M(x)=P(x1^|x)−P(x2^|x), где x1^ и x2^ являются первым и вторым наиболее вероятными классами.

Данная стратегия запроса выбирает примеры с наименьшим запасом (или маржой) между вероятностями двух наиболее вероятных классов, потому что чем меньше запас решения, тем более неопределенным оно является.

>>> import numpy as np
>>> proba = np.array([[0.1 , 0.85, 0.05],
...                   [0.6 , 0.3 , 0.1 ],
...                   [0.39, 0.61, 0.0 ]])
>>>
>>> proba
array([[0.1 , 0.85, 0.05],
       [0.6 , 0.3 , 0.1 ],
       [0.39, 0.61, 0.  ]])
>>> part = np.partition(-proba, 1, axis=1)
>>> part
array([[-0.85, -0.1 , -0.05],
       [-0.6 , -0.3 , -0.1 ],
       [-0.61, -0.39, -0.  ]])
>>> part[:, 0]
array([-0.85, -0.6 , -0.61])
>>> part[:, 1]
array([-0.1 , -0.3 , -0.39])
>>> margin = - part[:, 0] + part[:, 1]
>>> margin
array([0.75, 0.3 , 0.22])

В данном случае будет выбран третий семпл (третья строка массива), поскольку запас вероятности для этого примера минимален.

Энтропия классификации рассчитывается по формуле информационной энтропии  H(x)=−∑kpklog(pk), где pk это вероятность принадлежности выборки к k-му классу. Чем ближе распределение к равномерному, тем выше энтропия. Для нашего примера максимальная энтропия получена для 2-го примера.

[0.51818621, 0.89794572, 0.66874809]

Выглядит не очень сложно. Пожалуй, этой информации достаточно для понимания трех основных стратегий запросов. Более детально вы можете прочесть об этом в документации к пакету, а я лишь перевел и озвучил базовые моменты.

Пакетные стратегии запросов

Делать запрос по одному элементу и переобучать модель не всегда эффективно. Гораздо выгоднее промаркировать и выбрать сразу несколько экземпляров из неразмеченных данных. Для этого существует ряд запросов, наиболее известным из которых является семплирование ранжированной партии на основе функции подобия, например, косинусного расстояния. Данный метод оценивает, насколько хорошо исследуется пространство признаков в окрестностях x (немаркированного примера). После оценки экземпляр с наивысшей оценкой добавляется в обучающую выборку и удаляется из пула неразмеченных данных, после чего оценка пересчитывается и лучший экземпляр добавляется снова, пока количество примеров не достигнет заданного размера (размера батча). 

Запросы на основе информационной плотности

При использовании простых стратегий запросов, изложенных выше, никак не оценивается структура данных. Это может приводить к неоптимальным запросам. Для улучшения семплирования можно использовать меры информационной плотности, которые будут способствовать правильному выбору элементов неразмеченных данных. Здесь используется косинусное или эвклидово расстояние. Чем выше плотность информации, тем больше данный выбранный экземпляр похож на все остальные. 

Запросы по комитету классификаторов

Данный вид запросов устраняет некоторые недостатки простых видов запросов. Например, выборка элементов имеет тенденцию быть смещенной из-за особенностей конкретного классификатора. Некоторые важные элементы выборки могут быть пропущены. Данный эффект устраняется путем одновременного сохранения нескольких гипотез и выбором запросов, между которыми возникли разногласия. Таким образом, комитет классификаторов обучается каждый на своей копии выборки, а затем результаты взвешиваются. Другими разновидностями обучения на комитете классификаторов является бэггинг и бутстраппинг.

Я практически полностью покрыл функционал библиотеки в этом кратком описании. Для уточнения каких-то вопросов вы можете обратиться к документации.

Учимся активно

Я выбрал пакетную стратегию запросов, а также запросы по комитету классификаторов и провел ряд экспериментов. Пакетная стратегия запросов не показала хорошей производительности на новых данных сама по себе, однако, подав сформированный ею датасет в GMM, я начал получать интересные результаты. 

Рассмотрим пример реализации функции пакетного активного обучения:

def active_learner(data, labeled_size, unlabeled_size, batch_size, max_depth):
    X_raw = data[data.columns[1:-1]].to_numpy()
    y_raw = data[data.columns[-1]].to_numpy()

    # Isolate our examples for our labeled dataset.
    training_indices = np.random.randint(low=0, high=X_raw.shape[0] + 1, size=labeled_size)

    X_train = X_raw[training_indices]
    y_train = y_raw[training_indices]

    # fit the model on all data
    cl = AdaBoostClassifier(DecisionTreeClassifier(max_depth=max_depth), n_estimators=50, learning_rate = 0.01)
    cl.fit(X_raw, y_raw)
    print('Score for the passive learning: ', cl.score(X_raw, y_raw), ' with train size: ', data.shape[0])

    # Isolate the non-training examples we'll be querying.
    X_pool = np.delete(X_raw, training_indices, axis=0)
    y_pool = np.delete(y_raw, training_indices, axis=0)

    # Pre-set our batch sampling to retrieve 3 samples at a time.
    preset_batch = partial(uncertainty_batch_sampling, n_instances=batch_size)

    # Specify our core estimator along with it's active learning model.
    cl = AdaBoostClassifier(DecisionTreeClassifier(max_depth=3), n_estimators=50, learning_rate = 0.03)
    learner = ActiveLearner(estimator=cl, query_strategy=preset_batch, X_training=X_train, y_training=y_train)

На вход функции передается размеченный датасет, количество размеченных примеров, количество неразмеченных, размер батча для пакетного запроса меток и максимальная глубина дерева.

Из размеченного датасета случайным образом выбирается заданное количество примеров с метками для предобучения модели. Остальная часть датасета формирует пул, из которого будут запрашиваться примеры. В качестве базового классификатора я выбрал AdaBoost, который похож на CatBoost. После этого модель итеративно обучается:

    # Allow our model to query our unlabeled dataset for the most
    # informative points according to our query strategy (uncertainty sampling).
    N_QUERIES = unlabeled_size // batch_size

    for index in range(N_QUERIES):
        query_index, query_instance = learner.query(X_pool)

        # Teach our ActiveLearner model the record it has requested.
        X, y = X_pool[query_index], y_pool[query_index]
        learner.teach(X=X, y=y)

        # Remove the queried instance from the unlabeled pool.
        X_pool, y_pool = np.delete(
            X_pool, query_index, axis=0), np.delete(y_pool, query_index)

        # Calculate and report our model's accuracy.
        model_accuracy = learner.score(X_raw, y_raw)
        print('Accuracy after query {n}: {acc:0.4f}'.format(
            n=index + 1, acc=model_accuracy))

        # Save our model's performance for plotting.
        performance_history.append(model_accuracy)

    print('Score for the active learning with train size: ',
          learner.X_training.shape)     

Поскольку в результате такого полуконтролируемого обучения может произойти все что угодно, то и результат получается какой угодно. Однако, после некоторых манипуляций с настройками лернера, получились результаты, сопоставимые с результатами из предыдущей статьи. 

В идеале, точность классификации активного лернера на небольшом количестве размеченных данных должна превосходить точность аналогичного классификатора, если бы все данные были размечены.

>>> learned = active_learner(pr, 1000, 1000, 50)
Score for the passive learning:  0.5991245668429692  with train size:  5483
Accuracy after query 1: 0.5710
Accuracy after query 2: 0.5836
Accuracy after query 3: 0.5749
Accuracy after query 4: 0.5847
Accuracy after query 5: 0.5829
Accuracy after query 6: 0.5823
Accuracy after query 7: 0.5650
Accuracy after query 8: 0.5667
Accuracy after query 9: 0.5854
Accuracy after query 10: 0.5836
Accuracy after query 11: 0.5807
Accuracy after query 12: 0.5907
Accuracy after query 13: 0.5944
Accuracy after query 14: 0.5865
Accuracy after query 15: 0.5949
Accuracy after query 16: 0.5873
Accuracy after query 17: 0.5833
Accuracy after query 18: 0.5862
Accuracy after query 19: 0.5902
Accuracy after query 20: 0.6002
Score for the active learning with train size:  (2000, 8)

Из отчета следует, что классификатор, который обучался на всех размеченных данных, имеет точность ниже чем у активного лернера, который обучен всего на 2000 примеров. Наверное, это хорошо. 

Теперь мы можем отправить эту выборку в GMM модель, а затем обучить классификатор CatBoost.

# prepare data for CatBoost
catboost_df = pd.DataFrame(learned.X_training)
catboost_df['labels'] = learned.y_training

# perform GMM clasterizatin over dataset
X = catboost_df.copy()
gmm = mixture.GaussianMixture(
    n_components=75, max_iter=500, covariance_type='full', n_init=1).fit(X)

# sample new dataset
generated = gmm.sample(10000)
# make labels
gen = pd.DataFrame(generated[0])
gen.rename(columns={gen.columns[-1]: "labels"}, inplace=True)
gen.loc[gen['labels'] >= 0.5, 'labels'] = 1
gen.loc[gen['labels'] < 0.5, 'labels'] = 0
X = gen[gen.columns[:-1]]
y = gen[gen.columns[-1]]
pr = pd.DataFrame(X)
pr['labels'] = y

# fit CatBoost model and test it
model = fit_model(pr)
test_model(model, TEST_START, END_DATE)

Данный процесс можно повторять несколько раз, потому что на каждом этапе обработки данных существует элемент неопределенности, который не позволяет строить однозначные модели. После всех итераций были получены такие картинки в тестере (период обучения 1 год и тестовый период 5 лет):

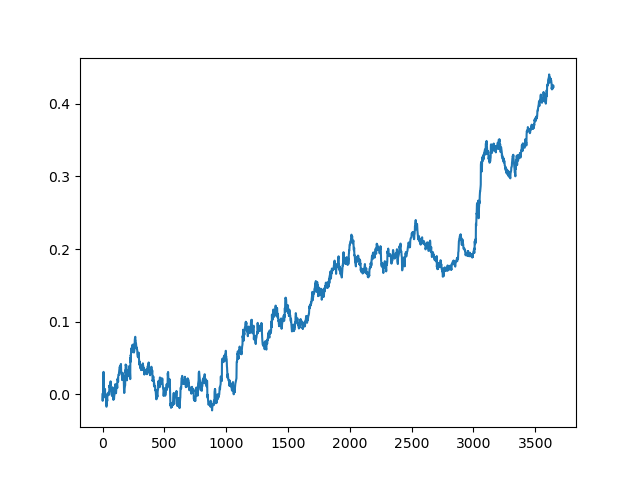
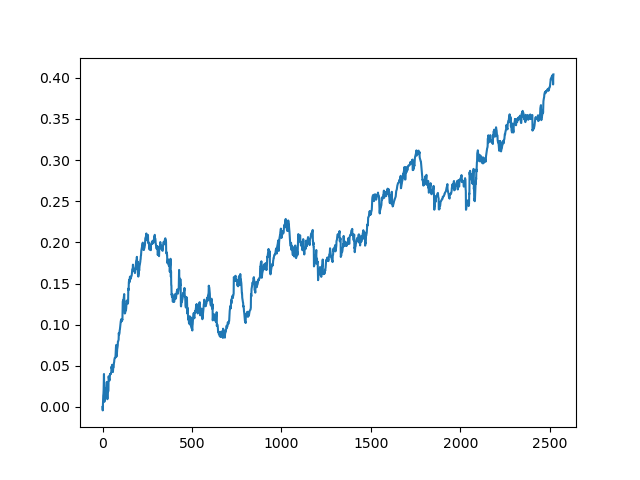
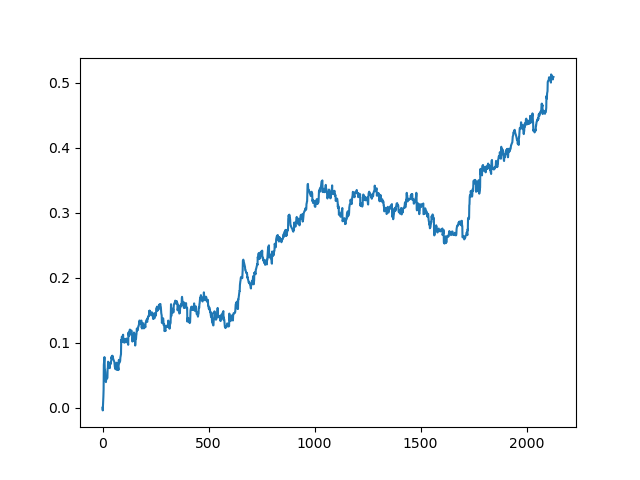
Конечно, эти изображения не являются каким-то эталоном, а лишь демонстрируют возможность получения прибыльных (на новых данных) моделей, которые можно перебирать. 

Давайте теперь реализуем функцию обучения на комитете классификаторов и посмотрим, что из этого получится:

def active_learner_committee(data, learners_number, labeled_size, unlabeled_size, batch_size):
    X_pool = data[data.columns[1:-1]].to_numpy()
    y_pool = data[data.columns[-1]].to_numpy()

    cl = AdaBoostClassifier(DecisionTreeClassifier(max_depth=3), n_estimators=50, learning_rate = 0.05)
    cl.fit(X_pool, y_pool)
    print('Score for the passive learning: ', cl.score(
        X_pool, y_pool), ' with train size: ', data.shape[0])

    # initializing Committee members
    learner_list = list()

    # Pre-set our batch sampling to retrieve 3 samples at a time.
    preset_batch = partial(uncertainty_batch_sampling, n_instances=batch_size)
    
    for member_idx in range(learners_number):
        # initial training data
        train_idx = np.random.choice(range(X_pool.shape[0]), size=labeled_size, replace=False)
        X_train = X_pool[train_idx]
        y_train = y_pool[train_idx]

        # creating a reduced copy of the data with the known instances removed
        X_pool = np.delete(X_pool, train_idx, axis=0)
        y_pool = np.delete(y_pool, train_idx)

        # initializing learner
        learner = ActiveLearner(
            estimator=AdaBoostClassifier(DecisionTreeClassifier(max_depth=2), n_estimators=50, learning_rate = 0.05),
            query_strategy=preset_batch,
            X_training=X_train, y_training=y_train
        )
        learner_list.append(learner)

    # assembling the committee
    committee = Committee(learner_list=learner_list)

    unqueried_score = committee.score(X_pool, y_pool)
    performance_history = [unqueried_score]

    N_QUERIES = unlabeled_size // batch_size

    for idx in range(N_QUERIES):
        query_idx, query_instance = committee.query(X_pool)
        committee.teach(
            X=X_pool[query_idx].reshape(1, -1),
            y=y_pool[query_idx].reshape(1, )
        )
        model_accuracy = committee.score(X_pool, y_pool)
        performance_history.append(model_accuracy)
        print('Accuracy after query {n}: {acc:0.4f}'.format(
            n=idx + 1, acc=model_accuracy))

        # remove queried instance from pool
        X_pool = np.delete(X_pool, query_idx, axis=0)
        y_pool = np.delete(y_pool, query_idx)

    return committee

Здесь я также выбрал пакетную стратегию запросов, чтобы не переобучать модель при каждом добавлении всего одного элемента (что медленно). В остальном я просто создал комитет из произвольного количества AdaBoost классификаторов (думается, что больше пяти добавлять не имеет смысла, но можно экспериментировать). 

Ниже приведен скоринг обучения комитета из пяти моделей с аналогичными настройками, что и для предыдущего метода:

>>> commetee = active_learner_committee(pr, 5, 1000, 1000, 50)
Score for the passive learning:  0.6533842794759825  with train size:  5496
Accuracy after query 1: 0.5927
Accuracy after query 2: 0.5818
Accuracy after query 3: 0.5668
Accuracy after query 4: 0.5862
Accuracy after query 5: 0.5874
Accuracy after query 6: 0.5906
Accuracy after query 7: 0.5918
Accuracy after query 8: 0.5910
Accuracy after query 9: 0.5820
Accuracy after query 10: 0.5934
Accuracy after query 11: 0.5864
Accuracy after query 12: 0.5753
Accuracy after query 13: 0.5868
Accuracy after query 14: 0.5921
Accuracy after query 15: 0.5809
Accuracy after query 16: 0.5842
Accuracy after query 17: 0.5833
Accuracy after query 18: 0.5783
Accuracy after query 19: 0.5732
Accuracy after query 20: 0.5828

Здесь комитет активных лернеров не дотянул до результата одного пассивного. Невозможно предположить, чем это вызвано. Возможно, просто случайный результат. Дальше я прогнал несколько раз полученный датасет по тому же принципу, что и в прошлый раз и получил такие случайные результаты на выбор:

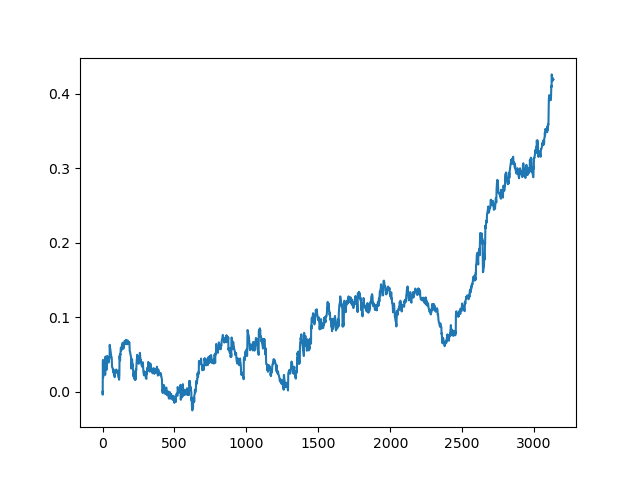
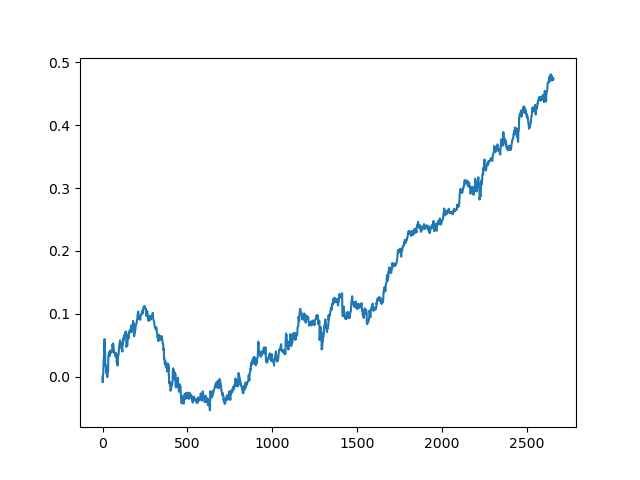
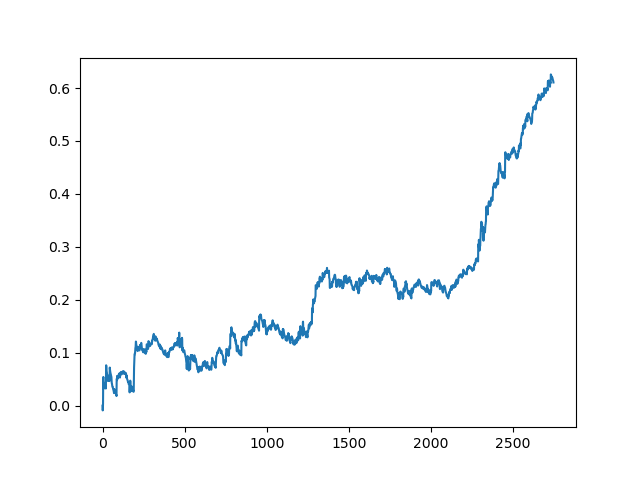
Заключение

В данной статье мы разобрались с активным обучением, которое оставило смешанные впечатления. С одной стороны, всегда заманчиво обучаться на небольшом количестве примеров, и эти модели действительно работают хорошо для некоторых классификационных задач. Однако, это все еще далеко от искусственного интеллекта. Такая модель не может сама найти устойчивые закономерности в мусорных данных, и для нее требуется более тщательная подготовка признаков и меток, в т. ч. на основе экспертной разметки. Я не увидел значительного прироста в качестве моделей, и был ли он вообще. В то же время, трудоемкость и время обучения моделей увеличилось, что является негативным фактором. Мне понравилась философия активного обучения и заимствование особенностей человеческого мышления. А аттаче файл со всеми функциями, вы можете поэкспериментировать самостоятельно, либо использовать эти модели каким-то другим оригинальным способом.