
Нейросети — это просто (Часть 6): Эксперименты с коэффициентом обучения нейронной сети
Содержание
- Введение
- 1. Проблематика вопроса
- 2. Эксперимент 1
- 3. Эксперимент 2
- 4. Эксперимент 3
- Заключение
- Ссылки
- Программы, используемые в статье
Введение
Мы уже познакомились с принципами работы и способами реализации полносвязного перцептрона, сверточных и рекуррентных сетей. Для обучения всех сетей мы использовали метод градиентного спуска. Данный метод заключается в определении ошибки предсказания сети на каждом шаге и корректировке весовых коэффициентов в сторону уменьшения ошибки. При этом на каждом шаге мы не полностью исключаем ошибку, а лишь немного корректируем веса для ее сокращения. Таким образом, мы пытаемся подобрать такие весовые коэффициенты, которые максимально близко повторят обучающую выборку на всем ее протяжении. И именно коэффициент обучения отвечает за скорость минимизации ошибки на каждом шаге.
1. Проблематика вопроса
В чем же проблема выбора коэффициента? Давайте очертим круг основных вопросов выбора коэффициента обучения.
1. Почему нельзя принять коэффициент равный "1" и сразу компенсировать ошибку или близким к этому значению?
При таком подходе мы получим нейронную сеть, переобученную под последнюю ситуацию. В результате будем принимать последующее решение, основываясь только на последних данных без учета истории.
2. В чем риск использования заведомо малого коэффициента, который даст возможность усреднить значения на всей выборке?
Первая проблема при таком подходе это период обучения нейронной сети. Двигаясь слишком мелкими шагами к цели, нам потребуется большое количество таких шагов. На это требуется время и ресурсы.
Вторая проблема такого подхода заключается в том, что дорога к цели не всегда бывает гладкой. На пути встречаются как впадины, так и подъемы. Двигаясь слишком малыми шагами, мы можем застрять в одной из таких впадин, приняв ее за глобальный минимум. При этом мы так никогда и не достигнем цели. Частично данная проблема решается использованием моментума в формуле обновления весов, но вопрос остается открытым.
3. В чем риск использования завышенного коэффициента, который даст возможность усреднить значения на некой дистанции и проходить локальные минимумы?
Попытка решить проблему локального минимума увеличением коэффициента обучения кроет в себе другую проблему: использование завышенного коэффициента обучения часто не позволяет свести ошибку к минимуму, т.к. при очередном обновлении весов их изменение будет больше требуемого и в результате мы "перелетим" через глобальный минимум. При последующем возврате получим аналогичную ситуацию. В результате мы будем колебаться в некой окрестности глобального минимума.
Указанные проблемы широко известны и часто встречаются в литературе, но нигде я не нашел четкого указания по выбору коэффициента (темпа) обучения. Все сводится к эмпирическому подбору коэффициента под каждую задачу. Также, в некоторых трудах предлагается в процессе обучения постепенно уменьшать коэффициент для минимизации риска 3, описанного выше.
В данной статье я предлагаю провести эксперименты по обучению одной нейронной сети с разными коэффициентами темпа обучения и посмотреть влияние данного параметра на обучение нейронной сети в целом.
2. Эксперимент 1
Для удобства проведения эксперимента вынесем переменную eta из класса CNeuronBaseOCL в глобальные переменны.
double eta=0.01; #include "NeuroNet.mqh"
и
class CNeuronBaseOCL : public CObject { protected: ........ ........ //--- //const double eta;
Теперь создадим 3 копии советника с различными параметрами темпа обучения (0,1; 0,01; 0,001). И создадим 4-й советник в котором зададим начальный темп обучения равный 0.01 и будем понижать его в 10 раз каждые 10 эпох. Для этого цикл обучения в функции Train дополним нижеследующим кодом.
if(discount>0) discount--; else { eta*=0.1; discount=10; }
Все 4 советника были одновременно запущены в одном терминале. Для эксперимента взяты параметры, применяемые ранее для тестирования советников: инструмент EURUSD, таймфрейм H1, на вход подаются данные за 20 последовательных свечей, обучение проводится на истории за 2 последних года. Таким образом, обучающая выборка составила немногим более 12,4 тыс. баров.
Все советники были инициализированы случайными весами в диапазоне от -1 до 1, исключая нулевые значения.
К сожалению, советник с темпом обучения равным 0,1 продемонстрировал ошибку близкую к 1, и поэтому на графиках не будет представлен. Динамика обучения остальных советников представлена на графиках ниже.
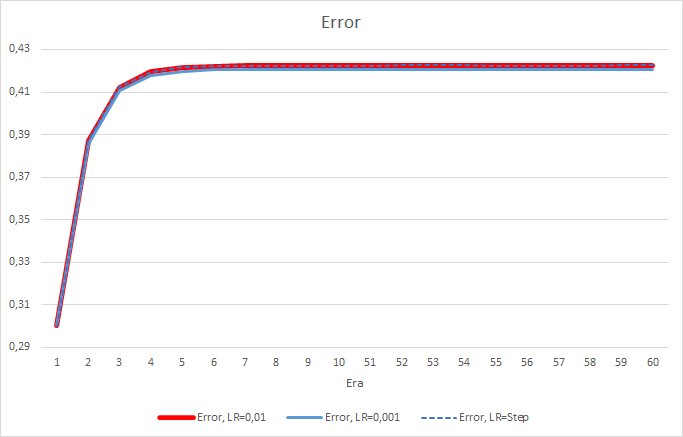
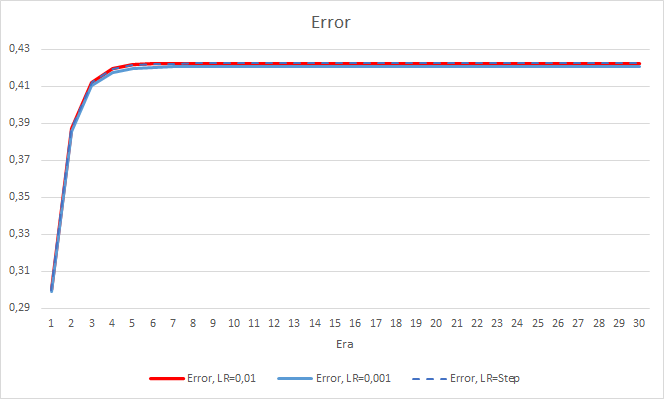
Буквально после 5 эпох ошибка всех советников достигла отметки 0.42, где и продолжала колебаться все оставшееся время. Следует отметить, что ошибка советника с темпом обучения равным 0.001 была немногим ниже. Отличия наблюдались в 3-ем знаке после запятой (0.420 против 0.422 2-х других советников).
Траектория ошибки советника с изменяемым темпом обучения повторяет линию ошибки советника с коэффициентом обучения равным 0.01. Это вполне ожидаемо на первых десяти эпохах, но с понижением коэффициента отклонения не наблюдаются.
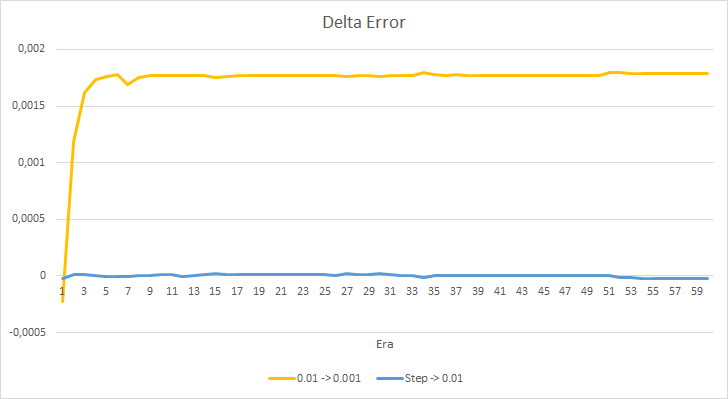
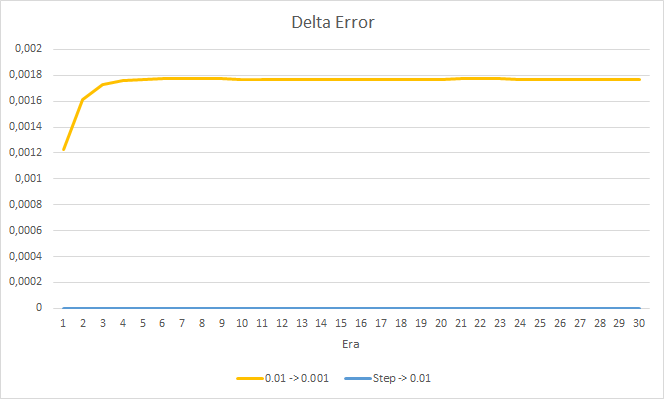
Посмотрим детальнее на разницу между ошибками советников в эксперименте. Практически на протяжении всего эксперимента разница между ошибками советников с постоянными темпами обучения 0.01 и 0.001 колеблется в районе отметки 0.0018. При этом понижение коэффициента обучения в советнике каждые 10 эпох почти не оказывает влияния и отклонение от советника с коэффициентом 0.01 (равный начальному коэффициенту обучения) колеблется около "0".
Полученные показатели ошибки показывают, что в нашем случае не применим темп обучения равный 0.1, а вот использование темпа обучения 0.01 и ниже дают схожие результаты с ошибкой около 42%.
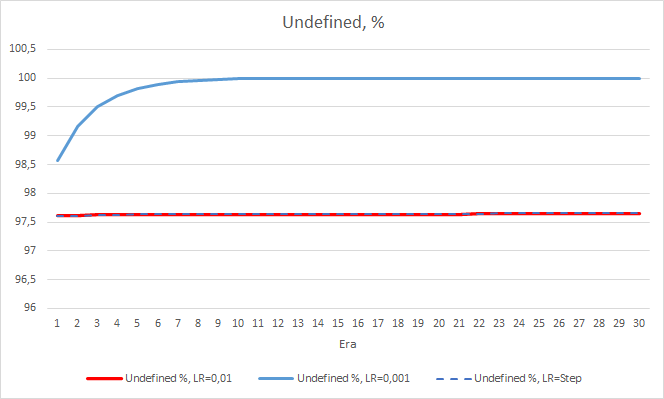
Картина со статистической ошибкой нейронной сети понятна, а как это отразится на работе нашего советника? Посмотрим на количество пропущенных фракталов. К сожалению, во время эксперимента показатели всех советников по данному показателю неутешительны, все они близки к 100% пропуска фракталов. При этом если советник с темпом обучения равным 0.01 определяет порядка 2.5% фракталов, то при коэффициенте обучения равном 0,001 пропускаются 100% фракталов. Следует отметить, у советника с темпом обучения 0.01 после 52 эпохи наметилась тенденция к снижению числа пропущенных фракталов. В то время, как у советника с переменным коэффициентом обучения такой тенденции нет.
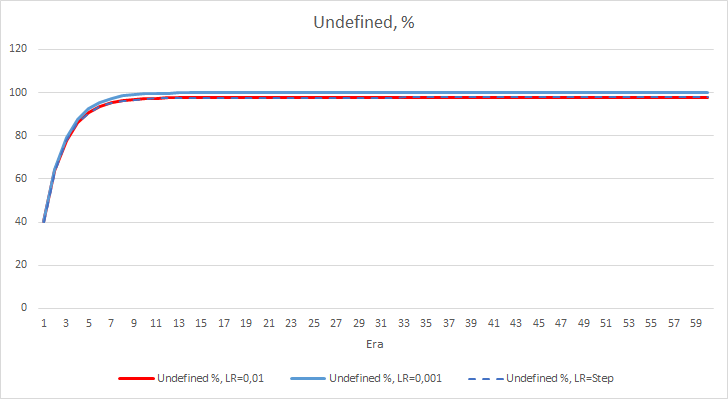
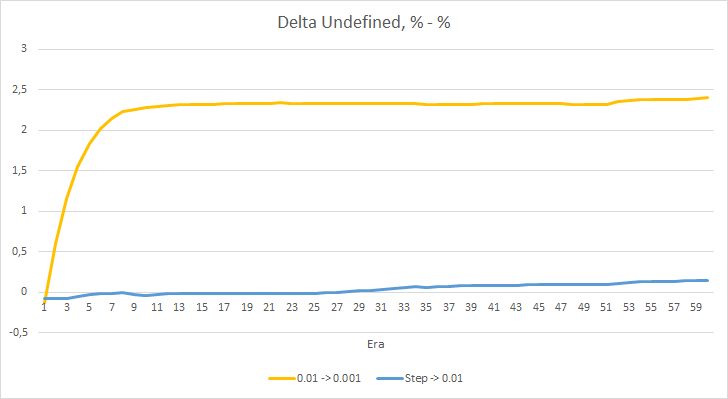
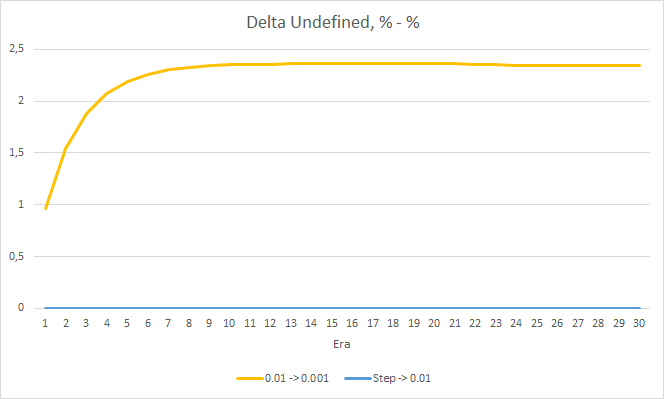
График дельт процента пропущенных фракталов также демонстрирует постепенный рост разницы в пользу советника с темпом обучения 0.01.
Мы рассмотрели 2 показателя работы нейронной сети и пока видим, что советник с меньшим темпом обучения имеет меньшую ошибку, но при этом пропускает фракталы. Посмотрим на третий показатель - "попадание" предсказанных фракталов.
Представленные ниже графики демонстрируют рост процента "попадания" в процессе обучением советников с темпом обучения 0.01 и с динамически снижаемым коэффициентом. При этом при понижении темпа обучения снижается и скорость роста данного показателя. У советника с темпом обучения 0.001 процента "попадания" застыл около "0", что вполне ожидаемо, так как он пропускает 100% фракталов.
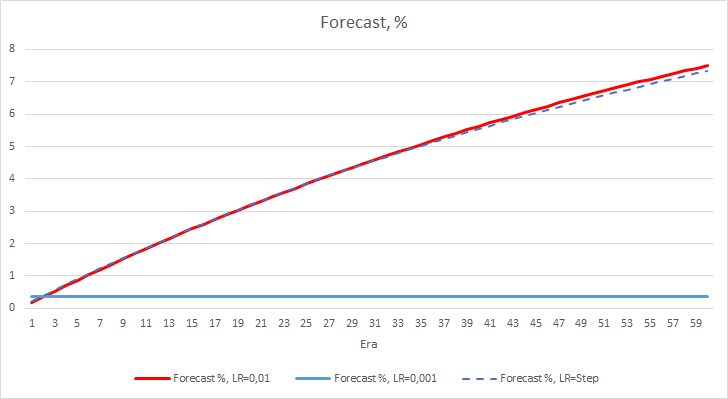
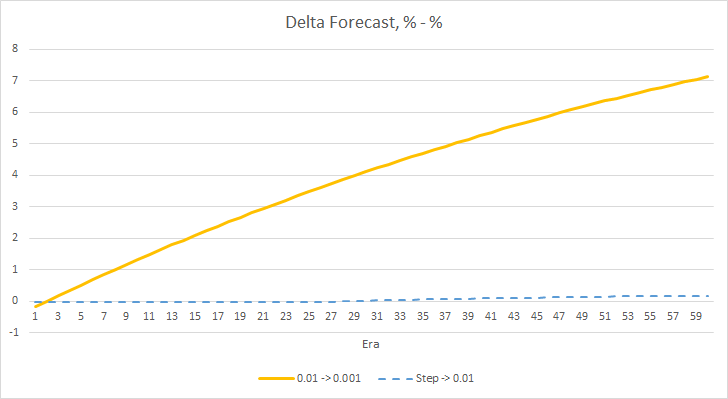
Проведенный эксперимент подсказывает нам об оптимальности использования темпа обучения близкого к 0.01 для обучения нейронной сети в нашей задаче. При этом постепенное снижение коэффициента обучения не дало положительного результата. Возможно, эффект от понижения коэффициента будет другой, если его изменять не через 10 эпох, а реже. Возможно, через 100 или 1000 эпох. Но это также нужно проверять экспериментальным путем.
3. Эксперимент 2
В первом эксперименте матрицы весов нейронных сетей были инициализированы случайным образом. И, конечно, все советники имели различные начальные состояния. Чтобы исключить влияние случайности на чистоту эксперимента загрузим во все 3 советника матрицу весов, полученную после предыдущего эксперимента от советника с темпом обучения равном 0.01 и продолжим обучение еще на 30 эпох.
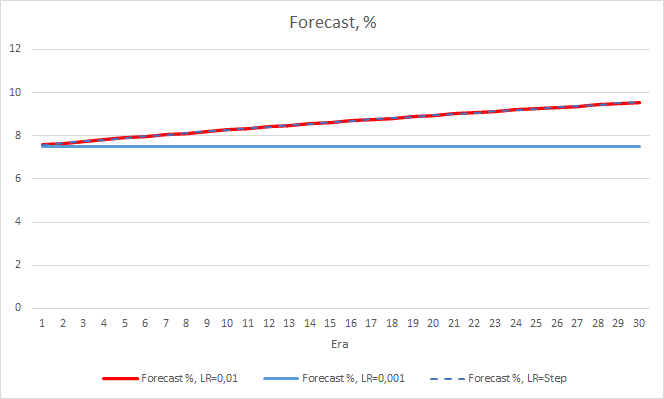
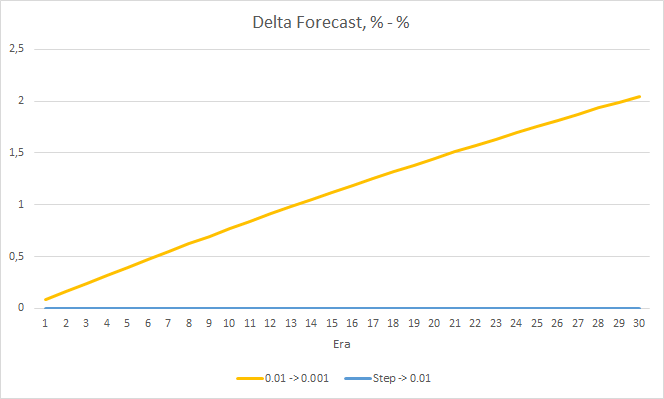
Проведенное обучение подтверждает полученные ранее результаты. Мы также наблюдаем среднюю ошибку в районе 0.42 по всем трем советникам. При этом у советника с меньшим темпом обучения (0.001) ошибка немного меньше, на те же 0.0018. Влияние постепенного снижение коэффициента обучения практически равно "0".
По проценту пропущенных фракталов так же подтверждаются полученные ранее результаты. Советник с меньшим коэффициентом обучения за 10 эпох приблизился к 100% пропущенных фракталов, т.е. советник неспособен указать фракталы. Два других советника держатся на уровне 97.6%. Влияние постепенного снижение темпа обучения близко к "0".
Процент "попадания" советника с темпом обучения 0.01 продолжает постепенно расти. А постепенное снижение темпа обучения не оказывает влияния на показатель.
4. Эксперимент 3
Третий эксперимент является небольшим отступлением от темы статьи, но его идея появилась в процессе проведения первых двух экспериментов. Поэтому решил поделиться и этой мыслью. Наблюдая за обучением нейронной сети, я обратил внимание на тот факт, что вероятность отсутствия фрактала колеблется в районе 60-70 % и редко опускается ниже 50%. В то время, как вероятность появления фрактала, будь то в бай или селл, колеблется около 20-30%. И это вполне закономерно, т. к. на графике гораздо меньше фракталов, чем свечей внутри тенденций. Таким образом, наша нейронная сеть переобучается и мы получаем результаты, приведенные выше. Практически 100% фракталов пропускаем, и только редкие удается "поймать".
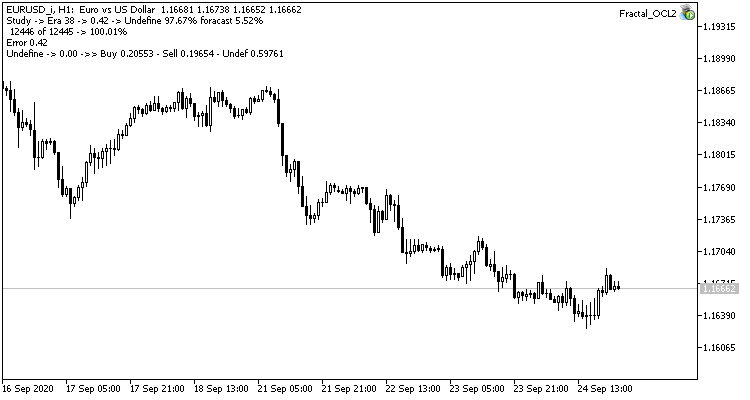
Для решения этой проблемы, я решил немного компенсировать не равномерность выборки и при отсутствии фрактала в эталонном значении при обучении сети указал 0.5 вместо 1.
TempData.Add((double)buy); TempData.Add((double)sell); TempData.Add((double)((!buy && !sell) ? 0.5 : 0));
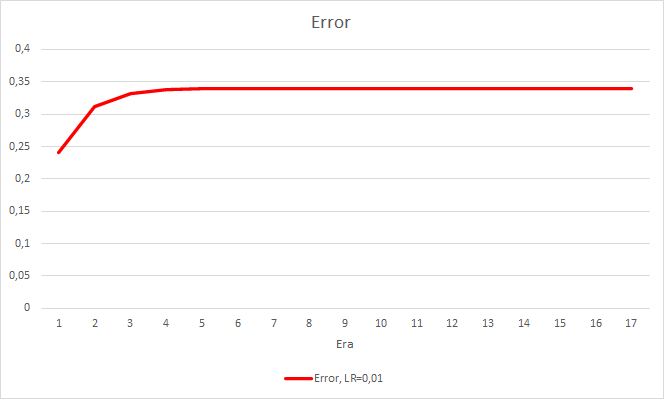
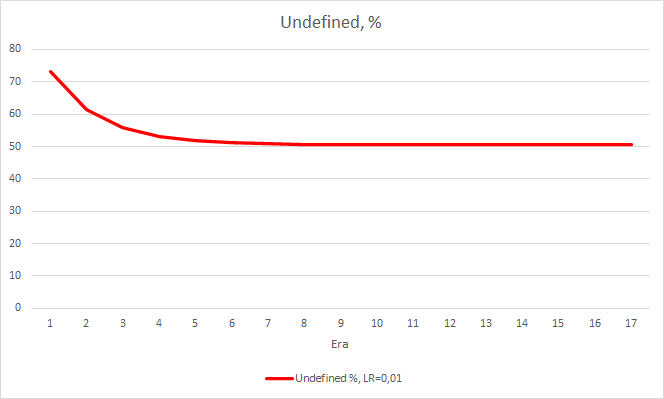
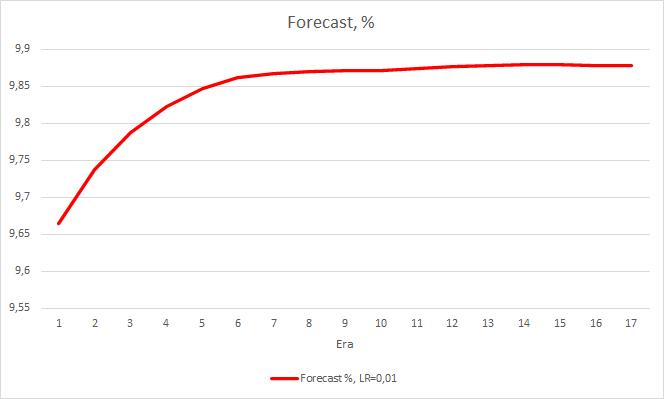
Такой шаг дал свои результаты. Запустив советник с темпом обучения 0.01 и матрицей весов после предыдущих экспериментов после 5 эпох обучения, видим стабилизацию ошибки около 0.34. При этом доля пропущенных фракталов снизилась до 51% и "попадание" поднялось 9.88%. На графике можно заметить, что советник дает сигналы группами, тем самым определяя некоторые зоны. Очевидно, что идея требует дополнительной проработки и тестирования, но полученные результаты говорят о состоятельности подобного подхода.
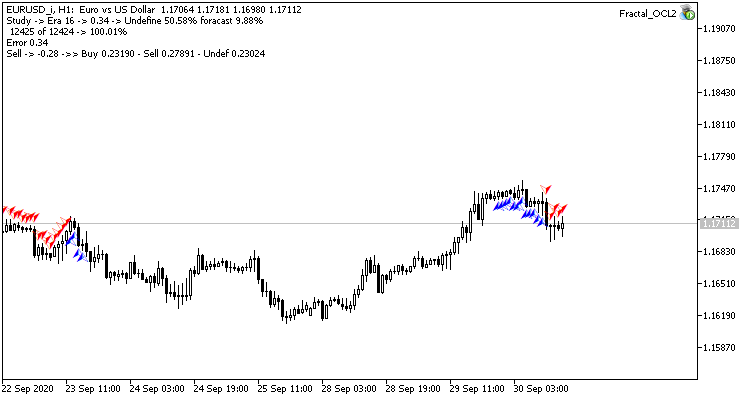
Заключение
В статье было проведено 3 эксперимента. Первые 2 эксперимента показали важность правильного подбора коэффициента обучения нейронной сети. От его правильного подбора зависит общий результат обучения нейронной сети. Но на данный момент нет четкого правила по выбору темпа обучения. Поэтому, на практике приходится подбирать его экспериментальным путем.
Третий эксперимент показал, что не стандартный подход к решению задачи может улучшить общий результат. Но применение каждого решения должно быть подтверждено экспериментальным путем.
Ссылки
- Нейросети - это просто
- Нейросети - это просто (Часть 2): обучение и тестирование сети
- Нейросети - это просто (Часть 3): сверточные сети
- Нейросети - это просто (Часть 4): рекуррентные сети
- Нейросети — это просто (Часть 5): многопоточные вычисления в OpenCL
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Fractal_OCL1.mq5 | Советник | Советник с нейронной сетью классификации(3 нейрона в выходном слое) с использованием технологии OpenCL. Темп обучения 0.1 |
| 2 | Fractal_OCL2.mq5 | Советник | Советник с нейронной сетью классификации(3 нейрона в выходном слое) с использованием технологии OpenCL. Темп обучения 0.01 |
| 3 | Fractal_OCL3.mq5 | Советник | Советник с нейронной сетью классификации(3 нейрона в выходном слое) с использованием технологии OpenCL. Темп обучения 0.001 |
| 4 | Fractal_OCL_step.mq5 | Советник | Советник с нейронной сетью классификации(3 нейрона в выходном слое) с использованием технологии OpenCL. Темп обучения с понижением в 10 раз от 0.01 каждые 10 эпох |
| 5 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 6 | NeuroNet.cl | Библиотека | Библиотека кода программы OpenCL |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Набор инструментов для ручной разметки графиков и торговли (Часть II). Рисование разметки
Набор инструментов для ручной разметки графиков и торговли (Часть II). Рисование разметки
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
"..при отсутствии фрактала в эталонном значении при обучении сети указал 0.5 вместо 1."
Почему именно 0.5, откуда эта цифра?
"..при отсутствии фрактала в эталонном значении при обучении сети указал 0.5 вместо 1."
Почему именно 0.5, откуда эта цифра?
В процессе обучения модель учит вероятностное распределение каждого из 3 событий. Т.к. вероятность отсутствия фрактала значительно выше вероятности его появления, то мы искусственно её занижаем. Указываем 0.5, так как при таком значении мы приходим примерно к равному уровню максимальных вероятностей событий. И их можно сравнивать.
Согласен, что такой подход весьма спорный и продиктован наблюдениями из обучающей выборки.
Похоже что данные не нормализованы, так и должно быть или это тоже работает?
Похоже что данные не нормализованы, так и должно быть или это тоже работает?
О нормализации данных речь пойдет немного позже.
О нормализации данных речь пойдет немного позже.