Нейросети — это просто (Часть 4): Рекуррентные сети

MetaTrader 5 — Торговые системы | 9 сентября 2020, 11:28

8 911

Dmitriy Gizlyk

Содержание

Введение

Продолжаем изучение нейронных сетей. Ранее мы уже рассмотрели многослойный перцептрон и сверточные нейронный сети. Все они работают со статичными данными в рамках марковских процессов, когда последующее состояние системы зависит только от ее текущего состояния и не зависит от состояния системы в прошлом. Сейчас я предлагаю посмотреть в сторону Рекуррентных Нейронных Сетей (Recurrent Neural Network). Это особый вид нейронных сетей, призванный работать с временными последовательностями и на сегодняшний день являющийся лидером в данном направлении.

1. Отличительные особенности рекуррентных нейронных сетей

Рассмотренные ранее типы нейронных сетей работают с заранее заданным объемом данных. В нашем же случае при работе с графиками цен трудно сказать, каким будет идеальным размер анализируемых данных. Разные закономерности могут проявляться в различные временные интервалы. Да и сами эти интервалы не всегда статичны и могут варьироваться в зависимости от текущей ситуации. Какие-то события могут быть редкими на рынке, но с большой долей вероятности отрабатываться. И хорошо, если такое событие осталось в рамках анализируемого окна. Но как только оно выпадает из него, то нейронная сеть уже не примет его во внимание. Хотя, возможно, именно в этот момент рынок будет отрабатывать реакцию на это событие. Увеличение анализируемого окна ведет к росту потребления вычислительных ресурсов и, как следствие, потребуется больше времени на принятие решения.

Для решения данной проблемы работы с временными рядами было предложено использование в нейронных сетях рекуррентных нейронов. Это попытка реализации краткосрочной памяти в нейронных сетях, когда на вход нейрона вместе с информацией о текущем состоянии системы подается и предыдущее состояние этого же нейрона. Такое решение основано на предположении о том, что значение на выходе нейрона учитывает влияние всех факторов (в том числе и свое предыдущее состояние) и на следующем шаге передаст "все свои знания" в свое будущее состояние. По аналогии с нами, когда мы совершаем свои действия на основе своего опыта и действий, совершенных нами ранее. Срок такой памяти и ее влияние на текущее состояния нейрона будет зависеть от весовых коэффициентов.

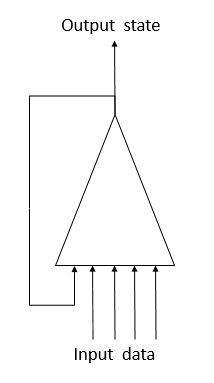
К сожалению, столь простое решение не лишено недостатков. Подобный подход позволяет сохранить "память" на коротком временном отрезке. Цикличность умножения сигнала на коэффициент меньше "1" и применение функции активации нейрона ведет к постепенному затуханию сигнала с ростом количества таких циклов. Для решения данной проблемы в 1997 году Зепп Хохрайтер и Юрген Шмидху́бер предложили использовать архитектуру "Долгая краткосрочная память" (Long short-term memory - LSTM). На сегодняшний день алгоритм LTSM считается одним из лучших для решения задач классификации и прогнозирования временных рядов, когда значимые события разделены во времени и растянуты по временным интервалам.

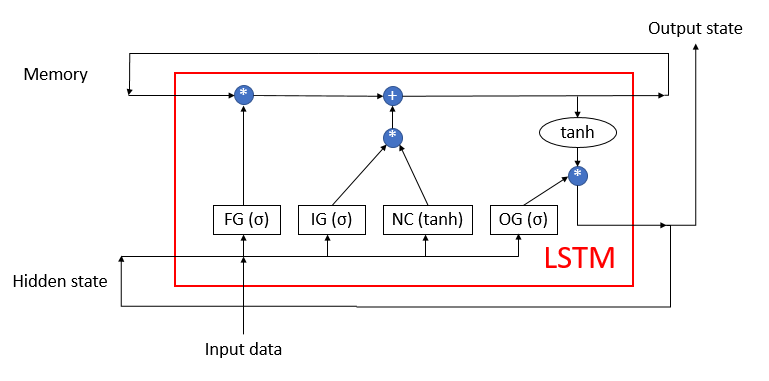
LSTM сложно назвать нейроном. Скорее он уже является нейронной сетью с 3-мя каналами входа данных и 3-мя каналами выхода данных. Из них только по 2-м каналам осуществляется обмен данным с окружающим миров (один для входа и один для выхода). А остальные четыре канала замкнуты попарно для циклического обмена информацией ("Memory" - память и "Hidden state" - скрытое состояние).

Внутри блока LSTM содержится 2 основных потока информации, которые связаны между собой 4-мя полносвязными нейронными слоями. Все нейронные слои содержат одинаковое количество нейронов, которое равно размеру выходного потока и потока памяти. Рассмотрим более детально алгоритм.

Поток данных Memory (память) служит для хранения и передачи во времени важной информации. На начальной стадии инициализируется нулевыми значениями и заполняется в процессе работы нейронной сети. Можно сравнить с живым человеком, который рождается без знаний и обучается на протяжении всей жизни.

Поток Hidden state (скрытое состояние) предназначен для передачи во времени выходного состояния системы. Размер канала данных равен каналу данных "памяти".

Каналы Input data (входные данные) и Output stata (выходное состояние) предназначены для обмена информацией с окружающим миром.

На вход алгоритма поступаю 3-и потока данных:

Input data - описывает текущее состояние системы.
Memory и Hidden state - получаем из предыдущего состояния.

Вначале работы алгоритма информация из Input data и HIdden state объединяются в единый массив данных, который в последующем подается на все 4 скрытых нейронных слоя LSTM.

Первый нейронный слой Forget gate (врата забывания) определяет какую из полученной информации в памяти можно забыть, а какую нужно помнить. Организован в виде полносвязного нейронного слоя с сигмоидной функцией активации. Количество нейронов в слое соответствует количеству ячеек памяти в потоке Memory. Каждый нейрон слоя получает на входе суммарный массив данных потоков Input data и Hidden state, а на выходе выдает число в диапазоне от 0 (полностью забыть) до 1 (сохранить в памяти). Поэлементное произведение выходных данных нейронного слоя с потоком памяти возвращает скорректированную память.

На следующем шаге алгоритм определяет какую из полученной на данном шаге информацию необходимо сохранить в памяти. Для этого используются 2 нейронных слоя:

New Content (новый контент) — полносвязный нейронный слой с гиперболическим тангенсом в качестве функции активации нормализует полученную информации в диапазоне от -1 до 1.
Input gate (входные врата) — полносвязный нейронный слой с сигмоидой в качестве функции активации. Аналогичен Forget gate и определяет какую новую информации нужно запомнить.

Поэлементное произведение New Content и Input gate прибавляется к значениям ячеек памяти. В результате данных операций получаем обновленное состояние памяти, которое впоследствии передается на вход следующего цикла итераций.

После обновления памяти сформируем значения выходного потока. Для этого по аналогии с Forget gate и Input gate пересчитаем Output gate (ворота выходного сигнала), нормализуем текущее значение памяти с помощью гиперболического тангенса. Поэлементное произведение двух полученных массивов данных дает массив выходного сигнала, который выдается из LSTM во внешний мир. Этот же массив данных передадим на следующий цикл итераций в качестве потока скрытого состояния.

2. Принципы обучения рекуррентных нейронных сетей

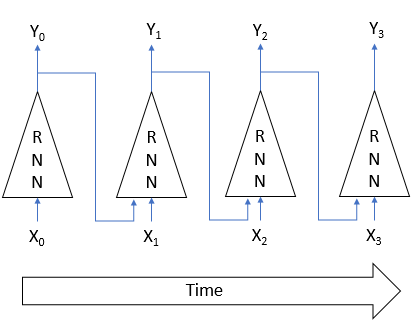
Обучение рекуррентных нейронных сетей осуществляется уже хорошо известным нам методом обратного распространения ошибки. По аналогии с обучением сверточных нейронных сетей, цикличность процесса во времени раскладывают в многослойный перцептрон. В таком перцептроне каждый временной отрезок выступает в роли скрытого слоя. Только для всех слоев такого перцептрона используется одна матрица весовых коэффициентов. Поэтому для корректировки весов берем сумму градиентов по всем слоям, и дельту весовых коэффициентов считаем один раз для суммарного по всем слоям градиента.

3. Построение рекуррентной нейронной сети

Для построения своей рекуррентной нейронной сети мы будем использовать LSTM блоки. И начнем мы с создания класса CNeuronLSTM. С целью сохранения структуры наследования классов, созданной в предыдущей статье, создадим новый класс наследником класса CNeuronProof.

class CNeuronLSTM    :  public CNeuronProof
  {
protected:
   CLayer            *ForgetGate;
   CLayer            *InputGate;
   CLayer            *OutputGate;
   CLayer            *NewContent;
   CArrayDouble      *Memory;
   CArrayDouble      *Input;
   CArrayDouble      *InputGradient;
   //---
   virtual bool      feedForward(CLayer *prevLayer);
   virtual bool      calcHiddenGradients(CLayer *&nextLayer);
   virtual bool      updateInputWeights(CLayer *&prevLayer);
   virtual bool      updateInputWeights(CLayer *gate, CArrayDouble *input_data);
   virtual bool      InitLayer(CLayer *layer, int numOutputs, int numOutputs);
   virtual CArrayDouble *CalculateGate(CLayer *gate, CArrayDouble *sequence);

public:
                     CNeuronLSTM(void);
                    ~CNeuronLSTM(void);
   virtual bool      Init(uint numOutputs,uint myIndex,int window, int step, int units_count);
   //---
   virtual CLayer    *getOutputLayer(void)  { return OutputLayer;  }
   virtual bool      calcInputGradients(CLayer *prevLayer) ;
   virtual bool      calcInputGradients(CNeuronBase *prevNeuron, uint index) ;
   //--- methods for working with files
   virtual bool      Save( int const file_handle);
   virtual bool      Load( int const file_handle);
   virtual int       Type(void)   const   {  return defNeuronLSTM;   }
  };

Родительский класс уже содержит слой выходных нейронов OutputLayer. Добавим еще 4 нейронных слоя, необходимых для функционирования алгоритма: ForgetGate, InputGate, OutputGate и NewContent. Также добавим 3 массива для хранения данных "памяти", объединения Input data и Hidden state, а также градиента ошибок входящих данных. Наименование и функционал методов класса соответствуют рассмотренным ранее. Тем не менее в их коде есть отличия, необходимые для функционирования алгоритма. Рассмотрим детальнее основные методы.

3.1. Метод инициализации класса.

Метод инициализации класса в параметрах получает основную информации о создаваемом блоке. Названия параметров метода сохранились от базового класса, но некоторые получили иной смысл:

numOutputs — количество исходящих связей. Используются, когда за слоем LSTM блоков идет полносвязный слой;
myIndex — индекс нейрона в слое. Используется для идентификации блока;
window — размер канала Input data;
step — не используется;
units_count — ширина выходного канала и количество нейронов в скрытых слоях блока. Все нейронные слои блока содержат одинаковое количество нейронов.

bool CNeuronLSTM::Init(uint numOutputs,uint myIndex,int window,int step,int units_count)
  {
   if(units_count<=0)
      return false;
//--- Init Layers
   if(!CNeuronProof::Init(numOutputs,myIndex,window,step,units_count))
      return false;
   if(!InitLayer(ForgetGate,units_count,window+units_count))
      return false;
   if(!InitLayer(InputGate,units_count,window+units_count))
      return false;
   if(!InitLayer(OutputGate,units_count,window+units_count))
      return false;
   if(!InitLayer(NewContent,units_count,window+units_count))
      return false;
   if(!Memory.Reserve(units_count))
      return false;
   for(int i=0; i<units_count; i++)
      if(!Memory.Add(0))
         return false;
//---
   return true;
  }

Внутри метода сначала проверим, чтобы в нейронных слоях блока было создано как минимум по одному нейрону. Затем вызовем соответствующий метод базового класса. После его успешного завершения произведем инициализацию скрытых слоев блока, операции повторяющиеся для каждого слоя выведем в отдельный метод InitLayer. По завершении инициализации нейронных слоев инициализируем массив памяти нулевыми значениями.

Метод инициализации нейронного слоя InitLayer в параметрах получает указатель на объект инициализируемого нейронного слоя, количество нейронов в слое и количество исходящих соединений. В начале метода проверим действительность полученного указателя. Если указатель недействительный, создадим новый экземпляр класса нейронного слоя. При действительности указателя очистим слой от нейронов.

bool CNeuronLSTM::InitLayer(CLayer *layer,int numUnits, int numOutputs)
  {
   if(CheckPointer(layer)==POINTER_INVALID)
     {
      layer=new CLayer(numOutputs);
      if(CheckPointer(layer)==POINTER_INVALID)
         return false;
     }
   else
      layer.Clear();

Заполним слой необходимым количеством нейронов. В случае возникновения ошибки на любом из этапов метода, выходим из функции с результатом false.

   if(!layer.Reserve(numUnits))
      return false;
//---
   CNeuron *temp;
   for(int i=0; i<numUnits; i++)
     {
      temp=new CNeuron();
      if(CheckPointer(temp)==POINTER_INVALID)
         return false;
      if(!temp.Init(numOutputs+1,i))
         return false;
      if(!layer.Add(temp))
         return false;
     }
//---
   return true;
  }

После успешного завершения всех итераций выходим из метода с результатом true.

3.2. Прямой проход.

Прямой проход реализован в методе feedForward. В параметрах метод получает указатель на предшествующий нейронный слой. В начале метода проверяем действительность полученного указателя, а также наличие нейронов в предшествующем слое. Также проверим действительность массива для входных данных. Если объект еще не создан, то создадим новый экземпляр класса. При наличии уже созданного объекта очистим массив.

bool CNeuronLSTM::feedForward(CLayer *prevLayer)
  {
   if(CheckPointer(prevLayer)==POINTER_INVALID || prevLayer.Total()<=0)
      return false;
   CNeuronBase *temp;
   CConnection *temp_con;
   if(CheckPointer(Input)==POINTER_INVALID)
     {
      Input=new CArrayDouble();
      if(CheckPointer(Input)==POINTER_INVALID)
         return false;
     }
   else
      Input.Clear();

Далее объединим данные о текущем состоянии системы и данные о состоянии на предыдущем временном интервале в единый массив входных данных Input.

   int total=prevLayer.Total();
   if(!Input.Reserve(total+OutputLayer.Total()))
      return false;
   for(int i=0; i<total; i++)
     {
      temp=prevLayer.At(i);
      if(CheckPointer(temp)==POINTER_INVALID || !Input.Add(temp.getOutputVal()))
         return false;
     }
   total=OutputLayer.Total();
   for(int i=0; i<total; i++)
     {
      temp=OutputLayer.At(i);
      if(CheckPointer(temp)==POINTER_INVALID || !Input.Add(temp.getOutputVal()))
         return false;
     }
   int total_data=Input.Total();

Пересчитаем значение гейтов. Как и при инициализации, повторяющиеся для каждого гейта операции вынесем в отдельный метод CalculateGate. Здесь же мы вызываем данный метод с передачей в него указателей на обрабатываемый гейт и массив исходных данных.

//--- Calculated forget gate
   CArrayDouble *forget_gate=CalculateGate(ForgetGate,Input);
   if(CheckPointer(forget_gate)==POINTER_INVALID)
      return false;
//--- Calculated input gate
   CArrayDouble *input_gate=CalculateGate(InputGate,Input);
   if(CheckPointer(input_gate)==POINTER_INVALID)
      return false;
//--- Calculated output gate
   CArrayDouble *output_gate=CalculateGate(OutputGate,Input);
   if(CheckPointer(output_gate)==POINTER_INVALID)
      return false;

Пересчитаем и нормализуем входящие данные в массив new_content.

//--- Calculated new content
   CArrayDouble *new_content=new CArrayDouble();
   if(CheckPointer(new_content)==POINTER_INVALID)
      return false;
   total=NewContent.Total();
   for(int i=0; i<total; i++)
     {
      temp=NewContent.At(i);
      if(CheckPointer(temp)==POINTER_INVALID)
         return false;
      double val=0;
      for(int c=0; c<total_data; c++)
        {
         temp_con=temp.Connections.At(c);
         if(CheckPointer(temp_con)==POINTER_INVALID)
            return false;
         val+=temp_con.weight*Input.At(c);
        }
      val=TanhFunction(val);
      temp.setOutputVal(val);
      if(!new_content.Add(val))
         return false;
     }

И в заключение, после всех выполненных промежуточных расчетов пересчитаем массив "памяти" и определим выходные данные.

//--- Calculated output sequences
   for(int i=0; i<total; i++)
     {
      double value=Memory.At(i)*forget_gate.At(i)+new_content.At(i)*input_gate.At(i);
      if(!Memory.Update(i,value))
         return false;
      temp=OutputLayer.At(i);
      value=TanhFunction(value)*output_gate.At(i);
      temp.setOutputVal(value);
     }

Затем удалим массивы промежуточных данных и выходим из метод с результатом true.

   delete forget_gate;
   delete input_gate;
   delete new_content;
   delete output_gate;
//---
   return true;
  }

В упомянутом выше методе CalculateGate осуществляется умножение матрицы весовых коэффициентов на вектор исходных данных с последующей нормализацией данных через сигмоидную функцию активации. В параметрах данный метод получает 2 указателя на объекты нейронного слоя и исходной последовательности данных. И первым делом проверяем действительность полученных указателей.

CArrayDouble *CNeuronLSTM::CalculateGate(CLayer *gate,CArrayDouble *sequence)
  {
   CNeuronBase *temp;
   CConnection *temp_con;
   CArrayDouble *result=new CArrayDouble();
   if(CheckPointer(gate)==POINTER_INVALID)
      return NULL;

Далее организуем цикл по перебору всех нейронов.

   int total=gate.Total();
   int total_data=sequence.Total();
   for(int i=0; i<total; i++)
     {
      temp=gate.At(i);
      if(CheckPointer(temp)==POINTER_INVALID)
        {
         delete result;
         return NULL;
        }

После проверки действительности указателя в последовательности на объект нейрона организовываем вложенный цикл по перебору всех весовых коэффициентов нейрона с подсчетом суммы произведений последних на соответствующий элемент в массиве исходных данных.

      double val=0;
      for(int c=0; c<total_data; c++)
        {
         temp_con=temp.Connections.At(c);
         if(CheckPointer(temp_con)==POINTER_INVALID)
           {
            delete result;
            return NULL;
           }
         val+=temp_con.weight*(sequence.At(c)==DBL_MAX ? 1 : sequence.At(c));
        }

Полученная сумма произведений пропускается через функцию активации. Результат записывается в выходное значение нейрона и добавляется в массив. После успешного перебора всех нейронов в слое выходим из метода, вернув массив результатов. При возникновении ошибки на каком-либо этапе вычислений метод вернет пустое значение.

      val=SigmoidFunction(val);
      temp.setOutputVal(val);
      if(!result.Add(val))
        {
         delete result;
         return NULL;
        }
     }
//---
   return result;
  }

3.3. Расчет градиентов ошибки.

Расчет градиентов ошибки осуществляется в методе calcHiddenGradients, который в параметрах получает указатель на последующий слой нейронов. В начале метода проверим актуальность ранее созданного объекта для хранения последовательности градиентов ошибки к исходным данным. Если объект еще не создан, то создадим его новый экземпляр. При наличии ранее созданного объекта, очистим массив данных. Также объявим внутренние переменные и экземпляры классов.

bool CNeuronLSTM::calcHiddenGradients(CLayer *&nextLayer)
  {
   if(CheckPointer(InputGradient)==POINTER_INVALID)
     {
      InputGradient=new CArrayDouble();
      if(CheckPointer(InputGradient)==POINTER_INVALID)
         return false;
     }
   else
      InputGradient.Clear();
//---
   int total=OutputLayer.Total();
   CNeuron *temp;
   CArrayDouble *MemoryGradient=new CArrayDouble();
   CNeuron *gate;
   CConnection *con;

Далее посчитаем градиент ошибки для выходного слоя нейронов, пришедший от последующего нейронного слоя.

   for(int i=0; i<total; i++)
     {
      temp=OutputLayer.At(i);
      if(CheckPointer(temp)==POINTER_INVALID)
         return false;
      temp.setGradient(temp.sumDOW(nextLayer));
     }

Распространим полученный градиент на все внутренние нейронные слои LSTM.

   if(CheckPointer(MemoryGradient)==POINTER_INVALID)
      return false;
   if(!MemoryGradient.Reserve(total))
      return false;
   for(int i=0; i<total; i++)
     {
      temp=OutputLayer.At(i);
      gate=OutputGate.At(i);
      if(CheckPointer(gate)==POINTER_INVALID)
         return false;
      double value=temp.getGradient()*gate.getOutputVal();
      value=TanhFunctionDerivative(Memory.At(i))*value;
      if(i>=MemoryGradient.Total())
        {
         if(!MemoryGradient.Add(value))
            return false;
        }
      else
        {
         value=MemoryGradient.At(i)+value;
         if(!MemoryGradient.Update(i,value))
            return false;
        }
      gate.setGradient(gate.getOutputVal()!=0 && temp.getGradient()!=0 ? temp.getGradient()*temp.getOutputVal()*SigmoidFunctionDerivative(gate.getOutputVal())/gate.getOutputVal() : 0);
      //--- Calcculated gates and new content gradients
      gate=ForgetGate.At(i);
      if(CheckPointer(gate)==POINTER_INVALID)
         return false;
      gate.setGradient(gate.getOutputVal()!=0 && value!=0? value*SigmoidFunctionDerivative(gate.getOutputVal()) : 0);
      gate=InputGate.At(i);
      temp=NewContent.At(i);
      if(CheckPointer(gate)==POINTER_INVALID)
         return false;
      gate.setGradient(gate.getOutputVal()!=0 && value!=0 ? value*temp.getOutputVal()*SigmoidFunctionDerivative(gate.getOutputVal()) : 0);
      temp.setGradient(temp.getOutputVal()!=0 && value!=0 ? value*gate.getOutputVal()*TanhFunctionDerivative(temp.getOutputVal()) : 0);
     }

После подсчета градиентов на внутренних нейронных слоях посчитаем градиент ошибки для последовательности исходных данных.

//--- Calculated input gradients
   int total_inp=temp.getConnections().Total();
   for(int n=0; n<total_inp; n++)
     {
      double value=0;
      for(int i=0; i<total; i++)
        {
         temp=ForgetGate.At(i);
         con=temp.getConnections().At(n);
         value+=temp.getGradient()*con.weight;
         //---
         temp=InputGate.At(i);
         con=temp.getConnections().At(n);
         value+=temp.getGradient()*con.weight;
         //---
         temp=OutputGate.At(i);
         con=temp.getConnections().At(n);
         value+=temp.getGradient()*con.weight;
         //---
         temp=NewContent.At(i);
         con=temp.getConnections().At(n);
         value+=temp.getGradient()*con.weight;
        }
      if(InputGradient.Total()>=n)
        {
         if(!InputGradient.Add(value))
            return false;
        }
      else
         if(!InputGradient.Update(n,value))
            return false;
     }

По завершении пересчета всех градиентов удалим не нужные объекты и выйдем из метода с результатом true.

   delete MemoryGradient;
//---
   return true;
  }

Хочу обратить Ваше внимание на такой момент: в теоретической части говорилось о необходимости развертывания последовательности во времени и пересчета градиентов ошибок на каждом временном этапе. Здесь этого не сделано, т. к. используется обучающий коэффициент много меньше 1 и влияние градиента ошибки на предыдущих временных отрезках будет настолько минимальным, что им можно пренебречь для повышения общей производительности алгоритма.

3.4. Обновление весовых коэффициентов.

И вполне естественно, что после получения градиентов ошибок мы корректируем весовые коэффициенты всех нейронных слоев LSTM. Данная задача решается в методе updateInputWeights, который получает в своих параметрах указатель на предыдущий нейронный слой. Сразу скажу, что передача в параметрах указателя на предыдущий слой сделана только с для сохранения структуры наследования.

В начале метода проверим действительность полученного указателя и наличие массива исходных данных. После успешной проверки указателей проводим непосредственно корректировку весовых коэффициентов внутренних нейронных слоев. Как и ранее, повторяющиеся действия я вынес в отдельный метод updateInputWeights с указателями на конкретный нейронный слой и массив исходных данных в параметрах. Здесь же мы поочередно вызываем вспомогательный метод для каждого нейронного слоя.

bool CNeuronLSTM::updateInputWeights(CLayer *&prevLayer)
  {
   if(CheckPointer(prevLayer)==POINTER_INVALID || CheckPointer(Input)==POINTER_INVALID)
      return false;
//---
   if(!updateInputWeights(ForgetGate,Input) || !updateInputWeights(InputGate,Input) || !updateInputWeights(OutputGate,Input)
      || !updateInputWeights(NewContent,Input))
     {
      return false;
     }
//---
   return true;
  }

Рассмотрим операции, выполняемые в методе updateInputWeights(CLayer *gate,CArrayDouble *input_data). В начале метода проверим действительность полученных в параметрах указателей и объявим внутренние переменные.

bool CNeuronLSTM::updateInputWeights(CLayer *gate,CArrayDouble *input_data)
  {
   if(CheckPointer(gate)==POINTER_INVALID || CheckPointer(input_data)==POINTER_INVALID)
      return false;
   CNeuronBase *neuron;
   CConnection *con;
   int total_n=gate.Total();
   int total_data=input_data.Total();

Организуем вложенные циклы по перебору всех нейронов в слое и весов в нейронах с корректировкой матрицы весов. Формула корректировки весов та же, что рассмотренная ранее для CNeuron::updateInputWeights(CArrayObj *&prevLayer). Невозможность использования созданного ранее метода обусловлена лишь тем, что ранее мы использовали связи нейрона для соединения с последующим слоем, а сейчас мы их используем для связи с предыдущим слоем.

   for(int n=0; n<total_n; n++)
     {
      neuron=gate.At(n);
      if(CheckPointer(neuron)==POINTER_INVALID)
         return false;
      for(int i=0; i<total_data; i++)
        {
         con=neuron.getConnections().At(i);
         if(CheckPointer(con)==POINTER_INVALID)
            return false;
         double data=input_data.At(i);
         con.weight+=con.deltaWeight=(neuron.getGradient()!=0 && data!=0 ? eta*neuron.getGradient()*(data!=DBL_MAX ? data : 1) : 0)+alpha*con.deltaWeight;
        }
     }
//---
   return true;
  }

После обновления матрицы весов выходим из метода с результатом true.

После создания класса внесем небольшие корректировки в диспетчеры базового класса CNeuronBase, чтобы они могли правильно обрабатывать экземпляры нового класса. С полным кодом всех методов и функций можно ознакомиться во вложении.

4. Тестирование

Тестирование работы созданного нами блока LSTM осуществлялось в тех же условиях, что и предыдущее тестирование сверточных сетей. Для тестирования был создан советник Fractal_LSTM. По существу, это тот же Fractal_conv из предыдущей статьи, только в функции OnInit в блоке задания структуры нейронной сети сверточный и подвыборочный слои заменены на слой из 4 блоков LSTM (по аналогии с 4-мя фильтрами сверточной сети).

      //---
      desc=new CLayerDescription();
      if(CheckPointer(desc)==POINTER_INVALID)
         return INIT_FAILED;
      desc.count=4;
      desc.type=defNeuronLSTM;
      desc.window=(int)HistoryBars*12;
      desc.step=(int)HistoryBars/2;
      if(!Topology.Add(desc))
         return INIT_FAILED;

Других изменений в код советника не вносились. С полным кодом советника и классов можно ознакомиться во вложении.

Вполне естественно, что наличие 4-х внутренних нейронных слоев в каждом блоке LSTM и сложность самого алгоритма сказались на производительности, скорость работы такой нейронной сети несколько ниже рассмотренной ранее сверточной сети. Но при этом среднеквадратичная ошибка работы рекуррентной сети значительно меньше.

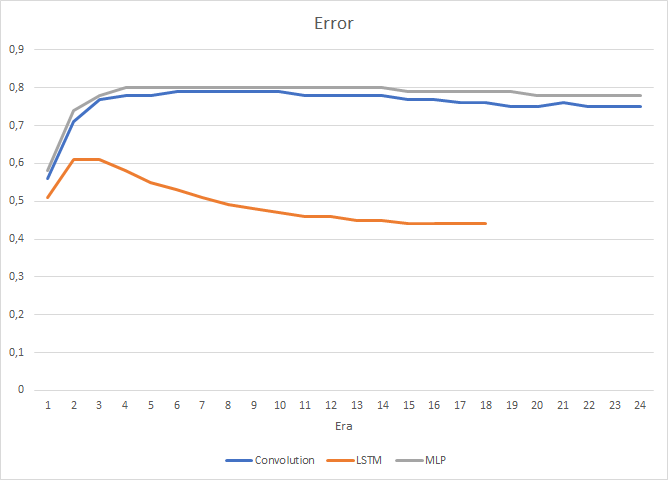
При этом в процессе обучения рекуррентной нейронной сети график точности попадания в цель имеет ярко выраженный, практически прямолинейный, восходящий тренд.

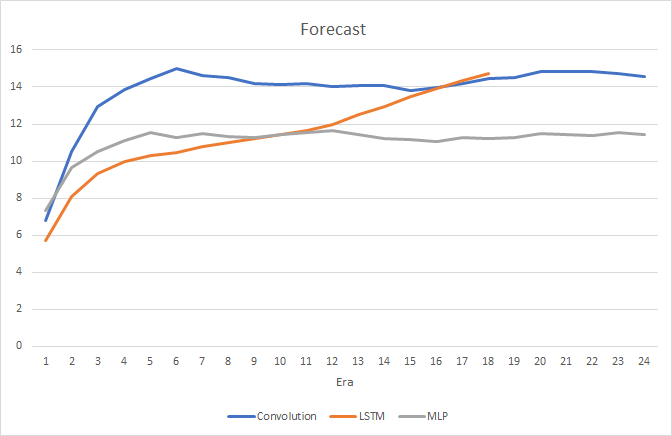
На ценовом графике видны лишь редкие указатели на предсказанные фракталы. Напомню, что при предыдущих тестах ценовой график был практически усеян метками.

Тестирование рекуррентной нейронной сети

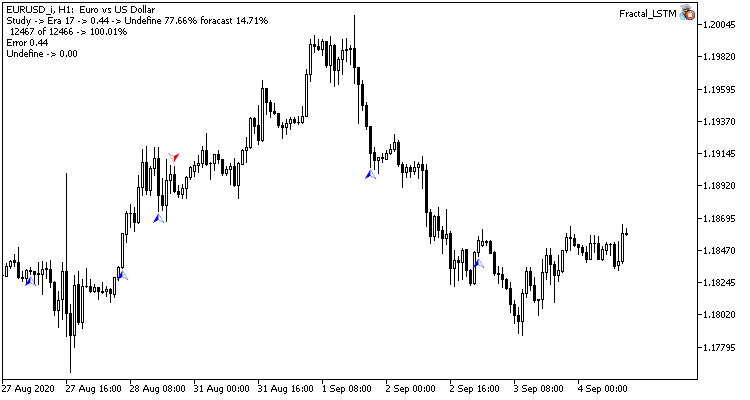
Заключение

В данной статье мы рассмотрели алгоритм работы рекуррентных нейронных сетей, построили LSTM блок и протестировали на реальных данных работу построенной нейронной сети. В сравнении с рассмотренными ранее типами нейронных сетей, рекуррентные сети требуют больших трудозатрат как на прямой проход, так и в процессе обучения. Но в тоже время показывают лучшие результаты работы, и это подтверждается проведенными тестами.

Ссылки

Программы, используемые в статье

#	Имя	Тип	Описание
1	Fractal.mq5	Советник	Советник с нейронной сетью регрессии (1 нейрон в выходном слое)
2	Fractal_2.mq5	Советник	Советник с нейронной сетью классификации (3 нейрона в выходном слое)
3	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети (перцептрона)
4	Fractal_conv.mq5	Советник	Советник со сверточной нейронной сетью классификации (3 нейрона в выходном слое)
5	Fractal_LSTM.mq5	Советник	Советник с рекуррентной нейронной сетью классификации (3 нейрона в выходном слое)

Прикрепленные файлы |

Загрузить ZIP

MQL5.zip (32.06 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Последние комментарии | Перейти к обсуждению на форуме трейдеров (4)

Aleksandr Masterskikh | 10 сент. 2020 в 16:23

Нейросети - очень нужная тема для трейдинга.

В то же время, нейросети должны учитывать природу процесса.

Финансовые рынки - это поведенческие системы, причём процесс движения цен здесь является нестационарным.

В рамках теории импульсного равновесия поведенческий фактор учтён - это конкретные параметры - "элементарная структура (М-форма)", "побуждающая амплитуда", "активный" импульс", и "сверхактивны импульс".

Было бы интересно дать эту информацию нейросети, как опорную.

Tatiana Savkevych | 20 окт. 2020 в 21:24

Очень интересная работа.

Roman Korotchenko | 3 июл. 2022 в 11:33

Увлекательное исследование и разбор деталей. Профессиональность автора не вызывает сомнений - реализация программных блоков это подтверждает. Вопрос возникает следующий: Если в программах MQL5 разрешается использовать Python и, соответственно, Keras, TensorFlow, PyTorch, то было бы проще и перспективнее реализовать нейросети этими средствами, используя богатый инструментарий из набора?

Dmitriy Gizlyk | 3 июл. 2022 в 13:25

Roman Korotchenko #:

Здесь несколько причин.
1. Данная статья позволяет увидеть принципы работы алгоритма. Если Вам это не интересно, всегда можно использовать готовые библиотеки Python и других языков программирования.
2. Первая интеграция с Python была добавлена 12 июня 2019 build 2085 в которой можно было только получать котировки. С тех пор возможности интеграции постоянно расширяются. Но и сейчас она не полная. Возможности MQL5 шире.
3. Многие здесь не профессиональные программисты. И для них, изучение интеграции и ещё одного языка программирования может быть затруднительно. Возможно, кому-то может показаться и статья трудной для понимания, но они всегда могут воспользоваться приложенным готовым кодом для своих разработок.

Ну и посмотрите на Python. Указанные Вами библиотеки тоже когда-то были созданы и используют интеграцию с другими языками программирования, о которой пользователь может даже не догадываться. И создание подобных библиотек на MQL5 только расширяет его возможности.

Брутфорс-подход к поиску закономерностей

В данной статье мы будем искать закономерности на рынке, создавать советников на их основе и проверять, как долго эти закономерности сохраняют работоспособность и вообще, сохраняют ли они ее.

Пишем Twitter-клиент для MetaTrader 4 и MetaTrader 5 без использования DLL

Хотите получать твиты или публиковать свои торговые сигналы в Твиттере? Больше не нужно искать решения — в этой серии статей мы рассмотрим, как работать с Твиттером без использования DLL. Мы вместе реализуем Tweeter API с помощью MQL. В первой статье начнем с возможностей аутентификации и авторизации в с Twitter API.

Работа с таймсериями в библиотеке DoEasy (Часть 52): Кроссплатформенность мультипериодных мультисимвольных однобуферных стандартных индикаторов

В статье рассмотрим создание мультисимвольного мультипериодного стандартного индикатора Accumulation/Distribution. Чтобы программы, написанные под устаревшую платформу MetaTrader 4, основанные на данной библиотеке, могли нормально работать при переходе на MetaTrader 5, мы немного доработаем классы библиотеки касаемо индикаторов.

Торговля на форекс и ее базовая математика

Статья ставит целью максимально просто и быстро описать основные особенности торговли на форекс, поделиться простыми истинами с новичками. Ну и постараться ответить на наиболее волнующие вопросы в трейдерской среде, а также написать простенький индикатор.