Redes neurais em trading: Redução de consumo de memória com o método de otimização Adam-mini

Introdução

Ao começar a explorar redes neurais, discutimos diferentes abordagens para otimizar os parâmetros dos modelos. Em trabalho, utilizamos diversas estratégias. Pessoalmente, uso frequentemente o método Adam, que ajusta adaptativamente a taxa de aprendizado ideal para cada parâmetro do modelo. No entanto, essa adaptabilidade tem um custo. O algoritmo Adam usa momentos de primeira e segunda ordem para cada parâmetro, o que demanda o dobro da memória do próprio modelo. Esse alto consumo de memória torna-se um obstáculo significativo no treinamento de modelos grandes. Na prática, para lidar com esse consumo elevado, é necessário fazer offloading para o CPU, o que aumenta a latência e desacelera o treinamento. Diante desses desafios, torna-se ainda mais relevante buscar novos métodos ou aprimorar os já conhecidos para otimizar os parâmetros dos modelos. 

Uma solução interessante foi apresentada no artigo "Adam-mini: Use Fewer Learning Rates To Gain More", publicado em julho de 2024. Os autores propuseram uma modificação no método Adam que mantém seu desempenho. O novo otimizador, chamado Adam-mini, divide os parâmetros do modelo em blocos e atribui uma única taxa de aprendizado para cada bloco, proporcionando as seguintes vantagens:

• Simplicidade: o Adam-mini reduz significativamente o número de taxas de aprendizado utilizadas pelo Adam, diminuindo o consumo de memória em cerca de 45 a 50%.
• Eficiência: apesar da economia de recursos, o Adam-mini apresenta desempenho comparável ou até superior ao método Adam básico.
  

1. O algoritmo Adam-mini

Os autores do Adam-mini exploram o papel de v (momento de segunda ordem) no Adam e suas possibilidades de melhoria. No Adam, v fornece uma taxa de aprendizado individual para cada parâmetro. Foi observado que o Hessiano em Transformers e outras redes neurais apresenta uma estrutura quase diagonal em blocos. Cada bloco de um Transformer possui uma distribuição de autovalores consideravelmente distinta. Dessa forma, os Transformers requerem taxas de aprendizado diferentes para cada bloco, a fim de lidar com a heterogeneidade desses autovalores, o que é viabilizado pelo uso de v no Adam.

No entanto, o Adam faz muito mais: ele atribui uma taxa de aprendizado não apenas para cada bloco, mas também para cada parâmetro. É importante ressaltar que o número de parâmetros é muito maior que o de blocos. Isso levanta a seguinte questão: é realmente necessário usar uma taxa de aprendizado individual para cada parâmetro? Se não for, quanto podemos economizar?

Os autores do método investigam essa questão em problemas gerais de otimização e chegam às seguintes conclusões:

• O Adam supera o método que utiliza uma única taxa ótima de aprendizado. Isso era esperado, já que o Adam aplica taxas de aprendizado diferentes a diferentes parâmetros.
• Contudo, ao selecionar um subbloco específico com Hessiano denso, observa-se que o método com uma única taxa de aprendizado ótima supera o Adam.
• Portanto, taxas de aprendizado ótimas aplicadas à versão "em blocos" do gradiente descendente podem melhorar a eficiência do processo de treinamento do problema original.

Para problemas gerais com Hessiano em formato de bloco diagonal, um maior número de taxas de aprendizado não necessariamente oferece benefícios adicionais. Em particular, para cada sub-bloco denso, uma única taxa de aprendizado (bem ajustada) é suficiente para alcançar o melhor desempenho.

Fenômenos semelhantes são observados em modelos baseados nessa arquitetura. Os autores do Adam-mini realizam uma série de experimentos com um Transformer de quatro camadas e constatam que, nesses modelos, é possível alcançar um desempenho igual ou superior utilizando um número muito menor de taxas de aprendizado em comparação com o Adam.

Resta a questão de como encontrar as taxas de aprendizado ideais.

O objetivo do Adam-mini é reduzir o uso de recursos relacionados às taxas de aprendizado no método Adam, sem exigir uma busca intensiva em grades para otimizá-las.

O Adam-mini é composto por duas etapas. A Etapa 1 é necessária apenas na inicialização.

Primeiramente, dividimos os parâmetros do modelo em blocos. No caso do Transformer, os autores sugerem dividir todas as Queries e Keys por cabeças de atenção. Em outros casos, utiliza-se um único momento de segunda ordem para cada camada.

Os blocos de Embeddings são tratados separadamente. Para esses blocos, é preferível usar o método Adam clássico, pois o grande número de valores nulos nos embeddings de elementos individuais causa um forte desvio na distribuição média em relação à distribuição da variável original.

Na segunda etapa do algoritmo, utiliza-se uma única taxa de aprendizado para cada bloco de parâmetros (exceto os blocos de Embeddings). Para escolher eficientemente a taxa de aprendizado adequada em cada bloco, o Adam-mini substitui o quadrado do gradiente do erro pelo seu valor médio. Assim como no Adam clássico, os autores aplicam uma média móvel a esses valores médios.

De acordo com os autores do método, no Transformer, o Adam-mini reduz o número de taxas de aprendizado do total de parâmetros para a soma do tamanho das camadas de embeddings, da camada de saída e do número de blocos em outras camadas. Assim, a economia de memória depende da proporção de parâmetros não relacionados a embeddings no modelo.

O Adam-mini pode alcançar maior throughput em comparação ao Adam, especialmente em ambientes com recursos de hardware limitados. Isso ocorre por duas razões. Primeiro, o Adam-mini não adiciona carga computacional extra às regras de atualização. Além disso, ele reduz significativamente a quantidade de operações de extração de raízes quadradas e divisão de tensores utilizadas no Adam.

Em segundo lugar, com a redução do uso de memória, o Adam-mini permite o suporte a lotes maiores de GPU, ao mesmo tempo em que minimiza a comunicação entre GPU e CPU, um gargalo conhecido em sistemas computacionais.

Graças a essas características, o Adam-mini pode reduzir o tempo total de pré-treinamento de modelos grandes.

O Adam-mini projeta a taxa de aprendizado para cada subbloco denso do Hessiano utilizando o valor médio de v no Adam para esse bloco. Embora esse design priorize a eficiência computacional, ele pode não ser o mais otimizado. Felizmente, o modelo atual é suficiente para alcançar desempenho igual ou ligeiramente superior ao Adam, com consumo de memória consideravelmente reduzido.

2. Implementação com MQL5

Depois de discutir os aspectos teóricos do Adam-mini, passamos à aplicação prática usando MQL5. Neste artigo, implementaremos nossa própria visão das abordagens descritas por meio da MQL5.

Devo mencionar que esta implementação difere significativamente de nossos projetos anteriores. Geralmente, desenvolvemos novos métodos dentro de uma única classe da camada do modelo. Desta vez, no entanto, será necessário modificar diversas classes existentes. Isso ocorre porque cada classe previamente criada contém o método updateInputWeights, herdado ou redefinido, que implementa o algoritmo de atualização dos parâmetros do modelo para aquela camada.

Existem, é claro, métodos updateInputWeights em algumas classes que servem como soluções arquitetônicas mais complexas, nas quais apenas são chamados métodos equivalentes de objetos internos. Um exemplo seria o Decodificador, discutido em um artigo anterior. Nesses casos, o algoritmo não depende do método de otimização utilizado. 

bool CNeuronSTNNDecoder::updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *Context)
  {
   if(!cEncoder.UpdateInputWeights(NeuronOCL, Context))
      return false;
   if(!CNeuronMLCrossAttentionMLKV::updateInputWeights(cEncoder.AsObject(), Context))
      return false;
//---
   return true;
  }

Ao descer pela hierarquia de chamadas, sempre chegamos às "peças-chave" fundamentais em que o algoritmo principal de atualização dos parâmetros do modelo é implementado.

2.1 Implementação do Adam-mini na camada totalmente conectada básica

Um desses componentes é a nossa classe base para camadas totalmente conectadas, a CNeuronBaseOCL. Portanto, iniciaremos nosso trabalho com ela.

É importante lembrar que a maioria das tarefas computacionais foi transferida para o GPU, possibilitando cálculos em múltiplos threads. Esse processo não será uma exceção. Assim, utilizaremos um programa OpenCL para criar um novo kernel chamado UpdateWeightsAdamMini.

Antes de escrever o código do programa, discutiremos brevemente a solução arquitetural planejada.

O novo método de otimização Adam-mini difere do Adam clássico principalmente no que se refere ao algoritmo de cálculo do momento de segunda ordem v. No Adam-mini, em vez de calcular o gradiente do erro para cada parâmetro individualmente, os autores propõem usar o valor médio de um grupo. Embora o algoritmo para calcular essa média seja simples, ele libera uma quantidade significativa de memória, já que apenas um valor do momento de segunda ordem é armazenado para cada grupo.

Por outro lado, não seria eficiente calcular a média de todo o bloco em cada thread separadamente. Para camadas totalmente conectadas, os autores do Adam-mini recomendam usar uma única taxa de aprendizado. Assim, repetir o cálculo da média do gradiente de erro para todos os parâmetros da camada em cada thread é, no mínimo, ineficaz. Além disso, considerando que esse processo envolve múltiplos acessos à memória global, que é relativamente custosa, torna-se evidente a necessidade de paralelizar o processo em múltiplos threads, minimizando os acessos à memória global. Isso, porém, levanta a questão de como organizar a troca de dados entre threads.

Em trabalhos anteriores, já abordamos o intercâmbio de dados dentro de grupos locais com sincronização de threads. No entanto, consolidar todo o processo de atualização de parâmetros de uma camada em um único grupo local não parece ser a melhor solução. Portanto, nesta implementação, decidiu-se aumentar ligeiramente o número de momentos de segunda ordem calculados, igualando-os ao tamanho do tensor de resultados.

Lembre-se de que o número de parâmetros de uma camada totalmente conectada é igual ao produto do tamanho do tensor de entrada pelo tamanho do tensor de saída. O uso de um parâmetro de viés para cada neurônio adiciona um número de parâmetros equivalente ao tamanho do tensor de saída. O Adam clássico armazena a mesma quantidade de valores para os momentos de primeira e segunda ordens. Na implementação do Adam-mini, reduzimos significativamente a quantidade de valores para o momento de segunda ordem.

Agora, discutamos o processo de cálculo do valor médio do momento de segunda ordem. O gradiente do erro de um parâmetro é o produto entre o gradiente do erro na saída da camada (ajustado pela derivada da função de ativação) e o valor correspondente da entrada.

O valor médio do quadrado dos gradientes pode ser calculado da seguinte forma:

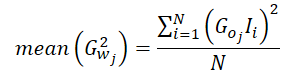
Como calculamos o gradiente médio do erro por neurônio da camada de saída em nossa implementação, o gradiente de erro deste neurônio pode ser isolado da fórmula.

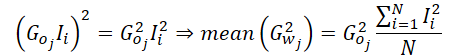
Portanto, ao calcular o valor médio do momento de segunda ordem, basta determinar o valor médio dos quadrados dos dados de entrada, eliminando a necessidade de acessar o buffer de gradientes de erro da camada de saída localizado na memória global. Depois, aplicamos o valor do gradiente de erro uma única vez, multiplicando seu quadrado pelo valor médio calculado. O resultado final pode ser distribuído por todo o grupo de trabalho local para os cálculos subsequentes.

Com uma compreensão clara do algoritmo, podemos passar à implementação no código do kernel UpdateWeightsAdamMini. Os parâmetros deste kernel são quase idênticos aos do kernel do método Adam clássico, incluindo cinco buffers de dados e três constantes:

• matrix_w: matriz de parâmetros da camada;
• matrix_g: tensor de gradientes de erro na saída da camada;
• matrix_i: buffer de dados de entrada;
• matrix_m: tensor de momentos de primeira ordem;
• matrix_v: tensor de momentos de segunda ordem;
• l: taxa de aprendizado;
• b1: coeficiente de suavização dos momentos de primeira ordem (ß1);
• b2: coeficiente de suavização dos momentos de segunda ordem (ß2);

__kernel void UpdateWeightsAdamMini(__global float *matrix_w, 
                                    __global const float *matrix_g,
                                    __global const float *matrix_i,
                                    __global float *matrix_m,
                                    __global float *matrix_v,
                                    const float l,
                                    const float b1,
                                    const float b2 
                                   )
  {
//--- inputs
   const size_t i = get_local_id(0);
   const size_t inputs = get_local_size(0) - 1;
//--- outputs
   const size_t o = get_global_id(1);
   const size_t outputs = get_global_size(1);

O kernel será executado em um espaço de tarefas bidimensional. A primeira dimensão corresponde ao número de dados de entrada mais o elemento de viés, enquanto a segunda dimensão reflete o tamanho do tensor de saída. Dentro do kernel, identificamos imediatamente o fluxo em ambas as dimensões.

Vale notar que combinamos os fluxos em grupos de trabalho baseados na primeira dimensão do espaço de tarefas.

Em seguida, criamos um array na memória local do contexto para a troca de dados entre os fluxos do grupo de trabalho.

   __local float temp[LOCAL_ARRAY_SIZE];
   const int ls = min((uint)LOCAL_ARRAY_SIZE, (uint)inputs);

No próximo passo, calculamos o valor médio do quadrado desses dados. Como o valor do buffer de entrada também será necessário no cálculo do momento de primeira ordem, cada fluxo inicialmente acessa um valor correspondente do buffer global de entrada.

   const float inp = (i < inputs ? matrix_i[i] : 1.0f);

Em seguida, criamos um laço com sincronização entre threads, no qual cada thread adiciona o valor quadrático do respectivo elemento dos dados de entrada ao array local.

   int count = 0;
   do
     {
      if(count == (i / ls))
        {
         int shift = i % ls;
         temp[shift] = (count == 0 ? 0 : temp[shift]) + ((isnan(inp) || isinf(inp)) ? 0 : inp*inp);
        }
      count++;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count * ls < inputs);

Depois disso, somamos os valores dos elementos do array local.

//--- sum
   count = (ls + 1) / 2;
   do
     {
      if(i < count && (i + count) < ls)
        {
         temp[i] += temp[i + count];
         temp[i + count] = 0;
        }
      count = (count + 1) / 2;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Dentro de um único thread, calculamos o momento de segunda ordem e armazenamos o resultado no elemento de índice 0 do array local.

Além disso, lembramos que o acesso à memória local é significativamente mais rápido do que o acesso ao buffer da memória global. Para reduzir essas operações, o gradiente do erro da camada atual é carregado no elemento de índice 1 do array local. Dessa forma, as operações subsequentes realizadas pelos outros threads do grupo de trabalho acessam diretamente a memória local, evitando a necessidade de acessar a memória global.

A sincronização dos threads do grupo de trabalho é obrigatória.

//--- calc v
   if(i == 0)
     {
      temp[1] = matrix_g[o];
      if(isnan(temp[1]) || isinf(temp[1]))
         temp[1] = 0;
      temp[0] /= inputs;
      if(isnan(temp[0]) || isinf(temp[0]))
         temp[0] = 1;
      float v = matrix_v[o];
      if(isnan(v) || isinf(v))
         v = 1;
      temp[0] = b2 * v + (1 - b2) * pow(temp[1], 2) * temp[0];
      matrix_v[o] = temp[0];
     }
   barrier(CLK_LOCAL_MEM_FENCE);

Note que o momento de segunda ordem é imediatamente salvo no buffer global. Esse passo simples elimina acessos desnecessários a esse buffer por outros threads do grupo de trabalho e evita atrasos causados por múltiplos acessos simultâneos a um mesmo elemento da memória global. 

Em seguida, o algoritmo segue os passos do método Adam clássico. Primeiro, determinamos o deslocamento no tensor de parâmetros treináveis e carregamos o valor atual do parâmetro em análise a partir do buffer global.

   const int wi = o * (inputs + 1) + i;
   float weight = matrix_w[wi];
   if(isnan(weight) || isinf(weight))
      weight = 0;

Calculamos o valor do momento de primeira ordem.

   float m = matrix_m[wi];
   if(isnan(m) || isinf(m))
      m = 0;
//--- calc m
   m = b1 * m + (1 - b1) * temp[1] * inp;
   if(isnan(m) || isinf(m))
      m = 0;

Determinamos o tamanho do ajuste do parâmetro.

   float delta = l * (m / (sqrt(temp[0]) + 1.0e-37f) - (l1 * sign(weight) + l2 * weight));
   if(isnan(delta) || isinf(delta))
      delta = 0;

Corrigimos o valor do parâmetro e salvamos o novo valor no buffer global.

   if(delta > 0)
      matrix_w[wi] = clamp(weight + delta, -MAX_WEIGHT, MAX_WEIGHT);
   matrix_m[wi] = m;
  }

Nesse ponto, também armazenamos o valor do momento de primeira ordem e finalizamos o kernel.

Após fazer as alterações no programa OpenCL, precisamos realizar ajustes no programa principal. Primeiramente, adicionamos o novo método de otimização ao nosso conjunto de enumerações.

//+------------------------------------------------------------------+
/// Enum of optimization method used                                 |
//+------------------------------------------------------------------+
enum ENUM_OPTIMIZATION
  {
   SGD,        ///< Stochastic gradient descent
   ADAM,       ///< Adam
   ADAM_MINI   ///< Adam-mini
  };

Depois, modificamos o método CNeuronBaseOCL::updateInputWeights. No bloco de declaração de variáveis, incluímos um array para descrever o tamanho do grupo de trabalho local (local_work_size, destacado no código). Nesse estágio, não atribuiremos valores ao array, pois eles serão necessários apenas ao usar o método de otimização correspondente.

bool CNeuronBaseOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(CheckPointer(OpenCL) == POINTER_INVALID || CheckPointer(NeuronOCL) == POINTER_INVALID)
      return false;
   uint global_work_offset[2] = {0, 0};
   uint global_work_size[2], local_work_size[2];
   global_work_size[0] = Neurons();
   global_work_size[1] = NeuronOCL.Neurons() + 1;
   uint rest = 0;
   float lt = lr;

O algoritmo então se ramifica de acordo com o método de otimização selecionado. Os procedimentos para ordenar os kernels dos métodos de otimização já discutidos permanecem inalterados, portanto não entraremos em detalhes.

   switch(NeuronOCL.Optimization())
     {
      case SGD:
.........
.........
.........
         break;
      case ADAM:
........
........
........
         break;

Vamos revisar o código adicionado. Primeiro, passamos os parâmetros necessários para o funcionamento correto do kernel.

      case ADAM_MINI:
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdamMini, def_k_wuam_matrix_w,
                                                           NeuronOCL.getWeightsIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdamMini, def_k_wuam_matrix_g,
                                                                    getGradientIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdamMini, def_k_wuam_matrix_i, 
                                                            NeuronOCL.getOutputIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdamMini, def_k_wuam_matrix_m, 
                                                     NeuronOCL.getFirstMomentumIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdamMini, def_k_wuam_matrix_v, 
                                                    NeuronOCL.getSecondMomentumIndex()))
            return false;
         lt = (float)(lr * sqrt(1 - pow(b2, (float)t)) / (1 - pow(b1, (float)t)));
         if(!OpenCL.SetArgument(def_k_UpdateWeightsAdamMini, def_k_wuam_l, lt))
            return false;
         if(!OpenCL.SetArgument(def_k_UpdateWeightsAdamMini, def_k_wuam_b1, b1))
            return false;
         if(!OpenCL.SetArgument(def_k_UpdateWeightsAdamMini, def_k_wuam_b2, b2))
            return false;

Em seguida, definimos os espaços de trabalho para a execução global do kernel e para cada grupo de trabalho.

         global_work_size[0] = NeuronOCL.Neurons() + 1;
         global_work_size[1] = Neurons();
         local_work_size[0] = global_work_size[0];
         local_work_size[1] = 1;

É importante notar que, na primeira dimensão, tanto para o espaço global quanto para o grupo de trabalho, especificamos um valor que é um elemento maior que o tamanho da camada de entrada. Esse elemento adicional corresponde ao parâmetro de viés. Na segunda dimensão, o espaço global define o número de elementos na camada de neurônios atual, enquanto o grupo de trabalho é limitado a um elemento, o que corresponde ao trabalho de uma única unidade do grupo no neurônio atual.

Após a preparação, o kernel é enfileirado para execução.

         ResetLastError();
         if(!OpenCL.Execute(def_k_UpdateWeightsAdamMini, 2, global_work_offset, global_work_size, 
                                                                                local_work_size))
           {
            printf("Error of execution kernel UpdateWeightsAdamMini: %d", GetLastError());
            return false;
           }
         t++;
         break;
      default:
         return false;
         break;
     }
//---
   return true;
  }

Também adicionamos uma saída com resultado negativo caso seja especificado um método de otimização de parâmetros incorreto.

Com isso, concluímos o trabalho no método de atualização de parâmetros da camada base totalmente conectada CNeuronBaseOCL::updateInputWeights. Porém, é crucial lembrar do objetivo das alterações realizadas: reduzir o consumo de memória ao usar o método de otimização Adam. Assim, é necessário revisar o método de inicialização da classe CNeuronBaseOCL::Init para reduzir o tamanho do buffer de momentos de segunda ordem ao optar pelo método de otimização Adam-mini. Como essas alterações são pontuais, não apresentarei o algoritmo completo, mas apenas o trecho de inicialização do buffer correspondente.

         if(CheckPointer(SecondMomentum) == POINTER_INVALID)
           {
            SecondMomentum = new CBufferFloat();
            if(CheckPointer(SecondMomentum) == POINTER_INVALID)
               return false;
           }
         if(!SecondMomentum.BufferInit((optimization == ADAM_MINI ? numOutputs : count), 0))
            return false;
         if(!SecondMomentum.BufferCreate(OpenCL))
            return false;

O código completo desse método, bem como os demais programas usados neste artigo, estão disponíveis no anexo. Lá, você encontrará o código completo para consulta.

2.2 Adam-mini na camada convolucional

Outro "bloco fundamental" amplamente utilizado em diversas arquiteturas, incluindo Transformers, é a camada convolucional (conv2d layer).

A adição do método de otimização Adam-mini ao seu funcional apresenta particularidades relacionadas às especificidades dessa camada. Ao contrário da camada totalmente conectada, na qual cada parâmetro treinável é usado para transferir valores entre um único neurônio da entrada e um único neurônio da camada atual, a camada convolucional tem menos parâmetros, mas seu uso é mais abrangente.

Vale lembrar que usamos as camadas convolucionais para criar as entidades Query, Key e Value no contexto dos algoritmos Transformer. Essas entidades apresentam especificidades próprias para a implementação do método Adam-mini.

Todos esses aspectos devem ser considerados ao implementar o Adam-mini em camadas convolucionais.

Assim como no caso da camada totalmente conectada, iniciaremos nosso trabalho no programa OpenCL. Aqui, criaremos o kernel UpdateWeightsConvAdamMini. Além das variáveis já conhecidas, são adicionadas duas constantes aos parâmetros deste kernel: o tamanho da sequência de entrada e o passo da janela de convolução.

__kernel void UpdateWeightsConvAdamMini(__global float *matrix_w,  
                                        __global const float *matrix_i,
                                        __global float *matrix_m,      
                                        __global float *matrix_v,      
                                        const int inputs,              
                                        const float l,              
                                        const float b1,             
                                        const float b2,             
                                        int step                    
                                       )
  {
//--- window in
   const size_t i = get_global_id(0);
   const size_t window_in = get_global_size(0) - 1;
//--- window out
   const size_t f = get_global_id(1);
   const size_t window_out = get_global_size(1);
//--- head window out
   const size_t f_h = get_local_id(1);
   const size_t window_out_h = get_local_size(1);
//--- variable
   const size_t v = get_global_id(2);
   const size_t variables = get_global_size(2);

É importante notar que não especificamos o tamanho da janela de entrada nem o número de filtros utilizados nos parâmetros do kernel. Esses parâmetros, juntamente com outros dois, são definidos no espaço de tarefas, o que merece atenção.

Planejamos executar este kernel em um espaço de tarefas tridimensional. A primeira dimensão corresponde ao tamanho da janela de entrada, mais um elemento para o viés. Nesse sentido, há uma semelhança com o espaço de tarefas da camada totalmente conectada.

A segunda dimensão do espaço de tarefas representa o número de filtros utilizados. Nesse caso, há uma ligação lógica com a dimensionalidade dos resultados da camada totalmente conectada.

No entanto, os grupos de trabalho não serão criados para cada filtro individual, mas sim agrupados por cabeças de atenção da arquitetura Transformer.

O usuário pode especificar apenas um filtro de convolução por cabeça de atenção. Nesse caso, cada filtro de convolução recebe uma taxa de aprendizado individual, semelhante à implementação para a camada totalmente conectada.

A terceira dimensão do espaço de tarefas foi criada para lidar com séries temporais multimodais, em que cada sequência unária utiliza seus próprios filtros de convolução. Para esses filtros, também criamos momentos de segunda ordem separados, possibilitando taxas de aprendizado adaptativas.

Aqui, é muito importante distinguir entre "cabeças de atenção" e "séries temporais unitárias". Apesar de algumas semelhanças, esses conceitos não devem ser confundidos. Séries temporais unitárias dividem o tensor de entrada, enquanto cabeças de atenção dividem o tensor de resultados.

No corpo do kernel, após identificar o fluxo em todas as dimensões do espaço de tarefas, determinamos as constantes de deslocamento nos buffers globais de dados.

//--- constants
   const int total = (inputs - window_in + step - 1) / step;
   const int shift_var_in = v * inputs;
   const int shift_var_out = v * total * window_out;
   const int shift_w = (f + v * window_out) * (window_in + 1) + i;

Em seguida, criamos um array local para troca de informações entre os threads do grupo de trabalho.

   __local float temp[LOCAL_ARRAY_SIZE];
   const int ls = min((uint)window_in, (uint)LOCAL_ARRAY_SIZE);

Após essa preparação, reunimos os gradientes de erro para cada parâmetro.

//--- calc gradient
   float grad = 0;
   for(int t = 0; t < total; t++)
     {
      if(i != window_in && (i + t * window_in) >= inputs)
         break;
      float gt = matrix_g[t * window_out + f + shift_var_out] *
                 (i == window_in ? 1 : matrix_i[i + t * step + shift_var_in]);
      if(!(isnan(gt) || isinf(gt)))
         grad += gt;
     }

Nesta etapa, cada fluxo global coleta completamente os gradientes de erro de todos os elementos sob sua influência. Diferentemente da camada totalmente conectada, nesta etapa multiplicamos diretamente o valor do elemento de entrada pelo gradiente de erro correspondente aos resultados.

Depois, coletamos os gradientes de erro obtidos para somar os valores quadráticos nos elementos do array local, agora no contexto do grupo de trabalho. Para isso, organizamos um sistema de laços aninhados com sincronização obrigatória dos threads. O laço externo corresponde ao número de filtros dentro do grupo de trabalho, enquanto o laço interno reúne os gradientes de erro de todos os parâmetros de um único filtro.  

//--- calc sum grad
   int count;
   for(int h = 0; h < window_out_h; h++)
     {
      count = 0;
      do
        {
         if(h == f_h)
           {
            if(count == (i / ls))
              {
               int shift = i % ls;
               temp[shift] = ((count == 0 && h == 0) ? 0 : temp[shift]) + 
                             ((isnan(grad) || isinf(grad)) ? 0 : grad * grad);
              }
           }
         count++;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while((count * ls) < window_in);
     }

Em seguida, somamos os valores do array local.

   count = (ls + 1) / 2;
   do
     {
      if(i < count && (i + count) < ls && f_h == 0)
        {
         temp[i] += temp[i + count];
         temp[i + count] = 0;
        }
      count = (count + 1) / 2;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Determinamos o valor do momento de segunda ordem do grupo atual.

//--- calc v
   if(i == 0 && f_h == 0)
     {
      temp[0] /= (window_in * window_out_h);
      if(isnan(temp[0]) || isinf(temp[0]))
         temp[0] = 1;
      int head = f / window_out_h;
      float v = matrix_v[head];
      if(isnan(v) || isinf(v))
         v = 1;
      temp[0] = clamp(b2 * v + (1 - b2) * temp[0], 1.0e-6f, 1.0e6f);
      matrix_v[head] = temp[0];
     }
   barrier(CLK_LOCAL_MEM_FENCE);

Depois, repetimos o algoritmo do método Adam clássico. Calculamos o momento de primeira ordem.

//--- calc m
   float mt = clamp(b1 * matrix_m[shift_w] + (1 - b1) * grad, -1.0e5f, 1.0e5f);
   if(isnan(mt) || isinf(mt))
      mt = 0;

Ajustamos o valor do parâmetro analisado.

   float weight = clamp(matrix_w[shift_w] + l * mt / sqrt(temp[0]), -MAX_WEIGHT, MAX_WEIGHT);

E salvamos os valores obtidos.

   if(!(isnan(weight) || isinf(weight)))
      matrix_w[shift_w] = weight;
   matrix_m[shift_w] = mt;
  }

Com o kernel criado no lado OpenCL, passamos a trabalhar na aplicação principal. Assim como na camada totalmente conectada, o kernel criado é chamado no método CNeuronConvOCL::updateInputWeights. O algoritmo para essa chamada segue um padrão semelhante ao apresentado para a camada totalmente conectada. Para uma camada convolucional convencional, usamos um filtro de atenção por cabeça e uma sequência unitária. Dessa maneira, a dimensionalidade do espaço de tarefas adota o formato descrito.

   uint global_work_offset_am[3] = { 0, 0, 0 };
   uint global_work_size_am[3] = { iWindow + 1, iWindowOut, iVariables };
   uint local_work_size_am[3] = { global_work_size_am[0], 1, 1 };

O código completo desse método, bem como os demais programas usados neste artigo, estão disponíveis no anexo.

O código completo deste método está disponível no anexo para consulta. Gostaria de acrescentar algumas observações sobre o uso do kernel criado na implementação de classes que utilizam a arquitetura Transformer. Por exemplo, considere a classe CNeuronMLMHAttentionOCL, usada como classe base para construir diversos algoritmos.

Vale lembrar que a classe CNeuronMLMHAttentionOCL não possui camadas convolucionais em sua estrutura, no sentido convencional. Ela organiza matrizes de buffers e redefine todos os métodos. A atualização de parâmetros das camadas convolucionais é realizada no método ConvolutionUpdateWeights. Como esse método é usado para operar diferentes camadas convolucionais, adicionamos dois parâmetros adicionais: o número de cabeças de atenção (heads) e o número de sequências unitárias (variables). Para evitar problemas ao chamar esse método de outras classes, esses novos parâmetros recebem valores padrão.

bool CNeuronMLMHAttentionOCL::ConvolutuionUpdateWeights(CBufferFloat *weights, 
                                                        CBufferFloat *gradient, 
                                                        CBufferFloat *inputs, 
                                                        CBufferFloat *momentum1, 
                                                        CBufferFloat *momentum2, 
                                                        uint window, uint window_out, 
                                                        uint step = 0, uint heads = 0, 
                                                        uint variables = 1)
  {
   if(CheckPointer(OpenCL) == POINTER_INVALID || CheckPointer(weights) == POINTER_INVALID || 
      CheckPointer(gradient) == POINTER_INVALID || CheckPointer(inputs) == POINTER_INVALID  || 
      CheckPointer(momentum1) == POINTER_INVALID)
      return false;

No corpo do método, verificamos inicialmente os ponteiros para os buffers de dados, recebidos como parâmetros da função chamada.

Em seguida, verificamos o valor do parâmetro de passo da janela de convolução. Caso seja "0", ajustamos o passo para corresponder ao tamanho da janela de convolução.

   if(step == 0)
      step = window;

Observe que, neste caso, utilizamos tipos de dados sem sinal para os parâmetros. Consequentemente, esses parâmetros não podem ter valores negativos. O controle de valores excessivamente altos para esses parâmetros fica a cargo do usuário.

Definimos os espaços de tarefas. Neste caso, o kernel do método de otimização Adam-mini utiliza um espaço tridimensional, diferente do espaço unidimensional utilizado por outros métodos de otimização. Por isso, alocamos arrays separados para sua especificação. 

   uint global_work_offset[1] = {0};
   uint global_work_size[1];
   global_work_size[0] = weights.Total();
   uint global_work_offset_am[3] = {0, 0, 0};
   uint global_work_size_am[3] = {window, window_out, 1};
   uint local_work_size_am[3] = {window, (heads > 0 ? window_out / heads : 1), variables};

Observe a segunda dimensão do espaço de tarefas do grupo de trabalho. Se o número de cabeças de atenção não for especificado nos parâmetros do método, será utilizada uma taxa de aprendizado separada para cada filtro. Caso contrário, calculamos o número de filtros por cabeça de atenção dividindo o total de filtros pelo número total de cabeças.

Essa abordagem foi adotada para acomodar diferentes cenários de uso do método. Na classe CNeuronMLMHAttentionOCL, os filtros convolucionais são utilizados tanto para formar as entidades Query, Key e Value quanto para projetar dados (como na camada de redução de dimensionalidade do multi-head attention e no bloco FeedForward).

A próxima etapa consiste em dividir o algoritmo de acordo com o método de otimização de parâmetros utilizado. Assim como na análise dos algoritmos da camada totalmente conectada, não abordaremos os métodos de otimização já implementados, concentrando-nos apenas no bloco referente ao Adam-mini.

   if(weights.GetIndex() < 0)
      return false;
   float lt = 0;
   switch(optimization)
     {
      case SGD:
........
........
........
         break;
      case ADAM:
........
........
........
         break;
      case ADAM_MINI:
         if(CheckPointer(momentum2) == POINTER_INVALID)
            return false;
         if(gradient.GetIndex() < 0)
            return false;
         if(inputs.GetIndex() < 0)
            return false;
         if(momentum1.GetIndex() < 0)
            return false;
         if(momentum2.GetIndex() < 0)
            return false;

Aqui, verificamos a validade dos ponteiros para buffers de dados no contexto do OpenCL e, em seguida, passamos todos os parâmetros necessários para o kernel.

         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsConvAdamMini, def_k_wucam_matrix_w, 
                                                                         weights.GetIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsConvAdamMini, def_k_wucam_matrix_g, 
                                                                        gradient.GetIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsConvAdamMini, def_k_wucam_matrix_i, 
                                                                          inputs.GetIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsConvAdamMini, def_k_wucam_matrix_m, 
                                                                       momentum1.GetIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsConvAdamMini, def_k_wucam_matrix_v, 
                                                                       momentum2.GetIndex()))
            return false;
         lt = (float)(lr * sqrt(1 - pow(b2, t)) / (1 - pow(b1, t)));
         if(!OpenCL.SetArgument(def_k_UpdateWeightsConvAdamMini, def_k_wucam_inputs, 
                                                                            inputs.Total()))
            return false;
         if(!OpenCL.SetArgument(def_k_UpdateWeightsConvAdamMini, def_k_wucam_l, lt))
            return false;
         if(!OpenCL.SetArgument(def_k_UpdateWeightsConvAdamMini, def_k_wucam_b1, b1))
            return false;
         if(!OpenCL.SetArgument(def_k_UpdateWeightsConvAdamMini, def_k_wucam_b2, b2))
            return false;
         if(!OpenCL.SetArgument(def_k_UpdateWeightsConvAdamMini, def_k_wucam_step, (int)step))
            return false;

O espaço de tarefas já foi definido anteriormente, restando apenas enfileirar o kernel para execução.

         ResetLastError();
         if(!OpenCL.Execute(def_k_UpdateWeightsConvAdamMini, 3, global_work_offset_am, 
                                              global_work_size_am, local_work_size_am))
           {
            string error;
            CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error);
            printf("Error of execution kernel %s Adam-Mini: %s", __FUNCSIG__, error);
            return false;
           }
         t++;
         break;
      //---
      default:
         printf("Error of optimization type %s: %s", __FUNCSIG__, EnumToString(optimization));
         return false;
     }

Também adicionamos uma mensagem de erro caso seja especificado um tipo incorreto de otimização de parâmetros.

O restante do método, no que diz respeito à normalização dos parâmetros do modelo, permanece inalterado.

   global_work_size[0] = window_out;
   OpenCL.SetArgumentBuffer(def_k_NormilizeWeights, def_k_norm_buffer, weights.GetIndex());
   OpenCL.SetArgument(def_k_NormilizeWeights, def_k_norm_dimension, (int)window + 1);
   if(!OpenCL.Execute(def_k_NormilizeWeights, 1, global_work_offset, global_work_size))
     {
      string error;
      CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error);
      printf("Error of execution kernel %s Normalize: %s", __FUNCSIG__, error);
      return false;
     }
//---
   return true;
  }

Além disso, ajustamos os tamanhos dos buffers de dados criados para armazenar os momentos de segunda ordem nos métodos de inicialização das classes mencionadas, de forma semelhante ao algoritmo apresentado para a modernização da camada totalmente conectada. No entanto, esses detalhes não serão explorados aqui, pois são alterações pontuais disponíveis no anexo para consulta.

3. Testes

A implementação do método Adam-mini foi descrita para dois dos principais componentes de nossas arquiteturas. Agora é hora de analisar a eficácia dos métodos propostos.

Nesta abordagem, apresentamos um novo método de otimização. Para avaliar sua eficácia, é lógico analisar o processo de treinamento de um modelo utilizando diferentes métodos de otimização.

Para o experimento, utilizei os modelos descritos no artigo sobre o algoritmo TPM e modifiquei apenas o método de otimização de parâmetros nas arquiteturas dos modelos.

É desnecessário dizer que, com essa abordagem, todos os programas de treinamento dos modelos, o conjunto de dados e o processo de treinamento permaneceram inalterados.

Lembro que o treinamento foi realizado com dados históricos do par EURUSD no intervalo de tempo H1 para o ano de 2023. Os parâmetros de todos os indicadores permaneceram os mesmos.

Ao testar o modelo treinado, obtivemos resultados bastante semelhantes aos do método clássico Adam. Abaixo, estão apresentados os resultados do teste com dados de janeiro de 2024.

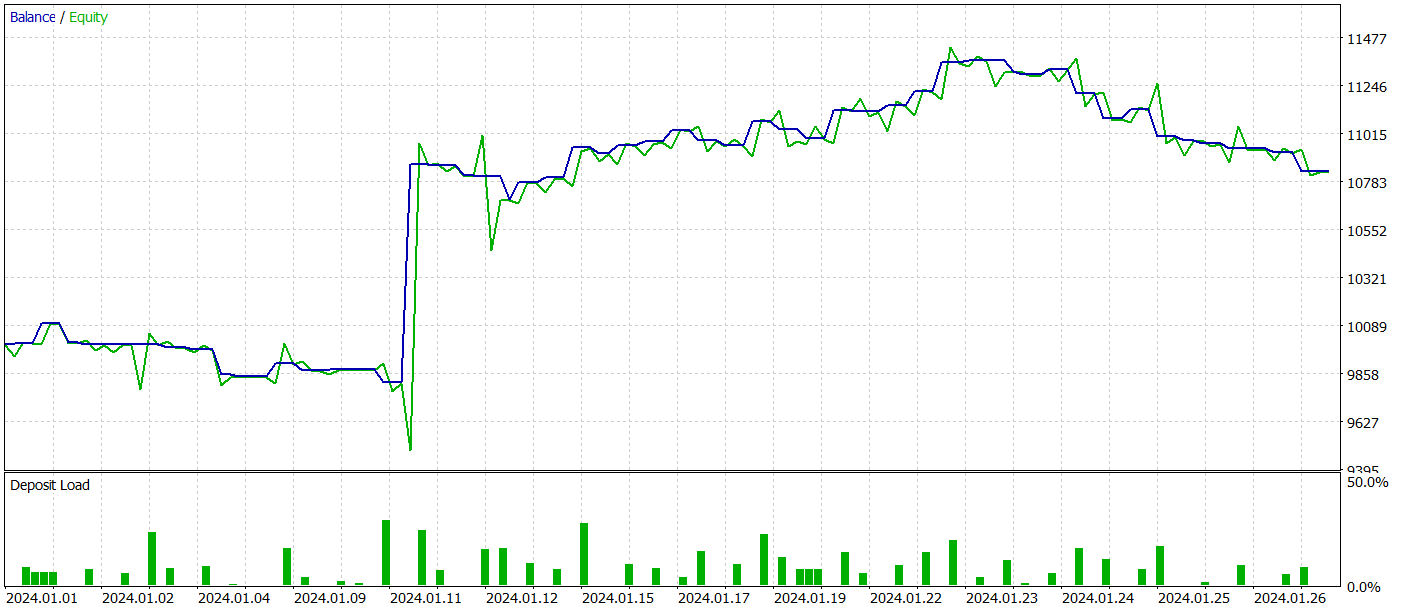
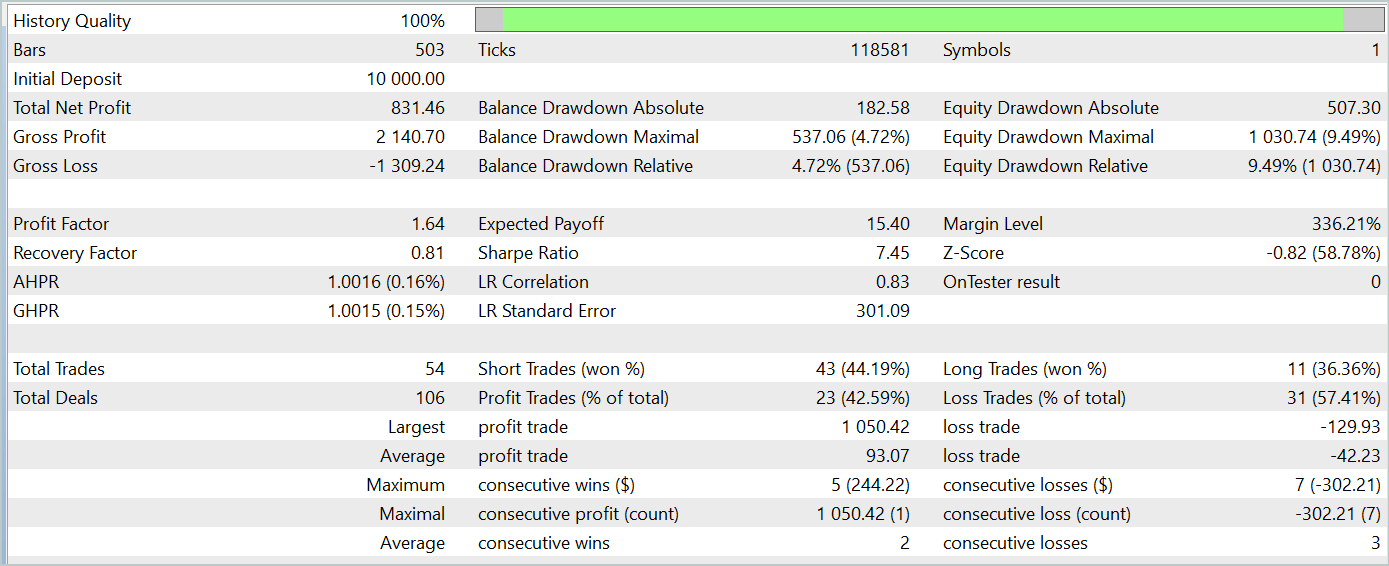
Nesse contexto, é importante ressaltar que o objetivo principal dos autores do Adam-mini é reduzir o consumo de memória sem comprometer a qualidade do treinamento. E o método proposto cumpre bem essa tarefa.

Considerações finais

Nesta discussão, exploramos o Adam-mini, um novo método de otimização projetado para reduzir o uso de memória e aumentar a eficiência no treinamento de grandes modelos de linguagem. O Adam-mini atinge esse objetivo ao reduzir o número de taxas de aprendizado necessárias para somar o tamanho da camada de embedding, o tamanho da camada de saída e o número de blocos em outras camadas. Sua simplicidade, flexibilidade e eficiência fazem deste método uma ferramenta promissora para ampla aplicação no campo do aprendizado profundo.

A parte prática do artigo demonstrou a implementação do método proposto em tipos básicos de camadas neurais. Os resultados dos testes realizados corroboram as melhorias apresentadas pelos autores.

Referências

Adam-mini: Use Fewer Learning Rates To Gain More

Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA para coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA para coleta de exemplos com Real-ORL
3	Study.mq5	Expert Advisor	EA para treinamento de modelos
4	StudyEncoder.mq5	Expert Advisor	EA para treinamento do codificador
5	Test.mq5	Expert Advisor	EA para testar o modelo
6	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema
7	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação de redes neurais
8	NeuroNet.cl	Biblioteca	Biblioteca de código OpenCL