Redes neuronales en el trading: Reducción del consumo de memoria con el método de optimización Adam (Adam-mini)

Introducción

Comenzando nuestra introducción a las redes neuronales, analizaremos varios enfoques para optimizar los parámetros de los modelos. En nuestro trabajo utilizaremos distintos enfoques. Personalmente, suelo usar el método Adam, que permite ajustar de forma adaptativa la velocidad de aprendizaje óptima de cada parámetro del modelo. No obstante, esta adaptabilidad tiene un precio. El algoritmo Adam usa momentos de primer y segundo orden para cada parámetro del modelo cuyo almacenamiento consume una memoria 2 veces superior al tamaño del propio modelo. Este consumo de memoria se ha convertido en un obstáculo importante a la hora de entrenar modelos de gran tamaño. En la práctica, para mantener el algoritmo con un alto consumo de memoria, debe utilizarse la descarga a la CPU, lo cual aumenta la latencia y ralentiza el proceso de entrenamiento. A la luz de estos problemas, se hace más urgente la búsqueda de nuevos métodos de optimización de los parámetros de los modelos o la mejora de los ya conocidos. 

Una solución interesante se expone en el artículo "Adam-mini: Use Fewer Learning Rates To Gain More", publicado en julio de 2024. Sus autores proponen una modificación del método Adam sin comprometer su rendimiento. Un nuevo optimizador denominado Adam-mini divide los parámetros del modelo en bloques, selecciona una velocidad de aprendizaje para cada uno de ellos y presenta las siguientes ventajas:

• Facilidad: Adam-mini reduce significativamente el número de velocidades de aprendizaje utilizadas en Adam, lo que se traduce en una reducción del 45-50% del consumo de memoria.
• Eficiencia: A pesar del ahorro de recursos, Adam-mini muestra un rendimiento comparable o incluso superior al del método Adam básico.
  

1. Algoritmo Adam-mini

Los autores del método Adam-mini investigan el papel de v (momento de 2º orden) en Adam y las posibilidades de mejorarlo. En el método de Adam, v ofrece una velocidad de aprendizaje individualizada para cada parámetro. Se observa que la hessiana en el Transformer y diversas redes neuronales tienen una estructura casi diagonal de bloques. Y cada bloque del Transformer tiene una distribución de valores propios significativamente diferente. En consecuencia, el Transformer requiere diferentes velocidades de aprendizaje de los bloques individuales para controlar la heterogeneidad de los valores propios. Y esto puede garantizarse usando v en Adam.

No obstante, Adam hace mucho más que eso: asigna una velocidad de aprendizaje individual no solo para cada bloque, sino también para cada parámetro. Observe que el número de parámetros es mucho mayor que el número de bloques. Esto nos plantea una pregunta: ¿Es necesario usar un velocidad de aprendizaje individualizada para cada parámetro? Y si no, ¿cuánto podemos ahorrar?

Los autores del método analizan primero esta cuestión en problemas generales de optimización y llegan a las siguientes conclusiones:

• Adam supera al método con una única velocidad de aprendizaje óptima. Esto es de esperar, ya que Adam aplica distintas velocidades de aprendizaje a distintos parámetros.
• Pero si seleccionamos un subbloque separado con hessiana densa del problema general, encontraremos que el método con una velocidad de aprendizaje óptima supera a Adam.
• Por ello: las velocidades de aprendizaje óptimas aplicadas a la versión "en bloque" del descenso de gradiente mejorarán la eficacia del proceso de aprendizaje en el problema original.

Para las tareas generales con hessianas en bloque diagonal, una mayor velocidad de aprendizaje no aportará necesariamente un beneficio adicional. En concreto, para cada subbloque denso, bastará con una única (pero buena) velocidad de aprendizaje para lograr el mejor rendimiento.

Fenómenos similares se observan en los modelos que utilizan la arquitectura del Transformer. Los autores del método Adam-mini realizan una serie de experimentos con un Transformer de 4 capas y observan que es posible lograr un rendimiento similar o incluso mejor en este tipo de modelos con velocidades de aprendizaje muy inferiores a las de Adam.

Queda, eso sí, la cuestión de cómo encontrar las velocidades óptimas de aprendizaje.

El objetivo del método Adam-mini es reducir el uso de recursos para las velocidades de aprendizaje del método Adam sin tener que realizar una búsqueda intensiva de las mismas en la red.

Adam-mini consta de dos etapas. La primera solo será necesaria en la inicialización.

En primer lugar, dividiremos los parámetros del modelo en bloques. En el caso del Transformer, los autores del método sugieren dividir todas las Query y Keys por cabezas de atención. En todos los demás casos, se utilizará un único momento de 2º orden para cada capa.

Los bloques incorporados destacan por separado. Para ellos, resultará prefiere el método Adam clásico, ya que el gran número de valores cero en las incorporaciones de los elementos individuales provocará un fuerte desplazamiento de la distribución de los valores medios con respecto a la distribución de la variable original.

En el segundo paso del algoritmo, se utilizará una velocidad de aprendizaje para cada bloque de parámetros (fuera de los bloques de incorporación). Para seleccionar con eficacia la velocidad de aprendizaje adecuada en cada bloque, Adam-mini simplemente sustituirá el cuadrado del gradiente de error en el Adam normal por su valor medio. Los autores del método aplican a estas medias una media móvil, como en el Adam clásico.

Según la intención de los autores del método, para el Transformer Adam-mini reducirá las velocidades de aprendizaje del número de todos los parámetros hasta la suma del tamaño de la capa de incorporación, la capa de resultados y el número de bloques en otras capas. Así, la fracción de memoria reducida dependerá de la fracción de parámetros no integrados en el modelo.

Adam-mini puede alcanzar un mayor rendimiento que Adam, sobre todo con recursos de hardware limitados. Esto se debe a dos razones. En primer lugar, Adam-mini no añade ninguna carga computacional adicional en sus reglas de actualización. Además, Adam-mini reduce sustancialmente el número de operaciones de extracción de raíces cuadradas y de división tensorial en Adam.

En segundo lugar, reduciendo la memoria, Adam-mini puede admitir paquetes de mayor tamaño en la GPU y, al mismo tiempo, reducir la comunicación entre la GPU y la CPU, que es uno de los principales cuellos de botella conocidos.

Gracias a estas características, Adam-mini puede reducir el tiempo total de preentrenamiento de los modelos grandes.

Adam-mini proyecta la velocidad de aprendizaje para cada subbloque hessiano denso utilizando el valor v Adam medio en dicho bloque. Un diseño así consigue un cálculo menos costoso, pero que puede no ser óptimo. Por fortuna, el diseño actual resulta suficiente para lograr un rendimiento igual o ligeramente superior al de Adam con un uso de memoria significativamente menor.

2. Implementación con MQL5

Tras repasar las cuestiones teóricas del método Adam-mini propuesto, vamos a abordar la parte práctica de nuestro trabajo. En este artículo implementaremos nuestra propia visión de los enfoques descritos usando MQL5.

Debemos decir que este trabajo resultará bastante diferente de lo que hacemos en la mayoría de los artículos. Mientras que normalmente implementamos nuevos enfoques dentro de una única clase de capa de nuestro modelo, ahora deberemos realizar adiciones a varias clases creadas previamente. Lo que ocurre es que cada clase que creamos anteriormente contiene un método heredado o redefinido updateInputWeights que construye un algoritmo para actualizar los parámetros del modelo dentro de la capa dada.

Obviamente, existen updateInputWeights de clases separadas, normalmente arquitecturas complejas que simplemente llaman a los métodos homónimos de los objetos anidados. Un ejemplo sería el decodificador del que hablamos en el artículo anterior. Su algoritmo es independiente del método de optimización utilizado, 

bool CNeuronSTNNDecoder::updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *Context)
  {
   if(!cEncoder.UpdateInputWeights(NeuronOCL, Context))
      return false;
   if(!CNeuronMLCrossAttentionMLKV::updateInputWeights(cEncoder.AsObject(), Context))
      return false;
//---
   return true;
  }

pero a medida que descendamos por la jerarquía de llamadas, siempre llegaremos a los "caballos de batalla" subyacentes en los que se construye el algoritmo básico para actualizar los parámetros del modelo.

2.1 Implementación de Adam-mini en la capa básica completamente conectada

Una de estas clases será nuestra capa básica completamente conectada CNeuronBaseOCL. En consecuencia, comenzaremos nuestro trabajo con ella.

Y aquí deberemos recordar que hemos colocado la mayor parte de las tareas computacionales en la GPU para organizar los cálculos multiflujo. Este proceso no será una excepción. En consecuencia, recurriremos a un programa OpenCL en el que crearemos un nuevo kernel UpdateWeightsAdamMini.

Pero antes de escribir el código de nuestro programa, hablaremos un poco de la arquitectura que estamos construyendo.

En primer lugar, debemos señalar que, en general, el nuevo método de optimización Adam-mini solo diferirá del método Adam clásico en el algoritmo de cálculo del momento v de 2º orden. Aquí, en lugar del gradiente de error de cada parámetro individual, los autores del método proponen usar la media del grupo. El algoritmo para calcular la media simple no resulta complicado, pero de esta forma liberaremos una cantidad considerable de memoria, ya que solo almacenaremos 1 valor del momento de 2º orden para cada grupo.

Por otro lado, no querríamos repetir el cálculo de la media de todo el bloque en cada flujo individual. Recordemos que para una capa totalmente conectada, los autores del método Adam-mini proponen usar solo 1 velocidad de aprendizaje. En consecuencia, repetir el cálculo del valor medio del gradiente de error del parámetro de la capa en el flujo de cada parámetro individual del modelo parecerá, por decirlo suavemente, poco eficiente. Y si además consideramos que este proceso implicará muchas referencias a memoria global "costosa", querremos paralelizar este proceso en varios flujos separados con referencias minimizadas a la memoria global. Pero aquí surge inmediatamente una cuestión importante: la organización del proceso de intercambio de datos entre flujos.

En artículos anteriores ya hemos aprendido a intercambiar datos dentro de un grupo local con sincronización de flujos. Sin embargo, combinar todo el proceso de actualización de los parámetros de una capa dentro de un grupo local no parece nada atractivo. Por ello , en esta implementación, hemos decidido aumentar ligeramente el número de momentos de 2º orden calculados hasta el tamaño del tensor resultante.

Recordemos que el número de parámetros de una capa totalmente conectada será igual al producto del tamaño del tensor de datos de origen por el tamaño del tensor de resultados, mientras que el uso de un parámetro de desplazamiento para cada neurona añadirá otro número de parámetros igual al tamaño del tensor de resultados. El Adam clásico conservará el mismo número de valores para los momentos 1 y 2. Dentro de la aplicación del método Adam-mini, reduciremos significativamente el número de valores de momentos de 2º orden.

Ahora vamos a hablar un poco del proceso de cálculo del valor medio del momento de 2º orden. El gradiente de error del parámetro 1 será igual al producto del gradiente del error de salida de la capa (corregido por la derivada de la función de activación) y el valor correspondiente de los datos de origen.

Como consecuencia, el valor medio del cuadrado de los gradientes podría calcularse del siguiente modo:

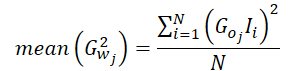
No resulta difícil ver que, como en nuestra implementación calculamos el gradiente de error medio de 1 neurona de la capa de resultados, el gradiente de error de esta neurona puede ponerse fuera de paréntesis.

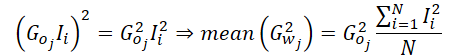
Así, al calcular la media del momento de 2º orden en nuestra implementación, solo necesitaremos calcular la media de los cuadrados de los datos de origen, eliminando las referencias al búfer de gradiente de error a nivel de los resultados, que se encuentra en la memoria global. Y solo entonces tomar el valor del gradiente de error 1 vez y multiplicar su cuadrado por la media obtenida. A continuación, solo tendremos que propagar el valor obtenido a todo el grupo local para los cálculos posteriores.

Ahora que tenemos una idea clara del algoritmo de las operaciones, podemos proceder a implementarlo en el código del kernel UpdateWeightsAdamMini. Los parámetros de este kernel serán casi idénticos a los del kernel correspondiente del método Adam clásico, e incluyen 5 búferes de datos y 3 constantes:

• matrix_w — matriz de parámetros de la capa;
• matrix_g — tensor de gradientes de error a la salida de la capa;
• matrix_i — búfer de datos de origen;
• matrix_m — tensor de momentos de 1º orden;
• matrix_v — tensor de momentos de 2º orden;
• l — velocidad de aprendizaje;
• b1 — coeficiente de suavizado de momentos de 1º orden (ß1);
• b2 — coeficiente de suavizado de momentos de 2º orden (ß2);

__kernel void UpdateWeightsAdamMini(__global float *matrix_w, 
                                    __global const float *matrix_g,
                                    __global const float *matrix_i,
                                    __global float *matrix_m,
                                    __global float *matrix_v,
                                    const float l,
                                    const float b1,
                                    const float b2 
                                   )
  {
//--- inputs
   const size_t i = get_local_id(0);
   const size_t inputs = get_local_size(0) - 1;
//--- outputs
   const size_t o = get_global_id(1);
   const size_t outputs = get_global_size(1);

La ejecución del kernel se planificará en un espacio de tareas bidimensional. La primera dimensión se corresponderá con el número de datos de origen más un elemento de desplazamiento, mientras que la segunda será el tamaño del tensor de resultados. En el cuerpo del kernel, identificaremos directamente el flujo en ambas dimensiones.

Aquí debemos notar que agruparemos los flujos en grupos de trabajo a lo largo de 1 dimensión del espacio de tareas.

Luego organizaremos un array en la memoria local del contexto para intercambiar datos entre los flujos del grupo de trabajo.

   __local float temp[LOCAL_ARRAY_SIZE];
   const int ls = min((uint)LOCAL_ARRAY_SIZE, (uint)inputs);

A continuación calcularemos el cuadrado medio de los datos de origen. Como, al calcular el momento de 1º orden, necesitaremos el valor del búfer de datos de origen, cada subproceso tomará primero 1 valor correspondiente del búfer de datos de origen global.

   const float inp = (i < inputs ? matrix_i[i] : 1.0f);

Y luego organizaremos un ciclo con sincronización del trabajo de los flujos, dentro del cual cada flujo añadirá al array local el valor cuadrático de su elemento de los datos de origen.

   int count = 0;
   do
     {
      if(count == (i / ls))
        {
         int shift = i % ls;
         temp[shift] = (count == 0 ? 0 : temp[shift]) + ((isnan(inp) || isinf(inp)) ? 0 : inp*inp);
        }
      count++;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count * ls < inputs);

A continuación, sumaremos los valores de los elementos del array local.

//--- sum
   count = (ls + 1) / 2;
   do
     {
      if(i < count && (i + count) < ls)
        {
         temp[i] += temp[i + count];
         temp[i + count] = 0;
        }
      count = (count + 1) / 2;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Dentro de un único flujo, organizaremos el cálculo de un momento de 2º orden y lo almacenaremos en un elemento de array local con índice 0.

Además, recordemos que acceder al array de memoria local resulta mucho más rápido que trabajar con el búfer de memoria global. Por lo tanto, para reducir las operaciones de acceso a la memoria global, tomaremos el gradiente de error al nivel de los resultados de la capa actual y lo almacenaremos en un elemento del array local con el índice 1. De este modo, los demás elementos del grupo de trabajo tomarán un valor de la memoria local en lugar de acceder a la memoria global al realizar operaciones posteriores.

Deberemos sincronizar los flujos del grupo de trabajo.

//--- calc v
   if(i == 0)
     {
      temp[1] = matrix_g[o];
      if(isnan(temp[1]) || isinf(temp[1]))
         temp[1] = 0;
      temp[0] /= inputs;
      if(isnan(temp[0]) || isinf(temp[0]))
         temp[0] = 1;
      float v = matrix_v[o];
      if(isnan(v) || isinf(v))
         v = 1;
      temp[0] = b2 * v + (1 - b2) * pow(temp[1], 2) * temp[0];
      matrix_v[o] = temp[0];
     }
   barrier(CLK_LOCAL_MEM_FENCE);

Observe que almacenaremos inmediatamente el valor del momento de 2º orden en el búfer de datos globales. Este sencillo paso nos permitirá eliminar accesos innecesarios a la memoria global desde otros flujos del grupo de trabajo, al tiempo que evitamos los retrasos derivados de accesos simultáneos a un elemento del búfer global desde diferentes flujos. 

A continuación, nuestro algoritmo repetirá las operaciones del método Adam clásico. Aquí definiremos un desplazamiento en el tensor de los parámetros a entrenar y cargaremos el valor actual del parámetro analizado desde el búfer de memoria global.

   const int wi = o * (inputs + 1) + i;
   float weight = matrix_w[wi];
   if(isnan(weight) || isinf(weight))
      weight = 0;

Luego calcularemos el valor del momento de 1º orden.

   float m = matrix_m[wi];
   if(isnan(m) || isinf(m))
      m = 0;
//--- calc m
   m = b1 * m + (1 - b1) * temp[1] * inp;
   if(isnan(m) || isinf(m))
      m = 0;

Determinaremos el tamaño del ajuste de los parámetros.

   float delta = l * (m / (sqrt(temp[0]) + 1.0e-37f) - (l1 * sign(weight) + l2 * weight));
   if(isnan(delta) || isinf(delta))
      delta = 0;

Después ajustaremos el valor del parámetro y guardaremos su nuevo valor en el búfer de datos global.

   if(delta > 0)
      matrix_w[wi] = clamp(weight + delta, -MAX_WEIGHT, MAX_WEIGHT);
   matrix_m[wi] = m;
  }

Aquí almacenaremos el valor del momento de 1º orden y finalizaremos el kernel.

Tras realizar los cambios en la parte OpenCL del programa, también tendremos que hacer una serie de ediciones en el programa principal. En primer lugar, añadiremos un nuevo método de optimización a nuestra enumeración.

//+------------------------------------------------------------------+
/// Enum of optimization method used                                 |
//+------------------------------------------------------------------+
enum ENUM_OPTIMIZATION
  {
   SGD,        ///< Stochastic gradient descent
   ADAM,       ///< Adam
   ADAM_MINI   ///< Adam-mini
  };

Después de eso, realizaremos modificaciones en el método CNeuronBaseOCL::updateInputWeights. Aquí, en el bloque de declaración de variables, añadiremos un array que describirá el tamaño del grupo de trabajo local_work_size (subrayado en el código siguiente). En esta fase, no le asignaremos valores, ya que solo serán necesarios al utilizar el método de optimización correspondiente.

bool CNeuronBaseOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(CheckPointer(OpenCL) == POINTER_INVALID || CheckPointer(NeuronOCL) == POINTER_INVALID)
      return false;
   uint global_work_offset[2] = {0, 0};
   uint global_work_size[2], local_work_size[2];
   global_work_size[0] = Neurons();
   global_work_size[1] = NeuronOCL.Neurons() + 1;
   uint rest = 0;
   float lt = lr;

El algoritmo se ramificará según el método seleccionado para optimizar los parámetros del modelo. Los algoritmos para colocar el kernel en la cola de ejecución de los métodos de optimización discutidos anteriormente permanecerán inalterados y no nos detendremos en ellos.

   switch(NeuronOCL.Optimization())
     {
      case SGD:
.........
.........
.........
         break;
      case ADAM:
........
........
........
         break;

Analizaremos solo el código añadido. Primero transmitiremos los parámetros necesarios para que el kernel funcione correctamente.

      case ADAM_MINI:
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdamMini, def_k_wuam_matrix_w,
                                                           NeuronOCL.getWeightsIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdamMini, def_k_wuam_matrix_g,
                                                                    getGradientIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdamMini, def_k_wuam_matrix_i, 
                                                            NeuronOCL.getOutputIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdamMini, def_k_wuam_matrix_m, 
                                                     NeuronOCL.getFirstMomentumIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdamMini, def_k_wuam_matrix_v, 
                                                    NeuronOCL.getSecondMomentumIndex()))
            return false;
         lt = (float)(lr * sqrt(1 - pow(b2, (float)t)) / (1 - pow(b1, (float)t)));
         if(!OpenCL.SetArgument(def_k_UpdateWeightsAdamMini, def_k_wuam_l, lt))
            return false;
         if(!OpenCL.SetArgument(def_k_UpdateWeightsAdamMini, def_k_wuam_b1, b1))
            return false;
         if(!OpenCL.SetArgument(def_k_UpdateWeightsAdamMini, def_k_wuam_b2, b2))
            return false;

Después definiremos los espacios de tareas del kernel de trabajo global y del grupo de trabajo individual.

         global_work_size[0] = NeuronOCL.Neurons() + 1;
         global_work_size[1] = Neurons();
         local_work_size[0] = global_work_size[0];
         local_work_size[1] = 1;

Observe que en la primera dimensión, tanto a nivel global como para el grupo de trabajo, indicaremos un valor 1 elemento mayor que el tamaño de la capa de datos de origen. Este será nuestro parámetro de desplazamiento. Pero en la segunda dimensión, a nivel global especificaremos el número de elementos en la capa neuronal actual. Mientras que para un grupo de trabajo en esta dimensión, especificaremos 1 elemento, lo cual se corresponde con el grupo de trabajo que opera dentro de 1 neurona de la capa actual.

El trabajo preparatorio realizado irá seguido de la colocación del kernel en la cola de ejecución.

         ResetLastError();
         if(!OpenCL.Execute(def_k_UpdateWeightsAdamMini, 2, global_work_offset, global_work_size, 
                                                                                local_work_size))
           {
            printf("Error of execution kernel UpdateWeightsAdamMini: %d", GetLastError());
            return false;
           }
         t++;
         break;
      default:
         return false;
         break;
     }
//---
   return true;
  }

Y luego añadiremos una salida con un resultado negativo al especificar un método de optimización de parámetros incorrecto.

Con esto completaremos el método de actualización de parámetros de la capa completamente conectada básica CNeuronBaseOCL::updateInputWeights. Pero aquí deberemos recordar la finalidad de estas operaciones: reducir el consumo de memoria usando el método de optimización Adam. Por ello, tendremos que dirigir nuestra atención al método de inicialización de la clase CNeuronBaseOCL::Init y reducir en este el tamaño del búfer de momentos de 2º orden al elegir el método de optimización de los parámetros Adam-mini. Como las ediciones serán de carácter puntual, no ofreceremos una descripción completa del algoritmo del método en el ámbito de este artículo. Solo presentaremos el bloque de inicialización del búfer correspondiente.

         if(CheckPointer(SecondMomentum) == POINTER_INVALID)
           {
            SecondMomentum = new CBufferFloat();
            if(CheckPointer(SecondMomentum) == POINTER_INVALID)
               return false;
           }
         if(!SecondMomentum.BufferInit((optimization == ADAM_MINI ? numOutputs : count), 0))
            return false;
         if(!SecondMomentum.BufferCreate(OpenCL))
            return false;

Usted mismo podrá leer el código completo de este método en el archivo adjunto. Allí se presentará también el código completo de todos los programas utilizados en la elaboración de este artículo.

2.2 Adam-mini en la capa convolucional

Otro "ladrillo básico" que utilizaremos ampliamente en otras arquitecturas, incluyendo el Transformer, es la capa convolucional.

Debemos decir que la adición del método de optimización de parámetros Adam-mini a su funcionalidad tiene sus propias especificidades. Y en primer lugar, esto se debe a las particularidades de la propia capa. A diferencia de la capa completamente conectada, en la que cada parámetro entrenado se utiliza para transmitir el valor de solo 1 neurona de los datos de origen a solo 1 neurona de la capa actual, La capa convolucional suele tener muchos menos parámetros, pero su uso está más extendido.

También querría recordarle que son precisamente las capas convolucionales las que utilizaremos para formar las entidades Query, Key y Value dentro de los algoritmos del Transformer. Y estas entidades tendrán su propia aplicación específica del método Adam-mini.

Y todos estos puntos deberemos considerarlos a la hora de implementar el método Adam-mini dentro de la capa convolucional.

Al igual que sucede con la capa totalmente conectada, empezaremos nuestro trabajo por el lado OpenCL del programa. Aquí es donde crearemos el kernel UpdateWeightsConvAdamMini. En los parámetros del kernel especificado, además de las variables ya conocidas, añadiremos 2 constantes: el tamaño de la secuencia de datos de origen y el paso de la ventana convolucional.

__kernel void UpdateWeightsConvAdamMini(__global float *matrix_w,  
                                        __global const float *matrix_i,
                                        __global float *matrix_m,      
                                        __global float *matrix_v,      
                                        const int inputs,              
                                        const float l,              
                                        const float b1,             
                                        const float b2,             
                                        int step                    
                                       )
  {
//--- window in
   const size_t i = get_global_id(0);
   const size_t window_in = get_global_size(0) - 1;
//--- window out
   const size_t f = get_global_id(1);
   const size_t window_out = get_global_size(1);
//--- head window out
   const size_t f_h = get_local_id(1);
   const size_t window_out_h = get_local_size(1);
//--- variable
   const size_t v = get_global_id(2);
   const size_t variables = get_global_size(2);

Observe que en los parámetros del kernel no se especifica el tamaño de la ventana de datos de origen ni el número de filtros utilizados. Estos parámetros y otros 2 se colocarán en el espacio de tareas. Merece la pena prestarle atención.

Tenemos previsto llamar este kernel en un espacio tridimensional de tareas. La primera dimensión se corresponderá con el tamaño de la ventana de datos de origen más 1 elemento de desplazamiento. Aquí podemos ver alguna conexión con el espacio de tareas de la capa totalmente conectada.

La segunda dimensión del espacio de tareas se corresponderá con el número de filtros utilizados. Y aquí la conexión lógica con la dimensionalidad de los resultados de la capa totalmente conectada resulta obvia,

salvo que no crearemos grupos de trabajo para cada filtro convolucional individual, sino que los agruparemos según las cabezas de atención de la arquitectura del Transformer.

Tenga en cuenta que el usuario solo podrá especificar 1 filtro convolucional por cabeza. Y en ese caso, cada filtro convolucional recibirá una velocidad de aprendizaje individual similar a nuestra implementación de la capa completamente conectada.

Luego crearemos la tercera dimensión del espacio de tareas para trabajar con las series temporales multidimensionales, cuando se utilizan filtros convolucionales personalizados para secuencias unitarias individuales. Para ellas, también crearemos momentos de 2º orden independientes para organizar las velocidades de aprendizaje adaptativas.

Aquí existe una fina línea entre "cabezas de atención" y "series temporales unitarias" que no debe confundirse. A pesar de que tienen algunas similitudes, nunca deberá sustituirse un concepto por otro. Las series temporales unitarias comparten el tensor de los datos de origen, mientras que las cabezas de atención comparten el tensor de resultados.

En el cuerpo del kernel, tras identificar el flujo en todas las dimensiones del espacio de tareas, definiremos las constantes de desplazamiento básicas en los búferes de datos globales.

//--- constants
   const int total = (inputs - window_in + step - 1) / step;
   const int shift_var_in = v * inputs;
   const int shift_var_out = v * total * window_out;
   const int shift_w = (f + v * window_out) * (window_in + 1) + i;

Y crearemos un array de intercambio de datos de grupo de trabajo local.

   __local float temp[LOCAL_ARRAY_SIZE];
   const int ls = min((uint)window_in, (uint)LOCAL_ARRAY_SIZE);

Una vez realizado el trabajo preparatorio, recopilaremos los gradientes de error para cada parámetro.

//--- calc gradient
   float grad = 0;
   for(int t = 0; t < total; t++)
     {
      if(i != window_in && (i + t * window_in) >= inputs)
         break;
      float gt = matrix_g[t * window_out + f + shift_var_out] *
                 (i == window_in ? 1 : matrix_i[i + t * step + shift_var_in]);
      if(!(isnan(gt) || isinf(gt)))
         grad += gt;
     }

Tenga en cuenta que, en este caso, cada flujo global recogerá al completo los gradientes de error de todos los elementos a los que afecta. Y aquí, a diferencia de la capa completamente conectada, multiplicaremos directamente el valor del elemento de los datos de origen por el gradiente de error correspondiente de los resultados.

A continuación, recopilaremos los gradientes de error obtenidos para sumar los valores cuadráticos en los elementos del array local, pero ya dentro del grupo de trabajo. Para ello organizaremos un sistema de ciclos anidados con sincronización obligatoria de los flujos. El ciclo exterior se corresponderá con el número de filtros del grupo de trabajo, mientras que el ciclo anidado recogerá los gradientes de error de todos los parámetros de un único filtro.  

//--- calc sum grad
   int count;
   for(int h = 0; h < window_out_h; h++)
     {
      count = 0;
      do
        {
         if(h == f_h)
           {
            if(count == (i / ls))
              {
               int shift = i % ls;
               temp[shift] = ((count == 0 && h == 0) ? 0 : temp[shift]) + 
                             ((isnan(grad) || isinf(grad)) ? 0 : grad * grad);
              }
           }
         count++;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while((count * ls) < window_in);
     }

A continuación, sumaremos los valores del array local.

   count = (ls + 1) / 2;
   do
     {
      if(i < count && (i + count) < ls && f_h == 0)
        {
         temp[i] += temp[i + count];
         temp[i + count] = 0;
        }
      count = (count + 1) / 2;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Y determinaremos el valor del momento de 2º orden del grupo actual.

//--- calc v
   if(i == 0 && f_h == 0)
     {
      temp[0] /= (window_in * window_out_h);
      if(isnan(temp[0]) || isinf(temp[0]))
         temp[0] = 1;
      int head = f / window_out_h;
      float v = matrix_v[head];
      if(isnan(v) || isinf(v))
         v = 1;
      temp[0] = clamp(b2 * v + (1 - b2) * temp[0], 1.0e-6f, 1.0e6f);
      matrix_v[head] = temp[0];
     }
   barrier(CLK_LOCAL_MEM_FENCE);

Y luego repetiremos el algoritmo del método Adam clásico. Aquí definiremos un momento de 1º orden.

//--- calc m
   float mt = clamp(b1 * matrix_m[shift_w] + (1 - b1) * grad, -1.0e5f, 1.0e5f);
   if(isnan(mt) || isinf(mt))
      mt = 0;

Después ajustaremos el valor del parámetro analizado.

   float weight = clamp(matrix_w[shift_w] + l * mt / sqrt(temp[0]), -MAX_WEIGHT, MAX_WEIGHT);

Y guardaremos los valores obtenidos.

   if(!(isnan(weight) || isinf(weight)))
      matrix_w[shift_w] = weight;
   matrix_m[shift_w] = mt;
  }

Tras crear el kernel en el lado OpenCL, pasaremos a trabajar en el programa principal. Al igual que en el caso de la capa totalmente conectada, organizaremos la llamada al kernel creado anteriormente en el método CNeuronConvOCL::updateInputWeights. El algoritmo para llamarla recordará al presentado anteriormente para una capa totalmente conectada. Para una capa convolucional regular, utilizaremos 1 filtro para cada cabeza de atención, y también usaremos 1 secuencia unitaria. Así, la dimensionalidad del espacio de tareas adoptará la siguiente forma.

   uint global_work_offset_am[3] = { 0, 0, 0 };
   uint global_work_size_am[3] = { iWindow + 1, iWindowOut, iVariables };
   uint local_work_size_am[3] = { global_work_size_am[0], 1, 1 };

Usted mismo podrá leer el código completo de este método en el archivo adjunto.

Sin embargo, querría añadir unas palabras sobre el uso del kernel creado dentro de la implementación de clases utilizando la arquitectura del Transformer. Como ejemplo, analizaremos la clase CNeuronMLMHAttentionOCL. Esta clase es la que usaremos como clase madre para construir otros algoritmos.

Recordemos que la clase CNeuronMLMHAttentionOCL no contiene capas convolucionales en el sentido habitual. Organizará los arrays de búferes y redefinirá todos los métodos. Los parámetros de las capas convolucionales se actualizarán en el método ConvolutuionUpdateWeights. Como este método se utiliza para organizar el funcionamiento de diferentes capas convolucionales, añadiremos 2 parámetros adicionales: el número de cabezas (heads) y las secuencias unitarias (variables). Para evitar problemas con las llamadas a este método desde otras clases, los nuevos parámetros obtendrán valores por defecto.

bool CNeuronMLMHAttentionOCL::ConvolutuionUpdateWeights(CBufferFloat *weights, 
                                                        CBufferFloat *gradient, 
                                                        CBufferFloat *inputs, 
                                                        CBufferFloat *momentum1, 
                                                        CBufferFloat *momentum2, 
                                                        uint window, uint window_out, 
                                                        uint step = 0, uint heads = 0, 
                                                        uint variables = 1)
  {
   if(CheckPointer(OpenCL) == POINTER_INVALID || CheckPointer(weights) == POINTER_INVALID || 
      CheckPointer(gradient) == POINTER_INVALID || CheckPointer(inputs) == POINTER_INVALID  || 
      CheckPointer(momentum1) == POINTER_INVALID)
      return false;

En el cuerpo del método, primero comprobaremos los punteros a los búferes de datos que el método recibe como parámetros del programa que realiza la llamada.

A continuación, comprobaremos el valor del parámetro de paso de la ventana convolucional. Si es igual a "0", entonces daremos un paso igual a la ventana convolucional.

   if(step == 0)
      step = window;

Tenga en cuenta que en este caso estamos usando un tipo de datos sin signo para los parámetros. Por consiguiente, no podrán contener valores negativos. Dejaremos al usuario el control de los valores sobreestimados de los parámetros.

A continuación definiremos los espacios de tareas. En este caso, el kernel del método de optimización de Adam-mini utilizará un espacio de tareas tridimensional distinto del unidimensional de otros métodos de optimización. Por ello, asignaremos arrays aparte para su indicación. 

   uint global_work_offset[1] = {0};
   uint global_work_size[1];
   global_work_size[0] = weights.Total();
   uint global_work_offset_am[3] = {0, 0, 0};
   uint global_work_size_am[3] = {window, window_out, 1};
   uint local_work_size_am[3] = {window, (heads > 0 ? window_out / heads : 1), variables};

Observe la 2ª dimensión del espacio de tareas del grupo de trabajo. Si el número de cabezas de atención usadas no se especifica en los parámetros del método, se utilizará una velocidad de aprendizaje distinta para cada filtro. En caso contrario, calcularemos el número de filtros de una cabeza de atención como la relación entre el número total de filtros y el número de cabezas de atención.

Este enfoque se ha adoptado para considerar los distintos escenarios en los que se utiliza el método. De hecho, dentro de la clase CNeuronMLMHAttentionOCL, las capas convolucionales se utilizarán tanto para formar las entidades Query, Key y Value, como para la proyección de los datos (dentro de la capa de reducción de la dimensionalidad del bloque de atención multicabeza y el bloque FeedForward).

El siguiente paso consistirá en dividir el algoritmo según el método utilizado para optimizar los parámetros del modelo. Al igual que en el examen de los algoritmos de capa completamente conectada, no nos detendremos en los algoritmos de organización del funcionamiento de los métodos de optimización aplicados anteriormente. Analizaremos solo el bloque del método Adam-mini.

   if(weights.GetIndex() < 0)
      return false;
   float lt = 0;
   switch(optimization)
     {
      case SGD:
........
........
........
         break;
      case ADAM:
........
........
........
         break;
      case ADAM_MINI:
         if(CheckPointer(momentum2) == POINTER_INVALID)
            return false;
         if(gradient.GetIndex() < 0)
            return false;
         if(inputs.GetIndex() < 0)
            return false;
         if(momentum1.GetIndex() < 0)
            return false;
         if(momentum2.GetIndex() < 0)
            return false;

Aquí comprobaremos la relevancia de los punteros a búferes de datos en el contexto de OpenCL. Después transmitiremos todos los parámetros necesarios al kernel.

         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsConvAdamMini, def_k_wucam_matrix_w, 
                                                                         weights.GetIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsConvAdamMini, def_k_wucam_matrix_g, 
                                                                        gradient.GetIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsConvAdamMini, def_k_wucam_matrix_i, 
                                                                          inputs.GetIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsConvAdamMini, def_k_wucam_matrix_m, 
                                                                       momentum1.GetIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsConvAdamMini, def_k_wucam_matrix_v, 
                                                                       momentum2.GetIndex()))
            return false;
         lt = (float)(lr * sqrt(1 - pow(b2, t)) / (1 - pow(b1, t)));
         if(!OpenCL.SetArgument(def_k_UpdateWeightsConvAdamMini, def_k_wucam_inputs, 
                                                                            inputs.Total()))
            return false;
         if(!OpenCL.SetArgument(def_k_UpdateWeightsConvAdamMini, def_k_wucam_l, lt))
            return false;
         if(!OpenCL.SetArgument(def_k_UpdateWeightsConvAdamMini, def_k_wucam_b1, b1))
            return false;
         if(!OpenCL.SetArgument(def_k_UpdateWeightsConvAdamMini, def_k_wucam_b2, b2))
            return false;
         if(!OpenCL.SetArgument(def_k_UpdateWeightsConvAdamMini, def_k_wucam_step, (int)step))
            return false;

Ya hemos mencionado antes el espacio de tareas. Y ahora todo lo que deberemos hacer es poner el kernel en la cola de ejecución.

         ResetLastError();
         if(!OpenCL.Execute(def_k_UpdateWeightsConvAdamMini, 3, global_work_offset_am, 
                                              global_work_size_am, local_work_size_am))
           {
            string error;
            CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error);
            printf("Error of execution kernel %s Adam-Mini: %s", __FUNCSIG__, error);
            return false;
           }
         t++;
         break;
      //---
      default:
         printf("Error of optimization type %s: %s", __FUNCSIG__, EnumToString(optimization));
         return false;
     }

También añadiremos un mensaje de error si se especifica un tipo de optimización de parámetros incorrecto.

El código adicional del método en cuanto a la normalización de los parámetros del modelo se ha mantenido sin cambios.

   global_work_size[0] = window_out;
   OpenCL.SetArgumentBuffer(def_k_NormilizeWeights, def_k_norm_buffer, weights.GetIndex());
   OpenCL.SetArgument(def_k_NormilizeWeights, def_k_norm_dimension, (int)window + 1);
   if(!OpenCL.Execute(def_k_NormilizeWeights, 1, global_work_offset, global_work_size))
     {
      string error;
      CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error);
      printf("Error of execution kernel %s Normalize: %s", __FUNCSIG__, error);
      return false;
     }
//---
   return true;
  }

Además, en los métodos de inicialización de las clases anteriores, modificaremos el tamaño de los búferes de datos creados para almacenar los momentos de 2º orden, de forma similar al algoritmo presentado al describir la actualización de la capa completamente conectada. Pero no nos detendremos en ello en el marco de este artículo. Son solo de modificaciones puntuales que podrá ver usted mismo en el archivo adjunto.

3. Simulación

Arriba se describe la implementación del método Adam-mini en las 2 clases básicas de nuestros modelos. Ahora es el momento de analizar la eficacia de los enfoques propuestos.

Tenga en cuenta que en este artículo hemos aplicado un nuevo método de optimización. Y para evaluar el rendimiento de un método de optimización, será lógico analizar el proceso de entrenamiento de un mismo modelo con distintos métodos de optimización.

Para nuestro experimento hemos tomado los modelos del artículo sobre el algoritmo TPM y cambiado solo el método de optimización de parámetros en la arquitectura de los modelos.

Sobra decir que, con este planteamiento, todos los programas de entrenamiento de modelos, la muestra de entrenamiento y el proceso de entrenamiento han permanecido inalterados.

Permítanme recordarles que el entrenamiento de los modelos se realizará con los datos históricos de 2023 para el instrumento EURUSD y el marco temporal H1. Los parámetros de todos los indicadores se usarán por defecto.

Al probar el modelo entrenado, hemos obtenido resultados bastante similares a los del entrenamiento del modelo con la ayuda del método Adam clásico. A continuación le presentamos los resultados de la prueba del modelo entrenado con los datos de enero de 2024.

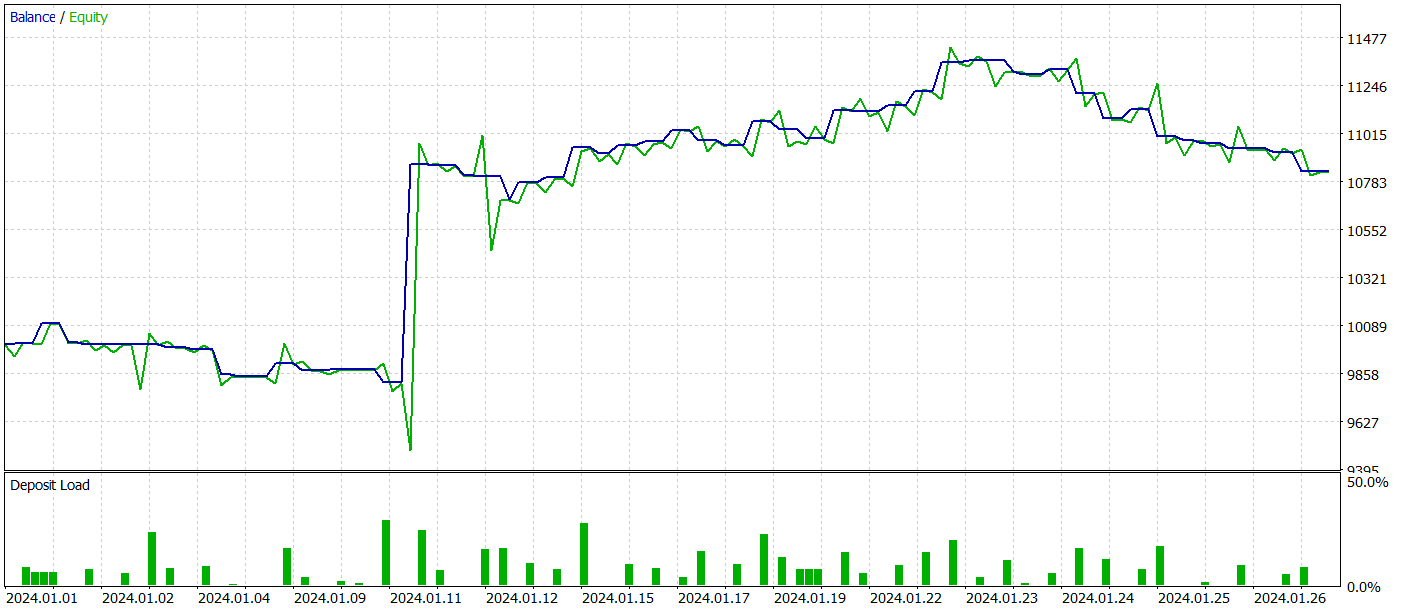
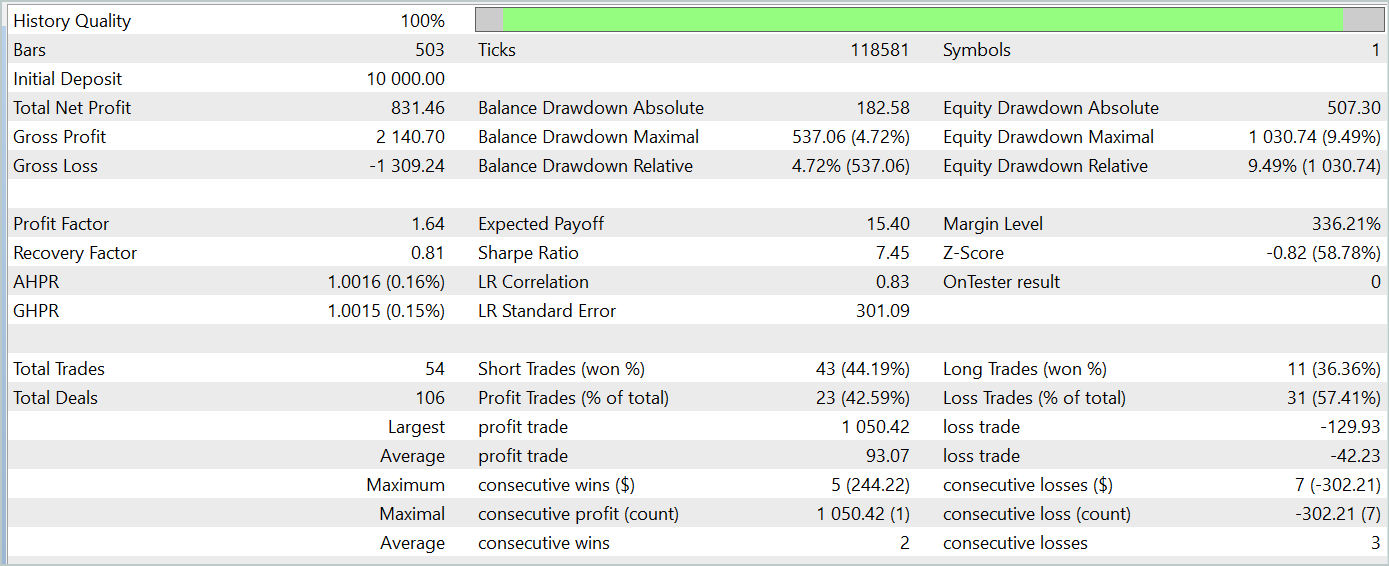
Aquí conviene recordar que el principal objetivo de los autores del método de optimización Adam-mini es reducir el consumo de memoria del modelo sin degradar la calidad del entrenamiento. Y el método presentado cumple con esta tarea.

Conclusión

En este artículo, nos hemos familiarizado con el nuevo método de optimización Adam-mini, diseñado para reducir el uso de memoria y aumentar el rendimiento al entrenar modelos lingüísticos de gran tamaño. Adam-mini lo logra reduciendo el número de velocidades de aprendizaje necesarios a la suma del tamaño de la capa de incorporación, el tamaño de la capa de resultados y el número de bloques en otras capas. Su simplicidad, flexibilidad y eficiencia hacen del método presentado una herramienta prometedora de amplia aplicación en el aprendizaje profundo.

En la parte práctica del trabajo, hemos demostrado la implementación del método propuesto en tipos básicos de capas neuronales. Y los resultados de las pruebas realizadas confirman las mejoras anunciadas por los autores del método.

Enlaces

Adam-mini: Use Fewer Learning Rates To Gain More

Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor de recopilación de ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de Modelos
4	StudyEncoder.mq5	Asesor	Asesor de entrenamiento del Codificador
5	Test.mq5	Asesor	Asesor para la prueba de modelos
6	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema.
7	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
8	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL