
Redes Neurais de Maneira Fácil(Parte 7): Métodos de otimização adaptativos
Conteúdo
- Introdução
- 1. Características distintivas dos métodos de otimização adaptativa
- 1.1. Método do Gradiente Adaptativo (AdaGrad)
- 1.2. Método RMSProp
- 1.3. Método Adadelta
- 1.4. Método de Estimativa do Momento Adaptativo (Adam)
- 2. Implementação
- 2.1. Construindo o kernel em OpenCL
- 2.2. Alterações no código da classe neuron do programa principal
- 2.3. Alterações no código da classe que não usa OpenCL
- 2.4. Alterações no código da classe de rede neural do programa principal
- 3. Teste
- Conclusões
- Referências
- Programas utilizados no artigo
Introdução
Nos artigos anteriores, nós usamos diferentes tipos de neurônios, mas sempre usamos o gradiente descendente estocástico para treinar a rede neural. Este método provavelmente pode ser chamado de básico, e suas variações são frequentemente utilizadas na prática. No entanto, existem muitos outros métodos de treinamento de rede neural. Hoje, eu proponho estudar os métodos de aprendizado adaptativos. Esta família de métodos permite a mudança da taxa de aprendizado do neurônio durante o treinamento da rede neural.
1. Características distintivas dos métodos de otimização adaptativa
Você sabe que nem todas as características alimentadas em uma rede neural têm o mesmo efeito no resultado final. Alguns parâmetros podem conter muito ruído e mudar com mais frequência do que outros, com diferentes amplitudes. Amostras de outros parâmetros podem conter valores raros que podem passar despercebidos ao treinar a rede neural com uma taxa de aprendizado fixa. Uma das desvantagens do método gradiente descendente estocástico previamente considerado é a indisponibilidade de mecanismos de otimização em tais amostras. Como resultado, o processo de aprendizagem pode parar no mínimo local. Este problema pode ser resolvido usando métodos adaptativos para treinar as redes neurais. Esses métodos permitem a mudança dinâmica da taxa de aprendizado no processo de treinamento da rede neural. Existem vários desses métodos e suas variações. Vamos considerar o mais popular deles.
1.1. Método do Gradiente Adaptativo (AdaGrad)
O Método do Gradiente Adaptativo foi proposto em 2011. Ele é uma variação do método do gradiente descendente estocástico. Ao comparar as fórmulas matemáticas desses métodos, nós podemos facilmente notar uma diferença: a taxa de aprendizado em AdaGrad é dividida pela raiz quadrada da soma dos quadrados dos gradientes para todas as iterações de treinamento anteriores. Essa abordagem permite reduzir a taxa de aprendizado dos parâmetros atualizados com frequência.
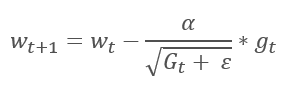
A principal desvantagem deste método decorre de sua fórmula: a soma dos quadrados dos gradientes só pode crescer e, portanto, a taxa de aprendizado tende a 0. Isso acabará por fazer com que o treinamento pare.
A utilização deste método requer cálculos adicionais e a alocação de memória adicional para armazenar a soma dos quadrados dos gradientes para cada neurônio.
1.2. Método RMSProp
A continuação lógica do método AdaGrad é o método RMSProp. Para evitar a queda da taxa de aprendizado para 0, a soma dos quadrados dos gradientes anteriores foi substituída pela média exponencial dos gradientes quadrados no denominador da fórmula usada para atualizar os pesos. Essa abordagem elimina o crescimento constante e infinito do valor no denominador. Além disso, dá maior atenção aos últimos valores do gradiente que caracterizam o estado atual do modelo.
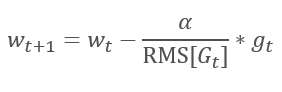
1.3. Método Adadelta
O método adaptativo Adadelta foi proposto quase que de maneira simultânea ao RMSProp. Este método é semelhante e usa uma média exponencial da soma dos quadrados dos gradientes no denominador da fórmula usada para atualizar os pesos. Mas, ao contrário do RMSProp, este método recusa completamente a taxa de aprendizado na fórmula de atualização e a substitui por uma média exponencial da soma dos quadrados das alterações anteriores no parâmetro analisado.
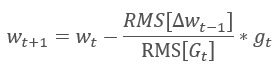
Esta abordagem permite remover a taxa de aprendizado da fórmula usada para atualizar os pesos e criar um algoritmo de aprendizagem altamente adaptável. No entanto, esse método requer iterações adicionais de cálculos e alocação de memória para armazenar um valor adicional em cada neurônio.
1.4. Método de Estimativa do Momento Adaptativo (Adam)
Em 2014, Diederik P. Kingma e Jimmy Lei Ba propuseram o Método de Estimativa de Momento Adaptativo (Adam). Segundo os autores, o método combina as vantagens dos métodos AdaGrad e RMSProp e funciona bem para o treinamento on-line. Este método mostra os resultados consistentemente bons em diferentes amostras. Geralmente é recomendado a sua utilização por padrão em vários pacotes.
O método é baseado no cálculo da média exponencial dos gradientes m e a média exponencial do quadrado dos gradientes v. Cada média exponencial tem seu próprio hiperparâmetro ß que determina o período da média.
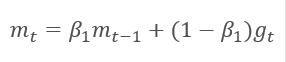
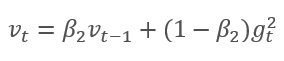
Os autores sugerem o uso padrão de ß1 em 0.9 e ß2 em 0.999. Nesse caso m0 e v0 assumem valores iguais a zero. Com esses parâmetros, as fórmulas apresentadas acima retornam valores próximos de 0 no início do treinamento, e assim a taxa de aprendizado no início será baixa. Para agilizar o processo de aprendizagem, os autores sugerem corrigir o momento obtido.
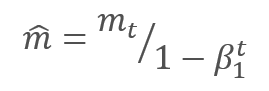
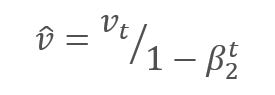
Os parâmetros são atualizados ajustando para a proporção do momento do gradiente corrigido m para a raiz quadrada do momento corrigido do quadrado do gradiente v. Para evitar a divisão por zero, a constante Ɛ próxima de 0 é adicionada ao denominador. A razão resultante é ajustada pelo fator de aprendizado α, que neste caso é o limite superior do passo de aprendizado. Os autores sugerem o uso de α em 0.001 por padrão.
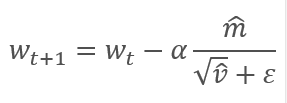
2. Implementação
Depois de considerar os aspectos teóricos, nós podemos proceder à implementação prática. Eu proponho implementar o método de Adam com os hiperparâmetros padrão oferecidos pelos autores. Além disso, você pode tentar outras variações de hiperparâmetros.
A rede neural construída anteriormente usava o gradiente descendente estocástico para o treinamento, que já foi implementado - algoritmo backpropagation. A funcionalidade de retropropagação existente pode ser usada para implementar o método de Adam. Nós precisamos apenas implementar o algoritmo de atualização de peso. Essa funcionalidade é realizada pelo método updateInputWeights, que é implementado em cada classe de neurônios. Obviamente, nós não excluiremos o algoritmo gradiente descendente estocástico criado anteriormente. Vamos criar um algoritmo alternativo que possibilite a escolha do método de treinamento a ser utilizado.
2.1. Construindo o kernel em OpenCL
Considere a implementação do método Adam para a classe CNeuronBaseOCL. Primeiro, criamos o kernel UpdateWeightsAdam para implementar o método em OpenCL. Os ponteiros para as seguintes matrizes serão passados para o kernel em parâmetros:
- matriz de pesos — matrix_w,
- matriz de erro dos gradientes — matrix_g,
- matriz dos dados de entrada — matrix_i,
- matriz das médias exponenciais dos gradientes — matrix_m,
- matriz das médias exponenciais do quadrado dos gradientes — matrix_v.
__kernel void UpdateWeightsAdam(__global double *matrix_w, __global double *matrix_g, __global double *matrix_i, __global double *matrix_m, __global double *matrix_v, int inputs, double l, double b1, double b2)
Além disso, nos parâmetros do kernel, passamos o tamanho da matriz contendo os dados de entrada e os hiperparâmetros do algoritmo de Adam.
No início do kernel, obtemos os números de série do fluxo em duas dimensões, que indicarão os números dos neurônios das camadas atual e anterior, respectivamente. Usando os números recebidos, determinamos o número inicial do elemento processado nos buffers. Preste atenção que o número do fluxo resultante na segunda dimensão é multiplicado por "4". Isso porque, para reduzir o número de fluxos e o tempo total de execução do programa, nós usaremos os cálculos vetoriais com os vetores de 4 elementos.
{
int i=get_global_id(0);
int j=get_global_id(1);
int wi=i*(inputs+1)+j*4;
Após determinar a posição dos elementos processados nos buffers de dados, declaramos as variáveis do vetor e preenchemos eles com os valores correspondentes. Usamos o método descrito anteriormente e preenchemos os dados perdidos em vetores com zeros.
double4 m, v, weight, inp; switch(inputs-j*4) { case 0: inp=(double4)(1,0,0,0); weight=(double4)(matrix_w[wi],0,0,0); m=(double4)(matrix_m[wi],0,0,0); v=(double4)(matrix_v[wi],0,0,0); break; case 1: inp=(double4)(matrix_i[j],1,0,0); weight=(double4)(matrix_w[wi],matrix_w[wi+1],0,0); m=(double4)(matrix_m[wi],matrix_m[wi+1],0,0); v=(double4)(matrix_v[wi],matrix_v[wi+1],0,0); break; case 2: inp=(double4)(matrix_i[j],matrix_i[j+1],1,0); weight=(double4)(matrix_w[wi],matrix_w[wi+1],matrix_w[wi+2],0); m=(double4)(matrix_m[wi],matrix_m[wi+1],matrix_m[wi+2],0); v=(double4)(matrix_v[wi],matrix_v[wi+1],matrix_v[wi+2],0); break; case 3: inp=(double4)(matrix_i[j],matrix_i[j+1],matrix_i[j+2],1); weight=(double4)(matrix_w[wi],matrix_w[wi+1],matrix_w[wi+2],matrix_w[wi+3]); m=(double4)(matrix_m[wi],matrix_m[wi+1],matrix_m[wi+2],matrix_m[wi+3]); v=(double4)(matrix_v[wi],matrix_v[wi+1],matrix_v[wi+2],matrix_v[wi+3]); break; default: inp=(double4)(matrix_i[j],matrix_i[j+1],matrix_i[j+2],matrix_i[j+3]); weight=(double4)(matrix_w[wi],matrix_w[wi+1],matrix_w[wi+2],matrix_w[wi+3]); m=(double4)(matrix_m[wi],matrix_m[wi+1],matrix_m[wi+2],matrix_m[wi+3]); v=(double4)(matrix_v[wi],matrix_v[wi+1],matrix_v[wi+2],matrix_v[wi+3]); break; }
O vetor gradiente é obtido multiplicando o gradiente do neurônio atual pelo vetor de dados de entrada.
double4 g=matrix_g[i]*inp;
Em seguida, calculamos as médias exponenciais do gradiente e do quadrado do gradiente.
double4 mt=b1*m+(1-b1)*g; double4 vt=b2*v+(1-b2)*pow(g,2)+0.00000001;
Calculamos os deltas de alteração do parâmetro.
double4 delta=l*mt/sqrt(vt);
Observe que nós não ajustamos os momentos recebidos no kernel. Este passo é omitido intencionalmente aqui. Já que ß1 e ß2 são iguais para todos os neurônios, e t, que aqui é o número de iterações das atualizações dos parâmetros dos neurônios, também é o mesmo para todos os neurônios, então o fator de correção também será o mesmo para todos os neurônios. É por isso que não recalcularemos o fator para cada neurônio, mas o calcularemos uma vez no código do programa principal e passaremos para o kernel o coeficiente de aprendizagem ajustado por este valor.
Depois de calcular os deltas, nós precisamos apenas ajustar os coeficientes de peso e atualizar os momentos calculados nos buffers. Em seguida, saímos do kernel.
switch(inputs-j*4) { case 2: matrix_w[wi+2]+=delta.s2; matrix_m[wi+2]=mt.s2; matrix_v[wi+2]=vt.s2; case 1: matrix_w[wi+1]+=delta.s1; matrix_m[wi+1]=mt.s1; matrix_v[wi+1]=vt.s1; case 0: matrix_w[wi]+=delta.s0; matrix_m[wi]=mt.s0; matrix_v[wi]=vt.s0; break; default: matrix_w[wi]+=delta.s0; matrix_m[wi]=mt.s0; matrix_v[wi]=vt.s0; matrix_w[wi+1]+=delta.s1; matrix_m[wi+1]=mt.s1; matrix_v[wi+1]=vt.s1; matrix_w[wi+2]+=delta.s2; matrix_m[wi+2]=mt.s2; matrix_v[wi+2]=vt.s2; matrix_w[wi+3]+=delta.s3; matrix_m[wi+3]=mt.s3; matrix_v[wi+3]=vt.s3; break; } };
Este código tem outro truque. Preste atenção na ordem inversa dos casos case no operador switch. Também, o operador break só é usado após o case 0 e o caso default. Essa abordagem permite evitar a duplicação do mesmo código para todas as variantes.
2.2. Alterações no código da classe neuron do programa principal
Depois de construir o kernel, nós precisamos fazer as alterações no código do programa principal. Primeiro, adicionamos as constantes ao bloco 'define' para trabalhar com o kernel.
#define def_k_UpdateWeightsAdam 4 #define def_k_uwa_matrix_w 0 #define def_k_uwa_matrix_g 1 #define def_k_uwa_matrix_i 2 #define def_k_uwa_matrix_m 3 #define def_k_uwa_matrix_v 4 #define def_k_uwa_inputs 5 #define def_k_uwa_l 6 #define def_k_uwa_b1 7 #define def_k_uwa_b2 8
Criamos as enumerações para indicar os métodos de treinamento e adicionamos os buffers de momento às enumerações.
enum ENUM_OPTIMIZATION { SGD, ADAM }; //--- enum ENUM_BUFFERS { WEIGHTS, DELTA_WEIGHTS, OUTPUT, GRADIENT, FIRST_MOMENTUM, SECOND_MOMENTUM };
Então, no corpo da classe CNeuronBaseOCL, adicionamos os buffers para armazenar os momentos, as constantes das médias exponenciais, o contador de iterações de treinamento e uma variável para armazenar o método de treinamento.
class CNeuronBaseOCL : public CObject { protected: ......... ......... .......... CBufferDouble *FirstMomentum; CBufferDouble *SecondMomentum; //--- ......... ......... const double b1; const double b2; int t; //--- ......... ......... ENUM_OPTIMIZATION optimization;
No construtor da classe, definimos os valores das constantes e inicializamos os buffers.
CNeuronBaseOCL::CNeuronBaseOCL(void) : alpha(momentum), activation(TANH), optimization(SGD), b1(0.9), b2(0.999), t(1) { OpenCL=NULL; Output=new CBufferDouble(); PrevOutput=new CBufferDouble(); Weights=new CBufferDouble(); DeltaWeights=new CBufferDouble(); Gradient=new CBufferDouble(); FirstMomentum=new CBufferDouble(); SecondMomentum=new CBufferDouble(); }
Não se esqueça de adicionar a remoção dos objetos do buffer no destrutor da classe.
CNeuronBaseOCL::~CNeuronBaseOCL(void) { if(CheckPointer(Output)!=POINTER_INVALID) delete Output; if(CheckPointer(PrevOutput)!=POINTER_INVALID) delete PrevOutput; if(CheckPointer(Weights)!=POINTER_INVALID) delete Weights; if(CheckPointer(DeltaWeights)!=POINTER_INVALID) delete DeltaWeights; if(CheckPointer(Gradient)!=POINTER_INVALID) delete Gradient; if(CheckPointer(FirstMomentum)!=POINTER_INVALID) delete FirstMomentum; if(CheckPointer(SecondMomentum)!=POINTER_INVALID) delete SecondMomentum; OpenCL=NULL; }
Nos parâmetros da função de inicialização da classe, adicionamos um método de treinamento e, dependendo do método de treinamento especificado, inicializamos os buffers. Se o gradiente descendente estocástico for usado para treinamento, inicializamos o buffer de deltas e removemos os buffers de momentos. Se o método de Adam for usado, inicializamos os buffers de momento e removemos o buffer de deltas.
bool CNeuronBaseOCL::Init(uint numOutputs,uint myIndex,COpenCLMy *open_cl,uint numNeurons, ENUM_OPTIMIZATION optimization_type) { if(CheckPointer(open_cl)==POINTER_INVALID || numNeurons<=0) return false; OpenCL=open_cl; optimization=optimization_type; //--- .................... .................... .................... .................... //--- if(numOutputs>0) { if(CheckPointer(Weights)==POINTER_INVALID) { Weights=new CBufferDouble(); if(CheckPointer(Weights)==POINTER_INVALID) return false; } int count=(int)((numNeurons+1)*numOutputs); if(!Weights.Reserve(count)) return false; for(int i=0;i<count;i++) { double weigh=(MathRand()+1)/32768.0-0.5; if(weigh==0) weigh=0.001; if(!Weights.Add(weigh)) return false; } if(!Weights.BufferCreate(OpenCL)) return false; //--- if(optimization==SGD) { if(CheckPointer(DeltaWeights)==POINTER_INVALID) { DeltaWeights=new CBufferDouble(); if(CheckPointer(DeltaWeights)==POINTER_INVALID) return false; } if(!DeltaWeights.BufferInit(count,0)) return false; if(!DeltaWeights.BufferCreate(OpenCL)) return false; if(CheckPointer(FirstMomentum)==POINTER_INVALID) delete FirstMomentum; if(CheckPointer(SecondMomentum)==POINTER_INVALID) delete SecondMomentum; } else { if(CheckPointer(DeltaWeights)==POINTER_INVALID) delete DeltaWeights; //--- if(CheckPointer(FirstMomentum)==POINTER_INVALID) { FirstMomentum=new CBufferDouble(); if(CheckPointer(FirstMomentum)==POINTER_INVALID) return false; } if(!FirstMomentum.BufferInit(count,0)) return false; if(!FirstMomentum.BufferCreate(OpenCL)) return false; //--- if(CheckPointer(SecondMomentum)==POINTER_INVALID) { SecondMomentum=new CBufferDouble(); if(CheckPointer(SecondMomentum)==POINTER_INVALID) return false; } if(!SecondMomentum.BufferInit(count,0)) return false; if(!SecondMomentum.BufferCreate(OpenCL)) return false; } } else { if(CheckPointer(Weights)!=POINTER_INVALID) delete Weights; if(CheckPointer(DeltaWeights)!=POINTER_INVALID) delete DeltaWeights; } //--- return true; }
Além disso, fazemos as alterações no método de atualização do peso updateInputWeights. Em primeiro lugar, criamos um algoritmo de ramificação dependendo do método de treinamento.
bool CNeuronBaseOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(OpenCL)==POINTER_INVALID || CheckPointer(NeuronOCL)==POINTER_INVALID) return false; uint global_work_offset[2]={0,0}; uint global_work_size[2]; global_work_size[0]=Neurons(); global_work_size[1]=NeuronOCL.Neurons(); if(optimization==SGD) {
Para o gradiente descendente estocástico, usamos o código inteiro sem modificações.
OpenCL.SetArgumentBuffer(def_k_UpdateWeightsMomentum,def_k_uwm_matrix_w,NeuronOCL.getWeightsIndex()); OpenCL.SetArgumentBuffer(def_k_UpdateWeightsMomentum,def_k_uwm_matrix_g,getGradientIndex()); OpenCL.SetArgumentBuffer(def_k_UpdateWeightsMomentum,def_k_uwm_matrix_i,NeuronOCL.getOutputIndex()); OpenCL.SetArgumentBuffer(def_k_UpdateWeightsMomentum,def_k_uwm_matrix_dw,NeuronOCL.getDeltaWeightsIndex()); OpenCL.SetArgument(def_k_UpdateWeightsMomentum,def_k_uwm_inputs,NeuronOCL.Neurons()); OpenCL.SetArgument(def_k_UpdateWeightsMomentum,def_k_uwm_learning_rates,eta); OpenCL.SetArgument(def_k_UpdateWeightsMomentum,def_k_uwm_momentum,alpha); ResetLastError(); if(!OpenCL.Execute(def_k_UpdateWeightsMomentum,2,global_work_offset,global_work_size)) { printf("Error of execution kernel UpdateWeightsMomentum: %d",GetLastError()); return false; } }
Na ramificação do método Adam, definimos os buffers de troca de dados para o kernel apropriado.
else { if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_w,NeuronOCL.getWeightsIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_g,getGradientIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_i,NeuronOCL.getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_m,NeuronOCL.getFirstMomentumIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdam,def_k_uwa_matrix_v,NeuronOCL.getSecondMomentumIndex())) return false;
Em seguida, ajustamos a taxa de aprendizado para a iteração de treinamento atual.
double lt=eta*sqrt(1-pow(b2,t))/(1-pow(b1,t));
Definimos os hiperparâmetros de treinamento.
if(!OpenCL.SetArgument(def_k_UpdateWeightsAdam,def_k_uwa_inputs,NeuronOCL.Neurons())) return false; if(!OpenCL.SetArgument(def_k_UpdateWeightsAdam,def_k_uwa_l,lt)) return false; if(!OpenCL.SetArgument(def_k_UpdateWeightsAdam,def_k_uwa_b1,b1)) return false; if(!OpenCL.SetArgument(def_k_UpdateWeightsAdam,def_k_uwa_b2,b2)) return false;
Como nós usamos os valores vetoriais para cálculos no kernel, reduzimos o número de threads na segunda dimensão em quatro vezes.
uint rest=global_work_size[1]%4; global_work_size[1]=(global_work_size[1]-rest)/4 + (rest>0 ? 1 : 0);
Uma vez que o trabalho preparatório foi feito, chamamos o kernel e aumentamos o contador de iterações de treinamento.
ResetLastError(); if(!OpenCL.Execute(def_k_UpdateWeightsAdam,2,global_work_offset,global_work_size)) { printf("Error of execution kernel UpdateWeightsAdam: %d",GetLastError()); return false; } t++; }
Após a ramificação, independentemente do método de treinamento, lemos os pesos recalculados. Como eu expliquei no artigo anterior, o buffer deve ser lido para as camadas ocultas também, porque essa operação não apenas lê os dados, mas também inicia a execução do kernel.
//--- return NeuronOCL.Weights.BufferRead(); }
Além das adições ao algoritmo de cálculo do método de treinamento, é necessário ajustar os métodos usados para armazenar e carregar as informações sobre os resultados de treinamento do neurônio anterior. No método Save, implementamos o armazenamento do método de treinamento e adicionamos o contador de iterações de treinamento.
bool CNeuronBaseOCL::Save(const int file_handle) { if(file_handle==INVALID_HANDLE) return false; if(FileWriteInteger(file_handle,Type())<INT_VALUE) return false; //--- if(FileWriteInteger(file_handle,(int)activation,INT_VALUE)<INT_VALUE) return false; if(FileWriteInteger(file_handle,(int)optimization,INT_VALUE)<INT_VALUE) return false; if(FileWriteInteger(file_handle,(int)t,INT_VALUE)<INT_VALUE) return false;
O armazenamento dos buffers que são comuns para ambos os métodos de treinamento não mudou.
if(CheckPointer(Output)==POINTER_INVALID || !Output.BufferRead() || !Output.Save(file_handle)) return false; if(CheckPointer(PrevOutput)==POINTER_INVALID || !PrevOutput.BufferRead() || !PrevOutput.Save(file_handle)) return false; if(CheckPointer(Gradient)==POINTER_INVALID || !Gradient.BufferRead() || !Gradient.Save(file_handle)) return false; //--- if(CheckPointer(Weights)==POINTER_INVALID) { FileWriteInteger(file_handle,0); return true; } else FileWriteInteger(file_handle,1); //--- if(CheckPointer(Weights)==POINTER_INVALID || !Weights.BufferRead() || !Weights.Save(file_handle)) return false;
Depois disso, criamos um algoritmo de ramificação para cada método de treinamento, enquanto salvamos os buffers específicos.
if(optimization==SGD) { if(CheckPointer(DeltaWeights)==POINTER_INVALID || !DeltaWeights.BufferRead() || !DeltaWeights.Save(file_handle)) return false; } else { if(CheckPointer(FirstMomentum)==POINTER_INVALID || !FirstMomentum.BufferRead() || !FirstMomentum.Save(file_handle)) return false; if(CheckPointer(SecondMomentum)==POINTER_INVALID || !SecondMomentum.BufferRead() || !SecondMomentum.Save(file_handle)) return false; } //--- return true; }
Em seguida, fazemos alterações semelhantes para o método Load.
O código completo de todos os métodos e funções está disponível em anexo.
2.3. Alterações no código da classe que não usa OpenCL
Para manter as condições de operação para todas as classes, alterações semelhantes ocorreram nas classes que trabalham em MQL5 puro, sem o uso do OpenCL.
Primeiro, adicionamos as variáveis para armazenar os dados de momento na classe CConnection e definimos os valores iniciais no construtor da classe.
class CConnection : public CObject { public: double weight; double deltaWeight; double mt; double vt; CConnection(double w) { weight=w; deltaWeight=0; mt=0; vt=0; }
Também é necessário adicionar o processamento de novas variáveis aos métodos que salvam e carregam os dados de conexão.
bool CConnection::Save(int file_handle) { ........... ........... ........... if(FileWriteDouble(file_handle,mt)<=0) return false; if(FileWriteDouble(file_handle,vt)<=0) return false; //--- return true; } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ bool CConnection::Load(int file_handle) { ............ ............ ............ mt=FileReadDouble(file_handle); vt=FileReadDouble(file_handle); //--- return true; }
Em seguida, adicionamos as variáveis para armazenar o método de otimização e o contador de iterações da atualização de peso para a classe do neurônio CNeuronBase.
class CNeuronBase : public CObject { protected: ......... ......... ......... ENUM_OPTIMIZATION optimization; const double b1; const double b2; int t;
Então, o método de inicialização do neurônio também precisa ser alterado. Adicionamos aos parâmetros do método uma variável para indicar o método de otimização e implementar o armazenamento na variável definida acima.
bool CNeuronBase::Init(uint numOutputs,uint myIndex, ENUM_OPTIMIZATION optimization_type) { optimization=optimization_type;
Depois disso, vamos criar a ramificação do algoritmo de acordo com o método de otimização, para o método updateInputWeights. Antes de percorrer as conexões, recalculamos a taxa de aprendizado ajustada e, em um loop, criamos dois ramos para calcular os pesos.
bool CNeuron::updateInputWeights(CLayer *&prevLayer) { if(CheckPointer(prevLayer)==POINTER_INVALID) return false; //--- double lt=eta*sqrt(1-pow(b2,t))/(1-pow(b1,t)); int total=prevLayer.Total(); for(int n=0; n<total && !IsStopped(); n++) { CNeuron *neuron= prevLayer.At(n); CConnection *con=neuron.Connections.At(m_myIndex); if(CheckPointer(con)==POINTER_INVALID) continue; if(optimization==SGD) con.weight+=con.deltaWeight=(gradient!=0 ? eta*neuron.getOutputVal()*gradient : 0)+(con.deltaWeight!=0 ? alpha*con.deltaWeight : 0); else { con.mt=b1*con.mt+(1-b1)*gradient; con.vt=b2*con.vt+(1-b2)*pow(gradient,2)+0.00000001; con.weight+=con.deltaWeight=lt*con.mt/sqrt(con.vt); t++; } } //--- return true; }
Adicionamos o processamento de novas variáveis aos métodos de save e load.
O código completo de todos os métodos é fornecido em anexo abaixo.
2.4. Alterações no código da classe de rede neural do programa principal
Além das alterações nas classes do neurônio, são necessárias alterações em outros objetos em nosso código. Em primeiro lugar, nós precisaremos passar as informações sobre o método de treinamento do programa principal para o neurônio. Os dados do programa principal são passados para a classe da rede neural por meio da classe CLayerDescription. Um método apropriado deve ser adicionado a esta classe para passar as informações sobre o método de treinamento.
class CLayerDescription : public CObject { public: CLayerDescription(void); ~CLayerDescription(void) {}; //--- int type; int count; int window; int step; ENUM_ACTIVATION activation; ENUM_OPTIMIZATION optimization; };
Agora, fazemos as adições finais ao construtor da classe da rede neural CNet. Adicionamos aqui uma indicação do método de otimização ao inicializar os neurônios da rede, aumentamos o número de kernels em OpenCL utilizados e declaramos um novo kernel de otimização - Adam. Abaixo está o código do construtor modificado com as alterações em destaque.
CNet::CNet(CArrayObj *Description)
{
if(CheckPointer(Description)==POINTER_INVALID)
return;
//---
int total=Description.Total();
if(total<=0)
return;
//---
layers=new CArrayLayer();
if(CheckPointer(layers)==POINTER_INVALID)
return;
//---
CLayer *temp;
CLayerDescription *desc=NULL, *next=NULL, *prev=NULL;
CNeuronBase *neuron=NULL;
CNeuronProof *neuron_p=NULL;
int output_count=0;
int temp_count=0;
//---
next=Description.At(1);
if(next.type==defNeuron || next.type==defNeuronBaseOCL)
{
opencl=new COpenCLMy();
if(CheckPointer(opencl)!=POINTER_INVALID && !opencl.Initialize(cl_program,true))
delete opencl;
}
else
{
if(CheckPointer(opencl)!=POINTER_INVALID)
delete opencl;
}
//---
for(int i=0; i<total; i++)
{
prev=desc;
desc=Description.At(i);
if((i+1)<total)
{
next=Description.At(i+1);
if(CheckPointer(next)==POINTER_INVALID)
return;
}
else
next=NULL;
int outputs=(next==NULL || (next.type!=defNeuron && next.type!=defNeuronBaseOCL) ? 0 : next.count);
temp=new CLayer(outputs);
int neurons=(desc.count+(desc.type==defNeuron || desc.type==defNeuronBaseOCL ? 1 : 0));
if(CheckPointer(opencl)!=POINTER_INVALID)
{
CNeuronBaseOCL *neuron_ocl=NULL;
switch(desc.type)
{
case defNeuron:
case defNeuronBaseOCL:
neuron_ocl=new CNeuronBaseOCL();
if(CheckPointer(neuron_ocl)==POINTER_INVALID)
{
delete temp;
return;
}
if(!neuron_ocl.Init(outputs,0,opencl,desc.count,desc.optimization))
{
delete temp;
return;
}
neuron_ocl.SetActivationFunction(desc.activation);
if(!temp.Add(neuron_ocl))
{
delete neuron_ocl;
delete temp;
return;
}
neuron_ocl=NULL;
break;
default:
return;
break;
}
}
else
for(int n=0; n<neurons; n++)
{
switch(desc.type)
{
case defNeuron:
neuron=new CNeuron();
if(CheckPointer(neuron)==POINTER_INVALID)
{
delete temp;
delete layers;
return;
}
neuron.Init(outputs,n,desc.optimization);
neuron.SetActivationFunction(desc.activation);
break;
case defNeuronConv:
neuron_p=new CNeuronConv();
if(CheckPointer(neuron_p)==POINTER_INVALID)
{
delete temp;
delete layers;
return;
}
if(CheckPointer(prev)!=POINTER_INVALID)
{
if(prev.type==defNeuron)
{
temp_count=(int)((prev.count-desc.window)%desc.step);
output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
}
else
if(n==0)
{
temp_count=(int)((output_count-desc.window)%desc.step);
output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
}
}
if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count,desc.optimization))
neuron=neuron_p;
break;
case defNeuronProof:
neuron_p=new CNeuronProof();
if(CheckPointer(neuron_p)==POINTER_INVALID)
{
delete temp;
delete layers;
return;
}
if(CheckPointer(prev)!=POINTER_INVALID)
{
if(prev.type==defNeuron)
{
temp_count=(int)((prev.count-desc.window)%desc.step);
output_count=(int)((prev.count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
}
else
if(n==0)
{
temp_count=(int)((output_count-desc.window)%desc.step);
output_count=(int)((output_count-desc.window-temp_count)/desc.step+(temp_count==0 ? 1 : 2));
}
}
if(neuron_p.Init(outputs,n,desc.window,desc.step,output_count,desc.optimization))
neuron=neuron_p;
break;
case defNeuronLSTM:
neuron_p=new CNeuronLSTM();
if(CheckPointer(neuron_p)==POINTER_INVALID)
{
delete temp;
delete layers;
return;
}
output_count=(next!=NULL ? next.window : desc.step);
if(neuron_p.Init(outputs,n,desc.window,1,output_count,desc.optimization))
neuron=neuron_p;
break;
}
if(!temp.Add(neuron))
{
delete temp;
delete layers;
return;
}
neuron=NULL;
}
if(!layers.Add(temp))
{
delete temp;
delete layers;
return;
}
}
//---
if(CheckPointer(opencl)==POINTER_INVALID)
return;
//--- create kernels
opencl.SetKernelsCount(5);
opencl.KernelCreate(def_k_FeedForward,"FeedForward");
opencl.KernelCreate(def_k_CaclOutputGradient,"CaclOutputGradient");
opencl.KernelCreate(def_k_CaclHiddenGradient,"CaclHiddenGradient");
opencl.KernelCreate(def_k_UpdateWeightsMomentum,"UpdateWeightsMomentum");
opencl.KernelCreate(def_k_UpdateWeightsAdam,"UpdateWeightsAdam");
//---
return;
}
O código completo de todas as classes e seus métodos está disponível no anexo.
3. Teste
O teste da otimização pelo método de Adam foi realizado sob as mesmas condições, que foram usados nos testes anteriormente: símbolo EURUSD, tempo gráfico H1, alimentando a rede com os dados das 20 velas consecutivas e o treinamento é executado usando o histórico dos últimos dois anos. O Expert Advisor Fractal_OCL_Adam foi criado para teste. Este Expert Advisor foi criado com base no EA Fractal_OCL especificando o método de otimização de Adam ao descrever a rede neural na função OnInit do programa principal.
desc.count=(int)HistoryBars*12; desc.type=defNeuron; desc.optimization=ADAM;
O número de camadas e neurônios não foi alterado.
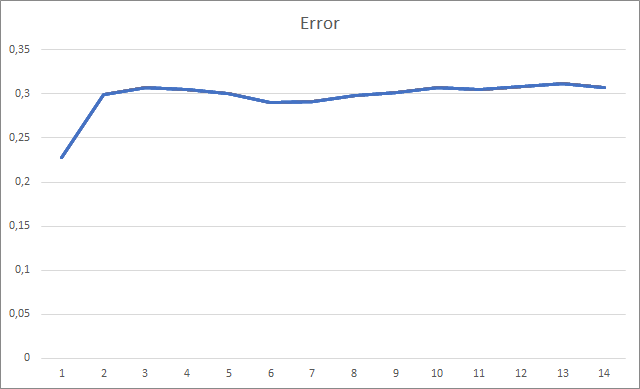
O Expert Advisor foi inicializado com os pesos aleatórios variando de -1 a 1, excluindo os valores iguais a zero. Durante o teste, já após a 2ª época de treinamento, o erro da rede neural estabilizou em torno de 30%. Como você deve se lembrar, ao aprender pelo método do gradiente descendente estocástico, o erro estabilizou em torno de 42% após a 5ª época de treinamento.
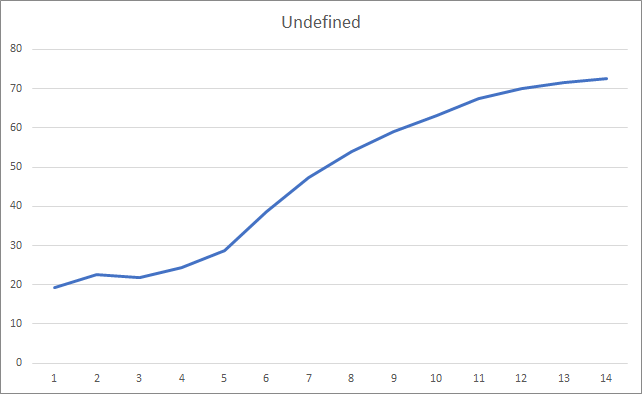
O gráfico dos fractais ausentes exibe um aumento gradual no valor ao longo de todo o treinamento. No entanto, após 12 épocas de treinamento, ocorre uma diminuição gradual na taxa de crescimento do valor. O valor foi igual a 72.5% a partir da 14ª época. Ao treinar uma rede neural semelhante usando o método gradiente descendente estocástico, a porcentagem de fractais ausentes após 10 épocas foi de 97-100% com diferentes taxas de aprendizado.
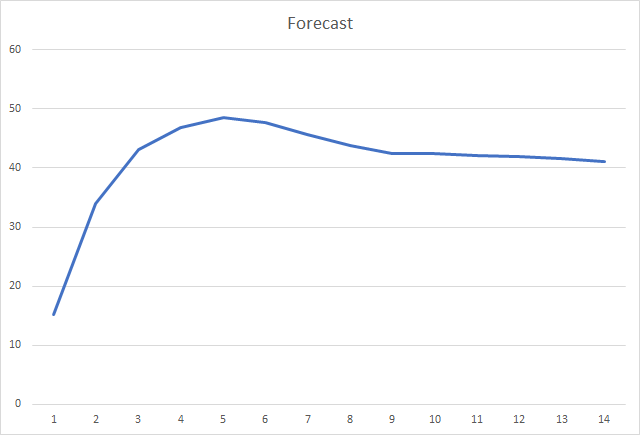
E, provavelmente, a métrica mais importante é a porcentagem de fractais definidos corretamente. Após a 5ª época de aprendizagem, o valor atingiu 48.6% e depois diminuiu gradativamente para 41.1%. Ao usar o método gradiente descendente estocástico, o valor não excedeu em 10% após 90 épocas.
Conclusões
O artigo considerou os métodos adaptativos para otimizar os parâmetros da rede neural. Nós adicionamos o método de otimização de Adam ao modelo de rede neural criado anteriormente. Durante o teste, a rede neural foi treinada usando o método de Adam. Os resultados superam os recebidos anteriormente, ao treinar uma rede neural semelhante usando o método gradiente descendente estocástico.
O trabalho realizado mostra o nosso progresso em direção ao objetivo.
Referências
- Redes neurais de maneira fácil
- Redes neurais de maneira fácil (Parte 2): Treinamento e teste da rede
- Redes Neurais de Maneira Fácil (Parte 3): Redes Convolucionais
- Redes Neurais de Maneira Fácil (Parte 4): Redes Recorrentes
- Redes Neurais de Maneira Fácil (Parte 5): Cálculos em Paralelo com o OpenCL
- Redes neurais de Maneira Fácil (Parte 6): Experimentos com a taxa de aprendizado da rede neural
- Adam: A Method for Stochastic Optimization
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Fractal_OCL_Adam.mq5 | Expert Advisor | Um EA com a rede neural de classificação (3 neurônios na camada de saída), usando a tecnologia OpenCL e o método de treinamento de Adam |
| 2 | NeuroNet.mqh | Biblioteca de classe | Uma biblioteca de classes para a criação de uma rede neural |
| 3 | NeuroNet.cl | Código Base | Biblioteca do código do programa OpenCL |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/8598
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Perceptron Multicamadas e o Algoritmo Backpropagation
Perceptron Multicamadas e o Algoritmo Backpropagation
 Gradient Boosting (CatBoost) no desenvolvimento de sistemas de negociação. Uma abordagem ingênua
Gradient Boosting (CatBoost) no desenvolvimento de sistemas de negociação. Uma abordagem ingênua
 Abordagem ideal para desenvolver e analisar sistemas de negociação
Abordagem ideal para desenvolver e analisar sistemas de negociação
 Redes neurais de Maneira Fácil (Parte 6): Experimentos com a taxa de aprendizado da rede neural
Redes neurais de Maneira Fácil (Parte 6): Experimentos com a taxa de aprendizado da rede neural
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Olá a todos. Quem já encontrou esse erro ao tentar ler um arquivo?
OnInit - 198 -> Erro de leitura de AUDNZD.......
Essa mensagem apenas informa que a rede pré-treinada não foi carregada. Se estiver executando o EA pela primeira vez, isso é normal e não preste atenção à mensagem. Se já tiver treinado a rede neural e quiser continuar a treiná-la, deverá verificar onde ocorreu o erro de leitura de dados do arquivo.
Infelizmente, você não especificou o código de erro para que possamos dizer mais.Essa mensagem informa apenas que a rede pré-treinada não foi carregada. Se estiver executando o EA pela primeira vez, isso é normal e não preste atenção à mensagem. Se você já tiver treinado a rede neural e quiser continuar a treiná-la, deverá verificar onde ocorreu o erro de leitura de dados do arquivo.
Infelizmente, você não especificou o código de erro para que possamos dizer mais.Olá.
Vou lhe contar mais sobre isso.
Ao iniciar o Expert Advisor pela primeira vez. Com essas modificações no código:
no registro, ele escreve isso:
KO 0 18:49:15.205 Core 1 NZDUSD: carregar 27 bytes de dados históricos para sincronizar em 0:00:00.001
FI 0 18:49:15.205 Core 1 NZDUSD: histórico sincronizado de 2016.01.04 a 2022.06.28
FF 0 18:49:15.205 Core 1 2019.01.01 00:00:00 OnInit - 202 -> Erro de leitura de AUDNZD_PERIOD_D1_ 20Fractal_OCL_Adam 1.nnw prev Net 0
CH 0 18:49:15.205 Core 1 2019.01.01 00:00:00 OpenCL: GPU device 'gfx902' selected
KN 0 18:49:15.205 Core 1 2019.01.01 00:00:00 Era 1 -> error 0.01 % forecast 0.01
QK 0 18:49:15.205 Core 1 2019.01.01 00:00:00 Arquivo a ser criado ChartScreenShot
HH 0 18:49:15.205 Core 1 2019.01.01 00:00:00 Era 2 -> erro 0.01 % previsão 0.01
CP 0 18:49:15.205 Core 1 2019.01.01 00:00:00 Arquivo a ser criado ChartScreenShot
PS 2 18:49:19.829 Core 1 desconectado
OL 0 18:49:19.829 Core 1 conexão fechada
NF 3 18:49:19.829 Tester parado pelo usuário
И в директории "C:\Users\Borys\AppData\Roaming\MetaQuotes\Tester\BA9DEC643240F2BF3709AAEF5784CBBC\Agent-127.0.0.1-3000\MQL5\Files"
Este arquivo foi criado:
Fractal_10000000.csv
com o seguinte conteúdo :
e assim por diante...
Ao reiniciar, o mesmo erro é exibido e o arquivo .csv é sobrescrito .
Ou seja, o Expert está sempre em treinamento porque não encontra o arquivo.
E a segunda pergunta, por favor, sugira o código (para ler os dados do neurônio de saída) para abrir ordens de compra e venda quando a rede estiver treinada.
Obrigado pelo artigo e pela resposta.
Olá.
Vou lhe contar mais sobre isso.
quando o Expert Advisor é iniciado pela primeira vez. Com essas modificações no código:
no registro, ele escreve isso:
KO 0 18:49:15.205 Core 1 NZDUSD: carregar 27 bytes de dados do histórico para sincronizar em 0:00:00.001
FI 0 18:49:15.205 Core 1 NZDUSD: histórico sincronizado de 2016.01.04 a 2022.06.28
FF 0 18:49:15.205 Core 1 2019.01.01 00:00:00 OnInit - 202 -> Erro de leitura AUDNZD_PERIOD_D1_ 20Fractal_OCL_Adam 1.nnw prev Net 0
CH 0 18:49:15.205 Core 1 2019.01.01 00:00:00 OpenCL: Dispositivo de GPU 'gfx902' selecionado
KN 0 18:49:15.205 Core 1 2019.01.01 00:00:00 Era 1 -> error 0.01 % forecast 0.01
QK 0 18:49:15.205 Core 1 2019.01.01 00:00:00 Arquivo a ser criado ChartScreenShot
HH 0 18:49:15.205 Core 1 2019.01.01 00:00:00 Era 2 -> erro 0,01 % previsão 0,01
CP 0 18:49:15.205 Core 1 2019.01.01 00:00:00 Um arquivo deve ser criado ChartScreenShot
PS 2 18:49:19.829 Core 1 desconectado
OL 0 18:49:19.829 Core 1 conexão fechada
NF 3 18:49:19.829 Testador interrompido pelo usuário
И в директории "C:\Users\Borys\AppData\Roaming\MetaQuotes\Tester\BA9DEC643240F2BF3709AAEF5784CBBC\Agent-127.0.0.1-3000\MQL5\Files"
Este arquivo foi criado:
Fractal_10000000.csv
com este conteúdo :
Etc...
Quando você o executa novamente, o mesmo erro é exibido e o arquivo .csv é sobrescrito .
Ou seja, o Expert Advisor está sempre em aprendizado porque não encontra o arquivo.
E a segunda pergunta: por favor, sugira o código (para ler os dados do neurônio de saída) para abrir ordens de compra e venda quando a rede for treinada.
Obrigado pelo artigo e pela resposta.
Boa noite, Boris.
Você está tentando treinar uma rede neural no testador de estratégias. Não recomendo que você faça isso. Certamente não sei quais alterações você fez na lógica de treinamento. No artigo, o treinamento do modelo foi organizado em um loop. E as iterações do ciclo foram repetidas até que o modelo estivesse totalmente treinado ou o EA fosse interrompido. E os dados históricos foram imediatamente carregados em matrizes dinâmicas na íntegra. Usei essa abordagem para executar o Expert Advisor em tempo real. O período de treinamento foi definido por um parâmetro externo.
Ao iniciar o Expert Advisor no testador de estratégia, o período de aprendizado especificado nos parâmetros é deslocado para a profundidade do histórico desde o início do período de teste. Além disso, cada agente no testador de estratégia MT5 trabalha em sua própria "sandbox" e salva arquivos nela. Portanto, quando você executa novamente o Expert Advisor no testador de estratégias, ele não encontra o arquivo do modelo treinado anteriormente.
Tente executar o Expert Advisor no modo em tempo real e verifique a criação de um arquivo com a extensão nnw depois que o EA parar de funcionar. Esse é o arquivo em que seu modelo treinado está gravado.
Quanto ao uso do modelo em negociações reais, você precisa passar a situação atual do mercado para os parâmetros do método Net.FeedForward. E, em seguida, obter os resultados do modelo usando o método Net.GetResult. Como resultado do último método, o buffer conterá os resultados do trabalho do modelo.
O Undefine, como no código anterior, não pode escrever 0,5 em vez de 0 para reduzir o número de indefinidos?
Ótimo e excelente trabalho, Dimitry! Seu esforço nesse caso é imenso.
E obrigado por compartilhar.
Uma pequena observação:
Experimentei o script, mas a retropropagação é executada antes do feedforward.
Minha sugestão seria fazer o feedforward primeiro e depois retropropagar o resultado correto.
Se os resultados corretos forem retropropagados depois de saber o que a rede pensa, você poderá ver uma redução nos fractais ausentes. Até 70% dos resultados poderiam ser refinados.
Também,
fazer isso:
poderia resultar em uma rede treinada prematuramente. portanto, devemos evitar isso.
Para o aprendizado da rede,
podemos começar com o otimizador Adam e uma taxa de aprendizado de0,001 e iterá-lo ao longo das épocas.
(ou)
para encontrar uma taxa de aprendizado melhor, podemos usar o teste de intervalo LR (LRRT)
Digamos que, se os padrões não estiverem funcionando, o melhor método para encontrar uma boa taxa de aprendizagem é o teste de faixa de taxa de aprendizagem.
Comece com uma taxa de aprendizado muito pequena (por exemplo,1e-7).
Em cada lote de treinamento, aumente gradualmente a taxa de aprendizagem exponencialmente.
Registre a perda de treinamento em cada etapa.
Trace o gráfico da perda versus a taxa de aprendizado.
Observe o gráfico. A perda diminuirá, depois se estabilizará e, de repente, aumentará. (a próxima taxa de aprendizado imediata é a ideal após esse aumento)
Precisamos da taxa de aprendizado mais rápida em que a perda ainda esteja diminuindo de forma consistente.
Mais uma vez, obrigado