Нейросети в трейдинге: Снижение потребления памяти методом оптимизации Adam (Adam-mini)

Введение

Начиная знакомство с нейронными сетями, мы обсуждали различные подходы к оптимизации параметров моделей. В своей работе мы используем разные подходы. Лично я наиболее часто использую метод Adam, который позволяет адаптивно настраивать оптимальную скорость обучения каждого параметра модели. Однако за эту адаптивность нужно платить. В алгоритме Adam используются моменты 1 и 2 порядка для каждого параметра модели, хранение которых потребляет память в 2 раза больше самой модели. Это потребление памяти стало серьезным препятствием при обучении больших моделей. На практике, для поддержания алгоритма с высоким потреблением памяти необходимо использовать выгрузку на CPU, что увеличивает задержку и замедляет процесс обучения. В свете указанных проблем становятся более актуальные вопросы поиска новых или совершенствование известных методов оптимизации параметров моделей. 

Одно из интересных решений было предложено в работе "Adam-mini: Use Fewer Learning Rates To Gain More", опубликованной в июле 2024 года. Её авторы предложили модификацию метода Adam без ущерба для его производительности. Новый оптимизатор под названием Adam-mini делит параметры модели на блоки, выбирает одну скорость обучения для каждого блока и имеет следующие преимущества:

• Легкость: Adam-mini значительно сокращает количество скоростей обучения, используемых в Adam, что позволяет сократить потребление памяти на 45—50%.
• Эффективность: Несмотря на экономию ресурсов, Adam-mini показывает сопоставимую или даже лучшую производительность, по сравнению с базовым методом Adam.
  

1. Алгоритм Adam-mini

Авторы метода Adam-mini исследуют роль v (момент 2 порядка) в Adam и возможности их улучшения. В методе Adam v предоставляет индивидуальную скорость обучения для каждого параметра. Отмечается, что гессиан в Transformer и различных нейронных сетей имеют почти блочно-диагональную структуру. И каждый блок Transformer имеет значительно отличающееся распределение собственных значений. Как следствие, Transformer для управления гетерогенностью собственных значений требует различные скорости обучения отдельных блоков. И это может быть обеспечено с помощью v в Adam.

Тем не менее Adam делает гораздо больше: он назначает индивидуальную скорость обучения не только для каждого блока, но и для каждого параметра. Обратите внимание, что количество параметров гораздо больше, чем количество блоков. Это порождает вопрос: Необходимо ли использовать индивидуальную скорость обучения для каждого параметра? Если нет, то насколько мы можем сэкономить?

Сначала авторы метода исследуют этот вопрос на общих задачах оптимизации и приходят к следующим выводам:

• Adam превосходит метод с одной оптимальной скоростью обучения. Это ожидаемо, поскольку Adam применяет разные скорости обучения к разным параметрам.
• Но если выбрать из общей проблемы отдельный подблок с плотным гессианом, то обнаруживается, что метод с одной оптимальной скоростью обучения превосходит Adam.
• Таким образом: оптимальные скорости обучения, примененные к "блочной" версии градиентного спуска, позволят повысить эффективность процесса обучения в исходной проблеме.

Для общих задач с блочно-диагональным гессианом большее количество скоростей обучения не обязательно приносит дополнительную выгоду. В частности, для каждого плотного подблока достаточно одной (но хорошей) скорости обучения для достижения лучшей производительности.

Аналогичные явления наблюдаются и в моделях с использованием архитектуры Transformer. Авторы метода Adam-mini проводят ряд экспериментов с 4-слойным Transformer и наблюдают, что в подобных моделях возможно достичь схожей или даже лучшей производительности с гораздо меньшим количеством скоростей обучения, чем у Adam.

Остается открытым вопрос, как находить оптимальные скорости обучения.

Цель метода Adam-mini — сократить использование ресурсов для скоростей обучения в методе Adam без необходимости трудоемкого их поиска по сетке.

Adam-mini состоит из двух шагов. Шаг 1 требуется только на инициализации.

Вначале делим параметры модели на блоки. В случае Transformer авторы метода предлагают делить все Query и Keys по головам внимания. Во всех остальных случаях используется один момент 2 порядка для каждого слоя.

Отдельно выделяются блоки Эмбедингов. Для них предпочтительнее использовать классический метод Adam, так как большое количество нулевых значений в эмбедингах отдельных элементов приводит к сильному смещению распределения средних значений от распределения исходной переменной.

На втором шаге алгоритма для каждого блока параметров (вне блоков Эмбедингов) используется одна скорость обучения. Для эффективного выбора подходящей скорости обучения в каждом блоке Adam-mini просто заменяет квадрат градиента ошибки в обычном Adam на его среднее значение. Авторы метода применяют скользящее среднее к этим средним значениям, как в классическом Adam.

По замыслу авторов метода, для Transformer Adam-mini снижает количество скоростей обучения с числа всех параметров до суммы размеров слоя эмбединга, слоя результатов и количества блоков в других слоях. Таким образом, доля сокращенной памяти зависит от доли параметров, не связанных со встраиванием, в модели.

Adam-mini может достигать большей пропускной способности по сравнению с Adam, особенно при ограниченных аппаратных ресурсах. Тому есть две причины. Во-первых, Adam-mini не добавляет дополнительной вычислительной нагрузки в своих правилах обновления. Кроме того, Adam-mini значительно сокращает количество операций извлечения квадратного корня и деления тензоров в Adam.

Во-вторых, благодаря сокращению памяти Adam-mini может поддерживать большие размеры пакетов на GPU, одновременно снижая коммуникацию между GPU и CPU, которая является известным основным "затором".

Благодаря этим свойствам Adam-mini может сократить общее время предварительного обучения больших моделей.

Adam-mini проектирует скорость обучения для каждого плотного подблока Гессиана, используя среднее значение v Adam в этом блоке. Такое проектирование достигает дешевых вычислений, но может быть не оптимальным. К счастью, текущий дизайн достаточен для достижения такой же или немного лучшей производительности по сравнению с Adam со значительно меньшими затратами памяти.

2. Реализация средствами MQL5

После рассмотрения теоретических вопросов предложенного метода Adam-mini мы переходим к практической части нашей статьи. В которой мы реализуем собственное видение описанных подходов средствами MQL5.

Должен сказать, что данная работа довольно отличается от проделываемой нами в большинстве статей. Если обычно мы реализовываем новые подходы в рамках класса отдельного слоя нашей модели, то сейчас нам предстоит внести дополнения в несколько ранее созданных классов. Дело в том, что каждый ранее созданный нами класс содержит переопределенный или унаследованный метод updateInputWeights, в котором построен алгоритм обновления параметров модели в рамках данного слоя.

Конечно, есть updateInputWeights отдельных классов, обычно сложных архитектурных решений, в которых лишь вызываются одноименные методы вложенных объектов. Примером может послужить рассмотренный в предыдущей статье Декодер. Их алгоритм не зависим от используемого метода оптимизации. 

bool CNeuronSTNNDecoder::updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *Context)
  {
   if(!cEncoder.UpdateInputWeights(NeuronOCL, Context))
      return false;
   if(!CNeuronMLCrossAttentionMLKV::updateInputWeights(cEncoder.AsObject(), Context))
      return false;
//---
   return true;
  }

Но, опускаясь по иерархии вызовов, мы всегда придем к основополагающим "рабочим лошадкам", в которых и построен основной алгоритм обновления параметров модели.

2.1 Внедрение Adam-mini в базовый полносвязный слой

Одним из таких классов является наш базовый полносвязный слой CNeuronBaseOCL. Соответственно, свою работу мы начнем именно с него.

И тут надо вспомнить, что большинство вычислительных задач мы вынесли на сторону GPU для организации многопоточных вычислений. Данный процесс не является исключением. Соответственно, мы обращаемся к OpenCL программе, где создадим новый кернел UpdateWeightsAdamMini.

Но пред написанием кода нашей программы давайте немного обсудим выстраиваемое архитектурное решение.

Прежде всего следует отметить, что по большому счету новый метод оптимизации Adam-mini от классического Adam отличается только в алгоритме вычисления момента 2 порядка v. Здесь вместо градиента ошибки каждого отдельного параметра авторы метода предлагают использовать среднее значение группы. Алгоритм вычисления простого среднего не сложный. Но таким образом мы высвобождаем значительное количество памяти, так как для каждой группы сохраняем только 1 значение момента 2 порядка.

С другой стороны, мы бы не хотели бы в каждом отдельном потоке повторять вычисление среднего значения всего блока. Напомню, что для полносвязного слоя авторы метода Adam-mini предлагают использовать только 1 скорость обучения. Следовательно, повторять вычисление среднего значения градиента ошибки параметров слоя в потоке каждого отдельного параметра модели выглядит, мягко говоря, не совсем эффективно. А если еще и учесть, что данный процесс связан с большим количеством обращений к "дорогой" глобальной памяти, то возникает желание распараллелить данный процесс по нескольким отдельным потокам с минимизацией обращений к глобальной памяти. Но тут сразу возникает вопрос организации процесса обмена данными между потоками.

В предыдущих работах мы с Вами уже научились обмениваться данными внутри локальной группы с синхронизацией работы потоков. Но объединять весь процесс обновления параметров одного слоя в рамках одной локальной группы выглядит совсем не привлекательно. Поэтому в рамках данной реализации было принято решение несколько увеличить количество вычисляемых моментов 2 порядка до размера тензора результатов.

Напомню, что количество параметров полносвязного слоя равно произведению размера тензора исходных данных на размер тензора результатов. А использование параметра смещения для каждого нейрона добавляет еще количество параметров, равное размеру тензора результатов. Классический Adam сохраняет столько же значений для 1 и 2 моментов. В рамках реализации метода Adam-mini мы значительно сокращаем количество значений момента 2 порядка.

Теперь давайте немного обсудим сам процесс вычисления среднего значения момента 2 порядка. Градиент ошибки 1 параметра равен произведению градиента ошибки на выходе слоя (скорректированного на производную функции активации) и соответствующего значения исходных данных.

Соответственно среднее значение квадрата градиентов можно вычислить следующим образом:

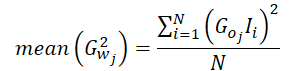
Не сложно заметить, что так как в своей реализации мы вычисляем средний градиент ошибки по 1 нейрону слоя результатов, то градиент ошибки этого нейрона можно вынести за скобки.

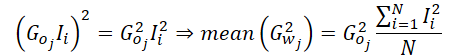
Таким образом, при вычислении среднего значения момента 2 порядка в нашей реализации нам достаточно посчитать среднее значение квадратов исходных данных, исключив обращения к буферу градиентов ошибки на уровне результатов, который находится в глобальной памяти. И только потом 1 раз взять значение градиента ошибки и умножить его квадрат на полученное среднее. Далее нам достаточно лишь распространить полученное значение по всей локальной группе для проведения последующих вычислений.

Теперь, когда у нас есть четкое представление об алгоритме операций мы можем перейти к реализации его в коде кернела UpdateWeightsAdamMini. Параметры данного кернела практически полностью повторяют соответствующий кернел классического метода Adam. Среди них 5 буферов данных и 3 константы:

• matrix_w — матрица параметров слоя;
• matrix_g — тензор градиентов ошибки на выходе слоя;
• matrix_i — буфер исходных данных;
• matrix_m — тензор моментов 1 порядка;
• matrix_v — тензор моментов 2 порядка;
• l — скорость обучения;
• b1 — коэффициент сглаживания моментов 1 порядка (ß1);
• b2 — коэффициент сглаживания моментов 2 порядка (ß2);

__kernel void UpdateWeightsAdamMini(__global float *matrix_w, 
                                    __global const float *matrix_g,
                                    __global const float *matrix_i,
                                    __global float *matrix_m,
                                    __global float *matrix_v,
                                    const float l,
                                    const float b1,
                                    const float b2 
                                   )
  {
//--- inputs
   const size_t i = get_local_id(0);
   const size_t inputs = get_local_size(0) - 1;
//--- outputs
   const size_t o = get_global_id(1);
   const size_t outputs = get_global_size(1);

Выполнение кернела планируется в 2 мерном пространстве задач. Первое измерение соответствует числу исходных данных плюс элемент смещения. А второе — размеру тензора результатов. В теле кернела мы сразу идентифицируем поток в обоих измерениях.

Здесь следует обратить внимание, что мы объединяем потоки в рабочие группы по 1 измерению пространства задач.

Далее мы организуем массив в локальной памяти контекста для обмена данными между потоками рабочей группы.

   __local float temp[LOCAL_ARRAY_SIZE];
   const int ls = min((uint)LOCAL_ARRAY_SIZE, (uint)inputs);

Следующим этапом мы переходим к вычислению среднего значения квадрата исходных данных. Так как значение из буфера исходных данных нам потребуется и при вычислении момента 1 порядка, то сначала каждый поток возьмет 1 соответствующе значение из глобального буфера исходных данных.

   const float inp = (i < inputs ? matrix_i[i] : 1.0f);

А затем организуем цикл с синхронизацией работы потоков, в рамках которого каждый поток добавит квадратичное значение своего элемента исходных данных в локальный массив.

   int count = 0;
   do
     {
      if(count == (i / ls))
        {
         int shift = i % ls;
         temp[shift] = (count == 0 ? 0 : temp[shift]) + ((isnan(inp) || isinf(inp)) ? 0 : inp*inp);
        }
      count++;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count * ls < inputs);

После чего мы суммируем значения элементов локального массива.

//--- sum
   count = (ls + 1) / 2;
   do
     {
      if(i < count && (i + count) < ls)
        {
         temp[i] += temp[i + count];
         temp[i + count] = 0;
        }
      count = (count + 1) / 2;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

В рамках одного потока мы организуем вычисление момента 2 порядка и сохраним его в элементе локального массива с индексом 0.

Кроме того, мы помним, что обращение к массиву локальной памяти гораздо быстрее работы с буфером глобальной памяти. Поэтому для сокращения операций обращения к глобальной памяти мы возьмем градиент ошибки на уровне результатов текущего слоя и сохраним в элементе локального массива с индексом 1. Таким образом, остальные элементы рабочей группы при выполнении последующих операциях вместо обращения к глобальной памяти возьмут значение из локальной.

В обязательном порядке синхронизируем работу потоков рабочей группы.

//--- calc v
   if(i == 0)
     {
      temp[1] = matrix_g[o];
      if(isnan(temp[1]) || isinf(temp[1]))
         temp[1] = 0;
      temp[0] /= inputs;
      if(isnan(temp[0]) || isinf(temp[0]))
         temp[0] = 1;
      float v = matrix_v[o];
      if(isnan(v) || isinf(v))
         v = 1;
      temp[0] = b2 * v + (1 - b2) * pow(temp[1], 2) * temp[0];
      matrix_v[o] = temp[0];
     }
   barrier(CLK_LOCAL_MEM_FENCE);

Обратите внимание, что мы сразу сохраняем значение момента 2 порядка в глобальном буфере данных. Этот простой шаг позволяет нам исключить излишние обращения к глобальной памяти из других потоков рабочей группы, а вместе с тем и задержки одновременного обращения к одному элементу глобального буфера из разных потоков. 

Далее наш алгоритм повторяет операции классического метода Adam. Здесь мы определяем смещение в тензоре обучаемых параметров и загрузим текущее значение анализируемого параметра из буфера глобальной памяти.

   const int wi = o * (inputs + 1) + i;
   float weight = matrix_w[wi];
   if(isnan(weight) || isinf(weight))
      weight = 0;

Посчитаем значение момента 1 порядка.

   float m = matrix_m[wi];
   if(isnan(m) || isinf(m))
      m = 0;
//--- calc m
   m = b1 * m + (1 - b1) * temp[1] * inp;
   if(isnan(m) || isinf(m))
      m = 0;

Определим размер корректировки параметра.

   float delta = l * (m / (sqrt(temp[0]) + 1.0e-37f) - (l1 * sign(weight) + l2 * weight));
   if(isnan(delta) || isinf(delta))
      delta = 0;

После чего скорректируем значение параметра и сохраним его новое значение в глобальном буфере данных.

   if(delta > 0)
      matrix_w[wi] = clamp(weight + delta, -MAX_WEIGHT, MAX_WEIGHT);
   matrix_m[wi] = m;
  }

Тут же мы сохраняем значение момента 1 порядка и завершаем работу кернела.

После внесения изменений на стороне OpenCL программы нам предстоит сделать ряд правок и в основной программе. Прежде всего мы добавим новый метод оптимизации в наше перечисление.

//+------------------------------------------------------------------+
/// Enum of optimization method used                                 |
//+------------------------------------------------------------------+
enum ENUM_OPTIMIZATION
  {
   SGD,        ///< Stochastic gradient descent
   ADAM,       ///< Adam
   ADAM_MINI   ///< Adam-mini
  };

После чего внесем правки в метод CNeuronBaseOCL::updateInputWeights. Здесь в блоке объявления переменных мы добавим массив описания размеров рабочей группы local_work_size (в коде ниже выделен подчеркиванием). На данном этапе мы не присваиваем ему значения, так как они будут необходимы только при использовании соответствующего метода оптимизации.

bool CNeuronBaseOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(CheckPointer(OpenCL) == POINTER_INVALID || CheckPointer(NeuronOCL) == POINTER_INVALID)
      return false;
   uint global_work_offset[2] = {0, 0};
   uint global_work_size[2], local_work_size[2];
   global_work_size[0] = Neurons();
   global_work_size[1] = NeuronOCL.Neurons() + 1;
   uint rest = 0;
   float lt = lr;

Далее идет разветвление алгоритма в зависимости от выбранного метода оптимизации параметров модели. Алгоритмы постановки в очередь выполнения кернелов ранее рассмотренных методов оптимизации остаются без изменений, и мы не будем на них останавливаться.

   switch(NeuronOCL.Optimization())
     {
      case SGD:
.........
.........
.........
         break;
      case ADAM:
........
........
........
         break;

Рассмотрим лишь добавленный код. Вначале мы передаем параметры, необходимые для корректной работы кернела.

      case ADAM_MINI:
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdamMini, def_k_wuam_matrix_w,
                                                           NeuronOCL.getWeightsIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdamMini, def_k_wuam_matrix_g,
                                                                    getGradientIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdamMini, def_k_wuam_matrix_i, 
                                                            NeuronOCL.getOutputIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdamMini, def_k_wuam_matrix_m, 
                                                     NeuronOCL.getFirstMomentumIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdamMini, def_k_wuam_matrix_v, 
                                                    NeuronOCL.getSecondMomentumIndex()))
            return false;
         lt = (float)(lr * sqrt(1 - pow(b2, (float)t)) / (1 - pow(b1, (float)t)));
         if(!OpenCL.SetArgument(def_k_UpdateWeightsAdamMini, def_k_wuam_l, lt))
            return false;
         if(!OpenCL.SetArgument(def_k_UpdateWeightsAdamMini, def_k_wuam_b1, b1))
            return false;
         if(!OpenCL.SetArgument(def_k_UpdateWeightsAdamMini, def_k_wuam_b2, b2))
            return false;

После чего определим пространства задач глобальной работы кернела и отдельной рабочей группы.

         global_work_size[0] = NeuronOCL.Neurons() + 1;
         global_work_size[1] = Neurons();
         local_work_size[0] = global_work_size[0];
         local_work_size[1] = 1;

Обратите внимание, что в первом измерении как глобально, так и для рабочей группы мы указываем значение на 1 элемент больше размера слоя исходных данных. Это наш параметр смещения. А вот во втором измерении глобально мы указываем количество элементов в текущем нейронном слое. В то время как для рабочей группы в этом измерении мы указываем 1 элемент. Что соответствует работе рабочей группы в рамках 1 нейрона текущего слоя.

За проведенной подготовительной работой следует постановка кернела в очередь выполнения.

         ResetLastError();
         if(!OpenCL.Execute(def_k_UpdateWeightsAdamMini, 2, global_work_offset, global_work_size, 
                                                                                local_work_size))
           {
            printf("Error of execution kernel UpdateWeightsAdamMini: %d", GetLastError());
            return false;
           }
         t++;
         break;
      default:
         return false;
         break;
     }
//---
   return true;
  }

И добавим выход с негативным результатом при указании не корректного метода оптимизации параметров.

На этом мы завершаем работу с методом обновления параметров базового полносвязного слоя CNeuronBaseOCL::updateInputWeights. Но тут стоит вспомнить о целях проделанных операций — сокращение потребления памяти при использовании метода оптимизации Adam. Следовательно, нам нужно обратить свое внимание на метод инициализации класса CNeuronBaseOCL::Init и в нем сократить размер буфера моментов 2 порядка при выборе метода оптимизации параметров Adam-mini. Так как правки носят точечный характер, я не буду в рамках статьи приводить полное описание алгоритма метода. Представлю лишь блок инициализации соответствующего буфера.

         if(CheckPointer(SecondMomentum) == POINTER_INVALID)
           {
            SecondMomentum = new CBufferFloat();
            if(CheckPointer(SecondMomentum) == POINTER_INVALID)
               return false;
           }
         if(!SecondMomentum.BufferInit((optimization == ADAM_MINI ? numOutputs : count), 0))
            return false;
         if(!SecondMomentum.BufferCreate(OpenCL))
            return false;

А с полным кодом данного метода Вы можете самостоятельно ознакомиться во вложении. Там же представлен полный код всех программ, используемых при подготовке данной статьи.

2.2 Adam-mini в сверточном слое

Еще один "базовый кирпичик", который широко используется нами в других архитектурах, включая Transformer, является сверточный слой.

Надо сказать, что добавление в его функционал метода оптимизации параметров Adam-mini имеет свою специфику. И прежде всего это связано со спецификой самого слоя. В отличие от полносвязного слоя, в котором каждый обучаемый параметр используется для передачи значения только 1 нейрона исходных данных только 1 нейрону текущего слоя. Сверточный слой обычно имеет значительно меньше параметров, но их использование более широкое.

Так же хочу напомнить, что именно сверточные слои мы используем для формирования сущностей Query, Key и Value в рамках работы алгоритмов Transformer. А эти сущности имеют свою специфику реализации метода Adam-mini.

И все эти моменты нам предстоит учесть при реализации метода Adam-mini в рамках сверточного слоя.

Как и в случае полносвязного слоя, свою работу мы начнем на стороне OpenCL программы. Здесь мы создаем кернел UpdateWeightsConvAdamMini. В параметрах указанного кернела помимо уже знакомых нам переменных добавляются 2 константы: размер последовательности исходных данных и шаг окна свертки.

__kernel void UpdateWeightsConvAdamMini(__global float *matrix_w,  
                                        __global const float *matrix_i,
                                        __global float *matrix_m,      
                                        __global float *matrix_v,      
                                        const int inputs,              
                                        const float l,              
                                        const float b1,             
                                        const float b2,             
                                        int step                    
                                       )
  {
//--- window in
   const size_t i = get_global_id(0);
   const size_t window_in = get_global_size(0) - 1;
//--- window out
   const size_t f = get_global_id(1);
   const size_t window_out = get_global_size(1);
//--- head window out
   const size_t f_h = get_local_id(1);
   const size_t window_out_h = get_local_size(1);
//--- variable
   const size_t v = get_global_id(2);
   const size_t variables = get_global_size(2);

Обратите внимание, что в параметрах кернела мы не указываем размер окна исходных данных и количество используемых фильтров. Эти параметры и 2 других вынесены в пространство задач. И на это стоит обратить внимание.

Данный кернел мы планируем вызывать в 3 мерном пространстве задач. Первое измерение соответствует размеру окна исходных данных плюс 1 элемент смещения. Здесь можно заметить некоторую связь с пространством задач полносвязного слоя.

Второе измерение пространства задач соответствует количеству используемых фильтров. И здесь очевидна логическая связь с размерностью результатов полносвязного слоя.

Только вот рабочие группы мы будем создавать ни по каждому отдельному фильтру свертки, а сгруппируем их по головам внимания архитектуры Transformer.

Обратите внимание, что пользователь имеет возможность указать только 1 фильтр свертки для каждой головы. И в таком случае каждый фильтр свертки получит индивидуальную скорость обучению аналогично нашей реализации полносвязного слоя.

Третье измерение пространства задач мы создали для работы с мультимодальными временными рядами. Когда для отдельных унитарных последовательностей используются собственные фильтры свертки. Для них мы так же создаем отдельные моменты 2 порядка для организации адаптивных скоростей обучения.

Здесь есть тонкая грань между "головами внимания" и "унитарными временными рядами", которую не следует путать. Несмотря на некоторое сходство, ни в коем случае нельзя одно понятие подменять другим. Унитарные временные ряды делят тензор исходных данных. В то время как головы внимания делят тензор результатов.

В теле кернела после идентификации потока во всех измерениях пространства задач мы определим основные константы смещения в глобальных буферах данных.

//--- constants
   const int total = (inputs - window_in + step - 1) / step;
   const int shift_var_in = v * inputs;
   const int shift_var_out = v * total * window_out;
   const int shift_w = (f + v * window_out) * (window_in + 1) + i;

И создадим локальный массив обмена данных рабочей группы.

   __local float temp[LOCAL_ARRAY_SIZE];
   const int ls = min((uint)window_in, (uint)LOCAL_ARRAY_SIZE);

После проведения подготовительной работы мы соберем градиенты ошибки по каждому параметру.

//--- calc gradient
   float grad = 0;
   for(int t = 0; t < total; t++)
     {
      if(i != window_in && (i + t * window_in) >= inputs)
         break;
      float gt = matrix_g[t * window_out + f + shift_var_out] *
                 (i == window_in ? 1 : matrix_i[i + t * step + shift_var_in]);
      if(!(isnan(gt) || isinf(gt)))
         grad += gt;
     }

Обратите внимание, в данном случае каждый глобальный поток полностью собирает градиенты ошибок со всех элементов, на которые он оказывает влияние. И здесь, в отличие от полносвязного слоя, мы сразу умножаем значение элемента исходных данных на соответствующий градиент ошибки результатов.

Далее мы собираем полученные градиенты ошибки для суммирования квадратичных значений в элементах локального массива, но уже в рамках рабочей группы. Для этого организуем систему вложенных циклов с обязательной синхронизацией потоков. Внешний цикл соответствует количеству фильтров в рамках рабочей группы. А вложенный цикл собирает градиенты ошибки со всех параметров одного фильтра.  

//--- calc sum grad
   int count;
   for(int h = 0; h < window_out_h; h++)
     {
      count = 0;
      do
        {
         if(h == f_h)
           {
            if(count == (i / ls))
              {
               int shift = i % ls;
               temp[shift] = ((count == 0 && h == 0) ? 0 : temp[shift]) + 
                             ((isnan(grad) || isinf(grad)) ? 0 : grad * grad);
              }
           }
         count++;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while((count * ls) < window_in);
     }

Затем мы суммируем значения локального массива.

   count = (ls + 1) / 2;
   do
     {
      if(i < count && (i + count) < ls && f_h == 0)
        {
         temp[i] += temp[i + count];
         temp[i + count] = 0;
        }
      count = (count + 1) / 2;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

И определим значение момента 2 порядка текущей группы.

//--- calc v
   if(i == 0 && f_h == 0)
     {
      temp[0] /= (window_in * window_out_h);
      if(isnan(temp[0]) || isinf(temp[0]))
         temp[0] = 1;
      int head = f / window_out_h;
      float v = matrix_v[head];
      if(isnan(v) || isinf(v))
         v = 1;
      temp[0] = clamp(b2 * v + (1 - b2) * temp[0], 1.0e-6f, 1.0e6f);
      matrix_v[head] = temp[0];
     }
   barrier(CLK_LOCAL_MEM_FENCE);

И далее повторяем алгоритм классического метода Adam. Здесь мы определяем момент 1 порядка.

//--- calc m
   float mt = clamp(b1 * matrix_m[shift_w] + (1 - b1) * grad, -1.0e5f, 1.0e5f);
   if(isnan(mt) || isinf(mt))
      mt = 0;

Корректируем значение анализируемого параметра.

   float weight = clamp(matrix_w[shift_w] + l * mt / sqrt(temp[0]), -MAX_WEIGHT, MAX_WEIGHT);

И сохраняем полученные значения.

   if(!(isnan(weight) || isinf(weight)))
      matrix_w[shift_w] = weight;
   matrix_m[shift_w] = mt;
  }

После создания кернела на стороне OpenCL мы переходим к работе над основной программой. Как и в случае полносвязного слоя, вызов выше созданного кернела мы организуем в методе CNeuronConvOCL::updateInputWeights. Алгоритм его вызова Вам напомнит выше представленный для полносвязного слоя. Для обычного сверточного слоя мы используем 1 фильтр для каждой головы внимания и используем 1 унитарную последовательность. Таким образом размерность пространства задач примет следующий вид.

   uint global_work_offset_am[3] = { 0, 0, 0 };
   uint global_work_size_am[3] = { iWindow + 1, iWindowOut, iVariables };
   uint local_work_size_am[3] = { global_work_size_am[0], 1, 1 };

А с полным кодом данного метода Вы можете самостоятельно ознакомиться во вложении.

Однако хочется добавить несколько слов об использовании созданного кернела в рамках реализации классов, использующих архитектуру Transformer. Для примера рассмотрим класс CNeuronMLMHAttentionOCL. Именно этот класс мы используем в качестве родительского для построения ряда других алгоритмов.

Напомню, что класс CNeuronMLMHAttentionOCL не содержит в своей структуре сверточные слои в обычном понимании. В нем организованы массивы буферов и переопределены все методы. Обновление параметров сверточных слоев осуществляется в методе ConvolutuionUpdateWeights. Так как данный метод используется для организации работы различных сверточных слоев, мы добавим 2 дополнительных параметра: количество голов внимания (heads) и унитарных последовательностей (variables). Для исключения проблем обращения к данному методу из других классов новые параметры получат значения по умолчанию.

bool CNeuronMLMHAttentionOCL::ConvolutuionUpdateWeights(CBufferFloat *weights, 
                                                        CBufferFloat *gradient, 
                                                        CBufferFloat *inputs, 
                                                        CBufferFloat *momentum1, 
                                                        CBufferFloat *momentum2, 
                                                        uint window, uint window_out, 
                                                        uint step = 0, uint heads = 0, 
                                                        uint variables = 1)
  {
   if(CheckPointer(OpenCL) == POINTER_INVALID || CheckPointer(weights) == POINTER_INVALID || 
      CheckPointer(gradient) == POINTER_INVALID || CheckPointer(inputs) == POINTER_INVALID  || 
      CheckPointer(momentum1) == POINTER_INVALID)
      return false;

В теле метода мы сначала проверяем указатели на буферы данных, которые метод получает в параметрах от вызывающей программы.

Далее мы проверяем значение параметра шага окна свертки. Если оно равно "0", то делаем шаг равный окну свертки.

   if(step == 0)
      step = window;

Обратите внимание, что в данном случае мы используем беззнаковый тип данных для параметров. Следовательно, они не могут содержать отрицательных значений. Контроль завышенных значений параметров мы оставляем за пользователем.

Затем мы определяем пространства задач. В данном случае кернел метода оптимизации Adam-mini использует 3 мерное пространства задач, которое отличается от одномерного для других методов оптимизации. Поэтому мы выделяем для его указания отдельные массивы. 

   uint global_work_offset[1] = {0};
   uint global_work_size[1];
   global_work_size[0] = weights.Total();
   uint global_work_offset_am[3] = {0, 0, 0};
   uint global_work_size_am[3] = {window, window_out, 1};
   uint local_work_size_am[3] = {window, (heads > 0 ? window_out / heads : 1), variables};

Посмотрите на 2 измерение пространства задач рабочей группы. Если в параметрах метода не указать количество используемых голов внимания, то для каждого фильтра используется отдельная скорость обучения. В противном случае мы вычисляем количество фильтров в одной голове внимания, как отношения общего количества фильтров к количеству голов внимания.

Такой подход был принят для удовлетворения различных сценариев использования данного метода. Ведь в рамках класса CNeuronMLMHAttentionOCL сверточные слои используются как для формирования сущностей Query, Key и Value, так и для проекции данных (в рамках слоя понижения размерности многоголового внимания и блока FeedForward).

Следующим этапом идет разделение алгоритма в зависимости от используемого метода оптимизации параметров модели. Как и при рассмотрении алгоритмов полносвязного слоя, мы не будем останавливаться на алгоритмах организации работы ранее реализованных методов оптимизации. Рассмотрим лишь блок метода Adam-mini.

   if(weights.GetIndex() < 0)
      return false;
   float lt = 0;
   switch(optimization)
     {
      case SGD:
........
........
........
         break;
      case ADAM:
........
........
........
         break;
      case ADAM_MINI:
         if(CheckPointer(momentum2) == POINTER_INVALID)
            return false;
         if(gradient.GetIndex() < 0)
            return false;
         if(inputs.GetIndex() < 0)
            return false;
         if(momentum1.GetIndex() < 0)
            return false;
         if(momentum2.GetIndex() < 0)
            return false;

Здесь мы проверяем актуальность указателей на буферы данных в контексте OpenCL. После чего передадим кернелу все необходимые параметры.

         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsConvAdamMini, def_k_wucam_matrix_w, 
                                                                         weights.GetIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsConvAdamMini, def_k_wucam_matrix_g, 
                                                                        gradient.GetIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsConvAdamMini, def_k_wucam_matrix_i, 
                                                                          inputs.GetIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsConvAdamMini, def_k_wucam_matrix_m, 
                                                                       momentum1.GetIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsConvAdamMini, def_k_wucam_matrix_v, 
                                                                       momentum2.GetIndex()))
            return false;
         lt = (float)(lr * sqrt(1 - pow(b2, t)) / (1 - pow(b1, t)));
         if(!OpenCL.SetArgument(def_k_UpdateWeightsConvAdamMini, def_k_wucam_inputs, 
                                                                            inputs.Total()))
            return false;
         if(!OpenCL.SetArgument(def_k_UpdateWeightsConvAdamMini, def_k_wucam_l, lt))
            return false;
         if(!OpenCL.SetArgument(def_k_UpdateWeightsConvAdamMini, def_k_wucam_b1, b1))
            return false;
         if(!OpenCL.SetArgument(def_k_UpdateWeightsConvAdamMini, def_k_wucam_b2, b2))
            return false;
         if(!OpenCL.SetArgument(def_k_UpdateWeightsConvAdamMini, def_k_wucam_step, (int)step))
            return false;

Пространство задач мы уже казали ранее. И сейчас нам остается лишь поставить кернел в очередь выполнения.

         ResetLastError();
         if(!OpenCL.Execute(def_k_UpdateWeightsConvAdamMini, 3, global_work_offset_am, 
                                              global_work_size_am, local_work_size_am))
           {
            string error;
            CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error);
            printf("Error of execution kernel %s Adam-Mini: %s", __FUNCSIG__, error);
            return false;
           }
         t++;
         break;
      //---
      default:
         printf("Error of optimization type %s: %s", __FUNCSIG__, EnumToString(optimization));
         return false;
     }

Мы так же добавим сообщение об ошибке при указании не корректного типа оптимизации параметров.

Дальнейший код метода в части нормализации параметров модели остался без изменений.

   global_work_size[0] = window_out;
   OpenCL.SetArgumentBuffer(def_k_NormilizeWeights, def_k_norm_buffer, weights.GetIndex());
   OpenCL.SetArgument(def_k_NormilizeWeights, def_k_norm_dimension, (int)window + 1);
   if(!OpenCL.Execute(def_k_NormilizeWeights, 1, global_work_offset, global_work_size))
     {
      string error;
      CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error);
      printf("Error of execution kernel %s Normalize: %s", __FUNCSIG__, error);
      return false;
     }
//---
   return true;
  }

Кроме того, в методах инициализации вышеуказанных классов мы изменяем размеры буферов данных, создаваемых для хранения моментов 2 порядка, аналогично алгоритму, представленному при описании модернизации полносвязного слоя. Но я не буду на этом останавливаться в рамках статьи. Это лишь точечные правки, с которыми Вы можете самостоятельно ознакомиться во вложении.

3. Тестирование

Выше представлено описание внедрения метода Adam-mini в 2 базовых класса наших моделей. И теперь пришло время посмотреть на эффективность предложенных подходов.

Обратите внимание, что в данной статье мы внедряли новый метод оптимизации. А для оценки эффективности работы метода оптимизации логично посмотреть на процесс обучения одной модели различными методами оптимизации.

Для своего эксперимента я взял модели из статьи об алгоритме TPM и изменил в архитектуре моделей только метод оптимизации параметров.

Излишне говорить, что при таком подходе все программы обучения моделей, обучающая выборка и процесс обучения остались неизменными.

Напомню, что обучение моделей осуществляется на исторических данных за весь 2023 год инструмента EURUSD таймфрейм H1. Параметры всех индикаторов используются по умолчанию.

При тестировании обученной модели мы получили результаты довольно схожие с обучением модели методом классического Adam. Результаты тестирования обученной модели на данных Января 2024 года представлены ниже.

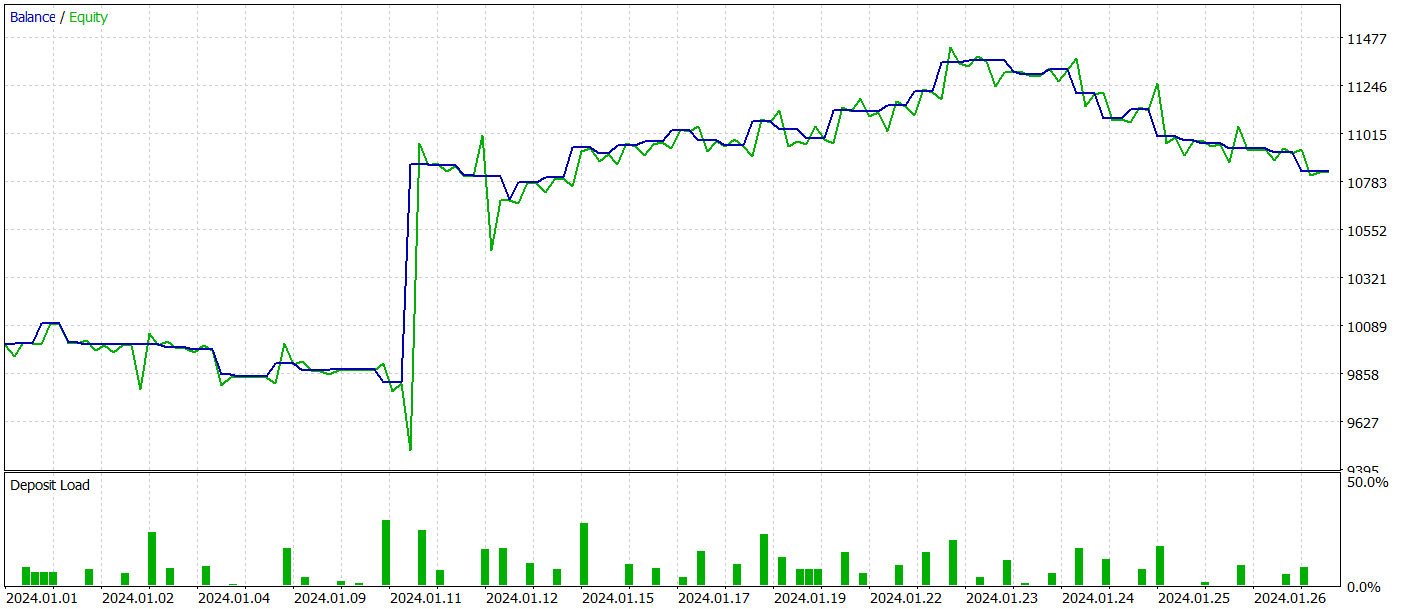
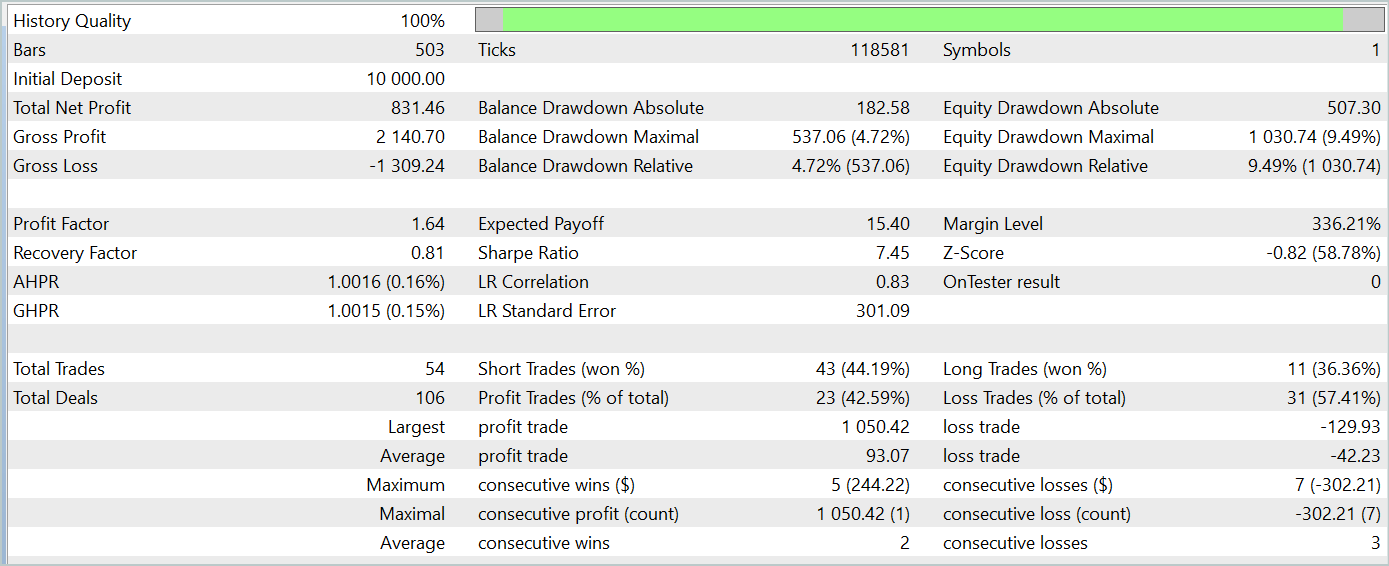
Здесь стоит напомнить, что основной целью авторов метода оптимизации Adam-mini является снижение потребления памяти модели без ухудшения качества обучения. И с этой задачей представленный метод справляется.

Заключение

В этой статье мы познакомились с новым методом оптимизации Adam-mini, который разработан с целью уменьшения использования памяти и увеличения пропускной способности при обучении крупных языковых моделей. Adam-mini достигает этого, сокращая количество необходимых скоростей обучения до суммы размера слоя эмбединга, размера слоя результатов и количества блоков в других слоях. Его простота, гибкость и эффективность делают представленный метод перспективным инструментом для широкого применения в области глубокого обучения.

В практической части статьи было продемонстрировано внедрение предложенного метода в базовые типы нейронных слоев. А результаты проведенных тестов подтверждают улучшения, заявленные авторами метода.

Ссылки

Adam-mini: Use Fewer Learning Rates To Gain More

Другие статьи серии

Программы, используемые в статье

#	Имя	Тип	Описание
1	Research.mq5	Советник	Советник сбора примеров
2	ResearchRealORL.mq5	Советник	Советник сбора примеров методом Real-ORL
3	Study.mq5	Советник	Советник обучения Моделей
4	StudyEncoder.mq5	Советник	Советник обучения Энкодера
5	Test.mq5	Советник	Советник для тестирования модели
6	Trajectory.mqh	Библиотека класса	Структура описания состояния системы
7	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
8	NeuroNet.cl	Библиотека	Библиотека кода программы OpenCL