Redes neurais em trading: Modelos "leves" para previsão de séries temporais
Introdução
Prever o movimento futuro dos preços é extremamente importante para construir estratégias de trading. Normalmente, para conseguir previsões precisas, é necessário usar modelos robustos e complexos de aprendizado profundo.
A base para previsões precisas de longo prazo de séries temporais reside na periodicidade e tendência inerentes aos dados. Além disso, sabe-se há muito tempo que os movimentos de preços dos pares de moedas estão intimamente ligados a sessões específicas de trading. Por exemplo, ao discretizarmos a série temporal de sequências diárias em momentos específicos do dia, cada subsequência mostrará tendências semelhantes ou consecutivas. Nesse caso, a periodicidade e a tendência da sequência original são decompostas e transformadas. Ou seja, os padrões periódicos se transformam na dinâmica entre as subsequências, enquanto os padrões de tendência são reinterpretados como características dentro de cada uma. Essa decomposição abre novas perspectivas para o desenvolvimento de modelos leves de previsão de longo prazo de séries temporais, o que chamou a atenção dos autores do artigo "SparseTSF: Modeling Long-term Time Series Forecasting with 1k Parameters".
Em seu trabalho, eles investigam, provavelmente pela primeira vez, como utilizar essa periodicidade e decomposição nos dados para construir modelos especializados na previsão de séries temporais. Isso lhes permitiu propor o algoritmo SparseTSF, um modelo extremamente leve para previsão de longo prazo de séries temporais.
Tecnicamente, foi proposta uma metodologia de previsão esparsa entre períodos. Primeiro, os dados brutos são divididos em sequências com periodicidade constante. Em seguida, a previsão é realizada para cada subsequência com discretização reduzida. Dessa maneira, o problema original de previsão de séries temporais é simplificado para a tarefa de previsão da tendência entre períodos.
Essa abordagem traz duas vantagens:
- separação eficiente da periodicidade dos dados e da tendência, permitindo que o modelo identifique e extraia de forma consistente características periódicas, enquanto se foca na previsão de mudanças na tendência;
- e compressão extrema do tamanho dos parâmetros do modelo, reduzindo significativamente a necessidade de recursos computacionais
1. Algoritmo SparseSTF
O problema da previsão de longo prazo de séries temporais (Long-term Time Series Forecasting — LTSF) consiste em prever valores futuros em um horizonte expandido usando dados observados anteriormente de séries temporais multivariadas. O principal objetivo do LTSF é estender o horizonte de previsão H, pois isso possibilita recomendações mais ricas e avançadas para aplicações práticas. No entanto, a ampliação do horizonte de previsão frequentemente resulta em um modelo mais complexo. Para resolver esse problema, os autores do método SparseTSF concentraram-se no desenvolvimento de modelos que fossem não apenas extremamente leves, mas também confiáveis e eficazes.
Os avanços recentes no campo do LTSF resultaram em uma mudança para abordagens de previsão independentes de canais ao lidar com dados de séries temporais multivariadas. Essa estratégia simplifica o processo de previsão ao focar em séries temporais univariadas individuais dentro do conjunto de dados, reduzindo a complexidade de lidar com relações entre canais. Como resultado, o objetivo principal dos modelos contemporâneos nos últimos anos mudou para previsões eficazes, modelando dependências de longo prazo, incluindo periodicidade e tendências, em sequências univariadas.
Considerando que os dados a serem previstos frequentemente exibem periodicidade constante e conhecida a priori, os autores do método SparseTSF propõem o uso de previsão esparsa entre períodos para melhorar a captura de dependências sequenciais de longo prazo, reduzindo a escala dos parâmetros do modelo. A solução proposta utiliza uma única camada linear para modelar o problema do LTSF.
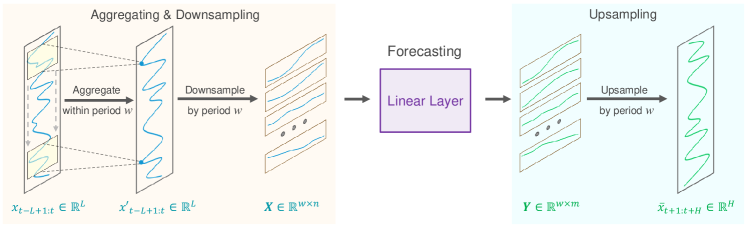
Supõe-se que uma série temporal Xt de comprimento L possui periodicidade w conhecida. O primeiro passo do algoritmo proposto é reduzir a discretização da sequência original em w subsequências de comprimento n (n=L/w). Em seguida, essas subsequências são submetidas a uma modelagem de previsão com parâmetros compartilhados. Como resultado dessa operação, obtemos w subsequências previstas, cada uma com comprimento m (m=H/w), que juntas formam a sequência completa prevista de comprimento H.
Intuitivamente, esse processo de previsão pode ser entendido como uma previsão deslizante com intervalo esparso w, realizada por uma camada completamente conectada que compartilha parâmetros durante um período constante w. Isso pode ser interpretado como um modelo que executa previsão deslizante esparsa por períodos.
Tecnicamente, o processo de redução da taxa de amostragem equivale a alterar a forma do tensor dos dados brutos Xt para uma matriz n*w, seguida pela transposição para w*n. A previsão da trajetória subsequente com deslizamento esparso equivale à aplicação de uma camada linear de tamanho n*m à última dimensão da matriz. Como resultado dessa operação, obtém-se uma matriz w*m.
Durante a ampliação da amostragem, são realizadas operações inversas: a transposição da matriz w*m, seguida pela reformatação em uma sequência completa de comprimento H.
No entanto, a abordagem proposta enfrenta dois desafios:
- Perda de informação, já que apenas um ponto de dados por período é utilizado para previsão, enquanto os demais são ignorados;
- Intensificação do impacto de valores atípicos, uma vez que a presença de valores extremos em subsequências com amostragem reduzida pode influenciar diretamente a previsão.
Para abordar esses problemas, os autores do método SparseTSF introduzem uma agregação deslizante na sequência original antes da previsão esparsa. Cada ponto de dados agregado inclui informações de outros pontos ao longo do período circundante, solucionando o primeiro problema. Além disso, como o valor agregado é essencialmente uma média ponderada dos pontos circundantes, ele atenua o impacto de valores atípicos, resolvendo assim o segundo problema.
Tecnicamente, essa agregação deslizante dos dados pode ser implementada utilizando uma camada convolucional com preenchimento zero.
Os dados de séries temporais frequentemente apresentam deslocamentos na distribuição entre os conjuntos de treinamento e teste. O uso de estratégias simples de normalização entre os dados brutos e a sequência prevista pode ajudar a mitigar esse problema. No algoritmo SparseTSF, utiliza-se uma estratégia direta de normalização. Especificamente, a média da sequência dos dados brutos é subtraída antes de o modelo ser alimentado com ela, e ela é adicionada de volta aos resultados obtidos.
Abaixo, é apresentada a visualização autoral do método SparseTSF.
2. Implementação em MQL5
Após abordar os aspectos teóricos do método SparseTSF, avançamos para a implementação dos métodos propostos utilizando MQL5. Para isso, criaremos uma nova classe chamada CNeuronSparseTSF dentro de nossa biblioteca.
2.1 Criação da classe SparseTSF
Nossa nova classe herdará a funcionalidade principal da classe base da camada completamente conectada, CNeuronBaseOCL. baixo, apresentamos a estrutura da classe CNeuronSparseTSF.
class CNeuronSparseTSF : public CNeuronBaseOCL { protected: CNeuronConvOCL cConvolution; CNeuronTransposeOCL acTranspose[4]; CNeuronConvOCL cForecast; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronSparseTSF(void) {}; ~CNeuronSparseTSF(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint sequence, uint variables, uint period, uint forecast, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronSparseTSF; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
Adicionaremos duas camadas convolucionais à estrutura da nova classe. Uma delas será responsável pela agregação de dados, enquanto a outra fará a previsão das sequências subsequentes. Além disso, utilizaremos uma série de transposições para reformatar os dados. Todos os objetos internos adicionados são declarados como estáticos, de modo que o construtor e o destrutor da classe permaneçam vazios. A inicialização direta do objeto da classe ocorre no método Init.
Nos parâmetros do método de inicialização, passamos os principais parâmetros do objeto a ser criado:
- sequence — comprimento da sequência de dados brutos;
- variables — número de parâmetros analisados (sequências unitárias nos dados brutos multimodais);
- period — periodicidade dos dados brutos;
- forecast — profundidade da previsão.
bool CNeuronSparseTSF::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint sequence, uint variables, uint period, uint forecast, ENUM_OPTIMIZATION optimization_type, uint batch ) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, forecast * variables, optimization_type, batch)) return false;
No corpo do método, como de costume, chamamos o método homônimo da classe pai, no qual já está implementado o processo de inicialização dos objetos e variáveis herdados.
Note que, ao chamar o método de inicialização da classe pai, especificamos o tamanho da camada como o produto da profundidade da previsão pelo número de sequências unitárias nos dados multimodais.
Após a inicialização bem-sucedida dos objetos e variáveis herdados, passamos à inicialização dos objetos internos adicionados. Essa inicialização será realizada na sequência em que ocorre a propagação para frente. Aqui, como se costuma dizer, "fiquem atentos às mãos". No nosso caso, é preciso ficar atento às dimensões do tensor dos dados sendo processados.
A camada de entrada espera receber um tensor de dados brutos com dimensão L*v, onde L é o comprimento da sequência de dados brutos e v é o número de séries unitárias nos dados multimodais. Conforme mencionado na primeira parte deste artigo, o método SparseTSF opera com base na lógica de previsão de sequências unitárias independentes. Para organizar tal processo, a matriz de dados brutos é transposta para v*L.
if(!acTranspose[0].Init(0, 0, OpenCL, sequence, variables, optimization, iBatch)) return false;
Em seguida, planejamos agregar os dados brutos utilizando uma camada convolucional. Nesta operação, aplicaremos uma convolução considerando dois períodos dos dados brutos, com um passo de um período. Para preservar as dimensões, o número de filtros de convolução será igual ao tamanho do período.
if(!cConvolution.Init(0, 1, OpenCL, 2 * period, period, period, sequence / period, variables, optimization, iBatch)) return false; cConvolution.SetActivationFunction(None);
É importante destacar que a agregação de dados será realizada em sequências unitárias independentes.
O próximo passo do algoritmo SparseTSF é a discretização dos dados brutos. Nesta etapa, os autores do método propõem alterar a dimensionalidade e transpor o tensor dos dados. No nosso caso, estamos lidando com buffers unidimensionais de dados. A alteração da dimensionalidade dos dados brutos é declarativa, ou seja, não implica uma realocação dos dados na memória. O mesmo não pode ser dito sobre a transposição, que reorganiza os dados de fato. Por isso, inicializamos em seguida a próxima camada responsável pela transposição dos dados.
if(!acTranspose[1].Init(0, 2, OpenCL, variables * sequence / period, period, optimization, iBatch)) return false;
Embora possa parecer um pouco estranho, é necessário usar uma segunda camada de transposição de dados. Afinal, à primeira vista, ele parece realizar a operação inversa à transposição anterior dos dados brutos. No entanto, isso não é verdade. Fiz questão de enfatizar as dimensões dos dados acima. O tamanho total do buffer de dados permanece inalterado — L*v. Apenas após a alteração declarativa da dimensionalidade da matriz de dados dizemos que seu tamanho é igual a (v * L/w) * w, onde w é a periodicidade dos dados brutos. Ao transpor essa expressão para w * (L/w * v), o buffer de dados resultante reflete uma sequência de etapas individuais da periodicidade dos dados brutos, preservando a independência das sequências unitárias dos dados.
Graficamente, o resultado das duas etapas de transposição de dados pode ser representado da seguinte forma:

Em seguida, utilizamos uma camada convolucional para realizar previsões independentes de passos individuais dentro da periodicidade dos dados brutos para sequências unitárias em um horizonte de planejamento definido.
if(!cForecast.Init(0, 3, OpenCL, sequence / period, sequence / period, forecast / period, variables, period, optimization, iBatch)) return false; cForecast.SetActivationFunction(TANH);
Note que o tamanho da janela de análise dos dados brutos e seu passo são iguais a sequence/period, enquanto o número de filtros da convolução é igual a forecast/period. Isso nos permite obter valores previstos para todo o horizonte de planejamento em uma única passagem. Além disso, utilizamos filtros separados para cada etapa do período dos dados analisados.
Como estamos assumindo que os dados estão normalizados, utilizamos a tangente hiperbólica como função de ativação para os valores previstos. Isso limita os resultados das previsões ao intervalo [-1, 1].
Posteriormente, é necessário reorganizar os valores previstos na sequência desejada. Essa operação é realizada por meio de duas camadas sequenciais de transposição de dados, que executam operações de inversão das reordenações anteriores.
if(!acTranspose[2].Init(0, 4, OpenCL, period, variables * forecast / period, optimization, iBatch)) return false; if(!acTranspose[3].Init(0, 5, OpenCL, variables, forecast, optimization, iBatch)) return false;
Para evitar cópias desnecessárias dos dados, organizamos a substituição dos buffers de resultados e dos gradientes de erro da camada atual.
if(!SetOutput(acTranspose[3].getOutput()) || !SetGradient(acTranspose[3].getGradient()) ) return false; //--- return true; }
A cada iteração, verificamos os resultados das operações realizadas. O resultado lógico final do método é retornado ao programa que o chamou.
É importante observar que, durante o processo de inicialização do objeto, não são armazenados os parâmetros da arquitetura da camada criada. Nesse caso, basta passar os parâmetros apropriados para os objetos internos. A arquitetura desses objetos determina claramente o funcionamento da classe, tornando desnecessário o armazenamento adicional dos parâmetros recebidos.
Após a inicialização do objeto da classe, avançamos para a criação do método de propagação para frente CNeuronSparseTSF::feedForward, no qual estruturamos o algoritmo do método SparseTSF, transmitindo os dados entre os objetos internos.
Nos parâmetros do método de propagação para frente, recebemos um ponteiro para o objeto da camada anterior, que contém os dados brutos.
bool CNeuronSparseTSF::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!acTranspose[0].FeedForward(NeuronOCL)) return false;
Como o algoritmo será implementado utilizando métodos previamente criados para os objetos internos, não serão feitas verificações adicionais sobre a validade do ponteiro recebido. Em vez disso, o transmitiremos diretamente ao método de propagação para a primeira camada de transposição de dados, que já inclui tais verificações juntamente com as operações de reordenação no buffer de dados. Apenas verificamos o resultado lógico das operações do método chamado.
Em seguida, ocorre a agregação dos dados por meio da chamada do método de propagação para frente da camada convolucional.
if(!cConvolution.FeedForward(acTranspose[0].AsObject())) return false;
De acordo com o algoritmo do método SparseTSF, os dados agregados são somados aos dados brutos. Contudo, para não alterar a sequência dos dados, somaremos a versão transposta dos dados brutos aos resultados da agregação.
if(!SumAndNormilize(cConvolution.getOutput(), acTranspose[0].getOutput(), cConvolution.getOutput(), 1, false)) return false;
O próximo passo é chamar o método de propagação para a próxima camada de transposição de dados, finalizando o processo de discretização da sequência original.
if(!acTranspose[1].FeedForward(cConvolution.AsObject())) return false;
Posteriormente, utilizamos a segunda camada convolucional interna para realizar a previsão da continuação mais provável da série temporal analisada.
if(!cForecast.FeedForward(acTranspose[1].AsObject())) return false;
Vale lembrar que a previsão das subsequências é baseada na análise de etapas individuais dentro da periodicidade especificada dos dados brutos. Realizamos previsões independentes para cada sequência unitária da série temporal multimodal dos dados brutos. Além disso, utilizam-se parâmetros treináveis exclusivos para cada etapa do ciclo fechado da periodicidade dos dados.
A reorganização dos valores previstos na ordem esperada da sequência de saída é realizada com duas camadas subsequentes de transposição de dados.
if(!acTranspose[2].FeedForward(cForecast.AsObject())) return false; if(!acTranspose[3].FeedForward(acTranspose[2].AsObject())) return false; //--- return true; }
Naturalmente, para a etapa de reorganização dos valores previstos no buffer de dados, poderíamos criar um novo kernel e substituir os dois níveis de transposição de dados por uma única chamada. Isso resultaria em um leve aumento de desempenho devido à eliminação de operações redundantes de transferência de dados. No entanto, considerando o tamanho do modelo, o ganho de desempenho seria insignificante. Por isso, neste experimento, decidimos priorizar a redução do código do programa e do esforço de desenvolvimento.
Observe que as operações do método de propagação para frente terminam com a execução dos métodos de propagação para frente dos objetos internos. Nesse processo, não é feita a transferência de valores para o buffer de resultados da camada atual, herdado da classe pai. No entanto, as camadas subsequentes do nosso modelo não têm acesso aos objetos internos e trabalham com os dados no buffer de resultados da camada atual. Esse aparente descompasso no fluxo de dados foi compensado por meio da substituição dos buffers de resultados e gradientes de erro durante a inicialização de nossa classe. Assim, o buffer de resultados da nossa camada recebeu um ponteiro para o buffer de resultados da última camada de transposição de dados. Com a execução da última operação de transposição, os dados são gravados no buffer de resultados da nossa camada, eliminando a necessidade de operações redundantes de transferência de dados entre objetos.
Como de costume, verificamos o resultado das operações em cada etapa e retornamos o valor lógico final ao programa chamador.
Com isso, concluímos a implementação da propagação para frente do método SparseTSF e avançamos para a construção dos algoritmos de propagação reversa. Nesta etapa, precisamos distribuir o gradiente de erro entre todos os participantes do processo, de acordo com sua influência no resultado, e ajustar os parâmetros do modelo para minimizar o erro de previsão da continuação da série temporal multimodal analisada.
O primeiro passo é construir o método de distribuição do gradiente de erro CNeuronSparseTSF::calcInputGradients. Assim como na propagação para frente, os parâmetros do método recebem um ponteiro para o objeto da camada anterior, onde, neste estágio, o gradiente de erro será registrado de acordo com a influência dos dados brutos no resultado do modelo.
bool CNeuronSparseTSF::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!acTranspose[2].calcHiddenGradients(acTranspose[3].AsObject())) return false;
A distribuição do gradiente de erro será feita seguindo as operações de propagação para frente, mas na ordem inversa. Como você sabe, devido à substituição dos ponteiros para os buffers de dados, o gradiente de erro recebido da camada subsequente do modelo é registrado diretamente no buffer da última camada interna de transposição de dados. Isso permite que passemos a trabalhar imediatamente com os objetos internos, sem a necessidade de realizar operações adicionais de transferência de dados.
Primeiro, conduzimos o gradiente de erro pelas duas camadas de transposição de dados para alcançar a discretização necessária dos gradientes.
if(!cForecast.calcHiddenGradients(acTranspose[2].AsObject())) return false;
Se necessário, ajustamos o gradiente obtido pela derivada da função de ativação da camada de previsão de dados.
if(cForecast.Activation() != None && !DeActivation(cForecast.getOutput(), cForecast.getGradient(), cForecast.getGradient(), cForecast.Activation())) return false;
Em seguida, descemos o gradiente de erro para o nível dos dados agregados.
if(!acTranspose[1].calcHiddenGradients(cForecast.AsObject())) return false; if(!cConvolution.calcHiddenGradients(acTranspose[1].AsObject())) return false;
Conduzimos o gradiente de erro através da camada de agregação.
if(!acTranspose[0].calcHiddenGradients(cConvolution.AsObject())) return false;
Lembre-se de que utilizamos conexões residuais para somar os dados agregados à sequência original durante a agregação dos dados. Consequentemente, o gradiente de erro também percorre dois fluxos de dados, e os valores dos dois buffers de gradiente de erro são somados.
if(!SumAndNormilize(cConvolution.getGradient(), acTranspose[0].getGradient(), acTranspose[0].getGradient(), 1, false)) return false;
Em seguida, transferimos o gradiente de erro resultante para o nível da camada anterior e, se necessário, ajustamos os valores pela derivada da função de ativação.
if(!NeuronOCL || !NeuronOCL.calcHiddenGradients(acTranspose[0].AsObject())) return false; if(NeuronOCL.Activation() != None && !DeActivation(NeuronOCL.getOutput(), NeuronOCL.getGradient(), NeuronOCL.getGradient(), NeuronOCL.Activation())) //--- return true; }
No final do método, retornamos o resultado lógico das operações para o programa que o chamou.
Após distribuir o gradiente de erro para todos os objetos de nosso modelo, de acordo com sua influência no resultado final, precisamos ajustar os parâmetros do modelo para minimizar o erro de previsão dos dados. Essa funcionalidade é realizada no método CNeuronSparseTSF::updateInputWeights. Aqui tudo é bastante simples e direto. Nossa nova classe contém apenas duas camadas convolucionais internas, que possuem parâmetros passíveis de treinamento. Como você sabe, as operações de transposição de dados não utilizam tais parâmetros. Portanto, no processo de ajuste dos parâmetros do modelo, basta chamar os métodos homônimos dessas camadas e verificar o resultado lógico das operações. Todo o processo de ajuste de parâmetros já está estruturado nesses objetos.
bool CNeuronSparseTSF::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(!cConvolution.UpdateInputWeights(acTranspose[0].AsObject())) return false; if(!cForecast.UpdateInputWeights(acTranspose[1].AsObject())) return false; //--- return true; }
Assim, concluímos a análise do algoritmo de construção dos principais métodos funcionais de nossa nova classe CNeuronSparseTSF. Todos os métodos auxiliares dessa classe foram construídos seguindo esquemas familiares das partes anteriores desta série de artigos. Por isso, não os abordaremos aqui e deixaremos que sejam estudados de forma independente. O código completo de todos os métodos da nova classe está disponível no anexo.
2.2 Arquitetura dos modelos treináveis
Acima, implementamos as principais abordagens do método SparseTSF utilizando MQL5 no escopo da nova classe CNeuronSparseTSF. Agora, precisamos integrar o objeto dessa classe ao nosso modelo. Como anteriormente, o algoritmo de previsão da série temporal será utilizado no modelo de Codificador do estado do ambiente. A arquitetura desse modelo está definida no método CreateCodificadorDescriptions, e um ponteiro para o objeto de array dinâmico onde será registrada a arquitetura do modelo criado é passado como parâmetro.
bool CreateEncoderDescriptions(CArrayObj *encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
No corpo do método, verificamos a validade do ponteiro recebido e, se necessário, criamos um novo objeto de array dinâmico.
Em seguida, como de costume, utilizamos uma camada completamente conectada básica para registrar os dados brutos.
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM_MINI; if(!encoder.Add(descr)) { delete descr; return false; }
Os dados "crus", não processados, são passados diretamente para o modelo, o que nos permite minimizar o trabalho de preparação de dados na parte principal do programa. O pré-processamento dos dados recebidos ocorre na camada de normalização em lote.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Após a camada de normalização em lote, adicionamos nossa nova camada do método SparseTSF.
if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSparseTSF; descr.count = HistoryBars; descr.window = BarDescr;
Lembro que, para o treinamento e teste dos modelos nesta série de artigos, utilizamos dados históricos do intervalo de tempo H1. Nessas condições, definimos o tamanho do período dos dados brutos como 24, o que corresponde a um dia de calendário.
descr.step = 24; descr.window_out = NForecast; descr.activation = None; descr.optimization = ADAM_MINI; if(!encoder.Add(descr)) { delete descr; return false; }
É importante notar que o uso dos modelos apresentados não se limita ao intervalo de tempo H1. No entanto, testar e treinar diferentes modelos sob condições idênticas nos permite avaliar o desempenho e minimizar a influência de fatores externos na eficácia deles.
Embora o método SparseTSF pareça simples, ele é bastante complexo e autossuficiente. Para obter a previsão desejada do movimento futuro dos preços, basta adicionar os indicadores de distribuição dos dados brutos extraídos em lote na camada de normalização.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = BarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; }
Para alinhar as características de frequência dos valores previstos, utilizamos as abordagens do método FreDF.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast; descr.step = int(true); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
Como se pode notar, a arquitetura do modelo de Codificador do estado do ambiente resultou bastante concisa. Isso corresponde perfeitamente à leveza declarada pelos autores do método SparseTSF.
Os modelos Ator e Crítico foram transferidos sem alterações do artigo anterior. O mesmo se aplica aos programas de treinamento e à interação com o ambiente. Por isso, não nos aprofundaremos nesses aspectos nesta parte do artigo. O código completo de todos os programas e classes utilizados na preparação deste artigo está disponível no anexo.
3. Testes
Nas seções anteriores, exploramos os aspectos teóricos do método SparseTSF e implementamos as abordagens propostas pelos autores utilizando MQL5. Agora, chegou o momento de avaliar a eficácia desses métodos na previsão do movimento futuro dos preços com base em dados históricos reais. Também verificaremos a possibilidade de usar essas previsões para elaborar uma política eficaz de ações para o Ator.
Durante a construção do novo modelo, não realizamos alterações na estrutura dos dados brutos nem nos resultados esperados. Isso nos permitiu usar os programas de interação com o ambiente e de treinamento de modelos das pesquisas anteriores sem alterações. Também foi possível utilizar os conjuntos de dados de treinamento previamente coletados para o treinamento inicial do modelo. Dessa maneira, treinamos o Codificador do estado do ambiente usando o buffer de reprodução de experiências das versões anteriores dos modelos.
Como você deve se lembrar, o Codificador do estado do ambiente trabalha apenas com o movimento dos preços e os valores dos indicadores analisados, que são independentes das ações do Ator. Portanto, do ponto de vista do Codificador, todas as passagens pela amostra de treinamento em um mesmo intervalo histórico são idênticas. Isso nos permite treinar o modelo do Codificador sem a necessidade de atualizar a amostra de treinamento. Além disso, a leveza do modelo proposto reduz significativamente os custos de recursos e o tempo necessários para o treinamento do Codificador.
Não se pode dizer que o treinamento do modelo resultou em previsões precisas para os estados subsequentes. No entanto, a qualidade geral das previsões é comparável à de modelos mais complexos, que exigem mais recursos e tempo para serem treinados. Dessa forma, podemos afirmar que, em parte, alcançamos o resultado desejado.
A segunda etapa foi o treinamento da política do Ator com base nos valores previstos. Nesse estágio, realizamos um treinamento iterativo dos modelos, com atualização periódica da amostra de treinamento. Isso nos permite manter uma amostra de treinamento atualizada, com recompensas reais relacionadas à distribuição de ações, semelhante à política atual do Ator. Devo admitir que fiquei agradavelmente surpreso: previsões aparentemente pouco expressivas sobre o movimento futuro dos preços mostraram-se suficientemente informativas para a construção de políticas do Ator capazes de gerar lucro, tanto na amostra de treinamento quanto na de teste.
Vale lembrar que, para o treinamento dos modelos, utilizamos dados históricos do par EURUSD no intervalo de tempo H1 para todo o ano de 2023. Os parâmetros padrão são utilizados para todos os indicadores analisados. O teste dos modelos treinados foi realizado com dados históricos de janeiro de 2024, mantendo todos os demais parâmetros inalterados. Dessa forma, aproximamos o teste do modelo o máximo possível das condições reais de sua utilização.
A seguir, são apresentados os resultados do teste do modelo treinado.


Durante o período de teste, o modelo realizou 81 operações. Houve uma distribuição quase equilibrada entre posições curtas e longas: 42 e 39, respectivamente. Mais de 60% das operações foram fechadas com lucro, o que permitiu alcançar um fator de 1,33.
Uma das características do método SparseTSF é a previsão dos dados em etapas individuais dentro do período de ciclicidade dos dados brutos. Lembro que, no modelo treinado do Codificador do estado do ambiente, analisamos dados horários com um período de ciclicidade de 24 horas. Nesse aspecto, a análise do desempenho do modelo por hora é particularmente interessante.
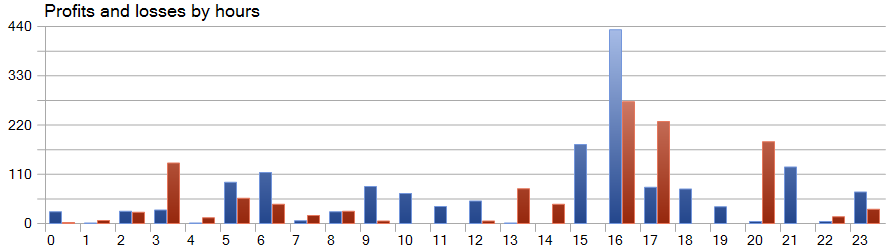
No gráfico apresentado, observa-se praticamente a ausência de perdas na primeira metade da sessão europeia, entre 9h e 12h. A duração média de retenção das operações, de 1 hora e 6 minutos, indica um desvio mínimo entre a abertura das operações e a realização de lucros ou perdas. A máxima rentabilidade foi observada no início da sessão americana, entre 15h e 16h.
Considerações finais
Neste artigo, exploramos o método SparseTSF, que demonstra vantagens no campo da previsão de séries temporais graças à sua arquitetura leve e ao uso eficiente de recursos. O emprego de um número mínimo de parâmetros torna o modelo proposto especialmente útil para aplicações com recursos computacionais limitados e prazos curtos de tomada de decisão.
O SparseTSF permite analisar etapas individuais de séries temporais com periodicidade definida e realizar previsões independentes para cada sequência unitária, proporcionando alta flexibilidade e adaptabilidade ao modelo.
Na parte prática do artigo, implementamos os métodos propostos utilizando MQL5, treinamos e testamos o modelo com dados históricos reais. Como resultado, obtivemos um modelo capaz de gerar lucros tanto na amostra de treinamento quanto na de teste, comprovando a eficácia dos métodos propostos.
No entanto, gostaria de lembrar novamente que este artigo apresenta programas destinados apenas à demonstração de uma das possíveis implementações dos métodos propostos e seu uso. Os programas apresentados, entretanto, não estão prontos para aplicação em mercados financeiros reais.
Referências
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA para coleta de exemplos |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA para coleta de exemplos pelo método Real-ORL |
| 3 | Study.mq5 | Expert Advisor | EA para treinamento de Modelos |
| 4 | StudyEncoder.mq5 | Expert Advisor | EA para treinamento do Codificador |
| 5 | Test.mq5 | Expert Advisor | EA para testar o modelo |
| 6 | Trajectory.mqh | Biblioteca de classe | Estrutura de descrição do estado do sistema |
| 7 | NeuroNet.mqh | Biblioteca de classe | Biblioteca de classes para criação de redes neurais |
| 8 | NeuroNet.cl | Biblioteca | Biblioteca de código do programa OpenCL |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/15392
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Redes neurais em trading: Usando modelos de linguagem para previsão de séries temporais
Redes neurais em trading: Usando modelos de linguagem para previsão de séries temporais
 Algoritmo de comportamento social adaptativo — Adaptive Social Behavior Optimization (ASBO): Evolução em duas fases
Algoritmo de comportamento social adaptativo — Adaptive Social Behavior Optimization (ASBO): Evolução em duas fases
 Aprendendo MQL5 do iniciante ao profissional (Parte IV): Sobre Arrays, Funções e Variáveis Globais do Terminal
Aprendendo MQL5 do iniciante ao profissional (Parte IV): Sobre Arrays, Funções e Variáveis Globais do Terminal
 Redes neurais em trading: Redução de consumo de memória com o método de otimização Adam-mini
Redes neurais em trading: Redução de consumo de memória com o método de otimização Adam-mini
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso