Neuronale Netze im Handel: Verringerung des Speicherverbrauchs mit der Adam-mini-Optimierung

Einführung

Als wir anfingen, uns mit neuronalen Netzen zu beschäftigen, haben wir verschiedene Ansätze zur Optimierung der Modellparameter diskutiert. Wir verwendeten bei unserer Arbeit verschiedene Ansätze. Am häufigsten verwende ich die Methode Adam, die eine adaptive Anpassung der optimalen Lernrate für jeden Modellparameter ermöglicht. Diese Anpassungsfähigkeit hat jedoch ihren Preis. Der Adam-Algorithmus verwendet Schätzungen des ersten und zweiten Moments für jeden Modellparameter und benötigt den Speicher des Modells selbst. Dieser Speicherverbrauch stellt ein erhebliches Problem beim Training großer Modelle dar. In der Praxis führt die Aufrechterhaltung eines Algorithmus mit derart hohen Speicheranforderungen häufig dazu, dass Berechnungen auf die CPU ausgelagert werden müssen, was die Latenzzeit erhöht und den Trainingsprozess verlangsamt. Angesichts dieser Herausforderungen ist die Suche nach neuen Optimierungsmethoden oder Verbesserungen bestehender Techniken immer wichtiger geworden. 

Eine vielversprechende Lösung wurde im Juli 2024 in dem Artikel „Use Fewer Learning Rates To Gain More“ (Mit weniger Lernraten mehr erreichen) veröffentlicht. Die Autoren haben eine Modifikation des Adam-Optimierers eingeführt, die dessen Leistung beibehält und gleichzeitig den Speicherverbrauch reduziert. Der neue Optimierer, genannt Adam-mini, unterteilt die Modellparameter in Blöcke, weist jedem Block eine einzige Lernrate zu und bietet folgende Vorteile:

• Leichtgewichtig: Adam-mini reduziert die Anzahl der in Adam verwendeten Lernraten erheblich, wodurch der Speicherverbrauch um 45-50% gesenkt werden kann.
• Effizient: Trotz des geringeren Ressourcenverbrauchs erreicht Adam-mini eine Leistung, die mit der des Standard-Adams vergleichbar oder sogar besser ist.
  

1. Der Adam-mini-Algorithmus

Die Autoren von Adam-mini analysieren die Rolle von v (die Schätzung des zweiten Moments) in Adam und untersuchen Möglichkeiten, diese zu optimieren. In Adam liefert v eine individuelle Lernrate für jeden Parameter. Es wurde beobachtet, dass die hessische Matrix in Transformer-Architekturen und anderen neuronalen Netzen dazu neigt, eine nahezu blockdiagonale Struktur aufzuweisen. Außerdem weist jeder Transformer-Block unterschiedliche Eigenwertverteilungen auf. Infolgedessen benötigen Transformer unterschiedliche Lernraten für verschiedene Blöcke, um die Eigenwert-Heterogenität zu bewältigen. Diese Funktion kann von v in Adam bereitgestellt werden.

Adam weist jedoch nicht nur jedem Block Lernraten zu, sondern auch jedem einzelnen Parameter. Beachten Sie, dass die Anzahl der Parameter die Anzahl der Blöcke bei weitem übersteigt. Dies wirft die Frage auf: Ist es notwendig, jedem Parameter eine eigene Lernrate zuzuordnen? Wenn nicht, wie viel können wir optimieren?

Die Autoren untersuchen diese Frage für allgemeine Optimierungsaufgaben und kommen zu folgenden Ergebnissen:

• Adam schneidet besser ab als eine einzige Methode mit optimaler Lernrate. Dies ist zu erwarten, da Adam auf verschiedene Parameter unterschiedliche Lernraten anwendet.
• Innerhalb eines dichten, hessischen Teilblocks kann jedoch eine einzige optimale Lernrate die Leistung von Adam übertreffen.
• Die Anwendung optimaler Lernraten auf ein „blockweises“ Gradientenabstiegskonzept erhöht daher die Trainingseffizienz.

Bei allgemeinen Optimierungsproblemen mit einer blockdiagonalen Hessian bringt eine Erhöhung der Anzahl der Lernraten nicht unbedingt zusätzliche Vorteile. Für jeden dichten Unterblock reicht eine einzige gut gewählte Lernrate aus, um eine optimale Leistung zu erzielen.

Ein ähnliches Verhalten ist bei Architekturen auf Basis eines Transformers zu beobachten. Die Autoren des Adam-mini führen Experimente mit einem 4-Schicht-Transformer durch und stellen fest, dass solche Modelle eine vergleichbare oder bessere Leistung mit deutlich geringeren Lernraten als Adam erzielen können.

Damit bleibt die Frage offen, wie die optimale Lernrate effizient bestimmt werden kann.

Das Ziel von Adam-mini ist es, den Speicherverbrauch für die Lernraten in Adam zu reduzieren, ohne dass eine erschöpfende Gittersuche erforderlich ist.

Adam-mini besteht aus zwei Schritten. Schritt 1 ist nur für die Initialisierung erforderlich.

Zunächst unterteilen wir die Modellparameter in Blöcke. Im Falle von Transformer schlagen die Autoren der Methode vor, alle Entitäten Query (Abfrage) und Key (Schlüssel) auf der Grundlage von Aufmerksamkeitsköpfen zu gruppieren. In allen anderen Fällen wird für jede Schicht eine Schätzung des zweiten Moments verwendet.

Einbettungsschichten werden gesondert behandelt. Bei Einbettungen ist das klassische Adam nach wie vor vorzuziehen, da Einbettungen viele Nullwerte enthalten und ihre Mittelwertverteilung erheblich von der Verteilung der Originalvariablen abweicht.

Im zweiten Schritt des Algorithmus wird für jeden Block von Parametern (außerhalb der Einbettungsblöcke) eine Lernrate verwendet. Um die geeignete Lernrate in jedem Block effektiv auszuwählen, ersetzt Adam-mini einfach den quadrierten Gradienten in Adam durch seinen Mittelwert. Die Autoren der Methode wenden auf diese Mittelwerte einen gleitenden Durchschnitt an, wie beim klassischen Adam.

Adam-mini reduziert die Anzahl der Lernraten in Transformers von einer pro Parameter auf die Summe der Größe der Einbettungsschicht, der Größe der Ausgabeschicht und der Anzahl der Nicht-Einbettungsblöcke. Das Ausmaß der Speichereinsparungen hängt vom Anteil der nicht eingebetteten Parameter im Modell ab.

Adam-mini kann im Vergleich zu Adam einen höheren Durchsatz erreichen, insbesondere bei begrenzten Hardware-Ressourcen. Hierfür gibt es zwei Gründe. Erstens verursacht Adam-mini durch seine Aktualisierungsregeln keine zusätzliche Rechenlast. Außerdem reduziert Adam-mini die Anzahl der Quadratwurzel- und Tensordivisionsoperationen, die in Adam verwendet werden, erheblich.

Zweitens kann Adam-mini aufgrund der geringeren Speichernutzung größere Stapelgrößen auf der GPU unterstützen und gleichzeitig die Kommunikation von GPU-zu-CPU, einen weiteren großen Engpass beim Training, reduzieren.

Diese Verbesserungen ermöglichen es Adam-mini, das Pretraining großer Modelle zu beschleunigen, indem sowohl der Speicherverbrauch als auch die Rechenkosten reduziert werden.

Adam-mini projiziert eine Lernrate für jeden dichten hessischen Unterblock unter Verwendung des v Adam-Mittelwerts innerhalb jedes Blocks. Dieser Ansatz kann rechnerisch effizient sein, ist aber möglicherweise nicht ganz optimal. Das derzeitige Design reicht jedoch aus, um eine Leistung zu erzielen, die mit der von Adam vergleichbar oder sogar leicht besser ist, und gleichzeitig den Speicherbedarf erheblich zu senken.

2. Implementierung in MQL5

Nachdem wir uns mit den theoretischen Aspekten der Methode Adam-Mini beschäftigt haben, kommen wir nun zum praktischen Teil unseres Artikels. In diesem Teil setzen wir unsere eigene Vision der beschriebenen Ansätze mit MQL5 um.

Bitte beachten Sie, dass sich diese Arbeit erheblich von der Arbeit in früheren Artikeln unterscheidet. Normalerweise implementieren wir neue Ansätze im Rahmen einer einzigen Schichtklasse in unserem Modell. In diesem Fall müssen wir jedoch Änderungen an bereits entwickelten Klassen vornehmen. Das liegt daran, dass jede dieser Klassen eine überschriebene oder abgeleitete Methode updateInputWeights enthält, die den Algorithmus für die Aktualisierung der Modellparameter auf der Ebene der Schichten definiert.

Natürlich gehören einige updateInputWeights-Methoden zu komplexen Architekturkomponenten, bei denen wir einfach die entsprechenden Methoden der verschachtelten Objekte aufrufen. Ein gutes Beispiel dafür ist der Decoder, der in unserem letzten Artikel beschrieben wurde. In solchen Fällen bleibt der Algorithmus unabhängig von der gewählten Optimierungsmethode. 

bool CNeuronSTNNDecoder::updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *Context)
  {
   if(!cEncoder.UpdateInputWeights(NeuronOCL, Context))
      return false;
   if(!CNeuronMLCrossAttentionMLKV::updateInputWeights(cEncoder.AsObject(), Context))
      return false;
//---
   return true;
  }

Wenn wir die Hierarchie der Funktionsaufrufe weiter nach unten gehen, gelangen wir immer zu den grundlegenden „Arbeitspferden“, wo der Hauptalgorithmus zur Aktualisierung der Parameter implementiert ist.

2.1 Implementierung von Adam-mini in der grundlegenden, vollständig vernetzten Schicht

Eine solche Klasse ist unsere Basisschicht CNeuronBaseOCL, die vollständig vernetzt ist. Deshalb werden wir unsere Arbeit hier beginnen.

Es ist wichtig, daran zu denken, dass die meisten Berechnungsaufgaben auf der GPU-Seite zur parallelen Verarbeitung implementiert werden. Dieser Prozess bildet da keine Ausnahme. Folglich werden wir mit einem OpenCL-Programm interagieren, in dem wir einen neuen Kernel namens UpdateWeightsAdamMini erstellen werden.

Bevor wir uns mit dem eigentlichen Code befassen, wollen wir kurz auf unsere architektonische Lösung eingehen.

Erstens liegt der Hauptunterschied zwischen den Optimierungsverfahren Adam-Mini und dem klassischen Adam vor allem in der Berechnung des Moments zweiter Ordnung v. Anstelle der Steigung jedes einzelnen Parameters schlagen die Autoren von Adam-mini vor, den Durchschnittswert einer Gruppe zu verwenden. Der Algorithmus zur Berechnung dieses einfachen Durchschnitts ist einfach. Auf diese Weise wird eine erhebliche Menge an Speicherplatz frei, da für jede Gruppe nur ein einziger Wert für das Moment zweiter Ordnung gespeichert wird.

Andererseits wollen wir die Berechnung des Mittelwerts für den gesamten Block nicht in jedem einzelnen Thread wiederholen. Erinnern Sie sich daran, dass die Adam-Mini-Methode für die vollständig verknüpfte Schicht die Verwendung von nur einer Lernrate vorschlägt. Die Neuberechnung des Mittelwerts der Steigung für jeden Parameter der Schicht in jedem Thread erscheint daher, gelinde gesagt, nicht effizient. In Anbetracht der hohen Kosten für den Zugriff auf den globalen Speicher besteht die beste Lösung darin, diesen Prozess über mehrere Threads zu parallelisieren und gleichzeitig den Zugriff auf den globalen Speicher zu minimieren. Dies wirft jedoch sofort die Frage auf, wie der Datenaustausch zwischen Threads organisiert werden kann.

In früheren Artikeln haben wir bereits gelernt, wie man Daten innerhalb einer lokalen Gruppe mit Thread-Synchronisierung austauscht. Die Organisation des gesamten Parameteraktualisierungsprozesses einer Ebene innerhalb einer einzigen lokalen Gruppe erscheint jedoch nicht besonders attraktiv. Daher habe ich in dieser Implementierung beschlossen, die Anzahl der berechneten Momente zweiter Ordnung zu erhöhen, um die Größe des Ergebnistensors anzupassen.

Wie wir wissen, ist die Anzahl der Parameter in einer vollständig verknüpften Schicht das Produkt aus der Größe des Eingabetensors und der Größe des Ergebnistensors. Zusätzlich wird durch die Verwendung eines Bias-Parameters für jedes Neuron die Anzahl der Parameter entsprechend der Größe des Ergebnissensors erhöht. Der „klassische“ Adam speichert eine gleiche Anzahl von Werten für das erste und zweite Moment. In der Implementierung von Adam-mini wird die Anzahl der gespeicherten Momentwerte zweiter Ordnung erheblich reduziert.

Lassen Sie uns nun ein wenig über den Prozess der Berechnung des Durchschnittswerts des Moments zweiter Ordnung sprechen. Der Fehlergradient eines Parameters ist gleich dem Produkt aus dem Fehlergradienten am Schichtausgang (korrigiert durch die Ableitung der Aktivierungsfunktion) und dem entsprechenden Eingabewert.

Der Durchschnitt der quadrierten Steigungen kann also wie folgt berechnet werden:

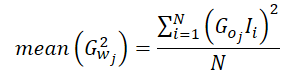
Da unsere Implementierung den durchschnittlichen Gradienten für ein einzelnes Neuron in der Ergebnisschicht berechnet, können wir den Gradienten dieses Neurons aus der Gleichung herausrechnen.

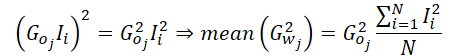
Das bedeutet, dass wir in unserer Implementierung des durchschnittlichen Moments zweiter Ordnung nur die durchschnittlichen quadrierten Werte der Eingabedaten berechnen müssen. Auf diese Weise entfällt der häufige Zugriff auf den globalen Speicher, in dem der Ausgangsgradient gespeichert ist. Nachdem wir diesen Mittelwert ermittelt haben, nehmen wir den Ausgangsgradienten nur einmal, quadrieren ihn und multiplizieren ihn mit dem berechneten Mittelwert. Schließlich verteilen wir den resultierenden Wert für weitere Berechnungen einfach auf die lokale Gruppe.

Da wir nun ein klares Verständnis des Berechnungsprozesses haben, können wir mit der Implementierung im Kernel von UpdateWeightsAdamMini fortfahren. Die Parameter dieses Kernels sind nahezu identisch mit denen des klassischen Adam. Dazu gehören 5 Datenpuffer und 3 Konstanten:

• matrix_w — Matrix der Schichtparameter;
• matrix_g — der Fehlergradiententensor am Ausgang der Schicht;
• matrix_i — Eingangsdatenpuffer;
• matrix_m — der Momententensor erster Ordnung;
• matrix_v — der Momententensor zweiter Ordnung;
• l — Lernrate;
• b1 — Glättungskoeffizient der Momente erster Ordnung (ß1);
• b2 — Glättungskoeffizient der Momente zweiter Ordnung (ß2);

__kernel void UpdateWeightsAdamMini(__global float *matrix_w, 
                                    __global const float *matrix_g,
                                    __global const float *matrix_i,
                                    __global float *matrix_m,
                                    __global float *matrix_v,
                                    const float l,
                                    const float b1,
                                    const float b2 
                                   )
  {
//--- inputs
   const size_t i = get_local_id(0);
   const size_t inputs = get_local_size(0) - 1;
//--- outputs
   const size_t o = get_global_id(1);
   const size_t outputs = get_global_size(1);

Die Durchführung des Kernels wird in einem 2-dimensionalen Aufgabenraum geplant. Die erste Dimension entspricht der Anzahl der Eingabewerte plus dem Offset-Element. Die zweite ist die Größe des Ergebnistensors. Im Hauptteil des Kernels identifizieren wir zunächst den Thread in beiden Dimensionen.

Beachten Sie, dass wir Threads entlang einer Dimension des Aufgabenraums zu Arbeitsgruppen zusammenfassen.

Als Nächstes organisieren wir ein Array im lokalen Kontextspeicher für den Datenaustausch zwischen den Threads der Arbeitsgruppe.

   __local float temp[LOCAL_ARRAY_SIZE];
   const int ls = min((uint)LOCAL_ARRAY_SIZE, (uint)inputs);

Der nächste Schritt ist die Berechnung des durchschnittlichen quadratischen Werts der Eingabedaten. Da der Eingangsdatenpuffer auch für die Berechnung des Moments erster Ordnung benötigt wird, holt sich jeder Thread zunächst den entsprechenden Wert aus dem globalen Eingangsdatenpuffer.

   const float inp = (i < inputs ? matrix_i[i] : 1.0f);

Dann implementieren wir eine Schleife mit Thread-Synchronisation, in der jeder Thread den quadrierten Wert seines Eingangsdatenelements zu einem lokalen Array hinzufügt.

   int count = 0;
   do
     {
      if(count == (i / ls))
        {
         int shift = i % ls;
         temp[shift] = (count == 0 ? 0 : temp[shift]) + ((isnan(inp) || isinf(inp)) ? 0 : inp*inp);
        }
      count++;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count * ls < inputs);

Danach addieren wir die Werte der Elemente des lokalen Arrays.

//--- sum
   count = (ls + 1) / 2;
   do
     {
      if(i < count && (i + count) < ls)
        {
         temp[i] += temp[i + count];
         temp[i + count] = 0;
        }
      count = (count + 1) / 2;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Innerhalb eines Threads implementieren wir die Berechnung des Moments zweiter Ordnung und speichern sie in dem lokalen Array-Element mit dem Index 0.

Wir erinnern uns auch daran, dass der Zugriff auf ein lokales Speicherfeld viel schneller ist als der Zugriff auf einen globalen Speicherpuffer. Um die Anzahl der globalen Speicherzugriffe zu reduzieren, nehmen wir den Fehlergradienten auf der Ebene der aktuellen Schichtergebnisse und speichern ihn in dem lokalen Array-Element mit dem Index 1. Daher werden die übrigen Elemente der Arbeitsgruppe bei der Durchführung nachfolgender Operationen den Wert aus dem lokalen Speicher übernehmen, anstatt auf den globalen Speicher zuzugreifen.

Achten Sie darauf, die Arbeit der Arbeitsgruppen-Threads zu synchronisieren.

//--- calc v
   if(i == 0)
     {
      temp[1] = matrix_g[o];
      if(isnan(temp[1]) || isinf(temp[1]))
         temp[1] = 0;
      temp[0] /= inputs;
      if(isnan(temp[0]) || isinf(temp[0]))
         temp[0] = 1;
      float v = matrix_v[o];
      if(isnan(v) || isinf(v))
         v = 1;
      temp[0] = b2 * v + (1 - b2) * pow(temp[1], 2) * temp[0];
      matrix_v[o] = temp[0];
     }
   barrier(CLK_LOCAL_MEM_FENCE);

Beachten Sie, dass wir den Momentwert zweiter Ordnung sofort im globalen Datenpuffer speichern. Dieser einfache Schritt trägt dazu bei, unnötige globale Speicherzugriffe von anderen Threads innerhalb der Arbeitsgruppe zu vermeiden, wodurch Verzögerungen durch den gleichzeitigen Zugriff auf dasselbe globale Pufferelement von mehreren Threads aus verringert werden. 

Danach folgt unser Algorithmus den Operationen der klassischen Adam-Methode. In diesem Stadium bestimmen wir den Offset im Tensor der trainierbaren Parameter und laden den aktuellen Wert des analysierten Parameters aus dem globalen Speicherpuffer.

   const int wi = o * (inputs + 1) + i;
   float weight = matrix_w[wi];
   if(isnan(weight) || isinf(weight))
      weight = 0;

Wir berechnen den Wert des Moments erster Ordnung

   float m = matrix_m[wi];
   if(isnan(m) || isinf(m))
      m = 0;
//--- calc m
   m = b1 * m + (1 - b1) * temp[1] * inp;
   if(isnan(m) || isinf(m))
      m = 0;

und bestimmen die Größe der Parameteranpassung.

   float delta = l * (m / (sqrt(temp[0]) + 1.0e-37f) - (l1 * sign(weight) + l2 * weight));
   if(isnan(delta) || isinf(delta))
      delta = 0;

Danach korrigieren wir den Parameterwert und speichern den neuen Wert im globalen Datenpuffer.

   if(delta > 0)
      matrix_w[wi] = clamp(weight + delta, -MAX_WEIGHT, MAX_WEIGHT);
   matrix_m[wi] = m;
  }

Hier speichern wir den Wert des Moments erster Ordnung und schließen die Kerneloperation ab.

Nachdem wir Änderungen auf der OpenCL-Seite vorgenommen haben, müssen wir eine Reihe von Änderungen am Hauptprogramm vornehmen. Zunächst werden wir eine neue Optimierungsmethode in unsere Aufzählung aufnehmen.

//+------------------------------------------------------------------+
/// Enum of optimization method used                                 |
//+------------------------------------------------------------------+
enum ENUM_OPTIMIZATION
  {
   SGD,        ///< Stochastic gradient descent
   ADAM,       ///< Adam
   ADAM_MINI   ///< Adam-mini
  };

Danach werden wir Änderungen an der Methode CNeuronBaseOCL::updateInputWeights vornehmen. Hier im Block der Variablendeklaration fügen wir ein Array hinzu, das die Größe der Arbeitsgruppe beschreibt, local_work_size (im folgenden Code unterstrichen). In diesem Stadium weisen wir ihm keine Werte zu, da sie erst bei der Anwendung der entsprechenden Optimierungsmethode benötigt werden.

bool CNeuronBaseOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL)
  {
   if(CheckPointer(OpenCL) == POINTER_INVALID || CheckPointer(NeuronOCL) == POINTER_INVALID)
      return false;
   uint global_work_offset[2] = {0, 0};
   uint global_work_size[2], local_work_size[2];
   global_work_size[0] = Neurons();
   global_work_size[1] = NeuronOCL.Neurons() + 1;
   uint rest = 0;
   float lt = lr;

Danach folgt die Verzweigung des Algorithmus in Abhängigkeit von der gewählten Methode zur Optimierung der Modellparameter. Wir werden die gleichen Algorithmen für die Warteschlangen der Kernel für die Ausführung verwenden, wie wir sie in den zuvor betrachteten Optimierungsmethoden verwendet haben, sodass wir nicht näher darauf eingehen werden.

   switch(NeuronOCL.Optimization())
     {
      case SGD:
.........
.........
.........
         break;
      case ADAM:
........
........
........
         break;

Schauen wir uns einfach den hinzugefügten Code an. Zunächst werden die Parameter übergeben, die der Kernel benötigt, um korrekt zu arbeiten.

      case ADAM_MINI:
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdamMini, def_k_wuam_matrix_w,
                                                           NeuronOCL.getWeightsIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdamMini, def_k_wuam_matrix_g,
                                                                    getGradientIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdamMini, def_k_wuam_matrix_i, 
                                                            NeuronOCL.getOutputIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdamMini, def_k_wuam_matrix_m, 
                                                     NeuronOCL.getFirstMomentumIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsAdamMini, def_k_wuam_matrix_v, 
                                                    NeuronOCL.getSecondMomentumIndex()))
            return false;
         lt = (float)(lr * sqrt(1 - pow(b2, (float)t)) / (1 - pow(b1, (float)t)));
         if(!OpenCL.SetArgument(def_k_UpdateWeightsAdamMini, def_k_wuam_l, lt))
            return false;
         if(!OpenCL.SetArgument(def_k_UpdateWeightsAdamMini, def_k_wuam_b1, b1))
            return false;
         if(!OpenCL.SetArgument(def_k_UpdateWeightsAdamMini, def_k_wuam_b2, b2))
            return false;

Danach werden wir die Aufgabenbereiche der globalen Arbeit des Kernels und einer separaten Arbeitsgruppe definieren.

         global_work_size[0] = NeuronOCL.Neurons() + 1;
         global_work_size[1] = Neurons();
         local_work_size[0] = global_work_size[0];
         local_work_size[1] = 1;

Beachten Sie, dass wir in der ersten Dimension sowohl global als auch für die Arbeitsgruppe einen Wert angeben, der um 1 Element größer ist als die Größe der Eingabedatenschicht. Dies ist unser Offset-Parameter. In der zweiten Dimension geben wir jedoch global die Anzahl der Elemente in der aktuellen neuronalen Schicht an. Für die Arbeitsgruppe geben wir 1 Element in dieser Dimension an. Dies entspricht den Operationen der Arbeitsgruppe innerhalb eines Neurons der aktuellen Schicht.

Nachdem die vorbereitenden Arbeiten abgeschlossen sind, wird der Kernel in die Ausführungswarteschlange gestellt.

         ResetLastError();
         if(!OpenCL.Execute(def_k_UpdateWeightsAdamMini, 2, global_work_offset, global_work_size, 
                                                                                local_work_size))
           {
            printf("Error of execution kernel UpdateWeightsAdamMini: %d", GetLastError());
            return false;
           }
         t++;
         break;
      default:
         return false;
         break;
     }
//---
   return true;
  }

Und wir fügen einen Exit mit einem negativen Ergebnis hinzu, falls eine falsche Optimierungsmethode angegeben wird.

Damit ist die Implementierung der Parameteraktualisierungsmethode für die grundlegende voll verknüpfte Schicht CNeuronBaseOCL::updateInputWeights abgeschlossen. Erinnern wir uns jedoch an das Hauptziel dieser Änderungen: die Verringerung des Speicherverbrauchs bei Verwendung der Adam-Optimierungsmethode. Daher muss auch die Initialisierungsmethode CNeuronBaseOCL::Init angepasst werden, um die Größe des Momentpuffers zweiter Ordnung zu verringern, wenn die Optimierungsmethode Adam-mini gewählt wird. Da es sich um minimale und gezielte Änderungen handelt, werde ich in diesem Artikel keine vollständige Beschreibung des Methodenalgorithmus geben. Stattdessen werde ich nur den Initialisierungsblock für den entsprechenden Puffer vorstellen.

         if(CheckPointer(SecondMomentum) == POINTER_INVALID)
           {
            SecondMomentum = new CBufferFloat();
            if(CheckPointer(SecondMomentum) == POINTER_INVALID)
               return false;
           }
         if(!SecondMomentum.BufferInit((optimization == ADAM_MINI ? numOutputs : count), 0))
            return false;
         if(!SecondMomentum.BufferCreate(OpenCL))
            return false;

Die vollständige Implementierung dieser Methode finden Sie in den beigefügten Dateien, zusammen mit dem vollständigen Code für alle Programme, die bei der Erstellung dieses Artikels verwendet wurden.

2.2 Adam-mini in der Faltungsschicht

Ein weiterer grundlegender Baustein, der in verschiedenen Architekturen, einschließlich Transformer, weit verbreitet ist, ist die Faltungsschicht.

Die Integration der Adam-mini-Optimierungsmethode in seine Funktionalität hat einige einzigartige Aspekte, die in erster Linie auf die spezifische Natur von Faltungsschichten zurückzuführen sind. Im Gegensatz zu vollständig verknüpften Schichten, bei denen jeder trainierbare Parameter dafür verantwortlich ist, den Wert nur eines Eingangsneurons an nur ein Neuron in der aktuellen Schicht zu übertragen, haben Faltungsschichten in der Regel weniger Parameter, aber jeder Parameter wird intensiver genutzt.

Darüber hinaus ist es wichtig zu wissen, dass wir Faltungsschichten verwenden, um die Entitäten von Query, Key und Value (Abfrage, Schlüssen, Wert) in den Transformer-Algorithmen zu erzeugen. Diese Einheiten erfordern eine spezielle Implementierung der Methode Adam-mini.

All diese Faktoren müssen bei der Implementierung der Adam-mini-Methode in einer Faltungsschicht berücksichtigt werden.

Wie bei der vollständig verbundenen Schicht beginnen wir mit der Implementierung der Methode auf der Seite von OpenCL. Hier erstellen wir den Kernel UpdateWeightsConvAdamMini. Zusätzlich zu den bekannten Variablen führt dieser Kernel zwei neue Konstanten ein: die Sequenzlänge der Eingabedaten und die Schrittweite des Faltungsfensters.

__kernel void UpdateWeightsConvAdamMini(__global float *matrix_w,  
                                        __global const float *matrix_i,
                                        __global float *matrix_m,      
                                        __global float *matrix_v,      
                                        const int inputs,              
                                        const float l,              
                                        const float b1,             
                                        const float b2,             
                                        int step                    
                                       )
  {
//--- window in
   const size_t i = get_global_id(0);
   const size_t window_in = get_global_size(0) - 1;
//--- window out
   const size_t f = get_global_id(1);
   const size_t window_out = get_global_size(1);
//--- head window out
   const size_t f_h = get_local_id(1);
   const size_t window_out_h = get_local_size(1);
//--- variable
   const size_t v = get_global_id(2);
   const size_t variables = get_global_size(2);

Bitte beachten Sie, dass wir in den Kernel-Parametern die Größe des Eingangsdatenfensters und die Anzahl der verwendeten Filter nicht angeben. Diese und zwei weitere Parameter werden in den Aufgabenbereich verschoben, was ein wichtiger Aspekt ist.

Dieser Kernel ist so konzipiert, dass er in einem dreidimensionalen Aufgabenraum ausgeführt werden kann: Die erste Dimension entspricht der Größe des Eingabefensters plus einem zusätzlichen Element für die Verzerrung. Hier können wir eine gewisse Ähnlichkeit mit dem Aufgabenraum der voll vernetzten Schicht feststellen.

Die zweite Dimension stellt die Anzahl der verwendeten Filter dar, was logischerweise der Ausgangsdimensionalität der vollständig verknüpften Schicht entspricht.

Was die Arbeitsgruppen angeht, so werden wir sie nicht für jeden einzelnen Faltungsfilter erstellen, sondern sie nach den Aufmerksamkeitsköpfen der Transformer-Architektur gruppieren.

Bitte beachten Sie, dass der Nutzer für jeden Kopf nur einen Faltungsfilter angeben kann. In diesem Fall erhält jeder Faltungsfilter eine individuelle Lernrate, ähnlich wie bei unserer Implementierung einer vollständig verbundenen Schicht.

Die dritte Dimension wird eingeführt, um multimodale Zeitreihen zu verarbeiten, bei denen einzelne unitäre Sequenzen ihre eigenen Faltungsfilter haben. Für sie werden auch separate Momente zweiter Ordnung geschaffen, um adaptive Lernraten zu ermöglichen.

Es muss zwischen „Aufmerksamkeitsköpfen“ und „einheitlichen Zeitreihen“ unterschieden werden, da sie nicht verwechselt werden dürfen. Auch wenn sie ähnlich aussehen, haben sie unterschiedliche Aufgaben. Unitäre Zeitreihen teilen den Eingangstensor. Aufmerksamkeitsköpfe unterteilen den Ausgangstensor.

Im Kernel werden nach der Identifizierung des Threads in allen Dimensionen des Aufgabenraums die wichtigsten Offset-Konstanten in den globalen Datenpuffern definiert.

//--- constants
   const int total = (inputs - window_in + step - 1) / step;
   const int shift_var_in = v * inputs;
   const int shift_var_out = v * total * window_out;
   const int shift_w = (f + v * window_out) * (window_in + 1) + i;

Wir erstellen ein lokales Array für den Datenaustausch in der Arbeitsgruppe.

   __local float temp[LOCAL_ARRAY_SIZE];
   const int ls = min((uint)window_in, (uint)LOCAL_ARRAY_SIZE);

Nach den vorbereitenden Arbeiten werden wir für jeden Parameter Fehlergradienten sammeln.

//--- calc gradient
   float grad = 0;
   for(int t = 0; t < total; t++)
     {
      if(i != window_in && (i + t * window_in) >= inputs)
         break;
      float gt = matrix_g[t * window_out + f + shift_var_out] *
                 (i == window_in ? 1 : matrix_i[i + t * step + shift_var_in]);
      if(!(isnan(gt) || isinf(gt)))
         grad += gt;
     }

Beachten Sie, dass in diesem Fall jeder globale Thread die Fehlergradienten von allen Elementen, die er beeinflusst, vollständig sammelt. Anders als bei der vollständig verknüpften Schicht wird hier der Wert des Eingangsdatenelements sofort mit dem entsprechenden Fehlergradienten der Ergebnisse multipliziert.

Als Nächstes werden die berechneten Fehlergradienten akkumuliert, um ihre quadrierten Werte innerhalb eines lokalen Arrays zu summieren, jetzt aber auf Arbeitsgruppenebene. Um dies zu erreichen, implementieren wir eine verschachtelte Schleifenstruktur mit obligatorischer Thread-Synchronisation. Die äußere Schleife entspricht der Anzahl der Filter innerhalb der Arbeitsgruppe. Die innere Schleife sammelt die Fehlergradienten aus allen Parametern eines einzelnen Filters.  

//--- calc sum grad
   int count;
   for(int h = 0; h < window_out_h; h++)
     {
      count = 0;
      do
        {
         if(h == f_h)
           {
            if(count == (i / ls))
              {
               int shift = i % ls;
               temp[shift] = ((count == 0 && h == 0) ? 0 : temp[shift]) + 
                             ((isnan(grad) || isinf(grad)) ? 0 : grad * grad);
              }
           }
         count++;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while((count * ls) < window_in);
     }

Dann summieren wir die Werte des lokalen Arrays.

   count = (ls + 1) / 2;
   do
     {
      if(i < count && (i + count) < ls && f_h == 0)
        {
         temp[i] += temp[i + count];
         temp[i + count] = 0;
        }
      count = (count + 1) / 2;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Wir werden auch den Wert des Moments zweiter Ordnung der aktuellen Gruppe bestimmen.

//--- calc v
   if(i == 0 && f_h == 0)
     {
      temp[0] /= (window_in * window_out_h);
      if(isnan(temp[0]) || isinf(temp[0]))
         temp[0] = 1;
      int head = f / window_out_h;
      float v = matrix_v[head];
      if(isnan(v) || isinf(v))
         v = 1;
      temp[0] = clamp(b2 * v + (1 - b2) * temp[0], 1.0e-6f, 1.0e6f);
      matrix_v[head] = temp[0];
     }
   barrier(CLK_LOCAL_MEM_FENCE);

Anschließend wiederholen wir den Algorithmus der klassischen Methode Adam. Hier definieren wir das Moment erster Ordnung.

//--- calc m
   float mt = clamp(b1 * matrix_m[shift_w] + (1 - b1) * grad, -1.0e5f, 1.0e5f);
   if(isnan(mt) || isinf(mt))
      mt = 0;

Wir passen den Wert des analysierten Parameters an.

   float weight = clamp(matrix_w[shift_w] + l * mt / sqrt(temp[0]), -MAX_WEIGHT, MAX_WEIGHT);

Und wir speichern die erhaltenen Werte.

   if(!(isnan(weight) || isinf(weight)))
      matrix_w[shift_w] = weight;
   matrix_m[shift_w] = mt;
  }

Nachdem wir den Kernel auf der OpenCL-Seite erstellt haben, gehen wir zur Arbeit am Hauptprogramm über. Wie im Fall einer vollständig verbundenen Schicht implementieren wir den Aufruf des oben erstellten Kerns in der Methode CNeuronConvOCL::updateInputWeights. Der Algorithmus für den Aufruf ist ähnlich wie der oben beschriebene für eine vollständig verbundene Schicht. Bei einer normalen Faltungsschicht verwenden wir einen Filter für jeden Aufmerksamkeitskopf und eine unitäre Sequenz. Die Dimension des Aufgabenraums hat also die folgende Form.

   uint global_work_offset_am[3] = { 0, 0, 0 };
   uint global_work_size_am[3] = { iWindow + 1, iWindowOut, iVariables };
   uint local_work_size_am[3] = { global_work_size_am[0], 1, 1 };

Die vollständige Implementierung dieser Methode finden Sie in den beigefügten Dateien,

Ich möchte jedoch noch ein paar Worte über die Verwendung des erstellten Kerns bei der Implementierung von Klassen hinzufügen, die die Transformer-Architektur nutzen. Betrachten wir als Beispiel die Klasse CNeuronMLMHAttentionOCL. Diese Klasse dient als übergeordnete Klasse für die Erstellung einer Vielzahl anderer Algorithmen.

Es ist wichtig zu beachten, dass die Klasse CNeuronMLMHAttentionOCL keine Faltungsschichten im herkömmlichen Sinne enthält. Stattdessen organisiert sie Puffer-Arrays und überschreibt alle relevanten Methoden. Die Parameteraktualisierungen für die Faltungsschichten werden in der Methode ConvolutionUpdateWeights behandelt. Da diese Methode zur Verwaltung verschiedener Faltungsschichten verwendet wird, fügen wir zwei zusätzliche Parameter hinzu: die Anzahl der Aufmerksamkeitsköpfe (heads) und die Anzahl der unitären Sequenzen (Variablen). Um mögliche Probleme beim Zugriff auf diese Methode von anderen Klassen aus zu vermeiden, werden diese neuen Parameter mit Standardwerten versehen.

bool CNeuronMLMHAttentionOCL::ConvolutuionUpdateWeights(CBufferFloat *weights, 
                                                        CBufferFloat *gradient, 
                                                        CBufferFloat *inputs, 
                                                        CBufferFloat *momentum1, 
                                                        CBufferFloat *momentum2, 
                                                        uint window, uint window_out, 
                                                        uint step = 0, uint heads = 0, 
                                                        uint variables = 1)
  {
   if(CheckPointer(OpenCL) == POINTER_INVALID || CheckPointer(weights) == POINTER_INVALID || 
      CheckPointer(gradient) == POINTER_INVALID || CheckPointer(inputs) == POINTER_INVALID  || 
      CheckPointer(momentum1) == POINTER_INVALID)
      return false;

Im Methodenrumpf werden zunächst die Zeiger auf die Datenpuffer geprüft, die die Methode als Parameter vom Aufrufer erhält.

Als Nächstes überprüfen wir den Wert des Parameters für die Schrittweite des Faltungsfensters (Step). Wenn er gleich „0“ ist, dann wird der Schritt gleich dem Faltungsfenster gemacht.

   if(step == 0)
      step = window;

Beachten Sie, dass wir in diesem Fall den Datentyp ohne Vorzeichen für die Parameter verwenden. Daher können sie keine negativen Werte enthalten. Die Kontrolle über die überhöhten Parameterwerte überlassen wir dem Nutzer.

Dann definieren wir Aufgabenräume. In diesem Fall verwendet der Kernel der Adam-Mini-Optimierungsmethode einen dreidimensionalen Aufgabenraum, der sich von dem eindimensionalen unterscheidet, der von anderen Optimierungsmethoden verwendet wird. Aus diesem Grund werden separate Arrays zugewiesen, um sie anzuzeigen. 

   uint global_work_offset[1] = {0};
   uint global_work_size[1];
   global_work_size[0] = weights.Total();
   uint global_work_offset_am[3] = {0, 0, 0};
   uint global_work_size_am[3] = {window, window_out, 1};
   uint local_work_size_am[3] = {window, (heads > 0 ? window_out / heads : 1), variables};

Werfen wir einen Blick auf die zweite Dimension des Aufgabenraums der Arbeitsgruppe. Wird die Anzahl der Aufmerksamkeitsköpfe nicht in den Methodenparametern angegeben, so hat jeder Filter eine eigene Lernrate. Wenn die Anzahl der Aufmerksamkeitsköpfe angegeben ist, wird die Anzahl der Filter pro Aufmerksamkeitskopf berechnet, indem die Gesamtzahl der Filter durch die Anzahl der Aufmerksamkeitsköpfe geteilt wird.

Dieser Ansatz wurde gewählt, um verschiedenen Anwendungsszenarien dieser Methode gerecht zu werden. Innerhalb der Klasse CNeuronMLMHAttentionOCL werden Faltungsschichten sowohl zur Bildung der Entitäten von Query-, Key- und Value als auch zur Datenprojektion (innerhalb der Multi-Head-Attention-Downsampling-Schicht und des FeedForward-Blocks) verwendet.

Der nächste Schritt besteht darin, den Algorithmus je nach der für die Modellparameter verwendeten Optimierungsmethode zu trennen. Genau wie bei der Diskussion über den Algorithmus für vollständig verknüpfte Schichten werden wir nicht im Detail darauf eingehen, wie die bisher implementierten Optimierungsmethoden funktionieren. Wir werden nur den Methodenblock von Adam-mini besprechen.

   if(weights.GetIndex() < 0)
      return false;
   float lt = 0;
   switch(optimization)
     {
      case SGD:
........
........
........
         break;
      case ADAM:
........
........
........
         break;
      case ADAM_MINI:
         if(CheckPointer(momentum2) == POINTER_INVALID)
            return false;
         if(gradient.GetIndex() < 0)
            return false;
         if(inputs.GetIndex() < 0)
            return false;
         if(momentum1.GetIndex() < 0)
            return false;
         if(momentum2.GetIndex() < 0)
            return false;

Hier prüfen wir die Relevanz von Zeigern auf Datenpuffer im Kontext von OpenCL. Danach werden wir alle notwendigen Parameter an den Kernel übergeben.

         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsConvAdamMini, def_k_wucam_matrix_w, 
                                                                         weights.GetIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsConvAdamMini, def_k_wucam_matrix_g, 
                                                                        gradient.GetIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsConvAdamMini, def_k_wucam_matrix_i, 
                                                                          inputs.GetIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsConvAdamMini, def_k_wucam_matrix_m, 
                                                                       momentum1.GetIndex()))
            return false;
         if(!OpenCL.SetArgumentBuffer(def_k_UpdateWeightsConvAdamMini, def_k_wucam_matrix_v, 
                                                                       momentum2.GetIndex()))
            return false;
         lt = (float)(lr * sqrt(1 - pow(b2, t)) / (1 - pow(b1, t)));
         if(!OpenCL.SetArgument(def_k_UpdateWeightsConvAdamMini, def_k_wucam_inputs, 
                                                                            inputs.Total()))
            return false;
         if(!OpenCL.SetArgument(def_k_UpdateWeightsConvAdamMini, def_k_wucam_l, lt))
            return false;
         if(!OpenCL.SetArgument(def_k_UpdateWeightsConvAdamMini, def_k_wucam_b1, b1))
            return false;
         if(!OpenCL.SetArgument(def_k_UpdateWeightsConvAdamMini, def_k_wucam_b2, b2))
            return false;
         if(!OpenCL.SetArgument(def_k_UpdateWeightsConvAdamMini, def_k_wucam_step, (int)step))
            return false;

Wir haben den Aufgabenbereich bereits früher gezeigt. Jetzt müssen wir nur noch den Kernel in die Ausführungswarteschlange stellen.

         ResetLastError();
         if(!OpenCL.Execute(def_k_UpdateWeightsConvAdamMini, 3, global_work_offset_am, 
                                              global_work_size_am, local_work_size_am))
           {
            string error;
            CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error);
            printf("Error of execution kernel %s Adam-Mini: %s", __FUNCSIG__, error);
            return false;
           }
         t++;
         break;
      //---
      default:
         printf("Error of optimization type %s: %s", __FUNCSIG__, EnumToString(optimization));
         return false;
     }

Wir werden auch eine Fehlermeldung hinzufügen, wenn eine falsche Art der Parameteroptimierung angegeben wird.

Der weitere Code der Methode in Bezug auf die Normalisierung der Modellparameter blieb unverändert.

   global_work_size[0] = window_out;
   OpenCL.SetArgumentBuffer(def_k_NormilizeWeights, def_k_norm_buffer, weights.GetIndex());
   OpenCL.SetArgument(def_k_NormilizeWeights, def_k_norm_dimension, (int)window + 1);
   if(!OpenCL.Execute(def_k_NormilizeWeights, 1, global_work_offset, global_work_size))
     {
      string error;
      CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error);
      printf("Error of execution kernel %s Normalize: %s", __FUNCSIG__, error);
      return false;
     }
//---
   return true;
  }

Darüber hinaus ändern wir in den Initialisierungsmethoden der oben genannten Klassen die Größe der Datenpuffer, die zur Speicherung von Momenten zweiter Ordnung angelegt werden, ähnlich wie bei dem Algorithmus, der bei der Beschreibung der Änderungen in der vollständig verbundenen Schicht vorgestellt wurde. Ich werde in diesem Artikel jedoch nicht näher darauf eingehen. Dabei handelt es sich nur um kleinere Änderungen, die Sie im Anhang nachlesen können.

3. Tests

Die Implementierung der Methode Adam-mini in zwei Basisklassen unserer Modelle wurde oben beschrieben. Nun ist es an der Zeit, die Wirksamkeit des vorgeschlagenen Ansatzes zu bewerten.

In diesem Artikel haben wir eine neue Optimierungsmethode vorgestellt. Um die Effektivität dieser Optimierungsmethode zu beurteilen, ist es logisch, den Trainingsprozess eines Modells mit verschiedenen Optimierungstechniken zu beobachten.

Für dieses Experiment habe ich die Modelle aus dem Algorithmus TPM und änderte die Architektur der Modelle, wobei ich nur die Methode zur Optimierung der Parameter änderte.

Es versteht sich von selbst, dass bei diesem Ansatz alle Trainingsprogramme, Datensätze und der Trainingsprozess unverändert bleiben.

Zur Erinnerung: Die Modelle wurden mit historischen Daten für das gesamte Jahr 2023 trainiert, wobei EURUSD mit dem Zeitrahmen H1 verwendet wurde. Die Parameter aller Indikatoren wurden auf Standardwerte gesetzt.

Beim Testen des trainierten Modells erzielten wir ähnliche Ergebnisse wie bei dem mit der klassischen Adam-Methode trainierten Modell. Die Testergebnisse für die Daten vom Januar 2024 werden im Folgenden vorgestellt.

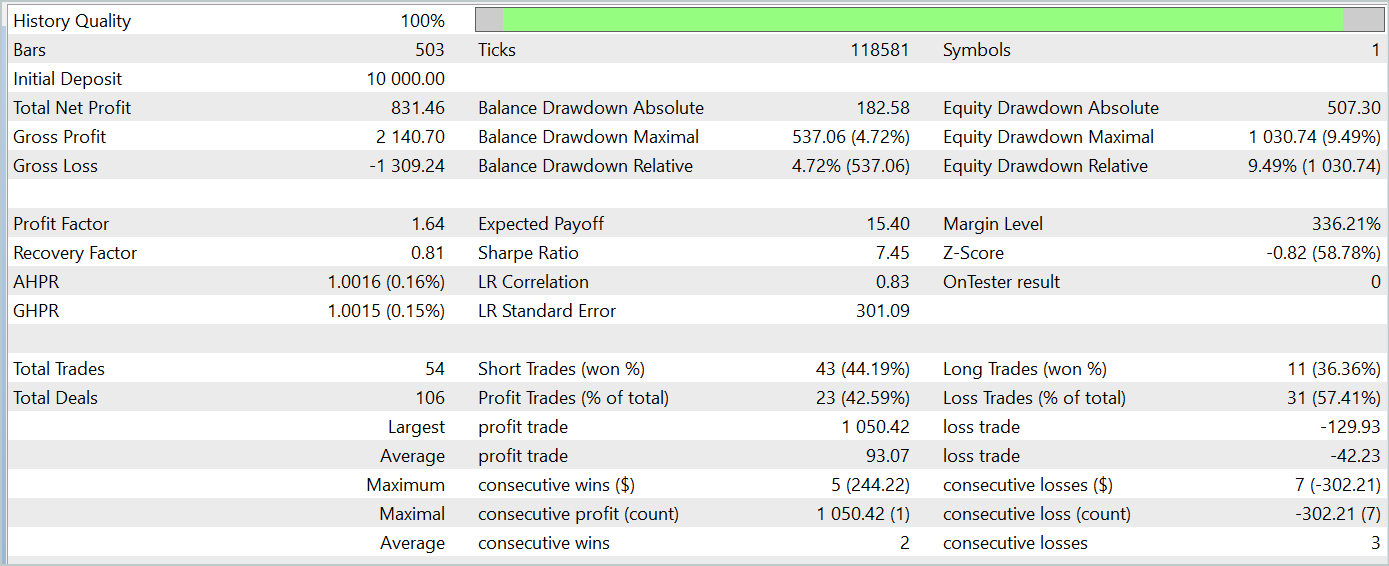
Es ist wichtig zu beachten, dass das Hauptziel der Adam-mini Optimierungsmethode darin besteht, den Speicherverbrauch zu reduzieren, ohne die Qualität des Trainings zu beeinträchtigen. Mit der vorgeschlagenen Methode wird dieses Ziel erfolgreich erreicht.

Schlussfolgerung

In diesem Artikel stellen wir eine neue Optimierungsmethode Adam-mini vor, die entwickelt wurde, um die Speichernutzung zu reduzieren und den Durchsatz beim Training großer Sprachmodelle zu erhöhen. Adam-mini erreicht dies, indem es die Anzahl der erforderlichen Lernraten auf die Summe aus der Größe der Einbettungsschicht, der Größe der Ergebnisschicht und der Anzahl der Blöcke in anderen Schichten reduziert. Seine Einfachheit, Flexibilität und Effizienz machen es zu einem vielversprechenden Werkzeug für eine breite Anwendung im Deep Learning.

Der praktische Teil des Artikels demonstriert die Integration der vorgeschlagenen Methode in die grundlegenden Arten von neuronalen Schichten. Die Ergebnisse der Tests bestätigen die von den Autoren der Methode angegebenen Verbesserungen.

Referenzen

Adam-mini: Use Fewer Learning Rates To Gain More

Weitere Artikel aus dieser Serie

Programme, die im diesem Artikel verwendet werden

#	Name	Typ	Beschreibung
1	Research.mq5	Expert Advisor	Beispielsammlung EA
2	ResearchRealORL.mq5	Expert Advisor	EA zum Sammeln von Beispielen mit der Real-ORL-Methode
3	Study.mq5	Expert Advisor	Modelltraining EA
4	StudyEncoder.mq5	Expert Advisor	Trainings-EA des Encoders
5	Test.mq5	Expert Advisor	Trainings-EA für das Model
6	Trajectory.mqh	Klassenbibliothek	Struktur der Systemzustandsbeschreibung
7	NeuroNet.mqh	Klassenbibliothek	Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes
8	NeuroNet.cl	Code Base	Die Bibliothek des Programmcodes von OpenCL