Estudando a previsão conformal de séries temporais financeiras

Introdução

MAPIE ou "Model agnostic prediction interval estimator" é uma biblioteca Python de código aberto, desenvolvida para a avaliação quantitativa da incerteza e o controle de riscos em modelos de aprendizado de máquina. Ela permite calcular intervalos de previsão para tarefas de regressão, bem como conjuntos de previsão para classificação e séries temporais. Essa avaliação de incerteza é realizada com base em um conjunto especial de dados de "conformidade".

Uma das principais vantagens do MAPIE é seu caráter agnóstico em relação ao modelo, o que significa que essa biblioteca se pode usar com qualquer modelo compatível com a API scikit-learn, incluindo aqueles desenvolvidos com TensorFlow ou PyTorch por meio de wrappers apropriados. Essa característica simplifica significativamente a integração em pipelines analíticos existentes, já que os traders frequentemente utilizam uma ampla variedade de modelos de aprendizado de máquina, desde abordagens estatísticas tradicionais até redes neurais complexas, dependendo da classe de ativos ou de uma estratégia de negociação específica. A possibilidade de utilizar sem obstáculos modelos já testados para incluir a avaliação quantitativa da incerteza reduz substancialmente os custos de implementação e acelera a adaptação, o que é especialmente valioso em um ambiente financeiro dinâmico.

A biblioteca faz parte do ecossistema scikit-learn-contrib e se baseia nas áreas de previsão conformal e inferência independente de distribuição. Ela implementa algoritmos revisados por pares, que não dependem do modelo nem do caso de uso, e que possuem garantias teóricas com suposições mínimas sobre os dados e o modelo. Além da classificação padrão, o MAPIE também é capaz de controlar riscos para tarefas mais complexas, como classificação multiclasse e segmentação de imagens em visão computacional, fornecendo garantias probabilísticas para métricas como recall e precisão.

Sua capacidade de controlar riscos e garantir resultados probabilísticos posiciona o MAPIE não apenas como uma ferramenta de avaliação quantitativa da incerteza, mas como uma estrutura completa de gerenciamento de riscos. Em finanças, previsões pontuais são insuficientes, pois não transmitem o nível de confiança nem o erro potencial. O fornecimento de métricas de erro garantidas, por exemplo, 95% de cobertura, se traduz diretamente em risco mensurável quantitativamente. Isso permite que gestores de risco estabeleçam tolerâncias explícitas ao risco.

Por exemplo, se o modelo gera um sinal de "compra", mas a previsão conformal indica uma alta probabilidade de erro, o gestor de risco pode decidir reduzir a posição ou se abster da operação, controlando diretamente as perdas potenciais. Isso contribui para a tomada de decisões mais confiáveis em condições de incerteza, indo além da simples precisão da previsão.

Princípios básicos da previsão conformal: garantias agnósticas ao modelo, independentes da distribuição

A previsão conformal (PC) consiste em uma base estatística que gera conjuntos de previsão para tarefas de classificação ou intervalos de previsão para regressão com probabilidade de cobertura garantida. Isso significa que, para um determinado nível de confiança, por exemplo, 90%, o resultado verdadeiro estará dentro do conjunto ou intervalo previsto em, pelo menos, 90% dos casos.

A principal vantagem da PC está em sua "independência de distribuição": o método não se apoia em suposições rígidas sobre a distribuição subjacente dos dados ou sobre o próprio modelo. A única suposição fundamental é que os dados (pontos de treinamento e teste) são intercambiáveis, ou seja, foram extraídos da mesma distribuição, e a ordem deles não importa.

Essa suposição é mais fraca do que a suposição de independência e distribuição idêntica (i.i.d.) e, muitas vezes, pode ser justificada na prática. Diferentemente dos intervalos de previsão tradicionais, que apenas aproximam a cobertura, a PC oferece garantias para amostras finitas, assegurando o alcance do nível de cobertura especificado mesmo com dados limitados.

A garantia independente de distribuição da previsão conformal resolve diretamente um problema fundamental da modelagem financeira. Os dados financeiros, como é bem conhecido, não seguem uma distribuição normal, apresentam caudas pesadas e frequentemente violam suposições estatísticas típicas, como homocedasticidade ou independência dos incrementos.

Os intervalos de previsão tradicionais geralmente dependem dessas suposições (como a de resíduos normais) e fornecem apenas uma cobertura aproximada. A capacidade da PC de oferecer cobertura garantida sem tais suposições a torna, por natureza, mais robusta e confiável para aplicações financeiras, onde distribuições mal especificadas podem levar a uma subestimação significativa do risco. Isso significa que os níveis de confiança reportados são mais confiáveis em conjuntos de dados financeiros reais e complexos.

O processo de previsão conformal geralmente envolve o uso de um modelo de aprendizado de máquina treinado, a criação de um conjunto de dados de calibração (não visto pelo modelo durante o treinamento), o cálculo de "pontuações de conformidade" nesse conjunto e, em seguida, o uso do quantil dessas pontuações para definir os conjuntos de previsão. A transição de uma cobertura aproximada para uma cobertura garantida em amostras finitas muda fundamentalmente o cenário de regulação e de gerenciamento de riscos para modelos de aprendizado de máquina em finanças.

Em setores de alto risco, como finanças, os modelos frequentemente precisam demonstrar confiabilidade quantitativa e controle sobre métricas de erro. Isso difere dos métodos estatísticos tradicionais, nos quais "90% de confiança" pode ser apenas uma propriedade assintótica ou uma aproximação. Para o trader quantitativo, isso fornece uma base mais sólida para justificar estratégias de negociação ou a alocação de capital de risco.

Conjuntos de previsão versus previsões pontuais na classificação binária

Modelos tradicionais de classificação binária produzem um único rótulo previsto (por exemplo, "Comprar" ou "Vender") ou uma estimativa de probabilidade (por exemplo, 0.8 para "Comprar"). Essas são previsões pontuais. No entanto, a previsão conformal fornece um conjunto de previsão, que é um subconjunto das classes possíveis (por exemplo, {Comprar}, {Vender} ou {Comprar, Vender}). Esse conjunto garante conter o rótulo verdadeiro com uma determinada probabilidade.

Para a classificação binária, o conjunto de previsão pode ser:

• Um único classe (por exemplo, {Comprar} ou {Vender}), o que indica um alto grau de confiança.
• Ambas as classes (por exemplo, {Comprar, Vender}), o que indica incerteza ou ambiguidade.
• Um conjunto vazio {} (embora isso seja menos comum ao usar alguns métodos, como APS, e frequentemente indesejável), o que indica extrema incerteza ou que nenhuma classe atende ao limiar de confiança.

A "informatividade" do conjunto de previsão é inversamente proporcional ao seu tamanho: conjuntos menores (por exemplo, de classe única) são mais informativos do que conjuntos mais amplos (por exemplo, ambas as classes). A saída explícita de um conjunto, em vez de um único ponto, muda fundamentalmente o processo de tomada de decisão na classificação binária para finanças. Em vez de um simples sinal de "sim/não" ou "comprar/vender", o conjunto de previsão fornece uma medida direta da confiança do modelo.

Um conjunto de classe única, como {Comprar}, sugere um sinal forte, enquanto um conjunto de duas classes {Comprar, Vender} indica ambiguidade significativa. Isso permite aplicar uma estratégia de negociação mais refinada: executar operações com sinais de alta confiança e, para sinais ambíguos, ou se abster, ou reduzir o tamanho da posição, ou buscar informações adicionais. Esse é um mecanismo direto para integrar a incerteza em decisões financeiras acionáveis.

A "informatividade" dos conjuntos de previsão torna-se uma medida direta de acionabilidade e tolerância ao risco na negociação financeira. Um conjunto de previsão amplo e pouco informativo (por exemplo, {Comprar, Vender}) para uma transação significa que o modelo não consegue distinguir de forma confiável entre compra e venda no nível de confiança desejado. Para o analista quantitativo, isso não é um erro de previsão a ser corrigido, mas um sinal para não agir ou agir com extrema cautela. Isso permite gerenciar riscos de forma dinâmica: alocar mais capital para operações com conjuntos estreitos e altamente confiáveis e preservar capital evitando ou minimizando a exposição a operações com conjuntos amplos e incertos. Isso leva diretamente à otimização do perfil risco-retorno da estratégia de negociação.

Garantias teóricas: cobertura marginal e condicional

Os preditores conformais são "automaticamente válidos" no sentido de que seus conjuntos de previsão possuem uma probabilidade de cobertura igual ou superior ao nível de confiança especificado (1 - α) em média sobre todos os dados. Essa garantia é mantida independentemente do modelo base ou do processo de geração dos dados, desde que a suposição de intercambiabilidade seja atendida. Essa propriedade é conhecida como cobertura marginal.

Embora a cobertura marginal seja garantida, ela representa uma métrica média. Conceitos mais rigorosos, como a validade condicional, buscam garantias de cobertura condicionadas a propriedades específicas dos dados (por exemplo, por classe, por objeto, por rótulo). Os preditores conformais indutivos (uma versão computacionalmente eficiente) controlam principalmente a probabilidade de cobertura incondicional. Alcançar a validade condicional frequentemente exige modificações no método.

A distinção entre cobertura marginal e condicional é de importância fundamental para a classificação binária financeira, especialmente em conjuntos de dados desbalanceados, comuns em finanças (por exemplo, muitos sinais de "sem operação" ou "manter" em comparação com um número menor de sinais de "comprar" ou "vender").

A cobertura marginal garante que, em média, 90% das previsões estarão corretas. No entanto, se os sinais de "comprar" forem raros, o modelo pode alcançar 90% de cobertura marginal sendo muito preciso nos sinais de "vender", mas apresentando desempenho fraco nos sinais de "comprar". Isso pode resultar em significativas oportunidades desperdiçadas ou em perdas, caso os sinais de "comprar" sejam críticos.

A cobertura condicional, especialmente a cobertura por classe, garante que o nível de confiança desejado seja alcançado para cada classe individualmente. Isso é chave para assegurar a confiabilidade das previsões tanto para operações de "comprar" quanto de "vender", prevenindo vieses sistemáticos que podem comprometer a estratégia de negociação.

A busca pela validade condicional por meio de métodos como Mondrian Conformal Prediction resolve diretamente o problema de equidade e confiabilidade entre diferentes classes de resultados em aplicações financeiras. Em finanças, erros de previsão em determinadas classes (por exemplo, uma oportunidade rara, porém altamente lucrativa de "comprar", ou um "vender" crítico para evitar grandes perdas) podem ter custos desproporcionalmente elevados em comparação com erros em cenários mais comuns de "sem operação".

Ao garantir cobertura condicional, o sistema assegura um nível mínimo de confiabilidade para cada tipo de transação, e não apenas em média. Isso permite um tratamento mais justo dos diferentes sinais de negociação e aumenta a confiança na capacidade do modelo de lidar com condições de mercado diversas e eventos raros, o que é essencial para uma negociação algorítmica robusta.

Avaliações de conformidade: o núcleo da previsão conformal

As avaliações de conformidade (conformity scores) são o núcleo da previsão conformal; elas quantificam o quão "incomum" ou "não conforme" um novo ponto de dados é em comparação com os dados de calibração. O único requisito para a função de avaliação é que valores mais altos codifiquem uma pior correspondência entre os dados de entrada e seu rótulo hipotético. Essas avaliações são usadas para calcular o quantil (ponto de corte) a partir do conjunto de calibração, que então define o conjunto de previsão para novos pontos de teste.

O MAPIE implementa diversas avaliações de conformidade, incluindo simétricas (por exemplo, Absolute Residual Score para regressão) e assimétricas (por exemplo, Gamma Score para regressão), que influenciam a forma como os limites do intervalo de previsão são calculados. Para classificação, são usadas avaliações específicas, como LAC, APS e RAPS.

A escolha da avaliação de conformidade não é apenas um detalhe técnico, mas uma decisão estratégica, que afeta a utilidade prática e a interpretabilidade dos conjuntos de previsão. Diferentes avaliações de conformidade (por exemplo, LAC, APS) levam a comportamentos distintos na formação dos conjuntos de previsão.

Por exemplo, o LAC pode produzir conjuntos vazios em situações de alta incerteza, o que pode ser indesejável em finanças, pois não fornece nenhuma indicação. O APS, por sua construção, evita conjuntos vazios, sempre fornecendo algum conjunto de resultados plausíveis. Isso significa que a escolha da avaliação afeta diretamente como os exemplos "ruins" são representados e se o sistema consegue sempre fornecer uma resposta acionável (ainda que incerta). O trader quantitativo deve escolher a avaliação que corresponda ao nível desejado de informatividade e tolerância ao risco.

O conceito de "conformidade" permite definir um "valor atípico" ou uma observação "incomum" no contexto das previsões do modelo com base nos dados, o que é altamente relevante para a detecção de condições anômalas de negociação. Nos mercados financeiros, movimentos de preços incomuns, picos repentinos de volume ou notícias inesperadas podem levar ao surgimento de pontos de dados que se desviam significativamente dos padrões históricos.

Uma avaliação de conformidade alta para uma nova observação sinaliza que essa observação "não está conforme" com os padrões observados nos dados de calibração. Isso pode servir como um sistema de alerta precoce para anomalias de mercado ou mudanças de regime, incentivando a revisão da estratégia de negociação ou a suspensão temporária da negociação automatizada, atuando assim como uma ferramenta importanet de gerenciamento de riscos, que vai além da simples precisão do modelo.

Análise detalhada das avaliações de conformidade relevantes para classificação

O MAPIE oferece diversas avaliações de conformidade, cada uma com suas próprias características e aplicabilidade.

• Least Ambiguous Set-valued Classifier (LAC):

1. Cálculo: a avaliação de conformidade é definida como 1 - softmax_score_of_the_true_label.
2. Propriedades: abordagem simples, teoricamente garante cobertura marginal. Geralmente resulta em conjuntos de previsão pequenos.
3. Aplicabilidade/Limitações: tende a formar conjuntos de previsão vazios em caso de alta incerteza do modelo (por exemplo, próximo às fronteiras de decisão). Isso pode ser problemático em finanças, pois um conjunto vazio não fornece indicações acionáveis.

• Adaptive Prediction Sets (APS):

1. Cálculo: as avaliações de conformidade são calculadas somando as pontuações softmax ranqueadas de cada rótulo, da mais alta para a mais baixa, até que o rótulo verdadeiro seja alcançado.
2. Propriedades: supera o problema de conjuntos vazios do LAC; os conjuntos de previsão por definição não são vazios. Fornece garantias de cobertura marginal.
3. Aplicabilidade: mais robusto para aplicações financeiras, onde alguma forma de previsão (mesmo que incerta) é sempre preferível a um conjunto vazio.

• Regularized Adaptive Prediction Sets (RAPS):

1. Cálculo: semelhante ao APS, mas inclui um termo de regularização para reduzir o tamanho dos conjuntos de previsão.
2. Propriedades: visa equilibrar cobertura e eficiência por meio da regularização do tamanho do conjunto, mantendo as garantias de cobertura.
3. Aplicabilidade: útil em cenários em que o tamanho do conjunto de previsão (eficiência) é tão importante quanto a cobertura, já que conjuntos menores são mais acionáveis na negociação.

• Mondrian Conformal Prediction:

1. Cálculo: este método calcula quantis separados das avaliações de conformidade para cada classe. Isso permite a inclusão no conjunto de previsão levando em conta a classe.
2. Propriedades: fornece cobertura condicional (1 - α) para cada classe, o que é vital para tarefas binárias ou multiclasse desbalanceadas.
3. Aplicabilidade: fortemente recomendado para classificação binária financeira (comprar/vender), onde as classes podem ser desbalanceadas (por exemplo, menos sinais de "comprar" do que de "manter" ou "vender") ou possuir diferentes tolerâncias a erro. Isso garante que a confiabilidade do sinal de "comprar" seja assegurada independentemente do sinal de "vender".

A evolução das avaliações de conformidade de LAC para APS/RAPS reflete a necessidade prática de conjuntos de previsão acionáveis e informativos em aplicações reais. Embora o LAC seja conceitualmente simples, sua tendência a gerar conjuntos vazios é uma limitação significativa em finanças. Um conjunto de previsão vazio para uma decisão de compra/venda não fornece nenhuma orientação, interrompendo efetivamente o processo de tomada de decisão. APS e RAPS, ao garantirem conjuntos não vazios, asseguram que, mesmo sob alta incerteza, o modelo forneça alguns resultados plausíveis, permitindo uma decisão padrão de "manter" ou "reavaliar", em vez de uma paralisação completa. Isso garante continuidade operacional e gerenciamento de riscos.

O método Mondrian é um avanço criticamente importante para a classificação binária financeira, pois resolve diretamente o problema de classes desbalanceadas e do impacto diferenciado dos erros. Em cenários de compra/venda, os sinais de "comprar" podem ser raros, porém altamente lucrativos, enquanto os sinais de "vender" podem ser mais frequentes, mas individualmente menos significativos. Métodos conformais padrão fornecem cobertura marginal, o que pode significar que a cobertura para a classe rara de "comprar" fique abaixo do desejado, desde que a média geral seja alcançada. A capacidade do Mondrian de calcular quantis específicos por classe garante que o nível de confiança desejado seja mantido para cada classe individualmente.

Isso é fundamental para evitar a subcobertura sistemática de eventos críticos e raros (por exemplo, sinais fortes de compra) e, assim, leva a estratégias de negociação mais confiáveis e potencialmente mais lucrativas. Isso garante que a confiabilidade do modelo não seja apenas uma métrica média, mas seja mantida para o tipo específico de transação considerada.

Etapas da formação de conjuntos preditivos conformais para classificação

Vamos analisar o processo passo a passo:

1. Escolha da medida de não conformidade (ou "função de avaliação"): isso é extremamente importante. Para classificação, frequentemente é utilizada a saída de um classificador previamente treinado (por exemplo, regressão logística, máquinas de vetores de suporte, rede neural ou floresta aleatória). Seja f(x) a saída do classificador para a entrada x. Se f(x) fornecer probabilidades (por exemplo, a partir de uma camada softmax), uma boa medida de não conformidade para um ponto de dados (xi , yi ) pode ser:
• 1 - Probabilidade prevista da classe verdadeira: αi = 1 − P^(yi | xi ). Aqui, P^(yi | xi ) é a probabilidade prevista do rótulo verdadeiro yi para a entrada xi. Um valor pequeno de αi significa que o modelo está confiante em sua previsão para a classe verdadeira, indicando "conformidade". Um αi grande significa que o modelo está menos confiante, indicando "não conformidade".
• Baseada em escalonamento de temperatura do softmax: se o modelo fornecer logits, pode-se aplicar softmax para obter probabilidades. Nesse caso, a avaliação de não conformidade novamente será 1 − P(yi | xi).
• Distância até a superfície de decisão (para SVM): para modelos como SVM, que fornecem a distância com sinal até a superfície de decisão, a medida de não conformidade pode estar relacionada ao valor negativo dessa distância para pontos corretamente classificados ou ao valor positivo dessa distância para pontos classificados incorretamente.
2. Separação dos dados para calibração: para tornar as previsões estatisticamente válidas, é necessário calibrar nossas avaliações de não conformidade. Normalmente, isso é feito dividindo o conjunto de dados original em duas partes:
• Conjunto de treinamento: utilizado para treinar o classificador base (por exemplo, rede neural, SVM).
• Conjunto de calibração: um conjunto separado de pontos de dados, não utilizado no treinamento do classificador, mas usado para calcular as avaliações de não conformidade e determinar o limiar de confiança.
3. Cálculo das avaliações de não conformidade para os dados de calibração: para cada ponto de dados (xj , yj ) no conjunto de calibração, sua avaliação de não conformidade αj é calculada usando o classificador previamente treinado.
4. Ordenação das avaliações de não conformidade e determinação do quantil (1−δ): todas as avaliações de não conformidade do conjunto de calibração são ordenadas em ordem crescente: α(1) ≤ α(2) ≤ ⋯ ≤ α(m), onde m é o tamanho do conjunto de calibração.
   Agora é escolhido o nível de significância desejado δ ∈ (0,1). Esse δ representa a probabilidade de que o conjunto preditivo não contenha o rótulo verdadeiro. Por outro lado, 1−δ é a probabilidade de cobertura desejada. É necessário encontrar o quantil (1−δ) dessas avaliações. Mais precisamente, encontra-se o menor valor q tal que pelo menos (1−δ)×(m+1) avaliações de calibração sejam menores ou iguais a q. Uma forma comum de calcular esse limiar é: q = α(⌈(m+1)(1−δ)⌉).
   No entanto, para amostras finitas, a fim de garantir cobertura exata, muitas vezes é mais confiável considerar o quantil empírico (1−δ) ajustado para amostras finitas. Uma abordagem mais prática consiste em encontrar o menor α(k) tal que k/(m+1) ≥ 1−δ. Seja esse valor q^ .
5. Formação do conjunto preditivo para um novo ponto de teste: seja xtest o novo input para o qual queremos fazer uma previsão. Para cada rótulo possível k no conjunto de classes (por exemplo, 1, 2, …, C para C classes), suponha que ytest = k.
   Em seguida, é calculada a avaliação de não conformidade αtest,k para o par (xtest , k) usando a medida de não conformidade escolhida (por exemplo, 1−P^(k | xtest)).
   O conjunto preditivo Ytest para xtest é formado incluindo todos os rótulos k para os quais a avaliação de não conformidade αtest,k é menor ou igual ao limiar q^ determinado no passo 4: Ytest = {k ∈ {1, …, C} | αtest,k ≤ q^ }

Componentes-chave do MapieClassifier

MapieClassifier é a classe principal no MAPIE para gerar conjuntos de previsão em tarefas de classificação. Ele foi projetado para ser compatível com qualquer estimador do scikit-learn que possua os métodos fit, predict e predict_proba. Se nenhum estimador for fornecido, LogisticRegression é utilizado por padrão.

O parâmetro cv permite o uso de diferentes estratégias de validação cruzada (por exemplo, "split", "crossval", "prefit") para o cálculo das avaliações de conformidade, influenciando a distinção entre os métodos jackknife e CV. A opção "prefit" pressupõe que o estimador já esteja treinado, e todos os dados fornecidos sejam usados para calibrar as previsões por meio do cálculo das avaliações. O processo envolve a divisão dos dados em conjuntos de treinamento, calibração e teste, o treinamento do modelo base no conjunto de treinamento e, em seguida, o uso do MAPIE para "conformalizar" o modelo no conjunto de calibração.

A opção cv="prefit" é extremamente prática para aplicações financeiras, onde os modelos frequentemente são treinados ou re-treinados continuamente em grandes conjuntos de dados. Em tempo real ou em negociações de alta frequência, os modelos são frequentemente atualizados ou treinados com dados em fluxo contínuo. A capacidade de usar um modelo previamente treinado e, em seguida, calibrá-lo com um conjunto de dados separado significa que a etapa computacionalmente intensiva de treinamento não precisa ser repetida para a conformidade. Isso permite integrar de forma eficiente a avaliação quantitativa da incerteza em sistemas de negociação de alto desempenho já existentes, sem atrasos significativos.

O parâmetro method (agora obsoleto em favor de conformity_score) define o método de previsão conformal. A descontinuação do parâmetro method em favor de conformity_score representa uma transição para maior modularidade e controle explícito sobre o mecanismo central da previsão conformal. Essa decisão arquitetural permite que os usuários definam com precisão como a "não conformidade" é medida para seu problema específico. Para dados financeiros, onde diferentes tipos de erros ou incertezas podem ser mais críticos (por exemplo, a classificação incorreta de "comprar" em comparação com "vender"), essa modularidade possibilita ajustar com precisão o processo de avaliação quantitativa da incerteza para melhor alinhamento com métricas específicas de risco financeiro ou objetivos de negociação. Isso oferece aos usuários experientes a capacidade de personalizar o processo de conformidade além dos métodos predefinidos.

Conclusões da parte teórica e recomendações

A biblioteca MAPIE representa uma ferramenta poderosa para a avaliação quantitativa da incerteza em modelos de aprendizado de máquina, especialmente no contexto da classificação binária conformal para aplicações financeiras. Sua capacidade de fornecer garantias de cobertura independentes da distribuição, para amostras finitas, e de identificar explicitamente amostras "boas" e "ruins" aumenta significativamente a confiabilidade e o controle de riscos em ambientes financeiros de alto risco.

A capacidade do MAPIE de se integrar a qualquer modelo compatível com o scikit-learn oferece flexibilidade e reduz as barreiras de adoção em sistemas financeiros existentes. A transição de previsões pontuais para conjuntos de previsão permite decisões mais refinadas e bem informadas, incorporando explicitamente o grau de incerteza do modelo. Em particular, a distinção entre cobertura marginal e condicional é de importância para aplicações financeiras, onde a confiabilidade das previsões para classes raras, porém criticamente importantes (por exemplo, sinais fortes de compra), pode ter um impacto desproporcionalmente grande.

Recomendações:

• Prioridade às avaliações de conformidade: para a classificação binária em finanças, recomenda-se dar preferência a avaliações de conformidade como APS ou RAPS, pois elas garantem conjuntos de previsão não vazios, assegurando a continuidade do processo de tomada de decisão e sempre fornecendo alguma forma de saída acionável, mesmo em condições de alta incerteza.
• Uso do Mondrian Conformal Prediction: em cenários com classes desbalanceadas ou quando a cobertura condicional para tipos específicos de transações (por exemplo, sinais raros de compra) é crítica, deve-se considerar o uso do método Mondrian Conformal Prediction. Esse método fornece garantias de confiabilidade para cada classe individualmente, prevenindo a subcobertura sistemática de eventos importantes, porém raros.
• Validação cuidadosa de séries temporais: a aplicação da previsão conformal a séries temporais financeiras exige validação cuidadosa e consideração das violações da suposição de intercambiabilidade. Apesar da existência de ferramentas especializadas no MAPIE para séries temporais, como MapieTimeSeriesRegressor, elas devem ser combinadas com outros métodos específicos para séries temporais e com backtesting rigoroso, a fim de garantir robustez diante da não estacionariedade e de mudanças abruptas de mercado.
• Desenvolvimento de estratégias de negociação multinível: devem ser desenvolvidas estratégias de negociação que explorem a interpretabilidade dos conjuntos de previsão. Isso permite ajustar dinamicamente a exposição ao risco: por exemplo, executar operações de alta confiança (conjuntos de classe única) com capital total e, para operações de baixa confiança (conjuntos multiclasse), reduzir o tamanho da posição, aplicar hedge ou se abster de operar.

Aplicação prática da biblioteca MAPIE

Na biblioteca MAPIE, são implementadas duas formas de "conformalizar" as previsões dos modelos:

• Split conformal predictions
• Cross conformal predictions

O primeiro método divide os dados originais em subconjuntos de treino e validação. O primeiro é usado para treinar o classificador base, e o segundo para calibração e geração dos conjuntos de previsão. O segundo método divide o dataset em vários folds e utiliza treinamento e calibração cruzados. Vamos usar imediatamente o segundo, pois ele deve ser mais robusto devido à validação cruzada. Isso é análogo ao walk-forward em aprendizado de máquina, uma explicação para quem não está familiarizado com validação cruzada.

Primeiro, é necessário instalar o pacote MAPIE e importar o módulo:

pip install mapie
from mapie.classification import CrossConformalClassifier

Também devem estar instaladas e importadas bibliotecas adicionais, cuja lista é apresentada abaixo.

import pandas as pd
import math
from datetime import datetime
from catboost import CatBoostClassifier
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_predict
from sklearn.model_selection import StratifiedKFold
from bots.botlibs.labeling_lib import *
from bots.botlibs.tester_lib import test_model
from mapie.classification import CrossConformalClassifier
from sklearn.ensemble import RandomForestClassifier

Em seguida, eu escrevi uma função de teste que implementa o processo de conformidade e depois exibe exemplos ruins e bons com base nos conjuntos de previsão.

def meta_learners_mapie(n_estimators_rf: int,
                       max_depth_rf: int,
                       confidence_level: float = 0.9):
    
    dataset = get_labels(get_features(get_prices()), markup=hyper_params['markup'])
    data = dataset[(dataset.index < hyper_params['forward']) & 
                  (dataset.index > hyper_params['backward'])].copy()
    
    # Extract features and target
    feature_columns = list(data.columns[1:-2])
    X = data[feature_columns]
    y = data['labels']

    mapie_classifier = CrossConformalClassifier(
                        estimator=RandomForestClassifier(n_estimators=n_estimators_rf, 
                                                         max_depth=max_depth_rf),
                        confidence_level=confidence_level,
                        cv=5,
                        ).fit_conformalize(X, y)
    predicted, y_prediction_sets = mapie_classifier.predict_set(X)
    
    
    y_prediction_sets = np.squeeze(y_prediction_sets, axis=-1)
    # Calculate set sizes (sum across classes for each sample)
    set_sizes = np.sum(y_prediction_sets, axis=1)
    # Initialize meta_labels
    data['meta_labels'] = 0.0
    # Mark labels as "good" (1.0) only where prediction set size is exactly 1
    data.loc[set_sizes == 1, 'meta_labels'] = 1.0
    # Report statistics on prediction sets
    empty_sets = np.sum(set_sizes == 0)
    single_element_sets = np.sum(set_sizes == 1)
    multi_element_sets = np.sum(set_sizes >= 2)
    
    print(f"Empty sets (meta_labels=0): {empty_sets}")
    print(f"Single element sets (meta_labels=1): {single_element_sets}")
    print(f"Multi-element sets (meta_labels=0): {multi_element_sets}")

    # Return the dataset with features, original labels, and meta labels
    return data[feature_columns + ['labels', 'meta_labels']]

Como classificador base, vamos usar uma floresta aleatória da distribuição do scikit-learn, pois o pacote MAPIE suporta todos os classificadores desse pacote. A floresta aleatória é um modelo suficientemente forte e com configurações flexíveis, mas você pode usar outro modelo que considerar adequado para suas tarefas. Para isso, deve-se passar qualquer outro classificador como estimator no código destacado. Vale observar que esse classificador será usado apenas para gerar os conjuntos preditivos, enquanto as models finais continuam sendo treinadas com CatBoost. 

Vamos destrinchar a função meta_learners_mapie() passo a passo.

Definição da função e seus parâmetros:

def meta_learners_mapie(n_estimators_rf: int,
                       max_depth_rf: int,
                       confidence_level: float = 0.9):

A função recebe três argumentos:  

1. n_estimators_rf: quantidade de árvores na floresta aleatória (Random Forest), que será usada como modelo base.  
2. max_depth_rf: profundidade máxima de cada árvore na floresta aleatória.  
3. confidence_level: nível de confiança para a previsão conformal (por padrão 0.9, ou seja, 90%). Esse parâmetro determina o quão "largos" serão os conjuntos preditivos.

Carregamento e preparação dos dados:

dataset = get_labels(get_features(get_prices()), markup=hyper_params['markup'])
data = dataset[(dataset.index < hyper_params['forward']) &
              (dataset.index > hyper_params['backward'])].copy()

Primeiro ocorre o carregamento e o pré-processamento dos dados.

Pressupõe-se a existência de três funções auxiliares:  

• get_prices(): carrega os dados brutos (preços) 
• get_features(): extrai ou calcula as características (features) a partir dos dados obtidos por get_prices() 
• get_labels(): gera os rótulos-alvo (labels) com base nas features e no parâmetro markup do dicionário hyper_params.  

Em seguida, os dados são filtrados pelo índice temporal. Permanecem apenas os registros cujo índice esteja entre hyper_params['backward'] e hyper_params['forward']. O uso de .copy() serve para criar uma cópia do DataFrame filtrado, a fim de evitar problemas com SettingWithCopyWarning.

Extração dos atributos X e da variável alvo y:

feature_columns = list(data.columns[1:-2])
X = data[feature_columns]
y = data['labels']

• feature_columns: é criada uma lista com os nomes das colunas que serão utilizadas como atributos. São consideradas todas as colunas, exceto a primeira (índice 0) e as duas últimas. Isso é específico da estrutura de data. 
• X: é criado um DataFrame com os atributos, selecionando as colunas definidas em feature_columns.  
• y: é criada uma Series com os rótulos alvo a partir da coluna 'labels'.

Inicialização e treinamento do classificador conformal MAPIE:

mapie_classifier = CrossConformalClassifier(
                    estimator=RandomForestClassifier(n_estimators=n_estimators_rf,
                                                     max_depth=max_depth_rf),
                    confidence_level=confidence_level,
                    cv=5,
                    ).fit_conformalize(X, y)

• É criada uma instância do CrossConformalClassifier da biblioteca MAPIE. Essa é uma wrapper que adiciona capacidades de previsão conformal a qualquer modelo compatível com scikit-learn.  
• estimator: como modelo base (estimador), é utilizado o RandomForestClassifier do scikit-learn. São passados a ele os parâmetros n_estimators_rf e max_depth_rf recebidos pela função.  
• confidence_level: é utilizado o nível de confiança passado para a função.  cv=5: indica o uso de validação cruzada com 5 folds para a calibração do preditor conformal. Esse é o procedimento padrão no MAPIE para dividir os dados em conjuntos de treinamento e calibração.  
• .fit_conformalize(X, y): esse método treina o RandomForestClassifier base nos dados (X, y) e, simultaneamente, calibra o preditor conformal. Após essa etapa, o mapie_classifier está pronto para realizar previsões conformais.

Obtenção das previsões e dos conjuntos preditivos:

predicted, y_prediction_sets = mapie_classifier.predict_set(X)

mapie_classifier.predict_set(X): esse método gera duas saídas para os dados de entrada X:  

• predicted: previsões pontuais (uma classe para cada exemplo), de forma análoga ao método padrão .predict().  
• y_prediction_sets: este é o principal resultado da previsão conformal. Para cada exemplo dos dados, trata-se de um array (ou lista de arrays) que indica quais classes estão incluídas no conjunto preditivo com o confidence_level especificado. O conjunto preditivo é um conjunto de classes que, com probabilidade de pelo menos confidence_level, contém a classe verdadeira. Sua forma típica é (n_samples, n_classes, 1) ou (n_samples, n_classes), onde os valores são booleanos (True/False) ou 0/1, indicando a inclusão da classe no conjunto.

Processamento dos conjuntos preditivos:

y_prediction_sets = np.squeeze(y_prediction_sets, axis=-1)
set_sizes = np.sum(y_prediction_sets, axis=1)

• np.squeeze(y_prediction_sets, axis=-1): se y_prediction_sets possuir uma dimensão extra de tamanho 1 ao final (por exemplo, com forma (n_samples, n_classes, 1)), essa operação a remove, resultando na forma (n_samples, n_classes).  
• set_sizes = np.sum(y_prediction_sets, axis=1): para cada exemplo (ao longo do eixo 0), os valores em y_prediction_sets são somados ao longo das classes (eixo 1). Se y_prediction_sets contiver valores 0/1, essa soma fornece o número de classes incluídas no conjunto preditivo para cada exemplo. Ou seja, set_sizes é um array com os tamanhos dos conjuntos preditivos para cada observação.

Geração de meta-rótulos:

data['meta_labels'] = 0.0
data.loc[set_sizes == 1, 'meta_labels'] = 1.0

• data['meta_labels'] = 0.0: no DataFrame data é adicionada uma nova coluna 'meta_labels', que é inicializada com zeros.  
• data.loc[set_sizes == 1, 'meta_labels'] = 1.0: este é o passo-chave para a criação dos meta-rótulos. Para aqueles exemplos em que o tamanho do conjunto preditivo (set_sizes) é exatamente 1 (ou seja, o modelo, com o nível de confiança definido, prevê exatamente uma única classe), o valor na coluna 'meta_labels' é definido como 1.0. Isso significa que, para esses exemplos, o modelo está muito confiante em sua única classe prevista. Se o conjunto preditivo estiver vazio (tamanho 0) ou contiver várias classes (tamanho >= 2), o meta-rótulo permanece como 0.0.

Relatório sobre as estatísticas dos conjuntos preditivos:

empty_sets = np.sum(set_sizes == 0)
single_element_sets = np.sum(set_sizes == 1)
multi_element_sets = np.sum(set_sizes >= 2)

print(f"Empty sets (meta_labels=0): {empty_sets}")
print(f"Single element sets (meta_labels=1): {single_element_sets}")
print(f"Multi-element sets (meta_labels=0): {multi_element_sets}")

É contabilizada a quantidade de:  

• empty_sets: conjuntos preditivos vazios (o modelo não consegue selecionar nenhuma classe com o nível de confiança definido).  
• single_element_sets: conjuntos que contêm exatamente uma classe (previsões de alta confiança, para as quais meta_labels = 1).  
• multi_element_sets: conjuntos que contêm duas ou mais classes (o modelo não está confiante em uma única classe).  

Essas estatísticas são exibidas na saída, fornecendo uma visão de quão frequentemente o modelo gera previsões confiáveis e unívocas.

Retorno do resultado:

return data[feature_columns + ['labels', 'meta_labels']]

A função retorna um DataFrame contendo os atributos originais (feature_columns), os rótulos originais ('labels') e os novos meta-rótulos gerados ('meta_labels'). Esses meta-rótulos podem então ser utilizados, por exemplo, para treinar outro modelo (meta-modelo) ou para selecionar apenas as previsões mais confiáveis para ações posteriores.

Em resumo, a função utiliza a previsão conformal para identificar aquelas observações para as quais o modelo base (Random Forest) faz uma previsão com alto grau de confiança, indicando exatamente uma classe possível. Essas observações são marcadas com um meta-rótulo igual a 1.

Aprimoramento da função de conformidade

Após testar a função e avaliar os resultados, cheguei à conclusão de que ela possui uma limitação significativa. Apesar de lidar muito bem com a geração de conjuntos preditivos, sobre os quais a meta-modelo é treinada, o modelo base ainda é treinado sobre o dataset original, que pode conter muitos erros, fazendo com que ele generalize mal para novos dados. A meta-modelo corrige os erros do modelo base ao impedir que ele opere em situações de alta incerteza; no entanto, devido à fraca capacidade de generalização do modelo principal, todo o sistema ainda apresenta desempenho insatisfatório em um mercado não estacionário.

Vamos lembrar que, após o treinamento do classificador MAPIE, obtemos dois conjuntos de rótulos: as previsões do modelo (os próprios rótulos) e os conjuntos preditivos.

predicted, y_prediction_sets = mapie_classifier.predict_set(X)

Na função de conformidade original, apenas os conjuntos preditivos são utilizados para treinar a meta-modelo, enquanto o modelo base é treinado com os rótulos do dataset original. Porém, também podemos corrigir os rótulos do próprio modelo base, mantendo apenas aqueles nos quais o classificador MAPIE está mais confiante.

# Initialize meta_labels column with zeros
data['meta_labels'] = 0.0
# Set meta_labels to 1 where predicted labels match original labels
# Compare predicted values with the original labels in the dataset
data.loc[predicted == data['labels'], 'meta_labels'] = 1.0

No código apresentado acima, comparamos os rótulos previstos com os rótulos originais e formamos uma nova coluna 'meta_labels', que contém valores 1 quando os rótulos coincidem e 0 quando não coincidem. Em seguida, treinamos o classificador base apenas com aqueles exemplos cujos rótulos coincidiram.

A primeira parte da função de treinamento dos modelos finais agora terá a seguinte aparência:

def fit_final_models(dataset) -> list:
    # features for model\meta models. We learn main model only on filtered labels 
    X = dataset[dataset['meta_labels']==1]
    X = X[X.columns[1:-3]]
    X_meta = dataset[dataset.columns[1:-3]]
    # labels for model\meta models
    y = dataset[dataset['meta_labels']==1]
    y = y[y.columns[-3]]
    y_meta = dataset['conformal_labels']

Dessa forma, ambos os modelos passarão a retornar avaliações de maior qualidade após o treinamento, na medida do possível em séries temporais não estacionárias.

Treinamento e teste do algoritmo

Para verificar o método, vamos treinar 10 modelos em um laço na paridade cambial EURUSD, do início de 2020 até o início de 2025. Os dados restantes correspondem ao período forward.

hyper_params = {
    'symbol': 'EURUSD_H1',
    'export_path': '/Users/dmitrievsky/Library/Program Files/MetaTrader 5/MQL5/Include/Trend following/',
    'model_number': 0,
    'markup': 0.00010,
    'stop_loss':  0.00500,
    'take_profit': 0.00200,
    'periods': [i for i in range(5, 300, 30)],
    'backward': datetime(2020, 1, 1),
    'forward': datetime(2025, 1, 1),
}

models = []
for i in range(10):
    print('Learn ' + str(i) + ' model')
    models.append(fit_final_models(meta_learners_mapie(15, 5, confidence_level=0.90, CV_folds=5)))

A função meta_leaners_mapie será chamada com os seguintes argumentos:

• 15 árvores de decisão no Random Forest (classificador base)
• 5: profundidade de cada árvore de decisão
• nível de confiança do modelo de 90%
• número de folds para validação cruzada igual a cinco

Durante o processo de treinamento, as seguintes informações são exibidas:

Learn 9 model
Empty sets (meta_labels=0): 0
Single element sets (meta_labels=1): 6715
Multi-element sets (meta_labels=0): 22948
Correct predictions (meta_labels=1): 16638
Incorrect predictions (meta_labels=0): 13025
R2: 0.9931613891107195

• Empty sets: quantidade de conjuntos preditivos vazios, quando o modelo não está confiante em nenhum dos classes
• Single element sets: quantidade de conjuntos preditivos que contêm um único elemento. Nesses casos, o modelo está confiante com probabilidade de 0.9
• Multi-element sets: quantidade de conjuntos preditivos que contêm vários classes. Nesses exemplos, o modelo não está confiante
• Correct predictions: quantidade de rótulos corretamente previstos
• Incorrect predictions: quantidade de rótulos previstos incorretamente
• R2: avaliação da curva de balanço

Com base no relatório apresentado, é possível concluir que o dataset contém muitos dados ruidosos: 6715 previsões confiáveis contra 22948 não confiáveis. No entanto, nosso modelo tentará corrigir isso e utilizará apenas as confiáveis. Como resultado, o gráfico de balanço no testador terá a seguinte aparência.

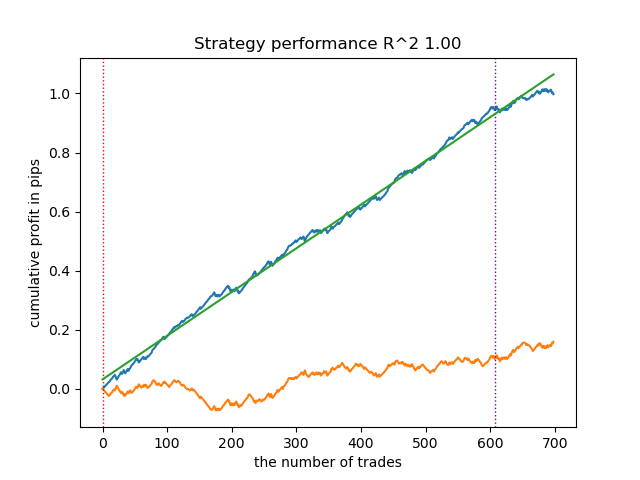
Uma característica distintiva desse algoritmo é que ambos os modelos (principal e meta) são treinados com alta Accuracy:

>>> models[-1][1].get_best_score()['validation']
{'Accuracy': 0.92, 'Logloss': 0.1990666082064606}

>>> models[-1][2].get_best_score()['validation']
{'Accuracy': 0.9647435897435898, 'Logloss': 0.10955056411224594}

Isso significa que agora uma grande parte da incerteza foi removida dos modelos em comparação com o dataset original, que contém muitos dados ruidosos. Adicionalmente, os modelos finais podem ser calibrados para obter limiares de tomada de decisão mais confiáveis, o que foge ao escopo deste artigo.

O que acontecerá se o nível de confiança (confidence_level) for reduzido de 0.9 para 0.6? Obteremos mais conjuntos que contêm o rótulo verdadeiro da classe com probabilidade de 60%, o que é refletido no relatório.

Learn 8 model
Empty sets (meta_labels=0): 0
Single element sets (meta_labels=1): 28647
Multi-element sets (meta_labels=0): 991
Correct predictions (meta_labels=1): 16999
Incorrect predictions (meta_labels=0): 12639
R2: 0.9850582205528567

Se no exemplo anterior os Single Element sets continham poucos exemplos, agora a quantidade deles passa a prevalecer sobre os Multi-element sets. Porém, a confiança em um desfecho bem-sucedido é muito menor. O gráfico de balanço reflete essa incerteza, pois passa a conter mais rebaixamentos.

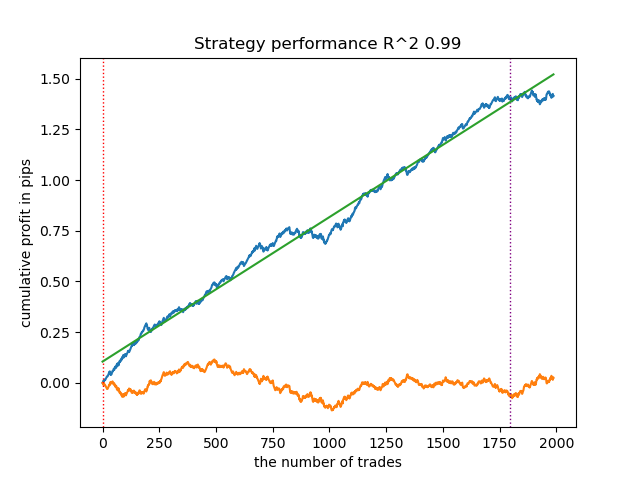
Dessa forma, ao regular o nível de confiança do modelo, é possível controlar os riscos associados a operações de negociação malsucedidas. Com isso, pode-se buscar um compromisso entre a quantidade de operações e a eficiência da negociação, ou a probabilidade de ocorrência de um cisne negro.

Exportação e teste dos modelos no terminal MetaTrader 5

A exportação dos modelos é realizada exatamente da mesma forma que em todos os artigos anteriores. Para um entendimento mais detalhado, recomendo a leitura deles.

export_model_to_ONNX(model = models[-1],
                     symbol = hyper_params['symbol'],
                     periods = hyper_params['periods'],
                     periods_meta = hyper_params['periods'],
                     model_number = hyper_params['model_number'],
                     export_path = hyper_params['export_path'])

Agora já é possível testar o algoritmo diretamente no terminal MetaTrader 5. O sistema de negociação mostrou-se robusto não apenas no período forward, mas também em um período passado, de 2017 a 2020.

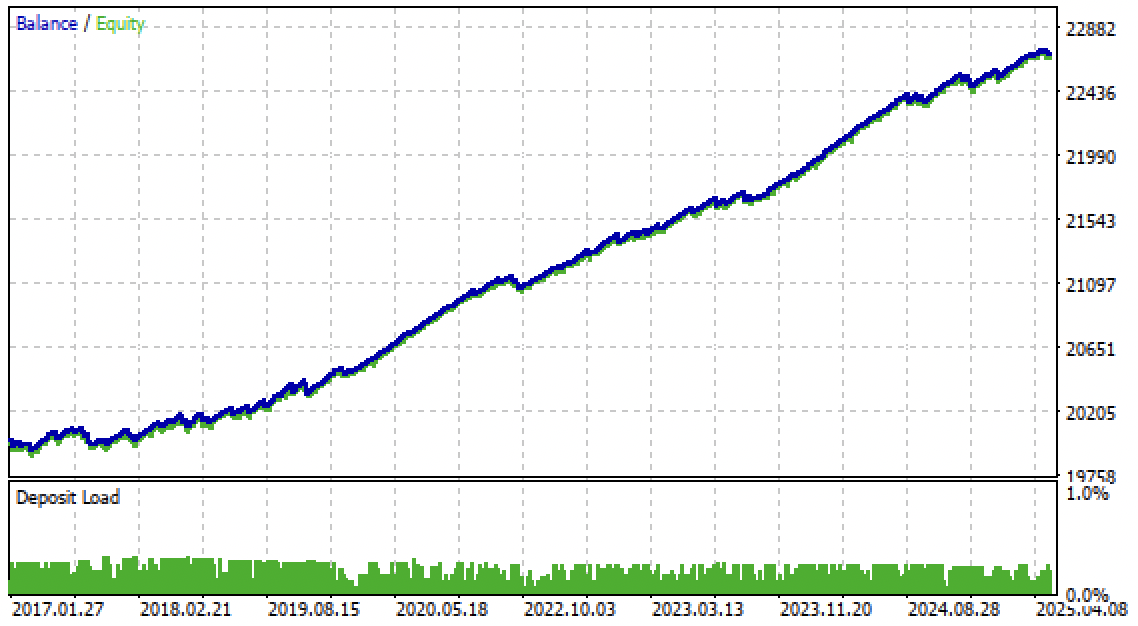
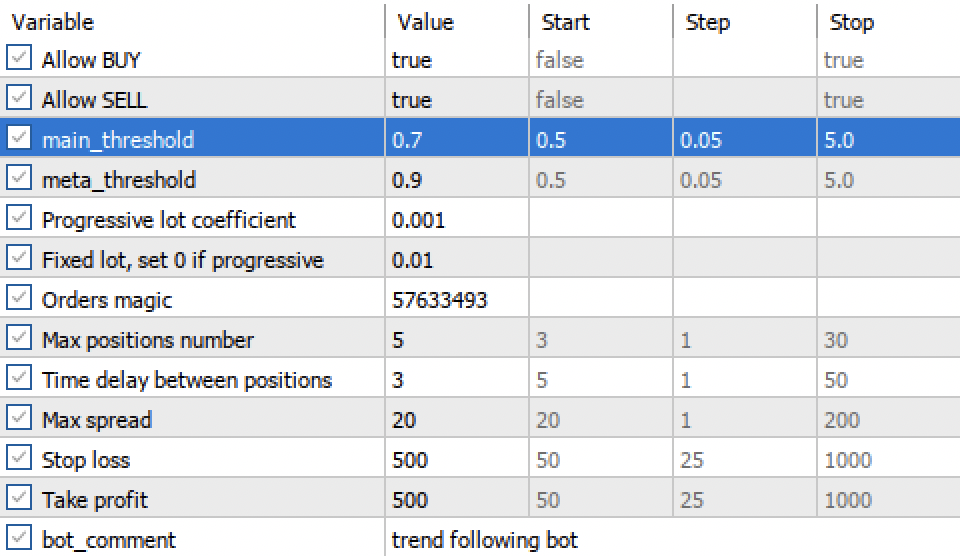
As configurações dos limiares main threshold e meta threshold agora permitem filtrar os sinais dos modelos com base na confiança. Quanto maior o limiar, mais conservadora e confiante é a negociação, porém com menor quantidade de operações.

Conclusão

Neste artigo, nos familiarizamos com as previsões conformais e com a biblioteca MAPIE, que as implementa. Essa abordagem é uma das mais modernas em aprendizado de máquina e permite focar no controle de riscos para os já existentes e variados modelos de aprendizado de máquina. As previsões conformais, por si só, não são uma forma de encontrar padrões nos dados. Elas apenas determinam o grau de confiança dos modelos existentes ao preverem exemplos específicos e permitem filtrar previsões confiáveis. Essa propriedade importante possibilita controlar o risco no trading por meio do ajuste do limiar de confiança ainda na fase de treinamento dos modelos.

O arquivo Python files.zip contém os seguintes arquivos para desenvolvimento no ambiente Python:

Nome do arquivo	Descrição
mapie causal.py	Script principal para o treinamento dos modelos
labeling_lib.py	Módulo atualizado com rotuladores de operações
tester_lib.py	Testador de estratégias customizado atualizado, baseado em aprendizado de máquina
export_lib.py	Módulo para exportação dos modelos para o terminal
EURUSD_H1.csv	Arquivo com cotações exportadas do terminal MetaTrader 5

O arquivo MQL5 files.zip contém os arquivos para o terminal MetaTrader 5:

Nome do arquivo	Descrição
mapie trader.ex5	Robô compilado deste artigo
mapie trader.mq5	Código-fonte do robô do artigo
pasta Include//Trend following	Contém os modelos ONNX e o arquivo de cabeçalho para conexão com o robô