
Redes neurais em trading: Rede neural espaço-temporal (STNN)
Introdução
A previsão de séries temporais é importante em diversas áreas, incluindo as finanças. Já estamos acostumados ao fato de que muitos sistemas reais permitem a medição de dados multidimensionais, que contêm informações ricas sobre a dinâmica da variável-alvo. No entanto, a análise eficaz e a previsão de séries temporais multidimensionais enfrentam o problema da "maldição da dimensionalidade". Assim, a escolha da janela de dados históricos analisados é muito importante. Frequentemente, ao usar uma janela insuficiente de dados analisados, o modelo de previsão tende a apresentar um desempenho insatisfatório e falha.
Para explorar informações multidimensionais, foi desenvolvida uma equação de transformação de informações espaço-temporais (STI), com base no teorema de incorporação com atraso. O STI transforma informações espaciais de variáveis multidimensionais em informações temporais futuras da variável-alvo, o que equivale ao aumento do tamanho da amostra e resolve o problema de dados de curto prazo.
Modelos baseados na arquitetura Transformer, já conhecidos por nós, processam sequências de dados e aprendem informações por meio do mecanismo de Self-Attention, modelando a interrelação entre variáveis independentemente da distância entre elas. Esses mecanismos podem capturar informações globais e focar no conteúdo importante, ajudando a mitigar a maldição da dimensionalidade.
Para resolver problemas de previsão de séries temporais, o artigo "Spatiotemporal Transformer Neural Network for Time-Series Forecasting" propôs o modelo Transformer Espacial-Temporal (STNN) para previsões eficazes de séries temporais multidimensionais de curto prazo em várias etapas, aproveitando as vantagens da equação STI e da estrutura Transformer.
Os autores do método destacam as seguintes vantagens dos enfoques propostos:
- A STNN utiliza a equação STI para transformar informações espaciais de variáveis multidimensionais em informações sobre a evolução temporal da variável-alvo, o que equivale a aumentar o tamanho da amostra.
- Foi proposto um mecanismo de atenção contínua para aumentar a precisão das previsões numéricas.
- A estrutura espacial do Self-Attention na STNN coleta informações espaciais precisas de variáveis multidimensionais, enquanto a estrutura temporal do Self-Attention é utilizada para capturar informações sobre a evolução temporal. A estrutura Transformer integra informações espaciais e temporais.
- O modelo STNN pode reconstruir o espaço de fase do sistema dinâmico para previsão de séries temporais.
1. Algoritmo STNN
O objetivo do modelo STNN é resolver de forma eficaz a equação não linear de transformação STI por meio do aprendizado do Transformer.
![]()
O modelo STNN utiliza a equação de transformação STI e inclui dois módulos de atenção específicos para realizar previsões em vários passos à frente. Como pode ser observado na equação apresentada acima, os dados brutos D-dimensionais no momento t (Xt são enviados para o Codificador, que extrai informações espaciais eficazes das variáveis de entrada.
Em seguida, as informações espaciais eficazes são transferidas para o Decodificador, que utiliza uma série temporal de comprimento L-1 da variável-alvo Y (𝐘t). O Decodificador extrai informações sobre a evolução temporal da variável-alvo. Depois disso, ele prevê os valores futuros da variável-alvo ao combinar informações espaciais das variáveis de entrada (𝐗t) com informações temporais da variável-alvo (𝐘t).
Note que a variável-alvo é uma das variáveis nos dados brutos multidimensionais X.
A transformação não linear STI é resolvida pelo par Codificador-Decodificador. O Codificador consiste em dois níveis. O primeiro é uma camada densamente conectada, enquanto o segundo é uma camada contínua espacial de atenção própria. Os autores do método STNN utilizam a camada contínua espacial do Self-Attention para extrair informações espaciais eficazes dos dados brutos multidimensionais 𝐗t.
A camada densamente conectada é usada para suavizar os dados brutos da série temporal multidimensional 𝐗t e filtrar ruídos. Os neurônios desta camada são descritos pela seguinte equação.
![]()
onde WFFN é a matriz de coeficientes,
bFFN é o viés,
ELU é a função de ativação.
A camada contínua espacial do Self-Attention recebe 𝐗t,FFN como entrada. Como a camada Self-Attention aceita uma série temporal multidimensional, o Codificador pode extrair informações espaciais a partir dos dados de entrada. Para obter informações espaciais eficazes (SSA), é proposto um mecanismo de atenção contínua da camada espacial do Self-Attention, cujo funcionamento pode ser descrito da seguinte forma.
Inicialmente, são geradas três matrizes de parâmetros treináveis (WQE, WKE e WVE)), que são utilizadas na camada espacial contínua do Self-Attention.
Em seguida, ao multiplicar os dados brutos 𝐗t,FFN pelas matrizes de pesos mencionadas acima, são geradas as entidades Query, Key e Value da camada contínua espacial do Self-Attention.
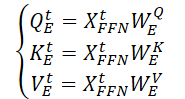
Ao realizar o produto escalar matricial, obtemos a expressão da informação espacial chave (SSAt) para os dados brutos 𝐗t.

onde dE é a dimensão das matrizes Query, Key e Value.
Os autores do método STNN destacam que, diferentemente do mecanismo clássico de atenção probabilística discreta, o mecanismo de atenção contínua proposto pode garantir a transmissão ininterrupta de dados do Codificador.
Na saída do Codificador, somamos o tensor da informação espacial chave aos dados brutos suavizados, normalizando-os em seguida. Isso ajuda a prevenir o rápido desaparecimento do gradiente e acelera a convergência do modelo.
![]()
O Decodificador combina informações espaciais precisas com a evolução temporal da variável-alvo. Em sua arquitetura, ele inclui duas camadas densamente conectadas: uma camada contínua temporal do Self-Attention e uma camada de atenção de transformação.
Os dados históricos da sequência da variável-alvo são fornecidos como entrada para o Decodificador. Assim como no Codificador, a representação eficaz dos dados brutos (𝐘t,FFN) é obtida após a filtragem de ruídos pela camada densamente conectada.
Posteriormente, os dados processados são direcionados à camada contínua temporal do Self-Attention, que se concentra nas informações históricas sobre a evolução temporal entre diferentes passos de tempo da variável-alvo. Como a influência do tempo é irreversível, definimos o estado atual da série temporal com base em informações históricas, mas não futuras. Assim, a camada de atenção temporal contínua emprega um mecanismo de atenção mascarada para excluir informações futuras. Vamos examinar essa operação em mais detalhes.
Primeiro, geramos três matrizes de parâmetros treináveis (WQD, WKD e WVD) para a camada temporal-espacial do Self-Attention. Em seguida, calculamos as respectivas matrizes das entidades Query, Key e Value.
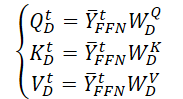
Realizamos o produto escalar matricial para obter informações sobre a evolução temporal da variável-alvo no intervalo histórico analisado.

Ao contrário do Codificador, aqui é adicionada uma máscara que anula a influência dos elementos subsequentes nos dados analisados. Dessa maneira, impedimos que o modelo "espreite o futuro" ao construir a função de evolução temporal da variável-alvo.
Em seguida, utilizamos uma conexão residual e normalizamos as informações sobre a evolução temporal da variável-alvo.
![]()
A camada de atenção contínua de transformação para a previsão dos valores futuros da variável-alvo combina informações sobre dependências espaciais (SSAt) com os dados da evolução temporal da variável-alvo (TSAt).

Aqui, também são utilizadas conexões residuais e normalização dos dados.
![]()
Na saída do Decodificador, os autores do método utilizam uma segunda camada densamente conectada para prever os valores da variável-alvo.
![]()
Durante o treinamento do modelo STNN, os autores usaram o MSE como função de perda e a regularização L2 para os parâmetros.
Abaixo, é apresentada a visualização autoral do método.

2. Implementação com MQL5
Após examinarmos os aspectos teóricos do método STNN, passamos para a parte prática do nosso artigo, na qual exploramos uma das opções de implementação dos enfoques propostos utilizando MQL5.
Como de costume, este artigo apresentará uma abordagem própria de implementação, que pode diferir da implementação original do método pelos autores. Além disso, nesta implementação, procuramos aproveitar ao máximo os recursos existentes, o que nos distanciou um pouco do método original. Abordaremos esse aspecto ao longo do processo de implementação das abordagens propostas.
Como você deve ter notado na descrição teórica do algoritmo STNN apresentada acima, ele inclui dois blocos principais: Codificador e Decodificador. Nosso trabalho também será dividido na implementação de duas classes correspondentes. Iniciaremos com a implementação do Codificador.
2.1 Codificador STNN
Implementaremos os algoritmos do Codificador no escopo da classe CNeuronSTNNEncoder. Os autores do método fizeram algumas alterações no algoritmo Self-Attention. No entanto, ele ainda mantém componentes básicos do enfoque clássico, sendo facilmente reconhecível. Por isso, para implementar a nova classe, utilizaremos os recursos existentes e herdamos a funcionalidade principal do algoritmo Self-Attention base da classe CNeuronMLMHAttentionMLKV. A estrutura geral da nova classe é apresentada a seguir.
class CNeuronSTNNEncoder : public CNeuronMLMHAttentionMLKV { protected: virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool AttentionOut(CBufferFloat *q, CBufferFloat *kv, CBufferFloat *scores, CBufferFloat *out) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronSTNNEncoder(void) {}; ~CNeuronSTNNEncoder(void) {}; //--- virtual int Type(void) override const { return defNeuronSTNNEncoder; } };
Como se pode notar, não há declarações de novas variáveis e objetos na nova classe. Além disso, a estrutura apresentada sequer redefine os métodos de inicialização de objetos. Há razões para isso. Como mencionado anteriormente, estamos aproveitando ao máximo os recursos disponíveis.
Inicialmente, vejamos as diferenças entre os enfoques propostos e os implementados anteriormente. Primeiramente, os autores do método STNN adicionaram uma camada densamente conectada antes do bloco Self-Attention. Tecnicamente, isso não representa um problema na declaração de objetos, mas apenas na implementação dos algoritmos de propagação para frente e de propagação reversa. Portanto, a implementação deste aspecto não interfere no algoritmo do método de inicialização.
O segundo ponto é que os autores do método STNN consideraram apenas uma camada densamente conectada. Já na abordagem clássica, cria-se um bloco com duas camadas densamente conectadas. Na minha opinião pessoal, o uso de um bloco com duas camadas densamente conectadas, embora aumente os custos computacionais, não reduz a qualidade do desempenho do modelo. Como experimento, para preservar ao máximo os recursos existentes, podemos utilizar duas camadas em vez de uma.
Além disso, os autores do método optaram por não usar a função SoftMax para normalizar os coeficientes de atenção. Em vez disso, utilizam uma exponencial simples do produto das matrizes Query e Key. A meu ver, a diferença do SoftMax está apenas na normalização dos dados e em um cálculo mais complexo. Em minha implementação, arriscarei usar a abordagem já implementada com o SoftMax.
Passamos, então, para a implementação dos algoritmos de propagação para a frente. Notei que os autores do método introduziram a máscara para os elementos subsequentes apenas no Decodificador. Isso gera certa inconsistência, pois a variável-alvo pode estar incluída no conjunto de dados brutos do Codificador. Porém, após um exame mais detalhado da visualização autoral do método, tudo se encaixa.

Os dados brutos do Codificador estão distantes do estado sendo analisado. Não posso julgar os motivos pelos quais os autores escolheram essa implementação. Contudo, acredito que o uso completo das informações disponíveis no momento da análise pode proporcionar mais dados e, potencialmente, melhorar a qualidade de nossas previsões. Por isso, em minha implementação, ajusto os dados brutos do Codificador para o momento atual e adiciono uma máscara, permitindo a análise das dependências apenas com os dados anteriores.
Para implementar a máscara nos dados, precisamos modificar o programa OpenCL. Aqui, faremos apenas ajustes pequenos no kernel MH2AttentionOut. Não utilizaremos um buffer de máscara adicional. Em vez disso, adotaremos uma abordagem mais simples. Adicionaremos apenas uma constante que determinará se a máscara deve ser aplicada e o mascaramento será integrado diretamente ao algoritmo do kernel.
__kernel void MH2AttentionOut(__global float *q, __global float *kv, __global float *score, __global float *out, int dimension, int heads_kv, int mask ///< 1 - calc only previous units, 0 - calc all ) { //--- init const int q_id = get_global_id(0); const int k = get_global_id(1); const int h = get_global_id(2); const int qunits = get_global_size(0); const int kunits = get_global_size(1); const int heads = get_global_size(2); const int h_kv = h % heads_kv; const int shift_q = dimension * (q_id * heads + h); const int shift_k = dimension * (2 * heads_kv * k + h_kv); const int shift_v = dimension * (2 * heads_kv * k + heads_kv + h_kv); const int shift_s = kunits * (q_id * heads + h) + k; const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE); float koef = sqrt((float)dimension); if(koef < 1) koef = 1; __local float temp[LOCAL_ARRAY_SIZE];
No corpo do kernel, faremos apenas ajustes pontuais no cálculo da soma das exponenciais.
//--- sum of exp uint count = 0; if(k < ls) { temp[k] = 0; do { if(mask == 0 || q_id <= (count * ls + k)) if((count * ls) < (kunits - k)) { float sum = 0; int sh_k = 2 * dimension * heads_kv * count * ls; for(int d = 0; d < dimension; d++) sum = q[shift_q + d] * kv[shift_k + d + sh_k]; sum = exp(sum / koef); if(isnan(sum)) sum = 0; temp[k] = temp[k] + sum; } count++; } while((count * ls + k) < kunits); } barrier(CLK_LOCAL_MEM_FENCE); count = min(ls, (uint)kunits);
Aqui, adicionaremos condições e calcularemos as exponenciais apenas para os elementos anteriores. Note que, ao criar os dados brutos para o modelo, eles são formados a partir das séries temporais de dados históricos de movimento de preços e indicadores. Neles, o bar atual possui o índice "0". Portanto, para mascarar os elementos na cronologia histórica, anulamos os coeficientes de dependência de todos os elementos cujo índice seja maior que o do Query analisado. Isso é observado no cálculo da soma das exponenciais e dos coeficientes de dependência (destacados no código).
//--- do { count = (count + 1) / 2; if(k < ls) temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : 0); if(k + count < ls) temp[k + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); //--- score float sum = temp[0]; float sc = 0; if(mask == 0 || q_id >= (count * ls + k)) if(sum != 0) { for(int d = 0; d < dimension; d++) sc = q[shift_q + d] * kv[shift_k + d]; sc = exp(sc / koef) / sum; if(isnan(sc)) sc = 0; } score[shift_s] = sc; barrier(CLK_LOCAL_MEM_FENCE);
No restante, o código do kernel permaneceu inalterado.
//--- out for(int d = 0; d < dimension; d++) { uint count = 0; if(k < ls) do { if((count * ls) < (kunits - k)) { float sum = kv[shift_v + d] * (count == 0 ? sc : score[shift_s + count * ls]); if(isnan(sum)) sum = 0; temp[k] = (count > 0 ? temp[k] : 0) + sum; } count++; } while((count * ls + k) < kunits); barrier(CLK_LOCAL_MEM_FENCE); //--- count = min(ls, (uint)kunits); do { count = (count + 1) / 2; if(k < ls) temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : 0); if(k + count < ls) temp[k + count] = 0; barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); //--- out[shift_q + d] = temp[0]; } }
É importante notar que, com essa implementação, simplesmente anulamos os coeficientes de dependência dos elementos subsequentes. Isso nos permitiu implementar o mascaramento com mínimas alterações no kernel de propagação para frente. Além disso, essa abordagem não exige ajustes nos kernels de propagação reversa, já que o "0" no coeficiente de dependência simplesmente anula o gradiente de erro nesses elementos da sequência.
Devo dizer que, com isso, concluímos o trabalho no lado do programa OpenCL para essa implementação e avançamos para o trabalho sobre nossa classe no programa principal.
Aqui, primeiramente, organizamos a chamada do kernel ajustado no método CNeuronSTNNEncoder::AttentionOut. O algoritmo de enfileiramento do kernel para execução permanece o mesmo, e acredito que seria redundante repeti-lo em cada artigo. Você pode consultar o código nos anexos. Quero apenas destacar a definição do parâmetro def_k_mh2ao_mask como "1" para realizar o mascaramento dos dados.
Na próxima etapa, implementamos o método de propagação para frente de nossa nova classe. Aqui, somos obrigados a redefinir o método para mover o bloco FeedForward antes do Self-Attention. É importante notar também que, ao contrário do Transformer clássico, o bloco FeedForward carece de conexões residuais e normalização de dados.
Antes de iniciar a implementação do algoritmo, é importante lembrar que, para evitar a cópia excessiva de dados no método de inicialização da classe pai, substituímos os ponteiros dos buffers de resultados de nossa camada e dos gradientes de erro pelos buffers equivalentes da última camada FeedForward. Aproveitamos a equivalência entre os tamanhos dos buffers de resultados do bloco de atenção e do FeedForward. Dessa forma, basta alterar a numeração ao acessar os buffers de dados correspondentes.
Agora, vejamos nossa implementação. Como anteriormente, recebemos um ponteiro para o objeto da camada anterior nos parâmetros do método, que nos fornece os dados brutos.
bool CNeuronSTNNEncoder::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(NeuronOCL) == POINTER_INVALID) return false;
Logo no início do método, verificamos a validade do ponteiro recebido. Em seguida, partimos diretamente para a construção do algoritmo de propagação para frente. Neste ponto, é importante destacar mais uma diferença em nossa implementação. Os autores do método STNN não especificam nem o número de camadas do Codificador nem a quantidade de cabeças de atenção. Com base na visualização e na descrição do método apresentadas anteriormente, é possível supor que haja apenas uma cabeça de atenção em uma camada do Codificador. Em nossa implementação, manteremos a abordagem clássica, com atenção multicabeças em uma arquitetura multicamadas. Assim, organizamos um laço para iterar sobre as camadas aninhadas do Codificador.
No corpo do laço, como mencionado anteriormente, os dados brutos passam primeiro pelo bloco FeedForward, onde são suavizados e filtrados.
CBufferFloat *kv = NULL; for(uint i = 0; (i < iLayers && !IsStopped()); i++) { //--- Feed Forward CBufferFloat *inputs = (i == 0 ? NeuronOCL.getOutput() : FF_Tensors.At(6 * i - 4)); CBufferFloat *temp = FF_Tensors.At(i * 6 + 1); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 1), inputs, temp, iWindow, 4 * iWindow, LReLU)) return false; inputs = FF_Tensors.At(i * 6); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 2), temp, inputs, 4 * iWindow, iWindow, None)) return false;
Depois, definimos as matrizes das entidades Query, Key e Value.
//--- Calculate Queries, Keys, Values CBufferFloat *q = QKV_Tensors.At(i * 2); if(IsStopped() || !ConvolutionForward(QKV_Weights.At(i * (optimization == SGD ? 2 : 3)), inputs, q, iWindow, iWindowKey * iHeads, None)) return false; if((i % iLayersToOneKV) == 0) { uint i_kv = i / iLayersToOneKV; kv = KV_Tensors.At(i_kv * 2); if(IsStopped() || !ConvolutionForward(KV_Weights.At(i_kv * (optimization == SGD ? 2 : 3)), inputs, kv, iWindow, 2 * iWindowKey * iHeadsKV, None)) return false; }
Note que, neste caso, utilizamos os métodos MLKV herdados da classe pai, o que permite o uso de um único buffer Key-Value para múltiplas cabeças de atenção e camadas de Self-Attention.
Com base nas entidades obtidas, determinamos os coeficientes de dependência, considerando o mascaramento dos dados.
//--- Score calculation and Multi-heads attention calculation temp = S_Tensors.At(i * 2); CBufferFloat *out = AO_Tensors.At(i * 2); if(IsStopped() || !AttentionOut(q, kv, temp, out)) return false;
Calculamos então o resultado da camada de atenção, levando em conta as conexões residuais e a normalização dos dados.
//--- Attention out calculation temp = FF_Tensors.At(i * 6 + 2); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9)), out, temp, iWindowKey * iHeads, iWindow, None)) return false; //--- Sum and normilize attention if(IsStopped() || !SumAndNormilize(temp, inputs, temp, iWindow, true)) return false; } //--- return true; }
Em seguida, passamos para a próxima camada aninhada. Quando todas as camadas forem processadas, o método será concluído.
De forma semelhante, mas em ordem inversa, construímos o algoritmo do método de distribuição do gradiente de erro CNeuronSTNNEncoder::calcInputGradients. Nos parâmetros, o método também recebe um ponteiro para o objeto da camada anterior, mas desta vez, será necessário transmitir a ele o gradiente de erro, correspondente à influência dos dados brutos sobre o resultado final do modelo.
bool CNeuronSTNNEncoder::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(CheckPointer(prevLayer) == POINTER_INVALID) return false; //--- CBufferFloat *out_grad = Gradient; CBufferFloat *kv_g = KV_Tensors.At(KV_Tensors.Total() - 1);
No corpo do método, como antes, verificamos a validade do ponteiro recebido e declaramos variáveis locais para armazenar temporariamente os ponteiros dos buffers de dados de trabalho.
Depois, declaramos um laço para percorrer as camadas aninhadas do Codificador em ordem inversa.
for(int i = int(iLayers - 1); (i >= 0 && !IsStopped()); i--) { if(i == int(iLayers - 1) || (i + 1) % iLayersToOneKV == 0) kv_g = KV_Tensors.At((i / iLayersToOneKV) * 2 + 1); //--- Split gradient to multi-heads if(IsStopped() || !ConvolutionInputGradients(FF_Weights.At(i * (optimization == SGD ? 6 : 9)), out_grad, AO_Tensors.At(i * 2), AO_Tensors.At(i * 2 + 1), iWindowKey * iHeads, iWindow, None)) return false;
No corpo do laço, primeiro distribuímos o gradiente de erro recebido da camada subsequente entre as cabeças de atenção. Em seguida, determinamos os erros nos níveis de entidades Query, Key e Value.
//--- Passing gradient to query, key and value if(i == int(iLayers - 1) || (i + 1) % iLayersToOneKV == 0) { if(IsStopped() || !AttentionInsideGradients(QKV_Tensors.At(i * 2), QKV_Tensors.At(i * 2 + 1), KV_Tensors.At((i / iLayersToOneKV) * 2), kv_g, S_Tensors.At(i * 2), AO_Tensors.At(i * 2 + 1))) return false; } else { if(IsStopped() || !AttentionInsideGradients(QKV_Tensors.At(i * 2), QKV_Tensors.At(i * 2 + 1), KV_Tensors.At((i / iLayersToOneKV) * 2), GetPointer(Temp), S_Tensors.At(i * 2), AO_Tensors.At(i * 2 + 1))) return false; if(IsStopped() || !SumAndNormilize(kv_g, GetPointer(Temp), kv_g, iWindowKey, false, 0, 0, 0, 1)) return false; }
Note a ramificação do algoritmo, relacionada às diferentes abordagens de distribuição do gradiente de erro até o tensor Key-Value, dependendo da camada atual.
Em seguida, transmitimos o gradiente de erro da entidade Query para o bloco FeedForward, considerando as conexões residuais.
CBufferFloat *inp = FF_Tensors.At(i * 6); CBufferFloat *temp = FF_Tensors.At(i * 6 + 3); if(IsStopped() || !ConvolutionInputGradients(QKV_Weights.At(i * (optimization == SGD ? 2 : 3)), QKV_Tensors.At(i * 2 + 1), inp, temp, iWindow, iWindowKey * iHeads, None)) return false; //--- Sum and normilize gradients if(IsStopped() || !SumAndNormilize(out_grad, temp, temp, iWindow, false, 0, 0, 0, 1)) return false;
Quando necessário, adicionamos os erros nas entidades Key e Value.
if((i % iLayersToOneKV) == 0) { if(IsStopped() || !ConvolutionInputGradients(KV_Weights.At(i / iLayersToOneKV * (optimization == SGD ? 2 : 3)), kv_g, inp, GetPointer(Temp), iWindow, 2 * iWindowKey * iHeadsKV, None)) return false; if(IsStopped() || !SumAndNormilize(GetPointer(Temp), temp, temp, iWindow, false, 0, 0, 0, 1)) return false; }
E passamos o gradiente de erro pelo bloco FeedForward.
//--- Passing gradient through feed forward layers if(IsStopped() || !ConvolutionInputGradients(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 2), out_grad, FF_Tensors.At(i * 6 + 1), FF_Tensors.At(i * 6 + 4), 4 * iWindow, iWindow, None)) return false; inp = (i > 0 ? FF_Tensors.At(i * 6 - 4) : prevLayer.getOutput()); temp = (i > 0 ? FF_Tensors.At(i * 6 - 1) : prevLayer.getGradient()); if(IsStopped() || !ConvolutionInputGradients(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 1), FF_Tensors.At(i * 6 + 4), inp, temp, iWindow, 4 * iWindow, LReLU)) return false; out_grad = temp; } //--- return true; }
As iterações do laço são repetidas até que todas as camadas aninhadas sejam processadas, concluindo com a transmissão do gradiente de erro para a camada anterior.
Após a distribuição do gradiente de erro, resta otimizar os parâmetros do modelo para minimizar o erro total de previsão. Essas operações são implementadas no método CNeuronSTNNEncoder::updateInputWeights. Seu algoritmo é idêntico ao método correspondente da classe pai, diferindo apenas na especificação dos buffers de dados. Por isso, não entraremos em detalhes sobre ele neste texto. Sugiro consultar esse método no anexo, onde também é possível encontrar o código completo da classe Codificador e todos os seus métodos.
2.2 Decodificador STNN
Após a implementação do Codificador, avançamos para a segunda parte do trabalho, que consiste em implementar o algoritmo do Decodificador do método STNN. Aqui, seguiremos os mesmos princípios utilizados na construção do Codificador. Em particular, nesta implementação, buscaremos aproveitar ao máximo os recursos anteriormente desenvolvidos.
Ao iniciar a implementação dos algoritmos do Decodificador, é importante observar que, diferentemente do Codificador, a nova classe será herdada de objetos de atenção cruzada. Isso se deve ao fato de que, nesta camada, precisaremos combinar informações espaciais e temporais. A estrutura completa da nova classe é apresentada a seguir.
class CNeuronSTNNDecoder : public CNeuronMLCrossAttentionMLKV { protected: CNeuronSTNNEncoder cEncoder; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *Context) override; virtual bool AttentionOut(CBufferFloat *q, CBufferFloat *kv, CBufferFloat *scores, CBufferFloat *out) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = None) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *Context) override; public: CNeuronSTNNDecoder(void) {}; ~CNeuronSTNNDecoder(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint window_kv, uint heads_kv, uint units_count, uint units_count_kv, uint layers, uint layers_to_one_kv, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronSTNNDecoder; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
Note que, nesta classe, declaramos um objeto aninhado do Codificador anteriormente criado. Contudo, é necessário destacar que, neste caso, esse objeto possui uma funcionalidade um pouco diferente.
Voltando à descrição teórica do método apresentada na primeira parte deste artigo, podemos identificar semelhanças entre os blocos de detecção de dependências espaciais e temporais. A diferença está nos dados brutos utilizados. No bloco de dependências espaciais, muitos parâmetros são analisados em um curto intervalo de tempo. No bloco de dependências temporais, a variável-alvo é analisada em um intervalo histórico específico. No entanto, os algoritmos são bastante semelhantes. Assim, nesta implementação, utilizamos o Codificador aninhado para detectar dependências temporais da variável-alvo.
Retomando a descrição dos algoritmos, a declaração de um objeto aninhado adicional, mesmo que estático, exige que redefinamos o método de inicialização da classe, Init. Apesar disso, nosso esforço em aproveitar ao máximo os recursos existentes é recompensado. O novo método de inicialização é extremamente simples.
bool CNeuronSTNNDecoder::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint window_kv, uint heads_kv, uint units_count, uint units_count_kv, uint layers, uint layers_to_one_kv, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!cEncoder.Init(0, 0, open_cl, window, window_key, heads, heads_kv, units_count, layers, layers_to_one_kv, optimization_type, batch)) return false; if(!CNeuronMLCrossAttentionMLKV::Init(numOutputs, myIndex, open_cl, window, window_key, heads, window_kv, heads_kv, units_count, units_count_kv, layers, layers_to_one_kv, optimization_type, batch)) return false; //--- return true; }
Nele, chamamos apenas os métodos homônimos do Codificador aninhado e da classe pai, utilizando os mesmos valores para os parâmetros de mesmo nome. Em seguida, verificamos o resultado das operações e retornamos o valor lógico obtido ao programa que o chamou.
Uma abordagem semelhante é observada nos métodos de propagação para frente e para trás. No método de propagação para frente, por exemplo, primeiro chamamos o método homônimo do Codificador para identificar as dependências temporais entre os valores da variável-alvo. Em seguida, comparamos as dependências temporais obtidas com as espaciais, que são fornecidas pelo Codificador do modelo STNN nos parâmetros de contexto deste método. Essa operação é realizada por meio da propagação para frente herdada da classe pai.
bool CNeuronSTNNDecoder::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *Context) { if(!cEncoder.FeedForward(NeuronOCL, Context)) return false; if(!CNeuronMLCrossAttentionMLKV::feedForward(cEncoder.AsObject(), Context)) return false; //--- return true; }
Aqui, é importante destacar alguns pontos nos quais nos desviamos do algoritmo proposto pelos autores do método STNN. Mantivemos, em geral, a concepção proposta, mas fizemos uma grande adaptação na implementação dos enfoques sugeridos.
Mantivemos os seguintes elementos:
- Identificação das dependências temporais;
- Comparação das dependências temporais com as espaciais para prever os valores da variável-alvo.
No entanto, como no caso do Codificador, utilizamos um bloco FeedForward composto por duas camadas densamente conectadas, em vez de uma única camada sugerida pelos autores do método. Isso aplica-se tanto à filtragem de dados antes da identificação das dependências temporais quanto à previsão dos valores da variável-alvo na saída do Decodificador.
Além disso, para implementar a atenção cruzada, utilizamos a propagação para frente da classe pai, que implementa o algoritmo clássico de atenção cruzada em múltiplas camadas, com conexões residuais nos blocos de atenção e FeedForward. Essa abordagem difere do algoritmo de atenção cruzada proposto pelos autores do método STNN.
Ainda assim, considero que essa implementação é válida, especialmente considerando o experimento de aproveitar ao máximo os recursos previamente desenvolvidos.
Outro ponto importante é que, apesar de utilizarmos uma estrutura em múltiplas camadas nos blocos de identificação de dependências temporais e na atenção cruzada, a arquitetura geral do Decodificador assume um caráter de camada única. Em outras palavras, primeiro identificamos as dependências temporais no Codificador aninhado em múltiplas camadas. Depois, o bloco de atenção cruzada em múltiplas camadas compara as dependências temporais e espaciais antes de prever os valores da variável-alvo.
Os métodos de propagação reversa seguem uma estrutura semelhante, mas não os abordaremos neste momento. Sugiro que você os consulte no anexo.
Com isso, concluímos a análise da arquitetura e dos algoritmos dos novos objetos. O código completo está disponível nos anexos deste artigo.
2.3 Arquitetura dos modelos
Após analisarmos os algoritmos de implementação dos enfoques propostos pelo método STNN, passamos à sua aplicação prática em modelos treináveis. Nesse contexto, é importante notar que o Codificador e o Decodificador no algoritmo proposto operam com diferentes dados brutos. Por isso, os destacamos em modelos separados, cuja arquitetura é apresentada no método CreateStateDescriptions.
Nos parâmetros do referido método, transmitiremos dois ponteiros de arrays dinâmicos para registrar a arquitetura dos modelos correspondentes.
bool CreateStateDescriptions(CArrayObj *&encoder, CArrayObj *&decoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; } //--- if(!decoder) { decoder = new CArrayObj(); if(!decoder) return false; }
No corpo do método, verificamos os ponteiros recebidos e, se necessário, criamos novas instâncias dos arrays.
Alimentamos o Codificador com o conjunto de dados não processados já conhecido.
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
O processamento inicial desses dados ocorre na camada de normalização em lote.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Depois disso, adicionamos a camada do Codificador STNN.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSTNNEncoder; descr.count = HistoryBars; descr.window = BarDescr; descr.window_out = 32; descr.layers = 4; descr.step = 2; { int ar[] = {8, 4}; if(ArrayCopy(descr.heads, ar) < (int)ar.Size()) return false; } descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Aqui, utilizamos quatro camadas aninhadas no Codificador, cada uma empregando oito cabeças de atenção para as entidades Query e quatro para o tensor Key-Value. Além disso, um único tensor Key-Value é compartilhado entre duas camadas aninhadas do Codificador.
Com isso, concluímos a arquitetura do modelo do Codificador. Os resultados de sua execução serão utilizados no Decodificador.
Na entrada do Decodificador, fornecemos os valores históricos da variável-alvo, cuja profundidade corresponde ao nosso horizonte de planejamento.
//--- Decoder decoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = (NForecast * ForecastBarDescr); descr.activation = None; descr.optimization = ADAM; if(!decoder.Add(descr)) { delete descr; return false; }
Também usamos aqui dados não processados, que são encaminhados para uma camada de normalização em lote.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!decoder.Add(descr)) { delete descr; return false; }
Em seguida, adicionamos a camada do Decodificador STNN, cuja arquitetura também conta com quatro camadas aninhadas de atenção temporal e atenção cruzada.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSTNNDecoder; { int ar[] = {NForecast, HistoryBars}; if(ArrayCopy(descr.units, ar) < (int)ar.Size()) return false; } { int ar[] = {ForecastBarDescr, BarDescr}; if(ArrayCopy(descr.windows, ar) < (int)ar.Size()) return false; } { int ar[] = {8, 4}; if(ArrayCopy(descr.heads, ar) < (int)ar.Size()) return false; } descr.window_out = 32; descr.layers = 4; descr.step = 2; descr.activation = None; descr.optimization = ADAM; if(!decoder.Add(descr)) { delete descr; return false; }
Na saída do Decodificador, esperamos obter os valores previstos da variável-alvo. A eles adicionamos indicadores estatísticos extraídos na camada de normalização em lote.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = ForecastBarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!decoder.Add(descr)) { delete descr; return false; }
Por fim, ajustamos as características de frequência da série temporal prevista.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = ForecastBarDescr; descr.count = NForecast; descr.step = int(true); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!decoder.Add(descr)) { delete descr; return false; } //--- return true; }
A arquitetura dos modelos Ator e Crítico foi transferida sem alterações de artigos anteriores e está apresentada no método CreateDescriptions, que você pode encontrar nos anexos deste artigo (arquivo ...\Experts\STNN\Trajectory.mqh).
2.4 Programas de treinamento de modelos
A separação do Codificador do estado do ambiente em dois modelos exigiu alterações nos programas de treinamento dos modelos. Vale destacar que, além da divisão do algoritmo em dois modelos, houve mudanças no bloco de preparação dos dados brutos e dos valores-alvo. As correções realizadas são ilustradas no exemplo do EA de treinamento do Codificador do estado do ambiente, localizado em ...\Experts\STNN\StudyEncoder.mq5.
Lembro que, no escopo deste EA, treinamos o modelo para prever o movimento futuro do preço em um horizonte de planejamento suficiente para tomar decisões de negociação em momentos específicos.
Neste artigo, não entraremos em detalhes sobre todos os procedimentos do programa, mas analisaremos apenas o método de treinamento das modelos, Train. Inicialmente, determinamos as probabilidades de seleção de trajetórias a partir do buffer de reprodução de experiência, considerando a eficácia real dessas trajetórias em dados históricos reais.
void Train(void) { //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9); //--- vector<float> result, target, state; matrix<float> mstate = matrix<float>::Zeros(1, NForecast * ForecastBarDescr); bool Stop = false;
Declaramos, então, o mínimo necessário de variáveis locais e realizamos o laço principal para o treinamento direto das modelos. O número de iterações do laço é definido pelo usuário nos parâmetros externos do EA.
uint ticks = GetTickCount(); //--- for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter ++) { int tr = SampleTrajectory(probability); int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - NForecast)); if(i <= 0) { iter--; continue; } state.Assign(Buffer[tr].States[i].state); if(MathAbs(state).Sum() == 0) { iter--; continue; }
No corpo do laço, amostramos uma trajetória e o estado correspondente para realizar as iterações de otimização do modelo. Primeiro, identificamos as dependências espaciais entre as variáveis analisadas por meio da chamada do método de propagação para frente do Codificador.
bStateE.AssignArray(state); //--- State Encoder if(!Encoder.feedForward((CBufferFloat*)GetPointer(bStateE), 1, false, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Em seguida, preparamos os dados brutos para o Decodificador. Em termos gerais, assumimos que o horizonte de planejamento é menor que a profundidade do histórico analisado. Assim, transferimos inicialmente os dados históricos do estado analisado para uma matriz. Ajustamos o tamanho dessa matriz de modo que cada linha represente os dados de um bar histórico. Depois, cortamos a matriz, deixando o número de linhas correspondente ao horizonte de planejamento e o número de colunas correspondente às variáveis-alvo.
mstate.Assign(state); mstate.Reshape(HistoryBars, BarDescr); mstate.Resize(NForecast, ForecastBarDescr); bStateD.AssignArray(mstate);
É importante destacar que, ao preparar o conjunto de treinamento para cada bar, gravamos inicialmente os parâmetros do movimento de preço, que serão previstos. Por isso, selecionamos as primeiras colunas da matriz.
Os valores da matriz resultante são transferidos para o buffer de dados, e realizamos a propagação para frente do Decodificador.
if(!Decoder.feedForward((CBufferFloat*)GetPointer(bStateD), 1, false, GetPointer(Encoder))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Após a propagação para frente, realizamos a otimização dos parâmetros do modelo. Para isso, é necessário preparar os valores-alvo das variáveis previstas. Essa operação é realizada de maneira semelhante à preparação dos dados brutos do Decodificador, mas utilizando os valores históricos subsequentes.
//--- Collect target data mstate.Assign(Buffer[tr].States[i + NForecast].state); mstate.Reshape(HistoryBars, BarDescr); mstate.Resize(NForecast, ForecastBarDescr); if(!Result.AssignArray(mstate)) continue;
Em seguida, realizamos a propagação reversa do Decodificador. Nesse estágio, otimizamos os parâmetros do Decodificador e transmitimos o gradiente de erro ao Codificador.
if(!Decoder.backProp(Result, GetPointer(Encoder))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Depois, otimizamos os parâmetros do Codificador.
if(!Encoder.backPropGradient((CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Finalmente, informamos o usuário sobre o progresso do processo de treinamento e passamos para a próxima iteração do laço de treinamento.
if(GetTickCount() - ticks > 500) { double percent = double(iter) * 100.0 / (Iterations); string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Decoder", percent, Decoder.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } }
Após a conclusão bem-sucedida de todas as iterações, registramos no log os resultados do treinamento das modelos e iniciamos o processo de encerramento do programa.
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Decoder", Decoder.getRecentAverageError()); ExpertRemove(); //--- }
Com isso, finalizamos a análise dos algoritmos de treinamento dos modelos. O código completo de todos os programas utilizados na preparação deste artigo pode ser encontrado no anexo.
3. Testes
Neste artigo, exploramos um novo método de previsão de séries temporais baseado em informações espaço-temporais utilizando a STNN. Implementamos nossa visão dos enfoques propostos com MQL5. Agora é o momento de avaliar os resultados do nosso trabalho.
Como de costume, utilizamos dados históricos do instrumento EURUSD no intervalo de tempo H1 ao longo de todo o ano de 2023 para treinar nossos modelos. Posteriormente, testamos os modelos treinados no testador de estratégias do MetaTrader 5 com dados de janeiro de 2024. É fácil perceber que o período de teste segue diretamente o período de treinamento, maximizando a proximidade com as condições reais de utilização dos modelos.
Para o treinamento do modelo de previsão do movimento de preço subsequente, usamos o conjunto de dados coletado durante a preparação dos artigos anteriores desta série. Como você sabe, o treinamento desse modelo é baseado apenas na análise de dados históricos de movimento de preços e indicadores. Como as ações do Agente não influenciam os dados analisados, é possível treinar o modelo Codificador do estado do ambiente sem a necessidade de atualizações periódicas do conjunto de treinamento.
Continuamos o treinamento da modelo até a estabilização do erro de previsão. Infelizmente, nesta etapa, enfrentamos uma decepção. Nosso modelo não conseguiu fornecer a previsão desejada para o movimento de preço subsequente, indicando apenas a direção geral da tendência.

Embora os valores digitalizados apresentem flutuações, elas são tão insignificantes que não são visíveis no gráfico. Isso levanta a questão: seriam essas flutuações suficientes para que nosso Ator construa uma estratégia lucrativa?
O treinamento das modelos do Ator e do Crítico foi realizado de maneira iterativa, com atualizações periódicas do conjunto de treinamento. Como você sabe, essas atualizações são necessárias para uma avaliação mais precisa das ações do Ator à medida que sua política evolui durante o treinamento.
Infelizmente, não conseguimos treinar uma política do Ator capaz de gerar lucros consistentes no conjunto de teste.
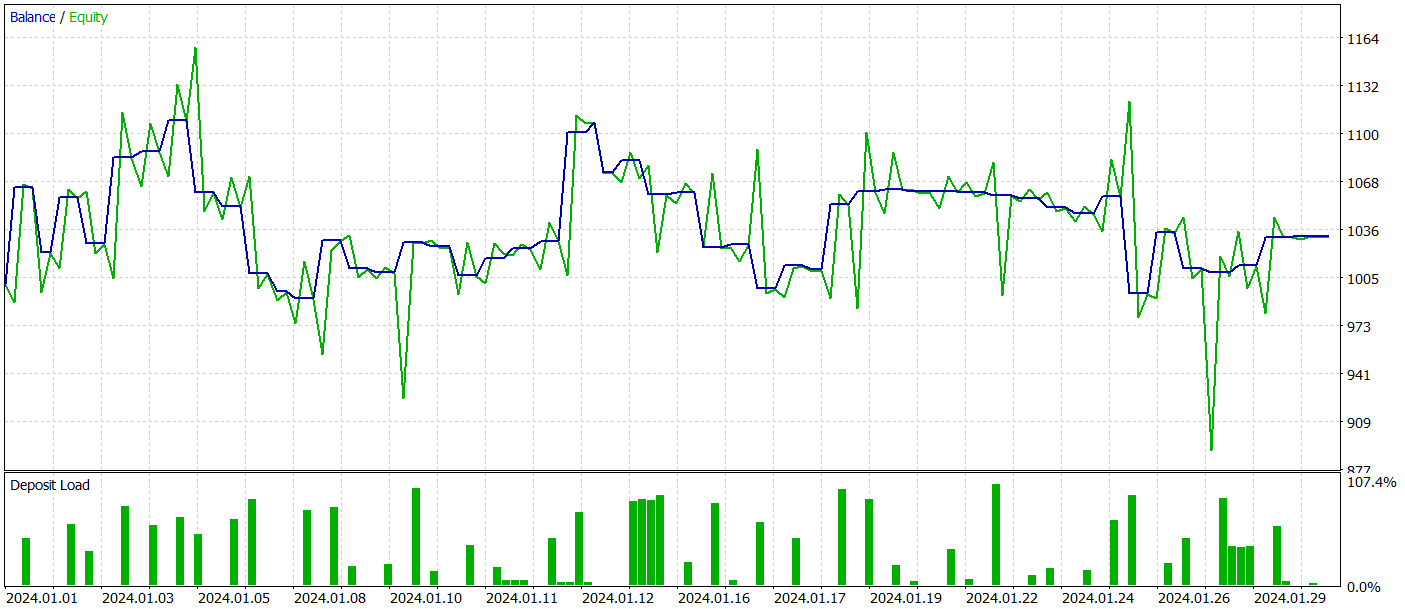

Reconhecemos, é claro, que foram feitas adaptações significativas em relação à implementação original do método durante sua implementação. Essas mudanças podem ter influenciado os resultados obtidos.
Considerações finais
Neste artigo, exploramos mais uma abordagem para a previsão de séries temporais baseada na Rede Neural Transformador Espaço-Temporal (STNN). Esse modelo combina as vantagens da equação de transformação de informações espaço-temporais (STI) com a estrutura Transformer, permitindo previsões eficientes de curto prazo em múltiplas etapas para séries temporais.
A STNN utiliza a equação STI, que transforma informações espaciais de variáveis multidimensionais em informações temporais da variável-alvo. Isso equivale a um aumento no tamanho da amostra e ajuda a resolver o problema da insuficiência de dados de curto prazo.
Para melhorar a precisão das previsões numéricas, foi proposto um mecanismo de atenção contínua na STNN, que permite que o modelo considere melhor os aspectos importantes dos dados.
Na parte prática do artigo, implementamos nossa visão dos enfoques propostos utilizando MQL5. No entanto, em nossa implementação, realizamos adaptações significativas em relação ao algoritmo original, o que pode ter influenciado os resultados dos experimentos.
Referências
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA para coleta de exemplos |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA para coleta de exemplos pelo método Real-ORL |
| 3 | Study.mq5 | Expert Advisor | EA para treinamento de Modelos |
| 4 | StudyEncoder.mq5 | Expert Advisor | EA para treinamento do Codificador |
| 5 | Test.mq5 | Expert Advisor | EA para teste do modelo |
| 6 | Trajectory.mqh | Biblioteca de classe | Estrutura de descrição do estado do sistema |
| 7 | NeuroNet.mqh | Biblioteca de classe | Biblioteca de classes para criação de redes neurais |
| 8 | NeuroNet.cl | Biblioteca | Biblioteca de código do programa OpenCL |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/15290
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Do básico ao intermediário: Template e Typename (II)
Do básico ao intermediário: Template e Typename (II)
 Simulação de mercado (Parte 03): Uma questão de performance
Simulação de mercado (Parte 03): Uma questão de performance
 Desenvolvimento de um EA baseado na estratégia de rompimento do intervalo de consolidação em MQL5
Desenvolvimento de um EA baseado na estratégia de rompimento do intervalo de consolidação em MQL5
 MetaTrader 5 no macOS
MetaTrader 5 no macOS
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso