Redes neurais em trading: Extração eficiente de características para classificação precisa (Construção de objetos)

Introdução

No artigo anterior, conhecemos os aspectos teóricos do framework Mantis, um modelo fundamental para classificação de séries temporais, livre do peso excessivo dos algoritmos de regressão e, ao mesmo tempo, sem perder precisão. Ele transforma os dados brutos da sequência analisada em sinais claros, com níveis de confiança compreensíveis, oferecendo uma nova qualidade de análise.

Imagine um modelo clássico de previsão: ele aprende a minimizar o erro de predição, mas frequentemente fracassa diante de picos repentinos de volatilidade. Esses algoritmos derivam junto com o mercado. São difíceis de adaptar. Estão sujeitos ao sobreajuste e não fornecem avaliações transparentes de confiabilidade. Precisamos de mais do que apenas a previsão de um valor futuro. Precisamos do reconhecimento do regime de mercado em tempo real, quando o preço se move segundo um cenário típico ou anômalo. É exatamente aqui que Mantis tem sua origem como um modelo treinado não tanto em regressão, mas no entendimento de padrões.

Na base do Mantis está a ideia de tokenização da série temporal, emprestada dos transformadores visuais. Em vez de escanear dezenas de milhares de ticks ou segundos, a série é dividida em um número estritamente definido de patches. Graças a isso, séries temporais de diferentes tamanhos são processadas com um número idêntico de passos, o que elimina a necessidade de redesenhar a arquitetura para diferentes escalas. Em seguida, ocorre a magia da atenção híbrida: em uma janela de visão, o modelo investiga microvariações por meio de convoluções e pooling, e em outra captura tendências de longo prazo, utilizando atenção global. A combinação desses dois pontos de vista permite que o modelo simultaneamente veja as menores oscilações e perceba o vetor geral de movimento.

O principal ingrediente secreto do modelo é o pré-treinamento contrastivo. Imagine duas versões levemente distorcidas de um mesmo fragmento da história de preços. O Mantis aprende a aproximar suas incorporações no espaço, como se comprimisse várias faixas de luz em um único feixe, e ao mesmo tempo a afastar segmentos completamente diferentes, como um elétron e um pósitron. Esse contraste fornece ao modelo uma percepção estável do padrão, o que é especialmente valioso diante de mudanças de amplitude, pequenos deslocamentos no tempo ou ruído não padrão.

O processo é finalizado com o escalonamento de temperatura, a calibração final das conclusões. O trader não se interessa apenas pelo fato de “reversão/não reversão”, mas pelo grau de confiança. O Mantis é capaz de fornecer não valores abstratos, mas probabilidades a posteriori plausíveis. A prática mostra: se o modelo afirma “80% de reversão”, então, na realidade, aproximadamente 80 de cada 100 desses sinais se mostram corretos.

O verdadeiro valor do Mantis se revela quando informações multicanais são alimentadas na entrada. Indicadores como RSI em sincronia, volumes, médias móveis e correlações entre pares de moedas formam um quadro complexo. A concatenação direta desses sinais leva a uma explosão no número de parâmetros, enquanto o processamento separado perde as relações cruzadas. A solução do Mantis são adaptadores leves, que comprimem as interações intercanal, preservando apenas o essencial, isto é, a força da relação entre os indicadores. O modelo economiza memória, e o trader economiza tempo de configuração.

Para compreender mais profundamente a arquitetura do Mantis, vamos percorrer suas etapas. A primeira fase é a convolução primária: a série temporal com d canais passa por uma camada com 256 saídas, formando uma representação densa. Em seguida, o tensor é dividido em partes iguais e o mean-pooling por canal transforma esses dados em 32 tokens, cada um carregando informação local.

Em paralelo, é construído um fluxo diferencial: as diferenças de primeira ordem dos dados originais aumentam a sensibilidade à dinâmica de curto prazo. Os dados obtidos percorrem o mesmo caminho de patching.

O terceiro e o quarto fluxo, estatísticos, coletam a média e o desvio padrão dos dados originais dentro das mesmas 32 janelas, transmitindo o pano de fundo geral de volatilidade e nível.

Esses quatro fluxos passam por projetores lineares individuais para alinhamento de dimensionalidade e, em seguida, são unificados e projetados em tokens globais de tamanho predefinido.

À sequência de tokens que codificam a sequência analisada é adicionado um token de classe e a codificação posicional senoidal, para que o modelo não perca a informação de ordem. Depois disso, os dados são introduzidos no transformador: 6 camadas, atenção multihead com 8 cabeças, normalização, FFN de dois níveis com GELU e Dropout de 10% na fase de treinamento.

O modelo foi treinado em 2 etapas. Na primeira, contrastiva, em um corpus unificado de dez datasets públicos, mais de 7 milhões de séries temporais, 100 épocas, batch 2048 em 4 NVIDIA Tesla V100. Isso lembra uma marcha forçada de treinamento intensivo. Na segunda etapa, é adicionada a cabeça de classificação e aplicada a calibração de temperatura das saídas. Essa abordagem bifásica permite alcançar uma combinação rara para redes neurais, alta precisão e interpretabilidade confiável.

Por fim, sobre a flexibilidade. Para lidar com tarefas de diferentes escalas e “calçar” os modelos com diferentes “botas” conforme o orçamento e a estrutura dos dados, os autores do framework Mantis propõem o uso de cinco tipos de adaptadores:

• PCA e Truncated SVD — métodos clássicos de redução linear de dimensionalidade, testados pelo tempo;
• Random Projection — uma forma rápida e simples, mas poderosa, de reduzir o vetor de características;
• Variance-Based Selector — seleciona apenas os canais mais expressivos com base na variância;
• Differentiable Linear Combiner (LComb) — um adaptador treinável que se ajusta à tarefa específica junto com o modelo principal.

Esses adaptadores permitem encontrar um compromisso entre velocidade e precisão, economizar recursos computacionais e, ao mesmo tempo, não perder ligações intercanal criticamente importantes.

No fim das contas, o Mantis representa não apenas um modelo, mas todo um complexo de engenharia para análise profunda de séries temporais. Sua força não está em palavras grandiosas, mas na execução detalhada: atenção cuidadosa a cada patch, conexão criteriosa entre contextos local e global, calibração rigorosa e compressão cuidadosa dos canais. Essa união entre análise e inteligência de máquina permite não adivinhar, mas agir com confiança, apoiando-se em estatísticas e princípios algorítmicos comprovados. Em uma era em que velocidade e precisão decidem tudo, o Mantis se torna o instrumento que ajuda a manter o equilíbrio no fio tênue do mercado.

A visualização autoral do framework Mantis é apresentada abaixo.

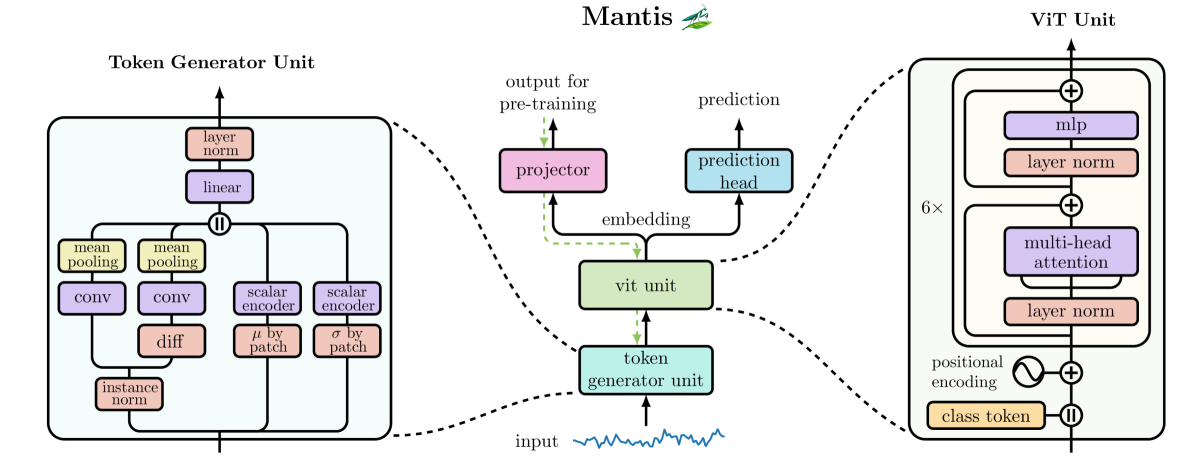
Na parte prática do artigo anterior, implementamos o componente básico de processamento de séries temporais, o módulo CNeuronConcatDiff. Esse objeto reuniu em si o algoritmo de cálculo da primeira diferença e o mecanismo de concatenação de tensores de diferentes fluxos de informação. A partir dele teve início a implementação prática do núcleo do framework Mantis.

Hoje continuaremos a construção dessa arquitetura, avançando para os próximos blocos fundamentais do modelo de redes neurais. Na etapa de planejamento, no artigo anterior, concordamos sobre a necessidade de introduzir a codificação temporal no fluxo de dados. Essa decisão foi motivada pelo desejo de melhorar a interpretabilidade e levar em conta a estrutura posicional dos dados originais, sem perder desempenho. Evidentemente, não vamos reinventar a roda, pois já dispomos de um objeto testado pelo tempo, o CMamba4CastEmbedding. Nós o criamos no âmbito do trabalho com o framework Mamba4Cast e agora ele se encaixa perfeitamente para a implementação dessa tarefa.

O próximo passo lógico é a organização do patching da série temporal. É exatamente nessa etapa que o modelo perde a dependência do comprimento da sequência original e passa a operar com um número fixo de fragmentos, independentemente da escala dos dados. Isso, sem exagero, é um dos módulos mais importantes na arquitetura do classificador, pois da sua implementação depende a estabilidade de todo o processamento subsequente. É por ele que começaremos o trabalho de hoje, passo a passo criaremos o mecanismo que dividirá o fluxo de informações originais em patches compactos e informativos.

Objeto de segmentação

Os autores do framework Mantis original abordaram a tarefa de segmentação de séries temporais por um caminho inesperado, porém elegante. Em vez do simples corte da sequência em segmentos iguais, eles propuseram transformar previamente os dados por meio de uma operação de convolução. E não apenas aplicar a convolução de forma protocolar, mas utilizá-la para converter uma série temporal unidimensional em um tensor multicanal. Essa ideia, à primeira vista, pode parecer excessiva, mas na prática oferece uma vantagem significativa: com o uso de convoluções com janelas pequenas, o modelo passa a sentir as oscilações locais do sinal e a capturar nuances importantes do comportamento do mercado, que de outra forma poderiam se perder no pano de fundo da tendência geral.

Após essa transformação, temos em mãos um tensor multicanal, no qual cada canal representa uma projeção separada da série original, isto é, uma mini-representação do sinal sob seu próprio ponto de vista. Esse tensor é então dividido de forma uniforme em um número fixo de fragmentos. Esses são os patches, os blocos de construção com os quais o modelo trabalhará a seguir. E é aqui que entra em cena a próxima etapa: a agregação de informações dentro de cada segmento.

Os autores do Mantis propuseram o uso da operação clássica de média por canal, conhecida como mean-pooling. Ela é simples, intuitiva e fornece uma representação suavizada adequada do segmento. Diferentemente do max-pooling, no qual permanece apenas o valor extremo, o mean-pooling preserva o contexto, permitindo que cada elemento da série temporal contribua para o token final. Isso é especialmente útil quando cada patch cobre um fragmento de dados suficientemente grande, pois nesses casos é necessário considerar todo o volume de informação, e não apenas picos e vales. Os tokens obtidos dessa forma formam uma representação compacta e informativa da estrutura temporal dos dados originais, adequada para posterior análise pelo transformador.

Entretanto, como mostra a prática, o mean-pooling pode ser excessivamente educado — pois ele suaviza não apenas a informação, mas também possíveis anomalias ou viradas bruscas na estrutura do sinal. Para um modelo fundamental, isso pode ser um compromisso aceitável: ele permanece simples, rápido e generalizável. Mas decidimos ir um pouco além. Em nossa implementação, substituímos o mean-pooling padrão por uma combinação de convolução por canal seguida de max-pooling.

O que isso oferece na prática? Primeiro, a convolução extrai características dentro de cada canal, garantindo uma filtragem primária e destacando mudanças locais. Em seguida, o max-pooling seleciona as manifestações mais expressivas dessas características. Essa abordagem torna o modelo mais afiado para a dinâmica da série temporal. Em vez de simplesmente fazer a média de tudo, ele fixa as características-chave e, portanto, reage de forma mais rápida e precisa a movimentos bruscos. Essa propriedade se torna criticamente importante em condições de trading de alta frequência ou ao trabalhar com ativos voláteis.

É precisamente graças a essa modificação do patching que o nosso classificador adquire a capacidade de se adaptar à forma e à estrutura de cada série temporal específica. Ele não apenas divide os dados em segmentos, mas analisa, extrai, filtra e avalia. Um patch, em um sistema desse tipo, deixa de ser apenas um fragmento do sinal e passa a ser um token completo, rico em informação, que carrega em si o contexto e a forma do sinal.

O algoritmo proposto foi implementado no âmbito da classe CNeuronMantisPatching. Trata-se de um módulo especializado, responsável pela segmentação da série temporal em patches estruturados e pela formação de uma representação de alto nível, adequada para processamento subsequente. É aqui que começa a verdadeira compreensão dos dados: de um simples fluxo unidimensional são extraídas regularidades locais, que são transformadas em descrições vetoriais densas.

A classe CNeuronMantisPatching é construída como um pipeline computacional em múltiplas etapas. Ela contém diversos objetos internos, cada um dos quais executa uma tarefa altamente especializada. A estrutura da classe é apresentada abaixo.

class CNeuronMantisPatching   :  public CNeuronTransposeOCL
  {
protected:
   CNeuronTransposeOCL     cToVarSeq;
   CNeuronConvOCL          cProjecting;
   CNeuronTransposeVRCOCL  cToVarProjSeq;
   CNeuronConvOCL          cPatchingProj;
   CNeuronProofOCL         cProof;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL)  override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL)  override;

public:
                     CNeuronMantisPatching(void) {};
                    ~CNeuronMantisPatching(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint count, uint patchs, uint variables,
                          uint embedding_size, uint patch_filters,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual int       Type(void)  override const {  return defNeuronMantisPatching; }
   //---
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
  };

Todos os objetos internos são declarados estaticamente, o que permite manter vazios o construtor e o destrutor da classe. A configuração deles é realizada no método Init, cujos parâmetros recebem um conjunto de constantes que permitem definir de forma inequívoca a arquitetura do objeto que está sendo criado.

bool CNeuronMantisPatching::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                 uint count, uint patchs, uint variables,
                                 uint embedding_size, uint patch_filters,
                                 ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronTransposeOCL::Init(numOutputs, myIndex, open_cl, variables * embedding_size,
                                                        patchs, optimization_type, batch))
      return false;

Vale ressaltar que, na entrada do objeto CNeuronMantisPatching, esperamos receber uma matriz de valores de uma série temporal multicanal, onde cada coluna é um canal separado. Além disso, cada canal representa uma sequência de medições numéricas ao longo do tempo. Em outras palavras, lidamos com uma matriz de dimensão [T * C], onde T é o número de passos temporais e C é o número de canais (variáveis).

Para organizar o processamento independente de canais individuais dentro do módulo, são utilizados objetos de transposição de dados. Isso é necessário para garantir o processamento separado ao longo das dimensões de canal e tempo, pois tal isolamento é difícil de implementar sem a movimentação explícita dos eixos. Além disso, a própria classe CNeuronMantisPatching herda de CNeuronTransposeOCL, o que possibilita executar a transposição inversa por meio da classe pai após a conclusão de todas as transformações, retornando o tensor de saída ao formato esperado.

E o primeiro passo do método de inicialização é a chamada do método homônimo da classe pai CNeuronTransposeOCL. É ele que prepara a estrutura básica e executa a inicialização preliminar dos parâmetros. Esse passo é necessário para o funcionamento correto de todos os mecanismos herdados.

Após a inicialização bem-sucedida da classe pai, inicia-se a configuração dos componentes internos. O primeiro deles que configuramos é o objeto cToVarSeq — que é uma camada de transposição de matriz responsável por fornecer acesso conveniente às sequências temporais individuais de cada canal. Sua tarefa é reorientar os dados de entrada de forma que cada canal se torne uma série temporal independente, adequada para a posterior convolução local.

   int index = 0;
   if(!cToVarSeq.Init(0, index, OpenCL, count, variables, optimization, iBatch))
      return false;

Em seguida, inicializamos o objeto de codificação local cProjecting. Trata-se de uma camada convolucional que desempenha o papel de "observador atento", percorrendo cada canal da série temporal com uma janela fixa de largura 3 e passo 1. Sua função é extrair padrões locais de curto prazo e mapeá-los para um espaço de dimensão fixa embedding_size.

   index++;
   if(!cProjecting.Init(0, index, OpenCL, 3, 1, embedding_size, count - 2, variables,
                                                               optimization, iBatch))
      return false;
   cProjecting.SetActivationFunction(SoftPlus);

É importante enfatizar que o processamento continua sendo estritamente por canal: cada canal é analisado de forma isolada, o que permite ao modelo se ajustar às características individuais dos sinais. Além disso, a cada canal corresponde um conjunto único de filtros convolucionais, o que confere ao processo uma flexibilidade e precisão adicionais.

O resultado dessa operação é um tensor de dimensão [C T' D], onde:

• C é o número de canais (características),
• T' é o comprimento do eixo temporal considerando o recorte após a convolução com janela 3,
• D é a dimensionalidade da nova representação após a codificação.

Esse tensor é uma forma localmente comprimida e já parcialmente estruturada dos dados originais, que servirá de base para a segmentação e agregação subsequentes. Assim, obtemos uma espécie de retrato condensado da dinâmica de curto prazo dentro de cada característica, algo que os métodos tradicionais de análise de séries temporais raramente conseguem capturar sem transformações pesadas e intensivas em recursos.

Em seguida, chega a etapa de segmentação. E aqui é importante compreender uma sutileza. A própria operação de segmentação, no nosso contexto, pressupõe a divisão dos dados ao longo do eixo temporal, isto é, a quebra da sequência em trechos de comprimento fixo. No entanto, no passo anterior, o resultado da convolução é apresentado na forma de um tensor em que o eixo temporal corresponde à segunda dimensão. Para facilitar o processamento subsequente e alinhar com a arquitetura das camadas seguintes, precisamos permutar os eixos.

Por isso, utilizamos um objeto de transposição de tensor tridimensional, trazendo o eixo temporal para o primeiro plano. Como resultado, obtemos um tensor com a nova estrutura [C D T'].

   index++;
   if(!cToVarProjSeq.Init(0, index, OpenCL, variables, count-2, embedding_size, optimization, iBatch))
      return false;

Essa representação dos dados é conveniente e lógica: agora podemos operar diretamente sobre a sequência no tempo, dividindo-a em fragmentos iguais, cada um dos quais será considerado um segmento semântico separado. Isso corresponde à nossa intenção inicial — passar da análise de pontos para a análise de padrões.

É exatamente nessa nova forma que o tensor segue para a próxima etapa, onde é realizada a operação principal de segmentação e agregação das informações. A tarefa central é dividir a sequência temporal em um número fixo de segmentos e extrair de cada um uma representação informativa. Contudo, como inicialmente nos é fornecido apenas o número necessário de segmentos (patchs), o primeiro passo é calcular o tamanho de um único segmento, isto é, quantos passos temporais entrarão em cada patch.

Depois disso, inicializamos a camada convolucional cPatchingProj, que será responsável pela segmentação. Ela utiliza uma janela igual ao tamanho calculado do patch e desliza ao longo do eixo temporal com o mesmo passo, o que garante a criação de segmentos não sobrepostos.

   index++;
   int patch_size = (int(count + patchs) - 3) / int(patchs);
   if(!cPatchingProj.Init(0, index, OpenCL, patch_size, patch_size, patch_filters,
                        patchs, variables * embedding_size, optimization, iBatch))
      return false;
   cPatchingProj.SetActivationFunction(SoftPlus);

É importante destacar que, diferentemente do simples mean-pooling, aqui é aplicada uma operação convolucional completa com múltiplos filtros (patch_filters). Isso permite que o modelo não apenas faça a média das informações dentro do segmento, mas extraia as características mais relevantes de cada trecho, reagindo a padrões locais característicos.

Após a passagem do tensor pela camada cPatchingProj, obtemos um tensor de quatro dimensões com tamanho [C × D × P × F], onde:

• P é o número de segmentos (patches),
• F é o número de filtros aplicados a cada patch.

Esse tensor contém representações enriquecidas de cada segmento de cada canal ao longo de todos os filtros. No entanto, o processamento posterior exige a agregação desses dados. É justamente aqui que se aplica a operação max-pooling ao longo da última dimensão — isto é, ao longo do eixo dos filtros F. Essa operação seleciona o valor mais expressivo em cada dimensão e permite eliminar filtros redundantes ou fracamente ativados. Após isso, a dimensionalidade do tensor passa a ser [C × D × P].

   index++;
   if(!cProof.Init(0, index, OpenCL, patch_filters, patch_filters, 
            patchs*variables*embedding_size, optimization, iBatch))
      return false;
//---
   return true;
  }

A transformação final dos dados é realizada por meio da classe pai, que já inicializamos anteriormente. Assim, concluímos a execução do método, retornando ao programa chamador o resultado lógico da realização das operações.

Vale notar que a arquitetura do CNeuronMantisPatching foi projetada com um alto grau de modularidade. Cada camada interna trabalha com os canais independentemente, o que torna a estrutura extremamente escalável. Independentemente do número de canais analisados, a lógica de processamento permanece a mesma, pois cada canal é tratado como um fluxo de dados autônomo.

Além disso, essa estrutura independente permite paralelizar os cálculos de maneira eficiente. Como todas as camadas neurais utilizadas são implementadas em OpenCL, elas usam automaticamente a GPU disponível ou qualquer outro dispositivo de computação compatível. Isso possibilita executar simultaneamente centenas de fluxos paralelos, processando canais individuais sem perda perceptível de tempo.

A lógica principal de funcionamento da classe CNeuronMantisPatching e a interação de seus componentes internos foram expostas em detalhe quando analisamos a estrutura do método de inicialização. É exatamente nele que, de forma sequencial, são montadas todas as etapas-chave de processamento de uma série temporal multicanal: da transposição primária até a segmentação e a agregação de informações.

Para não sobrecarregar o artigo com detalhes excessivos, omitimos deliberadamente a descrição dos métodos de propagação para frente (feedForward) e de propagação reversa (calcInputGradients, updateInputWeights). Neles, é implementada uma chamada estritamente sequencial dos métodos homônimos dos objetos internos, de acordo com a arquitetura do pipeline construído.

O código-fonte completo dessa classe, incluindo a implementação de todos os métodos auxiliares, está apresentado no anexo. Se desejar, o leitor pode consultá-lo por conta própria e estudar com mais profundidade todas as nuances técnicas.

Módulo de atenção

De acordo com a lógica geral do framework Mantis, a sequência da série temporal previamente processada, já na forma de tokens formados a partir dos patches de canais individuais, é enviada como entrada para o módulo Transformer. É aqui que ocorre o processamento final das informações espaço-temporais: à sequência de tokens é adicionado um token de classe e é incorporada a codificação posicional.

O token de classe serve como uma espécie de agregador de informações. Durante a passagem pelos 6 níveis do mecanismo multihead de autoatenção (Self-Attention), ele agrega a informação estrutural de toda a sequência. É justamente o seu valor na saída do transformador que é interpretado como o identificador de classe da série temporal analisada, seja no reconhecimento de uma fase de mercado, na classificação do estado dos indicadores ou na previsão do tipo de movimento futuro.

Na nossa implementação, fizemos certos ajustes nessa etapa. Antes de tudo, a codificação posicional foi excluída. O motivo é que a estrutura temporal da sequência já está explicitamente embutida nos próprios tokens graças à codificação temporal incorporada, emprestada da arquitetura Mamba4Cast. Essa abordagem permite codificar a posição absoluta e relativa de cada elemento dentro do canal, sem recorrer a vetores posicionais senoidais ou treináveis, como é comum em transformadores clássicos.

Essa substituição oferece imediatamente duas vantagens. Primeiro, torna o modelo menos sensível a deslocamentos e distorções da sequência original. Segundo, elimina a competição entre um código posicional rígido e o contexto temporal real que já está presente nos dados. Em séries temporais reais de mercado, isso permite aumentar a robustez do modelo, enquanto o transformador pode se concentrar no conteúdo do sinal de entrada.

Além disso, na implementação autoral do Mantis, na saída do Transformer é utilizado exclusivamente o token de classe — um vetor especial destinado à acumulação de informações generalizadas sobre a sequência. Esse token é previamente adicionado à sequência de entrada, percorre todas as camadas do transformador e é extraído na saída.

No entanto, na nossa implementação foi adotada uma decisão alternativa. Em vez da inserção tradicional do token de classe no início da sequência e de sua posterior extração, utilizamos um módulo de atenção cruzada (Cross-Attention). Sua característica principal é que o token de classe é fornecido como consulta principal (query), enquanto os tokens da sequência original atuam como contexto (keys e values). Essa configuração permite que o token de classe se concentre nos elementos mais significativos da sequência, minimizando o ruído e reforçando as conexões relevantes.

Além disso, aplicamos uma variante de atenção cruzada com canais independentes, na qual cada canal é analisado de forma isolada. Isso possibilita avaliar separadamente a contribuição de cada canal para o mecanismo de atenção. Essa abordagem é especialmente útil na análise de sinais multimodais ou heterogêneos, pois ajuda a evitar a dominância de um canal sobre os demais e a formar uma representação agregada objetiva de toda a estrutura da série temporal.

Dessa forma, o vetor-contêiner final, obtido na saída do bloco de atenção cruzada, já contém uma representação generalizada e equilibrada de toda a estrutura temporal, adequada para posterior classificação ou previsão.

Do ponto de vista técnico, tudo isso é implementado na classe CNeuronMantisAttentionUnit, que herda de CNeuronSoftMaxOCL. Isso significa que, na saída, obtemos imediatamente a probabilidade de a sequência analisada pertencer a uma ou outra classe. A estrutura do novo objeto é apresentada abaixo.

class CNeuronMantisAttentionUnit :  public CNeuronSoftMaxOCL
  {
protected:
   CNeuronBaseOCL                cClassToken[2];
   CNeuronMVCrossAttentionMLKV   cAttention;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL)  override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL)  override;

public:
                     CNeuronMantisAttentionUnit(void) {};
                    ~CNeuronMantisAttentionUnit(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint token_size, uint window, uint window_key, uint heads,
                          uint units_count, uint layers, uint variables,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual int       Type(void)  override const {  return defNeuronMantisAttentionUnit; }
   //---
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
  };

Dentro da nova classe, vemos 2 componentes principais:

• cClassToken[2] — uma MLP de duas camadas para geração do token de classe;
• cAttention — o próprio objeto de atenção cruzada multicamadas.

Todos os objetos internos são declarados estaticamente, o que permite manter vazios o construtor e o destrutor da classe. A inicialização dos objetos internos, como de costume, é realizada no método Init.

bool CNeuronMantisAttentionUnit::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                      uint token_size, uint window, uint window_key,
                                      uint heads, uint units_count, uint layers, uint variables,
                                      ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronSoftMaxOCL::Init(numOutputs, myIndex, open_cl, token_size, optimization_type, batch))
      return false;

Aqui, primeiro realizamos a chamada do método homônimo da classe pai, no qual, como você sabe, já está organizado o processo de inicialização dos objetos e interfaces herdados. E, após a execução bem-sucedida das operações do método da classe pai, passamos à inicialização dos objetos internos. Inicialmente, inicializamos a MLP de geração do token de classe treinável. A primeira camada sempre possui um único elemento de valor fixo, e a segunda, por meio de parâmetros treináveis, gera o token de classe do tamanho necessário.

   int index = 0;
   if(!cClassToken[0].Init(token_size, index, OpenCL, 1, optimization, iBatch))
      return false;
   if(!cClassToken[0].getOutput().Fill(1))
      return false;
   index++;
   if(!cClassToken[1].Init(0, index, OpenCL, token_size, optimization, iBatch))
      return false;
   cClassToken[1].SetActivationFunction(SIGMOID);

Com o objetivo de obter os elementos do token dentro de um intervalo de valores predefinido, utilizamos a função de ativação sigmoide na última camada.

No passo seguinte, inicializamos o bloco de atenção cruzada. Todas as informações sobre sua configuração são recebidas do usuário nos parâmetros do nosso método de inicialização.

   index++;
   if(!cAttention.Init(0, index, OpenCL, token_size, window_key, heads * variables, window,
                       heads, 1, units_count, layers, 1, 1, variables, optimization, iBatch))
      return false;
//---
   return true;
  }

E concluímos o trabalho do método, retornando ao programa chamador o resultado lógico da execução das operações.

De forma igualmente concisa é apresentado o método de propagação para frente feedForward. Nos parâmetros do método recebemos um ponteiro para o objeto de contexto da sequência analisada e imediatamente verificamos sua validade.

bool CNeuronMantisAttentionUnit::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

Em seguida, precisamos gerar o token de classe. Contudo, essa operação é realizada apenas durante o treinamento do modelo. No processo de utilização prática, os parâmetros do modelo não são alterados e, como consequência, o token de classe permanece fixo. Assim, não há necessidade de gerá-lo novamente a cada iteração.

//---
   if(bTrain)
     {
      if(!cClassToken[1].FeedForward(cClassToken[0].AsObject()))
         return false;
     }

O token de classe gerado, juntamente com o contexto da sequência analisada, é fornecido ao bloco de atenção.

   if(!cAttention.FeedForward(cClassToken[1].AsObject(), NeuronOCL.getOutput()))
      return false;

O resultado do funcionamento do bloco de atenção, o token de classe enriquecido, é encaminhado para a entrada da classe pai CNeuronSoftMaxOCL. Esse passo converte o valor de previsão em uma interpretação probabilística. Na saída, obtemos uma distribuição de probabilidades por classes.

   if(!CNeuronSoftMaxOCL::feedForward(cAttention.AsObject()))
      return false;
//---
   return true;
  }

Por fim, observamos que os métodos de propagação reversa (calcInputGradients e updateInputWeights) implementam a chamada sequencial das funções correspondentes dos componentes internos. O leitor pode estudar sua implementação de forma independente para compreender plenamente o processo de treinamento e atualização dos pesos no módulo CNeuronMantisAttentionUnit. O código-fonte completo dessa classe e de todos os seus métodos está apresentado no anexo.

Concluímos todo o volume de trabalhos planejados para hoje. No próximo artigo, analisaremos a arquitetura dos modelos e avaliaremos a eficácia das soluções implementadas com base em dados históricos reais.

Conclusão

Percorremos todo o caminho desde a preparação inicial dos dados — cálculo das primeiras diferenças, concatenação de características e codificação temporal com base no CMamba4CastEmbedding — até o processamento complexo de patches e a agregação inteligente por meio de atenção cruzada com o uso do token de classe. Cada etapa dessa cadeia — da transposição e convoluções locais ao max-pooling e à atenção multihead — foi cuidadosamente projetada para preservar o quadro mais completo possível da dinâmica temporal e, ao mesmo tempo, otimizar os recursos computacionais com foco no paralelismo em OpenCL.

Como resultado, obtivemos uma arquitetura modular, na qual é fácil ajustar o número de canais, o tamanho dos patches, a profundidade do embedding e o número de cabeças de atenção, sem alterar a lógica básica. Isso permite adaptar rapidamente o modelo aos mais diversos cenários financeiros — da negociação de alta frequência à análise de tendências de longo prazo.

Na próxima parte, apresentaremos o esquema completo do modelo treinável com base nos componentes descritos e mostraremos os resultados do seu funcionamento em dados históricos.

Links

• Mantis: Lightweight Calibrated Foundation Model for User-Friendly Time Series Classification
• Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	EA	EA coletor de exemplos
2	ResearchRealORL.mq5	EA	EA de coleta de exemplos pelo método Real-ORL
3	StudyContrast.mq5	EA	EA de treinamento contrastivo do codificador
4	Study.mq5	EA	EA de treinamento offline dos modelos
5	StudyOnline.mq5	EA	EA de treinamento online dos modelos
6	Test.mq5	EA	EA para teste do modelo
7	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema e da arquitetura dos modelos
8	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação da rede neural
9	NeuroNet.cl	Biblioteca	Biblioteca de código de programas em OpenCL