Redes neurais em trading: Generalização de séries temporais sem vinculação a dados (Módulos básicos do modelo)

Introdução

No artigo anterior, conhecemos o framework Mamba4Cast e seus componentes básicos: o SSM-módulo e os mecanismos de Prior-data Fitted Networks (PFNs). Esse framework estabelece uma base sólida para a previsão de séries temporais e pode se tornar uma ferramenta poderosa no arsenal do trader.

Mamba4Cast foi criado não para um longo aquecimento em cada nova série temporal, mas para entrar em operação de forma instantânea. Graças à ideia Zero-Shot Forecasting, o modelo é capaz de fornecer imediatamente previsões de alta qualidade em dados reais sem retreinamento e sem ajuste fino de hiperparâmetros. E o trader não precisa mais gastar dias escolhendo parâmetros ideais.

A base da alta velocidade de funcionamento do modelo está na complexidade linear dos SSM-módulos. Diferentemente dos transformadores, cuja complexidade computacional cresce quadraticamente com o comprimento da série, cada passo no Mamba4Cast é processado em tempo constante. Isso garante saída instantânea mesmo para sequências muito longas e latência mínima durante a inferência. Em um mundo em que a velocidade de tomada de decisão por vezes define o resultado de uma operação, essa vantagem é difícil de superestimar.

Além disso, Mamba4Cast fornece imediatamente uma previsão completa para todo o horizonte definido, em vez de gerá-la passo a passo. Essa abordagem permite evitar o acúmulo de erros, típico de modelos autorregressivos, e garante trajetórias mais estáveis do desenvolvimento futuro do evento. A estratégia de trading recebe a visão completa de uma só vez e, portanto, podemos contar com decisões seguras sem ressalvas desnecessárias.

Não menos importante é o método de treinamento em cenários sintéticos. O modelo foi alimentado com milhões de séries geradas artificialmente. Graças a isso, Mamba4Cast adquiriu uma intuição universal e aprendeu a operar de forma estável nas mais diversas condições. Essa abordagem o torna resistente a ruídos e a mudanças bruscas. Consequentemente, reduz-se o risco de falhas inesperadas em regime de utilização em massa.

Apesar de todo o poder dos mecanismos fundamentais, Mamba4Cast permanece econômico em termos de recursos. Experimentos realizados pelos autores do framework mostraram que, com precisão comparável às modernas modelos fundamentais baseados em transformadores, ele exige significativamente menos poder computacional. Isso permite executá-lo até mesmo em infraestruturas limitadas e incorporá-lo diretamente ao terminal de trading sem a necessidade de clusters GPU potentes.

É justamente a combinação de prontidão imediata para o trabalho, velocidade recorde de saída, previsão integral, resistência a ruídos e eficiência de recursos que torna Mamba4Cast uma ferramenta verdadeiramente revolucionária no campo da previsão de séries temporais.

A visualização autoral do framework Mamba4Cast é apresentada abaixo.

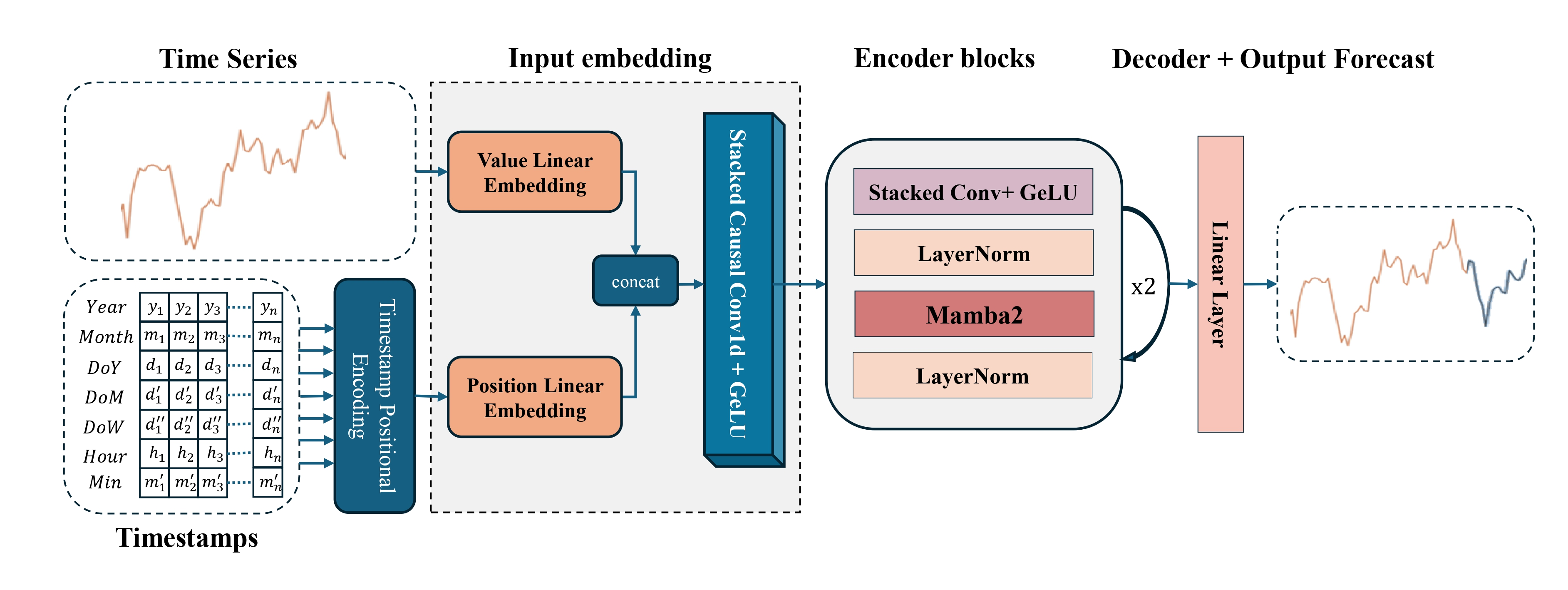
Na parte prática do artigo anterior, concluímos a construção do objeto de codificação temporal, o elemento-chave responsável pela representação posicional dos dados brutos na sequência temporal. Esse componente tornou-se o encerramento lógico do contorno geral de inicialização do modelo e uma parte importante da preparação arquitetural do sinal analisado. Sem ele, o framework simplesmente não conseguiria distinguir corretamente as dependências temporais.

Hoje continuaremos nosso trabalho exatamente a partir desse ponto.

Módulo de pré-processamento

A lógica de desenvolvimento é simples: antes de realizar quaisquer cálculos, prever o movimento do preço e gerar sinais de trading, é necessário preparar corretamente os dados. Como em qualquer sistema de aprendizado de máquina, o sucesso do modelo Mamba4Cast depende diretamente da qualidade do fluxo de dados analisado. Se ruído, valores em diferentes escalas ou estruturas irregulares chegarem à entrada, nem mesmo a arquitetura mais avançada será capaz de salvar a situação. Por isso, o foco central da nossa atenção é o bloco de pré-processamento de dados.

Esse módulo não é apenas uma etapa auxiliar. Ele atua como um elo de ligação entre os dados brutos de mercado e as entradas organizadas que o modelo é capaz de interpretar. Nele ocorrem normalização, escalonamento, formação de janelas, trabalho com máscaras e, o que é especialmente importante, a contextualização dos dados por meio de canais adicionais. Tudo isso prepara as informações analisadas para o processamento dentro do modelo principal e estabelece a base sobre a qual se constrói a previsão posterior.

Nossa tarefa não é simplesmente carregar os dados brutos na forma de cotações e leituras dos indicadores analisados. Devemos trazê-los a uma escala unificada, identificar os limites de janelas completas, destacar máscaras de valores indisponíveis e sincronizar todos os canais no tempo. Somente depois disso é possível transferir os dados para o codificador e esperar uma interpretação correta.

Na parte prática do artigo anterior, finalizamos a construção do objeto de codificação temporal, um dos componentes-chave do bloco de pré-processamento de dados, que desempenha um papel importante na arquitetura do Mamba4Cast. Esse elemento permite que o modelo perceba a sequência de eventos de mercado não como um conjunto abstrato de números, mas como informações estruturadas com uma determinada ordem e ritmo.

Para implementar a abordagem proposta, construiremos uma classe especializada CMamba4CastEmbeding, que ocupa uma posição central no bloco de pré-processamento dos dados brutos. A estrutura do objeto é apresentada abaixo.

class CMamba4CastEmbeding :   public CNeuronBaseOCL
  {
protected:
   CNeuronConvOCL             cProjection;
   CNeuronBatchNormOCL        cNorm;
   CNeuronTSPositionEncoder   cProjectionWithTE;
   //---
   virtual bool               feedForward(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool               feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override;
   virtual bool               updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool               calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CMamba4CastEmbeding(void) {};
                    ~CMamba4CastEmbeding(void) {};
   //---
   virtual bool               Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                   uint window, uint window_out, uint units_count, uint &periods[],
                                   ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int                Type(void) override  const   {  return defMamba4CastEmbeding;   }
   //---
   virtual bool               Save(int const file_handle) override;
   virtual bool               Load(int const file_handle) override;
   //---
   virtual bool               WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void               SetOpenCL(COpenCLMy *obj) override;
  };

A ideia principal consiste em transformar o fluxo de informações brutas em um contorno estruturado e informativo, adequado para as etapas posteriores de previsão. Para isso, aplica-se uma abordagem modular, em que a classe reúne vários módulos especializados, cada um responsável por uma transformação específica dos dados.

É importante observar que todos os objetos internos da classe CMamba4CastEmbeding são declarados de forma estática. Graças a isso, o construtor e o destrutor da classe podem permanecer vazios, pois não há necessidade de gerenciamento de memória dinâmica, já que os objetos são criados e destruídos automaticamente. Essa característica arquitetural simplifica a lógica do ciclo de vida do objeto, reduz o risco de vazamentos de memória e de erros potenciais associados à alocação dinâmica, o que é extremamente importante em ambientes de sistemas de trading de alto desempenho.

A inicialização direta de todos os módulos internos é realizada no método Init, em cujos parâmetros obtemos as principais características do objeto que está sendo criado.

bool CMamba4CastEmbeding::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                               uint window, uint window_out, uint units_count, uint &periods[],
                               ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(periods.Size() <= 0)
      return false;
   int freqs = (int(window_out / 2 + 2 * periods.Size()) - 1) / int(2 * periods.Size());
   if(freqs <= 0)
      return false;

No corpo do método, primeiro é verificada a presença de dados no array de períodos analisados da série temporal. Isso é necessário, pois a codificação temporal exige a existência de pelo menos um período para um cálculo correto. Em seguida, é calculado o valor do parâmetro freqs, que representa a quantidade de harmônicas de frequência para cada período.

A lógica de determinação do valor desse parâmetro exige uma explicação à parte. Um dos parâmetros do método de inicialização (window_out) indica a dimensionalidade do vetor de incorporação de um único passo temporal. Como já mencionado anteriormente, o mesmo recorte temporal de dados deve ser representado em duas formas, como um valor puro sem consideração do tempo e como uma combinação com características temporais incorporadas na forma de componentes harmônicos. Dessa maneira, a incorporação final contém ambos os tipos de representação. No entanto, o volume de memória alocado para essa representação é único. Portanto, para a codificação do componente temporal, podemos usar apenas metade do tamanho de incorporação definido pelo usuário. A outra metade é reservada para a projeção comum dos dados brutos.

Agora vamos analisar como exatamente essa metade é distribuída entre os componentes de frequência do codificador temporal. Os autores do framework Mamba4Cast utilizaram uma abordagem próxima à codificação posicional nos transformadores: para cada período especificado, são criadas funções seno e cosseno que descrevem a fase e a frequência das oscilações. Consequentemente, para cada componente de frequência de um período correspondem duas harmônicas, uma senoidal e uma cossenoidal. Isso significa que o número total de componentes de frequência deve ser, no mínimo, o dobro da quantidade de períodos indicados no array.

Para evitar confusão, a fórmula aqui é simples, mas exige atenção: dividimos metade do window_out pelo número de períodos especificados multiplicado por dois. O valor obtido mostra quantos componentes de frequência podem ser gerados para cada período. E esse número deve ser estritamente maior que zero, pois, caso seja igual a zero, o modelo não conseguirá criar sequer uma harmônica e, consequentemente, a codificação temporal simplesmente não ocorrerá.

Na prática, isso significa que, ao definir o tamanho da incorporação de um único passo temporal, é preciso partir não do desejo de aumentar o modelo, mas da necessidade real de cobrir cada um dos períodos com pelo menos um par de harmônicas.

Em seguida, é realizada a chamada do método homônimo da classe pai, onde já está organizado o processo de inicialização dos objetos e interfaces herdados.

if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_out * units_count, optimization_type, batch))
   return false;

E após sua execução bem-sucedida, passamos à inicialização sequencial dos módulos internos da nossa classe. O primeiro a ser inicializado é a camada convolucional de projeção dos dados brutos em uma representação compacta (cProjection).

int index = 0;
if(!cProjection.Init(0, index, OpenCL, window, window, window_out - 2 * freqs * periods.Size(), units_count,
                                                                                   1, optimization, iBatch))
   return false;
cProjection.SetActivationFunction(TANH);

Esse objeto é responsável por gerar a incorporação dos dados brutos sem a componente temporal. Utilizamos a função de ativação TANH para a transformação não linear dos dados, o que ajuda a destacar características relevantes ocultas nos fluxos numéricos brutos e a minimizar a influência de valores atípicos.

A camada de normalização em lote (cNorm) ajusta os valores obtidos, eliminando possíveis distorções e garantindo a estabilidade dos cálculos.

index++;
if(!cNorm.Init(0, index, OpenCL, cProjection.Neurons(), iBatch, optimization))
   return false;
cNorm.SetActivationFunction(None);

A funcionalidade de geração de incorporações considerando a componente temporal é executada pelo módulo de codificação temporal (cProjectionWithTE), o que é especialmente importante para a previsão de tendências sazonais e de mudanças dinâmicas no comportamento do mercado.

   index++;
   if(!cProjectionWithTE.Init(0, index, OpenCL, window, units_count, periods, freqs, optimization, iBatch))
      return false;
   SetActivationFunction(None);
//---
   return true;
  }

Dentro da lógica do framework, a passagem sequencial pelas etapas de inicialização garante que cada submódulo receba parâmetros corretamente compatibilizados, permitindo integrar de forma eficiente a informação temporal com os dados brutos.

Um dos estágios-chave do funcionamento do bloco CMamba4CastEmbedding é a execução do método feedForward, o mecanismo que garante a propagação para frente dos dados através de todos os elos da arquitetura de pré-processamento. É exatamente aqui que se forma a base para que os módulos subsequentes possam se apoiar não apenas em dados brutos, mas em representações devidamente preparadas, nas quais já estão consideradas tanto a estrutura do sinal original quanto seu contexto temporal.

bool CMamba4CastEmbeding::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)
  {
   if(!cProjection.FeedForward(NeuronOCL))
      return false;

O processo começa com o direcionamento dos dados analisados para o módulo cProjection. Trata-se de um bloco convolucional compacto, cuja principal tarefa é projetar o sinal original em um espaço oculto de características. Graças a esse passo, o sistema passa a focar imediatamente nas mudanças mais expressivas e significativas do fluxo de entrada.

Em seguida, as características obtidas são transmitidas ao módulo cNorm. Essa é uma camada de normalização que traz os valores para uma escala estável, eliminando saltos, valores atípicos e possíveis distorções na distribuição.

if(!cNorm.FeedForward(cProjection.AsObject()))
   return false;

Sem a normalização, arquiteturas profundas frequentemente começam a saturar ou, ao contrário, a perder o sinal do gradiente. Aqui, a normalização cumpre o papel de um estabilizador, alinhando o comportamento do modelo tanto no treinamento quanto na previsão.

No entanto, a particularidade da arquitetura Mamba4Cast reside no fluxo de informação a seguir. Em paralelo, os dados brutos são enviados para o cProjectionWithTE, o módulo responsável pela codificação temporal.

if(!cProjectionWithTE.FeedForward(NeuronOCL, SecondInput))
   return false;

Diferentemente da projeção inicial, onde são utilizadas apenas convoluções, aqui é conectado adicionalmente um segundo input, o SecondInput. É por meio dele que as marcas temporais, previamente preparadas para cada passo temporal, entram no processamento. Isso permite que o módulo não apenas se baseie nos valores, mas considere em qual contexto temporal específico eles surgiram, aumentando a sensibilidade do modelo a componentes sazonais, cíclicas e de fase do mercado.

A culminação desse processo é a operação de unificação. As representações finais obtidas a partir dos dois fluxos de informação são unidas em um único tensor por meio de concatenação.

   if(!Concat(cNorm.getOutput(), cProjectionWithTE.getOutput(), Output, cProjection.GetFilters(),
              cProjectionWithTE.GetWindowOut(), cProjection.GetUnits()))
      return false;
//---
   return true;
  }

O resultado obtido é uma representação densa e multinível de cada passo temporal, que carrega tanto características diretas quanto uma estrutura temporal enriquecida. E é justamente esse tipo de representação da sequência temporal que se torna a base para todo o trabalho subsequente do modelo.

Como é sabido, apenas a propagação para frente dos sinais não é suficiente para o treinamento de um modelo de rede neural. Para que o modelo possa se adaptar aos dados, é necessário organizar corretamente a propagação reversa do erro. Essa tarefa é resolvida exatamente pelo método calcInputGradients. Em essência, trata-se de um mecanismo interno de análise de erros, que é acionado após o modelo ter formado uma previsão e, então, precisar compreender onde exatamente ocorreu a imprecisão e como ela pode ser corrigida.

bool CMamba4CastEmbeding::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

Em primeiro lugar, o método verifica com qual objeto está trabalhando. Aqui é importante garantir que todos os elementos envolvidos no cálculo dos gradientes estejam corretamente inicializados. Após essa verificação, entra em ação o método DeConcat, destinado à decomposição do vetor de gradientes anteriormente unificado em dois fluxos de informação.

if(!DeConcat(cNorm.getGradient(), cProjectionWithTE.getGradient(), Gradient, cProjection.GetFilters(),
             cProjectionWithTE.GetWindowOut(), cProjection.GetUnits()))
   return false;

Recordemos que, na etapa de propagação para frente, as características normalizadas e as incorporações temporais foram unidas em um único fluxo. Agora, para treinar cada módulo separadamente, é necessário separá-las cuidadosamente, restaurando a estrutura original.

Após a separação dos sinais, inicia-se o processo principal, isto é, o cálculo dos gradientes de erro ao longo dos dois fluxos de informação até o nível dos dados brutos. Primeiramente, são executadas as operações com o caminho principal sem marcas temporais.

if(!cProjection.calcHiddenGradients(cNorm.AsObject()))
   return false;
if(!NeuronOCL.calcHiddenGradients(cProjection.AsObject()))
   return false;

Em seguida, a atenção se volta para o caminho do contexto temporal. Porém, antes de propagar o gradiente de erro, é necessário proteger os dados obtidos anteriormente. Para isso, inicialmente realizamos a substituição do ponteiro para o buffer de gradientes de erro do objeto de dados brutos. E somente depois disso executamos as operações de determinação da imprecisão.

   CBufferFloat *temp = NeuronOCL.getGradient();
   if(!NeuronOCL.SetGradient(NeuronOCL.getPrevOutput(), false) ||
      !NeuronOCL.calcHiddenGradients(cProjectionWithTE.AsObject()) ||
      !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, cProjection.GetWindow(), false, 0, 0, 0, 1) ||
      !NeuronOCL.SetGradient(temp, false)
     )
      return false;
//---
   return true;
  }

A etapa final consiste na soma dos dados dos dois fluxos de informação. Em seguida, os ponteiros para os buffers de dados são retornados ao estado original e o método encerra sua execução, previamente retornando à rotina chamadora o resultado lógico da realização das operações.

O resultado desse procedimento ajustado é a distribuição correta do gradiente de erro por toda a estrutura do módulo, o que permite garantir uma atualização equilibrada dos pesos.

Pela otimização dos coeficientes de peso em cada um dos submódulos é responsável o método updateInputWeights. A atualização é realizada por meio da chamada sequencial dos métodos homônimos dos objetos internos. Essa ordem passo a passo reflete o princípio do controle isolado dos pesos, o que permite acompanhar detalhadamente o processo de treinamento e introduzir alterações sem interferir na arquitetura geral do sistema. Caso ao menos uma das etapas de atualização falhe, o método retorna um erro, garantindo assim a integridade do estado atualizado do modelo.

Com o código do método updateInputWeights é possível se familiarizar no anexo do artigo. No mesmo local, é apresentado também o código completo da classe CMamba4CastEmbeding e de todos os seus métodos.

Em resumo, pode-se dizer que a classe CMamba4CastEmbeding não é apenas um conjunto de algoritmos para transformação de dados, mas um módulo elegantemente projetado, no qual cada função está intimamente entrelaçada com a lógica geral do framework Mamba4Cast. Ela garante um pré-processamento de alta qualidade dos dados brutos, permitindo que o modelo extraia de forma eficiente características relevantes, leve em conta a dinâmica temporal e seja treinado corretamente com base nos gradientes de erro obtidos.

Codificador

A próxima etapa do nosso trabalho passa a ser a construção dos objetos do Codificador, proposto pelos autores do framework Mamba4Cast, que desempenha um papel importante na extração e na estruturação de características para a previsão subsequente. A arquitetura desse bloco é baseada no uso de uma pilha de camadas convolucionais com janelas de convolução de diferentes tamanhos. Cada camada convolucional se concentra na extração de determinados aspectos dos dados brutos, e seus resultados são posteriormente unidos por meio de concatenação e normalizados para o processamento posterior pelo módulo Mamba. Ao mesmo tempo, a quantidade de repetições desse bloco é determinada pela profundidade de análise requerida, o que permite ao framework se adaptar a tarefas de diferentes níveis de complexidade.

Uma atenção especial nesse enfoque é atraída pela pilha de camadas convolucionais. O objeto de camada convolucional já foi implementado há bastante tempo em nossa biblioteca, e seu uso não apresenta dificuldades. No entanto, na abordagem padrão, cada camada convolucional é criada como um objeto separado e processada de forma sequencial. O uso de objetos com convoluções de tamanhos diferentes leva à criação de um grande número deles, e o processamento sequencial desses objetos aumenta significativamente a complexidade computacional do modelo e, consequentemente, o tempo de seu treinamento.

Para resolver esse problema, pensamos na criação de um objeto especial que seja capaz de realizar o processamento de várias camadas convolucionais em paralelo. Tal objeto permitirá iniciar o processamento dos dados simultaneamente em vários fluxos, o que reduzirá drasticamente o tempo de execução das operações. Dentro do novo objeto, será possível implementar mecanismos de distribuição de tarefas: o sinal original será alimentado simultaneamente em vários filtros convolucionais com diferentes tamanhos de janelas de convolução, e os resultados de seu funcionamento serão concatenados em um único tensor. Isso não apenas reduzirá a quantidade de objetos intermediários, como também garantirá um uso mais eficiente dos recursos computacionais, especialmente em condições de processamento multithread em modernas GPU.

A ideia não é nova. Anteriormente, já havíamos implementado o objeto CNeuronMultiWindowsConvOCL, que permitia aplicar operações convolucionais com diferentes tamanhos de janela. No entanto, seu algoritmo previa a existência de um bloco de dados separado para cada janela de convolução. Neste caso específico, porém, nos deparamos com uma tarefa diferente: é necessário processar o mesmo fluxo de informação utilizando diferentes janelas de convolução.

O problema reside no fato de que a alteração do tamanho da janela de convolução influencia a quantidade de operações de convolução possíveis. Com o aumento da janela de convolução, o número de posições nas quais é possível realizar a convolução diminui. Isso leva a uma situação em que a quantidade de fluxos de operações responsáveis pelos cálculos com diferentes tamanhos de janelas de convolução torna-se desbalanceada. E isso dificulta a execução paralela eficiente.

Para resolver esse problema, foi tomada a decisão de utilizar padding zero, isto é, a adição de zeros no início e no final do vetor analisado. Essa técnica permite estender o vetor até o comprimento necessário de modo que, independentemente do tamanho da janela de convolução, seja possível utilizar a mesma quantidade de fluxos de operações. Dessa forma, o número de operações de convolução passa a ser regulado apenas pelo tamanho do passo da janela de convolução, que utilizamos de forma unificada para todas as janelas, equilibrando a carga entre os fluxos paralelos e simplificando significativamente o processamento paralelo.

Toda a lógica principal é concentrada, no lado do programa OpenCL, em um kernel compacto, porém poderoso, FeedForwardMultWinConvWPad, que processa simultaneamente o mesmo fluxo de entrada por meio de várias janelas de convolução de diferentes comprimentos.

__kernel void FeedForwardMultWinConvWPad(__global const float *matrix_w,
                                         __global const float *matrix_i,
                                         __global float *matrix_o,
                                         __global const int *windows_in,
                                         const int inputs,
                                         const int step,
                                         const int window_out,
                                         const int activation
                                        )
  {
   const size_t id = get_global_id(0);
   const size_t id_w = get_global_id(1);
   const size_t v = get_global_id(2);
   const size_t outputs = get_global_size(0);
   const size_t windows_total = get_global_size(1);

Cada fluxo de operações é identificado por três coordenadas:

• id — índice do elemento no tensor de resultados,
• id_w — número da janela de convolução,
• v — identificador do fluxo unitário dos dados brutos.

Isso permite processar em paralelo múltiplas janelas de convolução, posições e sequências de dados brutos com diferentes parâmetros de operação.

No primeiro passo, o kernel determina o comprimento da janela de convolução atual window_in, obtendo-o do array windows_in pelo identificador da janela de convolução.

int window_in = windows_in[id_w];

Em seguida, é calculado o deslocamento da posição inicial da janela de convolução no buffer de dados brutos de acordo com o índice atual do elemento do tensor de resultados. Esse deslocamento é realizado levando em conta que o centro da janela deve coincidir com a posição id. Como os comprimentos das janelas podem ser diferentes, aplica-se a fórmula (window_in + 1) / 2, garantindo o alinhamento do centro da janela.

int window_in = windows_in[id_w];
int mid_win = (window_in + 1) / 2;
int shift_in = id * step - mid_win;
int shift_in_var = v * inputs;

O deslocamento shift_in_var é utilizado para o endereçamento correto da sequência unitária necessária no array global de dados brutos.

A etapa seguinte é o cálculo de shift_weight, o deslocamento dentro do array global de parâmetros treináveis. Como os pesos de cada janela estão dispostos sequencialmente uns após os outros, levando em conta seus comprimentos e o coeficiente de bias, é necessário somar os tamanhos de todos os blocos de pesos que precedem a janela atual id_w. Isso permite determinar com precisão a partir de qual posição começam os pesos da convolução atual.

int shift_weight = 0;
for(int w = 0; w < id_w; w++)
   shift_weight += (windows_in[w] + 1) * window_out;

Em seguida, é iniciado um laço interno que processa cada canal de saída w_out — que corresponde à dimensionalidade da incorporação no buffer de resultados obtido após a aplicação da convolução.

   for(int w_out = 0; w_out < window_out; w_out++)
     {
      float sum = matrix_w[shift_weight + window_in];
      //---
      for(int w = 0; w < window_in; w++)
         if((shift_in + w) >= 0 && (shift_in + w) < inputs)
            sum += IsNaNOrInf(matrix_i[shift_in_var + shift_in + w] * matrix_w[shift_weight + w], 0);
      //---
      int shift_out = (v * outputs + id) * window_out + w_out;
      matrix_o[shift_out] = Activation(sum, activation);
      shift_weight += window_in + 1;
     }
  }

Para cada um desses canais, é inicializada a variável sum, que inicialmente assume o valor do bias, o último elemento do bloco de pesos, e depois recebe a soma dos produtos dos valores dos dados brutos pelos pesos correspondentes. Nesse processo, é obrigatoriamente verificado se o índice atual não ultrapassa os limites do array de dados brutos. Caso isso ocorra — a operação é ignorada, o que é equivalente à aplicação de padding zero.

Quando o ciclo pela janela é concluído, o resultado é processado pela função de ativação. Seu tipo é definido pelo parâmetro activation, e a própria função é chamada por meio do wrapper auxiliar Activation. O valor final é gravado no buffer global de resultados matrix_o, levando em conta todos os deslocamentos.

Em seguida, o ponteiro para o bloco de pesos shift_weight é avançado para frente, pelo valor do tamanho da janela mais um (bias), a fim de passar para os pesos do próximo filtro. Dessa forma, dentro de um único fluxo ocorre o processamento sequencial de todos os canais, porém em paralelo para todas as janelas e todas as sequências unitárias de dados brutos.

O algoritmo resultante mostrou-se não apenas flexível, mas também excepcionalmente eficiente: convoluções de diferentes escalas são aplicadas aos dados simultaneamente, garantindo uma representação ampla e abrangente a partir de múltiplas perspectivas. O padding zero elimina a necessidade de cortar os dados manualmente ou alinhar a dimensionalidade da incorporação posteriormente. Tudo é feito de forma dinâmica, diretamente no momento da execução na GPU.

Uma implementação desse tipo demonstra um princípio-chave: alto desempenho não é obtido por meio da simplificação da lógica, mas sim através da divisão inteligente dos cálculos, do uso de processamento paralelo e do ajuste preciso de todas as etapas de transformação dos dados.

O próximo estágio importante é o cálculo dos gradientes de erro no nível dos dados brutos. Diferentemente da propagação para frente, aqui nos deparamos com uma tarefa mais complexa: não basta apenas passar os dados por um conjunto de filtros, é necessário, no caminho inverso, reunir a contribuição de cada filtro para o erro no nível dos resultados. Ao mesmo tempo, é preciso tratar corretamente os deslocamentos e preservar a consistência da forma dos dados.

Esse algoritmo é implementado no kernel OpenCL CalcHiddenGradientMultWinConvWPad. Sua função é agregar os gradientes de erro levando em conta todas as janelas de convolução de diferentes comprimentos e todos os canais de saída. Em outras palavras, ele reconstrói o erro que retorna à sequência original, considerando a não linearidade da ativação e a estrutura dos filtros.

__kernel void CalcHiddenGradientMultWinConvWPad(__global const float *matrix_w,
                                                __global const float *matrix_i,
                                                __global float *matrix_ig,
                                                __global const float *matrix_og,
                                                __global const int *windows_in,
                                                const int outputs,
                                                const int step,
                                                const int window_out,
                                                const int activation
                                               )
  {
   const size_t id_x = get_global_id(0);
   const size_t id_loc = get_local_id(1);
   const size_t id_win = id_loc / window_out;
   const size_t id_f = id_loc % window_out;
   const size_t v = get_global_id(2);
   const size_t inputs = get_global_size(0);
   const size_t size_loc = get_local_size(1);
   const size_t windows_total = size_loc / window_out;

Cada fluxo no kernel é responsável por um único elemento do gradiente no nível dos dados brutos:

• id_x — índice da posição na sequência original;
• id_loc — identificador local no grupo de trabalho, que é desmembrado em id_win (número da janela) e id_f (número do filtro no buffer de resultados);
• v — número da sequência unitária.

Também conhecemos o comprimento total da entrada inputs, o número de elementos na saída outputs e a quantidade de janelas windows_total.

Na primeira etapa, calcula-se o deslocamento shift_weight, que permite obter o início exato do bloco de pesos correspondente à janela e ao canal atuais. Aqui, assim como anteriormente, é necessário percorrer todas as janelas anteriores para somar cuidadosamente seus comprimentos e chegar à posição correta no array global de parâmetros matrix_w.

   __local float temp[LOCAL_ARRAY_SIZE];
   const uint ls = min((uint)size_loc, (uint)LOCAL_ARRAY_SIZE);
//---
   int window_in = windows_in[id_win];
   int shift_weight = id_f * (window_in + 1);
   for(int w = 0; w < id_win; w++)
      shift_weight += (windows_in[w] + 1) * window_out;

Após isso, determinamos o intervalo no buffer de resultados no qual o elemento analisado dos dados brutos poderia ter participado — shift_out. Esse valor é limitado inferiormente por zero e calculado como o maior índice de saída possível no qual a janela ainda pode abranger a posição id_x.

int shift_out = max((int)((id_x - window_in) / step), 0);

Mas isso ainda não é suficiente — em seguida, é iniciado um laço sobre todos os possíveis valores de saída out nos quais nosso elemento poderia ter participado durante a propagação para frente.

float grad = 0;
int mid_win = (window_in + 1) / 2;
for(int out = shift_out; out < outputs; out++)
  {
   int shift_in = out * step - mid_win;
   if(shift_in > id_x)
      break;
   int shift_w = id_x - shift_in;
   if(shift_w >= window_in)
      continue;
   int shift_g = ((v * outputs + out) * windows_total + id_win) * window_out + id_f;
   grad += IsNaNOrInf(matrix_w[shift_w + shift_weight] * matrix_og[shift_g], 0);
  }

A cada iteração desse laço, é verificado se id_x pertence à janela atual. Se pertencer, calcula-se o deslocamento local shift_w dentro da janela e a posição do gradiente de saída correspondente shift_g. Multiplicando o peso correspondente pelo gradiente de erro da saída matrix_og, obtemos a contribuição dessa convolução para o erro do elemento analisado. Todas essas contribuições são acumuladas na variável grad.

Nesse estágio, temos um gradiente parcial para cada fluxo. No entanto, é preciso considerar que, dentro do grupo de trabalho, podem existir vários fluxos responsáveis pelo mesmo id_x, porém para filtros e canais diferentes. Por isso, é introduzido um array intermediário na memória local temp, e é iniciado um laço de somatório com barreiras de sincronização. Inicialmente, cada fluxo grava seu valor em temp.

for(int i = 0; i < size_loc; i += ls)
  {
   if(i <= id_loc && (i + ls) > id_loc)
      temp[id_loc % ls] = (i == 0 ? 0 : temp[id_loc % ls]) + grad;
   barrier(CLK_LOCAL_MEM_FENCE);
  }

Em seguida, por meio de uma redução paralela, o array é somado em potências de dois, deixando em temp[0] o gradiente final considerando todos os canais e janelas.

uint count = ls;
do
  {
   count = (count + 1) / 2;
   if(id_loc < count && (id_loc + count) < ls)
     {
      temp[id_loc] += temp[id_loc + count];
      temp[id_loc + count] = 0;
     }
   barrier(CLK_LOCAL_MEM_FENCE);
  }
while(count > 1);

Por fim, apenas o fluxo com id_loc == 0 grava o valor final do gradiente de erro no array global matrix_ig. Porém, antes disso, é chamada a função Deactivation, que aplica a derivada da função de ativação ao valor de entrada matrix_i. Isso é fundamental: o gradiente deve ser ajustado levando em conta a forma da ativação, caso contrário o treinamento será incorreto.

 if(id_loc == 0)
    matrix_ig[v * inputs + id_x] = Deactivation(temp[0], matrix_i[v * inputs + id_x], activation);
}

Este é um dos trechos mais trabalhosos da propagação reversa. Graças à divisão dos cálculos por janelas e canais, bem como ao uso de memória local, alcança-se alta eficiência mesmo com um grande número de parâmetros. Em conjunto com a propagação para frente, esse estágio torna nosso algoritmo não apenas modular e escalável, mas também capaz de lidar com dependências muito complexas em séries temporais financeiras, sem perda de precisão ou desempenho.

O acorde final da sinfonia convolucional é a atualização dos pesos. Nesse estágio, convertemos os gradientes calculados em alterações reais nos parâmetros do modelo. E fazemos isso seguindo o clássico da otimização, o método Adam, complementado por deslocamentos para convoluções com janelas de diferentes larguras e levando em conta o padding zero. O kernel UpdateWeightsMultWinConvAdamWPad implementa cuidadosamente toda essa mecânica.

__kernel void UpdateWeightsMultWinConvAdamWPad(__global float *matrix_w,
                                               __global const float *matrix_og,
                                               __global const float *matrix_i,
                                               __global float *matrix_m,
                                               __global float *matrix_v,
                                               __global const int *windows_in,
                                               const int windows_total,
                                               const int window_out,
                                               const int inputs,
                                               const int step,
                                               const int outputs,
                                               const float l,
                                               const float b1,
                                               const float b2
                                              )
  {
   const size_t i = get_global_id(0);  // weight shift
   const size_t v = get_local_id(1);   // variable
   const size_t variables = get_local_size(1);

Cada fluxo nesse kernel é responsável por atualizar um parâmetro específico i, seja ele um coeficiente de filtro ou bias (deslocamento). A variável v representa aqui o índice da sequência unitária, enquanto variables é a quantidade total dessas sequências. Elas participam da soma dos gradientes ao longo de todo o fluxo de dados brutos, de modo que a atualização final seja mais estável.

Logo no início, o fluxo precisa determinar a qual filtro, a qual canal de saída e a qual peso específico corresponde o seu índice i. Isso é feito por meio de um laço sobre todas as janelas, no qual, com a ajuda de um contador cuidadoso shift_before, acompanha-se o deslocamento de cada janela no array linear de parâmetros treináveis.

   __local float temp[LOCAL_ARRAY_SIZE];
   const uint ls = min((uint)variables, (uint)LOCAL_ARRAY_SIZE);
//---
   int step_out = window_out * windows_total;
//---
   int shift_before = 0;
   int window = 0;
   int number_w = 0;
   for(int w = 0; w < windows_total; w++)
     {
      int win = windows_in[w];
      if(shift_before <= i &&
         (win + 1)*window_out > (i - shift_before))
        {
         window = win;
         number_w = w;
        }
      else
         shift_before += (win + 1) * window_out;
     }

Assim que identificamos a qual janela o índice i pertence, determinamos:

• window — a largura da janela do filtro;
• number_w — o número da janela;
• id_f — o número do filtro;
• shift_in — o deslocamento em relação ao início da janela (se for igual ao tamanho da janela, significa que se trata do bias).
• bias — um sinal lógico que indica se o elemento analisado é um parâmetro de deslocamento.

int shift_in = (i - shift_before) % (window + 1);
int shift_in_var = v * inputs;
bool bias = (shift_in == window);
int mid_win = (window + 1) / 2;
int id_f = (i - shift_before) / (window + 1);
int shift_out = number_w * window_out + id_f;
int shift_out_var = v * outputs * step_out;

No caso de um coeficiente de filtro comum, é iniciado um laço por todas as saídas out. Em cada saída, verificamos se a posição de entrada correspondente se encontra dentro dos limites dos dados válidos. Se estiver, realizamos o procedimento padrão: multiplicamos o gradiente de saída correspondente matrix_og pelo sinal de entrada matrix_i, acumulando os produtos em grad.

float grad = 0;
if(!bias)
  {
   for(int out = 0; out < outputs; out++)
     {
      int in = out * step - mid_win + shift_in;
      if(in >= inputs)
         break;
      if(in < 0)
         continue;
      //---
      grad += IsNaNOrInf(matrix_og[shift_out_var + shift_out + out * step_out] * matrix_i[shift_in_var + in], 0);
     }
  }
else
  {
   for(int out = 0; out < outputs; out++)
      grad += IsNaNOrInf(matrix_og[shift_out_var + shift_out + out * step_out], 0);
  }

Se, por outro lado, tratar-se de um parâmetro de deslocamento, então os dados brutos não participam do cálculo. Basta simplesmente somar os gradientes no nível dos resultados para todas as posições.

Em seguida — aplica-se uma técnica já conhecida: o somatório local por meio do array temp. O objetivo é acumular os gradientes de todas as sequências unitárias e reduzir a influência de valores atípicos. Novamente, utiliza-se uma árvore de redução com barreiras de sincronização, para somar corretamente os valores dentro do grupo de trabalho. E somente o fluxo com v == 0 (o primeiro na ordem) executa a atualização final do peso.

//--- sum
   for(int s = 0; s < (int)variables; s += ls)
     {
      if(v >= s && v < (s + ls))
         temp[v % ls] = (s == 0 ? 0 : temp[v % ls]) + grad;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
//---
   uint count = ls;
   do
     {
      count = (count + 1) / 2;
      if(v < count && (v + count) < ls)
        {
         temp[v] += temp[v + count];
         temp[v + count] = 0;
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

É aqui que entra em ação o algoritmo Adam:

1. Atualiza-se a primeira estimativa de momento do gradiente mt, com suavização exponencial por meio do coeficiente b1.
2. Atualiza-se a segunda estimativa de momento vt, que representa a variância do gradiente, com o coeficiente b2.
3. O peso é atualizado por meio da normalização mt / sqrt(vt) e escalonado pelo coeficiente da taxa de aprendizado l.
4. Todos os valores são rigidamente limitados com o uso de clamp, para evitar a divergência dos pesos e a divisão por zero.

 if(v == 0)
   {
    grad = temp[0];
    float mt = IsNaNOrInf(clamp(b1 * matrix_m[i] + (1 - b1) * grad, -1.0e5f, 1.0e5f), 0);
    float vt = IsNaNOrInf(clamp(b2 * matrix_v[i] + (1 - b2) * pow(grad, 2), 1.0e-6f, 1.0e6f), 1.0e-6f);
    float weight = clamp(matrix_w[i] + IsNaNOrInf(l * mt / sqrt(vt), 0), -MAX_WEIGHT, MAX_WEIGHT);
    matrix_w[i] = weight;
    matrix_m[i] = mt;
    matrix_v[i] = vt;
   }
}

Ao final, os valores atualizados são gravados novamente na memória global.

Em conjunto com as duas etapas anteriores (propagação para frente e propagação reversa do erro), esse mecanismo torna o bloco convolucional completamente autossuficiente, diferenciável e adequado para treinamento em uma arquitetura de rede neural profunda. E, o que é especialmente importante, ele é escalável e se adapta facilmente a um número arbitrário de janelas e canais. Isso confere ao modelo uma flexibilidade única no trabalho com séries temporais reais, não lineares e não estacionárias.

No lado do programa principal, toda a funcionalidade da convolução multicanal com padding zero está encapsulada na classe CNeuronMultiWindowsConvWPadOCL. Esse módulo herda do objeto da camada convolucional básica CNeuronConvOCL e serve como interface para o enfileiramento de todos os kernels OpenCL descritos acima.

A estrutura da classe é apresentada abaixo.

class CNeuronMultiWindowsConvWPadOCL    :  public CNeuronConvOCL
  {
protected:
   int               aiWindows[];
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronMultiWindowsConvWPadOCL(void) {  activation = SoftPlus;  iWindow = -1; }
                    ~CNeuronMultiWindowsConvWPadOCL(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint &windows[],
                          uint step, uint window_out, uint units_count, uint variables,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronMultiWindowsConvWPadOCL;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual void      SetOpenCL(COpenCLMy *obj);
   //---
   virtual uint               GetWindow(void) const { return aiWindows[0]; }
   virtual uint               GetWindowsSize(void) const { return aiWindows.Size(); }
   virtual uint               GetWindowOut(void) const { return iWindowOut; }
   virtual uint               GetUnits(void) const { return Neurons()/(iVariables*GetWindowsSize()*iWindowOut); }
  };

Essa classe oculta todas as complexidades da interação com OpenCL e permite integrar facilmente o bloco de convolução multiescalar à arquitetura geral do modelo. O código-fonte completo da classe, juntamente com a implementação de todos os métodos, está disponível no anexo do artigo e é destinado ao estudo independente pelo leitor.

Infelizmente, o formato do artigo possui suas limitações. E já esgotamos o volume disponível. A eficácia das abordagens implementadas será avaliada no próximo artigo.

Considerações finais

Neste artigo, demos continuidade ao desenvolvimento da implementação das abordagens propostas pelos autores do framework Mamba4Cast. E nos concentramos em dois módulos fundamentais: a incorporação dos dados brutos levando em conta a codificação temporal e a convolução multicanal com padding zero. O objeto CMamba4CastEmbedding demonstrou como, em um único bloco, é possível combinar a projeção de dados brutos com o código harmônico das marcas temporais. E os kernels OpenCL FeedForwardMultWinConvWPad, CalcHiddenGradientMultWinConvWPad e UpdateWeightsMultWinConvAdamWPad mostraram como implementar de forma eficiente o processamento paralelo com múltiplas janelas de convolução simultaneamente e garantir total diferenciabilidade durante o treinamento.

Dedicamos atenção especial não apenas ao desempenho: o ajuste fino dos deslocamentos, o balanceamento da carga entre os fluxos e a agregação cuidadosa dos gradientes por meio de reduções locais transformaram o bloco convolucional em uma ferramenta verdadeiramente escalável. Ao mesmo tempo, toda a lógica permanece transparente: a classe CNeuronMultiWindowsConvWPadOCL encapsula os detalhes da interação com OpenCL e permite integrar facilmente as soluções implementadas a qualquer modelo.

No próximo artigo, reuniremos todos os componentes desenvolvidos em um único modelo, iniciaremos seu treinamento com dados históricos reais e avaliaremos a eficácia das abordagens implementadas.

Referências

• Mamba4Cast: Efficient Zero-Shot Time Series Forecasting with State Space Models
• Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA de coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA de coleta de exemplos pelo método Real-ORL
3	Study.mq5	Expert Advisor	EA de treinamento offline de modelos
4	StudyOnline.mq5	Expert Advisor	EA de treinamento online de modelos
4	Test.mq5	Expert Advisor	EA para teste de modelo
5	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema e da arquitetura dos modelos
6	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação de redes neurais
7	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL