Redes neurais em trading: generalização de séries temporais sem vinculação a dados (Mamba4Cast)

Introdução

O mercado é algo teimoso e caprichoso. Ele não concede uma segunda chance àqueles que erram na avaliação dos sinais. Especialmente em nossa época, quando o fluxo de notícias se espalha mais rápido do que uma vela se forma em um gráfico de um minuto. O trader moderno não trabalha com o passado, mas com aquilo que ainda está apenas surgindo no fluxo de dados. Antecipar o surgimento de um padrão antes dos outros significa obter uma vantagem. Por isso, a exigência aos algoritmos modernos é uma só, prever antes que algo se torne evidente. E, de preferência, sem se afogar nas complexidades técnicas de configuração e manutenção do modelo.

Nessa corrida, os modelos tradicionais, como as arquiteturas recorrentes, já começam a patinar de forma perceptível. Eles lidam muito bem com padrões repetitivos, memorizam sequências com eficiência, mas frequentemente se perdem no comportamento caótico do mercado real. Têm dificuldade em capturar impulsos, não lidam bem com rupturas, apresentam desempenho fraco diante de valores atípicos e exigem ajustes para cada novo ambiente. O mercado atual exige uma ferramenta mais flexível e preditiva.

As arquiteturas baseadas em Transformer adicionaram inteligência e precisão, especialmente em tarefas com séries temporais longas. No entanto, junto com isso, trouxeram complexidade computacional e peso arquitetural. Com o crescimento do volume de dados e o aumento do horizonte de planejamento, esses modelos se tornam cada vez menos adequados para tarefas em tempo real. Na prática, isso significa mais recursos, mais tempo e mais esforço.

Nesse contexto surge o framework Mamba4Cast, apresentado no trabalho "Mamba4Cast: Efficient Zero-Shot Time Series Forecasting with State Space Models" Ele soa como um sopro de ar fresco e se baseia em duas ideias centrais, a arquitetura Mamba, leve, porém expressiva, e o conceito revolucionário de Prior-data Fitted Networks (PFNs). Juntas, elas formam a base para uma nova onda de abordagens de previsão de séries temporais, especialmente em áreas dinâmicas como o trading.

O conceito de PFN representa uma mudança radical de pensamento. Diferentemente dos enfoques clássicos, em que o modelo primeiro é pré-treinado em um conjunto de dados e depois passa por um longo ajuste fino em outro, os PFNs propõem treinar previamente o modelo em tarefas geradas sinteticamente. Ou seja, em vez de uma única tarefa real, o modelo é treinado em milhões de tarefas diferentes, ainda que imperfeitas. Isso o torna verdadeiramente universal e resistente ao novo. No trading, isso significa que o modelo não fica preso a um instrumento específico ou a determinados horizontes temporais, sendo capaz de se adaptar em tempo real.

O framework Mamba4Cast aplica o enfoque PFN de forma plena. Utilizando dados gerados sinteticamente, que cobrem uma ampla variedade de cenários, ele forma no modelo um vasto espectro comportamental. Graças a isso, o modelo adquire uma espécie de intuição, a capacidade de generalizar padrões mesmo em condições de alta volatilidade e dinâmica instável.

A segunda característica fundamental é a arquitetura Mamba, que se distingue pela complexidade computacional linear em relação ao comprimento da sequência. Diferentemente dos transformers, Mamba não exige operações quadráticas com matrizes de atenção e, por isso, é capaz de processar sequências longas de dados de entrada de forma rápida e econômica. O que é especialmente importante para o trader é que Mamba4Cast consegue prever uma janela inteira de valores futuros em uma única passagem. Isso reduz drasticamente os erros que surgem na previsão autorregressiva e permite reagir mais rapidamente às mudanças no cenário de mercado.

Além disso, graças à construção de previsões para vários passos à frente de uma só vez, o modelo é ideal para a criação de estratégias de trading complexas: desde a análise do sinal até a tomada direta da decisão de negociação. O Mamba4Cast pode se tornar não apenas um referencial, mas um verdadeiro núcleo do módulo de previsão em um sistema de trading automatizado.

Algoritmo do framework Mamba4Cast

O framework Mamba4Cast é um passo ousado e promissor na evolução dos sistemas de previsão de séries temporais. Em sua base está a combinação de uma fundamentação matemática rigorosa com algoritmos flexíveis de aprendizado profundo, capazes de enxergar o mercado como um ecossistema complexo, no qual passado, presente e futuro se entrelaçam em uma única imagem.

No enfoque tradicional, os modelos são treinados com dados históricos de um único ativo e depois repetem os padrões assimilados. Esse caminho trouxe excelentes resultados em seu tempo, mas hoje enfrenta limitações, os mercados tornam-se mais dinâmicos e os eventos menos previsíveis. Mamba4Cast propõe um caminho diferente, em vez de memorizar séries temporais específicas, utiliza-se a metodologia PFN (Prior-data Fitted Networks). Imagine que você treina um analista não com cotações reais de uma ação específica, mas com um número incontável de cenários sintéticos, aqui uma tendência, ali um flat, mais adiante uma calmaria antes da tempestade e, depois, uma explosão de notícias. Dessa forma, forma-se uma inteligência de mercado universal, pronta para atuar "fora da caixa" em qualquer instrumento.

O coração desse sistema é a arquitetura Mamba, baseada em State Space Modeling. Diferentemente das camadas de Self-Attention volumosas dos transformers, Mamba opera de forma linear em relação ao comprimento da sequência, o que lhe permite processar centenas e milhares de pontos temporais sem crescimento explosivo dos custos computacionais. Essa eficiência não apenas acelera os cálculos, como também abre caminho para a análise operacional de dados em tempo real, onde cada milissegundo conta. Essa solução permite economizar recursos e torna o sistema adequado para o processamento de fluxos de dados em tempo real em condições de alta volatilidade.

Na primeira etapa ocorre o escalonamento da série temporal original. Para isso, aplica-se a normalização Min-Max padrão, na qual cada valor xt é transformado segundo a fórmula:

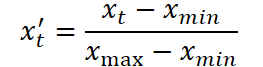
onde xmin e xmax são definidos pelo intervalo dentro do conjunto de treinamento. Isso elimina o desequilíbrio entre características com escalas diferentes e prepara os dados para um treinamento eficiente.

Em seguida começa a parte-chave do pré-processamento, a codificação posicional. As marcas temporais, como minuto, hora, dia da semana, dia do mês, mês e ano, são destacadas separadamente e transformadas em representações vetoriais. Aqui é utilizada um esquema sinusoidal de codificação, análoga à dos transformers, porém adaptada aos componentes periódicos das séries temporais. Para cada componente do tempo são calculadas várias harmônicas de senos e cossenos do produto do período por potências de dois:

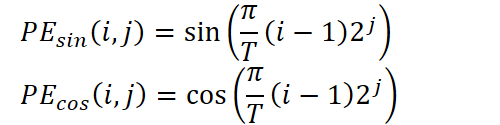
onde T é o período do componente correspondente, i é o índice do ponto temporal e j é o índice da frequência no espectro.

Esses vetores codificam dependências temporais em múltiplas escalas, permitindo que o modelo perceba a ciclicidade diária, a sazonalidade e as fases macroeconômicas.

Depois disso, eles são concatenados com os valores normalizados das próprias séries. O vetor resultante representa a incorporação de um ponto temporal.

O próximo passo é o processamento da sequência utilizando um conjunto de camadas convolucionais causais. Várias convoluções paralelas com janelas exclusivas permitem abranger diferentes escalas temporais. Cada convolução captura informações em seu próprio nível, desde as flutuações mais locais até as tendências de longo prazo. Os resultados do trabalho dessas camadas são combinados, formando uma representação enriquecida para cada ponto temporal. Isso é especialmente importante no contexto de dados financeiros, onde uma mesma vela pode carregar tanto um impulso de curto prazo quanto fazer parte de uma tendência ampla de mercado.

Em seguida, aplica-se uma projeção para um espaço de alta dimensionalidade, o que permite preparar os dados para a transferência ao bloco principal do modelo. Aqui também é conectado um inception-layer modificado, que combina convoluções de diferentes tamanhos, unindo características locais e globais. A ativação final em um ponto no tempo contém informações de diferentes níveis de generalização, mantendo ao mesmo tempo a dimensionalidade da saída e garantindo robustez a lacunas e ruído.

O coração da arquitetura são os blocos baseados no módulo Mamba, uma implementação inovadora de State Space Models (SSM) com complexidade linear em relação ao comprimento da sequência. Cada bloco implementa uma estrutura SSM generalizada, na qual o estado oculto é atualizado por meio das matrizes A, B, C, D, treinadas conjuntamente com os demais parâmetros do modelo:

Dessa forma, cada momento no tempo depende do estado anterior e da entrada atual. Isso garante uma memória estável de longo prazo e uma adaptação flexível ao contexto corrente. Após cada camada desse tipo, aplica-se Layer Normalization, que elimina vieses e normaliza a distribuição das ativações, tornando o treinamento mais estável. Em seguida, vem outra camada causal convolucional, que sustenta o fluxo de informações ao longo do eixo temporal.

A quantidade desses blocos no stack pode variar conforme a profundidade de generalização desejada. Os níveis inferiores se especializam na captura de padrões curtos, recuos rápidos, impulsos e oscilações provocadas por notícias. Os blocos superiores formam uma representação dos ciclos de mercado, movimentos sazonais e formações recorrentes. O stack funciona como um espectro neural, em que cada nível é responsável por sua própria faixa de frequência temporal.

A etapa final é a decodificação. Todas as ativações obtidas são projetadas por uma camada linear em um ou mais canais de saída. Se for necessário avaliar adicionalmente a incerteza, utiliza-se uma cabeça separada que prevê a dispersão em escala logarítmica:

Para tarefas de classificação, é utilizada uma cabeça SoftMax, que fornece as probabilidades das classes analisadas.

Uma característica do Mamba4Cast é sua capacidade de generalização Zero-Shot. Para alcançar isso, os autores propuseram uma etapa única de pré-treinamento em um amplo conjunto de dados sintéticos. Ele inclui séries temporais geradas por equações diferenciais estocásticas (SDE), padrões definidos manualmente, como reversões, consolidações e impulsos, e até regras generativas aleatórias.

O modelo é treinado simultaneamente com várias funções de perda: erro quadrático médio, log-verossimilhança negativa e entropia cruzada na mudança de regime. Isso permite formar uma representação universal e robusta dos padrões de mercado, capaz de se adaptar a novos ativos e a diferentes escalas temporais.

Tudo isso torna o Mamba4Cast não apenas um modelo experimental, mas uma base completa para a construção de sistemas de trading preditivos, algoritmos de avaliação de fases de mercado e previsão de volatilidade.

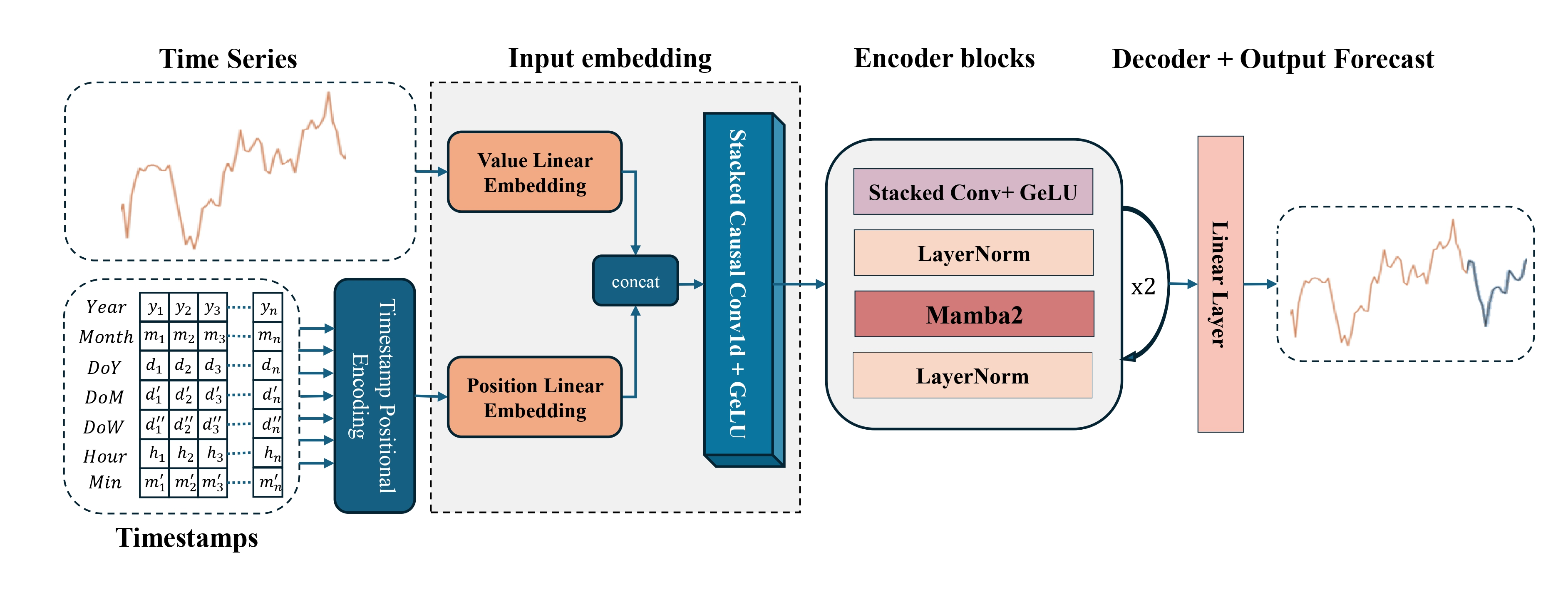
A visualização autoral do framework Mamba4Cast é apresentada abaixo.

Implementação com MQL5

Após um mergulho fundamental na arquitetura do Mamba4Cast, passamos para a parte mais prática, a implementação dos blocos-chave do framework com MQL5. E, antes de tudo, precisamos compreender o objeto de codificação posicional, sem o qual nenhum modelo preditivo moderno é capaz de perceber corretamente a sequência analisada como uma verdadeira escala temporal.

Em nossa biblioteca já existem implementações clássicas de incorporações posicionais, desde as simples seno-cosseno até tabelas treináveis, mas todas elas enxergam a série temporal como um conjunto de elementos consecutivos, sem levar em conta o momento de obtenção dos dados a partir do ambiente externo. Enquanto isso, os autores do Mamba4Cast insistem que cada passo deve ser codificado considerando o período real: minuto, hora, dia da semana, dia do mês, mês e até o ano, pois tudo isso influencia a dinâmica do mercado. O enfoque deles consiste em construir, para cada componente temporal, sua própria decomposição sinusoidal, e é exatamente a esse tratamento profundo do tempo que dedicaremos o primeiro bloco do trabalho prático.

Esse passo realmente define como o modelo irá enxergar o tempo: não apenas como uma sequência de barras, mas como um fluxo vivo de eventos com momentos claramente definidos. Sem uma consideração precisa das marcas temporais, até o algoritmo mais avançado perde o sentido, afinal, o mercado reage de maneira completamente diferente ao minuto, à hora e ao dia.

Codificação temporal no lado do OpenCL

Na nossa implementação, em vez de um enfoque sofisticado, porém pesado, com tabelas previamente calculadas de funções harmônicas, utilizamos um kernel OpenCL para o cálculo instantâneo do código posicional com base em marcas de tempo reais. Essa solução elimina a necessidade de manter na memória grandes matrizes de valores de seno e cosseno, remove degraus na transição entre um ponto e outro e simplifica ao máximo a lógica do EA.

No nosso enfoque, cada passo temporal chega ao kernel OpenCL já acompanhado de dois conjuntos de informações: características numéricas, como preço, volume e indicadores, e o tempo do evento. É exatamente esse momento que transformamos em um vetor que informa ao modelo quando ele ocorreu: no auge da sessão ou na calmaria do meio-dia de um fim de semana, no início do mês ou às vésperas de um novo ano.

As vantagens desse método são percebidas imediatamente. Em primeiro lugar, obtemos um código posicional absolutamente suave, nenhum salto entre índices vizinhos compromete a integridade dos embeddings. Em segundo lugar, a ausência de tabelas significa menos código, menos erros de sincronização e menos memória alocada na plataforma. Em terceiro lugar, o cálculo em tempo real torna o embedding ainda mais atual: não é necessário reconstruir tabelas ao mudar configurações ou períodos, basta alterar os valores dos períodos e o modelo se adapta instantaneamente aos novos requisitos.

O algoritmo de adição do código temporal aos dados analisados no lado do kernel OpenCL consiste em envolver cada barra com seu próprio vetor de harmônicas, refletindo em que ponto de cada ciclo ela foi formada. Nos parâmetros do kernel TSPositionEncoder são passados ponteiros para três matrizes:

• os dados de entrada data,
• a matriz de marcas de tempo time,
• a matriz de períodos period, que define a duração de cada ciclo de calendário.

__kernel void TSPositonEncoder(__global const float2* __attribute__((aligned(8))) data,
                               __global const float* time,
                               __global float2* __attribute__((aligned(8))) output,
                               __global const float* period
                              )
  {
   const int id = get_global_id(0);
   const int freq = get_global_id(1);
   const int p = get_global_id(2);
   const int total = get_global_size(0);
   const int freqs = get_global_size(1);
   const int periods = get_global_size(2);

Esse kernel planejamos executar em um espaço tridimensional de tarefas:

• o tamanho da sequência analisada (o número de passos temporais),
• a quantidade de harmônicas para cada período,
• o número de períodos.

E, no corpo do kernel, identificamos imediatamente o fluxo de execução atual em todas as dimensões do espaço de tarefas.

Primeiro, para cada ponto no tempo (índice id) e para cada harmônica (freq) dentro do período (p), o kernel calcula a coordenada dentro do período: o tempo real é dividido pela duração do ciclo, transformando o valor absoluto time[id] em um número de períodos completos, enquanto a parte fracionária é multiplicada por π e pela potência de dois 2^(freq+1). Isso permite obter o argumento val para o seno e o cosseno, em que a primeira harmônica cobre o ciclo inteiro, a segunda o divide ao meio, a terceira em quartos e assim por diante.

   const int shift = id * freqs + freq;
   const float2 d = data[shift * periods + p];
   const float t = time[id] / period[p];
   float val = M_PI_F * t * pow(2.0f, freq + 1);

Em seguida, esse valor é adicionado à incorporação original: OpenCL carrega um par de números de data correspondente ao tempo atual, à harmônica e ao ciclo, e então incrementa a primeira metade desse par com sin(val) e a segunda com cos(val). O vetor resultante é armazenado no buffer output. É exatamente essa operação colore cada ponto da série temporal com características adicionais, indicando de forma clara sua posição dentro dos padrões de calendário.

   output[shift * periods + p] = (float2)(d.s0 + sin(val), d.s1 + cos(val));
  }

A vantagem desse enfoque está no fato de que o cálculo é realizado na hora, diretamente no núcleo GPU, sem acesso a grandes tabelas e sem lógica no lado CPU. Quaisquer alterações, por exemplo, a adição de um novo período ou o aumento do número de harmônicas, se reduzem ao ajuste dos tamanhos da grade tridimensional de fluxos e dos valores no array period. Ao mesmo tempo, preservamos uma suavidade absoluta: seno e cosseno garantem uma representação contínua do tempo, e o paralelismo da GPU permite processar simultaneamente um grande número de pontos sem atrasos.

Como resultado, cada evento recebe seu próprio, único embedding, levando em conta não apenas o preço ou o volume, mas também o momento exato em que esse evento ocorreu. Isso fornece ao Mamba4Cast toda a profundidade do contexto e torna o algoritmo de previsão verdadeiramente consciente em relação ao tempo.

Como as marcas temporais dos eventos em nossa aplicação não são parâmetros treináveis, para o seu processamento basta implementar apenas a propagação para frente, isto é, a etapa de cálculo dos vetores embedding no núcleo OpenCL. Não precisamos distribuir gradientes de erro ao longo do tempo nem atualizar as próprias marcas. Isso permite excluir os processos de propagação reversa, simplificando ao máximo a arquitetura, e reduzir o cálculo do código posicional a uma função puramente determinística do tempo.

Objeto de codificação temporal

No lado do programa principal, os algoritmos de codificação temporal da sequência analisada são implementados na classe CNeuronTSPositionEncoder, cuja estrutura é apresentada abaixo.

class CNeuronTSPositionEncoder   :  public CNeuronBaseOCL
  {
protected:
   CNeuronConvOCL             cProjection;
   CNeuronBatchNormOCL        cNorm;
   CBufferFloat               cPeriods;
   //---
   virtual bool               AddPE(CBufferFloat *time);
   //---
   virtual bool               feedForward(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool               feedForward(CNeuronBaseOCL *NeuronOCL,
                                          CBufferFloat *SecondInput) override;
   virtual bool               updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool               calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronTSPositionEncoder(void) {};
                    ~CNeuronTSPositionEncoder(void) {};
   //---
   virtual bool               Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                   uint window, uint units_count, uint &periods[], uint freqs,
                                   ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int                Type(void) override  const   {  return defNeuronTSPositionEncoder;   }
   //---
   virtual bool               Save(int const file_handle) override;
   virtual bool               Load(int const file_handle) override;
   //---
   virtual bool               WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void               SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual uint               GetWindow(void) const { return cProjection.GetWindow(); }
   virtual uint               GetWindowOut(void) const { return cProjection.GetFilters(); }
   virtual uint               GetUnits(void) const { return cProjection.GetUnits(); }
  };

Na estrutura apresentada, chamam imediatamente a atenção três objetos internos que, à primeira vista, parecem redundantes considerando que a codificação temporal é executada no lado do OpenCL. No entanto, são justamente eles que garantem que qualquer sequência de dados analisados seja cuidadosamente empacotada e alinhada em escala antes que o contexto temporal seja adicionado.

Em primeiro lugar, cProjection recebe na entrada absolutamente quaisquer arrays de características provenientes da camada anterior da rede neural e os transforma em vetores uniformes de dimensionalidade fixa. Graças a isso, as demais partes do código não precisam se preocupar com quantas características existem nos dados nem como elas estão agrupadas, a saída de cProjection sempre tem uma forma previsível, pronta para a normalização em lote e para a codificação posicional.

Em segundo lugar, cNorm desempenha o papel de garante da estabilidade. Na prática, preços, volumes e quaisquer sinais estocásticos podem variar abruptamente ao longo de seus intervalos de valores. Se imediatamente após a projeção misturarmos a eles valores seno-cosseno no intervalo [-1,1], parte da informação corre o risco de ser perdida. Para evitar isso, passamos a saída de cProjection pela normalização em lote, trazendo a média para zero e a variância para um. Somente depois disso introduzimos as harmônicas do tempo. É exatamente nessa ordem que os atributos temporais se tornam uma extensão orgânica dos dados já processados, e não um ruído caótico.

Por fim, cPeriods armazena um conjunto constante de periodicidades dos ciclos temporais.

É justamente essa separação de responsabilidades que torna a classe simultaneamente flexível, pois aceita quaisquer dados de entrada, estável, pois sempre alinha tudo a uma forma consistente, e precisa, ao permitir uma continuidade absoluta da codificação temporal.

Para transformar a classe CNeuronTSPositionEncoder de uma construção declarativa em um nó funcional real, é necessário inicializar corretamente todos os seus componentes internos. É exatamente essa tarefa que o método Init resolve.

bool CNeuronTSPositionEncoder::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                    uint window, uint units_count, uint &periods[], uint freqs,
                                    ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, 2 * units_count * freqs * periods.Size(),
                                                                         optimization_type, batch))
      return false;

O método segue rigorosamente a lógica da arquitetura descrita anteriormente: projeção → normalização → adição de atributos temporais.

Na primeira etapa, é chamado o método homônimo da classe pai. Nele são definidos os parâmetros gerais do objeto. Observe que, ao especificar o tamanho do tensor de resultados, multiplicamos o produto dos parâmetros obtidos por 2. A razão disso é a representação de cada harmônica temporal na forma de dois componentes, seno e cosseno.

Em seguida, é inicializado o buffer dos ciclos temporais. Sua periodicidade é definida em segundos.

   cPeriods.BufferFree();
   if(!cPeriods.AssignArray(periods) ||
      !cPeriods.BufferCreate(OpenCL))
      return false;

Depois disso, inicializamos a camada de projeção dos dados de entrada para um espaço de dimensionalidade fixa: 2 × frequências × períodos. Esse tamanho corresponde ao número de canais que desejamos dotar de atributos temporais. Na prática, estamos configurando filtros que irão preparar cada fragmento da série temporal para a adição das fases temporais.

   int index = 0;
   if(!cProjection.Init(0, index, OpenCL, window, window, 2 * freqs * cPeriods.Total(), units_count,
                                                                           1, optimization, iBatch))
      return false;
   cProjection.SetActivationFunction(TANH);

O uso da função de ativação TANH na etapa de projeção não é apenas uma escolha estilística, mas uma solução prática para limitar a amplitude dos valores de saída ao intervalo [-1;1]. E isso traz imediatamente várias vantagens importantes.

Se os dados de entrada contêm ruído, saltos ou valores extremos, TANH atua como um limitador suave, suavizando desvios acentuados e tornando o comportamento do modelo mais estável. Isso é especialmente importante no contexto de séries temporais financeiras, onde velas repentinas ou picos de volume podem desorientar toda a rede.

Além disso, a função TANH fornece uma derivada suave em todo o intervalo de entrada, o que é importante para a propagação posterior do gradiente. Isso reduz o risco de saturação dos neurônios e contribui para uma convergência mais estável e rápida.

Assim que a convolução é concluída, seu resultado é encaminhado para cNorm, onde os valores médios e a escala são ajustados. Isso protege contra o afogamento dos sinais seno-cosseno em amplitudes excessivamente grandes e garante a confiabilidade do código temporal.

   index++;
   if(!cNorm.Init(0, index, OpenCL, cProjection.Neurons(), iBatch, optimization))
      return false;
   cNorm.SetActivationFunction(None);

O toque final: como o código temporal não é um nó treinável no sentido clássico, desativamos a ativação geral e simplesmente encaminhamos os gradientes das interfaces externas para cNorm.

   SetActivationFunction(None);
   if(!SetGradient(cNorm.getGradient(), true))
      return false;
//---
   return true;
  } 

Ao passar para a implementação da propagação para frente na classe CNeuronTSPositionEncoder, vale ressaltar que essa etapa representa o encerramento lógico de todo o procedimento de codificação temporal. É exatamente aqui que ocorre a união da informação projetada e normalizada da sequência original com a estrutura temporal detalhada na forma de harmônicas, calculadas a partir do tempo real de chegada dos dados.

O método feedForward divide cuidadosamente o processo em três estágios sequenciais. Observe também que, nos parâmetros do método, são passados ponteiros para 2 fontes de dados. Pelo fluxo principal de informações é apresentada a sequência analisada, enquanto pelo segundo fluxo são fornecidas as marcas temporais.

bool CNeuronTSPositionEncoder::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)
  {
   if(!cProjection.FeedForward(NeuronOCL))
      return false;

Inicialmente, é chamado o método de propagação para frente da camada de projeção dos dados de entrada. Nessa etapa, os dados de entrada de qualquer dimensionalidade são reduzidos a um número definido de características, garantindo o alinhamento das dimensões para a posterior sobreposição da quantidade especificada de harmônicas de informação temporal.

Em seguida, as projeções obtidas passam pela camada de normalização.

   if(!cNorm.FeedForward(cProjection.AsObject()))
      return false;

A tarefa da normalização é suavizar as diferenças estatísticas entre as características dos dados analisados e prepará-las para a soma com as harmônicas temporais.

E, por fim, o passo final é a chamada do método-wrapper do kernel de codificação temporal descrito anteriormente, que, em tempo real, para cada passo temporal e para cada frequência especificada, calcula as harmônicas seno-cosseno com base no valor atual da marca temporal e no conjunto de períodos definidos.

   return AddPE(SecondInput);
  }

Essa operação não depende de parâmetros sujeitos a treinamento e não requer propagação de gradiente, pois o tempo é um fator externo e determinístico.

Como resultado, na saída obtemos uma representação rica, que combina tanto as características semânticas dos dados quanto o contexto temporal preciso em que esses dados chegaram, não pelo número ordinal, mas pelo ritmo real dos eventos.

Os processos de propagação reversa na classe CNeuronTSPositionEncoder são extremamente concisos em sua estrutura, mas não perdem sua importância. Todos os cálculos se resumem ao esquema clássico de propagação do gradiente do erro até o nível dos dados de entrada. Nesse processo, o fluxo principal de cálculos passa por dois componentes-chave: a camada de projeção (cProjection) e a camada de normalização (cNorm). Cada um deles contém parâmetros treináveis e requer a otimização correspondente.

Na prática, isso significa que, ao chamar os métodos updateInputWeights e calcInputGradients, nosso objeto apenas delega sequencialmente o controle aos métodos correspondentes dos componentes internos.

Esse enfoque garante modularidade e reutilização da lógica: alterações no mecanismo de treinamento de uma camada específica se propagam automaticamente por todo o sistema, sem a necessidade de reescrever o código de nível superior. Isso é especialmente importante no contexto de arquiteturas de redes neurais escaláveis.

No entanto, aqui é necessário fazer uma observação importante. Apesar de o método de propagação para frente feedForward receber dois fluxos de informação: a sequência principal de dados de entrada e o array de marcas temporais, no processo de propagação reversa do erro participa apenas o fluxo principal de informações. E isso é absolutamente justificado.

A razão é que a codificação temporal em CNeuronTSPositionEncoder não possui parâmetros treináveis. Ela representa uma operação fixa e determinística sobre a marca temporal. Além disso, deliberadamente não propagamos o gradiente do erro até o nível das marcas temporais. Esses valores são externos em relação ao modelo e não devem ser alterados como resultado da otimização.

Essa lógica torna a arquitetura não apenas limpa e estável, mas também logicamente consistente: os dados temporais são utilizados para contextualização, mas não para aprendizado.

O código completo dessa classe e de todos os seus métodos está apresentado no anexo.

Chegamos suavemente aos limites razoáveis do formato do artigo. Os principais componentes da codificação temporal foram analisados, as ideias-chave foram implementadas e a arquitetura da camada recebeu uma materialização clara e bem estruturada no código. Mas, como se diz, não é tudo de uma vez.

Nossa implementação ainda não está concluída. Há muito trabalho pela frente, que exige um enfoque calmo e ponderado. Vamos fazer uma pequena pausa, respirar e continuar no próximo artigo.

Considerações finais

Neste artigo, conhecemos o framework Mamba4Cast, criado para resolver uma das tarefas fundamentais na análise de séries temporais — a construção de um modelo flexível e escalável, capaz de levar em conta a estrutura complexa de séries temporais dinâmicas. Vimos como os autores do framework contornaram as limitações tradicionais dos modelos clássicos, integrando os mais recentes enfoques arquiteturais, incluindo State Space Models (SSM), ampliados por um mecanismo de Causal Convolution, e complementando-os com uma codificação posicional precisa baseada em marcas temporais reais.

Ao mergulhar gradualmente na estrutura do framework, analisamos em detalhe a lógica de formação dos atributos temporais. Entendemos como, com a ajuda de funções harmônicas simples, porém poderosas, é possível transformar marcas de tempo cruas em incorporações significativas, refletindo a natureza cíclica dos processos de mercado. No exemplo da implementação em OpenCL, vimos como essas incorporações podem ser obtidas de forma eficiente diretamente no núcleo de computação, sem tabelas adicionais e sem atrasos.

Mas nosso trabalho ainda não terminou e vamos continuar no próximo artigo, onde mostraremos como as incorporações temporais interagem com os blocos arquiteturais do modelo, garantindo a integridade da análise e aumentando a precisão das previsões.

Referências

• Mamba4Cast: Efficient Zero-Shot Time Series Forecasting with State Space Models
• Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA de coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA de coleta de exemplos pelo método Real-ORL
3	Study.mq5	Expert Advisor	EA de treinamento offline de modelos
4	StudyOnline.mq5	Expert Advisor	EA de treinamento online de modelos
4	Test.mq5	Expert Advisor	EA para teste de modelo
5	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema e da arquitetura dos modelos
6	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação de redes neurais
7	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL