Redes neurais em trading: Extração eficiente de características para classificação precisa (Mantis)

Introdução

Em um mundo onde milissegundos e as menores oscilações de preço têm importância decisiva, os traders buscam ferramentas capazes não apenas de prever o movimento seguinte, mas também de classificar com precisão os padrões mais complexos nos gráficos. Nesse contexto, o modelo fundamental (foundation) Mantis, proposto no artigo "Mantis: Lightweight Calibrated Foundation Model for User-Friendly Time Series Classification", abre uma nova etapa na análise de séries temporais. Com sua leveza, arquitetura bem pensada e calibração superior, Mantis permite integrar rapidamente um classificador em sistemas de trading e obter intervalos de confiança confiáveis para o gerenciamento de risco.

Os autores observam que as abordagens clássicas, treinadas para prever valores subsequentes, muitas vezes se mostram excessivamente inertes, pois exigem uma reconfiguração cuidadosa para cada nova estratégia, e grandes saltos de volatilidade podem distorcer significativamente seu funcionamento. Ao mesmo tempo, nos últimos anos, os modelos foundation para previsão de séries apresentaram resultados impressionantes, porém são essencialmente voltados para regressão, e não para a classificação de regimes de mercado. Foi exatamente essa lacuna que os autores do framework preencheram, ao propor o framework Mantis com pré-treinamento contrastivo.

A ideia é simples e elegante: dividir a série temporal em uma sequência de patches e, em seguida, de forma semelhante ao Vision Transformer na visão computacional, aplicar uma atenção multifacetada. Ao mesmo tempo, o mecanismo clássico de atenção global possui complexidade quadrática, o que, para dados de alta frequência, se torna um gargalo. Para suavizar esse efeito, Mantis utiliza simultaneamente tokens locais, obtidos por meio de convoluções e pooling em janelas pequenas, e tokens globais, que acumulam informações sobre as tendências ao longo de todo o segmento. Essa combinação oferece uma escalabilidade quase linear em relação ao comprimento da série e preserva a capacidade de captar tanto pequenas flutuações quanto padrões de longo prazo.

O pré-treinamento contrastivo em Mantis tornou-se aquele ingrediente secreto que une diferentes ampliações de um mesmo fragmento temporal e, ao mesmo tempo, afasta séries radicalmente distintas. Como resultado, as incorporações de um mesmo padrão, com variações diferentes, se aproximam no espaço, enquanto eventos distintos se afastam. Essa estratégia permite que o modelo aprenda características robustas de diferentes padrões, apesar de picos e vales poderem se deslocar em amplitude e no tempo.

Um aspecto de extrema importância para o trader é a avaliação da segurança ao abrir uma posição: não basta apenas dizer "isso é uma reversão de tendência", é necessário entender o quanto o modelo está confiante em sua conclusão. Mantis resolve essa tarefa com um módulo embutido de escalonamento de temperatura, que ajusta os logits na saída de forma que as probabilidades a posteriori realmente reflitam a frequência de acerto em cada classe. Graças a isso, ao indicar "80% de probabilidade de reversão", o trader pode esperar que, aproximadamente, em quatro de cada cinco casos o sinal seja correto.

Atenção especial os autores também dedicaram à análise multimodal: no trading algorítmico, frequentemente são utilizados dezenas de indicadores simultaneamente (médias móveis, RSI, volumes, correlações de pares de moedas etc.). A simples união de todos os canais em um único, de alta dimensionalidade, leva a uma explosão no número de parâmetros e ao aumento das exigências de memória, enquanto a análise de sequências unitárias priva o modelo de informações sobre dependências entre canais. Por isso, os autores do framework incorporaram adaptadores leves, que comprimem as interações intercanal em um espaço compacto, sem perder as informações sobre as relações entre diferentes indicadores.

Para ilustrar a utilidade prática do Mantis, imagine um cenário de "flash crash" no mercado de criptomoedas: em questão de um segundo, o preço despenca alguns por cento e, em seguida, se recupera com a mesma rapidez. Um modelo clássico pode interpretar essa anomalia como ruído e ignorar o sinal de entrada. O Mantis, graças ao pré-treinamento em milhões de exemplos reais e sintéticos, entende que eventos desse tipo podem ser "falsos" ou "verdadeiros": ele emite o rótulo "anomalia de curta duração" ou "reversão real", com diferentes intervalos de confiança, permitindo que o trader desenvolva uma estratégia adequada de proteção de capital.

Outro caso vivo é a classificação de regimes do mercado de ações de empresas de tecnologia. Na fase de crescimento, os preços se movem quase de forma síncrona devido a um pano de fundo noticioso comum, enquanto no regime de correção cada ativo se comporta à sua maneira. O Mantis, graças aos adaptadores, capta essas discrepâncias intercanal: a baixa correlação entre ativos semelhantes se torna um sinal do início de um ciclo de correção, o que o modelo comunica com uma estimativa de confiança.

Algoritmo Mantis

O framework Mantis demonstra como uma arquitetura bem pensada e um treinamento cuidadoso transformam um conjunto de ideias em uma ferramenta confiável. O foundation-approach apresentado pelos autores do framework se apoia em quatro pilares-chave: tokenização de séries temporais, atenção híbrida, adaptadores para multidimensionalidade e pré-treinamento contrastivo Self-Supervised com calibração posterior.

A ideia central do Mantis está na recusa da divisão tradicional da série temporal em janelas fixas. Em vez disso, utiliza-se a divisão em um número fixo de patches, o que garante independência em relação ao comprimento da sequência de entrada e estabiliza os custos computacionais. Por exemplo, séries de comprimento 1024 e 2048 serão transformadas no mesmo número de patches, 32. Esse tipo de abordagem é criticamente importante no processamento em massa de séries temporais heterogêneas.

A formação da incorporação ocorre em várias etapas. Primeiro, aplica-se uma camada convolucional com 256 canais de saída. Essa camada transforma a série temporal em uma representação espacial mais compacta. Em seguida, cada um dos 32 patches é agregado por meio da operação de média (mean pooling), resultando em um tensor de dimensionalidade (32, 256). Cada patch codifica características locais da série temporal, incluindo picos, oscilações e a microestrutura do movimento de preços.

Em paralelo, é criado um segundo fluxo de dados, o diferencial. Ele é construído com base nas diferenças de primeira ordem entre valores adjacentes da série temporal. Essa transformação ajuda a eliminar tendências de longo prazo e a reforçar sinais associados à dinâmica de curto prazo. Ela é especialmente útil em situações em que o interesse recai sobre desvios em relação a um nível estável ou movimentos bruscos próximos a níveis de suporte e resistência.

Ambos os fluxos passam pelo mesmo procedimento de processamento, isto é, convolução, média e normalização. Na saída, obtêm-se dois conjuntos de patches, cada um com 32 tokens de dimensionalidade 256. Isso fornece ao modelo informações equivalentes tanto sobre a forma do sinal quanto sobre suas mudanças ao longo do tempo.

Adicionalmente, são extraídos mais dois tipos de informação, escalas e volatilidade. Para isso, a série temporal é dividida em 32 janelas iguais, em cada uma das quais são calculados o valor médio e o desvio padrão. Essas estatísticas são codificadas por meio do Multi-Scaled Scalar Encoder, permitindo transmitir ao modelo uma representação das características de fundo do sinal. Dessa forma, o modelo recebe imediatamente quatro fluxos, valores normalizados, diferenciais, valores médios e desvios padrão.

Os quatro fluxos de dados obtidos são unidos por meio de concatenação. Antes disso, eles passam por projetores lineares individuais para alinhar a dimensionalidade. Em seguida, as incorporações combinadas atravessam uma camada de projeção com aplicação posterior de Layer Normalization, formando a representação final da série temporal na forma de 32 tokens de dimensionalidade 256. Esses tokens são contêineres universais que contêm informações comportamentais e estatísticas sobre o mercado.

O passo seguinte na arquitetura é a adição do class-token, um vetor treinável cuja tarefa é agregar informações de todos os tokens. Isso permite que o modelo forme a representação final da série, considerando tanto regularidades locais quanto globais. Para preservar a informação sobre a ordem dos patches, aplica-se a codificação posicional senoidal, após o que os dados seguem para o bloco Transformer.

Transformer inclui 6 camadas. Cada camada contém Multi-Head Attention com 8 cabeças, uma camada de normalização e um bloco Feed-Forward de duas camadas com ativação GELU. Na etapa de pré-treinamento, aplica-se dropout com probabilidade de 10%, o que ajuda a evitar o sobreajuste. Após a passagem por todas as camadas, utiliza-se o vetor de saída do class-token, que forma a incorporação final da sequência.

O Mantis é treinado em uma abordagem Self-Supervised com o uso de aprendizado contrastivo. O modelo aplica diversas ampliações da série temporal dos dados brutos. Em particular, o método RandomCropResize, no qual de 0 a 20% da sequência é removido aleatoriamente, e a parte restante é esticada novamente até o comprimento original. Isso preserva a estrutura geral do sinal, sem violar a ordem dos eventos.

Para cada exemplo xi do batch, são escolhidas aleatoriamente duas ampliações. As representações obtidas passam pela cabeça de projeção e são comparadas por similaridade cosseno.

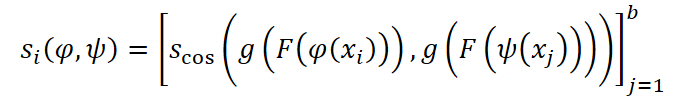
Em seguida, é calculada a função de perda de entropia cruzada.

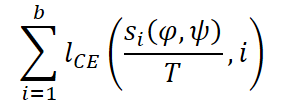
Os autores do framework, em seu trabalho, realizaram o pré-treinamento do modelo em um conjunto combinado de 10 datasets, com volume superior a 7 milhões de séries temporais. O treinamento durou 100 épocas. Foi utilizado um batch de 2048 e quatro GPU Tesla V100-32GB.

Na etapa de ajuste fino, foi acoplada uma cabeça de classificação ao embedding. Os valores preditivos obtidos passam por calibração de temperatura (temperature scaling), permitindo minimizar o erro de calibração esperado e interpretar os resultados do modelo em forma probabilística.

Entretanto, a natureza multivariada das séries temporais permanece como um dos principais desafios. Diferentes tarefas podem envolver diferentes números de canais, o que exige a adaptação do modelo. Assim como outros modelos foundation, Mantis é treinado de forma univariada e aplica o mesmo mecanismo a cada canal. Isso não apenas aumenta a carga sobre os recursos computacionais, como também ignora correlações intercanal.

Para resolver essas limitações, os autores do framework propõem o uso de adaptadores de canais, isto é, uma função a que transforma os d canais originais em dnew. Essa abordagem permite adaptar os dados de entrada ao orçamento computacional, preservar a estrutura temporal e garantir compatibilidade com qualquer modelo.

Aqui, os autores do framework Mantis consideram cinco variantes de adaptadores. As quatro primeiras são métodos clássicos de redução de dimensionalidade:

• PCA (Principal Component Analysis): encontra um espaço ortogonal no qual o máximo da variância está concentrado em um número menor de componentes;
• Truncated SVD: semelhante ao PCA, mas opera sobre a matriz não centralizada;
• Random Projection: mapeamento linear aleatório para um espaço de menor dimensionalidade;
• Variance-Based Selector: seleção dos canais mais variáveis.

Os dados para esses adaptadores são convertidos para a forma (n*t, d), onde n é o número de exemplos. A matriz procurada W implementa a projeção dos canais.

O quinto adaptador, Differentiable Linear Combiner (LComb), é treinado juntamente com o modelo principal por meio do ajuste de parâmetros no processo de propagação reversa. Isso permite levar em conta o contexto da tarefa e alcançar maior precisão.

Como resultado, o Mantis torna-se adequado para uma ampla gama de tarefas, sem perder a estrutura temporal dos dados nem as inter-relações entre canais. O modelo permanece universal e eficiente, mesmo em condições de cenários multivariados reais.

A visualização autoral do framework Mantis é apresentada abaixo.

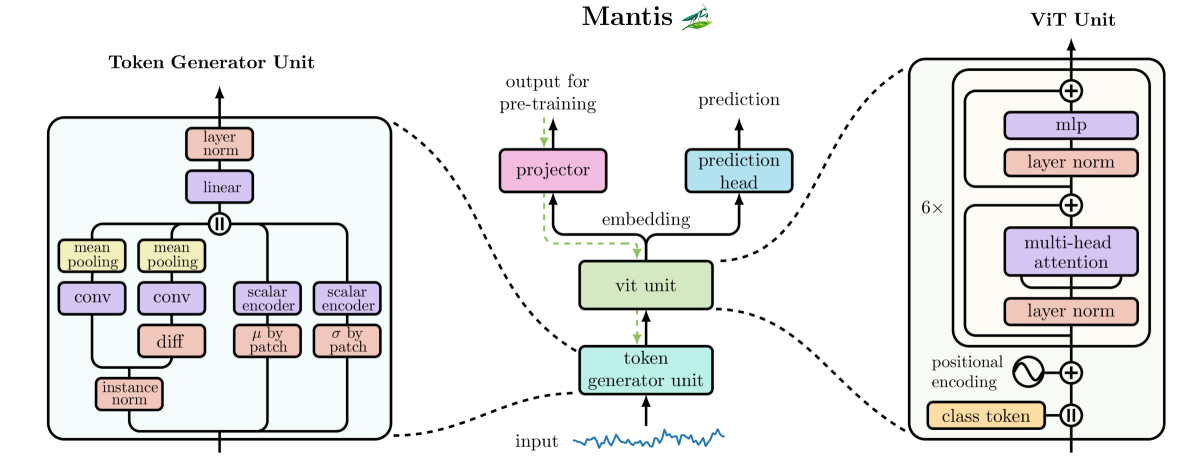
Implementação com MQL5

Após uma análise aprofundada dos aspectos teóricos do framework Mantis, chega o momento de passar para o mais interessante, sua implementação prática. É justamente aqui, no âmago do código real, que as ideias ganham forma e os princípios abstratos começam a gerar valor. No centro da nossa atenção está a implementação de software das principais decisões arquiteturais do framework por meio da linguagem MQL5. Apesar da alta complexidade dos conceitos, temos diante de nós uma tarefa clara e ambiciosa: construir um modelo capaz de processar de forma eficiente dados reais de mercado, adaptar-se à volatilidade e, ao mesmo tempo, permanecer o mais econômico possível em termos de recursos.

Discussão das abordagens

Antes de iniciar a escrita do código, como é próprio da prática de engenharia, é necessário desenvolver uma estratégia. Sem um plano claro, nenhuma arquitetura resiste à pressão do mercado real. Nosso caminho começa com uma reflexão sistêmica: o que exatamente queremos implementar, quais são os papéis dos componentes individuais e onde podem se esconder potenciais gargalos. É importante não apenas reescrever as ideias dos autores, mas adaptá-las à nossa tarefa e às condições do MQL5, que possuem suas próprias limitações e particularidades.

No centro da implementação está a formação dos tokens. É justamente aqui que se estabelecem as bases do sucesso futuro do modelo, pois Transformer não consegue trabalhar de forma eficiente com dados brutos. Ele necessita de uma entrada na forma de sequências de tokens, cada um dos quais carrega uma representação comprimida, porém expressiva, de um trecho da série temporal.

A arquitetura original do Mantis propõe o uso de um esquema multicanal, incluindo séries de desvios, valores médios e desvios padrão dos segmentos. No entanto, em condições de entradas normalizadas, com as quais nossos modelos trabalham na maioria das vezes, a informatividade dos fluxos de valores médios e desvios padrão é reduzida. Optamos conscientemente por abrir mão desses canais, apostando em dois fluxos-chave: a série temporal original e sua primeira diferença. Essa combinação permite considerar simultaneamente tanto os níveis globais quanto as mudanças locais, uma espécie de compromisso entre estabilidade e sensibilidade.

O processo de preparação desses fluxos começa com a normalização da série temporal original. Trata-se de uma etapa importante, que permite suavizar oscilações de grande escala e aumentar a robustez do modelo a valores atípicos. Em seguida, aplica-se a operação de diferenciação, por meio da qual é calculada a diferença entre observações vizinhas. A série resultante apresenta uma reação intensificada a mudanças abruptas, o que é especialmente valioso ao tentar captar impulsos ou reversões do mercado. Depois disso, ambas as séries são unidas em um tensor com dois canais, onde cada canal representa um fluxo informacional separado.

Entretanto, apenas a união não é suficiente. Apesar da riqueza de informações contidas na série temporal multicanal, ao modelo falta criticamente conhecimento sobre o contexto temporal. Os Transformers, como se sabe, não possuem uma capacidade intrínseca de compreender a ordem dos elementos na sequência original e, por isso, necessitam de informações adicionais que descrevam a posição de cada observação em relação às demais.

Na implementação original do Mantis, essa tarefa foi resolvida por meio da adição de codificação posicional senoidal, semelhante àquela proposta no artigo Attention is All You Need. Esse tipo de abordagem é conveniente por sua universalidade e portabilidade, pois não requer treinamento e funciona bem em tarefas de naturezas diversas. Ao mesmo tempo, a codificação é adicionada já após a união dos canais e a segmentação em patches.

No entanto, propomos um caminho diferente. Antes de cortar a sequência em fragmentos, introduzimos uma codificação temporal, de forma semelhante ao framework Mamba4Cast. Essa codificação não apenas indica a posição de um ponto na grade temporal, mas também transmite informações sobre a estrutura temporal da série, permitindo que o modelo capte sazonalidades ocultas, padrões recorrentes, assimetrias e a ritmicidade dos dados de mercado. Diferentemente da codificação senoidal, a codificação temporal é mais sensível à microestrutura do mercado e consegue capturar regularidades que se estendem para além da janela atualmente analisada.

Somente após a adição dessa codificação podemos avançar para a próxima etapa lógica, a segmentação dos canais. Esse passo desempenha o papel de um tipo de filtro, que transforma a informação temporalmente enriquecida em uma forma conveniente para o modelo. Em outras palavras, a essa altura os dados já carregam não apenas o valor e a derivada, mas também uma camada adicional de contexto, que revela sua dinâmica comportamental ao longo do tempo. Isso facilita significativamente a tarefa do modelo de extrair dependências complexas e torna seu funcionamento mais resistente ao ruído do mercado.

Sobre as mudanças no algoritmo de segmentação, proponho falar um pouco mais adiante, quando chegarmos diretamente à sua implementação. Por enquanto, deixamos deliberadamente de lado a descrição dos demais blocos, para nos concentrarmos no fundamento, a transformação da série temporal em uma sequência informativa, padronizada e estruturada. É exatamente nessa etapa que se estabelece o sucesso de todo o modelo. Dados bem preparados permitem identificar padrões de forma eficiente, considerar corretamente a ordem dos eventos e distinguir comportamentos relevantes do mercado.

Agora, quando a base conceitual está construída e o roteiro definido, é hora de passar das palavras à ação. Nesse ponto começa a implementação direta do modelo, o momento em que a teoria se transforma em linhas de código. Começaremos pela parte mais básica e, ao mesmo tempo, extremamente importante, o pré-processamento da série temporal, cuja saída forma uma representação multicanal dos dados. É justamente aqui que ocorre a extração primária de características, que posteriormente determinará o que o Transformer verá e como irá interpretar. A tarefa é extrair dois fluxos, a série original e sua primeira diferença, e então uni-los em um único tensor. Tudo isso será implementado por meio do OpenCL.

Alterações no programa OpenCL

O uso do OpenCL é motivado pela necessidade de acelerar os cálculos, especialmente ao trabalhar com um grande número de séries temporais. A GPU permite paralelizar operações sobre muitas variáveis e acelerar a preparação dos dados sem sobrecarregar o processador principal. Por isso, em primeiro lugar implementamos um kernel especializado ConcatDiff. Sua tarefa é calcular simultaneamente a primeira diferença e concatenar o resultado obtido com os dados originais, formando assim um tensor com dois canais para cada segmento temporal.

Nos parâmetros desse kernel são passados apenas dois ponteiros para buffers de dados, um minimalismo testado pelo tempo. O primeiro é o array de entrada data, que contém as séries temporais analisadas, e o segundo é o buffer de saída output, no qual são armazenados os resultados dos cálculos. Essa abordagem torna a interface do kernel o mais simples e compreensível possível, eliminando carga desnecessária.

Como parâmetro adicional, utiliza-se a constante step, o passo com o qual a diferença é calculada. Essa inovação amplia significativamente a universalidade do algoritmo. Agora podemos calcular tanto a primeira diferença clássica, entre pontos adjacentes, quanto, por exemplo, a diferença entre o valor “agora” e “daqui a cinco passos”. Isso pode ser especialmente útil no contexto financeiro: esse parâmetro permite preparar características que refletem mudanças em diferentes horizontes temporais.

__kernel void ConcatDiff(__global const float* data,
                         __global float* output,
                         const int step)
  {
   const size_t i = get_global_id(0);
   const size_t v = get_local_id(1);
   const size_t inputs = get_local_size(0);
   const size_t variables = get_local_size(1);

Cada fluxo de execução recebe um par único de índices, o índice temporal i e o índice da sequência unitária v. Dessa forma, cada fluxo é responsável pelo processamento de um valor específico na matriz dos dados de entrada.

O array de dados de entrada data representa uma série temporal normalizada, apresentada em forma linear, com desdobramento ao longo do tempo e dos canais.

Em seguida, dentro do kernel, calculamos shift, o deslocamento no array data correspondente à posição temporal variável atual.

const int shift = i * variables;
const float d = data[shift + v];

Após obter o valor original d, passamos ao cálculo de sua primeira diferença ao longo do eixo temporal. Para isso, é tomada a diferença entre o valor atual e aquele localizado step passos adiante. Esse esquema é orientado à preparação de características-alvo que refletem a dinâmica local: crescimento ou queda, aceleração ou desaceleração da mudança. Ao mesmo tempo, é obrigatoriamente verificada a correção do índice, pois não devemos ultrapassar os limites do array.

float diff = 0;
if(step > 0 && (i + step) < inputs)
   diff = IsNaNOrInf(d - data[shift + step * variables + v], 0);

O cálculo da diferença é finalizado com a função de proteção IsNaNOrInf, que zera o resultado em caso de surgimento de NaN ou infinitos, o que é especialmente importante na presença de valores ausentes ou falhas nos dados.

Em seguida chega o estágio-chave, a formação do array de saída output. Aqui ocorre uma operação interessante: os dados são gravados em pares. Primeiro é registrado o valor original e, logo depois, o valor correspondente da primeira diferença. Como utilizamos um deslocamento duplicado por variáveis, isto é, o dobro de canais, o tensor final para cada ponto temporal contém dois valores para cada variável. Assim, a estrutura de output passa a ter dimensão (T * 2 * V), onde T é o número de passos temporais e V é o número de variáveis.

 output[2 * shift + v] = d;
 output[2 * shift + v + variables] = diff;
}

Essa solução permite, em uma única passagem, preparar os dados para alimentar o modelo: o tensor já contém tanto características estáticas quanto dinâmicas do mercado.

A aplicação do OpenCL nesse caso proporciona um ganho duplo: economiza-se tempo, graças ao processamento paralelo, e simplifica-se a lógica do código, já que todo o trabalho com índices e arrays é realizado dentro do kernel. Em vez de ciclos volumosos no lado do CPU, temos um bloco compacto e eficiente, facilmente escalável para dados de qualquer comprimento e largura.

Esse módulo torna-se o primeiro tijolo no fundamento de todo o modelo. Ele implementa a ideia central, a decomposição primária da série temporal em dois fluxos complementares. Os valores originais permitem observar níveis e tendências, enquanto a primeira diferença garante sensibilidade às mudanças, uma espécie de derivada que sinaliza momentos de inflexão. Em conjunto, eles criam uma representação equilibrada, resistente ao ruído e adaptativa a mudanças rápidas.

Aqui vale destacar especialmente uma característica arquitetural desta etapa: no kernel ConcatDiff não existem quaisquer parâmetros treináveis. Sua tarefa é exclusivamente funcional, isto é, realizar as operações lineares mais simples, extração dos valores e de suas diferenças, e unir os resultados em um único array. Tudo isso o torna excepcionalmente adequado para implementação no lado do OpenCL, onde operações de processamento massivamente paralelo, sem lógica de estado complexa, são particularmente eficientes.

Além disso, os próprios dados de entrada, considerando a especificidade das séries temporais financeiras, são perfeitamente razoáveis de serem tratados como constantes dentro de uma única iteração de preparação. Exatamente por isso, neste caso, não implementamos kernels para propagação reversa do gradiente do erro ou atualização de parâmetros. Tais tarefas são relevantes apenas para camadas treináveis que formam o modelo. Aqui, lidamos com o pré-processamento, uma etapa em que velocidade, confiabilidade e total determinismo dos cálculos são fundamentais.

O código completo do programa OpenCL é apresentado no anexo.

Objeto de cálculo da diferença

O próximo passo do nosso trabalho passa a ser a integração do kernel ConcatDiff na estrutura do programa principal. Para isso, criamos um objeto especializado, implementado na forma da classe CNeuronConcatDiff. Esse objeto desempenha o papel de interface entre a lógica de alto nível do modelo de redes neurais e o código OpenCL de baixo nível, sendo responsável pela preparação correta dos parâmetros, pela execução do kernel e pelo recebimento do resultado.

class CNeuronConcatDiff:  public CNeuronBaseOCL
  {
protected:
   uint              iUnits;
   uint              iVariables;
   uint              iStep;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override   { return true; }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronConcatDiff(void) :  iUnits(0), iVariables(1), iStep(1) {  activation = None; }
                    ~CNeuronConcatDiff(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint units_count, uint step, uint variables,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override  const   {  return defNeuronConcatDiff;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
  };

A própria classe inclui várias variáveis-chave:

• iUnits — o número de passos temporais,
• iVariables — o número de canais ou variáveis nos dados de entrada,
• iStep — o parâmetro de deslocamento que define o passo para o cálculo da diferença. Esse valor torna o componente universal, permitindo adaptá-lo a uma largura arbitrária da janela temporal ou à frequência de amostragem.

O construtor da classe inicializa os parâmetros-chave com valores padrão: um canal (iVariables = 1), passo igual a um (iStep = 1) e a função de ativação desativada (activation = None), o que é lógico, pois nosso componente opera no nível de pré-processamento e não deve introduzir não linearidades.

Também é implementado na classe o método de inicialização do objeto Init, em cujos parâmetros são passadas constantes que permitem interpretar de forma inequívoca a arquitetura do objeto criado.

bool CNeuronConcatDiff::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                             uint units_count, uint step, uint variables,
                             ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, 2 * units_count * variables, optimization_type, batch))
      return false;
   if(step<=0 || step >= units_count)
      return false;
//---
   iUnits = units_count;
   iVariables = variables;
   iStep = step;
//---
   return true;
  }

A lógica do método Init é extremamente simples e concisa. Em seu corpo, é chamada a função homônima da classe pai, levando em conta as particularidades da estrutura dos dados. Como unimos no array de saída os dados originais e os valores da primeira diferença, o volume do buffer de saída deve ser duplicado.

Após a inicialização da parte pai, todos os parâmetros recebidos na entrada são armazenados nas variáveis internas da classe. Isso permite utilizá-los posteriormente na formação dos parâmetros para o kernel OpenCL.

Essa abordagem torna o objeto flexível, independente e reutilizável.

Uma atenção especial é dedicada ao método virtual feedForward, que é responsável pelo processo de propagação para frente e, consequentemente, pela chamada do kernel OpenCL.

Nos parâmetros do método, recebemos um ponteiro para o objeto dos dados de entrada e imediatamente realizamos a verificação de sua validade. 

bool CNeuronConcatDiff::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!OpenCL || !NeuronOCL || !Output)
      return false;
   if(getOutputIndex() < 0)
      return false;

Após a passagem bem-sucedida pelo bloco de controles, é efetuado o enfileiramento do kernel ConcatDiff para execução. Aqui é utilizado um algoritmo que já lhe é familiar. Os valores previamente armazenados nas variáveis internas são usados para definir a dimensionalidade do espaço de tarefas. 

{
 uint global_work_offset[2] = {0};
 uint global_work_size[2] = {iUnits, iVariables};
 const int kernel = def_k_ConcatDiff;
 if(!OpenCL.SetArgumentBuffer(kernel, def_k_concdiff_data, NeuronOCL.getOutputIndex()))
   {
    printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel),
                                                               GetLastError(), __LINE__);
    return false;
   }
 if(!OpenCL.SetArgumentBuffer(kernel, def_k_concdiff_output, getOutputIndex()))
   {
    printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                               GetLastError(), __LINE__);
    return false;
   }
 if(!OpenCL.SetArgument(kernel, def_k_concdiff_step, iStep))
   {
    printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                               GetLastError(), __LINE__);
    return false;
   }
 //---
 if(!OpenCL.Execute(kernel, global_work_size.Size(), global_work_offset, global_work_size))
   {
    printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                               GetLastError(), __LINE__);
    return false;
   }
}

Entretanto, o trabalho do método feedForward não se encerra nesse ponto. O passo seguinte consiste na normalização do tensor formado, que, em essência, é a conversão dos dados para uma escala unificada, algo criticamente importante no treinamento de redes neurais. Além disso, aqui é implementada uma normalização separada por características (são normalizados os valores originais das variáveis) e por diferenças (são processados separadamente os valores da primeira diferença). Isso permite preservar a sensibilidade do modelo a mudanças bruscas na série temporal, sem perder a robustez frente a oscilações de grande escala.

     {
      uint global_work_offset[1] = {0};
      uint global_work_size[1] = {2 * iUnits};
      const int kernel = def_k_Normilize;
      if(!OpenCL.SetArgumentBuffer(kernel, def_k_norm_buffer, getOutputIndex()))
        {
         printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel),
                                                                    GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.SetArgument(kernel, def_k_norm_dimension, iVariables))
        {
         printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.Execute(kernel, global_work_size.Size(), global_work_offset, global_work_size))
        {
         string error;
         CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error);
         printf("Error of execution kernel %s: %d -> %s", OpenCL.GetKernelName(kernel), 
                                                                GetLastError(), error);
         return false;
        }
     }
//---
   return true;
  }

Esse tipo de pós-processamento permite aumentar significativamente a estabilidade do treinamento e acelerar a convergência do modelo, graças à unificação dos intervalos dos valores de entrada.

Vale dizer algumas palavras também sobre o método distribuição do gradiente do erro, calcInputGradients. Apesar de não criarmos um kernel de propagação reversa para essa camada, o método correspondente ainda assim é implementado.

Por quê? A resposta é simples. Isso nos permite inserir esse objeto em qualquer nível do modelo, sem o risco de quebrar a cadeia de propagação reversa do erro. Mesmo que o cálculo de gradientes próprios não seja necessário para essa camada, ela deve transmitir corretamente o sinal de erro adiante, ao nível dos objetos anteriores. Caso contrário, o treinamento de todo o modelo pode ser interrompido justamente nela, levando à estagnação do fluxo de gradientes e, como consequência, à impossibilidade de otimizar os parâmetros das camadas inferiores.

O algoritmo do método é simples e confiável. Obtemos um ponteiro para o objeto dos dados de entrada (NeuronOCL) e imediatamente verificamos sua validade.

bool CNeuronConcatDiff::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

Redirecionamos o gradiente do erro ao longo do fluxo informacional direto dos dados de entrada, acumulado no objeto atual, como sinal para a camada anterior. Esse processo é uma simples desconcatenação, sem quaisquer sofisticações computacionais.

if(!DeConcat(NeuronOCL.getGradient(), getPrevOutput(), getGradient(), iVariables, iVariables, iUnits))
   return false;

Se necessário, dependendo da arquitetura, o gradiente do erro pode ser ajustado pela derivada da função de ativação.

   if(NeuronOCL.Activation() != None)
      if(!DeActivation(NeuronOCL.getOutput(), NeuronOCL.getGradient(), NeuronOCL.getGradient(),
                                                                       NeuronOCL.Activation()))
         return false;
//---
   return true;
  }

Essa abordagem garante compatibilidade e flexibilidade da arquitetura. O objeto CNeuronConcatDiff não interfere na propagação dos gradientes e pode ser utilizado em modelos complexos, tanto nos níveis inferiores (próximos à entrada) quanto profundamente dentro do grafo computacional.

Com isso, concluímos a análise dos algoritmos de construção dos métodos da classe CNeuronConcatDiff. O código completo dessa classe e de todos os seus métodos pode ser consultado no anexo.

Gradualmente chegamos aos limites de um volume razoável para o artigo atual. Apesar disso, a parte principal do trabalho ainda está por vir. Até aqui, apenas lançamos o fundamento. No entanto, a história não termina aqui. Para não sobrecarregar o leitor e preservar a legibilidade do material, faremos uma breve pausa e continuaremos a implementação no próximo artigo desta série. Lá nos espera uma etapa não menos interessante e tecnicamente densa.

Considerações finais

Neste artigo, conhecemos o framework Mantis, que combina leveza e alta precisão. Os autores do framework propuseram uma abordagem inovadora para a formação de tokens, baseada em convolução e mean pooling, o que permite representar séries temporais de forma eficiente na forma de 32 tokens com dimensionalidade 256, reduzindo os custos computacionais em comparação com métodos tradicionais. O pré-treinamento contrastivo em exemplos provenientes de diversos datasets proporcionou uma representação de características robusta e transferível, superando abordagens análogas nos modos zero-shot e fine-tuning, além de alcançar um erro de calibração recorde baixo.

Na parte prática, é apresentada a implementação de uma camada-chave de pré-processamento de dados por meio de OpenCL e MQL5, garantindo uma preparação paralela e determinística dos tensores de entrada. No próximo artigo, continuaremos a implementação da nossa própria visão das abordagens propostas pelos autores do framework Mantis.

Links

• Mantis: Lightweight Calibrated Foundation Model for User-Friendly Time Series Classification
• Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA de coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA de coleta de exemplos pelo método Real-ORL
3	StudyContrast.mq5	Expert Advisor	EA de aprendizado contrastivo do codificador
4	Study.mq5	Expert Advisor	EA de treinamento offline dos modelos
5	StudyOnline.mq5	Expert Advisor	EA de treinamento online dos modelos
6	Test.mq5	Expert Advisor	EA para teste do modelo
7	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema e da arquitetura dos modelos
8	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação da rede neural
9	NeuroNet.cl	Biblioteca	Biblioteca de código do programa OpenCL