Redes neuronales: así de sencillo (Parte 97): Entrenamiento de un modelo con el MSFformer

MetaTrader 5 — Sistemas comerciales | 8 enero 2025, 10:07

151

Dmitriy Gizlyk

Introducción

En el artículo anterior construimos los módulos básicos del modelo MSFformer: CSCM y Skip-PAM. El módulo CSCM construye el árbol de características de las series temporales analizadas, mientras que el Skip-PAM extrae información de las series temporales a múltiples escalas usando un mecanismo de atención basado en un árbol de características temporales. En este artículo, continuaremos el trabajo iniciado; así, entrenaremos el modelo y evaluaremos su rendimiento con datos reales en el simulador de estrategias de MetaTrader 5.

1. Arquitectura de los modelos

Y antes de empezar a entrenar modelos, tendremos que realizar una serie de preparativos. Primero deberemos definir la arquitectura de los modelos. El método MSFformer se ha desarrollado para resolver problemas de previsión de series temporales. Por consiguiente, lo aplicaremos en el modelo de Codificador de estados del entorno, así como en otros métodos similares.

1.1 Arquitectura del Codificador del entorno

La arquitectura del Codificador de estado de entorno se especifica en el método CreateEncoderDescriptions. En los parámetros, este método obtiene el puntero al objeto de array dinámico en el que vamos a escribir la arquitectura del modelo.

bool CreateEncoderDescriptions(CArrayObj *encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }

En el cuerpo del método comprobaremos la relevancia del puntero obtenido y, de ser necesario, crearemos una nueva instancia del array dinámico.

Ahora vamos a pasar a la descripción propiamente dicha de la arquitectura del modelo. Para ello, suministraremos a la entrada del Codificador datos "brutos" que describan el estado actual del entorno. Como es habitual, usaremos un objeto de capa completamente conectada básica sin función de activación como capa de datos de origen. Su uso en este caso resulta innecesario, ya que escribiremos los datos de origen recibidos directamente en el búfer de resultados de la capa especificada.

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Aquí debemos notar que el tamaño de la capa de datos inicial que vamos a crear deberá coincidir exactamente con el tamaño del tensor de descripción del estado del entorno. Además, la descripción de las condiciones del entorno deberá ser idéntica en todas las fases de entrenamiento y explotación del modelo. Por lo tanto, para que la sincronización de los parámetros de los programas utilizados durante el entrenamiento y la explotación de los modelos resulte cómoda, introduciremos 2 parámetros en las constantes: el número de elementos de descripción de una vela (BarDescr) y la profundidad de la historia analizada (HistoryBars). Usaremos el producto de estas constantes para establecer el tamaño de la capa de datos inicial a crear.

Como ya hemos mencionado, tenemos previsto suministrar a la entrada del modelo los datos de entrada "brutos" (sin procesar). Por un lado, esto nos permitirá restar importancia a la sincronización de los bloques de preparación de los datos de origen en los programas de entrenamiento y explotación de modelos. Y esto es una buena noticia.

Por otro lado, no obstante, el uso de datos sin procesar suele reducir la eficacia del entrenamiento del modelo. Esto se debe a las grandes diferencias en el rendimiento estadístico de los distintos elementos de los datos de origen utilizados. Para minimizar el impacto de este factor, realizaremos el procesamiento inicial de los datos de origen directamente en nuestro modelo. Esta funcionalidad será realizada por una capa de normalización por lotes de datos. Su algoritmo está construido de tal forma que obtendremos todos los datos con una media cercana a "0" y una varianza en la salida igual a la unidad.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Luego introduciremos los datos de origen preparados y la serie temporal ya normalizada en la entrada del módulo de extracción de características CSCM.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronCSCMOCL;
   descr.count = HistoryBars;
   descr.window = BarDescr;

Tenga en cuenta que extraeremos las características dentro de series temporales unitarias. Y aquí especificaremos una longitud de la secuencia igual a la profundidad de la historia analizada, mientras que el número de secuencias unitarias será igual al tamaño del vector de descripción de una vela. Sin embargo, en la composición del tensor de descripción del estado del entorno en los artículos anteriores, solemos recopilar una matriz de datos en la que las filas se corresponden con las barras a analizar, mientras que las columnas se corresponden con las características. Por ello, especificaremos en los parámetros del CSCM la necesidad de transponer previamente los datos.

   descr.step = int(true);

Después extraeremos características en 3 niveles con tamaños de ventana de análisis de 6, 5 y 4 barras.

     {
      int temp[] = {6, 5, 4};
      if(!ArrayCopy(descr.windows, temp))
         return false;
     }

No usaremos la función de activación; asimismo, optimizaremos los parámetros del modelo usando el método Adam.

   descr.step = int(true);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

El módulo Skip-PAM sigue el algoritmo del método MSFformer. En nuestra implementación, añadiremos 3 capas Skip-PAM consecutivas con la misma configuración.

//--- layer 3 - 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSPyrAttentionMLKV;
   descr.count = HistoryBars;
   descr.window = BarDescr;

Aquí especificaremos un tamaño similar de la secuencia analizada, solo que en este caso ya estamos trabajando con una secuencia multimodal.

Luego indicaremos un tamaño del vector interno de descripción de las entidades Query, Key y Value de 32 elementos. Al mismo tiempo, el número de cabezas de atención para el tensor Key-Value será 2 veces menor.

   descr.window_out = 32;
     {
      int temp[] = {8, 4};
      if(!ArrayCopy(descr.heads, temp))
         return false;
     }
   descr.layers = 3;
   descr.activation = None;
   descr.optimization = ADAM;
   for(int l = 0; l < 3; l++)
      if(!encoder.Add(descr))
        {
         delete descr;
         return false;
        }

La pirámide de atención de cada Skip-PAM contendrá 3 niveles. Aquí también utilizaremos el método Adam para optimizar los parámetros del modelo.

A la salida del módulo Skip-PAM obtendremos un tensor cuyo tamaño se corresponderá con los datos de origen. Al mismo tiempo, su contenido se corregirá usando las dependencias entre los elementos de la secuencia analizada. Y después deberemos construir las trayectorias predictivas de la continuación de las series temporales multimodales de los datos iniciales. Nuestro plan consiste en construir trayectorias de previsión independientes para cada serie unitaria de la secuencia multimodal analizada. Para ello, primero transpondremos el tensor de datos obtenido del módulo Skip-PAM.

//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Después, usaremos 2 capas de convolución sucesivas que actuarán como MLP para las secuencias unitarias individuales.

//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = BarDescr;
   descr.window = HistoryBars;
   descr.step = HistoryBars;
   descr.window_out = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = BarDescr;
   descr.window = LatentCount;
   descr.step = LatentCount;
   descr.window_out = NForecast;
   descr.optimization = ADAM;
   descr.activation = TANH;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Observe que para organizar la similitud MLP en las capas convolucionales presentadas anteriormente, indicaremos tamaños iguales para la ventana analizada y para su tamaño de paso. En el primer caso, en el nivel de profundidad de la secuencia analizada, mientras que en el segundo caso será igual al número de filtros de la capa anterior. El número de bloques de convolución será igual al número de secuencias unitarias analizadas. Para crear no linealidad entre las capas de convolución, usaremos la función de activación LReLU.

Para la segunda capa de convolución, estableceremos un número de filtros igual al tamaño de la secuencia predicha, que en nuestro caso será fijado por la constante NForecast.

Además, para la segunda capa de convolución, utilizaremos la tangente hiperbólica (TANH) como función de activación. Debemos decir que la elección de la función de activación no es casual. Como recordará, en la entrada del modelo usamos una capa de normalización por lotes para preprocesar los datos de origen, que lleva los datos a la varianza unitaria y a una media cercana a "0". Según la regla de las 3 sigmas, aproximadamente 2/3 de los valores de una variable aleatoria distribuida normalmente no se alejarán más de 1 desviación típica de la media. Así, el uso de una tangente hiperbólica con un rango de valores (-1, 1) como función permite abarcar el 68% de los valores de la magnitud analizada, permitiéndonos, además, filtrar los "valores atípicos" situados más allá de la desviación típica de la media.

Debemos entender que nuestra intención no es aprender y predecir todas las fluctuaciones de la serie temporal analizada, dado que está llena de ruido diverso. Lo único que necesitamos es realizar una previsión lo suficientemente precisa como para construir una estrategia comercial rentable.

A continuación, utilizaremos la capa de transposición de datos para devolver los valores predichos a la representación de los datos originales.

//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = BarDescr;
   descr.window = NForecast;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Y luego les añadiremos las medidas estadísticas que sacamos antes en la capa de normalización por lotes.

//--- layer 10
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRevInDenormOCL;
   descr.count = BarDescr*NForecast;
   descr.activation = None;
   descr.optimization = ADAM;
   descr.layers=1;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Llegados a este punto, la arquitectura del modelo de Codificador de estados del entorno ya puede considerarse completa. De hecho, en esta forma ya se corresponde con el modelo presentado por los autores del método MSFformer. Aún así, añadiremos un toque final. En trabajos anteriores, hemos dicho que el paradigma de la predicción directa presupone la independencia de los pasos individuales en la secuencia de predicción. Y esto, como usted mismo notará, contradice la esencia de las series temporales. Por lo tanto, usaremos los desarrollos del método FreDF para coordinar los pasos individuales de la secuencia de previsión de las series temporales analizadas que hemos construido.

//--- layer 11
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFreDFOCL;
   descr.window = BarDescr;
   descr.count =  NForecast;
   descr.step = int(true);
   descr.probability = 0.7f;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

De esta forma, la arquitectura del Codificador tendrá un aspecto más acabado. Espero que mis comentarios le hayan ayudado a comprender la lógica incorporada en el modelo que hemos construido.

Llegados a este punto, ya hemos descrito las arquitecturas del modelo para predecir el próximo movimiento de los precios y podríamos seguir con el entrenamiento del modelo. Pero nuestro objetivo va más allá de la predicción de series temporales. Queremos entrenar un modelo capaz de realizar transacciones en los mercados financieros y generar beneficios. Y esto significa que todavía tendremos que crear un modelo de Actor que genere acciones comerciales y las ejecute en nuestro nombre. Asimismo, deberemos crear un modelo de Crítico que evalúe las operaciones generadas por el Actor y nos ayude a construir una estrategia comercial rentable.

1.2 Arquitectura del Actor y del Crítico

La descripción de la arquitectura de los modelos del Actor y el Crítico la crearemos en el método CreateDescriptions. En los parámetros, el método especificado recibirá los 2 punteros a los arrays dinámicos en los que guardaremos la descripción de las soluciones arquitectónicas creadas.

bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic)
  {
//---
   CLayerDescription *descr;
//---
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
   if(!critic)
     {
      critic = new CArrayObj();
      if(!critic)
         return false;
     }

Al igual que en el caso anterior, en el cuerpo del método comprobaremos primero la relevancia de los punteros recibidos y, de ser necesario, crearemos nuevas instancias de objetos de array dinámicos. Después procederemos a la descripción directa de las arquitecturas de los modelos creados.

El primero que crearemos será el modelo del Actor. Y antes de empezar a describir la solución arquitectónica, hablaremos un poco de los objetivos que nos hemos marcado para el modelo del Actor. Obviamente, su objetivo principal consistirá en generar las acciones óptimas para ejecutar una operación comercial. Pero, ¿cómo se supone que lo hará el modelo? Obviamente, el Actor deberá observar el movimiento de precios previsto que generará el Codificador de estado del entorno y determinar la dirección de la transacción. A continuación, deberemos examinar el estado actual de la cuenta y determinar nuestras opciones. El Actor determinará el volumen de la transacción, los riesgos y los objetivos en forma de stop-loss y take-profit. Precisamente en este paradigma describiremos la arquitectura del Actor.

Primero introduciremos un vector de descripción del estado de la cuenta en la entrada del modelo

//--- Actor
   actor.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = AccountDescr;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

que ejecutaremos a través de una capa completamente conectada.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = EmbeddingSize;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Y luego pondremos un bloque de atención cruzada de 9 capas anidadas en el que compararemos el estado de la cuenta actual y el movimiento previsto de los precios.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronMLCrossAttentionMLKV;
     {
      int temp[] = {1, BarDescr};
      ArrayCopy(descr.units, temp);
     }
     {
      int temp[] = {EmbeddingSize, NForecast};
      ArrayCopy(descr.windows, temp);
     }
     {
      int temp[] = {8, 4};
      ArrayCopy(descr.heads, temp);
     }
   descr.layers = 9;
   descr.step = 1;
   descr.window_out = 32;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Al igual que en el Codificador de estado del entorno, utilizaremos:

Un tamaño del vector de descripción de entidades internas de 32 elementos;
El número de cabezas de atención del tensor Key-Value será 2 veces menor que el del tensor Query.

En este caso, cada tensor Key-Value actuará dentro de una sola capa anidada.

A continuación, analizaremos los datos obtenidos utilizando un MLP de 3 capas.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 2 * NActions;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Y en la salida del modelo, generaremos un vector de acción utilizando una cabeza estocástica.

//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronVAEOCL;
   descr.count = NActions;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Recordemos que la cabeza estocástica que creamos generará las acciones "aleatorias" del Actor. La región admisible de estos valores aleatorios estará estrictamente limitada por los parámetros de distribución normal en forma de media y desviación típica aprendidos por la capa anterior. Así, en condiciones ideales, cuando la acción pueda definirse claramente, la varianza de la distribución de la variable aleatoria de la acción generada tenderá a "0". Por lo tanto, obtendremos un resultado cercano a la media aprendida en la salida del Actor. A medida que aumente la incertidumbre, también lo hará la varianza de las acciones generadas. Como consecuencia, obtendremos acciones aleatorias en la salida del Actor. Por ello, deberemos prestar más atención al proceso de comprobación del modelo entrenado cuando se utilizan políticas estocásticas. En igualdad de condiciones, una política entrenada debería generar resultados cercanos. La variación significativa de las 2 pruebas podría indicar un entrenamiento insuficiente del modelo.

Y, obviamente, las acciones generadas por el Actor deberán coordinarse entre sí. El nivel de stop loss deberá corresponderse con el riesgo aceptable en el volumen declarado de la transacción. Con ello, pretendemos excluir las transacciones multidireccionales. Coordinaremos las acciones del Actor utilizando la capa FreDF.

//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFreDFOCL;
   descr.window = NActions;
   descr.count =  1;
   descr.step = int(false);
   descr.probability = 0.7f;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

El modelo del Crítico tendrá una arquitectura similar, solo que sustituiremos el vector de descripciones del estado de la cuenta que recibe el Actor como entrada por el tensor de acciones que el Actor ha generado en el estado del entorno analizado. La ausencia de datos sobre el estado de la cuenta en la entrada del Crítico resulta fácil de explicar. Al fin y al cabo, los ingresos o pérdidas obtenidos no dependen de la cantidad de fondos en la cuenta, sino del volumen y la dirección de la posición abierta.

Para conocer más información sobre la arquitectura del Crítico, le sugiero que se familiarice con ella. El código completo de todos los programas usados en la elaboración de este artículo se encuentra en el anexo.

2. Asesores para la entrenamiento de modelos

Tras describir la arquitectura de los modelos entrenados, ahora hablaremos de los programas de entrenamiento de modelos. En este caso usaremos 2 asesores:

StudyEncoder.mq5 - asesor experto de entrenamiento del Codificador del estado del entorno.
Study.mq5 - entrenamiento de la política del Actor.

2.1 Programa de entrenamiento del Codificador

En "StudyEncoder.mq5" entrenaremos el modelo del Codificador para predecir el próximo movimiento del precio y los valores de los indicadores analizados. No se sorprenda de que gastemos recursos en prever indicadores de análisis aparentemente superfluos. Estamos acostumbrados a que los indicadores se usen para identificar zonas de sobrecompra y sobreventa, para determinar la fuerza de una tendencia o para encontrar puntos de inversión del movimiento de los precios. No obstante, a la hora de construir indicadores, se suelen utilizar varios filtros digitales para minimizar el impacto del ruido inherente a los datos de origen del movimiento de los precios. Esto hace que los valores de los indicadores sean más suaves y, a menudo, más predecibles. Así, usando la previsión de los valores posteriores de los indicadores intentaremos aclarar y confirmar en cierta medida nuestras previsiones sobre la evolución de los precios.

En el método de inicialización "StudyEncoder.mq5", primero cargaremos los datos de la muestra de entrenamiento. Comentaremos sus métodos de recopilación un poco más adelante.

int OnInit()
  {
//---
   ResetLastError();
   if(!LoadTotalBase())
     {
      PrintFormat("Error of load study data: %d", GetLastError());
      return INIT_FAILED;
     }

Después trataremos de cargar un modelo preentrenado del Codificador del estado del entorno. Y aquí nos damos cuenta de que no siempre entrenaremos un modelo completamente nuevo inicializado con parámetros aleatorios. Resulta mucho más probable que tengamos que reentrenar un modelo cuyo entrenamiento inicial no haya logrado los resultados deseados.

//--- load models
   float temp;
   if(!Encoder.Load(FileName + "Enc.nnw", temp, temp, temp, dtStudied, true))
     {
      Print("Create new model");
      CArrayObj *encoder = new CArrayObj();
      if(!CreateEncoderDescriptions(encoder))
        {
         delete encoder;
         return INIT_FAILED;
        }
      if(!Encoder.Create(encoder))
        {
         delete encoder;
         return INIT_FAILED;
        }
      delete encoder;
     }

Si por alguna razón no logramos cargar el modelo preentrenado, llamaremos al método CreateEncoderDescriptions para generar la arquitectura del nuevo modelo. A continuación, inicializaremos el nuevo modelo de la arquitectura dada con parámetros aleatorios.

//---
   Encoder.getResults(Result);
   if(Result.Total() != NForecast * BarDescr)
     {
      PrintFormat("The scope of the Encoder does not match the forecast state count (%d <> %d)", 
                                                           NForecast * BarDescr, Result.Total());
      return INIT_FAILED;
     }
//---
   Encoder.GetLayerOutput(0, Result);
   if(Result.Total() != (HistoryBars * BarDescr))
     {
      PrintFormat("Input size of Encoder doesn't match state description (%d <> %d)", 
                                                       Result.Total(), (HistoryBars * BarDescr));
      return INIT_FAILED;
     }

Luego organizaremos un pequeño bloque de control de la arquitectura del modelo, en el que comprobaremos el tamaño de la capa de datos de entrada y del tensor de resultados. Obviamente, debemos entender que aquí las desviaciones serán casi imposibles al crear un nuevo modelo. Al fin y al cabo, para comprobar las dimensiones usamos las mismas constantes que empleamos para especificar los tamaños de las capas al describir la arquitectura del modelo. Este bloque de controles está más dirigido a detectar casos de carga de modelos preentrenados que no se ajusten a la muestra de entrenamiento usada.

Tras superar con éxito el bloque de control, todo lo que deberemos hacer es generar un evento personalizado para iniciar el proceso de entrenamiento del modelo y finalizar el método de inicialización del EA.

   if(!EventChartCustom(ChartID(), 1, 0, 0, "Init"))
     {
      PrintFormat("Error of create study event: %d", GetLastError());
      return INIT_FAILED;
     }
//---
   return(INIT_SUCCEEDED);
  }

El proceso inmediato de entrenamiento del modelo se construirá en el método Train.

void Train(void)
  {
//---
   vector<float> probability = GetProbTrajectories(Buffer, 0.9);

En el cuerpo del método, primero generaremos un vector de probabilidades para seleccionar las trayectorias de la muestra de entrenamiento. En este caso, el algoritmo se construirá de tal forma que las pasadas con un rendimiento máximo obtengan una mayor probabilidad. Obviamente, esto resultará más relevante cuando se entrene la política del Actor. Al fin y al cabo, el modelo del Codificador del estado de la cuenta no analiza ni el balance actual ni las posiciones abiertas. Funciona solo con el rendimiento de los indicadores analizados y el movimiento de los precios. No obstante, hemos dejado esta funcionalidad para mantener la unidad de la arquitectura de la solución de todos los programas usados.

A continuación declararemos las variables locales necesarias.

   vector<float> result, target, state;
   bool Stop = false;
//---
   uint ticks = GetTickCount();

Y organizaremos un ciclo de entrenamiento del modelo. El número de iteraciones de entrenamiento del modelo se especificará en los parámetros externos del programa.

   for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter ++)
     {
      int tr = SampleTrajectory(probability);
      int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - NForecast));
      if(i <= 0)
        {
         iter--;
         continue;
        }

En el cuerpo del ciclo, muestrearemos una trayectoria y el estado en ella a partir de la muestra de entrenamiento. Luego comprobaremos el estado seleccionado para los datos almacenados y, a continuación, transferiremos la información de la muestra de entrenamiento al búfer de datos.

      state.Assign(Buffer[tr].States[i].state);
      if(MathAbs(state).Sum()==0)
        {
         iter--;
         continue;
        }
      bState.AssignArray(state);

Partiendo de los datos entrenados, realizaremos una pasada directa del modelo entrenado.

      //--- State Encoder
      if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Sin embargo, no cargaremos los valores previstos resultantes. En esta fase, no nos interesan tanto los resultados de la predicción como su desviación respecto a los valores reales posteriores almacenados en la muestra de entrenamiento. Por ello, cargaremos los estados posteriores a partir de la muestra de entrenamiento.

      //--- Collect target data
      if(!Result.AssignArray(Buffer[tr].States[i + NForecast].state))
         continue;
      if(!Result.Resize(BarDescr * NForecast))
         continue;

Y prepararemos los valores verdaderos con los que vamos a comparar las predicciones resultantes. Introduciremos estos datos en los parámetros del método pasada inversa de nuestro modelo. Precisamente en él se optimizarán los parámetros del modelo para minimizar el error de predicción.

      if(!Encoder.backProp(Result,(CBufferFloat*)NULL))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Tras ejecutar con éxito las pasadas directa e inversa de nuestro modelo, todo lo que deberemos hacer es informar al usuario sobre el progreso del proceso de entrenamiento y pasar a la siguiente iteración del ciclo.

      if(GetTickCount() - ticks > 500)
        {
         double percent = double(iter) * 100.0 / (Iterations);
         string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Encoder", 
                                        percent, Encoder.getRecentAverageError());
         Comment(str);
         ticks = GetTickCount();
        }
     }

Debo admitir que el proceso de entrenamiento está estructurado de la forma más simple y sencilla posible. La duración del entrenamiento está determinada únicamente por el número de iteraciones del mismo, que el usuario especifica en los parámetros externos al iniciar el asesor experto. La salida anticipada del proceso de aprendizaje solo es posible si se produce un error o si el usuario cierra el programa en el terminal.

Una vez finalizado el proceso de entrenamiento, borraremos el campo de comentarios del gráfico del programa donde antes mostrábamos el progreso del entrenamiento.

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Encoder", Encoder.getRecentAverageError());
   ExpertRemove();
//---
  }

Luego enviaremos los resultados del entrenamiento al diario de registro de MetaTrader 5 e inicializaremos la finalización del programa actual. El modelo entrenado se guardará en el método OnDeinit. Encontrará el código completo del asesor en el archivo adjunto.

2.2 Algoritmo de entrenamiento del Actor

El segundo asesor experto "Study.mq5" está diseñado para entrenar la política del Actor. Al mismo tiempo, en el marco de este programa también se ejecutará el entrenamiento del modelo del Crítico.

Aquí debemos decir que el papel del Crítico es bastante específico: tendrá que dirigir al Actor para que actúe en la dirección correcta. Sin embargo, el propio Crítico no se utilizará en el explotación del modelo. En otras palabras, por paradójico que parezca, entrenaremos al Crítico para entrenar al Actor.

La estructura del asesor de entrenamiento del Actor resultará similar a la del programa de entrenamiento del Codificador comentado anteriormente. Y dentro del ámbito de este artículo, solo nos centraremos en el método de entrenamiento de modelos Train.

Al igual que en el programa anteriormente analizado, en el cuerpo del método primero generaremos el vector de probabilidades de la selección de trayectorias de la muestra de entrenamiento y declararemos las variables locales.

void Train(void)
  {
//---
   vector<float> probability = GetProbTrajectories(Buffer, 0.9);
//---
   vector<float> result, target, state;
   bool Stop = false;
//---
   uint ticks = GetTickCount();

Después declararemos un ciclo de entrenamiento, en cuyo cuerpo muestrearemos la trayectoria partiendo de la muestra de entrenamiento y el estado en ella.

   for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter ++)
     {
      int tr = SampleTrajectory(probability);
      int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2));
      if(i <= 0)
        {
         iter--;
         continue;
        }
      state.Assign(Buffer[tr].States[i].state);
      if(MathAbs(state).Sum()==0)
        {
         iter--;
         continue;
        }
      bState.AssignArray(state);

Aquí codificaremos la marca temporal que representaremos como un vector de armónicos sinusoidales de diferentes frecuencias.

      bTime.Clear();
      double time = (double)Buffer[tr].States[i].account[7];
      double x = time / (double)(D'2024.01.01' - D'2023.01.01');
      bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = time / (double)PeriodSeconds(PERIOD_MN1);
      bTime.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0));
      x = time / (double)PeriodSeconds(PERIOD_W1);
      bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      x = time / (double)PeriodSeconds(PERIOD_D1);
      bTime.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
      if(bTime.GetIndex() >= 0)
         bTime.BufferWrite();

Luego utilizaremos los datos recopilados para generar valores predictivos de la próxima evolución de los precios. Esta operación se realizará llamando al método de pasada directa del Codificador previamente entrenado.

      //--- State Encoder
      if(!Encoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false,(CBufferFloat*)NULL))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Como ya hemos dicho, para entrenar al Actor, tendremos que entrenar al Crítico. Después extraeremos de la muestra de entrenamiento las acciones realizadas por el Actor durante la recogida de la muestra de entrenamiento.

      //--- Critic
      bActions.AssignArray(Buffer[tr].States[i].action);
      if(bActions.GetIndex() >= 0)
         bActions.BufferWrite();

Y las suministraremos a la entrada de nuestro modelo de Crítico junto con el estado previsto del entorno.

      Critic.TrainMode(true);
      if(!Critic.feedForward((CBufferFloat*)GetPointer(bActions), 1, false, GetPointer(Encoder), LatentLayer))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Aquí debemos señalar que, a la entrada del Crítico, en lugar de los datos de predicción del próximo movimiento de precios y los indicadores futuros que se han entrenado en la salida del modelo, suministraremos el estado oculto del Codificador. Esto se debe a que, a la salida del Codificador, hemos añadido los parámetros estadísticos de la serie temporal original a los valores predichos. Por consiguiente, antes de procesar estos datos en el modelo del Crítico, tendremos que normalizarlos. Pero en su lugar, tomaremos el estado oculto del Codificador, que contiene los valores predichos sin los sesgos inherentes a los datos originales.

Como resultado de la pasada directa, el Crítico ha formado una cierta evaluación de las acciones del Actor, que, obviamente, en las primeras iteraciones de entrenamiento estará lejos de la recompensa real que el Actor ha obtenido al interactuar con el entorno. Luego extraeremos de la muestra de entrenamiento la recompensa real recibida por la acción realizada.

      result.Assign(Buffer[tr].States[i + 1].rewards);
      target.Assign(Buffer[tr].States[i + 2].rewards);
      result = result - target * DiscFactor;
      Result.AssignArray(result);
      if(!Critic.backProp(Result, (CNet *)GetPointer(Encoder), LatentLayer))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Y realizaremos una pasada inversa del Crítico para minimizar el error de evaluación de la acción.

A continuación, implementaremos el entrenamiento de la política del Actor. Para implementar su pasada directa, primero deberemos preparar el tensor de descripción del estado de la cuenta, que extraeremos de la muestra de entrenamiento.

      //--- Policy
      float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0];
      float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1];
      bAccount.Clear();
      bAccount.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance);
      bAccount.Add(Buffer[tr].States[i].account[1] / PrevBalance);
      bAccount.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity);
      bAccount.Add(Buffer[tr].States[i].account[2]);
      bAccount.Add(Buffer[tr].States[i].account[3]);
      bAccount.Add(Buffer[tr].States[i].account[4] / PrevBalance);
      bAccount.Add(Buffer[tr].States[i].account[5] / PrevBalance);
      bAccount.Add(Buffer[tr].States[i].account[6] / PrevBalance);
      bAccount.AddArray(GetPointer(bTime));
      if(bAccount.GetIndex() >= 0)
         bAccount.BufferWrite();

Y luego realizaremos una pasada directa del modelo transmitiendo el vector de descripción del estado de la cuenta y el estado oculto del Codificador en los parámetros del método.

      //--- Actor
      if(!Actor.feedForward((CBufferFloat*)GetPointer(bAccount), 1, false, GetPointer(Encoder), LatentLayer))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Obviamente, como resultado de la pasada directa del Actor, se ha formado algún vector de acción. Lo introduciremos junto con el estado latente del Codificador en la entrada del Crítico.

      Critic.TrainMode(false);
      if(!Critic.feedForward((CNet *)GetPointer(Actor), -1, (CNet*)GetPointer(Encoder), LatentLayer))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Tenga en cuenta que en este punto desactivaremos el modo de entrenamiento del Crítico. Ya que en este caso el modelo del Crítico solo se utilizará para transmitir el gradiente de error al Actor.

Después optimizaremos los parámetros del Actor, por así decirlo, en 2 direcciones. En primer lugar, se espera que nuestra muestra de entrenamiento tenga pasadas exitosas que produzcan ganancias durante el periodo de entrenamiento. Tomaremos dichas pasadas como referencia y, usando métodos de entrenamiento supervisado, mejoraremos la política de nuestro Actor ante tales acciones.

      if(Buffer[tr].States[0].rewards[0] > 0)
         if(!Actor.backProp(GetPointer(bActions), GetPointer(Encoder), LatentLayer))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            Stop = true;
            break;
           }

Por otro lado, deberemos ser conscientes de que las pasadas rentables serán significativamente inferiores a las no rentables. Y, obviamente, no deberemos ignorar la información que portan. Bien, durante el aprendizaje de la política del Actor, las pasadas no rentables serán tan útiles como las rentables. Si usamos las pasadas rentables a la hora de ajustar la política del Actor, las no rentables, en cambio, deberán usarse como punto de referencia. Pero, ¿en qué medida y en qué dirección? Además, incluso en las pasadas no rentables pueden existir transacciones rentables, y resulta deseable que conservemos esta información. Aquí es donde entra en juego el papel del Crítico en el proceso de entrenamiento de la política del Actor.

Se supone que durante el proceso de entrenamiento del Crítico, sus parámetros optimizarán algún tipo de función de dependencia entre la acción del Actor, el estado del entorno y la recompensa. Por lo tanto, si nos movemos hacia la maximización de la recompensa cuando el entorno no cambia, el gradiente de error apuntará en la dirección del ajuste de las acciones del Agente para aumentar la recompensa esperada. Esa es la propiedad que utilizaremos.

      Critic.getResults(Result);
      for(int c = 0; c < Result.Total(); c++)
        {
         float value = Result.At(c);
         if(value >= 0)
            Result.Update(c, value * 1.01f);
         else
            Result.Update(c, value * 0.99f);
        }

Ahora extraeremos la evaluación actual de las acciones por parte del Crítico. Luego aumentaremos el beneficio en un 1% y disminuiremos la pérdida en la misma cantidad. Estos serán nuestros valores objetivo en esta fase. Los transmitiremos a las operaciones de pasada inversa del Crítico y luego al Actor.

      if(!Critic.backProp(Result, (CNet *)GetPointer(Encoder), LatentLayer) ||
         !Actor.backPropGradient((CNet *)GetPointer(Encoder), LatentLayer, -1, true))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Querríamos recordarle que, en este momento, hemos desactivado el modo de entrenamiento para el Crítico, y eso significa que solo se utilizará para transmitir el gradiente de error al Actor; esta pasada inversa no ajustará los parámetros del Crítico. El Actor, por su parte, ajustará los parámetros del modelo en la dirección de la maximización de la recompensa esperada.

Entonces, todo lo que deberemos hacer es informar al usuario sobre el progreso del entrenamiento del modelo y pasar a la siguiente iteración del ciclo.

      //---
      if(GetTickCount() - ticks > 500)
        {
         double percent = double(iter) * 100.0 / (Iterations);
         string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Actor", 
                                          percent, Actor.getRecentAverageError());
         str += StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Critic", 
                                          percent, Critic.getRecentAverageError());
         Comment(str);
         ticks = GetTickCount();
        }
     }

Una vez finalizado el proceso de entrenamiento, borraremos el campo de comentarios del gráfico del instrumento. Después enviaremos los resultados del entrenamiento al diario de registro e iniciaremos el proceso de finalización del programa.

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Actor", Actor.getRecentAverageError());
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic", Critic.getRecentAverageError());
   ExpertRemove();
//---
  }

Con esto concluiremos nuestra revisión de los algoritmos para los programas de entrenamiento de modelos. Podrá ver el código completo de todos los programas utilizados en la preparación del artículo en el archivo adjunto.

3. Recopilación de la muestra de entrenamiento

El siguiente paso, igual de importante, consistirá en recopilar los datos para la muestra de entrenamiento. Aquí debemos decir que utilizaremos el simulador de estrategias de MetaTrader 5 para obtener datos reales sobre la interacción con el entorno. En él, realizaremos las pasadas sobre datos históricos. Y registraremos los resultados obtenidos en el archivo de muestras de entrenamiento.

Es bastante natural que antes de empezar el entrenamiento, nos surja la pregunta: ¿dónde podemos conseguir pasadas exitosas según la muestra de entrenamiento? Y debemos decir que aquí hay unas cuantas opciones. Probablemente la más obvia sea tomar la historia y "tirar" manualmente de las transacciones perfectas. Sin duda, este enfoque tiene su razón de ser, pero es un trabajo manual, y a medida que crezca la muestra de entrenamiento, también lo hará el esfuerzo a invertir, y al mismo tiempo, el tiempo para preparar la muestra de entrenamiento. Además, el uso de fuerza manual siempre da lugar a diversos errores achacados al "factor humano". Yo utilizo un frame para recopilar los datos primarios, Real-ORL, que ya hemos descrito con detalle en esta serie de artículos. Ahí también figura el código del programa, que se duplica en el archivo adjunto. No nos detendremos a estudiarlo.

La muestra inicial de entrenamiento recogida permite al modelo ofrecer una primera visión del entorno. Pero el mundo de los mercados financieros es tan polifacético que ninguna muestra de entrenamiento puede reproducirlo totalmente. Además, las dependencias que el modelo ha construido entre los indicadores analizados y las transacciones rentables pueden resultar falsas o incompletas, pues no había ejemplos en la muestra de entrenamiento presentada que pudieran revelar tales incoherencias. Por ello, tendremos que refinar la muestra de entrenamiento durante el mismo. Y esta vez el enfoque de recopilación de información adicional ya será distinto.

La cuestión es que en esta fase nos enfrentaremos a la tarea de optimizar la política del Actor aprendida. Y para cumplir dicha tarea necesitaremos datos lo suficientemente cercanos a la trayectoria de la política actual del Actor para entender la dirección del vector de cambio de la recompensa al darse cierta desviación de acciones respecto a la política actual. Con esta información en la mano, podremos aumentar el rendimiento de las políticas actuales avanzando en la dirección de una mayor recompensa.

Aquí también hay diferentes opciones. Y los planteamientos pueden cambiar por diversos factores. Esto incluye la dependencia respecto a la arquitectura del modelo. Por ejemplo, al utilizar una política estocástica, podemos simplemente ejecutar múltiples pasadas del Actor usando la política actual en el simulador de estrategias. La cabeza estocástica lo hará todo por nosotros. La dispersión de las acciones aleatorias del actor abarcará el espacio de acciones de interés, mientras que nosotros podremos realizar un preentrenamiento del modelo dados los datos actualizados. Sin embargo, si utilizamos una política del Actor estricta, en la que el modelo construya vínculos inequívocos entre el estado del entorno y la acción, podremos aprovechar la ventaja que supone añadir algo de ruido a las acciones del Agente para crear una especie de nube de acción en torno a la política del Actor actual.

En ambos casos, nos será cómodo utilizar el modo de optimización lenta del simulador de estrategias para recopilar los datos adicionales de las muestras de entrenamiento.

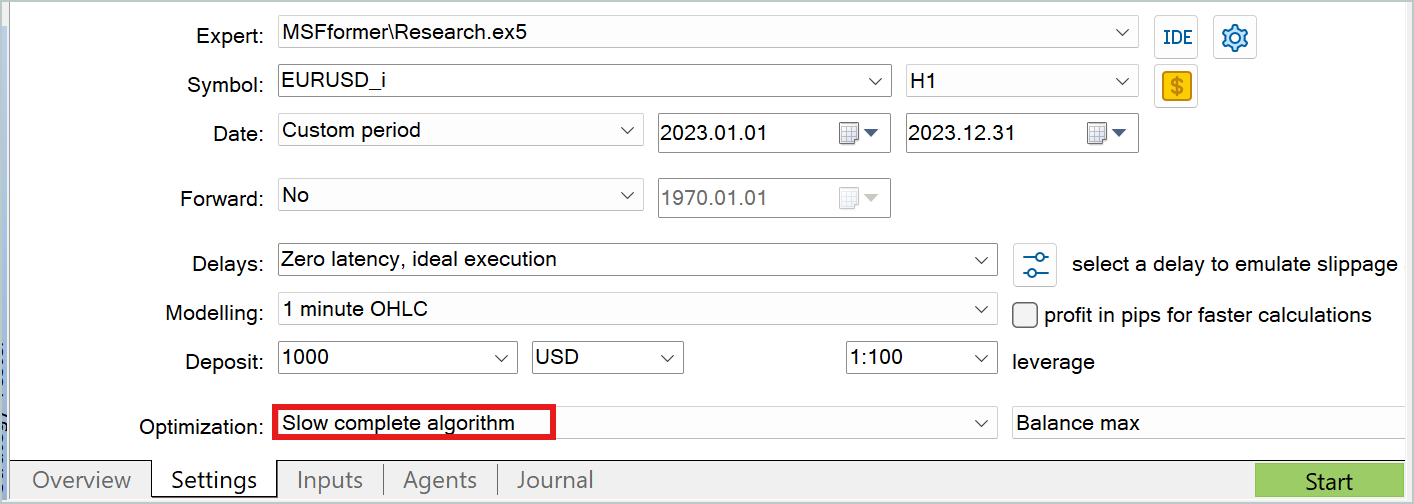
Permítanme que no me detenga en los detalles de los programas de interacción con el entorno. Ya hemos hablado muchas veces de ellos en esta serie de artículos. En el archivo adjunto figura el código completo de todos los programas utilizados en la elaboración de este artículo. También podrá consultar el código de los programas de interacción con el entorno.

4. Entrenamiento y prueba de los modelos

Tras repasar los algoritmos de todos los programas usados en el entrenamiento de modelos, podemos pasar directamente al proceso en sí. Entrenaremos los modelos presentados con datos históricos reales del marco temporal H1 de EURUSD. Además, utilizaremos el año 2023 completo como periodo de estudio.

En el intervalo histórico especificado, recopilaremos la muestra de entrenamiento primaria como hemos comentado anteriormente. Y precisamente con en ella realizaremos el entrenamiento del Codificador del entorno. Como ya hemos mencionado, el modelo del Codificador utilizará únicamente los datos históricos de los movimientos de precio y las lecturas de los indicadores analizados durante el entrenamiento. A mi juicio, resulta obvio que los datos especificados serán idénticos para todas las pasadas en un intervalo invariable de datos históricos. Por lo tanto, no tendrá sentido que refinemos la muestra de entrenamiento en esta fase. Y entrenaremos el modelo del Codificador con la muestra de entrenamiento inicial hasta obtener el resultado deseado.

Durante el entrenamiento, vigilaremos el error de predicción. Asimismo, dejaremos de entrenar el modelo cuando el error de predicción deje de disminuir y sus fluctuaciones se mantengan dentro de un rango pequeño.

Obviamente, tenemos curiosidad por ver qué ha sido capaz de aprender el modelo, aunque nuestro objetivo sea entrenar una política del Actor rentable. Aun así, he decidido saciar mi curiosidad y he comparado el cambio de precio previsto y el real con un conjunto de datos seleccionados aleatoriamente de la muestra de entrenamiento.

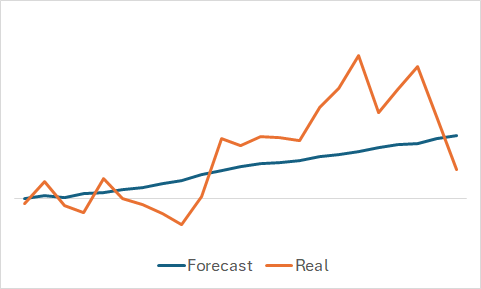
Como podemos ver en el gráfico presentado, el modelo ha sido capaz de captar la tendencia principal del próximo movimiento del precio.

Un gráfico bastante suave del movimiento del precio previsto, con fluctuaciones insignificantes, puede sugerir que quizá el modelo haya captado la tendencia general de la muestra de entrenamiento y pueda mostrar un patrón similar para todos los estados, independientemente de los datos reales. Para confirmar o negar esta suposición, tomaremos otro estado de la muestra de entrenamiento y realizaremos una comparación similar entre los movimientos de los precios previstos y reales.

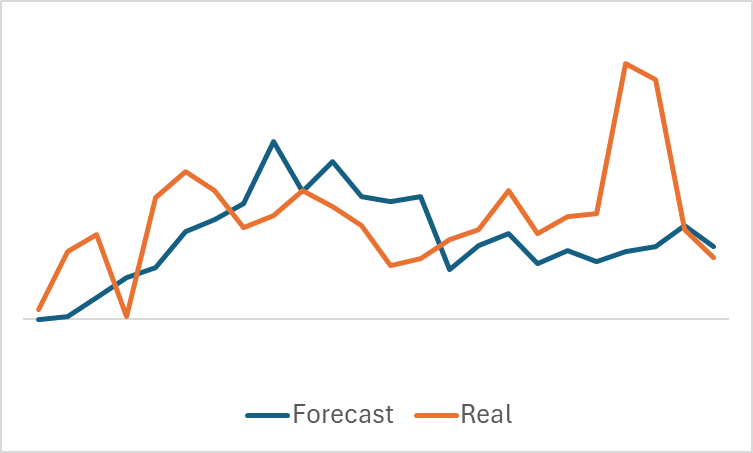
Aquí podemos ver ya fluctuaciones más significativas en los valores previstos del movimiento de los precios. No obstante, se aproximan bastante a los datos reales.

Una vez entrenado el modelo del Codificador de estados del entorno, podemos proceder al segundo paso: el entrenamiento de la política del Actor. Y este proceso será ya iterativo por naturaleza. La primera iteración de entrenamiento la realizaremos sobre los datos de la muestra de entrenamiento primaria. En esta etapa, daremos al modelo una representación inicial del entorno. Y con las pasadas rentables que hayamos podido recopilar utilizando el método Real-ORL, estaremos sentando las bases de nuestras futuras políticas.

En el entrenamiento de los modelos, al igual que en la primera etapa, nos orientaremos según las lecturas de error de los modelos. Y en el primer paso, le recomendaría orientarse según los valores de error del Crítico. Sí, necesitamos una política del actor que pueda generar ingresos, pero no olvidemos lo que hemos dicho antes: para entrenar al Actor necesitaremos entrenar al Crítico. Precisamente la construcción de las dependencias correspondientes dentro del Crítico será lo que nos ayude a ajustar la política del Actor en la dirección correcta.

Cuando el error de Crítico se detenga en un nivel sin signos de disminución adicional, deberemos ir al simulador de estrategias y recopilar datos adicionales utilizando el asesor experto "Research.mq5", que recomiendo ejecutar en el modo de optimización lenta.

A continuación, realizaremos un preentrenamiento de los modelos del Actor y el Crítico. Al principio del proceso de preentrenamiento de los modelos, se observa cierto aumento del error de ambos modelos, debido al procesamiento de los nuevos datos. Sin embargo, pronto notaremos un descenso gradual del error y nuevos mínimos.

De este modo, repetiremos las iteraciones de refinamiento de la muestra de entrenamiento y preentrenamiento de los modelos.

También me gustaría recordarle que la arquitectura del Actor presentada utiliza una cabeza estocástica que se caracteriza por una cierta aleatoriedad en las acciones. Por consiguiente, al probar la política del Actor entrenada, le recomendamos realizar varias pasadas en el segmento temporal de prueba. La política del Actor puede considerarse entrenada si podemos despreciar las desviaciones en las pasadas.

Al preparar este artículo, las pruebas del modelo entrenado se han realizado con los datos históricos de enero de 2024. Este intervalo temporal no formaba parte de la muestra de entrenamiento, lo cual significa que serán datos nuevos para el modelo, y la proximidad de los intervalos en la muestra de entrenamiento y en la prueba nos permite hablar de la comparabilidad de los datos.

Durante el entrenamiento, hemos obtenido un modelo capaz de generar beneficios tanto con los datos de la muestra de entrenamiento como en el periodo de prueba.

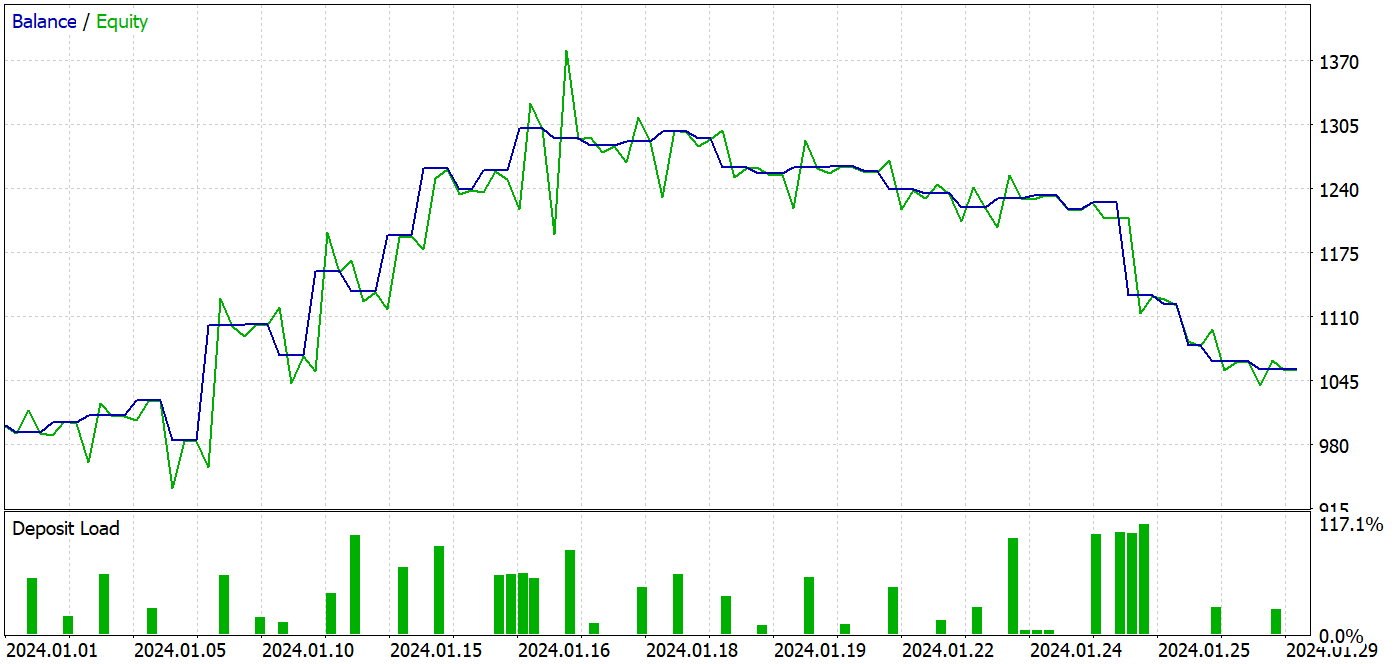
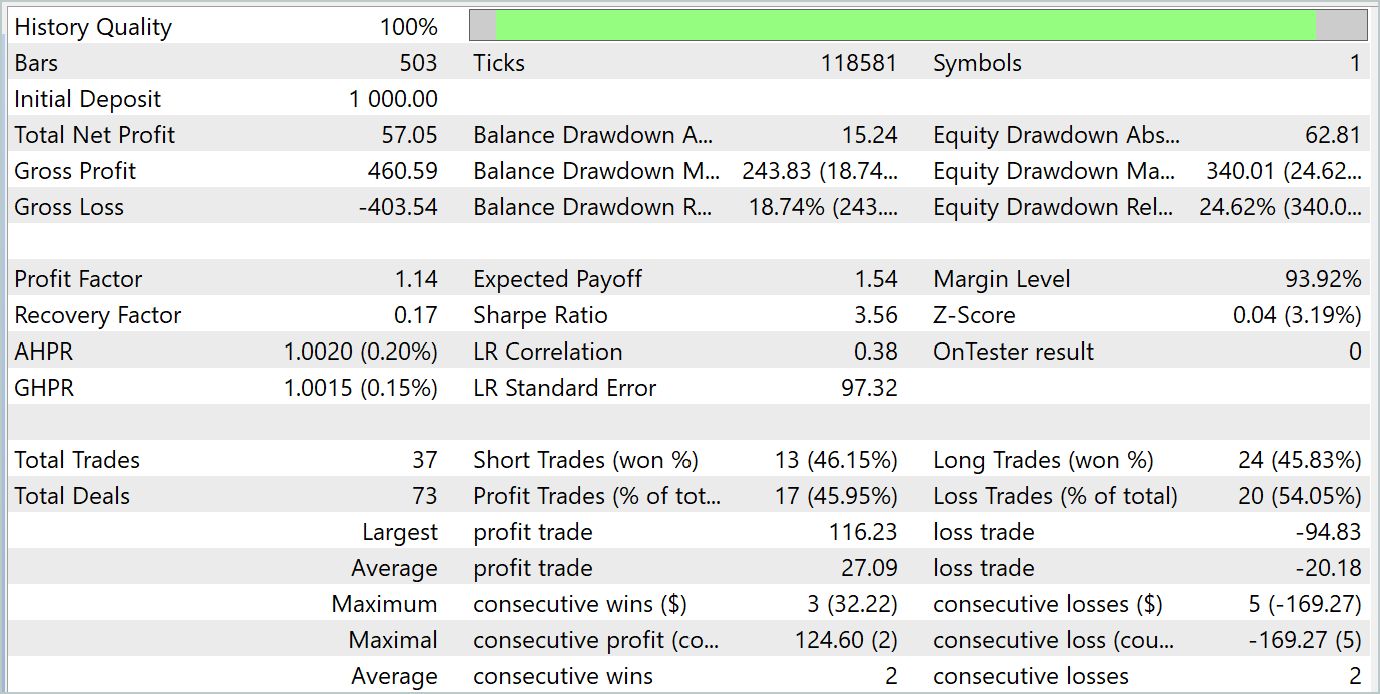
Durante el periodo de prueba, el modelo ha realizado 37 transacciones, 17 de las cuales se han cerrado con beneficios, lo cual supone casi el 46%. Cabe destacar que la proporción de transacciones rentables entre posiciones largas y cortas es casi igual. La desviación es solo del 0,32%, lo cual solo puede suponer un error de cálculo debido al reducido número de transacciones. Las transacciones rentables máximas y medias son superiores a las cifras correspondientes de las transacciones perdedoras. Esto nos ha permitido cerrar el periodo de pruebas con beneficios. El factor de beneficio, a su vez, ha sido 1,14. Sin embargo, resulta alarmante que los beneficios se hayan producido en la primera mitad del mes. Además, podemos observar un movimiento lateral del balance, y la última semana del mes ha estado marcada por un descenso.

Conclusión

En este artículo, hemos entrenado y probado el modelo utilizando los enfoques del método MSFformer. Según los resultados de las pruebas, hemos obtenido buenos resultados, lo cual nos permite hablar del carácter prometedor de los enfoques propuestos. No obstante, resulta llamativa la reducción del balance en la última semana del periodo de prueba, lo cual puede indicarnos la necesidad de introducir fases adicionales de entrenamiento del modelo.

Enlaces

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor de recopilación de ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de Modelos
4	StudyEncoder.mq5	Asesor	Asesor de entrenamiento del Codificador
5	Test.mq5	Asesor	Asesor para la prueba de modelos
6	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema.
7	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
8	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL

Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/15171

Archivos adjuntos |

Descargar ZIP

MQL5.zip (1378.56 KB)

Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Otros artículos del autor

Pasar a la discusión en el foro de los operadores

Creación de un modelo de restricción de tendencia de velas (Parte 6): Integración todo en uno

Un reto importante es la gestión de varias ventanas de gráficos del mismo par que ejecutan el mismo programa con diferentes funciones. Vamos a discutir cómo consolidar varias integraciones en un programa principal. Además, compartiremos ideas sobre la configuración del programa para imprimir en un diario y comentar el éxito de la emisión de señales en la interfaz de gráficos. Encontrará más información en este artículo a medida que avancemos en la serie de artículos.

Del básico al intermedio: Comando IF ELSE

En este artículo veremos cómo trabajar con el comando IF y su compañero ELSE. Este es el comando más importante y significativo que existe en cualquier lenguaje de programación. Sin embargo, aunque es muy sencillo de usar, a veces genera cierta confusión cuando nos falta experiencia en su uso y en los conceptos asociados. El contenido expuesto aquí tiene como objetivo exclusivamente la enseñanza didáctica. En ningún caso debe considerarse como una aplicación destinada a otro fin que no sea el aprendizaje y estudio de los conceptos presentados.

Algoritmo de búsqueda por vecindad — Across Neighbourhood Search (ANS)

El artículo revela el potencial del algoritmo ANS como paso importante en el desarrollo de métodos de optimización flexibles e inteligentes capaces de considerar la especificidad del problema y la dinámica del entorno en el espacio de búsqueda.

Del básico al intermedio: Paso por valor o por referencia

En este artículo entenderás en la práctica la diferencia entre el paso por valor y el paso por referencia. Aunque parece algo aparentemente sencillo y que no suele causar problemas, muchos programadores con una considerable experiencia suelen enfrentarse a verdaderos contratiempos con sus códigos, precisamente por este pequeño detalle. Saber cuándo, cómo y por qué usar un paso por valor o un paso por referencia marcará una gran diferencia en tu vida como programador. El contenido presentado aquí tiene como único objetivo la enseñanza. En ningún caso debe considerarse como una aplicación destinada a otro fin que no sea el aprendizaje y el estudio de los conceptos mostrados.