Redes neuronales en el trading: Representación lineal por partes de series temporales

Introducción

La mayoría de las veces, al hablar de la representación de una serie temporal, tenemos ante nosotros datos que suponen una secuencia de puntos registrados en orden cronológico. Sin embargo, a medida que aumenta la cantidad de información de origen, también se complica su análisis, con lo cual se reduce la eficacia del uso de la información disponible. Esto resulta especialmente importante al trabajar en mercados financieros en los que la pérdida de tiempo a la hora de analizar la información y tomar decisiones aumenta el riesgo de obtener beneficios por debajo de lo esperado y, a veces, de sufrir pérdidas. Y en este sentido, se reserva un papel especial a las ventajas de la reducción de la dimensionalidad de los datos, con el fin de aumentar la eficiencia y la eficacia de su análisis inteligente. Un enfoque para reducir la dimensionalidad de los datos sería la representación lineal por partes de las series temporales.

La representación lineal por partes de series temporales es un método de aproximación de una serie temporal usando funciones lineales en intervalos pequeños. Y en este artículo me gustaría presentar al lector el algoritmo de representación lineal bidireccional por partes de series temporales Bidirectional Piecewise Linear Representation (BPLR), que fue presentado en el artículo "Bidirectional piecewise linear representation of time series with application to collective anomaly detection". Este método se propuso para resolver los problemas derivados de la búsqueda de anomalías en las series temporales.

La detección de anomalías en las series temporales es el subcampo más importante en la minería de datos de series temporales. Su objetivo es identificar comportamientos inesperados en el conjunto de datos al completo. Como las anomalías suelen estar causadas por distintos mecanismos, carecen de criterios específicos para su definición. En la práctica, los datos que muestran un comportamiento esperado tienden a atraer más la atención, mientras que los datos anómalos suelen percibirse como ruido y posteriormente son ignorados o eliminados. Sin embargo, las anomalías pueden contener información útil, por lo que su detección resulta muy importante. La detección precisa de anomalías puede ayudarnos a mitigar efectos adversos innecesarios en diversos ámbitos como el entorno, la industria, las finanzas y otros.

Podemos clasificar las anomalías en las series temporales en las tres categorías siguientes:

1. Anomalías puntuales: un punto de datos se considera anómalo con respecto a otros puntos. Estas anomalías suelen deberse a los errores de medición, el mal funcionamiento de los sensores, los errores en la introducción de datos u otros sucesos excepcionales;
2. Anomalías contextuales: un dato se considera anómalo en un contexto determinado, pero no en otro;
3. Anomalías colectivas: subsecuencia de una serie temporal que presenta un comportamiento anómalo. Es todo un reto, ya que estas anomalías no pueden considerarse anormales en los análisis individuales; por el contrario, lo anormal es el comportamiento colectivo del grupo.

Las anomalías colectivas pueden ofrecer información valiosa sobre el sistema o proceso analizado, ya que pueden indicar un problema a nivel de grupo que debemos abordar. Así, la detección colectiva de anomalías puede ser una tarea importante en muchos ámbitos, como la ciberseguridad, las finanzas y la sanidad. En su trabajo, los autores del método BPLR se han centrado en identificar exactamente las anomalías colectivas.

La elevada dimensionalidad de los datos de series temporales requiere importantes recursos informáticos cuando se utilizan datos de origen para la detección de anomalías. No obstante, para mejorar la eficacia de la detección de anomalías, un enfoque típico consistiría en reducir primero la dimensionalidad y usar después una medida de distancia para realizar la tarea en el subespacio de representación transformado. Por lo tanto, los autores del método proponen un nuevo algoritmo de segmentación bidireccional para la representación lineal por partes BPLR. Con este método, la serie temporal original puede convertirse en una forma de expresión de baja dimensionalidad adecuada para un análisis eficaz.

El artículo también propone un nuevo algoritmo para medir la similitud, basado en la idea de la integración por partes (PI). Este realiza un cálculo eficiente de la medida de la similitud con un coste computacional relativamente bajo.

1. Algoritmo

La detección de anomalías basada en el método BPLR propuesto consta de dos etapas:

1. Representación de series temporales;
2. Medición de la similitud.

Antes de describir el algoritmo de representación de las series temporales en el método BPLR, debemos subrayar que el método está diseñado para resolver problemas de detección de anomalías. Se supone que la serie temporal analizada tiene cierta ciclicidad, y que el tamaño de esta puede obtenerse de forma experimental o a partir de un conocimiento a priori. Por lo tanto, toda la serie temporal original se divide en subsecuencias no solapadas cuyo tamaño será igual al ciclo supuesto de los datos de origen. Los autores del método intentan encontrar regiones anómalas comparando las subsecuencias obtenidas. A continuación, describiremos un algoritmo para representar una única subsecuencia que se repite para todos los elementos de la serie temporal analizada.

Para representar la serie temporal, necesitaremos encontrar varios conjuntos de puntos de segmentación en cada subsecuencia. Y luego convertir la subsecuencia original en un conjunto de segmentos lineales.

En primer lugar, para encontrar los puntos más probables de división de la subsecuencia en segmentos separados, identificaremos todos los posibles puntos de inversión de la tendencia (Trend Turning Points — TTP). Los autores del método distinguen 6 variantes de puntos de inversión de la tendencia.

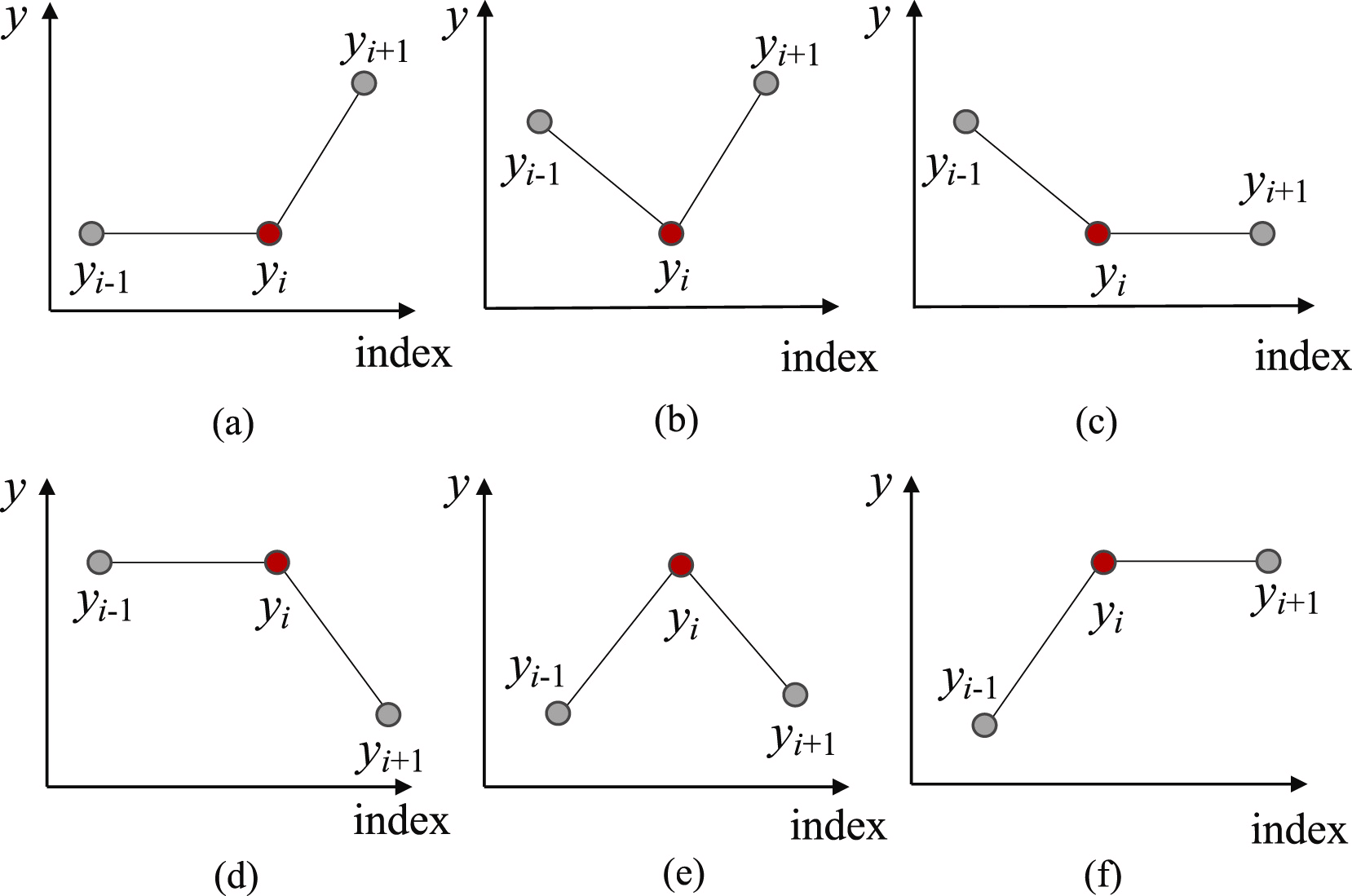
Y aquí debemos señalar que el primer y el último elemento de la subsecuencia se considerarán automáticamente puntos de inversión de la tendencia.

El siguiente paso consistirá en determinar la importancia de cada punto de inversión de tendencia encontrado. Los autores del método proponen usar la desviación de la media de la subsecuencia como medida de la importancia del TTP.

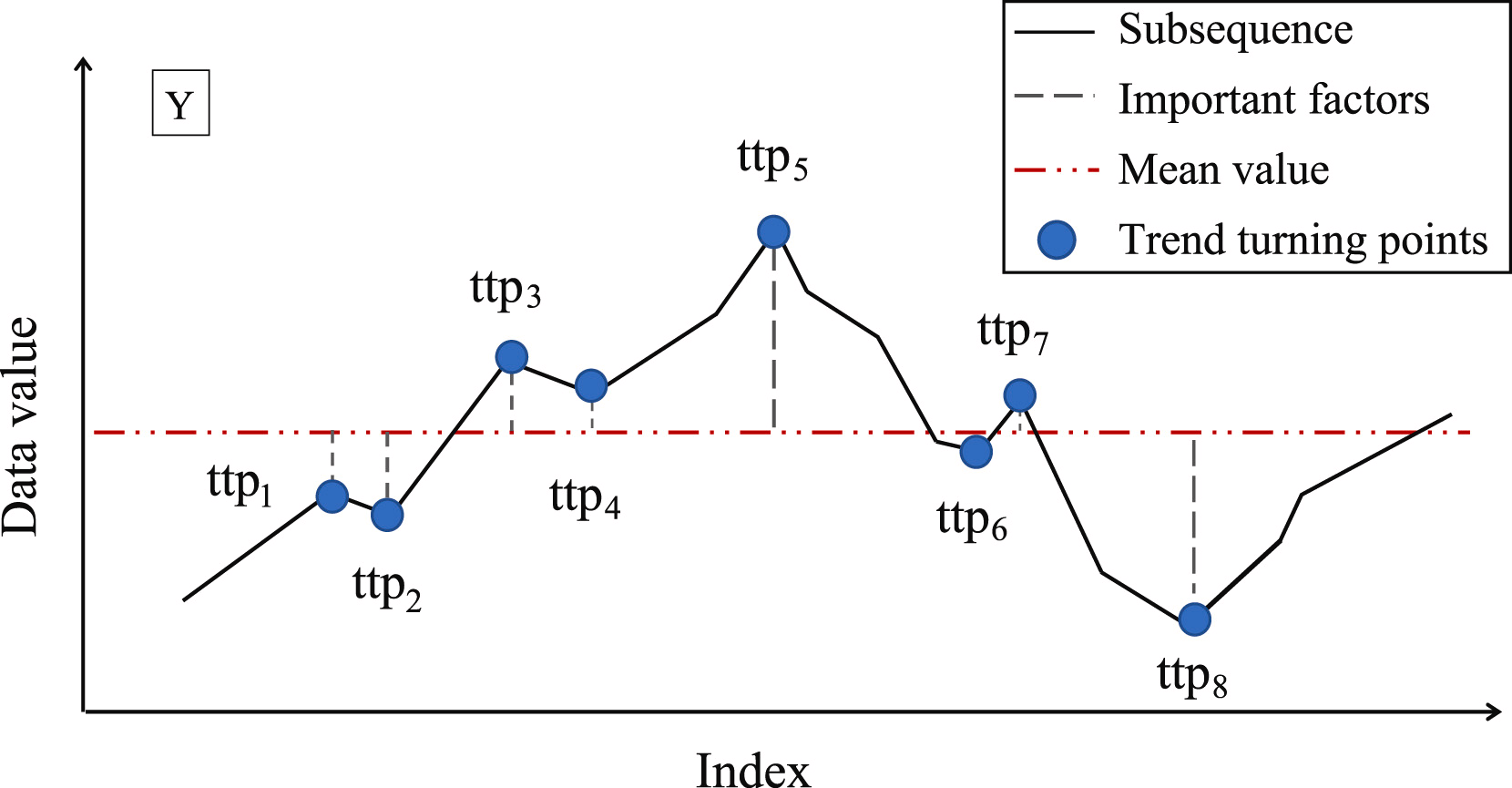
A continuación, los puntos de inversión de tendencia se clasificarán según su importancia. Los segmentos se identificarán iterativamente a partir de TTP1 con la máxima importancia en dos direcciones: antes y después de TTP1. Al mismo tiempo, se introducirá un hiperparámetro adicional δß para determinar la calidad del segmento que definirá la desviación máxima admisible de los puntos de la secuencia respecto a la línea del segmento.

Para determinar el punto de inicio del segmento precedente, enumeramos los elementos de la secuencia original en orden inverso a partir del TTP1 analizado, siempre que todos los elementos entre TTP1 y el candidato a inicio del segmento no estén más allá de δß. Si se encuentra un punto que esté fuera de los límites especificados, la iteración se detendrá, y luego se guardará el segmento. Si los puntos de inversión de tendencia encontrados anteriormente se encuentran dentro del área del segmento, se eliminarán.

Del mismo modo, se buscará el final del segmento en la dirección posterior a TTP1. Precisamente por la búsqueda de segmentos en las direcciones anterior y posterior al extremo, el método se denomina bidireccional.

Una vez determinados los puntos extremos de ambos segmentos, se repetirán las operaciones con el extremo siguiente. Las iteraciones se completarán cuando no queden puntos de inversión de tendencia sin procesar en el array.

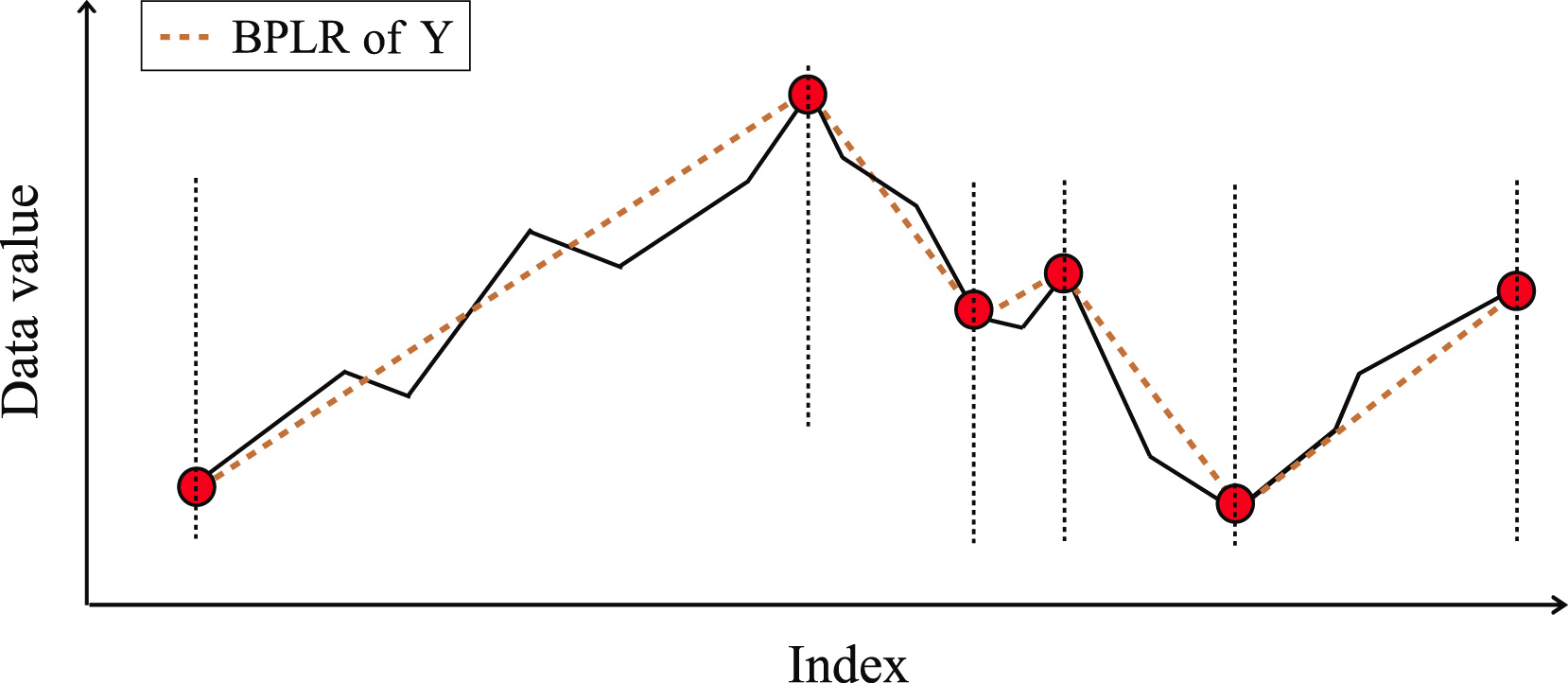
Para determinar la similitud de dos subsecuencias, se determinará el área de la figura formada por los segmentos de las secuencias analizadas.

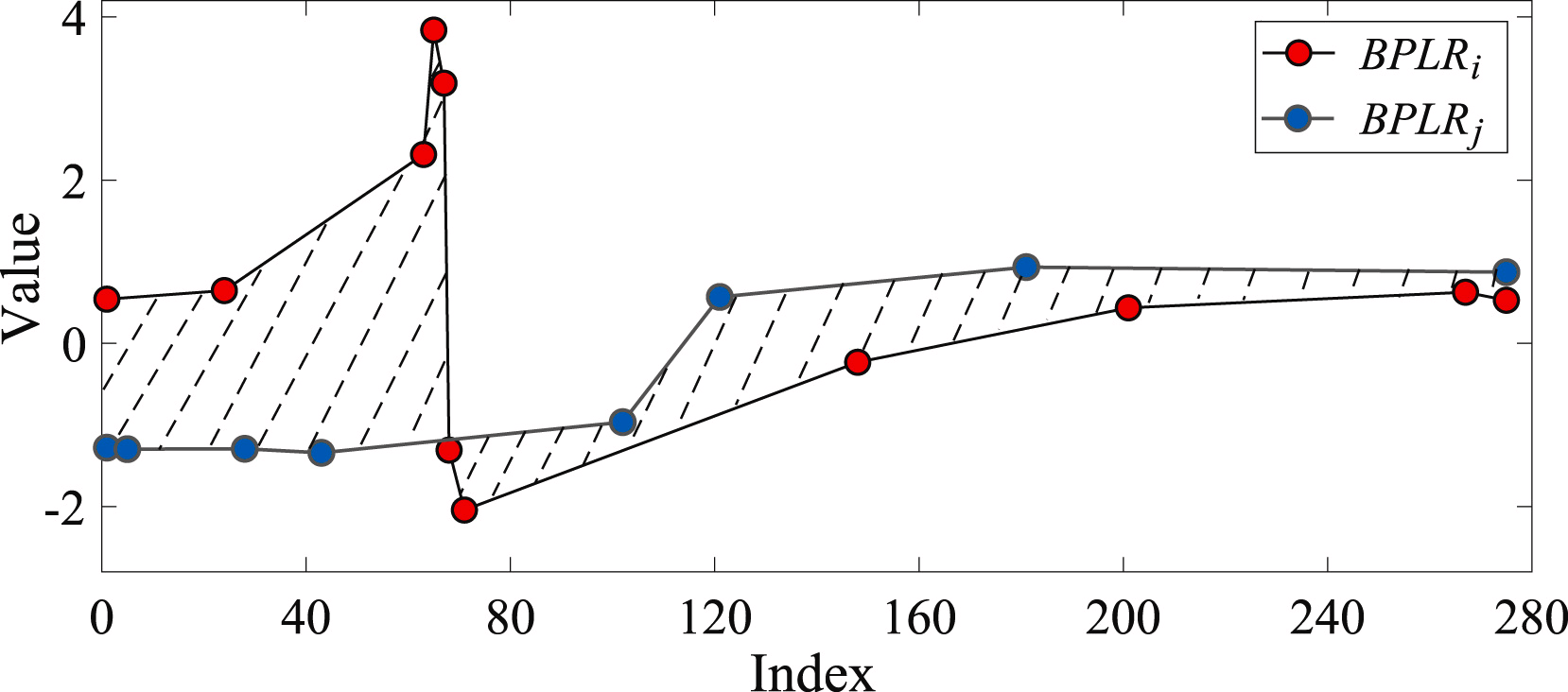
Para resolver el problema de la búsqueda de anomalías, los autores del método compilan una matriz de anomalías Mdist. A continuación, para cada subsecuencia individual, se calculará la desviación total con respecto a otras subsecuencias de la serie temporal Di analizada. En la práctica, Di será la suma de los elementos de la matriz Mdist en la fila i. Una subsecuencia anómala será la subsecuencia cuya desviación total difiera en una magnitud superior al umbral de error especificado del valor medio del índice similar de las demás subsecuencias.

En su artículo, los autores del método BPLR ofrecen resultados experimentales sobre datos sintéticos y reales que demuestran la eficacia de la solución propuesta.

2. Implementación con MQL5

Más arriba, nos hemos familiarizado con la representación teórica del método BPLR para encontrar subsecuencias anómalas de series temporales. Ahora, en la parte práctica de este artículo, implementaremos nuestra visión de los enfoques propuestos utilizando herramientas MQL5. Y aquí debemos advertirle de que solo aprovecharemos parcialmente las soluciones propuestas.

Permítanme decir de entrada que, en el ámbito de este artículo, no buscaremos anomalías en las series temporales. Los mercados financieros son tan dinámicos y diversos que podemos esperar que se produzcan desviaciones significativas entre dos secuencias no superpuestas.

Por otra parte, una representación alternativa de la serie temporal como una secuencia lineal por partes puede resultar muy útil. En el marco de nuestros artículos anteriores, ya hemos hablado de la utilidad de la segmentación de datos. Y la cuestión del tamaño del segmento sigue resultando de gran relevancia. En este caso, usaremos siempre segmentos de igual tamaño. Y el método de la representación lineal por partes permite utilizar tamaños de segmento dinámicos según la serie temporal analizada de datos de origen, lo que en cierta medida nos permite resolver la extracción de características de series temporales de diferentes escalas. Al mismo tiempo, la representación lineal por partes posee un tamaño fijo independientemente del tamaño del segmento, lo cual la hace cómoda para realizar análisis posteriores.

Lo mismo podemos decir de la representación de los segmentos. El propio nombre "representación lineal por partes" indica la representación de un segmento como una función lineal:

Como consecuencia de ello, indicaremos explícitamente la dirección de la tendencia principal en el segmento temporal. Y la posibilidad de comprimir los datos supone una ventaja añadida que reducirá la complejidad del modelo.

Obviamente, no dividiremos la serie temporal analizada en subsecuencias. Representaremos el conjunto completo de datos de entrada como una secuencia lineal por partes. Y nuestro modelo, basado en el análisis de los datos presentados, deberá sacar conclusiones y proponer la "única solución verdadera".

Bien, empezaremos nuestro trabajo construyendo el programa en el lado OpenCL.

2.1 Implementación en OpenCL

Como ya sabrá, para optimizar el coste del entrenamiento y la ejecución de nuestros modelos, hemos trasladado la mayor parte del cálculo al contexto de los dispositivos OpenCL, lo cual nos permitirá organizar el cálculo en un espacio multidimensional de flujos paralelos. Y esta aplicación no será una excepción en este sentido.

Para segmentar las series temporales analizadas, crearemos un kernel PLR.

__kernel void PLR(__global const float *inputs,
                  __global float *outputs,
                  __global int *isttp,
                  const int transpose,
                  const float min_step
                 )
  {
   const size_t i = get_global_id(0);
   const size_t lenth = get_global_size(0);
   const size_t v = get_global_id(1);
   const size_t variables = get_global_size(1);

En los parámetros, planeamos transmitir al kernel los punteros a 3 búferes de datos:

• inputs — resultados de origen
• outputs — resultados
• isttp — búfer de servicio para fijar los puntos de inversión de la tendencia

Además, añadiremos 2 constantes:

• transpose — indica la necesidad de transponer los datos de origen y los resultados
• min_step — desviación mínima de los elementos de la secuencia para fijar el TTP

El kernel lo llamaremos en el espacio bidimensional del problema según el número de elementos de la secuencia analizada y el número de secuencias unitarias de la serie temporal multidimensional. Como consecuencia, en el cuerpo del kernel, identificaremos directamente el subproceso actual en el espacio de tareas y, a continuación, definiremos las constantes de desplazamiento en el búfer de datos de origen.

//--- constants
   const int shift_in = ((bool)transpose ? (i * variables + v) : (v * lenth + i));
   const int step_in = ((bool)transpose ? variables : 1);

Tras un pequeño trabajo preparatorio, determinaremos la presencia de un punto de inversión de tendencia en la posición del elemento analizado. Los puntos extremos de la serie temporal analizada recibirán automáticamente el estatus de punto de inversión de tendencia, ya que son a priori los puntos extremos del segmento.

   float value = inputs[shift_in];
   bool bttp = false;
   if(i == 0 || i == lenth - 1)
      bttp = true;

En algunos casos, se buscará primero la desviación más próxima de los valores de la serie analizada en el valor mínimo necesario hasta el elemento actual de la secuencia. Al mismo tiempo mantendremos los valores mínimo y máximo en el intervalo a partir de los valores transmitidos.

   else
     {
      float prev = value;
      int prev_pos = i;
      float max_v = value;
      float max_pos = i;
      float min_v = value;
      float min_pos = i;
      while(fmax(fabs(prev - max_v), fabs(prev - min_v)) < min_step && prev_pos > 0)
        {
         prev_pos--;
         prev = inputs[shift_in - (i - prev_pos) * step_in];
         if(prev >= max_v && (prev - min_v) < min_step)
           {
            max_v = prev;
            max_pos = prev_pos;
           }
         if(prev <= min_v && (max_v - prev) < min_step)
           {
            min_v = prev;
            min_pos = prev_pos;
           }
        }

A continuación, buscaremos de forma similar el elemento siguiente con la desviación mínima requerida.

      //---
      float next = value;
      int next_pos = i;
      while(fmax(fabs(next - max_v), fabs(next - min_v)) < min_step && next_pos < (lenth - 1))
        {
         next_pos++;
         next = inputs[shift_in + (next_pos - i) * step_in];
         if(next > max_v && (next - min_v) < min_step)
           {
            max_v = next;
            max_pos = next_pos;
           }
         if(next < min_v && (max_v - next) < min_step)
           {
            min_v = next;
            min_pos = next_pos;
           }
        }

Y comprobaremos si el valor actual es un extremo.

      if(
         (value >= prev && value > next) ||
         (value > prev && value == next) ||
         (value <= prev && value < next) ||
         (value < prev && value == next)
      )
         if(max_pos == i || min_pos == i)
            bttp = true;
     }

Pero aquí deberemos recordar que al buscar elementos con la desviación mínima necesaria, podríamos recoger un cierto corredor de valores de varios elementos de la secuencia que formen alguna meseta del extremo. Por ello, un elemento recibirá una bandera de punto de inversión de tendencia solo si es un extremo en dicho corredor.

Luego guardaremos la bandera resultante y borraremos el búfer de resultados. Al hacerlo, sincronizaremos los flujos del grupo local.

//---
   isttp[shift_in] = (int)bttp;
   outputs[shift_in] = 0;
   barrier(CLK_LOCAL_MEM_FENCE);

Necesitaremos sincronizar los flujos para estar seguros de que todos los flujos de la serie temporal unitaria actual hayan registrado sus banderas de puntos de inversión de tendencia antes de las operaciones posteriores.

Las siguientes operaciones solo las realizarán los flujos en los que se haya definido un punto de inversión de tendencia. Los otros flujos simplemente no cumplirán las condiciones y prácticamente finalizarán las operaciones.

Aquí calcularemos primero la posición del extremo actual. Para ello, contaremos el número de banderas positivas en la posición actual del elemento, y almacenaremos prudentemente en una variable local la posición del punto de inversión de tendencia anterior en el búfer de datos de origen.

//--- calc position
   int pos = -1;
   int prev_in = 0;
   int prev_ttp = 0;
   if(bttp)
     {
      pos = 0;
      for(int p = 0; p < i; p++)
        {
         int current_in = ((bool)transpose ? (p * variables + v) : (v * lenth + p));
         if((bool)isttp[current_in])
           {
            pos++;
            prev_ttp = p;
            prev_in = current_in;
           }
        }
     }

A continuación, determinaremos los parámetros de la aproximación lineal de la tendencia del segmento actual.

//--- cacl tendency
   if(pos > 0 && pos < (lenth / 3))
     {
      float sum_x = 0;
      float sum_y = 0;
      float sum_xy = 0;
      float sum_xx = 0;
      int dist = i - prev_ttp;
      for(int p = 0; p < dist; p++)
        {
         float x = (float)(p);
         float y = inputs[prev_in + p * step_in];
         sum_x += x;
         sum_y += y;
         sum_xy += x * y;
         sum_xx += x * x;
        }
      float slope = (dist * sum_xy - sum_x * sum_y) / (dist > 1 ? (dist * sum_xx - sum_x * sum_x) : 1);
      float intercept = (sum_y - slope * sum_x) / dist;

Y guardaremos los resultados en el búfer de resultados.

      int shift_out = ((bool)transpose ? ((pos - 1) * 3 * variables + v) : (v * lenth + (pos - 1) * 3));
      outputs[shift_out] = slope;
      outputs[shift_out + 1 * step_in] = intercept;
      outputs[shift_out + 2 * step_in] = ((float)dist) / lenth;
     }

Aquí cabe señalar que caracterizaremos cada segmento obtenido usando 3 parámetros:

• slope — ángulo de inclinación de la línea de tendencia;
• intercept — desplazamiento de la línea de tendencia en el subespacio de los datos de origen;
• dist — longitud del segmento.

Probablemente deberíamos decir unas palabras sobre la representación de la duración de los segmentos. Creo que habrá adivinado que especificar la longitud de la secuencia con un valor entero, en este caso, no es el mejor resultado. Al fin y al cabo, resulta deseable disponer de un formato de representación de datos normalizado para que el modelo funcione eficazmente. Por ello, hemos decidido representar la duración del segmento como una fracción del tamaño total de la secuencia temporal unitaria analizada. Por lo tanto, dividiremos el número de elementos de un segmento por el número de elementos de toda la secuencia de la serie temporal unitaria. Y para no caer en la "trampa" de las operaciones con enteros, primero convertiremos el número de elementos del segmento de tipo int al tipo float.

Además, crearemos una rama de operaciones aparte para el último segmento. El hecho es que no sabemos el número de segmentos que se formarán en un momento concreto. De forma puramente hipotética, con fluctuaciones significativas de los elementos de la serie temporal y la presencia de puntos de inversión de tendencia en cada elemento de la serie temporal, en vez de compresión, podremos obtener 3 veces más valores. Obviamente, este giro de los acontecimientos resulta poco probable, sin embargo, no querríamos aumentar la cantidad de datos. Al mismo tiempo, tampoco querríamos perder datos.

Por ello, partiremos de un conocimiento a priori de la representación de series temporales en MQL5 y de la comprensión de la estructura de los datos analizados: los datos más recientes se encuentran al principio de nuestra serie temporal. Y es a ellos a quienes prestaremos más atención. Los datos del final de la ventana analizada tienen una mayor profundidad histórica y, como es de esperar, influirán menos en los acontecimientos posteriores, aunque no descartaremos tal influencia.

En consecuencia, para registrar los resultados, utilizaremos un tamaño de búfer de datos similar al tamaño del tensor de valores de la serie temporal de origen. Esto nos permitirá escribir segmentos de 3 veces la longitud de la secuencia (3 elementos para escribir 1 segmento). Esperamos que este volumen resulte más que suficiente. Sin embargo, debemos asegurarnos, y cuando haya más segmentos, fusionaremos los datos de los últimos segmentos en 1 para evitar la pérdida de datos.

   else
     {
      if(pos == (lenth / 3))
        {
         float sum_x = 0;
         float sum_y = 0;
         float sum_xy = 0;
         float sum_xx = 0;
         int dist = lenth - prev_ttp;
         for(int p = 0; p < dist; p++)
           {
            float x = (float)(p);
            float y = inputs[prev_in + p * step_in];
            sum_x += x;
            sum_y += y;
            sum_xy += x * y;
            sum_xx += x * x;
           }
         float slope = (dist * sum_xy - sum_x * sum_y) / (dist > 1 ? (dist * sum_xx - sum_x * sum_x) : 1);
         float intercept = (sum_y - slope * sum_x) / dist;
         int shift_out = ((bool)transpose ? ((pos - 1) * 3 * variables + v) : (v * lenth + (pos - 1) * 3));
         outputs[shift_out] = slope;
         outputs[shift_out + 1 * step_in] = intercept;
         outputs[shift_out + 2 * step_in] = ((float)dist) / lenth;
        }
     }
  }

En la mayoría de los casos, sin embargo, esperamos menos segmentos, y entonces los últimos elementos de nuestro búfer de resultados se rellenarán con valores nulos.

Aquí cabe señalar que el algoritmo presentado anteriormente no contiene parámetros entrenables y puede utilizarse en la fase de preparación preliminar de los datos de origen. Esto no implicará un proceso de retroceso ni una distribución del gradiente de error. No obstante, en el presente artículo prevemos aplicar este algoritmo en nuestros modelos. Y como consecuencia, necesitaremos implementar un algoritmo de pasada inversa para distribuir el gradiente de error de las capas neuronales posteriores a las anteriores. Al mismo tiempo, la ausencia de parámetros entrenables impedirá disponer de algoritmos para su optimización.

Así, como parte de nuestra implementación de algoritmos de pasada inversa, crearemos el kernel de distribución de gradiente de error PLRGradient.

__kernel void PLRGradient(__global float *inputs_gr,
                          __global const float *outputs,
                          __global const float *outputs_gr,
                          const int transpose
                         )
  {
   const size_t i = get_global_id(0);
   const size_t lenth = get_global_size(0);
   const size_t v = get_global_id(1);
   const size_t variables = get_global_size(1);

En los parámetros del kernel también transmitiremos los punteros a 3 búferes de datos. Solo que esta vez serán 2 búferes de gradiente de error (a nivel de datos de origen y de resultados) y un búfer de los resultados de la pasada directa de la capa actual. Además, añadiremos a los parámetros del kernel la ya conocida bandera de transposición de datos, que se utilizará para determinar los desplazamientos en los búferes de datos.

Tenemos previsto llamar al kernel en el mismo espacio de tareas bidimensional. La primera dimensión estará limitada por el tamaño de la secuencia de series temporales, mientras que la segunda estará limitada por el número de series temporales unitarias en los datos de entrada multimodales. En el cuerpo del kernel, identificaremos directamente el flujo actual en el espacio de tareas en todas las dimensiones.

El siguiente paso consistirá en definir las constantes de desplazamiento en los búferes de datos.

//--- constants
   const int shift_in = ((bool)transpose ? (i * variables + v) : (v * lenth + i));
   const int step_in = ((bool)transpose ? variables : 1);
   const int shift_out = ((bool)transpose ? v : (v * lenth));
   const int step_out = 3 * step_in;

Pero este no será el final del trabajo preparatorio. A continuación, deberemos encontrar el segmento en el que cae el elemento analizado de los datos de origen. Para ello, organizaremos un ciclo, en cuyo cuerpo sumaremos los tamaños de los segmentos, empezando por el primero. Las iteraciones del ciclo se repetirán hasta que encontremos un segmento que contenga el elemento deseado de los datos de origen.

//--- calc position
   int pos = -1;
   int prev_in = 0;
   int dist = 0;
   do
     {
      pos++;
      prev_in += dist;
      dist = (int)fmax(outputs[shift_out + pos * step_out + 2 * step_in] * lenth, 1);
     }
   while(!(prev_in <= i && (prev_in + dist) > i));

Tras completar las iteraciones del ciclo, obtendremos:

• pos — índice del segmento que contiene el elemento buscado de los datos de origen
• prev_in — desplazamiento en el búfer de datos de origen hasta el primer elemento del segmento
• dist — número de elementos del segmento

Para calcular las derivadas de primer orden de las operaciones de pasada directa, también necesitaremos la suma de las posiciones de los elementos del segmento y la suma de sus valores al cuadrado.

//--- calc constants
   float sum_x = 0;
   float sum_xx = 0;
   for(int p = 0; p < dist; p++)
     {
      float x = (float)(p);
      sum_x += x;
      sum_xx += x * x;
     }

Llegados a este punto, el trabajo preparatorio ha concluido y podemos calcular el gradiente de error. Comenzaremos extrayendo el gradiente de error para el ángulo de inclinación y el desplazamiento.

//--- get output gradient
   float grad_slope = outputs_gr[shift_out + pos * step_out];
   float grad_intercept = outputs_gr[shift_out + pos * step_out + step_in];

Vamos a recordar ahora la fórmula que utilizamos en el paso anterior para calcular el desplazamiento vertical de la línea de tendencia.

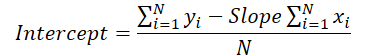
Podemos observar que el valor del ángulo de la línea se utiliza para calcular el desplazamiento. Por lo tanto, deberemos corregir el gradiente de error de la inclinación considerando su efecto en la corrección del desplazamiento. Para ello, hallaremos la derivada de la función de desplazamiento según el ángulo de inclinación.

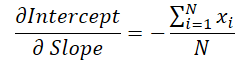
Luego multiplicaremos el valor obtenido por el gradiente de error de desplazamiento y añadiremos el resultado al gradiente de error de inclinación.

//--- calc gradient
   grad_slope -= sum_x / dist * grad_intercept;

Pasemos ahora a la fórmula para determinar el ángulo de inclinación.

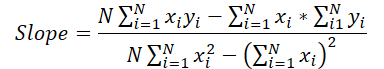
Podemos ver fácilmente que el denominador es en este caso una constante, y que podemos ajustar el gradiente de error de inclinación según dicha constante.

   grad_slope /= fmax(dist * sum_xx - sum_x * sum_x, 1);

Por último, veremos el efecto de los datos de origen en ambas fórmulas.

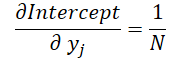
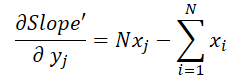
donde 1 ≤ j ≤ N y

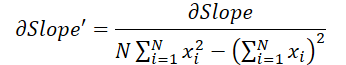
Armados con estas fórmulas, determinaremos el gradiente de error al nivel de los datos de origen.

   float grad = grad_intercept / dist;
   grad += (dist * (i - prev_in) - sum_x) * grad_slope;
   if(isnan(grad) || isinf(grad))
      grad = 0;

El resultado se almacenará en el elemento correspondiente del búfer de gradiente de datos de origen.

//--- save result
   inputs_gr[shift_in] = grad;
  }

Con esto damos por concluido nuestro trabajo en la parte del contexto OpenCL. Encontrará el código completo del programa OpenCL en el archivo adjunto.

2.2 Implementación de la nueva clase

Una vez completado el trabajo en la parte del contexto OpenCL, procederemos a trabajar con el código del programa principal. Aquí crearemos una nueva clase CNeuronPLROCL, que nos permitirá implementar el algoritmo anterior en nuestros modelos como una capa neuronal normal.

Como en la mayoría de los casos similares, la funcionalidad central del nuevo objeto heredará de nuestra clase básica de capas neuronales CNeuronBaseOCL. A continuación le mostraremos la estructura de la nueva clase.

class CNeuronPLROCL  :  public CNeuronBaseOCL
  {
protected:
   bool              bTranspose;
   int               icIsTTP;
   int               iVariables;
   int               iCount;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL)  { return true; }

public:
                     CNeuronPLROCL(void)  : bTranspose(false) {};
                    ~CNeuronPLROCL(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window_in, uint units_count, bool transpose, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronPLROCL;   }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

En la estructura presentada podemos observar la redefinición del conjunto estándar de métodos y la adición de diversas variables. Su nombre nos permitirá adivinar fácilmente la funcionalidad que se les asigna.

• bTranspose — bandera que indica la necesidad de transponer los datos de origen y los resultados
• iCount — tamaño de la secuencia analizada (profundidad de la historia)
• iVariables — número de parámetros analizados de series temporales multimodales (secuencias unitarias)

Y preste atención a lo siguiente: a pesar de que tenemos un búfer de datos auxiliar en los parámetros del kernel de pasada directa, no crearemos un búfer adicional en el lado del programa principal. Aquí solo almacenaremos el puntero al mismo en la variable local icIsTTP.

La ausencia de objetos internos nos permitirá dejar vacíos el constructor y el destructor de la clase, mientras que la inicialización del objeto se realizará en el método Init.

bool CNeuronPLROCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                         uint window_in, uint units_count, bool transpose, 
                         ENUM_OPTIMIZATION optimization_type, uint batch
                        )
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_in * units_count, optimization_type, batch))
      return false;

En los parámetros, el método obtendrá las constantes básicas para definir la arquitectura del objeto a crear. Y en el cuerpo de la clase llamaremos directamente al método homónimo de la clase padre, que ya implementará el control y la inicialización necesarios de los objetos y variables heredados.

A continuación guardaremos los parámetros de configuración del objeto a crear.

   iVariables = (int)window_in;
   iCount = (int)units_count;
   bTranspose = transpose;

Y para finalizar el método, crearemos un búfer de datos auxiliar en el lado del contexto OpenCL.

   icIsTTP = OpenCL.AddBuffer(sizeof(int) * Neurons(), CL_MEM_READ_WRITE);
   if(icIsTTP < 0)
      return false;
//---
   return true;
  }

Tras inicializar el objeto, procederemos a construir el algoritmo de pasada directa, que se implementará en el método feedForward. Aquí solo tendremos que invocar el mencionado kernel de pasada directa PLR. Pero hay un matiz a considerar: deberemos crear grupos locales para sincronizar los flujos dentro de series temporales unitarias tomadas por separado.

bool CNeuronPLROCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!OpenCL || !NeuronOCL || !NeuronOCL.getOutput())
      return false;
//---
   uint global_work_offset[2] = {0};
   uint global_work_size[2] = {iCount, iVariables};
   uint local_work_size[2] = {iCount, 1};

Para ello, definiremos un espacio de tareas global bidimensional. Para la primera dimensión especificaremos el tamaño de la secuencia que se va a analizar, y para la segunda, el número de series temporales unitarias. También especificaremos el tamaño del grupo local en el espacio de tareas bidimensional. En este caso, el tamaño de la primera dimensión se corresponderá con el valor global, mientras que en la segunda dimensión especificaremos 1. Así, cada grupo local obtendrá su propia secuencia unitaria.

A continuación, solo tendremos que transmitir los parámetros necesarios al kernel.

   ResetLastError();
   if(!OpenCL.SetArgumentBuffer(def_k_PLR, def_k_plr_inputs, NeuronOCL.getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_PLR, def_k_plr_outputs, getOutputIndex()))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgumentBuffer(def_k_PLR, def_k_plt_isttp, icIsTTP))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_PLR, def_k_plr_transpose, (int)bTranspose))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }
   if(!OpenCL.SetArgument(def_k_PLR, def_k_plr_step, (float)0.3))
     {
      printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__);
      return false;
     }

Y poner el kernel en la cola de ejecución.

//---
   if(!OpenCL.Execute(def_k_PLR, 2, global_work_offset, global_work_size, local_work_size))
     {
      printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError());
      return false;
     }
//---
   return true;
  }

Al mismo tiempo, no nos olvidaremos de controlar las operaciones en cada fase. Y al final del método retornaremos el valor lógico de los resultados del método al programa que realiza la llamada.

El algoritmo para el método de distribución de gradientes de error calcInputGradients se construirá de forma similar. Pero a diferencia del método de pasada directa, aquí no crearemos grupos locales, y cada flujo realizará sus operaciones independientemente de los demás. Podrá leer el código completo del método anterior en el archivo adjunto.

Como hemos mencionado antes, el objeto que estamos creando no contiene parámetros entrenables. Por lo tanto, hemos redefinido su método de optimización updateInputWeights únicamente para preservar la estructura general de los objetos y su compatibilidad durante la implementación. Este método siempre retornará true.

Con esto concluiremos nuestro análisis de los algoritmos para implementar los métodos de la nueva clase. Podrá leer el código completo de todos sus métodos, incluidos los no considerados en este artículo, en el archivo adjunto.

2.3 Arquitectura del modelo

En este artículo, hemos implementado uno de los algoritmos para la representación lineal por partes de series temporales y ahora podremos añadirlo a la arquitectura de nuestros modelos.

Para comprobar la eficacia de la aplicación propuesta, hemos introducido una nueva clase en la estructura del modelo del Codificador del estado del entorno. Y debemos decir que hemos simplificado al máximo la arquitectura del modelo, para así evaluar el impacto de la descomposición nominal de las series temporales en las tendencias lineales individuales.

Al igual que antes, describiremos la arquitectura del modelo en el método CreateEncoderDescriptions.

bool CreateEncoderDescriptions(CArrayObj *encoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }

En los parámetros, el método recibe el puntero a un objeto de array dinámico para registrar la arquitectura del modelo que se está creando. En el cuerpo del método comprobaremos directamente la relevancia del puntero recibido. A continuación, si es necesario, crearemos una nueva instancia de array dinámico.

Como de costumbre, suministraremos a la entrada del modelo información del entorno para una profundidad de historia determinada sin ningún procesamiento primario de datos.

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Y aquí debemos decir que el algoritmo de representación lineal por partes funciona igual de bien tanto con datos normalizados como con datos "brutos". Pero hay algunos matices.

En primer lugar, en nuestra aplicación utilizaremos el parámetro de desviación mínima necesaria de los valores de las series temporales para fijar el punto de inversión de la tendencia. Creo que sobra decir que necesitaremos una selección cuidadosa de este hiperparámetro para analizar cada serie temporal individual. El uso de un algoritmo para el análisis de series temporales multimodales cuyos valores de secuencias unitarias se encuentran en distribuciones diferentes, complica significativamente esta tarea y, en la mayoría de los casos, hace imposible el uso de un único hiperparámetro para todas las secuencias unitarias analizadas.

En segundo lugar, tenemos previsto usar los resultados del método PLR en modelos cuyo rendimiento sea significativamente mayor cuando se utilizan datos de entrada normalizados.

Obviamente, podemos utilizar la normalización de los resultados del método PLR antes de transmitirlos al modelo, pero incluso en este caso, el cambio dinámico del número de segmentos complicará la tarea.

Al mismo tiempo, el uso de la normalización de los datos de origen antes de introducirlos en la capa de representación lineal por partes simplificará enormemente todos los puntos anteriores. Llevar los datos de todas las secuencias unitarias a una única distribución nos permitirá utilizar un único hiperparámetro para analizar series temporales multimodales. Además, la normalización de la distribución de los datos de origen permitirá utilizar hiperparámetros promediados para secuencias originales completamente distintas. 

Recibiendo los datos normalizados en la entrada de la capa, tendremos secuencias normalizadas a la salida. Por ello, la siguiente capa de nuestro modelo será la capa de normalización por lotes.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

A continuación, transpondremos los datos de origen para trabajar con secuencias unitarias.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Por supuesto, cuando se trata de nuestra implementación del algoritmo PLR, en lugar de utilizar la capa de transposición de datos, parecería más eficiente utilizar el parámetro de transposición. No obstante, en este caso, el uso de la capa de transposición vendrá determinado por la posterior construcción de la arquitectura del modelo.

A continuación, dividiremos los datos preparados en segmentos lineales.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronPLROCL;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   descr.step = int(false);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Y utilizaremos un MLP de 3 capas para pronosticar secuencias unitarias individuales para un horizonte de planificación determinado.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = BarDescr;
   descr.window = HistoryBars;
   descr.step = HistoryBars;
   descr.window_out = LatentCount;
   descr.activation = LReLU;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = BarDescr;
   descr.window = LatentCount;
   descr.step = LatentCount;
   descr.window_out = LatentCount;
   descr.optimization = ADAM;
   descr.activation = SIGMOID;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = BarDescr;
   descr.window = LatentCount;
   descr.step = LatentCount;
   descr.window_out = NForecast;
   descr.optimization = ADAM;
   descr.activation = TANH;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Observe que utilizamos capas convolucionales con ventanas no solapadas para organizar la predicción condicionalmente independiente de los valores de secuencias unitarias individuales. Utilizamos la definición "predicción condicionalmente independiente" porque, para construir las trayectorias de previsión de todas las secuencias unitarias, se usan las mismas matrices de coeficientes de peso.

Transpondremos los valores predichos a una representación de los datos de origen.

//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronTransposeOCL;
   descr.count = BarDescr;
   descr.window = NForecast;
   descr.activation = None;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Y les añadiremos los parámetros estadísticos de la distribución extraídos al normalizar los datos de origen.

//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRevInDenormOCL;
   descr.count = BarDescr*NForecast;
   descr.activation = None;
   descr.optimization = ADAM;
   descr.layers=1;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

En la salida del modelo utilizaremos el funcionamiento del método FreDF para hacer coincidir los pasos individuales de las secuencias unitarias de previsión de las series temporales analizadas.

//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFreDFOCL;
   descr.window = BarDescr;
   descr.count =  NForecast;
   descr.step = int(true);
   descr.probability = 0.7f;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

Así, hemos construido un modelo de Codificador del entorno que combina esencialmente PLR y MLP para la previsión de series temporales.

3. Simulación

En la parte práctica de este trabajo, hemos implementado un algoritmo de representación lineal por partes de series temporales (PLR). El algoritmo propuesto no contiene parámetros entrenables e implica únicamente la transformación de las series temporales analizadas en una representación alternativa. También hemos presentado un modelo de previsión de series temporales bastante simplificado utilizando la capa CNeuronPLROCL creada. Ahora es el momento de evaluar la eficacia de los enfoques descritos.

Para entrenar el modelo del Codificador del entorno para predecir los indicadores posteriores de la serie temporal analizada, utilizaremos la muestra de entrenamiento recogida como parte del trabajo sobre el artículo anterior.

Permítame recordarle que para el entrenamiento del modelo hemos usado datos históricos reales de EURUSD del marco temporal H1 recopilados para todo el año 2023. Al entrenar el modelo de Codificador del entorno, este solo trabajará con los datos históricos de los movimientos de precio e indicadores analizados. Por ello, hemos entrenado el modelo hasta obtener el resultado deseado, sin necesidad de actualizar la muestra de entrenamiento.

Y hablando del entrenamiento de modelos, me gustaría mencionar la estabilidad del proceso. El modelo se entrena con bastante rapidez, sin picos repentinos en el error de predicción.

Al final, a pesar de la relativa simplicidad del modelo, hemos obtenido un resultado bastante bueno. Por ejemplo, a continuación le mostramos un gráfico comparativo del movimiento del precio objetivo y el previsto.

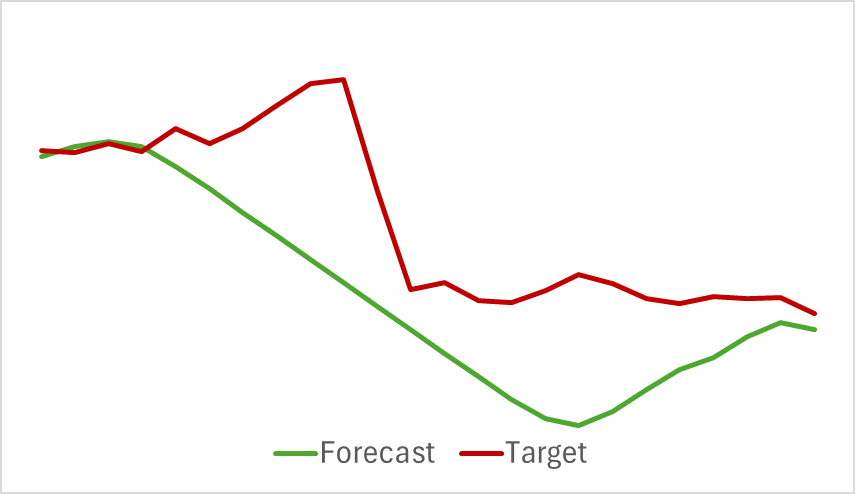
El gráfico muestra que el modelo ha sido capaz de captar las principales tendencias de la próxima evolución de los precios. Llama la atención el hecho de que con un horizonte de previsión de 24 horas tenemos valores bastante próximos al principio y al final de la trayectoria de previsión. Y solo el impulso del movimiento de precio de la trayectoria prevista se ha prolongado más en el tiempo.

Cabe añadir que las trayectorias previstas de los indicadores analizados tampoco arrojan malos resultados. A continuación le mostramos el gráfico de previsión del indicador RSI.

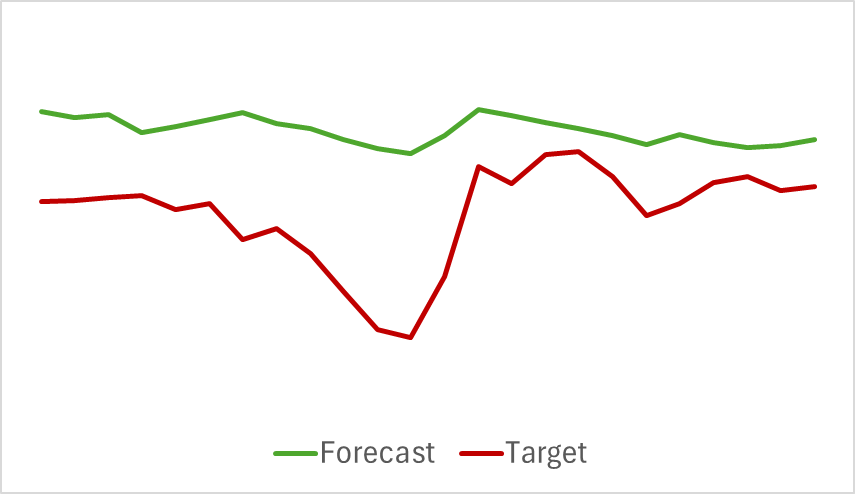
Los valores previstos del indicador se sitúan algo por encima de los valores reales y tienen una amplitud menor, pero podemos observar la coherencia en el tiempo y la dirección de los principales impulsos.

Me gustaría llamar la atención sobre el hecho de que las previsiones presentadas del movimiento de los precios y de los indicadores se refieren al mismo periodo temporal. Y si comparamos los dos gráficos presentados, podemos observar que el impulso principal de los valores previstos y reales de los indicadores coincide en el tiempo con el impulso principal del movimiento real de los precios.

Conclusión

En este artículo, nos hemos familiarizado con algunos métodos de representación alternativa de series temporales en forma de segmentación lineal por partes. En la parte práctica del artículo, hemos implementado una de las variantes de los enfoques propuestos. Y los resultados de los experimentos realizados muestran el potencial de los enfoques analizados.

Enlaces

Bidirectional piecewise linear representation of time series with application to collective anomaly detection

Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor de recopilación de ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de Modelos
4	StudyEncoder.mq5	Asesor	Asesor de entrenamiento del Codificador
5	Test.mq5	Asesor	Asesor para la prueba de modelos
6	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema.
7	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
8	NeuroNet.cl	Biblioteca	Biblioteca de código de programa OpenCL