
Automatisieren von Handelsstrategien in MQL5 (Teil 21): Verbesserung des Handels mit neuronalen Netzen durch adaptive Lernraten
Einführung
In unserem vorherigen Artikel (Teil 20) haben wir die Multi-Symbol-Strategie mit dem Commodity Channel Index (CCI) und dem Awesome Oscillator (AO) entwickelt, die eine Trendumkehr von mehrere Währungspaare handelt, automatisch mit einer robusten Signalerzeugung und Risikomanagement in MetaQuotes Language 5 (MQL5). In Teil 21 befassen wir uns mit einer Handelsstrategie auf der Basis von neuronalen Netzwerken, die durch einen Mechanismus einer adaptiven Lernrate erweitert wird, um die Vorhersagegenauigkeit für Marktbewegungen zu optimieren. Wir werden die folgenden Themen behandeln:
- Die Strategie der Lernrate adaptiver neuronaler Netze verstehen
- Implementierung in MetaQuotes Language 5 (MQL5)
- Testen und Optimieren der Adaption der Lernraten
- Schlussfolgerung
Am Ende haben Sie ein umfassendes Handelssystem in MetaQuotes Language 5 (MQL5), das neuronale Netze mit dynamischen Lernratenanpassungen nutzt und bereit ist für weitere Verfeinerungen - lassen Sie uns einsteigen!
Die Strategie der Lernrate adaptiver neuronaler Netze verstehen
In Teil 20 haben wir ein Multi-Symbol-Handelssystem entwickelt, das den Channel Index und den Awesome Oscillator nutzt und automatisierte Trendumkehr-Trades für mehrere Währungspaare ermöglicht. In Teil 21 tauchen wir nun in eine dynamische Handelsstrategie auf Basis eines neuronalen Netzes ein, die sich die Leistungsfähigkeit neuronaler Netze zunutze macht, die die miteinander verbundenen Neuronen des menschlichen Gehirns nachahmen, um Marktpreisbewegungen mit größerer Präzision vorherzusagen, indem verschiedene Marktindikatoren verarbeitet und der Lernprozess an die Marktvolatilität angepasst wird. Unser Ziel ist es, ein flexibles, hochleistungsfähiges Handelssystem zu entwickeln, das neuronale Netze nutzt, um komplexe Marktmuster zu analysieren und Geschäfte mit optimierter Genauigkeit durch einen adaptiven Mechanismus der Lernraten auszuführen.
Neuronale Netze arbeiten mit Schichten aus Knoten oder Neuronen, die aus einer Eingabeschicht, die Marktdaten erfasst, versteckten Schichten, die komplexe Muster aufdecken, und einer Ausgabeschicht bestehen, die Handelssignale generiert, z. B. die Vorhersage von Kursbewegungen nach oben oder unten. Die Vorwärtspropagation treibt die Daten durch diese Schichten, in denen die Neuronen die Eingaben mit Gewichten und Verzerrungen versehen und sie in Vorhersagen umwandeln. Siehe unten.
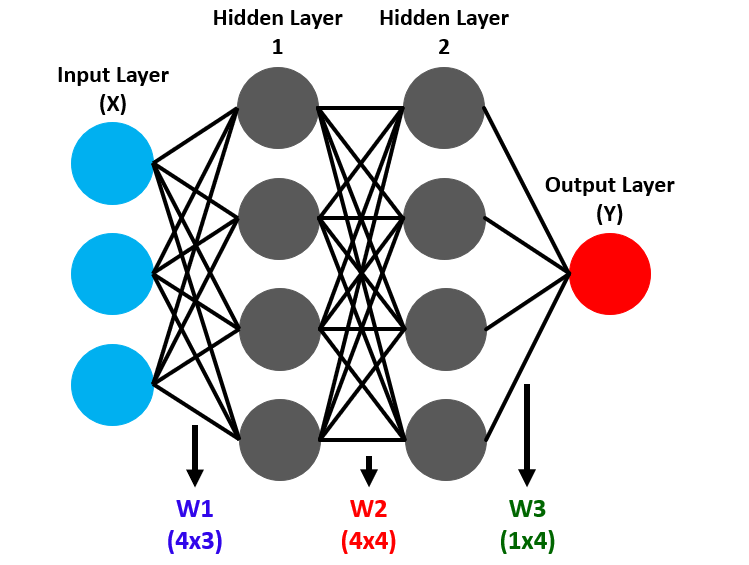
Eine entscheidende Komponente, die Aktivierungsfunktion, führt Nichtlinearität in diese Transformationen ein und ermöglicht es dem Netz, komplexe Beziehungen zu modellieren. Die Aktivierungsfunktion Sigmoid beispielsweise ordnet Werte einem Bereich von 0 bis 1 zu, wodurch sie sich ideal für binäre Klassifizierungsaufgaben wie Kauf- oder Verkaufsentscheidungen eignet. Backpropagation verfeinert diesen Prozess, indem es ausgehend von Vorhersagefehlern rückwärts arbeitet und die Gewichte und Verzerrungen anpasst, um die Genauigkeit im Laufe der Zeit zu verbessern. Siehe unten.
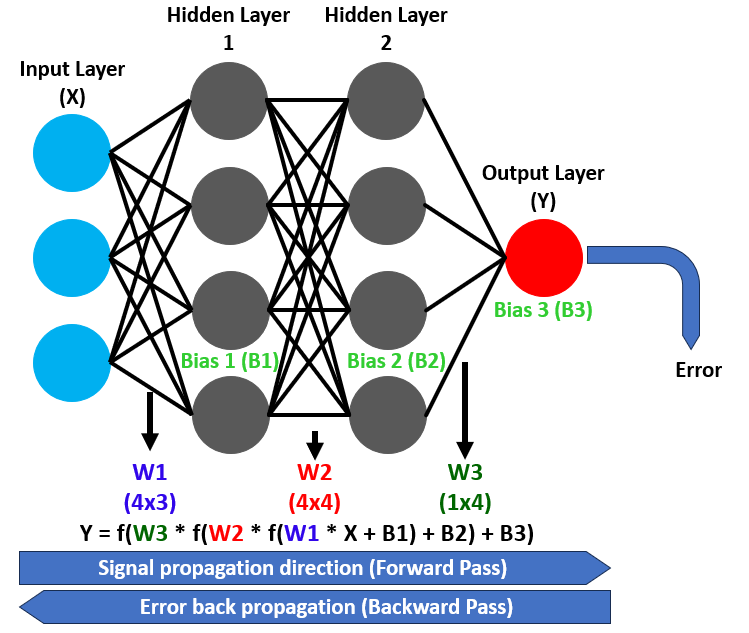
Um das Netzwerk dynamisch zu gestalten, planen wir die Implementierung einer adaptiven Lernstrategie, die die Geschwindigkeit der Aktualisierung der Gewichte während des BackpropagationLernens anpasst, wobei das Lernen beschleunigt wird, wenn die Vorhersagen mit den Marktergebnissen übereinstimmen, und die Geschwindigkeit verlangsamt, wenn die Fehler in die Höhe schnellen, um Stabilität zu gewährleisten.
Wir planen, ein System zu entwickeln, das Marktindikatoren wie gleitende Durchschnitte und Momentum-Metriken in die Eingabeschicht des neuronalen Netzes einspeist, sie durch versteckte Schichten verarbeitet, um Muster zu erkennen, und über die Ausgabeschicht zuverlässige Handelssignale erzeugt. Wir planen, die Aktivierungsfunktion Sigmoid zu verwenden, um die Neuronenausgaben zu transformieren und so glatte, interpretierbare Vorhersagen für Handelsentscheidungen zu gewährleisten. Wir haben uns dafür entschieden, weil wir so 2 Ausgabeoptionen haben. Hier ist ein Beispiel für andere Funktionen, die Sie verwenden können.
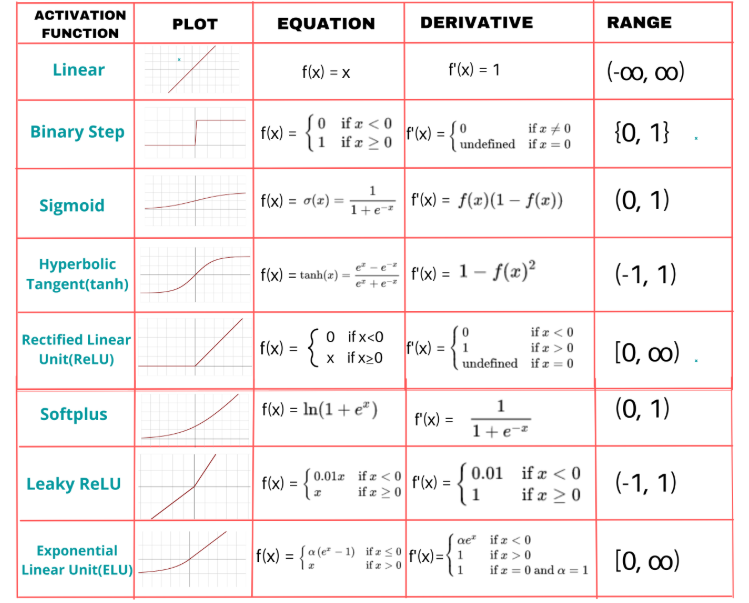
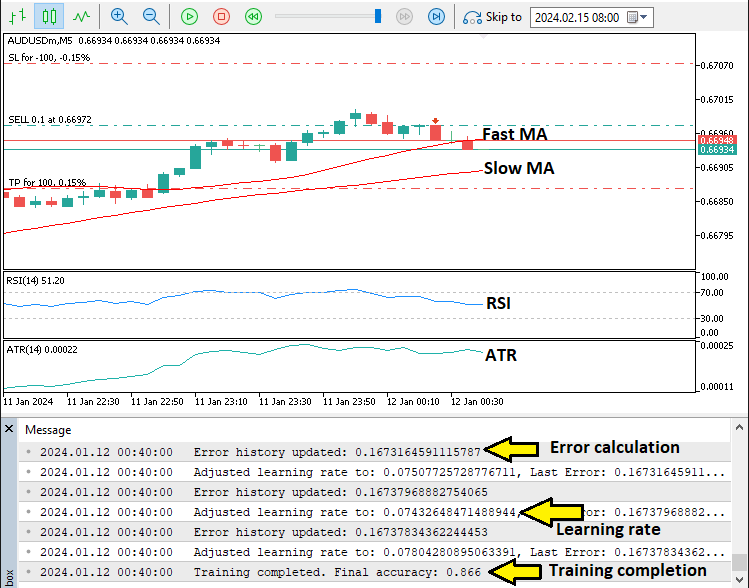
Darüber hinaus werden wir die Lernrate auf der Grundlage der Trainingsleistung dynamisch anpassen und die Anzahl der Neuronen der verborgenen Schicht an die Marktvolatilität anpassen, um ein reaktionsfähiges System zu schaffen, das Komplexität und Effizienz in Einklang bringt. Diese Strategie bildet die Grundlage für eine solide Umsetzung und gründliche Tests. Wir werden zwei gleitende Durchschnitte verwenden, den Relative Strength Index (RSI) und Average True Range (ATR), um die Eingaben zu liefern, und sobald wir Signale haben, werden wir den Handel eröffnen. Hier ist eine Visualisierung dessen, was wir nach der Implementierung erreichen wollen.
Implementation in MQL5
Um das Programm in MQL5 zu erstellen, öffnen wir den MetaEditor, gehen zum Navigator, suchen den Ordner der Indikatoren, klicken auf die Registerkarte „Neu“ und folgen den Anweisungen, um die Datei zu erstellen. Sobald dies geschehen ist, werden wir in der Programmierumgebung damit beginnen, einige Eingabevariablen, Strukturen und Klassen zu deklarieren, die wir verwenden werden, da wir einen objektorientierten Programmieransatz (OOP) anwenden wollen.
//+------------------------------------------------------------------+ //| Neural Networks Propagation EA.mq5 | //| Copyright 2025, Allan Munene Mutiiria. | //| https://t.me/Forex_Algo_Trader | //+------------------------------------------------------------------+ #property copyright "Copyright 2025, Allan Munene Mutiiria." #property link "https://t.me/Forex_Algo_Trader" #property version "1.00" #include <Trade/Trade.mqh> CTrade tradeObject; //--- Instantiate trade object for executing trades // Input parameters with clear, meaningful names input double LotSize = 0.1; // Lot Size input int StopLossPoints = 100; // Stop Loss (points) input int TakeProfitPoints = 100; // Take Profit (points) input int MinHiddenNeurons = 10; // Minimum Hidden Neurons input int MaxHiddenNeurons = 50; // Maximum Hidden Neurons input int TrainingBarCount = 1000; // Training Bars input double MinPredictionAccuracy = 0.7; // Minimum Prediction Accuracy input double MinLearningRate = 0.01; // Minimum Learning Rate input double MaxLearningRate = 0.5; // Maximum Learning Rate input string InputToHiddenWeights = "0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1"; // Input-to-Hidden Weights input string HiddenToOutputWeights = "0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1"; // Hidden-to-Output Weights input string HiddenBiases = "0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1,0.1,-0.1"; // Hidden Biases input string OutputBiases = "0.1,-0.1"; // Output Biases // Neural Network Structure Constants const int INPUT_NEURON_COUNT = 10; //--- Define number of input neurons const int OUTPUT_NEURON_COUNT = 2; //--- Define number of output neurons const int MAX_HISTORY_SIZE = 10; //--- Define maximum history size for accuracy and error tracking // Indicator handles int ma20IndicatorHandle; //--- Handle for 20-period moving average int ma50IndicatorHandle; //--- Handle for 50-period moving average int rsiIndicatorHandle; //--- Handle for RSI indicator int atrIndicatorHandle; //--- Handle for ATR indicator // Training related structures struct TrainingData { double inputValues[]; //--- Array to store input values for training double targetValues[]; //--- Array to store target values for training };
Hier legen wir den Grundstein für unsere auf neuronalen Netzen basierende Handelsstrategie mit adaptiven Lernraten, indem wir wesentliche Komponenten für die Handelsausführung und Datenverarbeitung initialisieren. Wir binden die Bibliothek „Trade.mqh“ ein und erstellen die Instanz „tradeObject“ der Klasse „CTrade“, um Handelsoperationen zu verwalten und die Ausführung von Kauf- und Verkaufsaufträgen auf der Grundlage von Prognosen durch ein neurales Netzwerk zu ermöglichen.
Wir definieren Eingabeparameter, um die Strategie zu konfigurieren, indem wir „LotSize“ zur Steuerung des Handelsvolumens, „StopLossPoints“ und „TakeProfitPoints“ für das Risikomanagement sowie „MinHiddenNeurons“ und „MaxHiddenNeurons“ zur Festlegung des Bereichs der versteckten Neuronen im neuronalen Netz festlegen. Zusätzlich geben wir „TrainingBarCount“ für die Anzahl der historischen Balken an, die für das Training verwendet werden, „MinPredictionAccuracy“ als Genauigkeitsschwelle und „MinLearningRate“ und „MaxLearningRate“ zur Begrenzung der adaptiven Lernrate. Wir bieten auch „InputToHiddenWeights“, „HiddenToOutputWeights“, „HiddenBiases“ und „OutputBiases“ als String-Eingaben für die Initialisierung von Gewichten und Biases des neuronalen Netzes an, die voreingestellte oder Standardkonfigurationen ermöglichen.
Als Nächstes legen wir Konstanten für die Struktur des neuronalen Netzes fest, indem wir „INPUT_NEURON_COUNT“ als 10 für die Marktdateneingänge, „OUTPUT_NEURON_COUNT“ als 2 für die Kauf-/Verkaufssignalausgänge und „MAX_HISTORY_SIZE“ als 10 definieren, um die Trainingsgenauigkeit und -fehler zu verfolgen. Wir erstellen die Indikator-Handles „ma20IndicatorHandle“, „ma50IndicatorHandle“, „rsiIndicatorHandle“ und „atrIndicatorHandle“, um auf die gleitenden Durchschnitte mit Periodenlängen von 20 bzw. 50, den RSI und Average True Range zu verweisen, um Marktdaten in das neuronale Netz einzuspeisen. Schließlich definieren wir die „TrainingData“-Struktur mit „inputValues“- und „targetValues“-Arrays, um Eingangsmerkmale und erwartete Ausgaben für das Training zu speichern und so eine organisierte Datenverwaltung für den Lernprozess des neuronalen Netzes zu gewährleisten. Wir werden Daten wie die folgenden speichern, wenn wir sie mit Werten füllen.
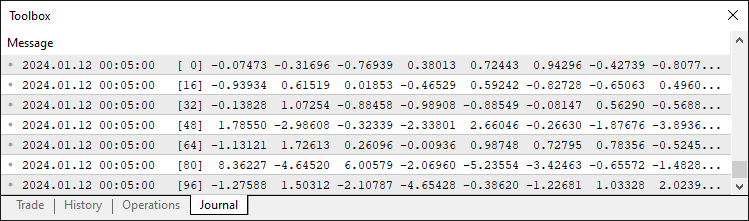
Als Nächstes müssen wir eine Klasse definieren, die die meisten der grundlegenden Mitgliedsvariablen enthält, die wir häufig verwenden müssen.
// Neural Network Class class CNeuralNetwork { private: int inputNeuronCount; //--- Number of input neurons int hiddenNeuronCount; //--- Number of hidden neurons int outputNeuronCount; //--- Number of output neurons double inputLayer[]; //--- Array for input layer values double hiddenLayer[]; //--- Array for hidden layer values double outputLayer[]; //--- Array for output layer values double inputToHiddenWeights[]; //--- Weights between input and hidden layers double hiddenToOutputWeights[];//--- Weights between hidden and output layers double hiddenLayerBiases[]; //--- Biases for hidden layer double outputLayerBiases[]; //--- Biases for output layer double outputDeltas[]; //--- Delta values for output layer double hiddenDeltas[]; //--- Delta values for hidden layer double trainingError; //--- Current training error double currentLearningRate; //--- Current learning rate double accuracyHistory[]; //--- History of training accuracy double errorHistory[]; //--- History of training errors int historyRecordCount; //--- Number of recorded history entries };
Hier implementieren wir die Kernstruktur unseres neuronalen Netzes, indem wir die Klasse „CNeuralNetwork“ erstellen. Wir definieren private Mitgliedsvariablen, um die Architektur des Netzwerks und den Trainingsprozess zu verwalten, beginnend mit „inputNeuronCount“, „hiddenNeuronCount“ und „outputNeuronCount“, um die Anzahl der Neuronen in der Eingabe-, der versteckten und der Ausgabeschicht festzulegen, die mit dem Design der Strategie für die Verarbeitung von Marktdaten und die Erzeugung von Handelssignalen übereinstimmen.
Wir richten Arrays ein, um die Werte der Schichten zu speichern, darunter „inputLayer“ für die Eingabe von Marktindikatoren, „hiddenLayer“ für die Verarbeitung von Zwischenmustern und „outputLayer“ für die Erstellung von Kauf-/Verkaufsprognosen. Für die Berechnungen des neuronalen Netzes erstellen wir die Arrays „inputToHiddenWeights“ und „hiddenToOutputWeights“ für die Gewichtungsverbindungen zwischen den Schichten sowie die Arrays „hiddenLayerBiases“ und „outputLayerBiases“ für die Bias-Anpassungen in den versteckten und den Ausgabeschichten. Für die Backpropagation definieren wir „outputDeltas“ und „hiddenDeltas“, um Fehlergradienten zu speichern und so die Aktualisierung von Gewichten und Verzerrungen während des Trainings zu ermöglichen.
Zusätzlich enthalten wir „trainingError“, um den aktuellen Fehler zu verfolgen, „currentLearningRate“, um die adaptive Lernrate zu verwalten, die Arrays „accuracyHistory“ und „errorHistory“, um die Trainingsleistung im Laufe der Zeit zu überwachen, und „historyRecordCount“, um die aufgezeichneten Einträge zu zählen, um sicherzustellen, dass das Netzwerk seinen Lernprozess dynamisch auf der Grundlage von Leistungstrends anpassen kann. Diese Klasse bildet die Grundlage für die Implementierung von Vorwärtspropagation, Backpropagation und adaptiven Lernratenanpassungen in nachfolgenden Funktionen. Innerhalb des privaten Zugriffsmodifikators können wir eine Methode zum Parsen von String-Eingaben in ein Array zur Verwendung definieren.
// Parse comma-separated string to array bool ParseStringToArray(string inputString, double &output[], int expectedSize) { //--- Check if input string is empty if(inputString == "") return false; string values[]; //--- Initialize array for parsed values ArrayResize(values, 0); //--- Split input string by comma int count = StringSplit(inputString, 44, values); //--- Check if string splitting failed if(count <= 0) { Print("Error: StringSplit failed for input: ", inputString, ". Error code: ", GetLastError()); return false; } //--- Verify correct number of values if(count != expectedSize) { Print("Error: Invalid number of values in input string. Expected: ", expectedSize, ", Got: ", count); return false; } //--- Resize output array to expected size ArrayResize(output, expectedSize); //--- Convert string values to doubles and normalize for(int i = 0; i < count; i++) { output[i] = StringToDouble(values[i]); //--- Clamp values between -1.0 and 1.0 if(MathAbs(output[i]) > 1.0) output[i] = MathMax(-1.0, MathMin(1.0, output[i])); } return true; }
Wir implementieren die Funktion „ParseStringToArray“ in der Klasse „CNeuralNetwork“, um kommagetrennte Strings für die Gewichte und Verzerrungen des neuronalen Netzes zu verarbeiten. Wir prüfen, ob „inputString“ leer ist und geben „false“ zurück, wenn es ungültig ist, und verwenden StringSplit mit einem Komma als Trennzeichen, um es in „values“ aufzuteilen. Wenn die Aufteilung fehlschlägt oder „count“ nicht mit „expectedSize“ übereinstimmt, werden Fehler mit Print protokolliert und „false“ zurückgegeben. Wir ändern die Größe von „output“ mit ArrayResize, konvertieren „values“ in Doubles mit StringToDouble, normalisieren sie zwischen -1.0 und 1.0 mit MathMax und MathMin, und geben „true“ für erfolgreiches Parsen zurück. Die übrigen Hilfsfunktionen können wie unten beschrieben im Modifikatorteil für den öffentlichen Zugriff deklariert werden, um sie später zu definieren.
public: CNeuralNetwork(int inputs, int hidden, int outputs); //--- Constructor void InitializeWeights(); //--- Initialize network weights double Sigmoid(double x); //--- Apply sigmoid activation function void ForwardPropagate(); //--- Perform forward propagation void Backpropagate(const double &targets[]); //--- Perform backpropagation void SetInput(double &inputs[]); //--- Set input values void GetOutput(double &outputs[]); //--- Retrieve output values double TrainOnHistoricalData(TrainingData &data[]); //--- Train on historical data void UpdateNetworkWithRecentData(); //--- Update with recent data void InitializeTraining(); //--- Initialize training arrays void ResizeNetwork(int newHiddenNeurons); //--- Resize network void AdjustLearningRate(); //--- Adjust learning rate dynamically double GetRecentAccuracy(); //--- Get recent training accuracy double GetRecentError(); //--- Get recent training error bool ShouldRetrain(); //--- Check if retraining is needed double CalculateDynamicNeurons(); //--- Calculate dynamic neuron count int GetHiddenNeurons() { return hiddenNeuronCount; //--- Get current hidden neuron count }
Hier definieren wir die öffentliche Schnittstelle der Klasse „CNeuralNetwork“. Wir erstellen den Konstruktor „CNeuralNetwork“ mit „inputs“, „hidden“ und „outputs“, um das Netz einzurichten, und „InitializeWeights“, um Gewichte und Verzerrungen zu konfigurieren. Wir implementieren „Sigmoid“ für die Aktivierung, „ForwardPropagate“ und „Backpropagate“ für die Verarbeitung und Aktualisierung auf der Grundlage von „Zielen“ sowie „SetInput“ und „GetOutput“ für die Handhabung von „Eingängen“ und „Ausgängen“.
Wir entwickeln „TrainOnHistoricalData“ mit „TrainingData“, „UpdateNetworkWithRecentData“ für aktuelle Daten, „InitializeTraining“ für Arrays, „ResizeNetwork“ für „newHiddenNeurons“, „AdjustLearningRate“ für dynamisches Lernen und „GetRecentAccuracy“, „GetRecentError“, „ShouldRetrain“, „CalculateDynamicNeurons“ und „GetHiddenNeurons“ zur Überwachung und Anpassung von „hiddenNeuronCount“. Wir können nun mit der Implementierung und Definition der Funktion wie folgt beginnen.
// Constructor CNeuralNetwork::CNeuralNetwork(int inputs, int hidden, int outputs) { //--- Set input neuron count inputNeuronCount = inputs; //--- Set output neuron count outputNeuronCount = outputs; //--- Initialize learning rate to minimum currentLearningRate = MinLearningRate; //--- Set hidden neuron count hiddenNeuronCount = hidden; //--- Ensure hidden neurons within bounds if(hiddenNeuronCount < MinHiddenNeurons) hiddenNeuronCount = MinHiddenNeurons; if(hiddenNeuronCount > MaxHiddenNeurons) hiddenNeuronCount = MaxHiddenNeurons; //--- Resize input layer array ArrayResize(inputLayer, inputs); //--- Resize hidden layer array ArrayResize(hiddenLayer, hiddenNeuronCount); //--- Resize output layer array ArrayResize(outputLayer, outputs); //--- Resize input-to-hidden weights array ArrayResize(inputToHiddenWeights, inputs * hiddenNeuronCount); //--- Resize hidden-to-output weights array ArrayResize(hiddenToOutputWeights, hiddenNeuronCount * outputs); //--- Resize hidden biases array ArrayResize(hiddenLayerBiases, hiddenNeuronCount); //--- Resize output biases array ArrayResize(outputLayerBiases, outputs); //--- Resize accuracy history array ArrayResize(accuracyHistory, MAX_HISTORY_SIZE); //--- Resize error history array ArrayResize(errorHistory, MAX_HISTORY_SIZE); //--- Initialize history record count historyRecordCount = 0; //--- Initialize training error trainingError = 0.0; //--- Initialize network weights InitializeWeights(); //--- Initialize training arrays InitializeTraining(); } // Initialize training arrays void CNeuralNetwork::InitializeTraining() { //--- Resize output deltas array ArrayResize(outputDeltas, outputNeuronCount); //--- Resize hidden deltas array ArrayResize(hiddenDeltas, hiddenNeuronCount); } // Initialize weights void CNeuralNetwork::InitializeWeights() { //--- Track if weights and biases are set bool isInputToHiddenWeightsSet = false; bool isHiddenToOutputWeightsSet = false; bool isHiddenBiasesSet = false; bool isOutputBiasesSet = false; double tempInputToHiddenWeights[]; double tempHiddenToOutputWeights[]; double tempHiddenBiases[]; double tempOutputBiases[]; //--- Parse and set input-to-hidden weights if provided if(InputToHiddenWeights != "" && ParseStringToArray(InputToHiddenWeights, tempInputToHiddenWeights, inputNeuronCount * hiddenNeuronCount)) { //--- Copy parsed weights to main array ArrayCopy(inputToHiddenWeights, tempInputToHiddenWeights); isInputToHiddenWeightsSet = true; //--- Log weight initialization Print("Initialized input-to-hidden weights from input: ", InputToHiddenWeights); } //--- Parse and set hidden-to-output weights if provided if(HiddenToOutputWeights != "" && ParseStringToArray(HiddenToOutputWeights, tempHiddenToOutputWeights, hiddenNeuronCount * outputNeuronCount)) { //--- Copy parsed weights to main array ArrayCopy(hiddenToOutputWeights, tempHiddenToOutputWeights); isHiddenToOutputWeightsSet = true; //--- Log weight initialization Print("Initialized hidden-to-output weights from input: ", HiddenToOutputWeights); } //--- Parse and set hidden biases if provided if(HiddenBiases != "" && ParseStringToArray(HiddenBiases, tempHiddenBiases, hiddenNeuronCount)) { //--- Copy parsed biases to main array ArrayCopy(hiddenLayerBiases, tempHiddenBiases); isHiddenBiasesSet = true; //--- Log bias initialization Print("Initialized hidden biases from input: ", HiddenBiases); } //--- Parse and set output biases if provided if(OutputBiases != "" && ParseStringToArray(OutputBiases, tempOutputBiases, outputNeuronCount)) { //--- Copy parsed biases to main array ArrayCopy(outputLayerBiases, tempOutputBiases); isOutputBiasesSet = true; //--- Log bias initialization Print("Initialized output biases from input: ", OutputBiases); } //--- Initialize input-to-hidden weights randomly if not set if(!isInputToHiddenWeightsSet) { for(int i = 0; i < ArraySize(inputToHiddenWeights); i++) inputToHiddenWeights[i] = (MathRand() / 32767.0) * 2 - 1; } //--- Initialize hidden-to-output weights randomly if not set if(!isHiddenToOutputWeightsSet) { for(int i = 0; i < ArraySize(hiddenToOutputWeights); i++) hiddenToOutputWeights[i] = (MathRand() / 32767.0) * 2 - 1; } //--- Initialize hidden biases randomly if not set if(!isHiddenBiasesSet) { for(int i = 0; i < ArraySize(hiddenLayerBiases); i++) hiddenLayerBiases[i] = (MathRand() / 32767.0) * 2 - 1; } //--- Initialize output biases randomly if not set if(!isOutputBiasesSet) { for(int i = 0; i < ArraySize(outputLayerBiases); i++) outputLayerBiases[i] = (MathRand() / 32767.0) * 2 - 1; } } // Sigmoid activation function double CNeuralNetwork::Sigmoid(double x) { //--- Compute and return sigmoid value return 1.0 / (1.0 + MathExp(-x)); } // Set input void CNeuralNetwork::SetInput(double &inputs[]) { //--- Check for input array size mismatch if(ArraySize(inputs) != inputNeuronCount) { Print("Error: Input array size mismatch. Expected: ", inputNeuronCount, ", Got: ", ArraySize(inputs)); return; } //--- Copy inputs to input layer ArrayCopy(inputLayer, inputs); } // Forward propagation void CNeuralNetwork::ForwardPropagate() { //--- Compute hidden layer values for(int j = 0; j < hiddenNeuronCount; j++) { double sum = 0; //--- Calculate weighted sum for hidden neuron for(int i = 0; i < inputNeuronCount; i++) sum += inputLayer[i] * inputToHiddenWeights[i * hiddenNeuronCount + j]; //--- Apply sigmoid activation hiddenLayer[j] = Sigmoid(sum + hiddenLayerBiases[j]); } //--- Compute output layer values for(int j = 0; j < outputNeuronCount; j++) { double sum = 0; //--- Calculate weighted sum for output neuron for(int i = 0; i < hiddenNeuronCount; i++) sum += hiddenLayer[i] * hiddenToOutputWeights[i * outputNeuronCount + j]; //--- Apply sigmoid activation outputLayer[j] = Sigmoid(sum + outputLayerBiases[j]); } } // Get output void CNeuralNetwork::GetOutput(double &outputs[]) { //--- Resize output array ArrayResize(outputs, outputNeuronCount); //--- Copy output layer to outputs ArrayCopy(outputs, outputLayer); } // Backpropagation void CNeuralNetwork::Backpropagate(const double &targets[]) { //--- Calculate output layer deltas for(int i = 0; i < outputNeuronCount; i++) { double output = outputLayer[i]; //--- Compute delta for output neuron outputDeltas[i] = output * (1 - output) * (targets[i] - output); } //--- Calculate hidden layer deltas for(int i = 0; i < hiddenNeuronCount; i++) { double error = 0; //--- Sum weighted errors from output layer for(int j = 0; j < outputNeuronCount; j++) error += outputDeltas[j] * hiddenToOutputWeights[i * outputNeuronCount + j]; double output = hiddenLayer[i]; //--- Compute delta for hidden neuron hiddenDeltas[i] = output * (1 - output) * error; } //--- Update hidden-to-output weights for(int i = 0; i < hiddenNeuronCount; i++) { for(int j = 0; j < outputNeuronCount; j++) { int idx = i * outputNeuronCount + j; //--- Adjust weight based on learning rate and delta hiddenToOutputWeights[idx] += currentLearningRate * outputDeltas[j] * hiddenLayer[i]; } } //--- Update input-to-hidden weights for(int i = 0; i < inputNeuronCount; i++) { for(int j = 0; j < hiddenNeuronCount; j++) { int idx = i * hiddenNeuronCount + j; //--- Adjust weight based on learning rate and delta inputToHiddenWeights[idx] += currentLearningRate * hiddenDeltas[j] * inputLayer[i]; } } //--- Update hidden biases for(int i = 0; i < hiddenNeuronCount; i++) //--- Adjust bias based on learning rate and delta hiddenLayerBiases[i] += currentLearningRate * hiddenDeltas[i]; //--- Update output biases for(int i = 0; i < outputNeuronCount; i++) //--- Adjust bias based on learning rate and delta outputLayerBiases[i] += currentLearningRate * outputDeltas[i]; } // Resize network (adjust hidden neurons) void CNeuralNetwork::ResizeNetwork(int newHiddenNeurons) { //--- Clamp new neuron count within bounds newHiddenNeurons = MathMax(MinHiddenNeurons, MathMin(newHiddenNeurons, MaxHiddenNeurons)); //--- Check if resizing is necessary if(newHiddenNeurons == hiddenNeuronCount) return; //--- Log resizing information Print("Resizing network. New hidden neurons: ", newHiddenNeurons, ", Previous: ", hiddenNeuronCount); //--- Update hidden neuron count hiddenNeuronCount = newHiddenNeurons; //--- Resize hidden layer array ArrayResize(hiddenLayer, hiddenNeuronCount); //--- Resize input-to-hidden weights array ArrayResize(inputToHiddenWeights, inputNeuronCount * hiddenNeuronCount); //--- Resize hidden-to-output weights array ArrayResize(hiddenToOutputWeights, hiddenNeuronCount * outputNeuronCount); //--- Resize hidden biases array ArrayResize(hiddenLayerBiases, hiddenNeuronCount); //--- Resize hidden deltas array ArrayResize(hiddenDeltas, hiddenNeuronCount); //--- Reinitialize weights InitializeWeights(); }
Hier implementieren wir wichtige Komponenten des neuronalen Netzes. Wir erstellen den Konstruktor „CNeuralNetwork“ und nehmen „inputs“, „hidden“ und „outputs“, um „inputNeuronCount“, „outputNeuronCount“ und „hiddenNeuronCount“, wobei letzterer zwischen „MinHiddenNeurons“ und „MaxHiddenNeurons“ geklemmt wird. Wir müssen nicht viel Zeit darauf verwenden, den Klassenprototyp zu erklären, da wir bereits im vorherigen Teil etwas Ähnliches getan haben.
Wir initialisieren dann „currentLearningRate“ auf „MinLearningRate“, ändern die Größe von Arrays wie „inputLayer“, „hiddenLayer“, „outputLayer“, „inputToHiddenWeights“, „hiddenToOutputWeights“, „hiddenLayerBiases“, „outputLayerBiases“, „accuracyHistory“ und „errorHistory“ mittels ArrayResize und rufen Sie „InitializeWeights“ und „InitializeTraining“ auf, um das Netz einzurichten.
Wir entwickeln die Funktion „InitializeTraining“, um die Größe der Arrays „outputDeltas“ und „hiddenDeltas“ für die Backpropagation zu ändern und die korrekte Speicherung des Fehlergradienten sicherzustellen. Die Funktion „InitializeWeights“ richtet Gewichte und Biases ein und verwendet „ParseStringToArray“, um „inputToHiddenWeights“, „hiddenToOutputWeights“, „hiddenLayerBiases“ zu ladenund „outputLayerBiases“ aus Eingaben wie „InputToHiddenWeights“, falls vorhanden, oder randomisiert sie mit MathRand zwischen -1 und 1, falls nicht, und protokolliert die Aktionen mit „Print“. Wir implementieren die Funktion „Sigmoid“, um den sigmoiden Aktivierungswert für ein gegebenes „x“ mit Hilfe der Funktion MathExp zu berechnen.
Die Funktion „SetInput“ kopiert „inputs“ in „inputLayer“, nachdem die Größe mit ArraySize überprüft wurde, und protokolliert Fehler mit „Print“, wenn sie nicht übereinstimmen. Wir erstellen die Funktion „ForwardPropagate“, um „hiddenLayer“- und „outputLayer“-Werte zu berechnen, indem wir gewichtete Summen und „Sigmoid“-Aktivierung mit „hiddenLayerBiases“ und „outputLayerBiases“ anwenden. Die Funktion „GetOutput“ ändert die Größe von „outputs“ mit „ArrayResize“ und kopiert „outputLayer“-Werte mit ArrayCopy.
Wir implementieren die Funktion „Backpropagate“ zur Berechnung von „outputDeltas“ und „hiddenDeltas“ aus „targets“ und aktualisieren „hiddenToOutputWeights“, „inputToHiddenWeights“, „hiddenLayerBiases“ und „outputLayerBiases“ unter Verwendung von „currentLearningRate“. Schließlich passt die Funktion „ResizeNetwork“ die „hiddenNeuronCount“ innerhalb der Grenzen an, ändert die Größe von Arrays wie „hiddenLayer“ und „hiddenDeltas“ und initialisiert die Gewichte mit „InitializeWeights“ und protokolliert die Änderungen mit „Print“. Wir müssen dann die Lernrate auf der Grundlage des Fehlertrends anpassen, also lassen Sie uns einen genaueren Blick darauf werfen.
// Adjust learning rate based on error trend void CNeuralNetwork::AdjustLearningRate() { //--- Check if enough history exists if(historyRecordCount < 2) return; //--- Get last and previous errors double lastError = errorHistory[historyRecordCount - 1]; double prevError = errorHistory[historyRecordCount - 2]; //--- Calculate error difference double errorDiff = lastError - prevError; //--- Increase learning rate if error decreased if(lastError < prevError) currentLearningRate = MathMin(currentLearningRate * 1.05, MaxLearningRate); //--- Decrease learning rate if error increased significantly else if(lastError > prevError * 1.2) currentLearningRate = MathMax(currentLearningRate * 0.9, MinLearningRate); //--- Slightly decrease learning rate otherwise else currentLearningRate = MathMax(currentLearningRate * 0.99, MinLearningRate); //--- Log learning rate adjustment Print("Adjusted learning rate to: ", currentLearningRate, ", Last Error: ", lastError, ", Prev Error: ", prevError, ", Error Diff: ", errorDiff); }
Wir implementieren den Mechanismus der adaptiven Lernrate, indem wir die Funktion „AdjustLearningRate“ innerhalb der Klasse „CNeuralNetwork“ erstellen. Wir prüfen, ob „historyRecordCount“ mindestens 2 ist, um sicherzustellen, dass genügend Daten im Array „errorHistory“ vorhanden sind, und brechen ab, wenn dies nicht der Fall ist, um ungültige Anpassungen zu vermeiden. Wir rufen den letzten Fehler als „lastError“ und den vorherigen Fehler als „prevError“ aus „errorHistory“ ab und berechnen dann ihre Differenz in „errorDiff“, um die Trainingsleistung zu bewerten.
Wir verwenden die Funktion MathMin, um „currentLearningRate“ um 5 % zu erhöhen, wenn „lastError“ kleiner als „prevError“ ist, und begrenzen sie auf „MaxLearningRate“, oder verwenden die Funktion MathMax, um sie um 10 % zu verringern, wenn „lastError“ „prevError“ um 20 % übersteigt, um sicherzustellen, dass sie über „MinLearningRate“ bleibt. Andernfalls wird „currentLearningRate“ mit Hilfe von „MathMax“ leicht um 1% reduziert. Schließlich verwenden wir die Funktion „Drucken“, um die angepassten Werte „currentLearningRate“, „lastError“, „prevError“ und „errorDiff“ zu protokollieren, was eine dynamische Optimierung des Lernprozesses des neuronalen Netzes ermöglicht. Anschließend verwenden wir den ATR-Indikator, um die Anzahl der versteckten Neuronen dynamisch zu berechnen, sodass wir sie an die Volatilität anpassen können.
// Calculate dynamic number of hidden neurons based on ATR double CNeuralNetwork::CalculateDynamicNeurons() { double atrValues[]; //--- Set ATR array as series ArraySetAsSeries(atrValues, true); //--- Copy ATR buffer if(CopyBuffer(atrIndicatorHandle, 0, 0, 10, atrValues) < 10) { Print("Error: Failed to copy ATR for dynamic neurons. Using default: ", hiddenNeuronCount); return hiddenNeuronCount; } //--- Calculate average ATR double avgATR = 0; for(int i = 0; i < 10; i++) avgATR += atrValues[i]; avgATR /= 10; //--- Get current close price double closePrice = iClose(_Symbol, PERIOD_CURRENT, 0); //--- Check for valid close price if(MathAbs(closePrice) < 0.000001) { Print("Error: Invalid close price for ATR ratio. Using default: ", hiddenNeuronCount); return hiddenNeuronCount; } //--- Calculate ATR ratio double atrRatio = atrValues[0] / closePrice; //--- Compute new neuron count int newNeurons = MinHiddenNeurons + (int)((MaxHiddenNeurons - MinHiddenNeurons) * MathMin(atrRatio * 100, 1.0)); //--- Return clamped neuron count return MathMax(MinHiddenNeurons, MathMin(newNeurons, MaxHiddenNeurons)); }
Um die Anzahl der versteckten Neuronen dynamisch an die Marktvolatilität anzupassen, deklarieren wir das Array „atrValues“ und verwenden die Funktion ArraySetAsSeries, um es als Zeitreihen-Array zu konfigurieren. Anschließend verwenden wir die Funktion CopyBuffer, um 10 Balken mit den Daten von Average True Range aus „atrIndicatorHandle“ in „atrValues“ einzulesen. Wenn „CopyBuffer“ weniger als 10 Werte abruft, verwenden wir die Funktion „Print“, um einen Fehler zu protokollieren und „hiddenNeuronCount“ als Standardwert zurückzugeben. Wir müssen das Array als Zeitreihe festlegen, damit die neuesten abgerufenen Daten in den Anfangsindizes abgebildet und als erste verwendet werden können. Hier ist eine Darstellung.
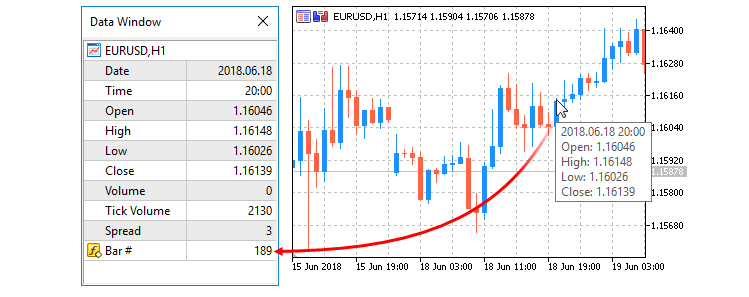
Wir berechnen die durchschnittliche ATR, indem wir die „atrValues“ über 10 Balken summieren und durch 10 dividieren und das Ergebnis in „avgATR“ speichern. Wir verwenden die Funktion iClose, um den aktuellen Schlusskurs in „closePrice“ für das _Symbol und „PERIOD_CURRENT“ zu erhalten. Wenn „closePrice“ nahe Null ist, verwenden wir die Funktion „Print“, um einen Fehler zu protokollieren und „hiddenNeuronCount“ zurückzugeben. Wir berechnen das ATR-Verhältnis als „atrValues[0]“ geteilt durch „closePrice“ und berechnen dann „newNeurons“, indem wir den Bereich zwischen „MinHiddenNeurons“ und „MaxHiddenNeurons“ mithilfe der Funktion MathMin auf das skalierte „atrRatio“ skalieren. Schließlich verwenden wir die Funktionen „mathmax“ und „mathmin“, um die angepasste Neuronenzahl festzuhalten und zurückzugeben, um eine dynamische Anpassung an die Marktbedingungen zu gewährleisten. Wir können nun den Rest der Trainings- und Aktualisierungsfunktionen wie folgt definieren.
// Train network on historical data double CNeuralNetwork::TrainOnHistoricalData(TrainingData &data[]) { const int maxEpochs = 100; //--- Maximum training epochs const double targetError = 0.01; //--- Target error threshold double accuracy = 0; //--- Training accuracy //--- Reset learning rate currentLearningRate = MinLearningRate; //--- Iterate through epochs for(int epoch = 0; epoch < maxEpochs; epoch++) { double totalError = 0; //--- Total error for epoch int correctPredictions = 0; //--- Count of correct predictions //--- Process each training sample for(int i = 0; i < ArraySize(data); i++) { //--- Check target array size if(ArraySize(data[i].targetValues) != outputNeuronCount) { Print("Error: Mismatch in targets size for training data at index ", i); continue; } //--- Set input values SetInput(data[i].inputValues); //--- Perform forward propagation ForwardPropagate(); double error = 0; //--- Calculate error for(int j = 0; j < outputNeuronCount; j++) error += MathPow(data[i].targetValues[j] - outputLayer[j], 2); totalError += error; //--- Check prediction correctness if((outputLayer[0] > outputLayer[1] && data[i].targetValues[0] > data[i].targetValues[1]) || (outputLayer[0] < outputLayer[1] && data[i].targetValues[0] < data[i].targetValues[1])) correctPredictions++; //--- Perform backpropagation Backpropagate(data[i].targetValues); } //--- Calculate accuracy accuracy = (double)correctPredictions / ArraySize(data); //--- Update training error trainingError = totalError / ArraySize(data); //--- Update history if(historyRecordCount < MAX_HISTORY_SIZE) { accuracyHistory[historyRecordCount] = accuracy; errorHistory[historyRecordCount] = trainingError; historyRecordCount++; } else { //--- Shift history arrays for(int i = 1; i < MAX_HISTORY_SIZE; i++) { accuracyHistory[i - 1] = accuracyHistory[i]; errorHistory[i - 1] = errorHistory[i]; } //--- Add new values accuracyHistory[MAX_HISTORY_SIZE - 1] = accuracy; errorHistory[MAX_HISTORY_SIZE - 1] = trainingError; } //--- Log error history update Print("Error history updated: ", errorHistory[historyRecordCount - 1]); //--- Adjust learning rate AdjustLearningRate(); //--- Log progress every 10 epochs if(epoch % 10 == 0) Print("Epoch ", epoch, ": Error = ", trainingError, ", Accuracy = ", accuracy); //--- Check for early stopping if(trainingError < targetError && accuracy >= MinPredictionAccuracy) break; } //--- Return final accuracy return accuracy; } // Update network with recent data void CNeuralNetwork::UpdateNetworkWithRecentData() { const int recentBarCount = 10; //--- Number of recent bars to process TrainingData recentData[]; //--- Collect recent training data if(!CollectTrainingData(recentData, recentBarCount)) return; //--- Process each recent data sample for(int i = 0; i < ArraySize(recentData); i++) { //--- Set input values SetInput(recentData[i].inputValues); //--- Perform forward propagation ForwardPropagate(); //--- Perform backpropagation Backpropagate(recentData[i].targetValues); } } // Get recent accuracy double CNeuralNetwork::GetRecentAccuracy() { //--- Check if history exists if(historyRecordCount == 0) return 0.0; //--- Return most recent accuracy return accuracyHistory[historyRecordCount - 1]; } // Get recent error double CNeuralNetwork::GetRecentError() { //--- Check if history exists if(historyRecordCount == 0) return 0.0; //--- Return most recent error return errorHistory[historyRecordCount - 1]; } // Check if retraining is needed bool CNeuralNetwork::ShouldRetrain() { //--- Check if enough history exists if(historyRecordCount < 2) return false; //--- Get recent metrics double recentAccuracy = GetRecentAccuracy(); double recentError = GetRecentError(); double prevError = errorHistory[historyRecordCount - 2]; //--- Determine if retraining is needed return (recentAccuracy < MinPredictionAccuracy || recentError > prevError * 1.5); }
Hier implementieren wir wichtige Trainings- und Aktualisierungsmechanismen für das neuronale Netz. Wir erstellen die Funktion „TrainOnHistoricalData“, um das Netz mit dem Array der Struktur „TrainingData“ zu trainieren, setzen „maxEpochs“ auf 100 und „targetError“ auf 0,01 und setzen „currentLearningRate“ auf „MinLearningRate“ zurück. Für jede Epoche iterieren wir durch „data“, überprüfen die Größe von „data[i].targetValues“ mit „outputNeuronCount“ und verwenden die Funktion „SetInput“, um „data[i].inputValues“ zu laden, gefolgt von der Funktion „ForwardPropagate“, um Vorhersagen zu berechnen. Wir berechnen den Fehler mit MathPow für „outputLayer“ gegenüber „data[i].targetValues“, verfolgen „correctPredictions“ und wenden die Funktion „Backpropagate“ mit „data[i].targetValues“ an.
Wir aktualisieren „accuracy“ und „trainingError“, speichern sie in „accuracyHistory“ und „errorHistory“ unter Verwendung von „historyRecordCount“, verschieben Arrays, wenn sie voll sind, protokollieren Aktualisierungen mit der Funktion „Print“ protokollieren und die Funktion „AdjustLearningRate“ verwenden, um den Lernprozess zu optimieren und frühzeitig zu stoppen, wenn „trainingError“ und „accuracy“ den Werten von „targetError“ und „MinPredictionAccuracy“ entsprechen.
Wir entwickeln die Funktion „UpdateNetworkWithRecentData“, um das Netzwerk zu verfeinern, wobei „recentBarCount“ auf 10 gesetzt wird, und verwenden die Funktion „CollectTrainingData“, um „recentData“ aufzufüllen, und iterieren, um „SetInput“, „ForwardPropagate“ und „Backpropagate“ für jede Probe anzuwenden. Die Funktion „GetRecentAccuracy“ gibt den letzten „accuracyHistory“-Wert oder 0,0 zurück, wenn „historyRecordCount“ Null ist, und die Funktion „GetRecentError“ tut dasselbe für „errorHistory“.
Wir erstellen die Funktion „ShouldRetrain“, um zu prüfen, ob „historyRecordCount“ mindestens 2 ist, und verwenden „GetRecentAccuracy“ und „GetRecentError“, um „recentAccuracy“ und „recentError“ mit „MinPredictionAccuracy“ und dem 1.das Fünffache des vorherigen „errorHistory“-Werts, wobei „true“ zurückgegeben wird, wenn ein erneutes Training erforderlich ist. Wir können nun eine Instanz der Klasse erstellen, die wir für die eigentliche Implementierung verwenden werden.
// Global neural network instance CNeuralNetwork *neuralNetwork; //--- Global neural network object
Wir legen den globalen Bereich für das neuronale Netz fest, indem wir den Zeiger „neuralNetwork“ auf eine Instanz der Klasse „CNeuralNetwork“ erstellen. Dieses globale Objekt ermöglicht den zentralen Zugriff auf die Funktionen des neuronalen Netzes, einschließlich Training, Forward Propagation, Backpropagation und adaptive Lernratenanpassung, und gewährleistet so eine nahtlose Integration in den gesamten Betrieb des Expert Advisors.
Indem wir „neuralNetwork“ global definieren, erleichtern wir seine Verwendung in Initialisierungs-, Tick-Verarbeitungs- und Deinitialisierungsfunktionen zur Verwaltung der Prognose- und Handelsfunktionen der Strategie. Wir können Funktionen definieren, um die Eingaben zu initialisieren und Trainingsdaten für die Modularität zu sammeln.
// Prepare inputs from market data void PrepareInputs(double &inputs[]) { //--- Resize inputs array if necessary if(ArraySize(inputs) != INPUT_NEURON_COUNT) ArrayResize(inputs, INPUT_NEURON_COUNT); double ma20Values[], ma50Values[], rsiValues[], atrValues[]; //--- Set arrays as series ArraySetAsSeries(ma20Values, true); ArraySetAsSeries(ma50Values, true); ArraySetAsSeries(rsiValues, true); ArraySetAsSeries(atrValues, true); //--- Copy MA20 buffer if(CopyBuffer(ma20IndicatorHandle, 0, 0, 2, ma20Values) <= 0) { Print("Error: Failed to copy MA20 buffer. Error code: ", GetLastError()); return; } //--- Copy MA50 buffer if(CopyBuffer(ma50IndicatorHandle, 0, 0, 2, ma50Values) <= 0) { Print("Error: Failed to copy MA50 buffer. Error code: ", GetLastError()); return; } //--- Copy RSI buffer if(CopyBuffer(rsiIndicatorHandle, 0, 0, 2, rsiValues) <= 0) { Print("Error: Failed to copy RSI buffer. Error code: ", GetLastError()); return; } //--- Copy ATR buffer if(CopyBuffer(atrIndicatorHandle, 0, 0, 2, atrValues) <= 0) { Print("Error: Failed to copy ATR buffer. Error code: ", GetLastError()); return; } //--- Check array sizes if(ArraySize(ma20Values) < 2 || ArraySize(ma50Values) < 2 || ArraySize(rsiValues) < 2 || ArraySize(atrValues) < 2) { Print("Error: Insufficient data in indicator arrays"); return; } //--- Get current market prices double closePrice = iClose(_Symbol, PERIOD_CURRENT, 0); double openPrice = iOpen(_Symbol, PERIOD_CURRENT, 0); double highPrice = iHigh(_Symbol, PERIOD_CURRENT, 0); double lowPrice = iLow(_Symbol, PERIOD_CURRENT, 0); //--- Calculate input features inputs[0] = (MathAbs(openPrice) > 0.000001) ? (closePrice - openPrice) / openPrice : 0; inputs[1] = (MathAbs(lowPrice) > 0.000001) ? (highPrice - lowPrice) / lowPrice : 0; inputs[2] = (MathAbs(ma20Values[0]) > 0.000001) ? (closePrice - ma20Values[0]) / ma20Values[0] : 0; inputs[3] = (MathAbs(ma50Values[0]) > 0.000001) ? (ma20Values[0] - ma50Values[0]) / ma50Values[0] : 0; inputs[4] = rsiValues[0] / 100.0; double highLowRange = highPrice - lowPrice; if(MathAbs(highLowRange) > 0.000001) { inputs[5] = (closePrice - lowPrice) / highLowRange; inputs[7] = MathAbs(closePrice - openPrice) / highLowRange; inputs[8] = (highPrice - closePrice) / highLowRange; inputs[9] = (closePrice - lowPrice) / highLowRange; } else { inputs[5] = 0; inputs[7] = 0; inputs[8] = 0; inputs[9] = 0; } inputs[6] = (MathAbs(closePrice) > 0.000001) ? atrValues[0] / closePrice : 0; //--- Log input preparation Print("Prepared inputs. Size: ", ArraySize(inputs)); } // Collect training data bool CollectTrainingData(TrainingData &data[], int barCount) { //--- Check output neuron count if(OUTPUT_NEURON_COUNT != 2) { Print("Error: OUTPUT_NEURON_COUNT must be 2 for binary classification."); return false; } //--- Resize data array ArrayResize(data, barCount); double ma20Values[], ma50Values[], rsiValues[], atrValues[]; //--- Set arrays as series ArraySetAsSeries(ma20Values, true); ArraySetAsSeries(ma50Values, true); ArraySetAsSeries(rsiValues, true); ArraySetAsSeries(atrValues, true); //--- Copy MA20 buffer if(CopyBuffer(ma20IndicatorHandle, 0, 0, barCount + 1, ma20Values) < barCount + 1) { Print("Error: Failed to copy MA20 buffer for training. Error code: ", GetLastError()); return false; } //--- Copy MA50 buffer if(CopyBuffer(ma50IndicatorHandle, 0, 0, barCount + 1, ma50Values) < barCount + 1) { Print("Error: Failed to copy MA50 buffer for training. Error code: ", GetLastError()); return false; } //--- Copy RSI buffer if(CopyBuffer(rsiIndicatorHandle, 0, 0, barCount + 1, rsiValues) < barCount + 1) { Print("Error: Failed to copy RSI buffer for training. Error code: ", GetLastError()); return false; } //--- Copy ATR buffer if(CopyBuffer(atrIndicatorHandle, 0, 0, barCount + 1, atrValues) < barCount + 1) { Print("Error: Failed to copy ATR buffer for training. Error code: ", GetLastError()); return false; } MqlRates priceData[]; //--- Set rates array as series ArraySetAsSeries(priceData, true); //--- Copy price data if(CopyRates(_Symbol, PERIOD_CURRENT, 0, barCount + 1, priceData) < barCount + 1) { Print("Error: Failed to copy rates for training. Error code: ", GetLastError()); return false; } //--- Process each bar for(int i = 0; i < barCount; i++) { //--- Resize input and target arrays ArrayResize(data[i].inputValues, INPUT_NEURON_COUNT); ArrayResize(data[i].targetValues, OUTPUT_NEURON_COUNT); //--- Get price data double closePrice = priceData[i].close; double openPrice = priceData[i].open; double highPrice = priceData[i].high; double lowPrice = priceData[i].low; double highLowRange = highPrice - lowPrice; //--- Calculate input features data[i].inputValues[0] = (MathAbs(openPrice) > 0.000001) ? (closePrice - openPrice) / openPrice : 0; data[i].inputValues[1] = (MathAbs(lowPrice) > 0.000001) ? (highPrice - lowPrice) / lowPrice : 0; data[i].inputValues[2] = (MathAbs(ma20Values[i]) > 0.000001) ? (closePrice - ma20Values[i]) / ma20Values[i] : 0; data[i].inputValues[3] = (MathAbs(ma50Values[i]) > 0.000001) ? (ma20Values[i] - ma50Values[i]) / ma50Values[i] : 0; data[i].inputValues[4] = rsiValues[i] / 100.0; if(MathAbs(highLowRange) > 0.000001) { data[i].inputValues[5] = (closePrice - lowPrice) / highLowRange; data[i].inputValues[7] = MathAbs(closePrice - openPrice) / highLowRange; data[i].inputValues[8] = (highPrice - closePrice) / highLowRange; data[i].inputValues[9] = (closePrice - lowPrice) / highLowRange; } data[i].inputValues[6] = (MathAbs(closePrice) > 0.000001) ? atrValues[i] / closePrice : 0; //--- Set target values based on price movement if(i < barCount - 1) { double futureClose = priceData[i + 1].close; double priceChange = futureClose - closePrice; if(priceChange > 0) { data[i].targetValues[0] = 1; data[i].targetValues[1] = 0; } else { data[i].targetValues[0] = 0; data[i].targetValues[1] = 1; } } else { data[i].targetValues[0] = 0; data[i].targetValues[1] = 0; } } //--- Return success return true; }
Hier implementieren wir die Datenvorbereitung, indem wir die Funktion „PrepareInputs“ erstellen, um Eingangsmerkmale für das neuronale Netz zu erzeugen. Wir verwenden die Funktion ArrayResize, um sicherzustellen, dass das Array „inputs“ mit „INPUT_NEURON_COUNT“ übereinstimmt, deklarieren dann die Arrays „ma20Values“, „ma50Values“, „rsiValues“ und „atrValues“ und setzen sie mit der Funktion ArraySetAsSeries als Zeitreihen. Wir verwenden die Funktion CopyBuffer, um zwei Balken von „ma20IndicatorHandle“, „ma50IndicatorHandle“, „rsiIndicatorHandle“ und „atrIndicatorHandle“ abzurufen, wobei wir Fehler mit der Funktion „Print“ protokollieren und bei Fehlern abbrechen.
Wir überprüfen die Array-Größen mit ArraySize, protokollieren Fehler mit „Print“, wenn sie nicht ausreichen, und verwenden iClose, „iOpen“, „iHigh“ und „iLow“, um aktuelle Preise in „closePrice“, „openPrice“, „highPrice“ und „lowPrice“ für _Symbol und PERIOD_CURRENT einzulesen. Wir berechnen Input-Merkmale für „inputs“, einschließlich normalisierter Preisdifferenzen, gleitender Durchschnittsabweichungen, RSI skaliert auf 0-1 und ATR relativ zu „closePrice“, behandeln Null-Divisionen mit MathAbs-Prüfungen und berechnen Range-basierte Merkmale für „highLowRange“. Wir protokollieren den Erfolg mit „Print“ und „ArraySize“.
Außerdem erstellen wir die Funktion „CollectTrainingData“, um Trainingsdaten im Array der Struktur „TrainingData“ für „barCount“-Balken vorzubereiten. Wir stellen sicher, dass „OUTPUT_NEURON_COUNT“ gleich 2 ist, verwenden „ArrayResize“, um die Größe von „data“ zu bestimmen, und verwenden „CopyBuffer“, um Daten von Indikator-Handles zu holen, und „CopyRates“ für Preisdaten in „priceData“, wobei Fehler mit „Print“ protokolliert werden, wenn sie fehlschlagen. Für jeden Balken verwenden wir „ArrayResize“, um „data[i].inputValues“ und „data[i].targetValues“ zu setzen, berechnen die Eingangsmerkmale ähnlich wie bei „PrepareInputs“ und setzen die Zielwerte in „data[i].targetValues“ auf der Grundlage der Preisbewegung in „priceData“, wobei bei Erfolg „true“ zurückgegeben wird. Anschließend müssen wir das Netz auf der Grundlage der empfangenen Daten trainieren.
// Train the neural network bool TrainNetwork() { //--- Log training start Print("Starting neural network training..."); TrainingData trainingData[]; //--- Collect training data if(!CollectTrainingData(trainingData, TrainingBarCount)) { Print("Failed to collect training data"); return false; } //--- Train network double accuracy = neuralNetwork.TrainOnHistoricalData(trainingData); //--- Log training completion Print("Training completed. Final accuracy: ", accuracy); //--- Return training success return (accuracy >= MinPredictionAccuracy); }
Wir erstellen die Funktion „TrainNetwork“ und verwenden die Funktion „Print“, um den Beginn des Trainings zu protokollieren. Anschließend deklarieren wir das Array „trainingData“ der Struktur „TrainingData“, um Eingabe- und Zielwerte zu speichern. Wir rufen die Funktion „CollectTrainingData“ auf, um „trainingData“ mit „TrainingBarCount“-Balken zu füllen, protokollieren einen Fehler mit „Print“ und geben „false“ zurück, wenn die Datensammlung fehlschlägt.
Wir verwenden die Funktion „TrainOnHistoricalData“ des „neuralNetwork“-Objekts, um das Netzwerk zu trainieren, speichern das Ergebnis in „accuracy“, protokollieren die Fertigstellung mit „Print“ einschließlich „accuracy“ und geben „true“ zurück, wenn „accuracy“ „MinPredictionAccuracy“ erfüllt oder übertrifft, um sicherzustellen, dass das Netzwerk für den Handel angemessen trainiert ist. Schließlich können wir eine Funktion zur Validierung der Handelssignale wie folgt erstellen.
// Validate Stop Loss and Take Profit levels bool CheckStopLossTakeprofit(ENUM_ORDER_TYPE orderType, double price, double stopLoss, double takeProfit) { //--- Get minimum stop level double stopLevel = SymbolInfoInteger(_Symbol, SYMBOL_TRADE_STOPS_LEVEL) * _Point; //--- Validate buy order if(orderType == ORDER_TYPE_BUY) { //--- Check stop loss distance if(MathAbs(price - stopLoss) < stopLevel) { Print("Buy Stop Loss too close. Minimum distance: ", stopLevel); return false; } //--- Check take profit distance if(MathAbs(takeProfit - price) < stopLevel) { Print("Buy Take Profit too close. Minimum distance: ", stopLevel); return false; } } //--- Validate sell order else if(orderType == ORDER_TYPE_SELL) { //--- Check stop loss distance if(MathAbs(stopLoss - price) < stopLevel) { Print("Sell Stop Loss too close. Minimum distance: ", stopLevel); return false; } //--- Check take profit distance if(MathAbs(price - takeProfit) < stopLevel) { Print("Sell Take Profit too close. Minimum distance: ", stopLevel); return false; } } //--- Return validation success return true; }
Hier erstellen wir lediglich eine boolesche Funktion zur Validierung der Handelspunkte, um potenzielle Fehler aufgrund von Broker-Einschränkungen zu vermeiden. Jetzt können wir das Programm mit der Ereignishandlung von OnInit initialisieren, indem wir die Indikatoren und Instanzen der neuronalen Klasse technisch initialisieren, um die schwere Arbeit wie unten beschrieben zu erledigen.
// Expert initialization function int OnInit() { //--- Initialize 20-period MA indicator ma20IndicatorHandle = iMA(_Symbol, PERIOD_CURRENT, 20, 0, MODE_SMA, PRICE_CLOSE); //--- Initialize 50-period MA indicator ma50IndicatorHandle = iMA(_Symbol, PERIOD_CURRENT, 50, 0, MODE_SMA, PRICE_CLOSE); //--- Initialize RSI indicator rsiIndicatorHandle = iRSI(_Symbol, PERIOD_CURRENT, 14, PRICE_CLOSE); //--- Initialize ATR indicator atrIndicatorHandle = iATR(_Symbol, PERIOD_CURRENT, 14); //--- Check MA20 handle if(ma20IndicatorHandle == INVALID_HANDLE) Print("Error: Failed to initialize MA20 handle. Error code: ", GetLastError()); //--- Check MA50 handle if(ma50IndicatorHandle == INVALID_HANDLE) Print("Error: Failed to initialize MA50 handle. Error code: ", GetLastError()); //--- Check RSI handle if(rsiIndicatorHandle == INVALID_HANDLE) Print("Error: Failed to initialize RSI handle. Error code: ", GetLastError()); //--- Check ATR handle if(atrIndicatorHandle == INVALID_HANDLE) Print("Error: Failed to initialize ATR handle. Error code: ", GetLastError()); //--- Check for any invalid handles if(ma20IndicatorHandle == INVALID_HANDLE || ma50IndicatorHandle == INVALID_HANDLE || rsiIndicatorHandle == INVALID_HANDLE || atrIndicatorHandle == INVALID_HANDLE) { Print("Error initializing indicators"); return INIT_FAILED; } //--- Create neural network instance neuralNetwork = new CNeuralNetwork(INPUT_NEURON_COUNT, MinHiddenNeurons, OUTPUT_NEURON_COUNT); //--- Check neural network creation if(neuralNetwork == NULL) { Print("Failed to create neural network"); return INIT_FAILED; } //--- Log initialization Print("Initializing neural network..."); //--- Return success return(INIT_SUCCEEDED); }
Wir implementieren die Initialisierungslogik in der Funktion OnInit. Wir verwenden die Funktion iMA zur Initialisierung von „ma20IndicatorHandle“ und „ma50IndicatorHandle“ für einfache gleitende Durchschnitte mit 20 und 50 Perioden auf „_Symbol“ und PERIOD_CURRENT mit „PRICE_CLOSE“, und die Funktionen „iRSI“ und iATR, um „rsiIndicatorHandle“ und „atrIndicatorHandle“ für die 14-Perioden-Indikatoren RSI und ATR zu setzen. Wir prüfen jedes Handle auf „INVALID_HANDLE“, protokollieren Fehler mit der Funktion „Print“ und „GetLastError“, wenn einer davon fehlschlägt, und geben INIT_FAILED zurück, wenn die Initialisierung eines Indikators fehlschlägt.
Wir erstellen eine neue Instanz der Klasse „CNeuralNetwork“ für „neuralNetwork“ und verwenden „INPUT_NEURON_COUNT“, „MinHiddenNeurons“ und „OUTPUT_NEURON_COUNT“, um die Netzstruktur einzurichten. Wenn „neuralNetwork“ „NULL“ ist, verwenden wir die Funktion „Print“, um den Fehler zu protokollieren und geben „INIT_FAILED“ zurück. Schließlich protokollieren wir die erfolgreiche Initialisierung mit „Print“ und geben INIT_SUCCEEDED zurück, um sicherzustellen, dass der Expert Advisor ordnungsgemäß für den Handel eingerichtet ist. Nach der Ausführung des Programms erhalten wir die folgende Ausgabe.
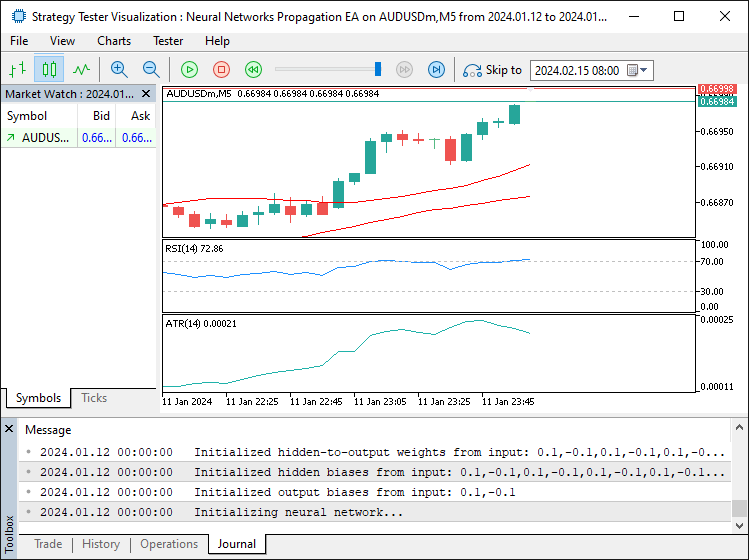
Aus dem Bild geht hervor, dass wir das Programm erfolgreich initialisiert haben. Da wir nun eine Instanz des neuronalen Netzes erstellt haben, müssen wir sie löschen, sobald wir das Programm entfernen. Hier ist die Logik, mit der wir das erreichen.
// Expert deinitialization function void OnDeinit(const int reason) { //--- Release MA20 indicator handle if(ma20IndicatorHandle != INVALID_HANDLE) IndicatorRelease(ma20IndicatorHandle); //--- Release MA50 indicator handle if(ma50IndicatorHandle != INVALID_HANDLE) IndicatorRelease(ma50IndicatorHandle); //--- Release RSI indicator handle if(rsiIndicatorHandle != INVALID_HANDLE) IndicatorRelease(rsiIndicatorHandle); //--- Release ATR indicator handle if(atrIndicatorHandle != INVALID_HANDLE) IndicatorRelease(atrIndicatorHandle); //--- Delete neural network instance if(neuralNetwork != NULL) delete neuralNetwork; //--- Log deinitialization Print("Expert Advisor deinitialized - ", EnumToString((ENUM_INIT_RETCODE)reason)); }
Wir implementieren den Bereinigungsprozess innerhalb der Funktion OnDeinit, wo wir die Funktion IndicatorRelease verwenden, um die Ressourcen für „ma20IndicatorHandle“, „ma50IndicatorHandle“, „rsiIndicatorHandle“ und „atrIndicatorHandle“ freizugeben, wenn diese nicht „INVALID_HANDLE“ sind, um die ordnungsgemäße Freigabe der gleitenden Durchschnitts-, RSI- und ATR-Indikator-Handles sicherzustellen. Wir prüfen, ob „neuralNetwork“ nicht „NULL“ ist, und verwenden den Operator „delete“, um die Instanz der Klasse „CNeuralNetwork“ freizugeben und das neuronale Netz zu bereinigen. Schließlich verwenden wir die Funktion „Print“ mit EnumToString, um den Deinitialisierungsgrund zu protokollieren und zu bestätigen, dass die Ressourcen des Expert Advisors ordnungsgemäß freigegeben wurden. Wird die Klasseninstanz nicht gelöscht, kommt es zu Speicherlecks, wie unten dargestellt.
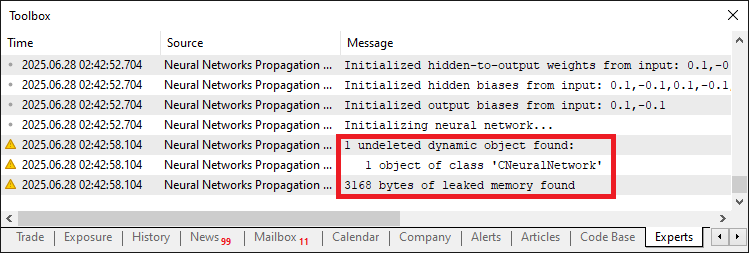
Sobald das Problem des Speicherlecks behoben ist, können wir die Hauptdatenerfassung, das Training und die Verwendung innerhalb des OnTick-Ereignishandlers implementieren.
// Expert tick function void OnTick() { static datetime lastBarTime = 0; //--- Track last processed bar time //--- Get current bar time datetime currentBarTime = iTime(_Symbol, PERIOD_CURRENT, 0); //--- Skip if same bar if(lastBarTime == currentBarTime) return; //--- Update last bar time lastBarTime = currentBarTime; //--- Calculate dynamic neuron count int newNeuronCount = (int)neuralNetwork.CalculateDynamicNeurons(); //--- Resize network if necessary if(newNeuronCount != neuralNetwork.GetHiddenNeurons()) neuralNetwork.ResizeNetwork(newNeuronCount); //--- Check if retraining is needed if(TimeCurrent() - iTime(_Symbol, PERIOD_CURRENT, TrainingBarCount) >= 12 * 3600 || neuralNetwork.ShouldRetrain()) { //--- Log training start Print("Starting network training..."); //--- Train network if(!TrainNetwork()) { Print("Training failed or insufficient accuracy"); return; } } //--- Update network with recent data neuralNetwork.UpdateNetworkWithRecentData(); //--- Check for open positions if(PositionsTotal() > 0) { //--- Iterate through positions for(int i = PositionsTotal() - 1; i >= 0; i--) { //--- Skip if position is for current symbol if(PositionGetSymbol(i) == _Symbol) return; } } //--- Prepare input data double currentInputs[]; ArrayResize(currentInputs, INPUT_NEURON_COUNT); PrepareInputs(currentInputs); //--- Verify input array size if(ArraySize(currentInputs) != INPUT_NEURON_COUNT) { Print("Error: Inputs array not properly initialized. Size: ", ArraySize(currentInputs)); return; } //--- Set network inputs neuralNetwork.SetInput(currentInputs); //--- Perform forward propagation neuralNetwork.ForwardPropagate(); double outputValues[]; //--- Resize output array ArrayResize(outputValues, OUTPUT_NEURON_COUNT); //--- Get network outputs neuralNetwork.GetOutput(outputValues); //--- Verify output array size if(ArraySize(outputValues) != OUTPUT_NEURON_COUNT) { Print("Error: Outputs array not properly initialized. Size: ", ArraySize(outputValues)); return; } //--- Get market prices double askPrice = SymbolInfoDouble(_Symbol, SYMBOL_ASK); double bidPrice = SymbolInfoDouble(_Symbol, SYMBOL_BID); //--- Calculate stop loss and take profit levels double buyStopLoss = NormalizeDouble(askPrice - StopLossPoints * _Point, _Digits); double buyTakeProfit = NormalizeDouble(askPrice + TakeProfitPoints * _Point, _Digits); double sellStopLoss = NormalizeDouble(bidPrice + StopLossPoints * _Point, _Digits); double sellTakeProfit = NormalizeDouble(bidPrice - TakeProfitPoints * _Point, _Digits); //--- Validate stop loss and take profit if(!CheckStopLossTakeprofit(ORDER_TYPE_BUY, askPrice, buyStopLoss, buyTakeProfit) || !CheckStopLossTakeprofit(ORDER_TYPE_SELL, bidPrice, sellStopLoss, sellTakeProfit)) { return; } // Trading logic const double CONFIDENCE_THRESHOLD = 0.8; //--- Confidence threshold for trading //--- Check for buy signal if(outputValues[0] > CONFIDENCE_THRESHOLD && outputValues[1] < (1 - CONFIDENCE_THRESHOLD)) { //--- Set trade magic number tradeObject.SetExpertMagicNumber(123456); //--- Place buy order if(tradeObject.Buy(LotSize, _Symbol, askPrice, buyStopLoss, buyTakeProfit, "Neural Buy")) { //--- Log successful buy order Print("Buy order placed - Signal Strength: ", outputValues[0]); } else { //--- Log buy order failure Print("Buy order failed. Error: ", GetLastError()); } } //--- Check for sell signal else if(outputValues[0] < (1 - CONFIDENCE_THRESHOLD) && outputValues[1] > CONFIDENCE_THRESHOLD) { //--- Set trade magic number tradeObject.SetExpertMagicNumber(123456); //--- Place sell order if(tradeObject.Sell(LotSize, _Symbol, bidPrice, sellStopLoss, sellTakeProfit, "Neural Sell")) { //--- Log successful sell order Print("Sell order placed - Signal Strength: ", outputValues[1]); } else { //--- Log sell order failure Print("Sell order failed. Error: ", GetLastError()); } } } //+------------------------------------------------------------------+
Hier implementieren wir die zentrale Handelslogik für die neuronale Netzwerkstrategie innerhalb der Funktion OnTick. Wir deklarieren „lastBarTime“, um den letzten verarbeiteten Balken zu verfolgen, und verwenden die Funktion iTime, um „currentBarTime“ für „_Symbol“ und PERIOD_CURRENT zu erhalten, und verlassen den Vorgang, wenn er unverändert bleibt, um nur neue Balken zu verarbeiten. Wir aktualisieren „lastBarTime“ und verwenden die Funktion „CalculateDynamicNeurons“, um „newNeuronCount“ zu berechnen, und rufen die Funktion „ResizeNetwork“ auf, wenn sie vom Ergebnis der Funktion „GetHiddenNeurons“ abweicht, um das Netz anzupassen.
Wir prüfen, ob ein erneutes Training erforderlich ist, indem wir TimeCurrent minus „iTime“ für „TrainingBarCount“ mit 12 Stunden oder mit der Funktion „ShouldRetrain“ vergleichen und dann die Funktion „TrainNetwork“ verwenden, um das erneute Training durchzuführen. Wir rufen die Funktion „UpdateNetworkWithRecentData“ auf, um das Netz zu verfeinern. Wenn PositionsTotal offene Positionen anzeigt, verwenden wir die Funktion „PositionGetSymbol“, um den Handel zu überspringen, wenn es welche für _Symbol gibt. Wir deklarieren „currentInputs“, ändern seine Größe mit „ArrayResize“ auf „INPUT_NEURON_COUNT“ und verwenden die Funktion „PrepareInputs“, um es zu füllen, wobei wir die Größe mit ArraySize überprüfen und Fehler mit „Print“ protokollieren.
Wir verwenden die Funktion „SetInput“, um „currentInputs“ zu laden, rufen die Funktion „ForwardPropagate“ auf, um Vorhersagen zu erstellen, und verwenden die Funktion „GetOutput“ Funktion, um „outputValues“ abzurufen, nachdem die Größe mit „ArrayResize“ auf „OUTPUT_NEURON_COUNT“ geändert wurde, und protokollieren Fehler mit „Print“, wenn sie ungültig sind. Wir holen „askPrice“ und „bidPrice“ mit SymbolInfoDouble, berechnen „buyStopLoss“, „buyTakeProfit“, „sellStopLoss“, und „sellTakeProfit“ unter Verwendung von NormalizeDouble mit „StopLossPoints“, „TakeProfitPoints“, „_Point“ und „_Digits“, und validieren Sie sie mit der Funktion „CheckStopLossTakeprofit“.
Für den Handel setzen wir „CONFIDENCE_THRESHOLD“ auf 0,8; wenn „outputValues[0]“ diesen Wert überschreitet und „outputValues[1]“ unter seinem Komplement liegt, verwenden wir die Funktion „tradeObject.Buy“, nachdem wir die magische Zahl mit „SetExpertMagicNumber“ gesetzt haben, und protokollieren Erfolg oder Misserfolg mit „Print“ und „GetLastError“. In ähnlicher Weise verwenden wir die Funktion „tradeObject.Sell“ für Verkaufssignale, um eine robuste Handelsausführung zu gewährleisten. Nach dem Kompilieren erhalten wir die folgende Ausgabe.
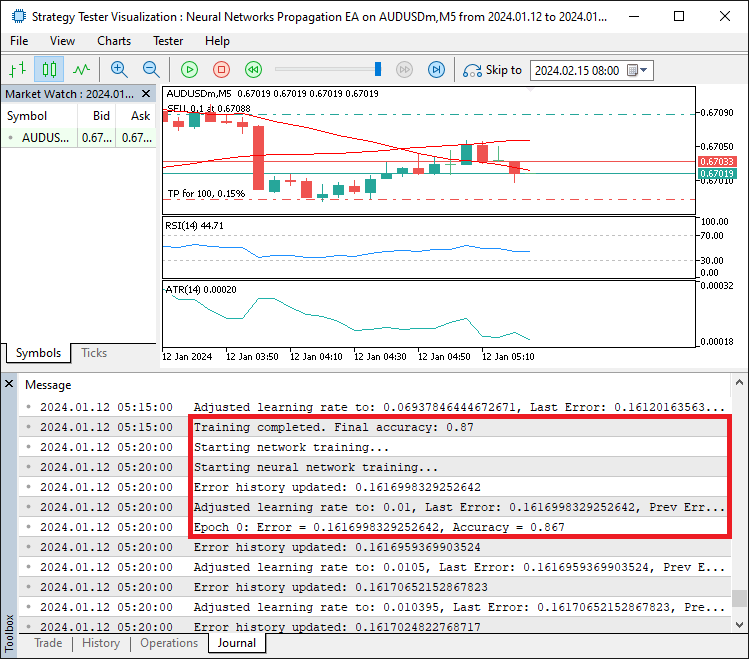
Aus dem Bild ist ersichtlich, dass wir das neuronale Netz trainieren, um Fehler zu erhalten, sie innerhalb der Epochen weiterzugeben und dann die Lernrate auf der Grundlage der Genauigkeit der Fehler anzupassen. Bleiben nur noch die Backtests des Programms, und das wird im nächsten Abschnitt behandelt.
Testen und Optimieren der Adaption der Lernraten
Nach einem gründlichen Backtest erhalten wir folgende Ergebnisse.
Backtest-Grafik:
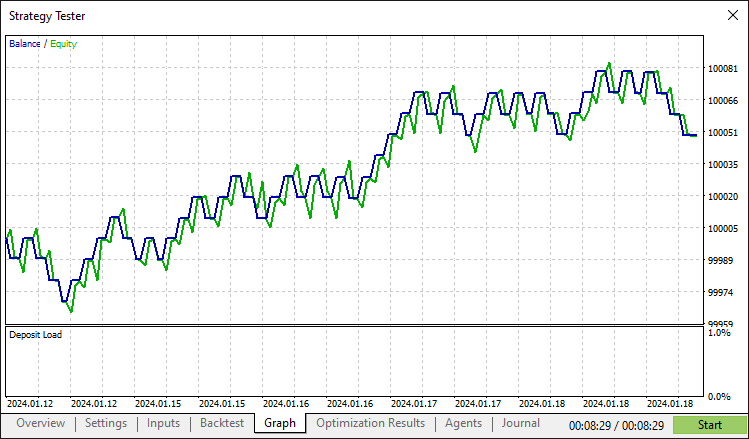
Bericht des Backtest:
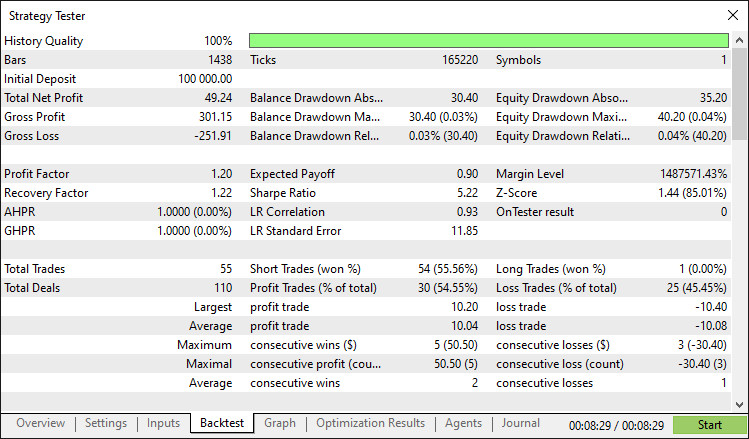
Schlussfolgerung
Zusammenfassend haben wir ein MQL5-Programm entwickelt, das eine Handelsstrategie mit einem neuronalen Netzwerk mit adaptive Lernraten implementiert und die Klasse „CNeuralNetwork“ zur Verarbeitung von Marktindikatoren und zur Ausführung von Trades mit dynamischen Anpassungen der Lerngeschwindigkeit und der Netzwerkgröße für eine optimale Leistung nutzt. Durch modulare Komponenten wie die Struktur „TrainingData“ und Funktionen wie „AdjustLearningRate“ und „TrainNetwork“ bietet dieses System ein flexibles Gerüst, das Sie durch die Feinabstimmung von Parametern oder die Integration zusätzlicher Marktindikatoren entsprechend Ihren Handelspräferenzen erweitern können.
Haftungsausschluss: Dieser Artikel ist nur für Bildungszwecke gedacht. Der Handel ist mit erheblichen finanziellen Risiken verbunden, und die Volatilität der Märkte kann zu Verlusten führen. Gründliche Backtests und sorgfältiges Risikomanagement sind entscheidend, bevor Sie dieses Programm auf den Live-Märkten einsetzen.
Mit Hilfe der vorgestellten Konzepte und Implementierungen können Sie dieses Handelssystem mit neuronalen Netzen verbessern oder seine Architektur anpassen, um neue Strategien zu entwickeln, die Ihnen den Weg zum algorithmischen Handel ebnen. Viel Spaß beim Handeln!
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/18660
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Entwicklung des Price Action Analysis Toolkit (Teil 31): Python-Engine für Kerzenmuster (I) - Manuelles Erkennen
Entwicklung des Price Action Analysis Toolkit (Teil 31): Python-Engine für Kerzenmuster (I) - Manuelles Erkennen
 MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 72): Verwendung der Muster von MACD und OBV mit überwachtem Lernen
MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 72): Verwendung der Muster von MACD und OBV mit überwachtem Lernen
 Formulierung eines dynamischen Multi-Pair EA (Teil 3): Mean-Reversion- und Momentum-Strategien
Formulierung eines dynamischen Multi-Pair EA (Teil 3): Mean-Reversion- und Momentum-Strategien
 Implementierung von praktischen Modulen aus anderen Sprachen in MQL5 (Teil 01): Aufbau der SQLite3-Bibliothek, inspiriert von Python
Implementierung von praktischen Modulen aus anderen Sprachen in MQL5 (Teil 01): Aufbau der SQLite3-Bibliothek, inspiriert von Python
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.