MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 72): Verwendung der Muster von MACD und OBV mit überwachtem Lernen

Einführung

In unserem letzten Artikel, in dem wir das Indikatorenpaar MACD und On-Balance-Volume-Oszillator (OBV) vorgestellt haben, haben wir 10 mögliche Signale untersucht, die aus der komplementären Paarung dieser Indikatoren generiert werden können. Wir testen immer 10 Signalmuster, die aus einem 2-Indikator-Paar abgeleitet sind, indem wir einen Vorwärtslauftest für ein Jahr durchführen, nachdem wir im Vorjahr ein Training oder eine Optimierung durchgeführt haben. Beim letzten Artikel konnte nur ein Signalmuster, Pattern-7, einen Vorwärtstest mit Gewinn beenden. Wir sind auf einige der Gründe eingegangen, warum diese Indikatorenkombination im Vergleich zu anderen von uns behandelten Indikatoren so schlecht abschneidet, was uns jedoch auch die Möglichkeit bietet, maschinelles Lernen zur Verbesserung einiger dieser Signalmuster zu nutzen.

Wir knüpfen daher an diesen Artikel an, indem wir untersuchen, ob und wie ein CNN-Netzwerk, das den rationalen quadratischen Kernel verwendet, die Interpretation und Anwendung von Indikatorsignalen unterstützen und vielleicht verbessern könnte. Der Rational-Quadratische (RQ) Kernel ist durch die folgende Formel definiert:

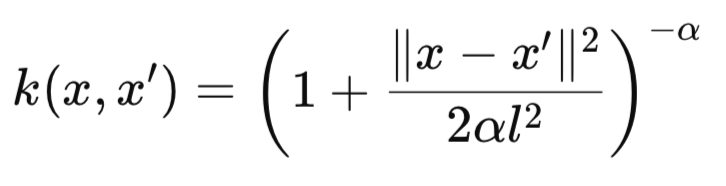
wobei:

• k(x,x′) ist der Kernelähnlichkeitswert zwischen zwei Eingaben x und x′. Er liegt zwischen 0 und 1, wobei Werte näher an 1 eine höhere Ähnlichkeit anzeigen.
  
  
• x und x′ sind zwei Eingangsvektoren (z. B. Scheiben eines 1D-Signals, Merkmalsvektoren oder Positionen in der Zeit). Sie können Einzelwerte (mit dim=1) oder Vektoren mit mehreren Dimensionen sein.
  
  
• ∥x-x′∥2 ist der quadrierte euklidische Abstand zwischen den beiden Eingangsvektoren. Sie misst, wie weit x und x′ in einem Merkmalsraum voneinander entfernt sind. Dieser Abstand kann mit dieser Formel berechnet werden:
• 
  

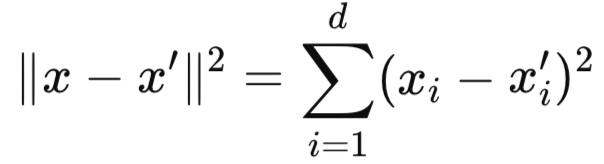
• l ist die Längenskala (oder charakteristische Skala) des Kernels. Sie bestimmt, wie schnell die Ähnlichkeit mit der Entfernung abnimmt:
• Kleines l: starker Abfall (lokale Empfindlichkeit).
• Großes l: langsamer Zerfall (große Ähnlichkeit).
  
  
• α oder Alpha ist der Skalenmischungsparameter (manchmal auch Formparameter genannt). Sie steuert die Gewichtung zwischen großen und kleinen Schwankungsbreiten:
  
  
• Wenn α → unendlich ist, wird der Kernel äquivalent zum quadratischen Exponentialkern (RBF-Kernel).
• Ein kleines α bedeutet, dass der Kernel schwerere Ausläufer hat, was Wechselwirkungen mit größerer Reichweite ermöglicht.

In unserer Implementierung des Rational Quadratic Kernel (RQK) in einem CNN verwenden wir ihn, um die Größe der Kernel und Kanäle des CNN festzulegen. Es gibt jedoch alternative Verwendungen und Anwendungen dieses Kerns innerhalb eines CNN, die vom Leser in Betracht gezogen werden können.

Alternative RQ-Kernel Anwendungen und Vorteile

An erster Stelle steht dabei die adaptive Aufmerksamkeitsmaskierung. In diesem Anwendungsfall baut der RQ-Kernel räumliche oder zeitliche Aufmerksamkeitsmasken innerhalb des CNN auf. Dies hilft bei der Segmentierung oder Zeitreihenprognose. Dabei werden Regionen mit hoher Ähnlichkeit zu einer Referenz, z. B. einem Schwerpunktfenster, hervorgehoben. Ein weiterer möglicher Verwendungszweck des RQ-Kerns könnte das entfernungsbewusste Pooling sein. In diesem Szenario werden nur Netzwerkaktivierungen innerhalb eines festgelegten Ähnlichkeitsschwellenwerts unter dem RQ-Kernel gepoolt, anstatt alles zu mitteln. Dies ermöglicht ein abstandsorientiertes, adaptives Pooling, das die Nähe der Merkmale berücksichtigt.

Eine weitere Anwendung kann die Skalierung der Bedeutung von Merkmalen sein. Hier würden die CNN-Kanäle auf eine gelernte, sanfte Art und Weise gewichtet werden. Schließlich könnte der RQ-Kernel verwendet werden, um Gewichte des CNN zu reduzieren oder zu „beschneiden“, deren Effekt, gemessen durch den Kernel, innerhalb des Eingaberaums des Netzes minimal ist. Die Gründe, warum dieser Kernel in CNNs eingesetzt werden kann und sollte, sind ebenfalls vielschichtig. Im Folgenden finden Sie eine Tabelle, die versucht, dies zusammenzufassen.

Robust gegenüber Ausreißern	Die langen Ausläufern der RQ-Kerne machen die Architektur weniger anfällig für räumliche oder zeitliche Anomalien.
Reibungslose Übergänge	Ein sanftes Abklingen des Kerns sorgt für weniger abrupte Darstellungsverschiebungen zwischen den Schichten. Dies ist gut für den Gradientenfluss.
Dynamische Architektur	Der Kernel verwendet eine datengesteuerte Auswahl der CNN-Kernelgröße oder Kanalerweiterung unter Verwendung von Ähnlichkeitsmaßen.

Dieses CNN-Design (conv-1d), das das RQ-Kernel verwendet, ist ideal für Eingaben mit 1-Dim-Größe, bei denen lokale Ähnlichkeit wichtig ist, wie z. B. bei den Finanzzeitreihen, die wir in diesem Artikel untersuchen. Andere mögliche geeignete Datentypen sind Audiosignale und die Erkennung binärer Muster. Bei der Verwendung dieses CNN ist es wichtig, die Eingangsvektoren auf den Bereich 0-1 zu normalisieren oder zu standardisieren, wie wir es in früheren Artikeln mit unseren Netzen getan haben. Die Form der Eingabe ist typischerweise (batch_size, input_length), wobei die Eingabevektoren mit 0en oder 1en gefüllt sind. 

Der RQ-Kernel hat eine Reihe wichtiger Hyperparameter, wie in seiner Formel oben erwähnt. An erster Stelle steht Alpha, das, wie in den Formelnotizen erwähnt, den Abfall der Ausläufer reguliert. Bei höheren Werten verhält sich der Kernel eher wie ein monolithischer Radialbasisfunktions-Kernel. Wenn dieser Wert jedoch verringert wird, wirkt das RQ-Kernel wie eine Kombination aus mehreren RBFs auf verschiedenen Skalen, die durch alpha gesteuert werden. Ein weiterer Hyperparameter ist die Längenskala, die die Empfindlichkeit der Ähnlichkeit gegenüber der Entfernung bestimmt.

Wenn unser Netz ein Klassifikator mit einer Wahrscheinlichkeitsverteilung ist, kann die BCE-Verlustfunktion beim Training verwendet werden. Angesichts unserer unkonventionellen Architektur können auch die richtige Initialisierung und die Planung der Lernrate von Bedeutung sein. Weitere Erweiterungen können auch durch das Hinzufügen von Restverbindungen zwischen den Schichten für eine bessere Gradientenausbreitung vorgenommen werden. Darüber hinaus kann die Integration des RQ-Kerns als Gating-Mechanismus erfolgen. Zwischen den Schichtenstapeln können auch auf Ähnlichkeit basierende Drop-outs verwendet werden.

Die Forschung weist darauf hin, dass RQ-Kerne Conv1D-Gewichte definieren und somit bestimmte Datenmuster erfassen. Diese Anwendung des Kernels reduziert den Gesamtparameterbedarf deutlich und verbessert auch die Interpretierbarkeit, könnte aber die Anpassungsfähigkeit im Vergleich zu gelernten Kerneln einschränken. Die Beweise für bessere Ergebnisse deuten auch auf die Verwendung dieses Kerns in Gaußschen Prozessschichten und die Optimierung von Hyperparametern bei der Entwicklung von CNNs im weiteren Sinne hin, wie in diesem Text über tiefe Gaußsche Prozesse mit Faltungskernen beschrieben. 

Die Verwendung von Kerneln definitiver Größe reduziert die erlernbaren Parameter und mildert die Überanpassung, insbesondere in Fällen, in denen die Daten begrenzt sind. Dies wurde in einer Klassifizierung von Maniok-Krankheiten veranschaulicht, die hierzu finden ist. Auch wenn die Interpretierbarkeit durch die Verwendung vorgegebener Kernel dazu beiträgt, einen Einblick in die Extraktion von Merkmalen zu erhalten – ein deutlicher Unterschied zu Black-Box-Kerneln – gibt es doch einige Bedenken hinsichtlich der Anpassungsfähigkeit. Fixierte Kerne passen sich in der Regel nicht so gut an Daten an wie lernende Kerne, was bei komplexen Aufgaben zu Leistungseinbußen führen kann. Dies geht aus der oben verlinkten Maniokstudie hervor, in der Hybridkerne besser abschnitten als einzelne RQ-Kerne. Ein Teil der Studienergebnisse wird im Folgenden vorgestellt:

Kernel-Typ	Genauigkeit
RQ-Kernel	88.5%
Quadratischer Exponential-Kernel	88.0%
Hybrider Kernel	90.1%

Unsere obige Tabelle aus der Maniok-Krankheitsstudie zeigt die leichten Leistungsunterschiede zwischen gelernten und festen Kernen. Es wird ein hybrider Ansatz empfohlen. In früheren Zeiten hatte der RQ-Kernel eine zweideutige Rolle. Wie in den obigen Links beschrieben, haben diese, diese und diese Studie dazu beigetragen, die Anwendung im Deep-Gaussian-Process insbesondere für Bilddaten und die Anpassung an Conv1D zu offenbaren. Die Studie über die Maniokkrankheit war ausschlaggebend für die Entscheidung, auf vordefinierte Gewichte zurückzugreifen, um ein Gleichgewicht zwischen festen und erlernten Ansätzen zu schaffen.

Beim Entwurf der verwendeten Netze wurde die Kernelgröße in Relation zu den Hyperparametern der Längenskala l gesetzt. Da mehrere Kanäle verschiedene Skalen erfassen, was der CNN-Praxis unterschiedlicher rezeptiver Felder entspricht, wurde bei der endgültigen Implementierung ein globales Durchschnitts-Pooling verwendet, um Flexibilität zu gewährleisten. Dies gewährleistete die Unabhängigkeit der Ausgabe von jeder Sequenzlänge und eignete sich auch gut für die skalare, 0-1-bereichsgebundene Ausgabe.

Das Netzwerk

Unsere Netzwerkimplementierung ist in Python, weil, wie wir in früheren Artikeln argumentiert haben, die Codierung und das Training in Python effizienter ist als die Durchführung der gleichen Aufgaben in MQL5. Wir implementieren ein CNN in Python, das seine Kernel und Kanäle mit dem RQ-Kernel wie folgt skaliert:

import torch
import torch.nn as nn
import torch.nn.functional as F

import pandas as pd
import numpy as np

class RationalQuadraticConv1D(nn.Module):
    def __init__(self, alpha=1.0, length_scale=1.0, input_length=100):
        super(RationalQuadraticConv1D, self).__init__()
        self.alpha = alpha
        self.length_scale = length_scale
        self.input_length = input_length

        # Deeper and wider design
        self.kernel_sizes, self.channels = self._design_architecture()

        self.conv_layers = nn.ModuleList()
        in_channels = 1

        for i, (out_channels, kernel_size) in enumerate(zip(self.channels, self.kernel_sizes)):
            layer = nn.Sequential(
                nn.Conv1d(in_channels, out_channels, kernel_size=kernel_size, padding=kernel_size // 2),
                nn.BatchNorm1d(out_channels),
                nn.ReLU(),
                nn.Dropout(0.2)
            )
            self.conv_layers.append(layer)
            in_channels = out_channels

        # Fully connected head to increase parameter count
        self.head = nn.Sequential(
            nn.AdaptiveAvgPool1d(1),
            nn.Flatten(),
            nn.Linear(in_channels, 128),
            nn.ReLU(),
            nn.Dropout(0.2),
            nn.Linear(128, 64),
            nn.ReLU(),
            nn.Linear(64, 1),
            nn.Sigmoid()
        )

    def _rq_kernel(self, x, x_prime):
        dist_sq = (x - x_prime) ** 2
        return (1 + dist_sq / (2 * self.alpha * self.length_scale ** 2)) ** -self.alpha

    def _design_architecture(self):
        x = torch.linspace(0, 1, self.input_length)
        center = 0.5
        responses = self._rq_kernel(x, center)
        thresholded = responses[responses > 0.01]  # allow more spread

        num_layers = 10
        kernel_sizes = [3 + (i % 4) * 2 for i in range(num_layers)]  # cyclic 3, 5, 7, 9
        channels = [32 * (i + 1) for i in range(num_layers)]  # 32, 64, ..., 320

        return kernel_sizes, channels

    def forward(self, x):
        x = x.unsqueeze(1)  # (B, 1, L)
        for layer in self.conv_layers:
            x = layer(x)
        return self.head(x)

Wir beginnen mit der Definition eines nutzerdefinierten PyTorch-Moduls, das als Eingaben einige der Schlüsselparameter hat, die wir oben in der RQ-Kernel-Formel hervorgehoben haben. Unsere Klasse, die wir als „RationalQuadraticConv1D“ bezeichnen, erbt von der Klasse „nn.Module“, die, wie wir in unseren früheren Artikeln gesehen haben, die Basisklasse für alle PyTorch-Module für neuronale Netzwerke ist. Der Konstruktor initialisiert drei wichtige RQ-Kernel-Parameter: alpha, length-scale und input-length. Alpha steuert, wie oben erwähnt, die Form des Kernels, die Längenskala bestimmt den Abstand, über den der Kernel abklingt, und die Eingabelänge soll die erwartete Größe/Länge des Eingabevektors erfassen.

Diese ersten Schritte sind wichtig, da sie die Grundlage des Modells bilden und die Anpassung des Verhaltens des Kerns ermöglichen. Dadurch wird auch sichergestellt, dass die Architektur den Abmessungen des Eingangsvektors entspricht. Die Einstellung von Alpha und der Längenskala sollte vorgenommen werden, um die Empfindlichkeit des Kernels gegenüber Unterschieden in den Eingaben anzupassen. Eine kleinere Längenskala würde sich beispielsweise auf lokale Muster konzentrieren, während ein größerer Wert breitere Ähnlichkeiten erfassen würde. Wie immer sollte die Eingabelänge überprüft werden, damit sie mit der Größe der Eingabedaten übereinstimmt. 

Nach der Initialisierung weisen wir die Kernelgrößen und die Anzahl der Kanäle für die Faltungsschichten dynamisch zu. Diese Codezeile ruft die Methode „_design_architecture“ auf (die später behandelt wird), um die Kernelgrößen und -kanäle auf der Grundlage des Ähnlichkeitsprofils des RQ-Kerns im Eingaberaum zu berechnen. Dies ist unser Ansatz für das Netzwerk, denn im Gegensatz zu traditionellen CNNs mit festen Architekturen passt dieser Ansatz die Modellstruktur an die Eigenschaften der Daten an. Dies kann die Effizienz und Effektivität der Merkmalsextraktion verbessern. Unser Ansatz der Anpassungsfähigkeit macht dieses Modell geeignet für Datensätze mit unterschiedlichen Ähnlichkeitsstrukturen. Die Überwachung der Ausgabe der Methode „_design_architecture“ ist wichtig, um sicherzustellen, dass die Architektur mit der Komplexität der Aufgabe übereinstimmt.

Danach bauen wir in den folgenden Codezeilen einen flexiblen Stapel von Faltungsschichten mit dynamischen Eigenschaften auf. Die Funktion „nn.ModuleList()“ erstellt einen Container für eine variable Anzahl von Faltungsschichten. Die Schleife iteriert über Paare von „out-channels“, d.h. die Anzahl der Ausgangskanäle, mit der „kernel-size“, die sich in diesem Fall auf die Größe des Faltungs-Kerns bezieht, wie sie aus „self.channels“ bzw. „self.kernel-size“ abgelesen werden. Jede Schicht „nn.Conv1D“ nimmt „in-channels“, beginnend bei 1 für die erste Schicht. Es gibt die Daten an „out-channels“ aus und verwendet „kernel-size“ mit padding, um die nächste Kernelgröße zu bestimmen, damit die Eingabelänge erhalten bleiben. Die „in-channels“ werden dann zu „out-channels“ für die nächste Schicht aktualisiert, wodurch eine Kette entsteht.

Dies ist wichtig, da die dynamische Konstruktion dem Modell eine maßgeschneiderte Anzahl von Schichten und Parametern ermöglicht. Gleichzeitig wird durch das Auffüllen sichergestellt, dass die Ausgabelänge mit der Eingabelänge übereinstimmt, was beim Umgang mit sequentiellen Daten von entscheidender Bedeutung ist. Größere Werte für die „Kernel-Größe“ erfassen tendenziell breitere Muster der Eingabedaten, während eine höhere Anzahl von „Out-Channels“ die Vielfalt der aus den Daten erfassten Merkmale erhöht. Wenn die Erhaltung der vollen Länge nicht wichtig ist, kann das Padding angepasst werden, z. B. auf 0 beim Downsampling.

Anschließend definieren wir das „endgültige“ Netz, das die Faltungsausgaben zu einem einzigen wahrscheinlichkeitsähnlichen Wert verarbeitet. Sie definiert eine Abfolge von Operationen, die „nn.AdaptiveAvgPool1D“, „nn.Flatten“, „nn.Linear“ und „nn.Sigmoid“ umfassen. Diese sind verantwortlich für: die Reduzierung der räumlichen Dimension auf 1 durch Mittelwertbildung über die Sequenz; die Umwandlung des Tensors in einen 1D-Vektor; die Zuordnung der abgeflachten Merkmale zu einem einzigen Ausgang; und die Ausgabe eines Wertes zwischen 0 und 1, der für die binäre Klassifizierung bzw. Regression geeignet ist. 

In diesem letzten Schritt werden die Merkmale zusammengeführt und eine aufgabenspezifische Ausgabe erstellt. Dies macht das Modell für Zwecke wie die binäre Klassifizierung oder die Wahrscheinlichkeitsschätzung verwendbar. Bei Mehrklassenaufgaben können die linearen und die Sigmoid-Schichten mit „nn.Linear(in_channels, num_classes)“ bzw. „nn.Softmax()“ ersetzt werden. Bei einer Regression müsste das Sigmoid gestrichen werden, da es sich besser für die Klassifizierung eignet.

In unserer Klasse haben wir eine Funktion, die die Ähnlichkeit zwischen Datenpunkten oder Vektoren berechnet. Dies ist die Funktion „_rq_kernel“. Diese Ähnlichkeit wird, wie zu erwarten, mit dem RQ-Kernel berechnet. Die Berechnungen erfassen den euklidischen Abstand zwischen x und x-prime. Es wird die oben beschriebene RQ-Kernel-Formel verwendet, die mit zunehmender Entfernung unter der Moderation von Alpha- und Längenskalen-Hyperparametern abnimmt. Der RQ-Kernel quantifiziert die Ähnlichkeit der Eingabedaten, was als Grundlage für die Gestaltung der CNN-Architektur dient.

Es ist flexibel, da es sowohl lokale als auch globale Muster erfassen kann. Ein größeres Alpha nähert sich einem Gaußschen Kernel an, während ein kleineres Alpha mehr Flexibilität bietet. Die Anpassung der Längenskala zur Kontrolle des Verfalls ist ebenfalls wichtig, wobei kleinere Werte die lokalen Ähnlichkeiten betonen.

Dies führt uns zu der Funktion „_design_architecture“, die wir in den obigen Anmerkungen vorgestellt haben. Die CNN-Architektur wird unter Verwendung des Abklingprofils des RQ-Kernels dynamisch entworfen bzw. aufgebaut. Der erste Schritt in dieser Funktion ist die Erstellung eines normalisierten Bereichs von Eingabepositionen. Dies ist das „x“. Dann legen wir den Referenzpunkt für die Ähnlichkeitsberechnungen fest, den wir als „Zentrum“ definieren. Anschließend wird die RQ-Kernel-Antwort für jede Position in Bezug auf das Zentrum berechnet (Antworten). Als Nächstes filtern wir Positionen für Kernel-Reaktionen, die 0,2 überschreiten, und konzentrieren uns gleichzeitig auf signifikante Regionen.

Anschließend skalieren wir die Kernelgrößen auf der Grundlage der Position und beginnen bei 3. Wir erhöhen dies mit der Entfernung vom „Zentrum“. Wir weisen den Regionen mit geringerer Ähnlichkeit vorläufig mehr Kanäle zu, beginnend bei 4. Schließlich geben wir Architektureinstellungen zurück, die den Entwurf auf drei Ebenen beschränken.

Diese Funktion passt das CNN an die Ähnlichkeitsstruktur der Daten an. Die Verwendung größerer Kernel ist gut für breitere Muster, und mehr Kanäle ermöglichen eine komplexere Merkmalsextraktion. Der Schwellenwert von 0,2 und die Skalierungsfaktoren von 4 für Kerne und 60 für Kanäle sind einstellbar. Die Anzahl der Schichten kann für Aufgaben, die eine tiefere Merkmalsextraktion erfordern, erhöht werden, doch sollte dies mit den Rechenkosten abgewogen werden.

Schließlich schließt die Vorwärtspass-Methode unsere Klasse „RationalQuadraticConv1D“ ab. Sie führt die Berechnungen des Modells von der Eingabe bis zur Ausgabe aus. Zunächst wird der Eingabe eine Kanaldimension hinzugefügt, um sie mit „nn.Conv1D“ kompatibel zu machen. Wir wenden dann jede Faltungsschicht an, gefolgt von einer ReLU-Aktivierung, um Nichtlinearität einzuführen. Anschließend wird das Ergebnis durch die letzten Schichten geleitet, um die endgültige Ausgabe zu erhalten. Unsere Funktion für den Vorwärtsdurchlauf definiert den Datenfluss des Modells, indem sie die dynamisch entwickelte Architektur nutzt, um die für die Prognosen verwendeten Merkmale zu erhalten.

Es muss sichergestellt werden, dass die Eingabeform dem Format (batch_size, input_length) entspricht und dass der verwendete Aktivierungstyp für die jeweilige Aufgabe geeignet ist. Formabweichungen können bei diesem Netz häufig vorkommen. Deshalb ist es wichtig, die Form der Eingabedaten bei jedem Schritt auszudrucken. Wir können uns nun ansehen, wie wir die Netzwerkeingänge setzen, indem wir die Indikatorimplementierungen in Python für den MACD und das OBV betrachten.

Der MACD

Unsere Indikatoren sind von Grund auf in Python kodiert, auch wenn es Bibliotheken und Module gibt, die einige dieser Probleme lösen können. Dies dient der reibungsloseren/ weniger speicherintensiven Kompilierung und Ausführung. Der MACD berechnet die MACD-Linie, die Signallinie und das Histogramm, die alle dazu beitragen, den Kurs des Vermögenswertes zu analysieren. Wir implementieren es in Python wie folgt:

def MACD(df, fast_period: int = 12, slow_period: int = 26, signal_period: int = 9) -> pd.DataFrame:
    """
    Calculate Moving Average Convergence Divergence (MACD) and append it to the input DataFrame.

    The MACD line is the difference between a fast and slow EMA.
    The Signal line is an EMA of the MACD line.
    The Histogram is the difference between the MACD and Signal lines.
    
    Args:
        df (pd.DataFrame): DataFrame with a 'close' column.
        fast_period (int): Lookback period for the fast EMA. Default is 12.
        slow_period (int): Lookback period for the slow EMA. Default is 26.
        signal_period (int): Lookback period for the Signal line EMA. Default is 9.
        
    Returns:
        pd.DataFrame: Input DataFrame with new 'MACD', 'Signal_Line', and 'MACD_Histogram' columns.
    """
    # Input validation
    if 'close' not in df.columns:
        raise ValueError("DataFrame must contain a 'close' column")
    if not all(p > 0 for p in [fast_period, slow_period, signal_period]):
        raise ValueError("All period values must be positive integers")
    if fast_period >= slow_period:
        raise ValueError("fast_period must be less than slow_period")

    # Create a copy to avoid modifying the original DataFrame
    result_df = df.copy()
    
    # Calculate Fast and Slow Exponential Moving Averages (EMA)
    ema_fast = result_df['close'].ewm(span=fast_period, adjust=False).mean()
    ema_slow = result_df['close'].ewm(span=slow_period, adjust=False).mean()
    
    # Calculate MACD line
    result_df['MACD'] = ema_fast - ema_slow
    
    # Calculate Signal line (EMA of MACD)
    result_df['Signal_Line'] = result_df['MACD'].ewm(span=signal_period, adjust=False).mean()
    
    # Calculate MACD Histogram
    result_df['MACD_Histogram'] = result_df['MACD'] - result_df['Signal_Line']
    
    return result_df

Das Format unserer Funktion entspricht dem bisher verwendeten Format eines Pandas-Datenrahmens mit einer Spalte für den Schlusskurs und den folgenden drei optionalen Integer-Parametern: die standardmäßig zugewiesene Fast-Periode (12), die standardmäßig zugewiesene Slow-Periode (26) und die Signalperiode (9). Die Verwendung eines Datenrahmens in den Eingaben, wie wir es getan haben, folgt dem Import von Preisdaten mit dem MT5 Python-Modul. Unsere Funktion liefert eine Kopie des Eingabedatenrahmens mit zusätzlichen Spalten für die Werte des MACD, der MACD-Linie und der Signallinie.

In den ersten Codezeilen wird überprüft, ob unser Eingabedatenrahmen eine Spalte mit Schlusskursen enthält, die die für die EMA-Berechnungen erforderlichen Schlusskurse liefert. Darüber hinaus stellen wir sicher, dass alle Periodenparameter positive ganze Zahlen sind, da sie auf Rückblickperioden verweisen. Darüber hinaus wird bei der Validierung überprüft, ob die schnelle Periode kleiner ist als die langsame Periode, sodass der MACD die Unterschiede zwischen kurzfristigen und langfristigen Trends widerspiegelt. Dieser Validierungsschritt beugt Laufzeitfehlern vor und sorgt dafür, dass die logische Konsistenz erhalten bleibt. Es ist immer wichtig, Fehlinterpretationen zu vermeiden, die zu unvorteilhaften Handelsentscheidungen führen könnten. 

Anschließend erstellen wir eine Kopie des Eingabedatenrahmens, die zur Speicherung unserer Ausgaben dient, wobei die Originaldaten erhalten bleiben. Auf diese Weise wird die Integrität von Eingaberahmen gewahrt, die für mehrere Funktionen verwendet werden könnten, deren Analysen nicht beschädigt werden müssen. In Python sorgt sie für Modularität und Wiederverwendbarkeit. Nachdem eine Kopie des Input-Frames erstellt wurde, verwenden wir die Pandas-Funktion des exponentiell gewichteten gleitenden Durchschnitts, um den EMA der Schlusskurse über die schnelle und langsame Periode zu berechnen. Dabei weisen wir dem Parameter adjust den Wert False zu, wodurch sichergestellt wird, dass die Standard-EMA-Formel verwendet wird und „span“ die Fenstergröße festlegt. Die Wahl der „Spanne“ hat einen direkten Einfluss auf die Empfindlichkeit, wobei kleinere Werte das EMA empfindlicher machen, während größere Werte das Rauschen glätten.

Sobald wir die Berechnung der schnellen und langsamen EMAs abgeschlossen haben, ordnen wir unsere erste neue Pandas-Reihe dem Ausgabedatenrahmen zu, den wir treffend als „MACD“ bezeichnen.  Damit wird die MACD-Linie im Wesentlichen als Differenz zwischen den schnellen und langsamen EMAs berechnet. Die MACD-Linie ist der Hauptindikator, der die Konvergenz oder Divergenz von langfristigen und kurzfristigen Kursbewegungen anzeigt. Zusammenfassend lässt sich sagen, dass ein positiver Wert einen Aufwärtstrend anzeigt, während ein negativer Wert auf einen Abwärtstrend hindeutet. Die Beobachtung der Richtung und des Ausmaßes der MACD-Linie kann als Kontrolle der Trendstärke dienen. Crossovers können Trendwechsel signalisieren.

Als Nächstes berechnen wir die Pandas-Reihe der Signallinien für unseren Ausgangsdatenrahmen. Hierbei handelt es sich um eine Berechnung der Signallinie als EMA der MACD-Linie über die „Signal-Periode“. Er glättet den MACD und die Signallinien, um eine Referenz für Handelssignale zu liefern. Auch das Kreuzen des MACD und der Signallinie ist ein wichtiger Entscheidungspunkt. Mit einem Standardzeitraum von 9 Jahren bietet dieser Puffer ein ausgewogenes Verhältnis zwischen Reaktionsfähigkeit und Glättung, kann aber je nach den Bedingungen des gehandelten Vermögenswerts noch fein abgestimmt werden.

Die letzte Pandas-Serie, die wir an den Ausgabedatenrahmen anhängen, ist das MACD-Histogramm. Damit wird die Differenz zwischen dem MACD-Puffer und dem Signallinienpuffer berechnet. Diese Berechnung hilft dabei, die Stärke des Momentums zu visualisieren, wobei es bei positive Werten steigt und bei negativen Werten fällt. Auch Vorzeichenwechsel im Histogramm können auf Umkehrungen hinweisen. Nachdem diese drei Pandas-Serien an den Ausgabedatenrahmen angehängt wurden, ist die Arbeit unserer Funktion abgeschlossen und sie gibt einfach diesen Datenrahmen zurück.

Der OBV

Diese Funktion berechnet das On-Balance-Volumen, einen Volumenindikator, der eine Analogie zwischen Preisänderungen und Volumen herstellt. Wir implementieren es in Python wie folgt:

def OBV(df) -> pd.DataFrame:
    """
    Calculate On-Balance Volume (OBV) and append it as an 'OBV' column 
    to the input DataFrame.

    OBV is a momentum indicator that uses volume flow to predict changes in stock price.
    
    Args:
        df (pd.DataFrame): DataFrame with 'close' and 'volume' columns.
        
    Returns:
        pd.DataFrame: Input DataFrame with a new 'OBV' column.
    """
    # Input validation
    if not all(col in df.columns for col in ['close', 'tick_volume']):
        raise ValueError("DataFrame must contain 'close' and 'volume' columns")

    # Create a copy to avoid modifying the original DataFrame
    result_df = df.copy()
    # print(result_df.columns)
    
    # Calculate the direction of price change
    # np.sign returns 1 for positive, -1 for negative, and 0 for zero change
    direction = np.sign(result_df['close'].diff())
    
    # Calculate the OBV
    # Multiply the volume by the direction of price movement
    # Then calculate the cumulative sum
    obv = (result_df['tick_volume'] * direction).cumsum()
    
    # The first value of diff() is NaN, so the first OBV will be NaN.
    # We can fill it with the first day's volume or 0. A common practice is to start at 0.
    result_df['OBV'] = obv.fillna(0)
    
    return result_df

Unser obiger Quellcode beginnt mit der Validierung des Datenrahmens, um sicherzustellen, dass er die erforderlichen Spalten des Schlusskurses und des Volumens von „tick-volume“ enthält. Wir stützen uns auf das Tick-Volumen, da dieses in den meisten Anlageklassen leichter verfügbar ist als das reale Volumen, das bei Devisenpaaren aufgrund ihrer dezentralen Natur schwer zu bekommen ist. Sobald diese Validierung abgeschlossen ist, erstellen wir eine Kopie des Eingabedatenrahmens, da wir beabsichtigen, die Eingabe zu ergänzen, und es ratsam sein könnte, die Integrität der Eingabe zu bewahren, wie bereits oben mit der MACD-Funktion argumentiert wurde. 

Auf dieser Grundlage berechnen wir die „Richtung“ der Schlusskursänderungen. Diese Berechnungen werden für aufeinanderfolgende Zeiträume durchgeführt. Die Funktion np.sign wird verwendet, um entweder -1, +1 oder 0 zu markieren; für Preissenkungen, Preiserhöhungen bzw. keine Preisänderungen. Dieser Schritt ist wichtig, um die Richtung der Kursbewegung festzulegen, die bestimmt, wie das Volumen im OBV akkumuliert wird. Dieser Schritt vereinfacht auch die Analyse von Preistrends, indem er sie in ein binäres Format umwandelt, das eine einfachere Integration mit Volumendaten ermöglicht. 

Nachdem der Richtungsvektor definiert ist, berechnen wir das OBV, d. h. das Produkt aus Volumen und dieser Richtung mit einer kumulativen Summe, um das OBV über die Zeit zu verfolgen. Das OBV akkumuliert volumenbasierte Kursbewegungen, indem es das Volumen in Zeiten der Hausse addiert und in Zeiten der Baisse abzieht. Der OBV-Wert kann also Kauf- oder Verkaufsdruck widerspiegeln. Der Trend des OBV ist wichtiger als sein absoluter Wert. Ein Vergleich seines Vorzeichens und der Kursrichtung kann bei der Trendbestätigung helfen.

Unsere nächste Codezeile füllt den NaN-Wert im ersten OBV-Eintrag, der ein Ergebnis der diff()-Berechnungen ist, da dies einen Vergleich verhindern würde. Diese Zeile fügt diesen OBV-Wert auch einer neuen OBV-Pandas-Reihe in unserem Ausgabe-Pandas-Datenrahmen hinzu. Die Wahl des OBV im speziellen Fall dieses Indikators ist praktisch, weil 0 ein neutraler Wert ist, der keinen Volumenschwung in eine der beiden Richtungen darstellt. Dies ist nicht dasselbe wie die Zuweisung von 0 zum Puffer der gleitenden Durchschnittspreise.

Frühere Notizen

Viele der Signalmuster im letzten Artikel, der diese Indikatorenkombination aus MACD und OBV vorstellte, haben den Vorwärtstest nicht bestanden. Nur Pattern-7 bestand einen Vorwärtstest, was eine enorme Minderleistung ist, wenn man bedenkt, dass normalerweise mindestens 6 der 10 getesteten Muster gewinnbringend ihren Vorwärtstest bestehen. Wir wählen also einige der sehr schlechten Ergebnisse aus dem letzten Artikel aus und sehen, ob wir durch die Anwendung von überwachtem Lernen bessere Ergebnisse erzielen können. Für diesen Artikel wählen wir daher 3 Muster aus den vorherigen 9 Nachzüglern aus. Diese sind Pattern-2, Pattern-3 und Pattern-5.

Pattern-2

Wir implementieren Pattern-2 in Python wie folgt;

def feature_2(macd_df, obv_df, price_df):
    """

    """
    feature = np.zeros((len(macd_df), 2))
    
    feature[:, 0] = ((price_df['low'] < price_df['low'].shift(1)) &
                     (macd_df['MACD_Histogram'] > macd_df['MACD_Histogram'].shift(1)) &
                     (obv_df['OBV'] > obv_df['OBV'].shift(1))).astype(int)
    
    feature[:, 1] = ((price_df['high'] > price_df['high'].shift(1)) &
                     (macd_df['MACD_Histogram'] < macd_df['MACD_Histogram'].shift(1)) &
                     (obv_df['OBV'] < obv_df['OBV'].shift(1))).astype(int)
    
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

Ein tieferes Tief und ein steigender MACD deuten auf eine versteckte Aufwärtsdivergenz hin, während ein höheres Hoch in Verbindung mit einem fallenden MACD ebenfalls auf eine versteckte Abwärtsdivergenz hindeutet. Dies wird mit der Bestätigung des Volumens kombiniert, wobei ein steigender OBV eine Akkumulation bestätigt, was ein Aufwärtssignal ist, während ein sinkender OBV eine Verteilung anzeigt, was ein Aufwärtssignal ist. Zusammenfassend lässt sich sagen, dass dieses Muster darauf abzielt, Divergenzen, die durch eine Abschwächung des Momentums trotz der Preisextreme entstehen, durch Signale mit Volumenfluss zu bestätigen.

Dieses Muster dient also dazu, Fortsetzungsmuster in Trends zu erkennen. Am zuverlässigsten ist er bei etablierten Trends wie Aufwärts- und Abwärtstrends. Außerdem sind oft 2 Balken Bestätigung erforderlich, bevor man sich voll darauf einlassen kann. Wir führen Tests mit einem CNN-Netzwerk durch, das den RQ-Kernel bei der Definition seiner Architektur einsetzt, während wir Eingangssignale aus diesem Muster aus dem Zeitraum 2023.01.01 bis 2025.01.01 nehmen, nachdem wir Training und Optimierungen über den Zeitraum 2023.01.01 bis 2024.01.01 auf dem Paar GBP JPY auf dem 4-Stunden-Zeitrahmen durchgeführt haben. Unser Testbericht lautet wie folgt:

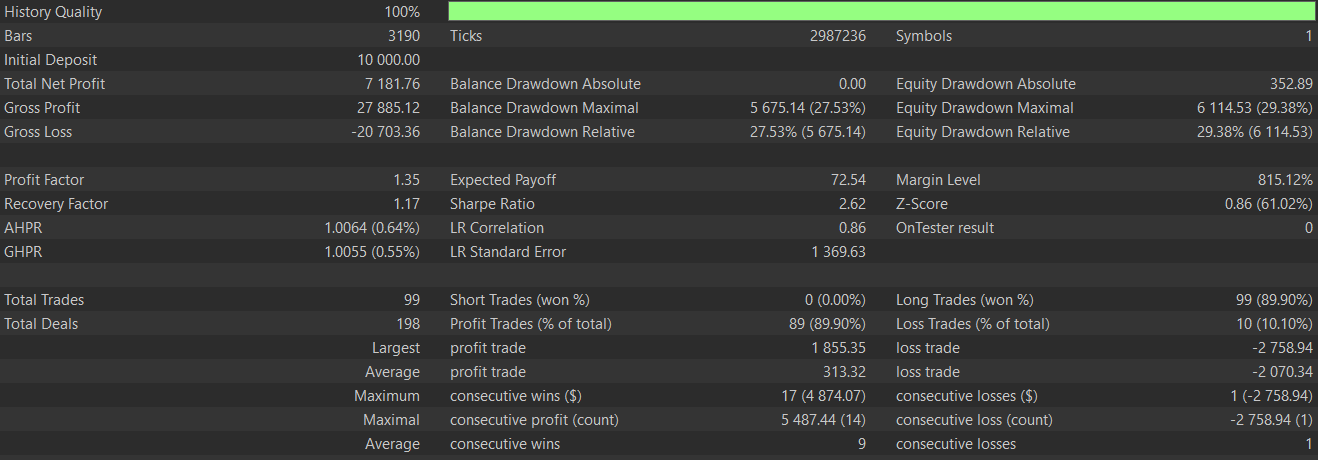
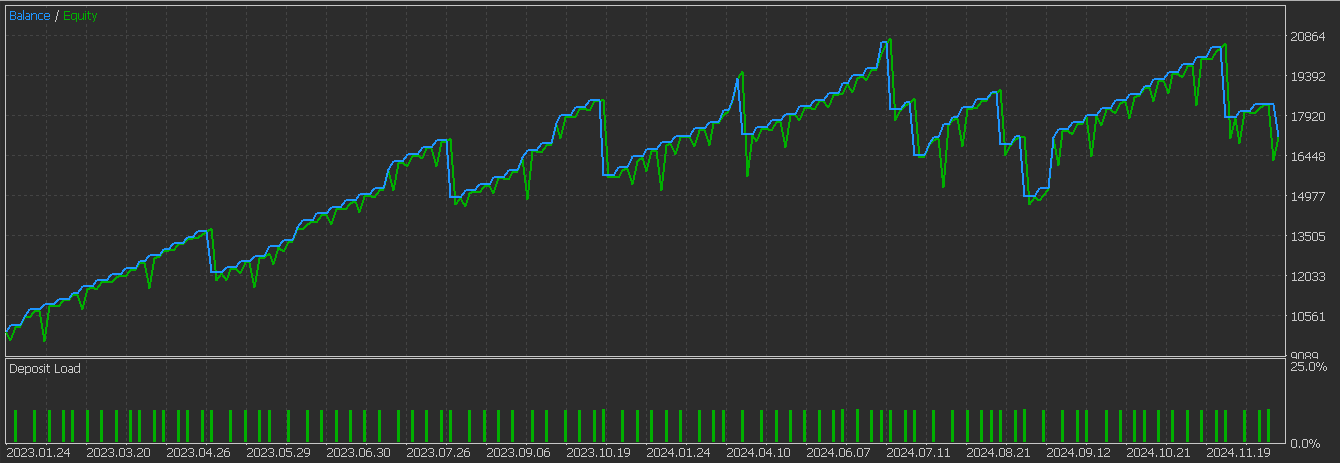
Im Vergleich zu den Ergebnissen des letzten Artikels ist eine deutliche Verbesserung festzustellen, sodass wir sagen können, dass unser überwachtes Lernmodell einen Unterschied gemacht hat. Wie immer werden vom Leser zusätzliche Sorgfalt und unabhängige Tests erwartet, bevor die hier vorgestellten Ideen auf Live-Konten angewendet werden können. Obwohl diese Artikel auf den automatisierten Handel ausgerichtet sind, könnte es für einige aufschlussreich sein, ein Gefühl dafür zu bekommen, wie die von uns beschriebenen Muster tatsächlich auf einem Chart aussehen. Zu diesem Zweck finden Sie unten das Aufwärtssignal für dieses Muster, dem Pattern-2.

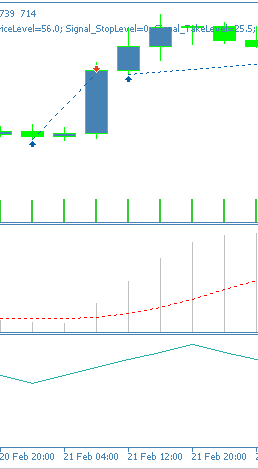
Pattern-3

Wir implementieren dieses Muster in Python wie folgt:

def feature_3(macd_df, obv_df, price_df):
    """
    """
    feature = np.zeros((len(macd_df), 2))
    
    feature[:, 0] = ((macd_df['MACD_Histogram'] > macd_df['MACD_Histogram'].shift(1)) &
                     (macd_df['MACD_Histogram'].shift(1) < macd_df['MACD_Histogram'].shift(2)) &
                     (obv_df['OBV'] > obv_df['OBV'].shift(1))).astype(int)
    
    feature[:, 1] = ((macd_df['MACD_Histogram'] < macd_df['MACD_Histogram'].shift(1)) &
                     (macd_df['MACD_Histogram'].shift(1) > macd_df['MACD_Histogram'].shift(2)) &
                     (obv_df['OBV'] < obv_df['OBV'].shift(1))).astype(int)
    
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

Dieses Muster sucht nach Umkehrungen im MACD-Histogramm, wobei ein Aufwärtssignal durch einen Tiefpunkt bestätigt wird, der durch einen Anstieg des Histogramms nach einem Rückgang gekennzeichnet ist. Das bärische Signal hingegen ist eine Spitzenbestätigung mit einem rückläufigen Histogramm, das in den letzten Balken gestiegen ist. Das Histogramm ist dazu gedacht, die Wendepunkte der Dynamik zu erfassen. Außerdem sind 3 Balken erforderlich, um das Muster von Tiefst- und Höchstständen richtig zu definieren und Fehlsignale zu vermeiden.

Parallel dazu würde das OBV eine Trendausrichtung liefern, bei der die Richtung des Volumens mit dem Preistrend übereinstimmen sollte, wobei positive Werte bullische Signale und negative Werte Aufwärtssignal bestätigen. Dies bestätigt auf dem Papier die institutionelle Beteiligung. Bei Tests unter ähnlichen Bedingungen wie bei Pattern-2 oben erhalten wir den folgenden Bericht, der auf einen Vorwärtstest hinzudeuten scheint:

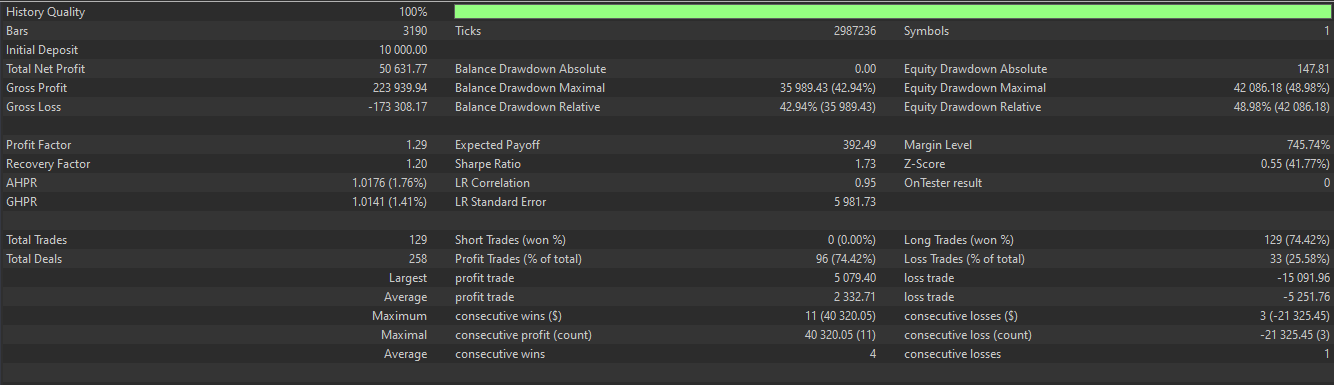
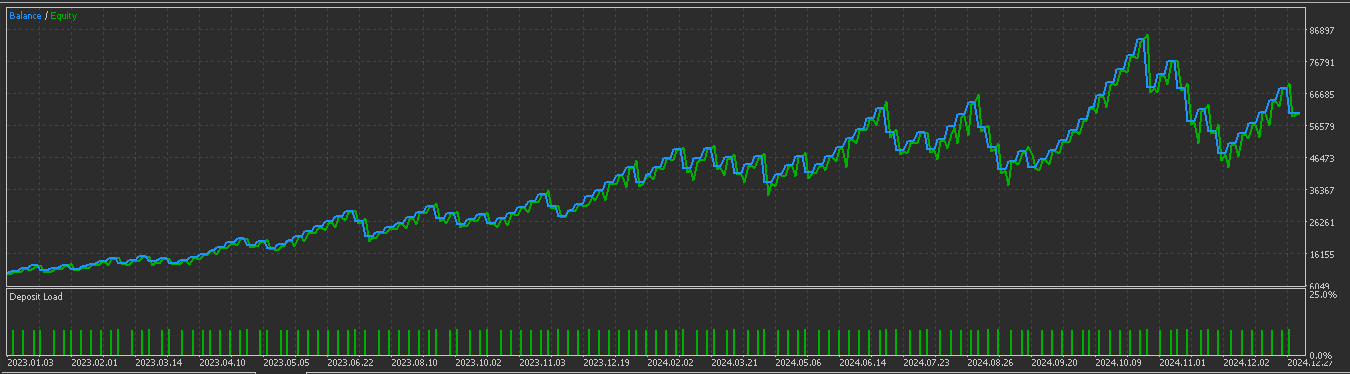
Dieses Signalmuster ist für Trendumkehrungen geeignet und kann bei überkauften/überverkauften Wendepunkten wirksam sein. Es werden mindestens 3 Balken der Preisentwicklung benötigt, daher werden die ersten 2 Balken der Reihe auf Null gesetzt, da sie keine Vergleichsdaten enthalten. Die Darstellung auf einem Chart kann für ein Aufwärtssignal wie folgt aussehen.

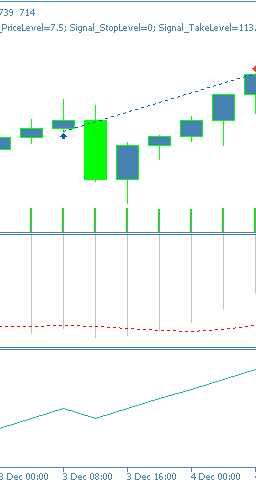
Pattern-5

Wir codieren dieses Muster in Python wie folgt:

def feature_5(macd_df, obv_df, price_df):
    """

    """
    feature = np.zeros((len(macd_df), 2))
    
    feature[:, 0] = ((macd_df['MACD_Histogram'] > macd_df['MACD_Histogram'].shift(1)) &
                     (macd_df['MACD_Histogram'] < 0.0) &
                     (obv_df['OBV'] > obv_df['OBV'].shift(1))).astype(int)
    
    feature[:, 1] = ((macd_df['MACD_Histogram'] < macd_df['MACD_Histogram'].shift(1)) &
                     (macd_df['MACD_Histogram'] > 0.0) &
                     (obv_df['OBV'] < obv_df['OBV'].shift(1))).astype(int)
    
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

Das Pattern-5 basiert auf dem Kontext der Nulllinie des MACD. Es zielt auf einen frühen Einstieg ab, wobei ein zinsbullisches Signal gesetzt wird, wenn der MACD im Baissebereich unter Null liegt, und ein bärisches, wenn der MACD über Null liegt. Die Verwendung eines 3rd-Party-Indikators, um eine Verschiebung der Dynamik zu signalisieren, wenn dieses Muster signalisiert wird, kann helfen, falsche Signale zu vermeiden. Der Filter für die Volumenrichtung sollte auch mit der Verschiebung des Volumenmomentums übereinstimmen, als Bestätigung für das Interesse der Institution.

Bei diesem Muster neigen die Aufwärtssignale dazu, in überverkauften Situationen mit steigendem Momentum zu verblassen, während die bärischen Signale in überkauften Situationen ebenfalls mit nachlassendem Momentum verblassen. Dieses Muster eignet sich besser für schwankende Märkte und setzt voraus, dass der MACD schwankt oder sich in einer Erholungsphase befindet. Das Testen dieses Musters nach dem Training und der Optimierung, so wie wir es mit den 2 anderen Mustern oben gemacht haben, ergibt den folgenden Testbericht:

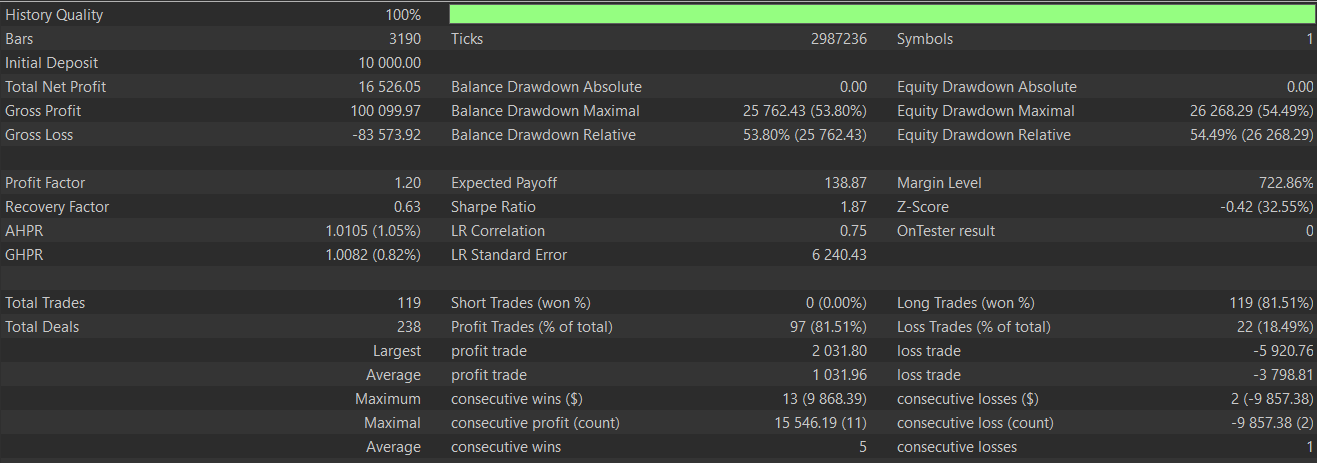
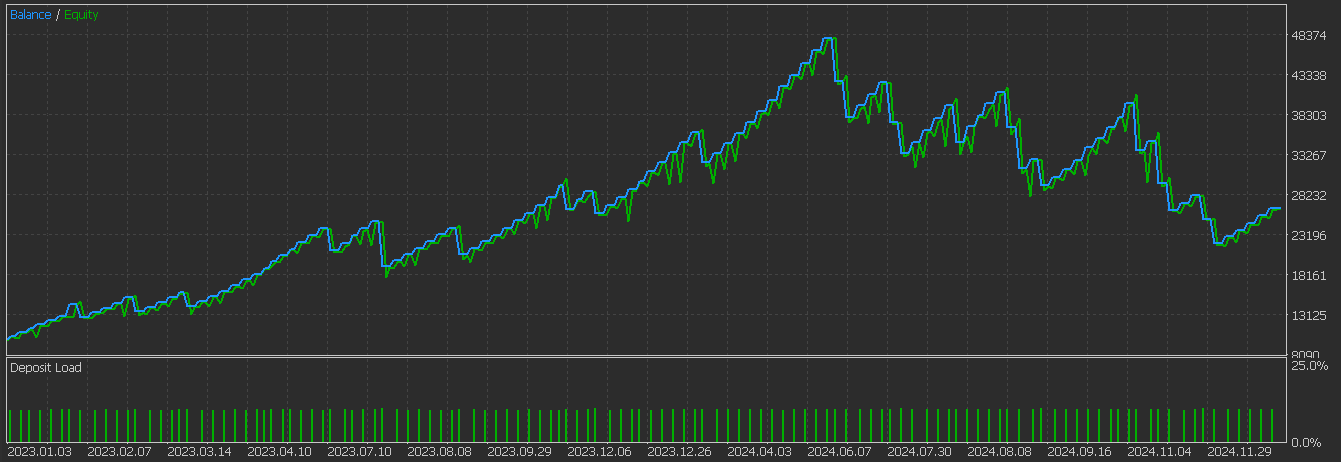
Von den 3 hier Getesteten scheint dies dasjenige zu sein, das noch Schwierigkeiten hat, einen Vorwärtstest zu bestehen. Dies könnte auf falsche MACD-Werte zurückzuführen sein, da der frühe Zeitpunkt noch nicht durch unabhängige Momentum-Pivots bestätigt wurde. Das Muster auf dem Chart ist ebenfalls wie folgt dargestellt:

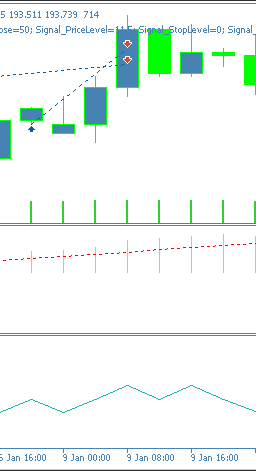
Schlussfolgerung

Zusammenfassend lässt sich sagen, dass wir die Indikatorenkombination aus MACD und OBV, die wir im letzten Artikel vorgestellt haben, wieder aufgegriffen haben, um zu sehen, ob wir die miserable Performance einiger ihrer Signalmuster verbessern können. Bei einem CNN mit überwachtem Lernen, das den rationalen quadratischen Kernel verwendet, um seine Kernel- und Kanalgrößen festzulegen, scheint dies für 2 der 3 erneut untersuchten Muster der Fall zu sein. Wir setzen das 3. Muster, das Pattern-5, düsteren Lauf zu schwachen Einstiegspunkten, die mehr Bestätigung erfordern.

Name	Beschreibung
WZ-72.mq5	Assistent Assemblierter Expert Advisor, dessen Header die enthaltenen Dateien beschreibt.
SignalWZ_72.mqh	Nutzerdefinierte Signalklassendatei für die Assistentengruppe
72_2.onnx	Python Exportiertes Netz für Signale des Pattern-2
72_3.onnx	Python Exportiertes Netz für Signale des Pattern-3
72_5.onnx	Pythion Exportiertes Netz für Signale des Pattern-5

Die angehängte nutzerdefinierte Signaldatei soll mit Hilfe des MQL5-Assistenten zu einem Expert Advisor zusammengestellt werden. Für neue Leser gibt es hier eine Anleitung, wie man das macht.