神经网络变得轻松(第八部分):关注机制
在之前的文章中,我们已经测试了组织规划神经网络的各种选项。 我们还研究了自图像处理算法中借鉴而来的卷积网络。 在本文中,我建议研究关注机制,它的出现为开发语言模型提供了动力。

MQL5 简介(第 1 部分):算法交易新手指南
通过我们的 MQL5 编程新手指南,进入算法交易的迷人领域。在揭开自动化交易世界的神秘面纱之际,让我们探索支持MetaTrader 5 的语言 MQL5 的精髓。从了解基础知识到迈出编码的第一步,本文是您即使没有编程背景也能释放算法交易潜力的关键。加入我们的旅程,在令人兴奋的 MQL5 世界里,体验简单与复杂的结合吧。
数据科学与机器学习(第 11 部分):朴素贝叶斯(Bayes),交易中的概率论
概率交易就像走钢丝一样 — 它需要精确、平衡和对风险的敏锐理解。 在交易世界中,概率就是一切。 这是成功与失败、盈利与亏损的区别。 通过利用概率的力量,交易者可以做出明智的决策,有效地管理风险,并实现他们的财务目标。 故此,无论您是经验丰富的投资者还是交易新手,了解概率都是解锁您的交易潜能的关键。 在本文中,我们将探索令人兴奋的概率交易世界,并向您展示如何将您的交易博弈提升到一个新的水平。

数据科学和机器学习(第 05 部分):决策树
决策树模仿人类的方式针对数据进行分类。 我们看看如何构建这棵树,并利用它们来分类和预测一些数据。 决策树算法的主要目标是将含有杂质的数据分离成纯节点或靠近节点。

神经网络变得轻松(第二十七部分):深度 Q-学习(DQN)
我们继续研究强化学习。 在本文中,我们将与深度 Q-学习方法打交道。 DeepMind 团队曾运用这种方法创建了一个模型,在玩 Atari 电脑游戏时其表现优于人类。 我认为评估该技术来解决交易问题的可能性将会很有益处。

神经网络实验(第 2 部分):智能神经网络优化
在本文中,我将利用实验和非标准方法开发一个可盈利的交易系统,并验证神经网络是否对交易者有任何帮助。 若在交易中运用神经网络的话, MetaTrader 5 完全可作为一款自给自足的工具。

如何在 MQL5 中使用 ONNX 模型
ONNX(开放式神经网络交换)是一种开源的机器学习模型格式。 在本文中,我们将研究如何创建 CNN-LSTM 模型,来预测金融时间序列。 我们还将展示如何在 MQL5 智能系统中运用创建的 ONNX 模型。

神经网络变得轻松(第七部分):自适应优化方法
在之前的文章中,我们利用随机梯度下降法针对网络中的所有神经元按照相同的学习率训练神经网络。 在本文中,我提议着眼于自适应学习方法,该方法能够改变每个神经元的学习率。 我们还将研究这种方法的利弊。
直推和主动机器学习中的梯度提升
在本文中,我们将探讨利用真实数据的主动机器学习方法,并讨论它们的优缺点。也许你会发现这些方法很有用,并将它们包含在你的机器学习模型库中。直推是由支持向量机(SVM)的共同发明者弗拉基米尔·瓦普尼克(Vladimir Vapnik)提出的。

神经网络变得轻松(第二十一部分):变分自动编码器(VAE)
在上一篇文章中,我们已熟悉了自动编码器算法。 像其它任何算法一样,它也有其优点和缺点。 在其原始实现中,自动编码器会尽可能多地将对象与训练样本分开。 这次我们将讨论如何应对它的一些缺点。

种群优化算法:灰狼优化器(GWO)
我们来研究一种最新的现代优化算法 — 灰狼优化。 测试函数的原始行为令该算法成为以前研究过的算法中最有趣的算法之一。 这是训练神经网络的顶级算法之一,具有许多变量的平滑函数。
数据科学与机器学习 — 神经网络(第 01 部分):前馈神经网络解密
许多人喜欢它们,但却只有少数人理解神经网络背后的整个操作。 在本文中,我尝试用淳朴的语言来解释前馈多层感知,解密其封闭大门背后的一切。

神经网络变得轻松(第三十五部分):内在好奇心模块
我们继续研究强化学习算法。 到目前为止,我们所研究的所有算法都需要创建一个奖励政策,从而令代理者能够每次从一个系统状态过渡到另一个系统状态的转换中估算其每个动作。 然而,这种方式人为因素相当大。 在实践中,动作和奖励之间存在一些时间滞后。 在本文中,我们将领略一种模型训练算法,该算法可以操控从动作到奖励的各种时间延迟。

神经网络变得轻松(第三十二部分):分布式 Q-学习
我们在本系列的早期文章中领略了 Q-学习方法。 此方法均化每次操作的奖励。 2017 年出现了两篇论文,在研究奖励分配函数时展现出了极大的成功。 我们来研究运用这种技术解决我们问题的可能性。

数据科学和机器学习(第 12 部分):自训练神经网络能否帮助您跑赢股市?
您是否厌倦了持续尝试预测股市? 您是否希望有一个水晶球来帮助您做出更明智的投资决策? 自训练神经网络可能是您一直在寻找的解决方案。 在本文中,我们将探讨这些强大的算法是否可以帮助您“乘风破浪”,并跑赢股市。 通过分析大量数据和识别形态,自训练神经网络通常可以做出比人类交易者更准确的预测。 发现如何使用这项尖端技术来最大化您的盈利,并制定更明智的投资决策。

神经网络变得轻松(第二十六部分):强化学习
我们继续研究机器学习方法。 自本文,我们开始另一个大话题,强化学习。 这种方式允许为模型设置某些策略来解决问题。 我们可以预期,强化学习的这种特性将为构建交易策略开辟新的视野。

用于时间序列挖掘的数据标签(第 5 部分):使用 Socket 在 EA 中进行应用和测试
本系列文章介绍了几种时间序列标注方法,可以创建符合大多数人工智能模型的数据,根据需求有针对性地进行数据标注,可以使训练出来的人工智能模型更符合预期设计,提高我们模型的准确性,甚至帮助模型实现质的飞跃!

在 ONNX 模型中使用 float16 和 float8 格式
用于表示机器学习模型的数据格式对其有效性起着至关重要的作用。近年来,出现了几种新类型的数据,专门为使用深度学习模型而设计。在本文中,我们将重点介绍两种新的数据格式,它们已在现代模型中广泛采用。
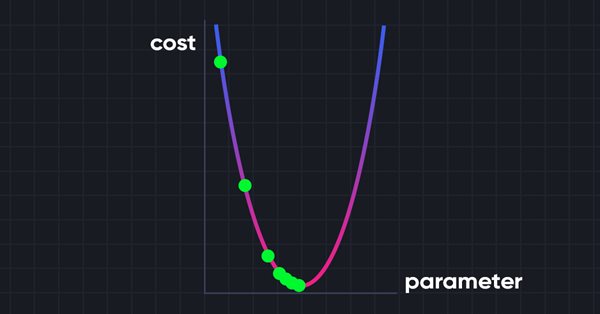
数据科学与机器学习(第 06 部分):梯度下降
梯度下降在训练神经网络和许多机器学习算法中起着重要作用。 它是一种快速而智能的算法,尽管它的工作令人印象深刻,但它仍然被许多数据科学家误解,我们来看看有关它的全部。
神经网络变得轻松(第三十四部分):全部参数化的分位数函数
我们继续研究分布式 Q-学习算法。 在之前的文章中,我们研究了分布式和分位数 Q-学习算法。 在第一种算法当中,我们训练了给定数值范围的概率。 在第二种算法中,我们用给定的概率训练了范围。 在这两个发行版中,我们采用了一个先验分布知识,并训练了另一个。 在本文中,我们将研究一种算法,其允许模型针对两种分布进行训练。

神经网络变得轻松(第十四部分):数据聚类
我的上一篇文章已经发表一年多了。 这令我有了大量时间考虑修改思路和发展新方法。 在这篇新文章中,我想转移一下以前使用的监督学习方法。 这次我们将深入研究无监督学习算法。 特别是,我们将考虑一种聚类算法 — k-均值。
使用 Python 和 MetaTrader5 python 软件包及 ONNX 模型文件进行深度学习预测和排序
本项目涉及在金融市场中使用 Python 进行基于深度学习的预测。我们将探索使用平均绝对误差(MAE)、均方误差(MSE)和R平方(R2)等关键指标测试模型性能的复杂性,并学习如何将所有内容打包到可执行文件中。我们还将制作一个 ONNX 模型文件以及它的 EA。

使用Python和MQL5开发机器人(第一部分):数据预处理
基于机器学习的交易机器人开发:详细指南本系列文章的第一篇将重点讨论数据的收集与准备以及特征的选择。该项目采用Python编程语言及其相关库,并结合MetaTrader 5平台来实现。

神经网络变得轻松(第九部分):操作归档
我们已经经历了很长一段路,并且函数库中的代码越来越庞大。 这令跟踪所有连接和依赖性变得难以维护。 因此,我建议为先前创建的代码创建文档,并保持伴随每个新步骤进行更新。 正确准备的文档将有助我们看到操作的完整性。
时间序列的频域表示:功率谱
在本文中,我们将讨论在频域中分析时间序列的相关方法。 构建预测模型时,强调检验时间序列功率谱的效用 在本文中,我们将讨论运用离散傅里叶变换(dft)在频域中分析时间序列获得的一些实用观点。
神经网络变得轻松(第四十四部分):动态学习技能
在上一篇文章中,我们讲解了 DIAYN 方法,它提供了学习各种技能的算法。 获得的技能可用在各种任务。 但这些技能可能非常难以预测,而这可能令它们难以运用。 在本文中,我们要研究一种针对学习可预测技能的算法。

MQL5 简介(第 3 部分):掌握 MQL5 的核心元素
在这篇便于初学者阅读的文章中,我们将为您揭开数组、自定义函数、预处理器和事件处理的神秘面纱,并对所有内容进行清晰讲解,让您可以轻松理解每一行代码,从而探索 MQL5 编程的基础知识。加入我们,用一种独特的方法释放 MQL5 的力量,确保每一步都能理解。本文为掌握 MQL5 奠定了基础,强调了对每行代码的解释,并提供了独特而丰富的学习体验。