
数据科学和机器学习(第 12 部分):自训练神经网络能否帮助您跑赢股市?
“我并不是说神经网络很容易。 您需要成为专家才能令这些事情发挥作用。 但是,这些专业知识可在更广泛的应用中为您提供服务。 从某种意义上说,以前用于特征设计的所有努力现在都投入到架构设计、损失函数设计、以及优化方案设计当中。 手工劳动已经提升到更高的抽象水平。“
斯特凡诺·索托(Stefano Soatto)
概述
如果您已经从事过一段时间的算法交易者,您很有可能听说过神经网络。 似乎它们总是制造圣杯交易机器人的一种推进途径,关于这一点我不太确定,因为最终获得一个可盈利的系统不光是将神经网络添加到交易机器人之中。 更不用说,您需要了解在使用神经网络时您自己的得失,因为即使是再小的细节也可能意味着成功或失败,即盈利或亏损。

坦率地讲,我认为神经网络对任何人都不起啥作用,特别若您不愿意弄脏自己的手,因为很多时候您需要花时间分析模型、预处理和缩放输入数据产生的错,以及我将在本文中讨论的更多内容。
我们从人工神经网络的定义开始本文。
什么是人工神经网络?
简而言之,人工神经网络,通常称为神经网络,是受到构成动物大脑的生物神经网络启发的一种计算系统。 若要理解神经网络的基本组件,请参阅本系列的上一篇文章。
在之前关于神经网络的文章中,我解释了有关前馈神经网络的基本知识。 在本文中,我们将探讨神经网络的前向验算和后向验算,即神经网络训练和测试。 我们还将根据最后讨论的所有内容创建一个交易机器人,并将见识我们的交易机器人的表现。
在多层感知器神经网络中,前层的所有神经元/节点都与第二层的节点互连,依此类推到从输入到输出的所有层。 这就是神经网络能够找出数据集中复杂关系的原因。 您拥有的神经层越多,您的模型就越能够理解数据集中的复杂关系。 这需要付出高昂的计算成本,并且不一定能保证模型的准确性,特别是如果模型过于复杂而问题却很简单。
在大多数情况下,单隐藏层就足以解决人们试图使用这些花哨的神经网络解决的大多数问题。 这就是为什么我们打算采用单层神经网络。
前向验算
前向验算中涉及的操作很简单,只需几行代码即可实现。 不过,为了令您的神经网络更灵活,您需要对矩阵和向量运算有深入的了解,因为它们是神经网络、以及我们在本系列中讨论的许多机器学习算法的构建模块。
需要知道的一件重要事情是人们试图使用神经网络解决的问题类型,因为不同的问题需要具有不同配置和不同输出的不同类型神经网络。
对于那些不知道以下问题类型的人,譬如是
- 回归问题
- 分类问题
回归问题是我们试图预测连续变量的问题,例如在交易中,我们经常试图预测市场的下一个价格点。 对于那些还没概念的人,我建议阅读线性回归。
这类问题可由回归神经网络解决。
02: 分类问题
分类问题是我们试图预测离散/非连续变量的问题。 在交易中,我们可以预测信号,比如 0 信号表示市场朝下,而 1 表示市场朝上。
这类问题由分类神经网络或形态识别神经网络解决,在 MATLAB 中它们被称为形态网络(patternnets)。
在本文中,我将通过尝试预测下一阶段市场价格走向来解决回归问题。
matrix CRegNeuralNets::ForwardPass(vector &input_v) { matrix INPUT = this.matrix_utils.VectorToMatrix(input_v); matrix OUTPUT; OUTPUT = W.MatMul(INPUT); //Weight X Inputs OUTPUT = OUTPUT + B; //Outputs + Bias OUTPUT.Activation(OUTPUT, ENUM_ACTIVATION_FUNCTION(A_FX)); //Activation Function return (OUTPUT); }
该前向验算函数易于阅读,但是当您尝试操作一切顺利时,您应该密切关注的最重要的地方是每一步的矩阵大小。
matrix INPUT = this.matrix_utils.VectorToMatrix(input_v);
这部分值得解释。由于此函数 VectorToMatrix 在向量中获取输入,这是由于即将发生矩阵运算,故这些输入需要采用矩阵形式。
始终记住:
- 第一个神经网络输入矩阵是 nx1 矩阵
- 权重矩阵为 HN x n;其中 HN 是当前隐藏层中的节点数,n 是来自前一层的输入数或来自输入矩阵的行数。
- 偏置矩阵的大小与层的输出大小相同。
了解这一点非常重要。 它将令您免于有一天在试图自己解决这个问题时淹没在不确定性之中。
我来展示一下我们正在研究的神经网络的架构,以便您清楚地明白我们正在做什么。
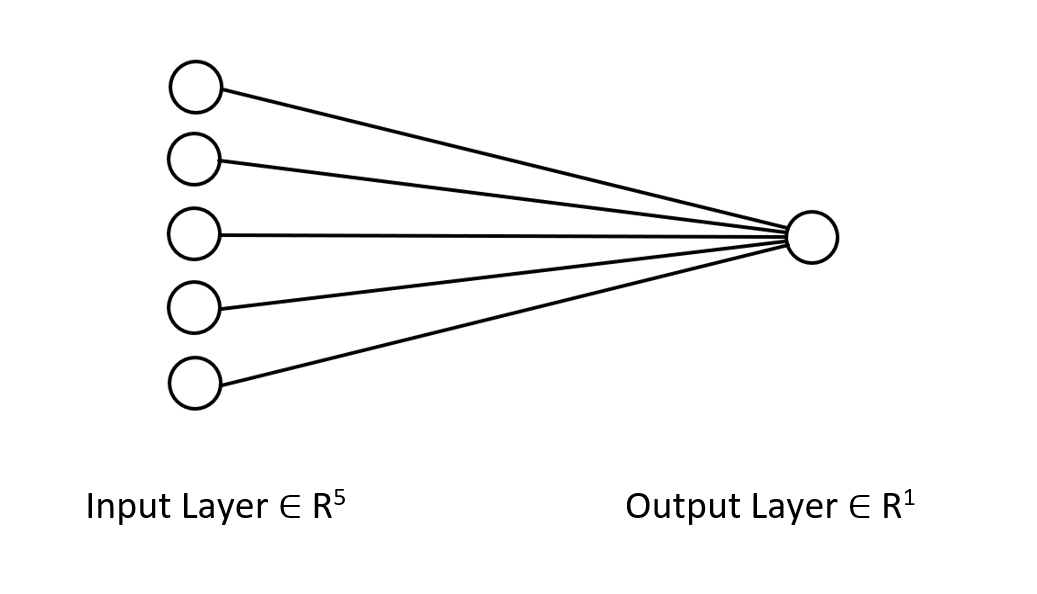
它只是一个单层神经网络,这就是为什么在我刚刚展示的函数中,您在前向验算中没有见到循环。 不过,如果您遵循相同的矩阵方法,并确保我上面解释的维度,您将能够实现任何复杂的架构。
您已经看到了 W 矩阵的前向验算,我们来看看如何为模型生成权重。
生成权重
为神经网络生成合适的权重不仅仅是初始化随机值的问题。 我学到了艰难的方式;得到错误结果会在反向验算中给您带来各种各样的麻烦,这会导致您怀疑,并开始调试您的已经硬编码且很复杂的代码。
不正确的权重初始化会令整个学习过程变得乏味和耗时。 网络可能会卡陷在局部最小值,并且收敛速度可能非常缓慢。
第一步是选择随机值,我更喜欢 42 的随机状态。
this.W = matrix_utils.Random(0.0, 1.0,1,m_inputs, RANDOM_STATE);
大多数人最终停在这一步,他们生成权重,并认为仅此而已。 选择随机变量后,我们需要使用 Glorot 或 He 初始化来初始化我们的权重。
Xavier/Glorot 初始化最适合 sigmoid 和 tanh 激活函数,而 He 初始化适用于 RELU 及其变体。
He 初始化
![]()
其中: n = 节点的输入数。
故此,在初始化权重后,权重归一化随之而来。
this.W = matrix_utils.Random(0.0, 1.0,1,m_inputs, RANDOM_STATE); this.W = this.W * 1/sqrt(m_inputs); //He initialization
由于该神经网络仅有一层,因此只有一个矩阵来承载权重。
激活函数
由于这是回归类型的神经网络,因此该网络的激活函数只是回归激活函数的变体。 RELU:
enum activation { AF_ELU_ = AF_ELU, AF_EXP_ = AF_EXP, AF_GELU_ = AF_GELU, AF_LINEAR_ = AF_LINEAR, AF_LRELU_ = AF_LRELU, AF_RELU_ = AF_RELU, AF_SELU_ = AF_SELU, AF_TRELU_ = AF_TRELU, AF_SOFTPLUS_ = AF_SOFTPLUS };
这些红色的激活函数,以及更多内容默认由标准库的矩阵提供,阅读更多。
损失函数
此回归神经网络的损失函数为:
enum loss { LOSS_MSE_ = LOSS_MSE, LOSS_MAE_ = LOSS_MAE, LOSS_MSLE_ = LOSS_MSLE, LOSS_HUBER_ = LOSS_HUBER };
标准库提供了更多激活函数,阅读更多。
使用增量规则的反向传播
增量(Delta)规则是一种梯度下降学习规则,用于更新单层神经网络中人工神经元输入的权重。 这是更通用的反向传播算法的特例。 对激活函数 g(x) 的神经元 j,第 j 神经元的权重 Wji 的增量规则给出如下:
![]()
其中:
![]() 是一个称为学习率的小常数
是一个称为学习率的小常数
![]() 是 g 的导数
是 g 的导数
g(x) 是神经元的激活函数
![]() 是目标输出
是目标输出
![]() 是实际输出
是实际输出
![]() 是第 i 个输入
是第 i 个输入
这太棒了,我们现在有一个公式,如此我们只需要实现它,对吗? 错!!!
这个公式的问题在于,尽管看起来很简单,但在将其转换为代码时却非常复杂,并且需要您编写一对 for 循环,神经网络中的这种练习会活生生地蚕食掉您的余生。我们需要拥有的正确公式是向我们显示矩阵运算的公式。 我来为您打造这个:
![]()
其中:
![]() = 权重矩阵的变化
= 权重矩阵的变化
![]() = 损失函数的导数
= 损失函数的导数
![]() = 逐元素矩阵乘法/哈达玛(Hadamard)乘积
= 逐元素矩阵乘法/哈达玛(Hadamard)乘积
![]() = 神经元激活矩阵的导数
= 神经元激活矩阵的导数
![]() = 输入矩阵。
= 输入矩阵。
L 矩阵始终与 O 矩阵具有相同的大小,并且右侧生成的矩阵需要与 W 矩阵具有相同的大小。 否则,您就抓瞎了。
我们看看转换为代码后的样子。
for (ulong iter=0; iter<m_rows; iter++) { OUTPUT = ForwardPass(m_x_matrix.Row(iter)); //forward pass pred = matrix_utils.MatrixToVector(OUTPUT); actual[0] = m_y_vector[iter]; preds[iter] = pred[0]; actuals[iter] = actual[0]; //--- INPUT = matrix_utils.VectorToMatrix(m_x_matrix.Row(iter)); vector loss_v = pred.LossGradient(actual, ENUM_LOSS_FUNCTION(L_FX)); LOSS_DX.Col(loss_v, 0); OUTPUT.Derivative(OUTPUT, ENUM_ACTIVATION_FUNCTION(A_FX)); OUTPUT = LOSS_DX * OUTPUT; INPUT = INPUT.Transpose(); DX_W = OUTPUT.MatMul(INPUT); this.W -= (alpha * DX_W); //Weights update by gradient descent }
使用 MQL5 提供的矩阵库替代·数组进行机器学习的好处是,您不必担心微积分,我的意思是您不必担心去寻找损失函数的导数,激活函数的导数 — 什么都没有。
为了训练模型,我们需要考虑两件事,至少目前,世代和学习率表示为 alpha。 如果您阅读过我之前关于梯度下降的文章,您就会知道我在说什么。
Epochs:单个 epoch 是指整个数据集完全向前和向后循环贯穿网络。 简单来说,当网络看到所有数据时。 世代数量越大,训练神经网络所需的时间就越长,学习效果就越好。
Alpha: 是您希望梯度下降算法在达到全局和局部最小值时采用的步长大小。 Alpha 通常是介于 0.1 和 0.00001 之间的小值。 此值越大,网络收敛越快,但跳过局部最小值的风险就越高。
下面是此增量规则的完整代码:
for (ulong epoch=0; epoch<epochs && !IsStopped(); epoch++) { for (ulong iter=0; iter<m_rows; iter++) { OUTPUT = ForwardPass(m_x_matrix.Row(iter)); pred = matrix_utils.MatrixToVector(OUTPUT); actual[0] = m_y_vector[iter]; preds[iter] = pred[0]; actuals[iter] = actual[0]; //--- INPUT = matrix_utils.VectorToMatrix(m_x_matrix.Row(iter)); vector loss_v = pred.LossGradient(actual, ENUM_LOSS_FUNCTION(L_FX)); LOSS_DX.Col(loss_v, 0); OUTPUT.Derivative(OUTPUT, ENUM_ACTIVATION_FUNCTION(A_FX)); OUTPUT = LOSS_DX * OUTPUT; INPUT = INPUT.Transpose(); DX_W = OUTPUT.MatMul(INPUT); this.W -= (alpha * DX_W); } printf("[ %d/%d ] Loss = %.8f | accuracy %.3f ",epoch+1,epochs,preds.Loss(actuals,ENUM_LOSS_FUNCTION(L_FX)),metrics.r_squared(actuals, preds)); }
现在一切都设置好了。 是时候训练神经网络,从而理解数据集中的一个小形态了。
#include <MALE5\Neural Networks\selftrain NN.mqh> #include <MALE5\matrix_utils.mqh> CRegNeuralNets *nn; CMatrixutils matrix_utils; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- matrix Matrix = { {1,2,3}, {2,3,5}, {3,4,7}, {4,5,9}, {5,6,11} }; matrix x_matrix; vector y_vector; matrix_utils.XandYSplitMatrices(Matrix,x_matrix,y_vector); nn = new CRegNeuralNets(x_matrix,y_vector,0.01,100, AF_RELU_, LOSS_MSE_); //Training the Network //--- return(INIT_SUCCEEDED); }
函数 XandYSplitMatrices 将我们的矩阵分别拆分为 x 和 y 矩阵和向量。
| X 矩阵 | Y 向量 |
|---|---|
| { {1, 2}, {2, 3}, {3, 4}, {4, 5}, {5, 6} } | {3}, {5}, {7}, {9}, {11} |
训练输出:
CS 0 20:30:00.878 Self Trained NN EA (Apple_Inc_(AAPL.O),H1) [1/100] Loss = 56.22401001 | accuracy -6.028 CS 0 20:30:00.879 Self Trained NN EA (Apple_Inc_(AAPL.O),H1) [2/100] Loss = 2.81560904 | accuracy 0.648 CS 0 20:30:00.879 Self Trained NN EA (Apple_Inc_(AAPL.O),H1) [3/100] Loss = 0.11757813 | accuracy 0.985 CS 0 20:30:00.879 Self Trained NN EA (Apple_Inc_(AAPL.O),H1) [4/100] Loss = 0.01186759 | accuracy 0.999 CS 0 20:30:00.879 Self Trained NN EA (Apple_Inc_(AAPL.O),H1) [5/100] Loss = 0.00127888 | accuracy 1.000 CS 0 20:30:00.879 Self Trained NN EA (Apple_Inc_(AAPL.O),H1) [6/100] Loss = 0.00197030 | accuracy 1.000 CS 0 20:30:00.879 Self Trained NN EA (Apple_Inc_(AAPL.O),H1) [7/100] Loss = 0.00173890 | accuracy 1.000 CS 0 20:30:00.879 Self Trained NN EA (Apple_Inc_(AAPL.O),H1) [8/100] Loss = 0.00178597 | accuracy 1.000 CS 0 20:30:00.879 Self Trained NN EA (Apple_Inc_(AAPL.O),H1) [9/100] Loss = 0.00177543 | accuracy 1.000 CS 0 20:30:00.879 Self Trained NN EA (Apple_Inc_(AAPL.O),H1) [10/100] Loss = 0.00177774 | accuracy 1.000 … … … CS 0 20:30:00.883 Self Trained NN EA (Apple_Inc_(AAPL.O),H1) [100/100] Loss = 0.00177732 | accuracy 1.000
仅在 5 个世代之后,神经网络的准确度为 100%。 这是个好消息,因为这个问题很容易,故此我期待更快的学习。
现在这个神经网络已经训练好了,我采用新值 {7,8} 来测试它。 您和我都知道结果是 15。
vector new_data = {7,8}; Print("Test "); Print(new_data," pred = ",nn.ForwardPass(new_data));
输出:
CS 0 20:37:36.331 Self Trained NN EA (Apple_Inc_(AAPL.O),H1) Test CS 0 20:37:36.331 Self Trained NN EA (Apple_Inc_(AAPL.O),H1) [7,8] pred = [[14.96557787153696]]
它给了我们大约 14.97。 15 只是一个双精度值,这就是为什么它附带了这些值,但是当四舍五入到整数有效数字时,输出将显示为 15。 这表明我们的神经网络现在能够自我学习。 太酷了!
我们为这个模型提供真实世界的数据集,观察它做什么。
在尝试预测纳斯达克(NAS 100)指数时,我使用特斯拉股票和苹果股票作为我的自变量。 我某次在网上读过 CNBC 的一篇文章,说有 6 只科技股占纳斯达克市值的一半,苹果和特斯拉股票就是其中的两只。 在这个例子中,我用这两只股票作为训练神经网络的自变量。
input string symbol_x = "Apple_Inc_(AAPL.O)"; input string symbol_x2 = "Tesco_(TSCO.L)"; input ENUM_COPY_RATES copy_rates_x = COPY_RATES_OPEN; input int n_samples = 100; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { matrix x_matrix(n_samples,2); vector y_vector; vector x_vector; //--- x_vector.CopyRates(symbol_x,PERIOD_CURRENT,copy_rates_x,0,n_samples); x_matrix.Col(x_vector, 0); x_vector.CopyRates(symbol_x2, PERIOD_CURRENT,copy_rates_x,0,n_samples); x_matrix.Col(x_vector, 1); y_vector.CopyRates(Symbol(), PERIOD_CURRENT,COPY_RATES_CLOSE,0,n_samples); nn = new CRegNeuralNets(x_matrix,y_vector,0.01,1000, AF_RELU_, LOSS_MSE_);
我的经纪人命名这些 symbol_x 和 symbol_x2 品种的方式可能与您的不同。 在使用测试 EA 之前,不要忘记修改它们,并将这些品种添加到市场观察之中。 y 品种是图表上的当前品种。 确保将此 EA 附加到纳斯达克图表上。
运行脚本后,我得到这些输出日志:
CS 0 21:29:20.698 Self Trained NN EA (NAS100,M30) [ 1/1000 ] Loss = 353809311769.08959961 | accuracy -27061631.733 CS 0 21:29:20.698 Self Trained NN EA (NAS100,M30) [ 2/1000 ] Loss = 149221473.48209998 | accuracy -11412.427 CS 0 21:29:20.699 Self Trained NN EA (NAS100,M30) [ 3/1000 ] Loss = 149221473.48209998 | accuracy -11412.427 CS 0 21:29:20.699 Self Trained NN EA (NAS100,M30) [ 4/1000 ] Loss = 149221473.48209998 | accuracy -11412.427 CS 0 21:29:20.699 Self Trained NN EA (NAS100,M30) [ 5/1000 ] Loss = 149221473.48209998 | accuracy -11412.427 CS 0 21:29:20.699 Self Trained NN EA (NAS100,M30) [ 6/1000 ] Loss = 149221473.48209998 | accuracy -11412.427 .... .... CS 0 21:29:20.886 Self Trained NN EA (NAS100,M30) [ 1000/1000 ] Loss = 149221473.48209998 | accuracy -11412.427
什么?! 这就是我们在做完所有这些事情之后得到的。 在神经网络中大部分时间都会发生这样的事情,这就是为什么无论您尝试什么框架和 Python 库,对神经网络有扎实的理解都非常重要,这样的事情经常发生。
规范化和缩放数据
我不能强调这有多重要,即使并非所有数据集在规范化时都能给出最佳结果,例如,当您规范化我们最初用来测试神经网络是否正常工作的简单数据集时,您会得到恼人的结果。 网络会像这些值一样返回值,甚至更糟的是,我尝试过。
有许多规范化技术。 其中使用最广泛的三种是:
最小-最大缩放器
这是一种规范化技术,可将数值特征的值缩放到固定范围 [0, 1]。 其公式如下:
x_norm = (x -x_min) / (x_max - x_min)
其中:
x = 原始特征
x_min = 要素的最小值
x_max = 要素的最大值
x_norm = 新规范化的要素值
为了选择规范化技术并规范化数据,您需要导入预处理库。 包括附在文章末尾的文件。
我决定在我们的神经网络库中添加规范化数据的能力。
CRegNeuralNets::CRegNeuralNets(matrix &xmatrix, vector &yvector,double alpha, uint epochs, activation ACTIVATION_FUNCTION, loss LOSS_FUNCTION, norm_technique NORM_METHOD)
您可以选择其中 norm_technique 规范化技术;
enum norm_technique { NORM_MIN_MAX_SCALER, //Min max scaler NORM_MEAN_NORM, //Mean normalization NORM_STANDARDIZATION, //standardization NORM_NONE //Do not normalize. };
在调用添加了规范化技术的类后,我能够获得合理的准确性。
nn = new CRegNeuralNets(x_matrix,y_vector,0.01,1000, AF_RELU_, LOSS_MSE_,NORM_MIN_MAX_SCALER);
输出:
CS 0 22:40:56.457 Self Trained NN EA (NAS100,M30) [ 1/1000 ] Loss = 0.19379434 | accuracy -0.581 CS 0 22:40:56.457 Self Trained NN EA (NAS100,M30) [ 2/1000 ] Loss = 0.07735744 | accuracy 0.369 CS 0 22:40:56.458 Self Trained NN EA (NAS100,M30) [ 3/1000 ] Loss = 0.04761891 | accuracy 0.611 CS 0 22:40:56.458 Self Trained NN EA (NAS100,M30) [ 4/1000 ] Loss = 0.03559318 | accuracy 0.710 CS 0 22:40:56.458 Self Trained NN EA (NAS100,M30) [ 5/1000 ] Loss = 0.02937830 | accuracy 0.760 CS 0 22:40:56.458 Self Trained NN EA (NAS100,M30) [ 6/1000 ] Loss = 0.02582918 | accuracy 0.789 CS 0 22:40:56.459 Self Trained NN EA (NAS100,M30) [ 7/1000 ] Loss = 0.02372224 | accuracy 0.806 CS 0 22:40:56.459 Self Trained NN EA (NAS100,M30) [ 8/1000 ] Loss = 0.02245222 | accuracy 0.817 CS 0 22:40:56.460 Self Trained NN EA (NAS100,M30) [ 9/1000 ] Loss = 0.02168207 | accuracy 0.823 CS 0 22:40:56.460 Self Trained NN EA (NAS100,M30 CS 0 22:40:56.623 Self Trained NN EA (NAS100,M30) [ 1000/1000 ] Loss = 0.02046533 | accuracy 0.833
我还必须承认,我没有在 1 小时内获得预期的结果,神经网络似乎在 30 分钟图表上得到了更好的准确性,而我懒得去搞明白这是什么原因。
好了,所以训练数据的准确率为 82.3%。 这是一个良好的准确性。 我们制定一个简单的交易策略,该网络将使用该策略来开仓交易。
我目前在 OnInit 函数中收集数据的方法并不可靠。 我将创建函数来训练网络,并将其放置在 Init 函数里。 我们的网络在一次生存期只能训练一次。 不过,您不必局限于这种方式。
void OnTick() { //--- if (!train_nn) TrainNetwork(); //Train the network only once train_nn = true; } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void TrainNetwork() { matrix x_matrix(n_samples,2); vector y_vector; vector x_vector; x_vector.CopyRates(symbol_x,PERIOD_CURRENT,copy_rates_x,0,n_samples); x_matrix.Col(x_vector, 0); x_vector.CopyRates(symbol_x2, PERIOD_CURRENT,copy_rates_x,0,n_samples); x_matrix.Col(x_vector, 1); y_vector.CopyRates(Symbol(), PERIOD_CURRENT,COPY_RATES_CLOSE,0,n_samples); nn = new CRegNeuralNets(x_matrix,y_vector,0.01,1000, AF_RELU_, LOSS_MSE_,NORM_MIN_MAX_SCALER); }
尽管这个训练函数似乎拥有我们抢占市场所需的一切,但它仍然不可靠。 我在日线时间帧内进行了测试,得到了 -77% 的准确率,在 H4 时间帧上,它返回的准确度为 -11234,或类似的数值。 当增加数据和练习不同的训练样本时,神经网络的训练精度与它给我的不一致。
解释其中的原因有很多,因为不同的问题需要不同的架构。 我猜不同时间帧内的一些市场形态对于这个单层神经网络来说可能太复杂了,因为增量规则只适用于单层神经网络。 我们暂时无法解决这个问题,如此我就在那些似乎能给我带来良好输出的时间帧内继续做。 不过,我们可以做一些事情来改善结果,并稍微解决这种不一致的行为。 这是用随机状态拆分数据。
数据拆分比您想象的更重要
如果您拥有来自机器学习的 python 背景,您可能已经见过来自 sklearn 的 train_test_split 函数。
将数据拆分为训练数据和测试数据的目的不仅是拆分数据,而且是随机化数据集,令其不按其原始顺序排列。 我来解释一下。由于神经网络和其它机器学习算法试图理解数据中的形态,因此按照数据的提取顺序排列数据可能对模型不利,因为它们也会理解由于数据的组织和排列方式而导致的形态。 这不是让模型学习的明智方法,因为排列不如变量中的形态重要。
void TrainNetwork() { //--- collecting the data matrix Matrix(n_samples,3); vector y_vector; vector x_vector; x_vector.CopyRates(symbol_x,PERIOD_CURRENT,copy_rates_x,0,n_samples); Matrix.Col(x_vector, 0); x_vector.CopyRates(symbol_x2, PERIOD_CURRENT,copy_rates_x,0,n_samples); Matrix.Col(x_vector, 1); y_vector.CopyRates(Symbol(), PERIOD_CURRENT,COPY_RATES_CLOSE,0,n_samples); Matrix.Col(y_vector, 2); //--- matrix x_train, x_test; vector y_train, y_test; matrix_utils.TrainTestSplitMatrices(Matrix, x_train, y_train, x_test, y_test, 0.7, 42); nn = new CRegNeuralNets(x_train,y_train,0.01,1000, AF_RELU_, LOSS_MSE_,NORM_MIN_MAX_SCALER); vector test_pred = nn.ForwardPass(x_test); printf("Testing Accuracy =%.3f",metrics.r_squared(y_test, test_pred)); }
收集训练数据后,在给定随机状态 42 的情况下,引入了函数 TrainTestSplitMatrices。
void TrainTestSplitMatrices(matrix &matrix_,matrix &x_train,vector &y_train,matrix &x_test, vector &y_test,double train_size=0.7,int random_state=-1)
实时市场预测
为了在 Ontick 函数进行实时预测,必须有代码来收集数据,并将其放入神经网络前向验算函数的输入向量之中。
void OnTick() { //--- if (!train_nn) TrainNetwork(); //Train the network only once train_nn = true; vector x1, x2; x1.CopyRates(symbol_x,PERIOD_CURRENT,copy_rates_x,0,1); //only the current candle x2.CopyRates(symbol_x2,PERIOD_CURRENT,copy_rates_x,0,1); //only the current candle vector inputs = {x1[0], x2[0]}; //current values of x1 and x2 instruments | Apple & Tesla matrix OUT = nn.ForwardPass(inputs); //Predicted Nasdaq value double pred = OUT[0][0]; Comment("pred ",OUT); }
现在,我们的神经网络就可以做出预测。 我们尝试在交易活动中使用它。 为此,我们将创建一个策略。
交易逻辑
交易逻辑很简单:如果神经网络预测的价格高于当前价格,则开仓做多交易,并以预测价格乘以某个输入值作为止盈,反之亦然。 在每笔交易中,止盈点数值乘以某个输入值作为止损放置。 以下在 MetaEditor 中的样子。
stops_level = (int)SymbolInfoInteger(Symbol(),SYMBOL_TRADE_STOPS_LEVEL); Lots = SymbolInfoDouble(Symbol(),SYMBOL_VOLUME_MIN); spread = (double)SymbolInfoInteger(Symbol(), SYMBOL_SPREAD); MqlTick ticks; SymbolInfoTick(Symbol(), ticks); if (MathAbs(pred - ticks.ask) + spread > stops_level) { if (pred > ticks.ask && !PosExist(POSITION_TYPE_BUY)) { target_gap = pred - ticks.bid; m_trade.Buy(Lots, Symbol(), ticks.ask, ticks.bid - ((target_gap*stop_loss) * Point()) , ticks.bid + ((target_gap*take_profit) * Point()),"Self Train NN | Buy"); } if (pred < ticks.bid && !PosExist(POSITION_TYPE_SELL)) { target_gap = ticks.ask - pred; m_trade.Sell(Lots, Symbol(), ticks.bid, ticks.ask + ((target_gap*stop_loss) * Point()), ticks.ask - ((target_gap*take_profit) * Point()), "Self Train NN | Sell"); } }
这就是我们的逻辑。 我们看看 EA 在 MT5 上的表现。
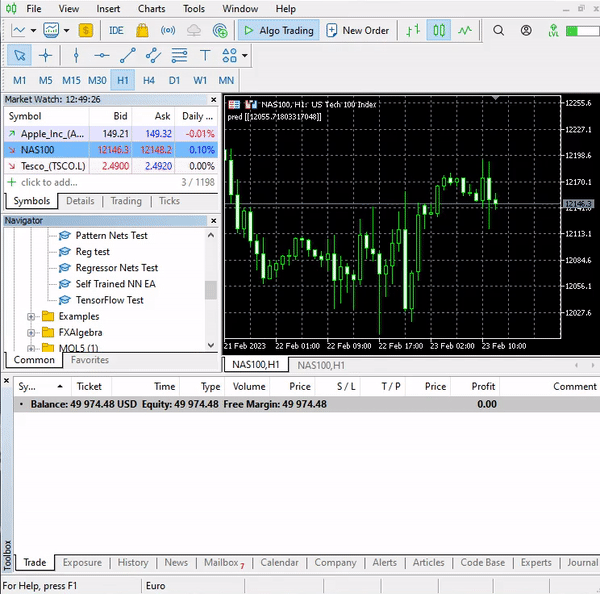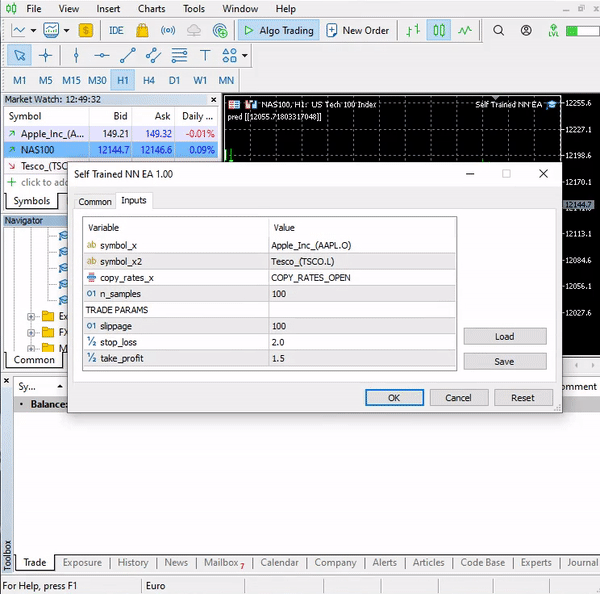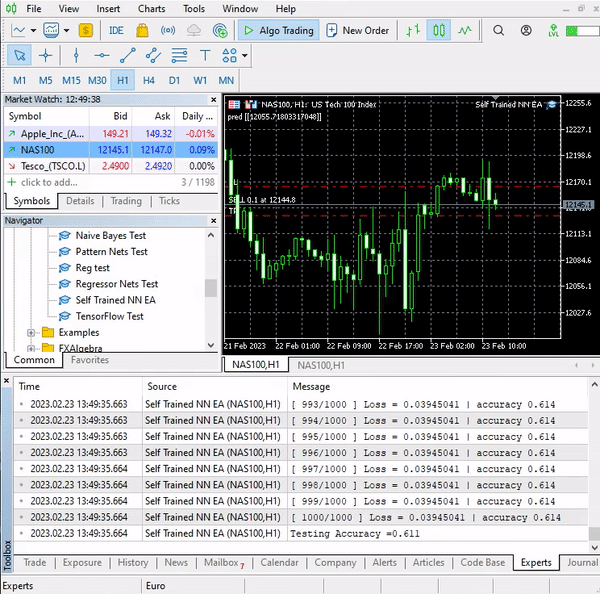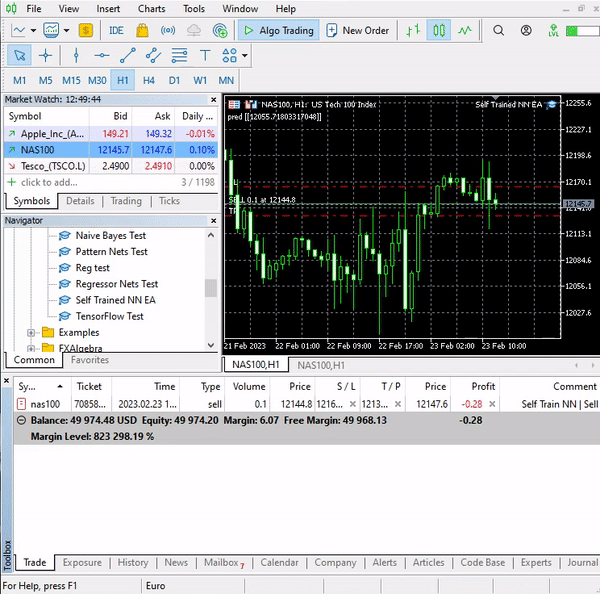
这个简单的智能系统现在可以自己进行交易。 我们目前无法评估其表现;这还为时过早。 我们跳到策略测试器。
策略测试器的结果
从策略测试器运行机器学习算法总是存在挑战,因为您必须确保算法平稳快速地运行,同时确保您最终能够获利。
我在 4 小时图表上运行了一个测试,从 2023.01.01 到 2023.02.23,基于真实跳价,我基于最近的跳价进行了测试,因为我怀疑它的质量比基于年度和月度要好得多。
由于我将训练模型的函数设置为在测试生命周期的第一个跳价时运行,因此训练和测试模型的过程是立即完成的。 我们先看看模型的表现如何,然后才能看到图表和策略测试器提供的所有内容。
CS 0 15:50:47.676 Tester NAS100,H4 (Pepperstone-Demo): generating based on real ticks CS 0 15:50:47.677 Tester NAS100,H4: testing of Experts\Advisors\Self Trained NN EA.ex5 from 2023.01.01 00:00 to 2023.02.23 00:00 started with inputs: CS 0 15:50:47.677 Tester symbol_x=Apple_Inc_(AAPL.O) CS 0 15:50:47.677 Tester symbol_x2=Tesco_(TSCO.L) CS 0 15:50:47.677 Tester copy_rates_x=1 CS 0 15:50:47.677 Tester n_samples=200 CS 0 15:50:47.677 Tester = CS 0 15:50:47.677 Tester slippage=100 CS 0 15:50:47.677 Tester stop_loss=2.0 CS 0 15:50:47.677 Tester take_profit=2.0 CS 3 15:50:49.209 Ticks NAS100 : 2023.02.21 23:59 - real ticks absent for 2 minutes out of 1379 total minute bars within a day CS 0 15:50:51.466 History Tesco_(TSCO.L),H4: history begins from 2022.01.04 08:00 CS 0 15:50:51.467 Self Trained NN EA (NAS100,H4) 2023.01.03 01:00:00 [ 1/1000 ] Loss = 0.14025037 | accuracy -1.524 CS 0 15:50:51.468 Self Trained NN EA (NAS100,H4) 2023.01.03 01:00:00 [ 2/1000 ] Loss = 0.05244676 | accuracy 0.056 CS 0 15:50:51.468 Self Trained NN EA (NAS100,H4) 2023.01.03 01:00:00 [ 3/1000 ] Loss = 0.04488896 | accuracy 0.192 CS 0 15:50:51.468 Self Trained NN EA (NAS100,H4) 2023.01.03 01:00:00 [ 4/1000 ] Loss = 0.04114715 | accuracy 0.259 CS 0 15:50:51.468 Self Trained NN EA (NAS100,H4) 2023.01.03 01:00:00 [ 5/1000 ] Loss = 0.03877407 | accuracy 0.302 CS 0 15:50:51.469 Self Trained NN EA (NAS100,H4) 2023.01.03 01:00:00 [ 6/1000 ] Loss = 0.03725228 | accuracy 0.329 CS 0 15:50:51.469 Self Trained NN EA (NAS100,H4) 2023.01.03 01:00:00 [ 7/1000 ] Loss = 0.03627591 | accuracy 0.347 CS 0 15:50:51.469 Self Trained NN EA (NAS100,H4) 2023.01.03 01:00:00 [ 8/1000 ] Loss = 0.03564933 | accuracy 0.358 CS 0 15:50:51.470 Self Trained NN EA (NAS100,H4) 2023.01.03 01:00:00 [ 9/1000 ] Loss = 0.03524708 | accuracy 0.366 CS 0 15:50:51.470 Self Trained NN EA (NAS100,H4) 2023.01.03 01:00:00 [ 10/1000 ] Loss = 0.03498872 | accuracy 0.370 CS 0 15:50:51.662 Self Trained NN EA (NAS100,H4) 2023.01.03 01:00:00 [ 1000/1000 ] Loss = 0.03452066 | accuracy 0.379 CS 0 15:50:51.662 Self Trained NN EA (NAS100,H4) 2023.01.03 01:00:00 Testing Accuracy =0.717
训练准确率为 37.9%,但测试准确率为 71.7%。 什么?!
我确定到底出了什么问题,但我确实怀疑训练质量。 始终确保您的训练和测试数据具有不错的质量,数据中的每个漏洞都可能导致不同的模型。 由于我们正在策略测试器上寻找良好的结果,我们必须确保回测结果来自我们投入大量精力构建的优良模型。
在策略测试结束时,结果并不令人惊讶,该 EA 的大部分开仓交易,以 78.27% 的亏损告终。
由于我们尚未针对止损和止盈目标进行优化,因此我认为针对这些值和其它参数进行优化是个好主意。
我运行了一个简短的优化,并挑选出以下值。 copy_rates_x: COPY_RATES_LOW, n_samples: 2950, Slippage: 1, Stop loss: 7.4, Take profit: 5.0.
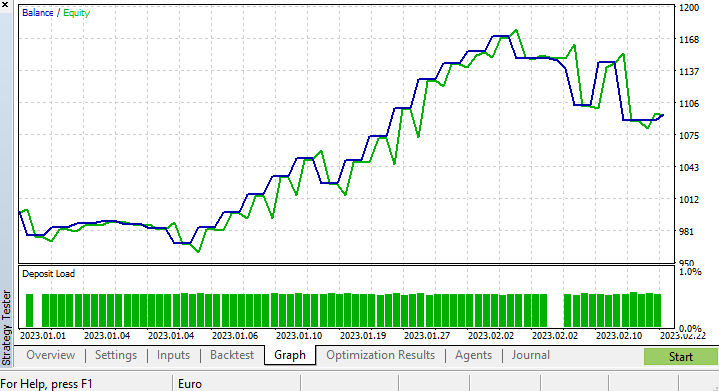
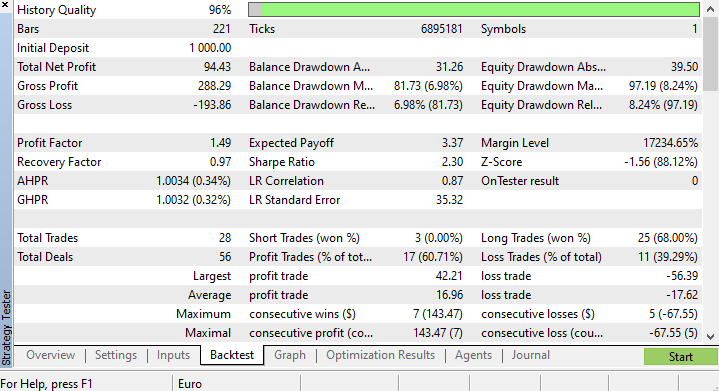
这一次,该模型在策略测试器开始时给出了 61.5% 的训练准确率,,和 63.5% 的测试准确率。 似乎很合理。
CS 0 17:11:52.100 Self Trained NN EA (NAS100,H4) 2023.01.03 01:00:00 [ 1000/1000 ] Loss = 0.05890808 | accuracy 0.615 CS 0 17:11:52.101 Self Trained NN EA (NAS100,H4) 2023.01.03 01:00:00 Testing Accuracy =0.635
最后的思考
增量规则适用于单层回归型神经网络,请记住这一点。 尽管使用了单层神经网络,但我们已经看到了当事情进展不顺利时如何构建和改进它。 单层神经网络只是线性回归模型的组合,作为一个团队一起工作来解决给定的问题。 例如:
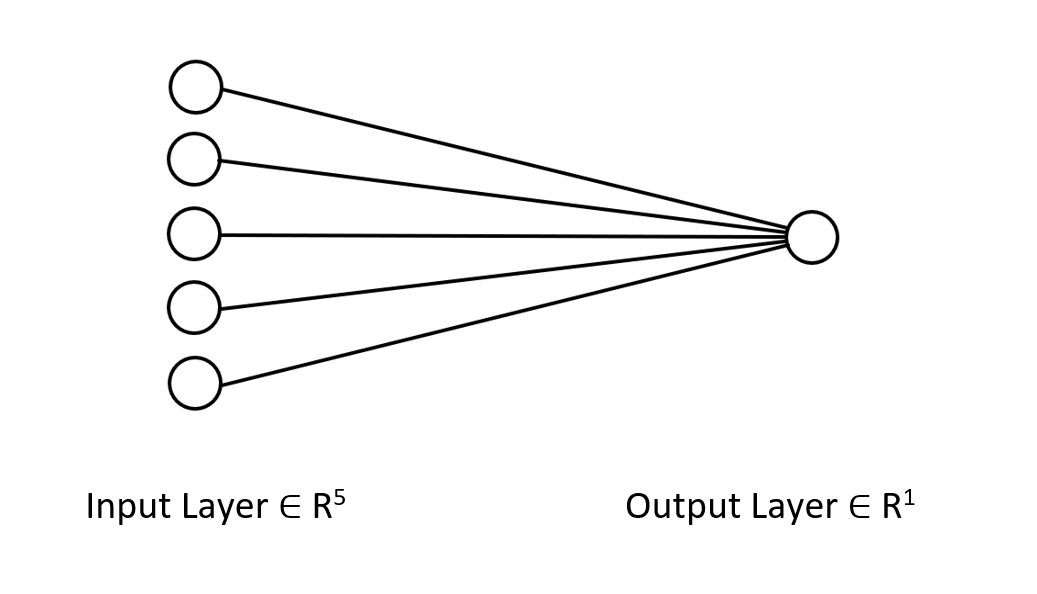
您可以将其视为处理同一问题的 5 个线性回归模型。 值得一提的是,这个神经网络无法理解变量中的复杂形态,所以如果不能理解,不要感到惊讶。 如前所述,增量规则是通用反向传播算法的构建模块,该算法用于深度学习中更复杂的神经网络。
我之所以构建神经网络,同时让自己受到错误的影响,是为了解释一点,以便您明白,即使神经网络能够学习形态,您也需要注意小细节,并把很多事情做好才能让它工作。
此致敬意。
在此存储库 https://github.com/MegaJoctan/MALE5 上跟踪该函数库和许多其它 ML 模型的开发进度。
附件表格:
| 文件 | 内容 & 用法 |
|---|---|
| metrics.mqh | 包含测量神经网络模型准确性的函数。 |
| preprocessing.mqh | 包含缩放和准备神经网络模型数据的函数 |
| matrix_utils.mqh | 矩阵操控的附加函数 |
| selftrain NN.mqh | 包含自训练神经网络的主包含文件 |
| Self Train NN EA.mq5 | 测试自训练神经网络的 EA |
参考文章:
免责声明:本文仅用于教学目的。 交易是一场有风险的游戏;您应该明白与之相关的风险。 对于因使用本文中讨论的类方法,而可能造成的任何损失或损害,作者概不负责。 资金损失风险必须在您能承受的范围之内。
本文由MetaQuotes Ltd译自英文
原文地址: https://www.mql5.com/en/articles/12209
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
一个很好的演示,展示了自我培训(调整) ML EA 的可能性。
目前仍处于 MQL ML 的早期阶段。希望随着时间的推移,越来越多的人会使用 MALE5。期待它的成熟。
如何保存和加载网络?