MetaTrader 5 / 交易系统
English Русский Español Deutsch 日本語 Português 한국어 Français Italiano Türkçe
preview
数据科学与机器学习 — 神经网络（第 01 部分）：前馈神经网络解密

数据科学与机器学习 — 神经网络（第 01 部分）：前馈神经网络解密

MetaTrader 5 — 交易系统 |
1 612 6
Omega J Msigwa
Omega J Msigwa

“...厌倦了知道太多，而理解太少。”

― Jan Karon, Home to Holly Springs

概述

神经网络听起来像是个稀奇的新事物，似乎是构建圣杯交易系统的一种前进方向，许多交易者对由神经网络构成的程序感到震惊，因为它们似乎擅长预测市场走势，基本上它们擅长接手的任何任务。 我也相信，在基于未经训练/从未见过的数据进行预测或分类方面，它们拥有巨大的潜力。

尽管它们可能很优秀，但它们需要由知识渊博的专业人士来构建，有时还需要优化，从而不仅确保多层感知器处于正确的架构中，而且所针对的问题类型适合神经网络来解决，而不仅仅是线性或逻辑回归模型的类型，亦或任何其它机器学习技术。

神经网络是一个很广泛的主论题，机器学习也是如此，一般来说，这就是为什么我决定为神经网络添加一个子标题，因为我将在本系列的另一个子标题中继续讲述机器学习的其它层面。

在本文中，我们将了解神经网络的基础知识，并回答一些我认为对于机器学习爱好者来说很重要的基本问题，以便他们掌握这个论题。

神经网络 101 篇文章


什么是人工神经网络？

人工神经网络（ANN），通常称为神经网络，是受构成动物大脑的生物神经网络启发的计算系统。


多层感知器对比深度神经网络

在讨论神经网络时，您经常听到人们提到一个术语多层感知器（MLP）。它只不过是最常见的神经网络类型。 MLP 是由输入层、隐藏层、和输出层组成的网络。 由于它们的简单性，故只需较短的时间来训练它们学习数据中的表意，并产生输出。

应用:

MLP 常用来应付不可线性分离的数据，例如回归分析。 由于它们的简单性，它们最适合复杂的分类任务和预测建模。 它们已被用于机器翻译、天气预报、欺诈检测、股票市场预测、信用评级预测，以及您能想到的许多其它方面。

另一方面，深度神经网络具有共同的结构，但唯一的区别是它们包含太多的隐藏层。 如果您的网络拥有三（3）个以上的隐藏层，就可将其视为深度神经网络。 由于它们的复杂性，它们需要经历很长周期基于输入数据来训练网络，此外，它们还需要具有专用处理单元的强大计算机，例如张量处理单元（TPU）和神经处理单元（NPU）。

应用:

DNN 由于其深层而成为强大的算法，因此它们通常用于处理复杂的计算任务，计算机视觉就是这些任务之一。

区别表:

MLP DNN
  少量隐藏层 大量隐藏层
  训练周期短 更长训练时间 
  允许 GPU 的设备就足够了 允许 TPU 的设备就足够了

现在，我们看看神经网络的类型。

神经网络有许多类型，但大致分为三（3）个主要类别;

  1. 前馈神经网络
  2. 卷积神经网络
  3. 递归神经网络

01: 前馈神经网络

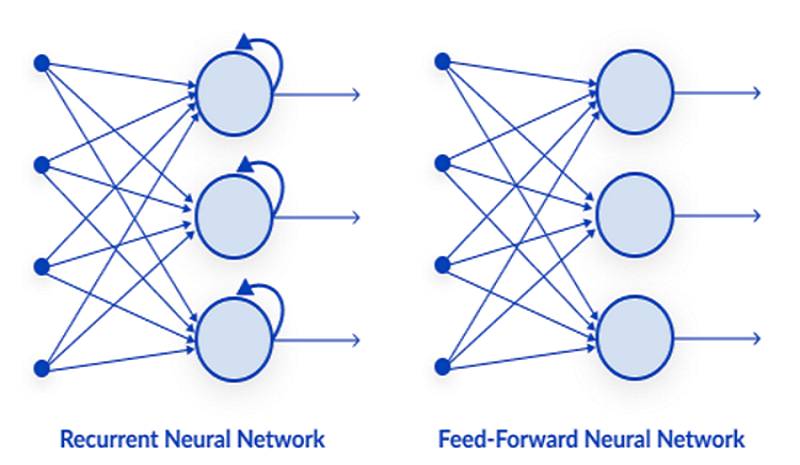
这是最简单的神经网络类型之一。 在前馈神经网络中，数据通过不同的输入节点，直至到达输出节点。 对比反向传播，此处的数据只往一个方向移动。

简单来说，反向传播在神经网络中执行与前馈相同的过程，其中数据从输入层传递到输出层，只是在反向传播中网络输出到达输出层后，它可以看到类的真实数值，并将其与它预测的值进行比较，模型查看它所做出的预测错误或正确的程度，如果预测错误，它会将数据向反馈回网络，并更新其参数，如此下次就可正确预测。 这是一种自学类型的算法。

02: 递归神经网络

递归神经网络是一种人工神经网络，其中特定层的输出被保存，并反馈到输入层。 这有助于提升神经层的预测。

常用递归神经网络解决的相关问题 

  • 时序数据
  • 文本数据
  • 音频数据

文本数据中最常见的用途是推荐 AI 应答的下一个单词，例如：How + are + you +?

递归网络对比前馈网络


03: 卷积神经网络 (CNN)

CNN 在深度学习社区中风靡一时。 它们在图像和视频处理项目中占据主导地位。 

例如，图像检测和分类 AI 均由卷积神经网络组成。

卷积神经网络示意图

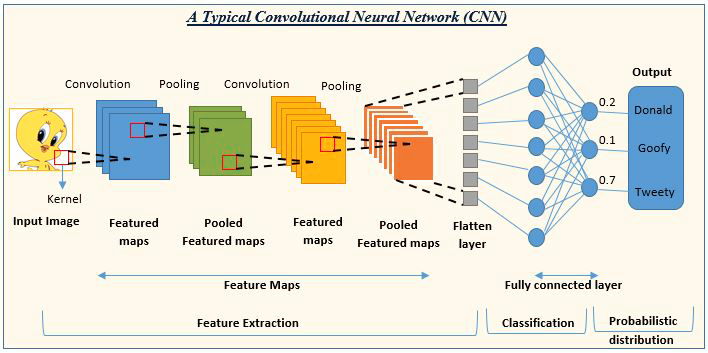
图像来源: analyticsvidhya.com

现在我们已看到神经网络的类型，我们将重点放到本文的主要主题前馈神经网络。


前馈神经网络

与其它更复杂的神经网络类型不同，它没有反向传播，这意味着数据在这种类型的神经网络中仅沿一个方向流动。 前馈神经网络可以有一个隐藏层，亦或有若干个隐藏层。

我们看看是什么驱动这个网络跳博

前馈神经网络

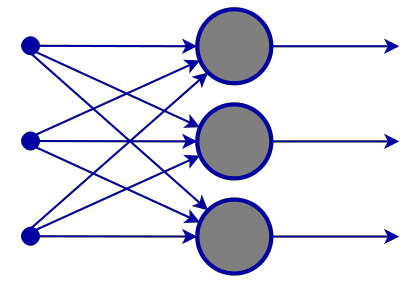
输入层

从神经网络的图像来看，它有一个输入层，但在内部很深，输入层只是一个表象。 在输入图层中不会执行任何计算。

隐藏层

隐藏层是网络中完成大部分操作的所在。

为了澄清这件事情，我们剖析第二个隐藏层节点。

第二个节点剖析

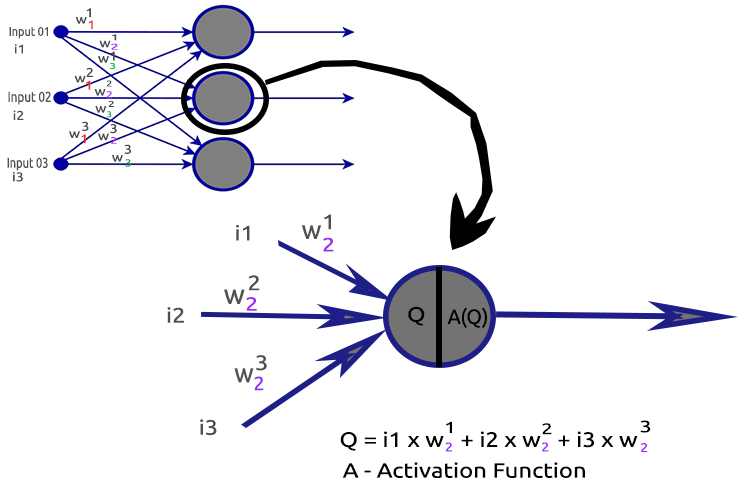
涉及的流程：

  1. 查找输入的点积及其各自的权重
  2. 将获得的点积添加到乖离率之中
  3. 第二个过程的结果传递给激活函数


什么是乖离率？

乖离率允许您围绕线性回归上下偏移，从而令预测线与数据更好地拟合。 这与线性回归线中的截距相同。

您将在 隐藏层中含有单节点的 MLP 是线性回归模型 章节更好地理解此参数的作用。

乖离率的重要性在这个堆栈中得到了很好的解释。


什么是权重？

权重反映的是输入的重要性，它们是您尝试求解的方程系数。 负权重会降低输出值，反之亦然。 当神经网络基于训练数据集上训练时，它会采用一组权重进行初始化。 这些权重随后会在训练期间优化，并筛选出最佳权重值。


什么是激活函数？

激活函数只不过是一个数学函数，它接受输入并产生输出。

激活函数的种类

有许多种激活函数及其变体，但以下是最常用的函数：

  1. Relu
  2. Sigmoid
  3. TanH
  4. Softmax

知晓哪个激活函数适用在哪里非常重要，我多次在网上看到有文章建议在无关紧要的地方使用激活函数，我已无语了。 我们来详阅这些。


01: RELU

RELU 代表整流线性激活函数。

这是神经网络中最常用的激活函数。 它是最简单的，易于编码，易于解释输出，这便是它如此受热捧的原因。 如果输入为正数，该函数将直接把输入值输出；否则，它输出零。

此为其逻辑

如果 x < 0 : 返回 0

否则 返回 x

此函数用于解决回归问题更佳

relu 示意图

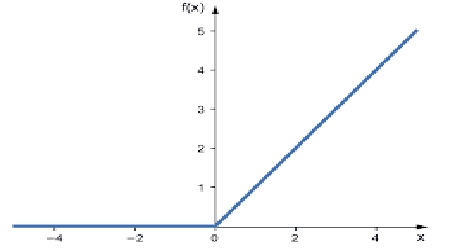
其输出范围从零到正无穷大。

此为 MQL5 代码:

double CNeuralNets::Relu(double z)
 {
   if (z < 0) return(0);
   else return(z);
 }

RELU 解决了 sigmoid 和 TanH 所遭遇的梯度消失问题（我们将在关于反向传播的文章中看到这是什么）。


02: Sigmoid

听起来耳熟吧？ 可还记得逻辑回归。

其公式如下。

sigmoid 激活函数

此函数用于分类问题更佳，尤其是，针对一个或仅两个类进行分类时。

其输出范围从零到一（概率项）。

sigmoid 图形

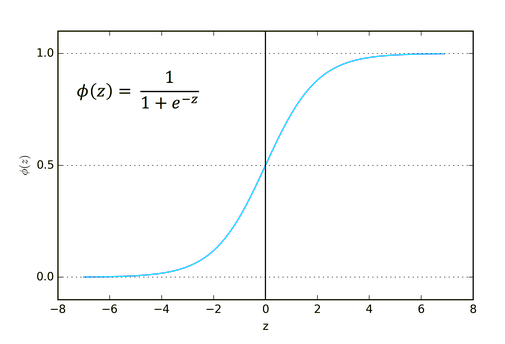
举例，您的网络在输出端有两个节点。 第一个节点针对猫，另一个节点针对狗。 您可以选择输出结果，如果第一个节点的输出大于 0.5，则表示它是一只猫，而相反则对应是一条狗。

此为 MQL5 代码:

double CNeuralNets::Sigmoid(double z)
 { 
   return(1.0/(1.0+MathPow(e,-z)));
 }

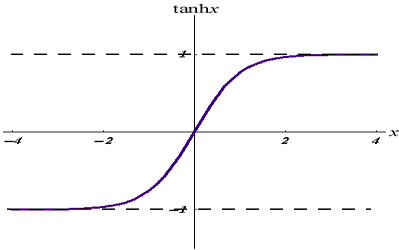
03: TanH

双曲正切函数。

给出它的公式:

tanh 公式

其图形如下所示：

tanh 激活函数示意图

该激活函数类似于 sigmoid，但更好。

其输出范围从 -1 到 1。

该函数用于多类分类神经网络更佳

其 MQL5 代码给出如下:

double CNeuralNets::tanh(double z)
 {
   return((MathPow(e,z) - MathPow(e,-z))/(MathPow(e,z) + MathPow(e,-z)));
 }

04: SoftMax

曾经有人问过，为什么没有 SoftMax 函数的图形。 与其它激活函数不同，SoftMax 不用在隐藏层，而仅用在输出层，且仅当您要将多类神经网络的输出转换为概率项时才应使用。

SoftMax 预测多项式概率分布。

softmax 激活函数公式

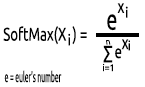
例如，回归神经网络的输出是 [1,3,2]，如果我们针对该输出应用 SoftMax 函数，则现在输出变为 [0.09003, 0.665240, 0.244728]。

该函数的输出范围为 0 到 1。

其 MQL5 代码则是:

void CNeuralNets::SoftMax(double &Nodes[])
 {
   double TempArr[];
   ArrayCopy(TempArr,Nodes);  ArrayFree(Nodes);
   
   double proba = 0, sum=0;
    
   for (int j=0; j<ArraySize(TempArr); j++)    sum += MathPow(e,TempArr[j]);
    
    for (int i=0; i<ArraySize(TempArr); i++)
      {
         proba = MathPow(e,TempArr[i])/sum;
         Nodes[i] = proba;
     } 
     
    ArrayFree(TempArr);
 }

现在，我们理解了隐藏层的单个神经元是由什么组成的，如此我们就可为它编写代码了。

void CNeuralNets::Neuron(int HLnodes,
                        double bias,
                        double &Weights[],
                        double &Inputs[],
                        double &Outputs[]
                       )
 {
   ArrayResize(Outputs,HLnodes);
   
   for (int i=0, w=0; i<HLnodes; i++)
    {
      double dot_prod = 0;
      for(int j=0; j<ArraySize(Inputs); j++, w++)
        {
            if (m_debug) printf("i %d  w %d = input %.2f x weight %.2f",i,w,Inputs[j],Weights[w]);
            dot_prod += Inputs[j]*Weights[w];
        }
        
      Outputs[i] = ActivationFx(dot_prod+bias);
    }     
 }

在 ActivationFx() 内部，我们可以在调用 NeuralNets 构造函数时选择哪个激活函数。

double CNeuralNets::ActivationFx(double Q)
 {
   switch(A_fx)
     {
      case  SIGMOID:
        return(Sigmoid(Q));
        break;
      case TANH:
         return(tanh(Q));
         break;
      case RELU:
         return(Relu(Q));
         break;
      default:
         Print("Unknown Activation Function");
        break;
     }
   return(0);
 }

代码的进一步解释：

函数 Neuron() 不仅仅是隐藏层内的单个节点，而且隐藏层的所有操作都会在该函数内执行。 所有隐藏层中的节点都具有与输入节点相同的大小，一直到最终输出节点，我之所以选择这种结构，是因为我即将在随机生成的数据集上应用此神经网络进行分类。

下面的函数 FeedForwardMLP() 是一个 NxN 结构，这意味着如果您有 3 个输入节点，且您选择 3 个隐藏层，那么您将在每个隐藏层上有 3 个隐藏节点查看图像。

nxn 神经网络

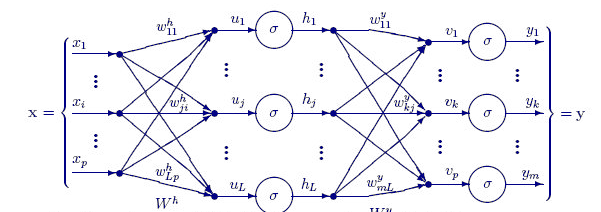
此处是 FeedForwardMLP() 函数：

void   CNeuralNets::FeedForwardMLP(int HiddenLayers,
           double &MLPInputs[],
           double &MLPWeights[],
           double &bias[],
           double &MLPOutput[])
 {
    
    double L_weights[], L_inputs[], L_Out[];
    
    ArrayCopy(L_inputs,MLPInputs);
    
    int HLnodes = ArraySize(MLPInputs);
    int no_weights = HLnodes*ArraySize(L_inputs);
    int weight_start = 0;
    
    for (int i=0; i<HiddenLayers; i++)
      {
        
        if (m_debug) printf("<< Hidden Layer %d >>",i+1);
        ArrayCopy(L_weights,MLPWeights,0,weight_start,no_weights);

        Neuron(HLnodes,bias[i],L_weights,L_inputs,L_Out);
        
        ArrayCopy(L_inputs,L_Out);
        ArrayFree(L_Out);
        
        ArrayFree(L_weights);
        
        weight_start += no_weights;
      }
     
    if (use_softmax)  SoftMax(L_inputs);
    ArrayCopy(MLPOutput,L_inputs);
    if (m_debug)
      {
       Print("\nFinal MLP output(s)");
       ArrayPrint(MLPOutput,5);
      }
 }

在神经网络中查找点积的操作可以通过矩阵运算来处理，但为了在第一篇文章中保持清晰和易于理解，我选择了循环方法，下次我们再运用矩阵乘法。


现在您已经看到了我为了构建函数库的缘故而默认选择的体系结构。 而这现在提出了一个关于神经网络架构的问题。

如果您去谷歌搜索神经网络的图像，您会遭受成千上万张具有不同神经网络结构的图像轰炸，例如：

神经网络架构


一个价值百万美元的问题是，什么是最好的神经网络架构？

“没有人像知道所有答案的人那样犯错”——托马斯·默顿（Thomas Merton）。

我们来分解一下，理解什么是必要的，以及哪些是不必要的。

输入层

构成该层的输入数量应等于特征数量（数据集中的列）。


输出层

判定大小（神经元数量）由分类神经网络数据集中的类数量决定，对于回归类型的问题，神经元的数量由所选模型配置确定。 对于回归器，一个输出层通常绰绰有余。

隐藏层

如果您的问题不太复杂，一、两个隐藏层就足够了，因为事实上两个隐藏层足以解决绝大多数问题。 但是，每个隐藏层中需要多少个节点？ 我不确定这一点，但我认为这取决于性能，您作为开发人员要探索和尝试不同的节点，去看看什么参数最适合特定类型的问题，在您开始玩这个之前，您应该掌握我们之前讨论的其它类型的神经网络。

在 stats.stackexchange.com 上有一个关于这个主题的极佳话题，链接在此。

我认为拥有与所有隐藏层的输入层相同数量的节点是前馈神经网络的理想选择，而这也是我在大多数时候选用的配置。

具有单个节点和单个隐藏层的 MLP 是线性模型。

如果您注意到神经网络隐藏层的单个节点内完成的操作，您就会注意到这一点：

Q = wi * Ii + b

同时，线性回归方程为;

Y = mi * xi + c

注意到有何相似之处吗？ 它们在理论上是一回事，此操作是线性回归器，这把我们带回隐藏层乖离率的重要性。 乖离率是线性模型的一个常数，其作用是增加模型的灵活性，从而拟合给定数据集，没有它，所有模型都将在 x 轴和 y 轴的零点（0）间传递。

无截距线性回归

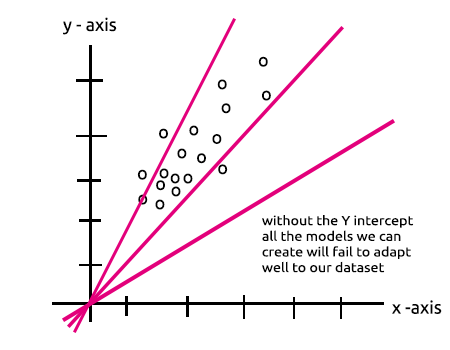
当训练神经网络时，权重和乖离率将被更新。 对于我们的模型，产生较少误差的参数将被保留，并记忆在测试数据集之中。

现在，为明确这一点，我来构建一个 MLP 为两个类分类。 在此之前，我先生成一个带有标记样本的随机数据集，我们将通过神经网络查看这些样本。 下面的函数制造随机数据集，第二个样本乘以 5，第一个样本乘以 2，只是为了得到不同尺度的数据。

void MakeBlobs(int size=10) 
 { 
     ArrayResize(data_blobs,size);
     for (int i=0; i<size; i++) 
       {   
         data_blobs[i].sample_1 = (i+1)*(2); 
         
         data_blobs[i].sample_2 = (i+1)*(5); 
         
         data_blobs[i].class_ = (int)round(nn.MathRandom(0,1));
       }  
 }

当我打印数据集时，此处是输出：

QK      0       18:27:57.298    TestScript (EURUSD,M1)  CNeural Nets Initialized activation = SIGMOID UseSoftMax = No
IR      0       18:27:57.298    TestScript (EURUSD,M1)      [sample_1] [sample_2] [class_]
LH      0       18:27:57.298    TestScript (EURUSD,M1)  [0]     2.0000     5.0000        0
GG      0       18:27:57.298    TestScript (EURUSD,M1)  [1]     4.0000    10.0000        0
NL      0       18:27:57.298    TestScript (EURUSD,M1)  [2]     6.0000    15.0000        1
HJ      0       18:27:57.298    TestScript (EURUSD,M1)  [3]     8.0000    20.0000        0
HQ      0       18:27:57.298    TestScript (EURUSD,M1)  [4]    10.0000    25.0000        1
OH      0       18:27:57.298    TestScript (EURUSD,M1)  [5]    12.0000    30.0000        1
JF      0       18:27:57.298    TestScript (EURUSD,M1)  [6]    14.0000    35.0000        0
DL      0       18:27:57.298    TestScript (EURUSD,M1)  [7]    16.0000    40.0000        1
QK      0       18:27:57.298    TestScript (EURUSD,M1)  [8]    18.0000    45.0000        0
QQ      0       18:27:57.298    TestScript (EURUSD,M1)  [9]    20.0000    50.0000        0

下一部分是生成随机权重值和乖离率，

     generate_weights(weights,ArraySize(Inputs));
     generate_bias(biases);

这是输出：

RG      0       18:27:57.298    TestScript (EURUSD,M1)  weights
QS      0       18:27:57.298    TestScript (EURUSD,M1)   0.7084 -0.3984  0.6182  0.6655 -0.3276  0.8846  0.5137  0.9371
NL      0       18:27:57.298    TestScript (EURUSD,M1)  biases
DD      0       18:27:57.298    TestScript (EURUSD,M1)  -0.5902  0.7384

现在我们看看脚本的 main 函数中的整个操作：

#include "NeuralNets.mqh";
CNeuralNets *nn;

input int batch_size =10;
input int hidden_layers =2;

data data_blobs[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---     
     nn = new CNeuralNets(SIGMOID);
           
     MakeBlobs(batch_size);
     
     ArrayPrint(data_blobs);
       
     double Inputs[],OutPuts[];
     
     ArrayResize(Inputs,2);     ArrayResize(OutPuts,2);
     
     double weights[], biases[];
     generate_weights(weights,ArraySize(Inputs));
     generate_bias(biases);
     
     Print("weights"); ArrayPrint(weights);
     Print("biases"); ArrayPrint(biases);
     
     for (int i=0; i<batch_size; i++)
       {
         Print("Dataset Iteration ",i);
         Inputs[0] = data_blobs[i].sample_1; Inputs[1]= data_blobs[i].sample_2;    
         nn.FeedForwardMLP(hidden_layers,Inputs,weights,biases,OutPuts);
       }
       
     delete(nn);    
  }

注意事项：

  • 乖离率的数量与隐藏层的数量相同。
  • 权重总数 = 输入数量的平方乘以隐藏层数量。 如此这般是因为我们的网络拥有与网络输入层/前一层相同数量的节点（从输入到输出的所有层都有相同数量的节点）。
  • 将遵循相同的原则，假设您有 3 个输入节点，则所有隐藏层都将有 3 个节点，除了最后一层，于此我们将要看到该如何处理它。

查看随机生成的数据集，您会注意到数据集中有两个输入特征 / 列，我选择了 2 个隐藏层，以下是我们的日志中关于我们的模型将如何执行计算的简述（在代码中将调试模式设置为 false 来防止这些日志输出）。

NL      0       18:27:57.298    TestScript (EURUSD,M1)  Dataset Iteration 0
EJ      0       18:27:57.298    TestScript (EURUSD,M1)  << Hidden Layer 1 >>
GO      0       18:27:57.298    TestScript (EURUSD,M1)  
NS      0       18:27:57.298    TestScript (EURUSD,M1)   HLNode 1
EI      0       18:27:57.298    TestScript (EURUSD,M1)  i 0  w 0 = input 2.00000 x weight 0.70837
FQ      0       18:27:57.298    TestScript (EURUSD,M1)  i 0  w 1 = input 5.00000 x weight -0.39838
QP      0       18:27:57.298    TestScript (EURUSD,M1)  dot_Product -0.57513 + bias -0.590 = -1.16534
RH      0       18:27:57.298    TestScript (EURUSD,M1)  Activation function Output =0.23770
CQ      0       18:27:57.298    TestScript (EURUSD,M1)  
OE      0       18:27:57.298    TestScript (EURUSD,M1)   HLNode 2
CO      0       18:27:57.298    TestScript (EURUSD,M1)  i 1  w 2 = input 2.00000 x weight 0.61823
FI      0       18:27:57.298    TestScript (EURUSD,M1)  i 1  w 3 = input 5.00000 x weight 0.66553
PN      0       18:27:57.298    TestScript (EURUSD,M1)  dot_Product 4.56409 + bias -0.590 = 3.97388
GM      0       18:27:57.298    TestScript (EURUSD,M1)  Activation function Output =0.98155
DI      0       18:27:57.298    TestScript (EURUSD,M1)  << Hidden Layer 2 >>
GL      0       18:27:57.298    TestScript (EURUSD,M1)  
NF      0       18:27:57.298    TestScript (EURUSD,M1)   HLNode 1
FH      0       18:27:57.298    TestScript (EURUSD,M1)  i 0  w 0 = input 0.23770 x weight -0.32764
ID      0       18:27:57.298    TestScript (EURUSD,M1)  i 0  w 1 = input 0.98155 x weight 0.88464
QO      0       18:27:57.298    TestScript (EURUSD,M1)  dot_Product 0.79044 + bias 0.738 = 1.52884
RK      0       18:27:57.298    TestScript (EURUSD,M1)  Activation function Output =0.82184
QG      0       18:27:57.298    TestScript (EURUSD,M1)  
IH      0       18:27:57.298    TestScript (EURUSD,M1)   HLNode 2
DQ      0       18:27:57.298    TestScript (EURUSD,M1)  i 1  w 2 = input 0.23770 x weight 0.51367
CJ      0       18:27:57.298    TestScript (EURUSD,M1)  i 1  w 3 = input 0.98155 x weight 0.93713
QJ      0       18:27:57.298    TestScript (EURUSD,M1)  dot_Product 1.04194 + bias 0.738 = 1.78034
JP      0       18:27:57.298    TestScript (EURUSD,M1)  Activation function Output =0.85574
EI      0       18:27:57.298    TestScript (EURUSD,M1)  
GS      0       18:27:57.298    TestScript (EURUSD,M1)  Final MLP output(s)
OF      0       18:27:57.298    TestScript (EURUSD,M1)  0.82184 0.85574
CN      0       18:27:57.298    TestScript (EURUSD,M1)  Dataset Iteration 1
KH      0       18:27:57.298    TestScript (EURUSD,M1)  << Hidden Layer 1 >>
EM      0       18:27:57.298    TestScript (EURUSD,M1)  
DQ      0       18:27:57.298    TestScript (EURUSD,M1)   HLNode 1
QH      0       18:27:57.298    TestScript (EURUSD,M1)  i 0  w 0 = input 4.00000 x weight 0.70837
PD      0       18:27:57.298    TestScript (EURUSD,M1)  i 0  w 1 = input 10.00000 x weight -0.39838
HR      0       18:27:57.298    TestScript (EURUSD,M1)  dot_Product -1.15027 + bias -0.590 = -1.74048
DJ      0       18:27:57.298    TestScript (EURUSD,M1)  Activation function Output =0.14925
OP      0       18:27:57.298    TestScript (EURUSD,M1)  
CK      0       18:27:57.298    TestScript (EURUSD,M1)   HLNode 2
MN      0       18:27:57.298    TestScript (EURUSD,M1)  i 1  w 2 = input 4.00000 x weight 0.61823
NH      0       18:27:57.298    TestScript (EURUSD,M1)  i 1  w 3 = input 10.00000 x weight 0.66553
HI      0       18:27:57.298    TestScript (EURUSD,M1)  dot_Product 9.12817 + bias -0.590 = 8.53796
FO      0       18:27:57.298    TestScript (EURUSD,M1)  Activation function Output =0.99980
RG      0       18:27:57.298    TestScript (EURUSD,M1)  << Hidden Layer 2 >>
IR      0       18:27:57.298    TestScript (EURUSD,M1)  
PD      0       18:27:57.298    TestScript (EURUSD,M1)   HLNode 1
RN      0       18:27:57.298    TestScript (EURUSD,M1)  i 0  w 0 = input 0.14925 x weight -0.32764
HF      0       18:27:57.298    TestScript (EURUSD,M1)  i 0  w 1 = input 0.99980 x weight 0.88464
EM      0       18:27:57.298    TestScript (EURUSD,M1)  dot_Product 0.83557 + bias 0.738 = 1.57397
EL      0       18:27:57.298    TestScript (EURUSD,M1)  Activation function Output =0.82835
KE      0       18:27:57.298    TestScript (EURUSD,M1)  
GN      0       18:27:57.298    TestScript (EURUSD,M1)   HLNode 2
LS      0       18:27:57.298    TestScript (EURUSD,M1)  i 1  w 2 = input 0.14925 x weight 0.51367
FL      0       18:27:57.298    TestScript (EURUSD,M1)  i 1  w 3 = input 0.99980 x weight 0.93713
KH      0       18:27:57.298    TestScript (EURUSD,M1)  dot_Product 1.01362 + bias 0.738 = 1.75202
IR      0       18:27:57.298    TestScript (EURUSD,M1)  Activation function Output =0.85221
OH      0       18:27:57.298    TestScript (EURUSD,M1)  
IM      0       18:27:57.298    TestScript (EURUSD,M1)  Final MLP output(s)
MH      0       18:27:57.298    TestScript (EURUSD,M1)  0.82835 0.85221

现在请注意所有迭代的最终 MLP 输出，您会注意到一个奇怪的行为，即输出趋向齐整的相同数值。 此问题有若干个起因，如在堆栈中讨论的那样，其中一个起因是在输出层中使用了错误的激活函数。 这就是 SoftMax 激活功能发挥作用的地方。

来自我的理解，sigmoid 函数仅在输出层中存在单个节点时才返回概率，它必须对一个类进行分类，在这种情况下，您需要 sigmoid 的输出来告诉您某物是否属于某个类，但在多类中这是另一个不同的故事。 如果我们对最终节点的输出求和，则大多数时候该值超过一（1），所以现在您知道它们不是概率，因为概率不能超过数值 1。

如果我们将 SoftMax 应用于最后一层，则输出就是。

第一次迭代输出 [0.4915  0.5085]，第二次迭代输出 [0.4940   0.5060]

在这种情况下，您可以将输出解释为 [属于类 0 的概率 属于类 1 的概率]。

好的，至少现在我们有概率，我们可以依靠它来解释来自我们网络的有意义的东西。

终考

我们还没有完成前馈神经网络，但至少现在您已经理解了理论和最重要的东西，这有助于您掌握 MQL5 中的神经网络。 设计的前馈神经网络是以分类为目的的神经网络，这意味着合适的激活函数是 sigmoid 和 tanh，具体取决于要在数据集中分类的样本和类数量。 我们无法更改输出层来返回我们想要推演的任何内容，也不是隐藏层中的节点，矩阵的引入会有助于把所有这些操作变成动态，如此我们就可以为任何任务构建一个非常标准的神经网络，这是本系列文章的目标，请保持更多关注。

知晓何时运用神经网络也是一件重要的事情，因为并非所有任务都需要由神经网络解决，如果一项任务可以通过线性回归来解决，那么线性模型也许会更胜于神经网络。 这是要牢记的事情之一。


GitHub 存储库: https://github.com/MegaJoctan/NeuralNetworks-MQL5

延伸阅读 | 书籍 | 参考

文章参考资料：


本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/11275

附加的文件 |
下载ZIP
NeuralNets.zip (13.56 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.

该作者的其他文章

最近评论 | 前往讨论 (6)
Omega J Msigwa
Omega J Msigwa | 12 8月 2022 在 20:28
Guilherme Mendonca #:

...

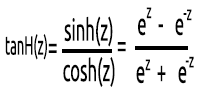
您能解释一下吗？或者举几个例子？

在策略测试仪上进行优化与优化神经网络参数之间的区别在于目标，在策略测试仪上，我们倾向于关注能提供最有利输出或至少是我们想要的交易结果的参数，这并不一定意味着神经网络有一个好的模型，能带来这样的结果。

有些人喜欢将权重和偏差作为基于神经网络系统的输入参数（粗略地说是前馈），但我认为使用策略测试仪进行优化基本上是在寻找最佳结果的随机值（寻找最优 值听起来像是靠运气），而如果我们使用随机梯度下降法进行优化，我们就会朝着每一步预测误差最小的模型前进

Guilherme Mendonca
Guilherme Mendonca | 12 8月 2022 在 20:47
Omega J Msigwa #:

在策略测试仪上进行优化与优化神经网络参数之间的区别在于目标，在策略测试仪上，我们倾向于关注能提供最有利输出或至少是我们想要的交易结果的参数，这并不一定意味着神经网络有一个好的模型，能带来这样的结果。

有些人喜欢将权重和偏差作为基于神经网络系统的输入参数（粗略地说是前馈），但我认为使用策略测试仪进行优化基本上是在寻找最佳结果的随机值（寻找最优 值听起来像是靠运气），而如果我们使用随机梯度下降法进行优化，我们就会朝着每一步预测误差最小的模型前进

感谢您的回复。

我明白你的意思了。

Xiaolei Liu
Xiaolei Liu | 14 8月 2022 在 16:55

为什么要从第一部分开始？

旧文章：

数据科学与机器学习（第 01 部分）：线性回归

https://www.mql5.com/zh/articles/10459

Omega J Msigwa
Omega J Msigwa | 14 8月 2022 在 20:20
Xiaolei Liu #:

为什么要从第一部分开始？

旧文章：

数据科学与机器学习（第 01 部分）：线性回归

https://www.mql5.com/zh/articles/10459

什么意思？

Liliya Yunusova
Liliya Yunusova | 18 8月 2022 在 16:49
Xiaolei Liu #:

为什么要从第一部分开始？

旧文章：

数据科学与机器学习（第 01 部分）：线性回归

https://www.mql5.com/zh/articles/10459

我猜这是神经网络子系列的第一部分。正在等待第二部分...
神经网络变得轻松（第二十三部分）：构建迁移学习工具 神经网络变得轻松（第二十三部分）：构建迁移学习工具
在本系列文章中，我们已经不止一次提到了迁移学习。 然而，都只是提及而已。 在本文中，我建议填补这一空白，并仔细研究迁移学习。
从头开始开发智能交易系统（第 26 部分）：面向未来（I） 从头开始开发智能交易系统（第 26 部分）：面向未来（I）
今天，我们将把我们的订单系统提升到一个新的层次。 但在此之前，我们需要解决少量问题。 我们现有的一些问题，是与在交易日里我们想要如何工作，以及我们做什么事情相关。
DoEasy. 控件 (第 14 部分): 命名图形元素的新算法。 继续操控 TabControl WinForms 对象 DoEasy. 控件 (第 14 部分): 命名图形元素的新算法。 继续操控 TabControl WinForms 对象
在本文中，我将创建一个新算法来为构建自定义图形的所有图形元素命名，并继续开发 TabControl WinForms 对象。
学习如何基于强力指数（Force Index）设计交易系统 学习如何基于强力指数（Force Index）设计交易系统
欢迎阅读我们系列中的新篇章，有关如何基于最流行的技术指标设计交易系统。 在本文中，我们将学习一个新的技术指标，以及如何运用强力指数（Force Index）指标创建交易系统。