数据科学与机器学习（第 06 部分）：梯度下降

MetaTrader 5 — 交易 | 4 十一月 2022, 10:04

1 360

Omega J Msigwa

过早优化在编程中是万恶之源

-唐纳德·高德纳（Donald Knuth）

概述

根据维基百科，梯度下降（通常也称为最陡下降）是一种一阶迭代优化算法，用于查找可微函数的局部最小值。这个思路是在当前点的函数梯度（或近似梯度）相反的方向重复步骤，因为这是最陡峭下降的方向。相反，沿梯度方向逐步执行会导致该函数的局部最大值；故该过程称为梯度上升。

基本上，梯度下降是一种优化算法，用于查找函数的最小值：

梯度下降文章 gif

梯度下降是机器学习中非常重要的算法，因为它可以帮助我们找到数据集最佳模型的参数。我先解释一下术语成本函数。

成本函数

有些人称之为亏损函数，它衡量我们的模型预测 x 和 y 值之间关系的计算好坏与否。

有很多衡量标准可判定模型的预如何测，但与所有那些不同的是，成本函数查找整个数据集的平均亏损，成本函数越大，我们的模型在数据集中查找关系就越差。

梯度下降旨在令成本函数最小化，因为具有最低成本函数的模型才是最佳模型。为了您能理解我刚刚解释的内容，我们看看下面的例子。

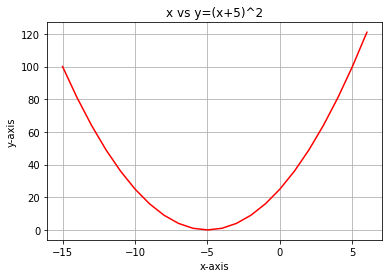
假设我们的成本函数是方程式

如果我们用 python 绘制这个函数的图形，它将是这样的：

pyplot

我们需要针对成本函数执行的第一步是用链式法则来区分成本函数：

方程式 y= (x+5)^2 是一个复合函数（一个函数含于另一个函数内部）。外部函数是 (x+5)^2 内部函数是 (x+5)。为了区分这一点，我们应用链式法则，请参见下图：

链式法则

如果你觉得这很难理解，在文末有一个我手工进行数学演算的视频链接。是的，现在我们刚刚得到的这个函数是梯度。找到方程梯度的过程是最重要的一步，我希望我的数学老师某天告诉我，微分函数的目的是为了得到函数的梯度。

这是第一步也是最重要的一步，下面是第二步。

步骤 02:

我们朝着梯度的负方向移动，在此提出了一个问题，我们应该移动多少？这就是学习曲率发挥作用的地方。

学习曲率

根据定义，这是向最小损失函数移动时，每次迭代的步长，以一个人下山坡为例，他们的步数是学习曲率，步数越小，到达山脚所需的时间就越长，反之亦然。

算法应将学习曲率保持在较小值，但也不要像 0.0001 那样太小了，这样做会增加程序执行时间，因为算法可能需要更长的时间才能达到最小值。与其对比，取较大数字作为学习曲率将导致算法跳过最小值，最终也许会导致您错过最小值目标。

默认学习曲率为 0.01。

我们来执行迭代，以便查看算法的工作原理。

第一次迭代：我们选择任何随机点作为我们算法的起点，我现在选择 0 作为 x 的第一个值，这是更新 x 值的公式

新值梯度下降

经历每次迭代，我们将朝下降低到函数的最小值，故此名曰梯度下降。 现在有意义吗？

现在有意义?

我们详细查看它是如何工作的。 6现在，我们在 2 次迭代中手动计算值，从而令您对正在发生的事情有一个坚实的理解：

第一次迭代:

公式: x1 = x0 - 学习曲率 * ( 2*(x+5) )

x1 = 0 - 0.01 * 0.01 * 2*(0+5)

x1 = -0.01 * 10

x1 = -0.1 (最终)

现在，最终我们通过将新值赋予旧值来更新该数值，并重复该过程，执行尽可能多的迭代，直至函数的最小值：

x0 = x1

第二次迭代:

x1 = -0.1 - 0.01 * 2*(-0.1+5)

x1 = -0.198

然后: x0 = x1

如果我们重复若干次此过程，则做开始的 10 次迭代的输出将是：

RS      0       17:15:16.793    gradient-descent test (EURUSD,M1)       Gradient Descent CostFunction CUSTOM
QQ      0       17:15:16.793    gradient-descent test (EURUSD,M1)       1 x0 = 0.0000000000 x1 = -0.1000000000 CostFunction = 10.0000000000
ES      0       17:15:16.793    gradient-descent test (EURUSD,M1)       2 x0 = -0.1000000000 x1 = -0.1980000000 CostFunction = 9.8000000000
PR      0       17:15:16.793    gradient-descent test (EURUSD,M1)       3 x0 = -0.1980000000 x1 = -0.2940400000 CostFunction = 9.6040000000
LE      0       17:15:16.793    gradient-descent test (EURUSD,M1)       4 x0 = -0.2940400000 x1 = -0.3881592000 CostFunction = 9.4119200000
JD      0       17:15:16.793    gradient-descent test (EURUSD,M1)       5 x0 = -0.3881592000 x1 = -0.4803960160 CostFunction = 9.2236816000
IG      0       17:15:16.793    gradient-descent test (EURUSD,M1)       6 x0 = -0.4803960160 x1 = -0.5707880957 CostFunction = 9.0392079680
IG      0       17:15:16.793    gradient-descent test (EURUSD,M1)       7 x0 = -0.5707880957 x1 = -0.6593723338 CostFunction = 8.8584238086
JF      0       17:15:16.793    gradient-descent test (EURUSD,M1)       8 x0 = -0.6593723338 x1 = -0.7461848871 CostFunction = 8.6812553325
NI      0       17:15:16.793    gradient-descent test (EURUSD,M1)       9 x0 = -0.7461848871 x1 = -0.8312611893 CostFunction = 8.5076302258
CK      0       17:15:16.793    gradient-descent test (EURUSD,M1)       10 x0 = -0.8312611893 x1 = -0.9146359656 CostFunction = 8.3374776213

我们也看看算法非常接近函数最小值时的其它十个数值：

GK      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1052 x0 = -4.9999999970 x1 = -4.9999999971 CostFunction = 0.0000000060
IH      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1053 x0 = -4.9999999971 x1 = -4.9999999971 CostFunction = 0.0000000059
NH      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1054 x0 = -4.9999999971 x1 = -4.9999999972 CostFunction = 0.0000000058
QI      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1055 x0 = -4.9999999972 x1 = -4.9999999972 CostFunction = 0.0000000057
II      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1056 x0 = -4.9999999972 x1 = -4.9999999973 CostFunction = 0.0000000055
RN      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1057 x0 = -4.9999999973 x1 = -4.9999999973 CostFunction = 0.0000000054
KN      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1058 x0 = -4.9999999973 x1 = -4.9999999974 CostFunction = 0.0000000053
JO      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1059 x0 = -4.9999999974 x1 = -4.9999999974 CostFunction = 0.0000000052
JO      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1060 x0 = -4.9999999974 x1 = -4.9999999975 CostFunction = 0.0000000051
QL      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1061 x0 = -4.9999999975 x1 = -4.9999999975 CostFunction = 0.0000000050
QL      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1062 x0 = -4.9999999975 x1 = -4.9999999976 CostFunction = 0.0000000049
HP      0       17:15:16.800    gradient-descent test (EURUSD,M1)       Local miminum found =-4.999999997546217

经过 1062（一千零六十二）次迭代，算法就能够达到此函数的局部最小值。

针对该算法需要注意的事情

查看成本函数的数值，您会注意到开始时数值的巨大变化，但到了成本函数的最后一个数值则变化难以察觉。

当梯度下降远未接近函数的最小值时，它会取较大的步长，但是，当接近函数的最小值时，它会取婴幼儿般的步长；这与您接近山脚时采取的行动相仿，所以现在您知道梯度下降非常聪明！

结束时本地最小值是

HP      0       17:15:16.800    gradient-descent test (EURUSD,M1)       Local miminum found =-4.999999997546217

这是准确的值，因为此函数的最小值为 -5.0！

真实的问题

梯度如何知道何时停止？看看若我们让算法保持迭代，直到无穷大，或者至少是计算机计算能力的尽头。

当成本函数为零，此刻我们知道梯度下降已经完成了它的工作。

现在我们用 MQL5 编写整个操作代码：

       while (true)
        {
           iterations++;
           
           x1 = x0 - m_learning_rate * CustomCostFunction(x0);
           
           printf("%d x0 = %.10f x1 = %.10f CostFunction = %.10f",iterations,x0,x1,CustomCostFunction(x0)); 
           
           if (NormalizeDouble(CustomCostFunction(x0),8) == 0) { Print("Local minimum found =",x0);  break;  }
              
           x0 = x1;
        }

以上的代码模块能够为我们带来我们想要的结果，但它在 CGradientDescent 类中并不孤单。函数 CustomCostFunction 是保持和计算我们的微分方程的地方，它是

double CGradientDescent::CustomCostFunction(double x)
 {
   return(2 * ( x + 5 ));
 }

目的是什么？

有人也许会自问，当您本可利用我们之前在本系列文章中讨论的以函数库，来创建默认线性模型时，所有这些计算的目的是什么。采用默认值创建的模型不一定是最佳模型，因此您需要让计算机学习误差最少模型的最佳参数。

我们这数篇文章距离构建人工神经网络更近了，为了让每个人都能够理解神经网络如何在反向传播和其它技术过程中学习（自学形态），而梯度下降是最流行的算法，能让这一切成为可能。如果对它没有坚实的理解，您可能永远无法理解这个过程，因为事情即将变得极其复杂。

回归模型的梯度下降

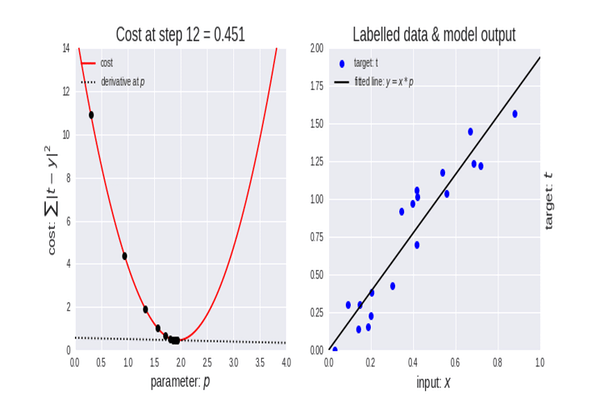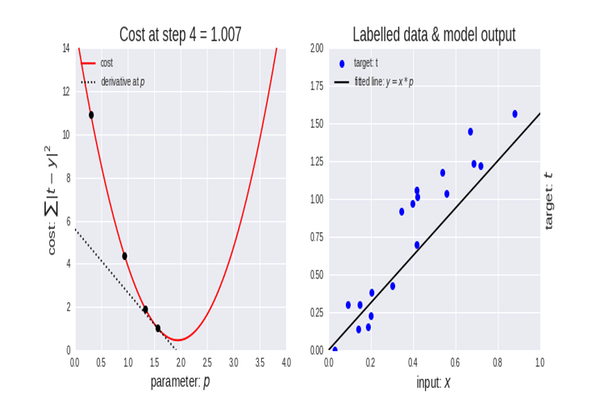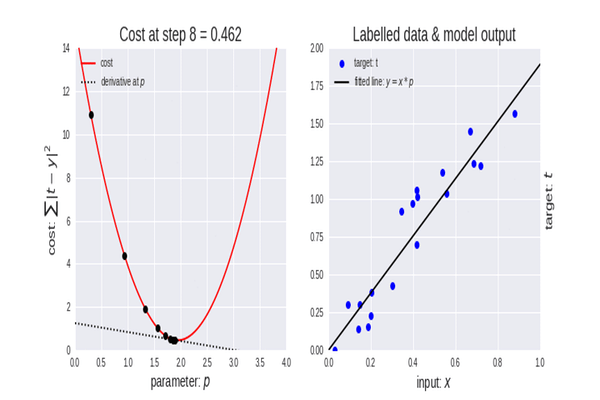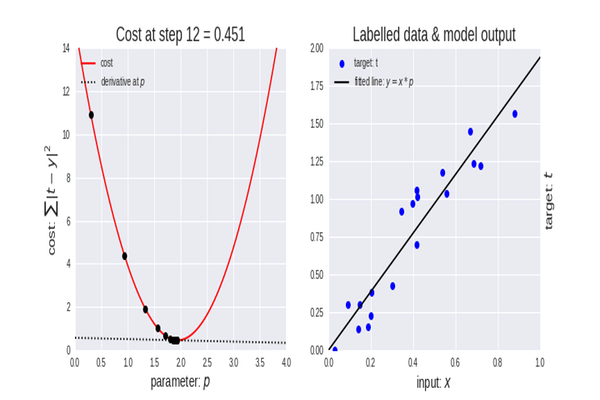
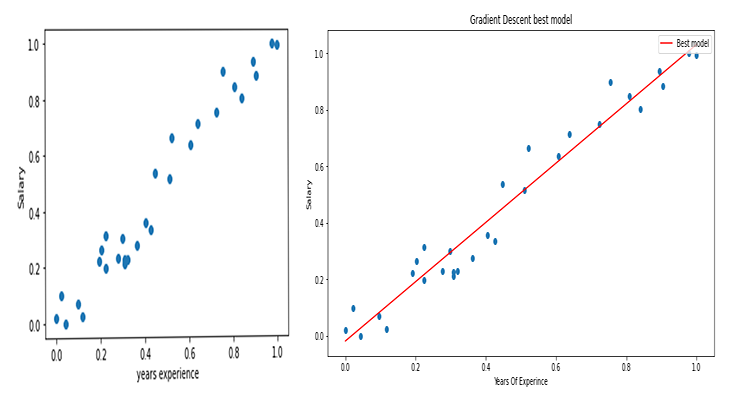
使用工资数据集，我们来构建利用梯度下降得到的最佳模型。

数据集概览

以 Python 数据可视化：

import pandas as pd 
import numpy as np
import matplotlib.pyplot as plt


data  = pd.read_csv(r"C:\Users\Omega Joctan\AppData\Roaming\MetaQuotes\Terminal\892B47EBC091D6EF95E3961284A76097\MQL5\Files\Salary_Data.csv")

print(data.head(10))

x = data["YearsExperience"]
y = data["Salary"]

plt.figure(figsize=(16,9))
plt.title("Experience vs Salary")
plt.scatter(x,y,c="green")
plt.xlabel(xlabel="Years of Experience")
plt.ylabel(ylabel="Salary")
plt.show()

这就是我们的图表：

工龄与工资

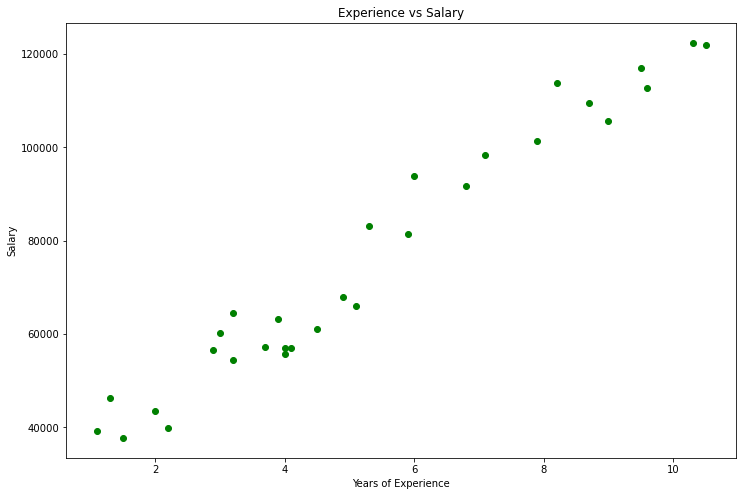
查看我们的数据集，您不禁会注意到该数据集是一个回归问题，但是我们可以有数百万个模型，来帮助我们进行预测，或我们想要实现的任何东西。

多模式

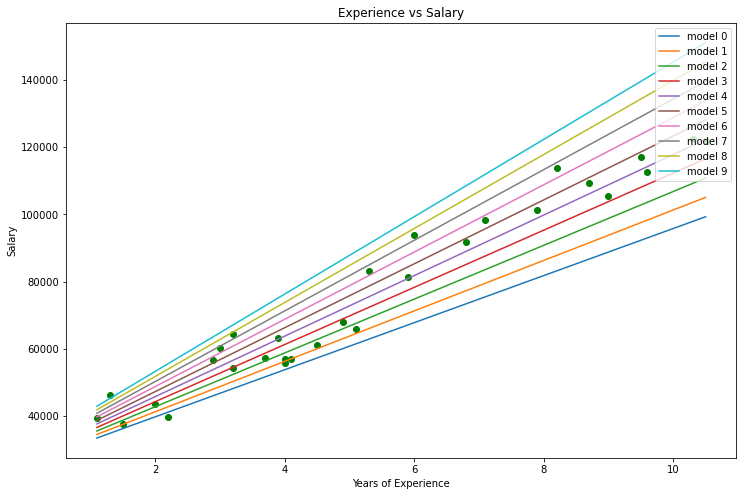
用来预测一个人的经验，以及他们的工资的最佳模型是什么？这就是我们需要去发掘的。但首先我们来推导针对我们回归模型的成本函数。

理论

让我带你回到线性回归。

我们知道一个事实，每个线性模型都有与之相关的误差。我们还知道，我们可以在此图形中创建数百万条线，并且最佳拟合线始终是误差最小的线。

成本函数表示我们的实际值和预测值之间的误差，我们可将成本函数的公式写成等式：

成本 = Y 真实 - Y 预测

鉴于我们看到误差的规模，我们提升至平方，我们的公式现在变成了

但我们正在寻找整个数据集中的误差，我们需要进行求和

最后，我们将误差的总和除以 m，即数据集中的项目数量：

线性回归成本函数

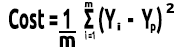
此处的视频是手工完成的整个数学过程。

现在我们有了成本函数，我们来为梯度下降进行编码，并为两者找到最佳参数。 X(Slope) 的斜率表示为 Bo ，以及 Y 截距表示为 B1

   
   double cost_B0=0, cost_B1=0;
   
   if (costFunction == MSE)
    {
      int iterations=0;
      for (int i=0; i<m_iterations; i++, iterations++)
        {
        
           cost_B0 = Mse(b0,b1,Intercept);
           cost_B1 = Mse(b0,b1,Slope);
           
           b0 = b0 - m_learning_rate * cost_B0; 
           b1 = b1 - m_learning_rate * cost_B1;
           
           printf("%d b0 = %.8f cost_B0 = %.8f B1 = %.8f cost_B1 = %.8f",iterations,b0,cost_B0,b1,cost_B1);
           
           DBL_MAX_MIN(b0); DBL_MAX_MIN(cost_B0); DBL_MAX_MIN(cost_B1);
           
           if (NormalizeDouble(cost_B0,8) == 0 && NormalizeDouble(cost_B1,8) == 0)  break; 
           
        }
      printf("%d Iterations Local Minima are\nB0(Intercept) = %.5f  ||  B1(Coefficient) = %.5f",iterations,b0,b1);    
    }

请注意梯度下降代码中的一些内容：

该过程仍然与我们之前执行的过程相同，但这次我们查找时，并一次性更新了两次 Bo 和 B1 的数值。
迭代次数有限，有人曾经说过，制作无限循环的最佳方法是使用 while 循环，我们这次不采用 while 循环，取而代之的是希望限制算法寻找最佳模型系数而进行的计算次数。
DBL_MAX_MIN 是一个用于调试目的的函数，负责检查并通知我们是否达到了计算机的数学极限。

这是算法操作的输出。 学习曲率 = 0.01 迭代 = 10000

PD      0       17:29:17.999    gradient-descent test (EURUSD,M1)       [20]  91738.0000  98273.0000 101302.0000 113812.0000 109431.0000 105582.0000 116969.0000 112635.0000 122391.0000 121872.0000
JS      0       17:29:17.999    gradient-descent test (EURUSD,M1)       Gradient Descent CostFunction MSE
RF      0       17:29:17.999    gradient-descent test (EURUSD,M1)       0 b0 = 1520.06000000 cost_B0 = -152006.00000000 B1 = 9547.97400000 cost_B1 = -954797.40000000
OP      0       17:29:17.999    gradient-descent test (EURUSD,M1)       1 b0 = 1995.08742960 cost_B0 = -47502.74296000 B1 = 12056.69235267 cost_B1 = -250871.83526667
LP      0       17:29:17.999    gradient-descent test (EURUSD,M1)       2 b0 = 2194.02117366 cost_B0 = -19893.37440646 B1 = 12707.81767044 cost_B1 = -65112.53177770
QN      0       17:29:17.999    gradient-descent test (EURUSD,M1)       3 b0 = 2319.78332575 cost_B0 = -12576.21520809 B1 = 12868.77569178 cost_B1 = -16095.80213357
LO      0       17:29:17.999    gradient-descent test (EURUSD,M1)       4 b0 = 2425.92576238 cost_B0 = -10614.24366387 B1 = 12900.42596039 cost_B1 = -3165.02686058
GH      0       17:29:17.999    gradient-descent test (EURUSD,M1)       5 b0 = 2526.58198175 cost_B0 = -10065.62193621 B1 = 12897.99808257 cost_B1 = 242.78778134
CJ      0       17:29:17.999    gradient-descent test (EURUSD,M1)       6 b0 = 2625.48307920 cost_B0 = -9890.10974571 B1 = 12886.62268517 cost_B1 = 1137.53974060
DD      0       17:29:17.999    gradient-descent test (EURUSD,M1)       7 b0 = 2723.61498028 cost_B0 = -9813.19010723 B1 = 12872.93147573 cost_B1 = 1369.12094310
HF      0       17:29:17.999    gradient-descent test (EURUSD,M1)       8 b0 = 2821.23916252 cost_B0 = -9762.41822398 B1 = 12858.67435081 cost_B1 = 1425.71249248

<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< Last Iterations >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

EI      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6672 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
NG      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6673 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
GD      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6674 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
PR      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6675 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
IS      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6676 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
RQ      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6677 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
KN      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6678 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
DL      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6679 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
RM      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6680 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
IK      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6681 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
PH      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6682 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
GF      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6683 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
MG      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6684 b0 = 25792.20019866 cost_B0 = -0.00000000 B1 = 9449.96232146 cost_B1 = 0.00000000
LE      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6684 Iterations Local Minima are
OJ      0       17:29:48.247    gradient-descent test (EURUSD,M1)       B0(Intercept) = 25792.20020  ||  B1(Coefficient) = 9449.96232

如果我们利用 matplotlib 绘制图形

最佳模型梯度下降

B A M，梯度下降已经能够成功地从我们尝试的 10000 个模型中获得最佳模型，太棒了，但我们错过了关键一步，可能会导致我们的模型行为异常，并让我们得到我们不想要的结果。

常规化线性回归输入变量数据

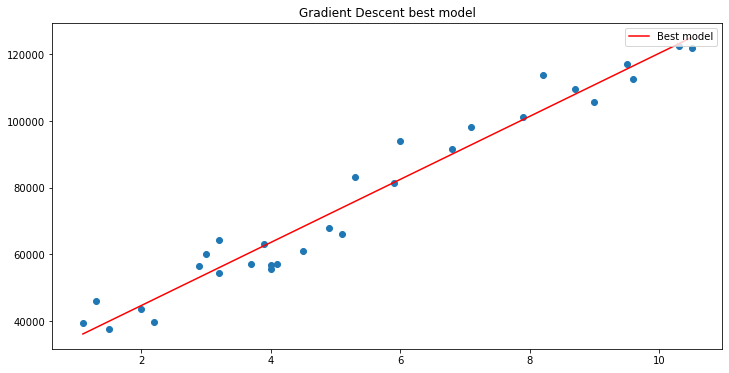
我们知道，对于不同的数据集，可以在不同的迭代之后找到最佳模型，有些可能需要 100 次迭代才能达到最佳模型，有些可能需要 10000 次或多达 100 万次迭代才能令成本函数变为零；更不用说如果我们得到错误的学习曲率，我们最终也许会错过局部最小值，而如果我们错过了该目标，我们的结局将达到计算机的数学极限，让我们在实践中看看这一点。

学习曲率 = 0.1 迭代 1000

我们只是触及了系统允许的最大双精度值。以下是我们的日志。

GM      0       17:28:14.819    gradient-descent test (EURUSD,M1)       Gradient Descent CostFunction MSE
OP      0       17:28:14.819    gradient-descent test (EURUSD,M1)       0 b0 = 15200.60000000 cost_B0 = -152006.00000000 B1 = 95479.74000000 cost_B1 = -954797.40000000
GR      0       17:28:14.819    gradient-descent test (EURUSD,M1)       1 b0 = -74102.05704000 cost_B0 = 893026.57040000 B1 = -512966.08473333 cost_B1 = 6084458.24733333
NM      0       17:28:14.819    gradient-descent test (EURUSD,M1)       2 b0 = 501030.91374462 cost_B0 = -5751329.70784622 B1 = 3356325.13824362 cost_B1 = -38692912.22976952
LH      0       17:28:14.819    gradient-descent test (EURUSD,M1)       3 b0 = -3150629.51591119 cost_B0 = 36516604.29655810 B1 = -21257352.71857720 cost_B1 = 246136778.56820822
KD      0       17:28:14.819    gradient-descent test (EURUSD,M1)       4 b0 = 20084177.14287909 cost_B0 = -232348066.58790281 B1 = 135309993.40314889 cost_B1 = -1565673461.21726084
OQ      0       17:28:14.819    gradient-descent test (EURUSD,M1)       5 b0 = -127706877.34210962 cost_B0 = 1477910544.84988713 B1 = -860620298.24803317 cost_B1 = 9959302916.51181984
FM      0       17:28:14.819    gradient-descent test (EURUSD,M1)       6 b0 = 812402202.33122230 cost_B0 = -9401090796.73331833 B1 = 5474519904.86084747 cost_B1 = -63351402031.08880615
JJ      0       17:28:14.819    gradient-descent test (EURUSD,M1)       7 b0 = -5167652856.43381691 cost_B0 = 59800550587.65039062 B1 = -34823489070.42410278 cost_B1 = 402980089752.84948730
MP      0       17:28:14.819    gradient-descent test (EURUSD,M1)       8 b0 = 32871653967.62362671 cost_B0 = -380393068240.57440186 B1 = 221513298448.70788574 cost_B1 = -2563367875191.31982422
MM      0       17:28:14.819    gradient-descent test (EURUSD,M1)       9 b0 = -209097460110.12799072 cost_B0 = 2419691140777.51611328 B1 = -1409052343513.33935547 cost_B1 = 16305656419620.47265625
HD      0       17:28:14.819    gradient-descent test (EURUSD,M1)       10 b0 = 1330075004152.67309570 cost_B0 = -15391724642628.00976562 B1 = 8963022367351.18359375 cost_B1 = -103720747108645.23437500
DP      0       17:28:14.819    gradient-descent test (EURUSD,M1)       11 b0 = -8460645083849.12207031 cost_B0 = 97907200880017.93750000 B1 = -57014041694401.67187500 cost_B1 = 659770640617528.50000000

这意味着，如果我们取了错误的学习曲率，那我们找到最佳模型的机会可能是微乎其微，而且我们最终触及计算机数学极限的可能性很高，就像您刚刚看到的警告一样。

但如果我尝试 0.01 作为此数据集的学习曲率，尽管训练过程会变慢很多，但我们最终不会遇到麻烦；若当我将此学习曲率用于此数据集时，我最终会触及数学极限，所以现在您知道每个数据集都有它的学习曲率，只是我们可能没有机会优化学习曲率，因为有时我们的复杂数据集有多个变量，这也是完成整个过程的低效途径。

针对所有这些的解决方案是常规化整个数据集，如此即可令其处于同一尺度，当我们在同一数轴上绘制数值时，这提高了可读性，也改善了训练时间，因为常规化后的数值通常在 0 到 1 的范围内，我们也不再需要担心学习曲率，因为一旦我们只有一个学习曲率参数，我们就可以将其应用到我们面临的任何数据集，例如 0.01 的学习曲率，更多有关规范化的信息，请参阅此处。

最后但同样重要的

我们还知道，我们的工资数据值是从 39,343 到 121,782 的中间值，而工龄是从 1.1到 10.5，如果我们的数据以这种方式持续，工资值会是巨大的，它们可能会让模型认为它们比任何值都重要，因此与工龄相比，它们将产生巨大的影响，我们需要所有自变量彼此间具有相同的影响力，现在您看到了数值常规化是如此重要。

(常规化) 最小-最大标量

在这种方式中，我们将数据常规化在 0 和 1 的范围内。公式给出如下：

常规化最小-最大-标量

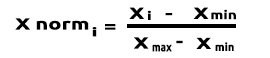
将此公式转换为 MQL5 中的代码行，则变为：

void CGradientDescent::MinMaxScaler(double &Array[])
 {
   double mean = Mean(Array);
   double max,min;
   double Norm[];
   
   ArrayResize(Norm,ArraySize(Array));
   
   max = Array[ArrayMaximum(Array)];   min = Array[ArrayMinimum(Array)];
   
    for (int i=0; i<ArraySize(Array); i++)
         Norm[i] = (Array[i] - min) / (max - min); 
   
   printf("Scaled data Mean = %.5f Std = %.5f",Mean(Norm),std(Norm));
   
   ArrayFree(Array);
   ArrayCopy(Array,Norm);
 }

函数 std() 只是为了在数据常规化之后，让我们知道标准偏差。这是它的代码：

double CGradientDescent::std(double &data[])
 {
   double mean =  Mean(data);
   double sum = 0;
   
    for (int i=0; i<ArraySize(data); i++)
       sum += MathPow(data[i] - mean,2);
    
    return(MathSqrt(sum/ArraySize(data)));  
 }

现在我们调用所有这些，并打印输出，来查看发生了什么：

void OnStart()
  {
//---
      string filename = "Salary_Data.csv";

      double XMatrix[];
      double YMatrix[];
      
      
      grad = new CGradientDescent(1, 0.01,1000);
      
      grad.ReadCsvCol(filename,1,XMatrix);
      grad.ReadCsvCol(filename,2,YMatrix);
       
      grad.MinMaxScaler(XMatrix);
      grad.MinMaxScaler(YMatrix);
      
      ArrayPrint("Normalized X",XMatrix);
      ArrayPrint("Normalized Y",YMatrix);
      
      
      grad.GradientDescentFunction(XMatrix,YMatrix,MSE);
      
      delete (grad);
  }

输出

OK      0       18:50:53.387    gradient-descent test (EURUSD,M1)       Scaled data Mean = 0.44823 Std = 0.29683
MG      0       18:50:53.387    gradient-descent test (EURUSD,M1)       Scaled data Mean = 0.45207 Std = 0.31838
MP      0       18:50:53.387    gradient-descent test (EURUSD,M1)       Normalized X
JG      0       18:50:53.387    gradient-descent test (EURUSD,M1)       [ 0] 0.0000 0.0213 0.0426 0.0957 0.1170 0.1915 0.2021 0.2234 0.2234 0.2766 0.2979 0.3085 0.3085 0.3191 0.3617
ER      0       18:50:53.387    gradient-descent test (EURUSD,M1)       [15] 0.4043 0.4255 0.4468 0.5106 0.5213 0.6064 0.6383 0.7234 0.7553 0.8085 0.8404 0.8936 0.9043 0.9787 1.0000
NQ      0       18:50:53.387    gradient-descent test (EURUSD,M1)       Normalized Y
IF      0       18:50:53.387    gradient-descent test (EURUSD,M1)       [ 0] 0.0190 0.1001 0.0000 0.0684 0.0255 0.2234 0.2648 0.1974 0.3155 0.2298 0.3011 0.2134 0.2271 0.2286 0.2762
IS      0       18:50:53.387    gradient-descent test (EURUSD,M1)       [15] 0.3568 0.3343 0.5358 0.5154 0.6639 0.6379 0.7151 0.7509 0.8987 0.8469 0.8015 0.9360 0.8848 1.0000 0.9939

图形现在将如下所示：

常规化价格图形

逻辑回归的梯度下降

我们已经看到了梯度下降的线性的一面，现在我们来看看逻辑方面。

在此，我们执行与线性回归部分相同的过程，因为所涉及的过程完全相同，只是区分逻辑回归的过程比线性模型的过程更复杂，我们先看看成本函数。

正如有关逻辑回归系列文章的第二篇所讨论的，逻辑回归模型的成本函数是二元交叉熵，又名对数损失，如下所示。

二元交叉熵或对数损失

现在我们先完成困难的部分，区分这个函数，来获取它的梯度。

找到导数之后

成本函数的导数

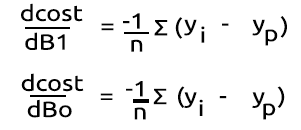
我们把代表二元交叉熵的 BCE 函数内的公式转换为 MQL5 代码。

double CGradientDescent::Bce(double Bo,double B1,Beta wrt)
 {
   double sum_sqr=0;
   double m = ArraySize(Y);
   double x[];
   
   MatrixColumn(m_XMatrix,x,2);
   
    if (wrt == Slope)
      for (int i=0; i<ArraySize(Y); i++)
        { 
          double Yp = Sigmoid(Bo+B1*x[i]);
          
          sum_sqr += (Y[i] - Yp) * x[i];
        }
        
    if (wrt == Intercept)
      for (int i=0; i<ArraySize(Y); i++)
         {
            double Yp = Sigmoid(Bo+B1*x[i]);
            sum_sqr += (Y[i] - Yp);
         } 
    return((-1/m)*sum_sqr);
 }

由于我们正在应对分类模型，因此我们选择的数据集是我们曾在逻辑回归中用过的泰坦尼克号数据集。我们的自变量是 Pclass (乘客类)，我们的另一个因变量是 Survived。

类与泰坦尼克数据集生存率

分类散点图

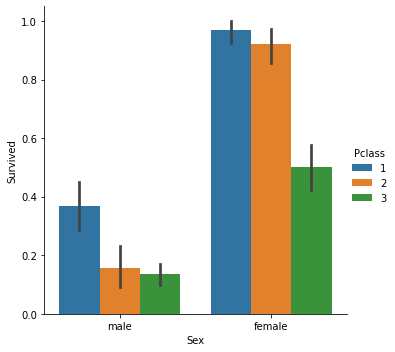
生存与类散点图

现在我们调用类的梯度下降，但这次采用BCE（二元交叉熵）作为我们的成本函数。

      filename = "titanic.csv";
      
      ZeroMemory(XMatrix);
      ZeroMemory(YMatrix);
      
      grad.ReadCsvCol(filename,3,XMatrix);
      grad.ReadCsvCol(filename,2,YMatrix);
      
      grad.GradientDescentFunction(XMatrix,YMatrix,BCE);
      
      delete (grad);

我们看看输出的结果：

CP      0       07:19:08.906    gradient-descent test (EURUSD,M1)       Gradient Descent CostFunction BCE
KD      0       07:19:08.906    gradient-descent test (EURUSD,M1)       0 b0 = -0.01161616 cost_B0 = 0.11616162 B1 = -0.04057239 cost_B1 = 0.40572391
FD      0       07:19:08.906    gradient-descent test (EURUSD,M1)       1 b0 = -0.02060337 cost_B0 = 0.08987211 B1 = -0.07436893 cost_B1 = 0.33796541
KE      0       07:19:08.906    gradient-descent test (EURUSD,M1)       2 b0 = -0.02743120 cost_B0 = 0.06827832 B1 = -0.10259883 cost_B1 = 0.28229898
QE      0       07:19:08.906    gradient-descent test (EURUSD,M1)       3 b0 = -0.03248925 cost_B0 = 0.05058047 B1 = -0.12626640 cost_B1 = 0.23667566
EE      0       07:19:08.907    gradient-descent test (EURUSD,M1)       4 b0 = -0.03609603 cost_B0 = 0.03606775 B1 = -0.14619252 cost_B1 = 0.19926123
CF      0       07:19:08.907    gradient-descent test (EURUSD,M1)       5 b0 = -0.03851035 cost_B0 = 0.02414322 B1 = -0.16304363 cost_B1 = 0.16851108
MF      0       07:19:08.907    gradient-descent test (EURUSD,M1)       6 b0 = -0.03994229 cost_B0 = 0.01431946 B1 = -0.17735996 cost_B1 = 0.14316329
JG      0       07:19:08.907    gradient-descent test (EURUSD,M1)       7 b0 = -0.04056266 cost_B0 = 0.00620364 B1 = -0.18958010 cost_B1 = 0.12220146
HE      0       07:19:08.907    gradient-descent test (EURUSD,M1)       8 b0 = -0.04051073 cost_B0 = -0.00051932 B1 = -0.20006123 cost_B1 = 0.10481129
ME      0       07:19:08.907    gradient-descent test (EURUSD,M1)       9 b0 = -0.03990051 cost_B0 = -0.00610216 B1 = -0.20909530 cost_B1 = 0.09034065
JQ      0       07:19:08.907    gradient-descent test (EURUSD,M1)       10 b0 = -0.03882570 cost_B0 = -0.01074812 B1 = -0.21692190 cost_B1 = 0.07826600
        <<<<<<  Last  10 iterations >>>>>>

FN      0       07:19:09.725    gradient-descent test (EURUSD,M1)       6935 b0 = 1.44678930 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
PN      0       07:19:09.725    gradient-descent test (EURUSD,M1)       6936 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
NM      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6937 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
KL      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6938 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
PK      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6939 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
RK      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6940 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
MJ      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6941 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
HI      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6942 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
CH      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6943 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
MH      0       07:19:09.727    gradient-descent test (EURUSD,M1)       6944 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
QG      0       07:19:09.727    gradient-descent test (EURUSD,M1)       6945 b0 = 1.44678931 cost_B0 = -0.00000000 B1 = -0.85010666 cost_B1 = 0.00000000
NG      0       07:19:09.727    gradient-descent test (EURUSD,M1)       6945 Iterations Local Minima are
MJ      0       07:19:09.727    gradient-descent test (EURUSD,M1)       B0(Intercept) = 1.44679  ||  B1(Coefficient) = -0.85011

我们不会像在线性回归中那样对逻辑回归的分类数据进行常规化或缩放。

这里有两个最重要的机器学习模型的梯度下降，我希望它是易于理解的，本文中助力很大的 python 代码，和数据集的链接在 GitHub 的存储库。

结束语

我们已经看到了一个自变量和一个因变量的梯度下降，对于多个自变量，您需要采用方程的向量/矩阵形式，我认为这一次任何人都可以轻松尝试并发现它们，因为我们有 MQL5 最近发布的针对矩阵的标准函数库，如需任何有关矩阵的帮助，请随时与我联系，我将非常乐意提供帮助。

此致敬意

了解有关微积分的更多信息：

本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/11200

附加的文件 |

下载ZIP

Gradient_Descent.zip (41.03 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.