
数据科学和机器学习(第 05 部分):决策树
什么是决策树?
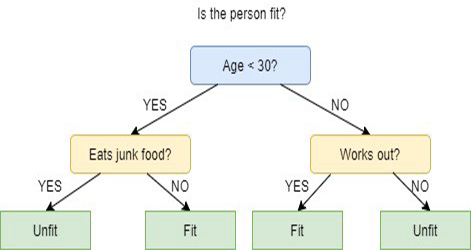
决策树是一种有监督的机器学习技术,可根据前一组问题的答案进行分类或预测。 模型是监督学习的一种形式,这意味着模型会基于包含所需分类的一组数据上进行训练和测试。
决策树也许并不总是提供明确的答案或决策,取而代之,它也许提供选项,如此数据科学家能够自行做出明智的决策。 决策树模仿人类的思维方式,故数据科学家往往很容易理解和解释结果。

术语警报!
在本系列的第一篇文章中,我忘了讲述有监督和无监督学习的术语,所以就就这里吧。
监督学习
有监督学习是一种创建人工智能(AI)的方式,其中计算机算法基于输入数据进行训练,并标记为特定输出,针对模型加以训练,直到它能够检测出底层形态,和输入数据与输出标签之间的关系,当前所未见的数据出现时启用它产生准确的结果。
与监督学习鲜明对比,在这种方法中,算法取用无标记的数据,并设计用于自行检测形态或相似性。
监督学习程序中常用的算法包括:
有监督和无监督学习之间的主要区别在于算法如何学习。 在无监督学习中,算法取无标记数据作为训练集合。 与监督学习不同,它没有正确的输出值;该算法判定数据中的形态和相似性,而不是将其与一些外部测量值相关联。换句话说,算法可以自由行事,从而掌握更多有关数据的信息,并找到人类不曾发现的有趣或意外的东西。
我们目前正经历监督学习,我们将在接下来的几篇文章中了解非监督学习。
决策树是如何工作的?
决策树运用多种算法来决定将一个节点拆分为两个或多个子集节点。 子节点的创建提升了子节点合量的均匀性。 换言之,我们可以说节点的纯度随着目标变量的增加而增加。 决策树算法把所有可用变量上的节点拆分,然后选择拆分最均匀的子节点。
算法选择基于目标变量的类型。
以下是决策树中采用的算法:
- ID3 > D3 扩展
- C4.5 > ID3 继承者
- CART > 分类和回归树
- CHAID > 卡方自动交叠检测,在计算分类树时执行多级分割
- MARS > 多元自适应回归样条
在本文中,我将基于 ID3 算法创建一棵决策树,我们将在本系列的下一篇文章中讨论和运用其它算法。
决策树的目标
决策树算法的主要目标是将含有杂质的数据分离为纯节点或靠近节点的数据,例如,在一个篮子中苹果与橘子混杂,当决策树根据苹果的颜色和大小进行训练时,会将其分离到它自己的篮子中,而橘子也会被分到自己的篮子里。
ID3 A算法
ID3 代表迭代二分法器 3,之所以这样命名是因为该算法在每个步骤迭代地(重复地)将特征二分法(划分)为两个或更多组。
由 Ross Quinlan 发明的 ID3 使用自上而下的贪婪方法来构建决策树。 简而言之,自上而下的贪婪方法意味着它从顶部开始构建树,而贪婪方法意味着在每次迭代时,我们选择当前时刻的最佳特征来创建节点。
通常,ID3 仅用于标称数据的分类问题(基本上,都是无法测量的数据)。
也就是说,有两种类型的决策树。
- 分类树
- 回归树
01: 分类树
分类树就如同我们将要在本文中学习的树,其中我们要分类的特征没有连续的数值或有序值。
分类树可将事物分类。
02: 回归树
它们是用有序值和连续值来构建的。
决策树预测数字值。
ID3 算法中的步骤
01: 它的起始以原始数据集作为根节点。
为了构建基准函数库,我们将采用在特定天气条件下打网球的简单数据集,此处是我们的数据集概况,这是一个小数据集(只有 14 行)。
为了采用此算法绘制决策树,我们需要了解哪些属性提供了所有属性中的最大信息增益,我来解释一下。
其中一个属性(列)必须是根节点作为开头,但是,如何决定哪一列是根节点? 这就是我们使用信息增益的地方。
信息增益
信息增益计算熵的减少,并测量给定特征分离,或目标分类的程度。 选择含有最高信息增益的特征作为最佳特征。
![]()
熵
熵是随机变量不确定性的度量,它表征给定样本中的杂质。
熵的公式是,
![]()
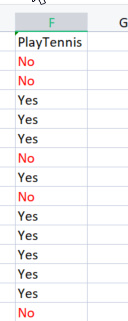
我们要做的第一件事是找到整个数据集的熵,这意味着找到目标变量的熵,因为所有这些列都投影到目标列 PlayTennis。
我们来编写一些代码,
我们确信知道,在找到目标变量的熵之前,我们需要将负值的总数标记为 No,将正值标记为 Yes,这些值可以帮助我们获得列中元素的概率,为了获得这些值,我们要编写代码,在熵函数中做这些事。
double CDecisionTree::Entropy(int &SampleNumbers[],int total) { double Entropy = 0; double entropy_out =0; //the value of entropy that will be returned for (int i=0; i<ArraySize(SampleNumbers); i++) { double probability1 = Proba(SampleNumbers[i],total); Entropy += probability1 * log2(probability1); } entropy_out = -Entropy; return(entropy_out); }
该函数乍一看很容易理解,特别是如果您已经阅读过公式,但请注意数组 SampleNumbers[],样本内部是列,我们也可以将样本称为类。例如,在这个目标列中,我们的样本是 Yes 和 No。
基于 TargetArray 列上成功运行函数,结果将导致
12:37:48.394 TestScript There are 5 No 12:37:48.394 TestScript There are 9 Yes 12:37:48.394 TestScript There are 2 classes 12:37:48.394 TestScript "No" "Yes" 12:37:48.394 TestScript 5 9 12:37:48.394 TestScript Total contents = 14
现在我们有了这些数字,我们继续用我们的公式来求熵
![]()
如果您注意到这个公式,您会注意到我们在这里处理的是以 2 为底的对数,它是二元对数(参阅读更多信息)为了找到以 2 为底的对数,我们将 log2 除以参数值的对数。
double CDecisionTree::log2(double value) { return (log10(value)/log10(2)); }
.因为底数是一样的,一切都很好。
我还编写了一个函数 Proba() 来帮助我们获得一类值的概率,如下所示。
double CDecisionTree::Proba(int number,double total) { return(number/total); }
屋里的大象。 为了找到我们列中某个元素的概率,我们要找到它出现的次数,再除以该列中所有元素的总数,您可能已经注意到有 5 个元素 No 和 9 个元素 Yes,因此,
no 的概率 = 5/14(元素总数) = 0.357142..
yes 的概率 = 9/14(同样的故事) = 0.6428571...
最后,找到属性/数据集列的熵
for (int i=0; i<ArraySize(SampleNumbers); i++) { double probability1 = Proba(SampleNumbers[i],total); Entropy += probability1 * log2(probability1); } entropy_out = -Entropy;
如果针对目标变量运行该函数,输出将为
13:37:54.273 TestScript Proba1 0.35714285714285715 13:37:54.273 TestScript Proba1 0.6428571428571429 13:37:54.273 TestScript Entropy of the entire dataset = 0.9402859586706309
太厉害了
现在我们知道了整个数据集的熵,基本上是 y 值的熵,且我们有查找熵的函数。 我们来查找数据集中每一列的熵。
现在我们得到了整个数据集的熵,下一步是找到每个自变量列中成员的熵,在自变量中查找这个熵的目的是帮助我们找到每个数据列的信息增益。
在我们利用我们的函数库查找 Outlook 列的熵之前,我们先以手工计算它,以便您可以清楚地了解正在执行的操作。
我们取 outlook 列与其目标变量进行比较。
Outlook 对比 PlayTennis 列
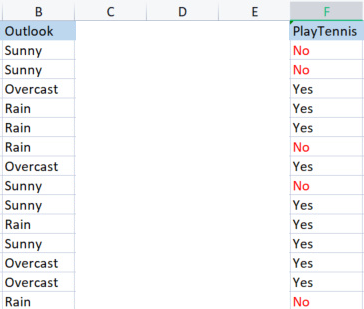
不同于我们如何查找整个数据集的熵(也被称为目标变量的熵),若要查找自变量的熵,我们必须将其引用指向目标变量,因为这是我们的目标,
Outlook 中的数值
我们有 3 个不同的值,分别是晴天、阴天和雨天,我们必须找到每个值相对于目标变量的熵
Samples(Sunny) (positive and negative samples of Sunny) = [2 Positive (The Yes's), 3 Negative(The No's)]
既然现在我们有了正数和负数,在晴天打网球的 Yes 概率为
概率1= 2(“Yes” 出现的次数) / 5(晴天总数)
故 2/5 = 0.4
与其对比
在晴天不打球的概率为 0.6,即 3/5 = 0.6
最后,晴天打球的熵为,参考公式
Entropy(Sunny) = - (P1*log2P1 + P2*log2P2)
Entropy(Sunny) = -(0.4*log2 0.4 + 0.6*log2 0.6)
Entropy(Sunny) = 0.97095
现在,我们来计算阴天的熵
阴天的样本。
正数样本 4 (在目标列的 Yes 样本),负数样本 0 (在目标列的 No 样本)。 这种情况属于例外。
ID3 算法中的异常
当有零(0)个负样本,而有多个正样本,或相反,有零(0)个正样本,同时有多个负样本,无论它何时发生,熵都绑定为零(0)。
我们说这是一个纯节点,不需要再拆分它,因为它具有同质样本,当我们绘制树时,您将更理解我的意思。
另一个例外是:
当正样本和负样本数量相等时,从数学上讲,熵将为 一(1)。
唯一需要我们高效处理的例外是当样本中存在零值时,因为零值可能导致除零,以下是新函数,具有处理此类异常的能力。
double CDecisionTree::Entropy(int &SampleNumbers[],int total) { double Entropy = 0; double entropy_out =0; //the value of entropy that will be returned for (int i=0; i<ArraySize(SampleNumbers); i++) { if (SampleNumbers[i] == 0) { Entropy = 0; break; } //Exception double probability1 = Proba(SampleNumbers[i],total); Entropy += probability1 * log2(probability1); } if (Entropy==0) entropy_out = 0; //handle the exception else entropy_out = -Entropy; return(entropy_out); }
最后,我们来查找雨天的熵
雨天样本:
有 3 个正样本(目标列中 “Yes” 样本)。
有 2 个负样本(目标列中 “No” 样本)。
最后是在雨天打网球的熵。
Entropy(Rain) = - (P1*log2P1 + P2*log2P2)
Entropy(Rain) = -(0.6*log2 0.6 + 0.4*log2 0.4)
Entropy(Rain) = 0.97095
以下是我们从 Outlook 列中获得的熵值
| 来自 Outlook 列的熵 |
|---|
| Entropy(Sunny) = 0.97095 |
| Entropy(Overcast) = 0 |
| Entropy(Rain) = 0.97095 |
因此,这就是如何手动查找样本的熵。如果我们利用我们的程序来查找这些熵,输出将是:
PD 0 13:47:20.571 TestScript <<<<<<<< Parent Entropy 0.94029 A = 0 >>>>>>>> FL 0 13:47:20.571 TestScript <<<<< C O L U M N Outlook >>>>> CL 0 13:47:20.571 TestScript << Sunny >> total > 5 MH 0 13:47:20.571 TestScript "No" "Yes" DM 0 13:47:20.571 TestScript 3 2 CQ 0 13:47:20.571 TestScript Entropy of Sunny = 0.97095 LD 0 13:47:20.571 TestScript << Overcast >> total > 4 OI 0 13:47:20.571 TestScript "No" "Yes" MJ 0 13:47:20.571 TestScript 0 4 CM 0 13:47:20.571 TestScript Entropy of Overcast = 0.00000 JD 0 13:47:20.571 TestScript << Rain >> total > 5 GN 0 13:47:20.571 TestScript "No" "Yes" JH 0 13:47:20.571 TestScript 2 3 HR 0 13:47:20.571 TestScript Entropy of Rain = 0.97095
我们将采用这些值,并用前面讨论的公式来查找整个数据的信息增益。
![]()
现在,我以手工来查找熵,这样您就可以理解隐藏在封闭的门户之后会发生什么。
信息增益(IG)= 整体数据集的熵 - 样本概率与其熵的乘积之和。
IG = E(dataset) - ( Prob(sunny) * E(sunny) + Prob(Overcast)*E(Overcast) + Prob(Rain)*E(Rain) )
IG = 0.9402 - ( 5/14 * (0.97095) + 4/14 * (0) + 5/14(0.97095) )
IG = 0.2467 (这是 Outlook 列的信息增益)
当我们将公式转换为代码时,将是:
double CDecisionTree::InformationGain(double parent_entropy, double &EntropyArr[], int &ClassNumbers[], int rows_) { double IG = 0; for (int i=0; i<ArraySize(EntropyArr); i++) { double prob = ClassNumbers[i]/double(rows_); IG += prob * EntropyArr[i]; } return(parent_entropy - IG); }
调用函数
if (m_debug) printf("<<<<<< Column Information Gain %.5f >>>>>> \n",IGArr[i]);
输出
PF 0 13:47:20.571 TestScript <<<<<< Column Information Gain 0.24675 >>>>>>
现在,我们必须针对所有列重复这个过程,并找到它们的信息增益。 输出为:
RH 0 13:47:20.571 TestScript (EURUSD,H1) Default Parent Entropy 0.9402859586706309 PD 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<<<< Parent Entropy 0.94029 A = 0 >>>>>>>> FL 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Outlook >>>>> CL 0 13:47:20.571 TestScript (EURUSD,H1) << Sunny >> total > 5 MH 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" DM 0 13:47:20.571 TestScript (EURUSD,H1) 3 2 CQ 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Sunny = 0.97095 LD 0 13:47:20.571 TestScript (EURUSD,H1) << Overcast >> total > 4 OI 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" MJ 0 13:47:20.571 TestScript (EURUSD,H1) 0 4 CM 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Overcast = 0.00000 JD 0 13:47:20.571 TestScript (EURUSD,H1) << Rain >> total > 5 GN 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" JH 0 13:47:20.571 TestScript (EURUSD,H1) 2 3 HR 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Rain = 0.97095 PF 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.24675 >>>>>> QP 0 13:47:20.571 TestScript (EURUSD,H1) KH 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Temp >>>>> PR 0 13:47:20.571 TestScript (EURUSD,H1) << Hot >> total > 4 QF 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" OS 0 13:47:20.571 TestScript (EURUSD,H1) 2 2 NK 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Hot = 1.00000 GO 0 13:47:20.571 TestScript (EURUSD,H1) << Mild >> total > 6 OD 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" KQ 0 13:47:20.571 TestScript (EURUSD,H1) 2 4 GJ 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Mild = 0.91830 HQ 0 13:47:20.571 TestScript (EURUSD,H1) << Cool >> total > 4 OJ 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" OO 0 13:47:20.571 TestScript (EURUSD,H1) 1 3 IH 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Cool = 0.81128 OR 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.02922 >>>>>> ID 0 13:47:20.571 TestScript (EURUSD,H1) HL 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Humidity >>>>> FH 0 13:47:20.571 TestScript (EURUSD,H1) << High >> total > 7 KM 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" HF 0 13:47:20.571 TestScript (EURUSD,H1) 4 3 GQ 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of High = 0.98523 QK 0 13:47:20.571 TestScript (EURUSD,H1) << Normal >> total > 7 GR 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" DD 0 13:47:20.571 TestScript (EURUSD,H1) 1 6 OF 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Normal = 0.59167 EJ 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.15184 >>>>>> EL 0 13:47:20.571 TestScript (EURUSD,H1) GE 0 13:47:20.571 TestScript (EURUSD,H1) <<<<< C O L U M N Wind >>>>> IQ 0 13:47:20.571 TestScript (EURUSD,H1) << Weak >> total > 8 GE 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" EO 0 13:47:20.571 TestScript (EURUSD,H1) 2 6 LI 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Weak = 0.81128 FS 0 13:47:20.571 TestScript (EURUSD,H1) << Strong >> total > 6 CK 0 13:47:20.571 TestScript (EURUSD,H1) "No" "Yes" ML 0 13:47:20.571 TestScript (EURUSD,H1) 3 3 HO 0 13:47:20.571 TestScript (EURUSD,H1) Entropy of Strong = 1.00000 LE 0 13:47:20.571 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.04813 >>>>>> IE 0 13:47:20.571 TestScript (EURUSD,H1)
既然现在我们已经得到了所有列的信息增益,我们将开始绘制决策树,如何做到?
这个初始过程旨在查找所有列的信息增益,从而令我们可以决定哪一列是根节点,比之所有其它列,信息增益最大的列将成为根节点,在这种情况下,Outlook 拥有最高的信息增益,如此它将成为决策树的根节点,我们现在就来绘制这棵树。
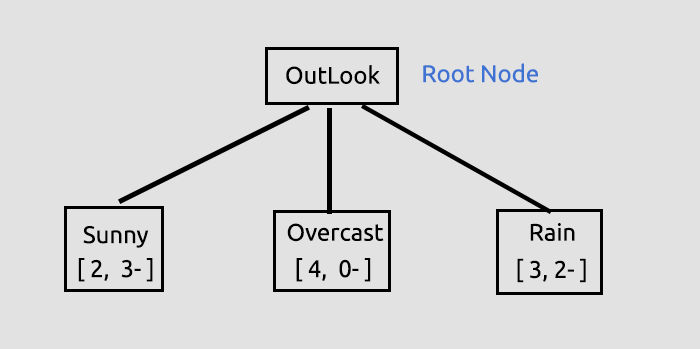
outlook 上的这些信息由函数库给出,当您运行本文末尾链接的测试脚本时,函数库处于默认调试模式时,故会打印大量信息。
信息增益是从其函数中获得的,然后存储在保存所有信息增益的双精度值数组之中,最后数组中的最大值就是我们的目标值。
//--- Finding the Information Gain ArrayResize(IGArr,i+1); //information gains matches the columns number IGArr[i] = InformationGain(P_EntropyArr[A],EntropyArr,ClassNumbers,rows); max_gain = ArrayMaximum(IGArr);输出为:
QR 0 13:47:20.571 TestScript (EURUSD,H1) Parent Noce will be Outlook with IG = 0.24675 IK 0 13:47:20.574 TestScript (EURUSD,H1) Parent Entropy Array and Class Numbers NL 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Overcast" "Rain" NH 0 13:47:20.574 TestScript (EURUSD,H1) 0.9710 0.0000 0.9710 FR 0 13:47:20.574 TestScript (EURUSD,H1) 5 4 5
关于这棵树的更多解释,我们已针对性的绘制。
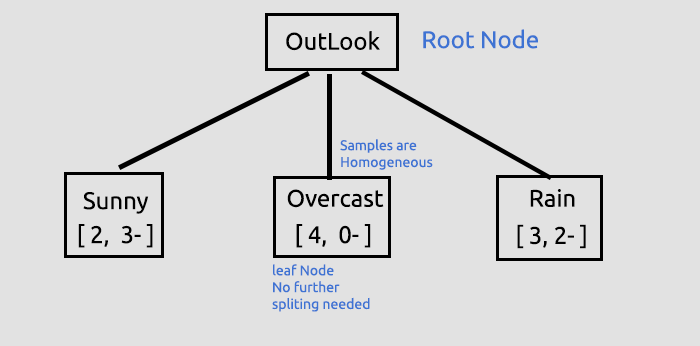
这第一个关键步骤,就是我们要找到根节点,并将该根节点拆分为分支和第一片叶,我们还将继续拆分数据,直到无任何数据可拆分,在此我们将继续此过程,将分支拆分为晴天项、雨天项。
阴天由同质项组成(它是纯粹的),所以我们说它已经完全被分类,当进入到决策树时,我们称它为一片叶子。 它不会生成分支。
但是,在进一步分解数据之前,我们需要对现有数据集执行一些关键步骤。
对剩余数据集矩阵进行分类
我们必须对剩余的数据集矩阵进行分类,以便将含有相同值的行按升序排列,这有助于创建含有相同内容的分支和叶片(我们渴望达成的一些东西)。
void CDecisionTree::MatrixClassify(string &dataArr[],string &Classes[], int cols) { string ClassifiedArr[]; ArrayResize(ClassifiedArr,ArraySize(dataArr)); int fill_start = 0, fill_ends = 0; int index = 0; for (int i = 0; i<ArraySize(Classes); i++) { int start = 0; int curr_col = 0; for (int j = 0; j<ArraySize(dataArr); j++) { curr_col++; if (Classes[i] == dataArr[j]) { //printf("Classes[%d] = %s dataArr[%d] = %s ",i,Classes[i],j,dataArr[j]); if (curr_col == 1) fill_start = j; else { if (j>curr_col) fill_start = j - (curr_col-1); else fill_start = (curr_col-1) - j; fill_start = fill_start; //Print("j ",j," j-currcol ",j-(curr_col-1)," curr_col ",curr_col," columns ",cols," fill start ",fill_start ); } fill_ends = fill_start + cols; //printf("fillstart %d fillends %d j index = %d i = %d ",fill_start,fill_ends,j,i); //--- //if (ArraySize(ClassifiedArr) >= ArraySize(dataArr)) break; //Print("ArraySize Classified Arr ",ArraySize(ClassifiedArr)," dataArr size ",ArraySize(dataArr)," i ",i); for (int k=fill_start; k<fill_ends; k++) { index++; //printf(" k %d index %d",k,index); //printf("dataArr[%d] = %s index = %d",k,dataArr[k],index-1); ClassifiedArr[index-1] = dataArr[k]; } if (index >= ArraySize(dataArr)) break; //might be infinite loop if this occurs } if (curr_col == cols) curr_col = 0; } if (index >= ArraySize(dataArr)) break; //might be infinite loop if this occurs } ArrayCopy(dataArr,ClassifiedArr); ArrayFree(ClassifiedArr); }
为什么注释掉如此多的代码?我们的函数库仍然需要改进,且这些注释的行都是为了调试,希望您能用到它们。
当我们调用这个函数并打印输出时,我们将得到
JG 0 13:47:20.574 TestScript (EURUSD,H1) Classified matrix dataset KL 0 13:47:20.574 TestScript (EURUSD,H1) "Outlook" "Temp" "Humidity" "Wind" "PlayTennis " GS 0 13:47:20.574 TestScript (EURUSD,H1) [ QF 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Weak" "No" DN 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Strong" "No" JF 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Mild" "High" "Weak" "No" ND 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Cool" "Normal" "Weak" "Yes" PN 0 13:47:20.574 TestScript (EURUSD,H1) "Sunny" "Mild" "Normal" "Strong" "Yes" EH 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Hot" "High" "Weak" "Yes" MH 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Cool" "Normal" "Strong" "Yes" MN 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Mild" "High" "Strong" "Yes" DN 0 13:47:20.574 TestScript (EURUSD,H1) "Overcast" "Hot" "Normal" "Weak" "Yes" MG 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Weak" "Yes" QO 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Weak" "Yes" LN 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Strong" "No" LE 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Mild" "Normal" "Weak" "Yes" FE 0 13:47:20.574 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Strong" "No" GS 0 13:47:20.574 TestScript (EURUSD,H1) ] DH 0 13:47:20.574 TestScript (EURUSD,H1) columns = 5 rows = 70
太厉害了,这个函数的工作如同魔术一样
好了,下一个关键步骤是
从数据集中删除叶节点
在所有处理过程的下一次迭代之前,我们完成了到此刻为止的全部工作,最重要的是删除叶节点,因为它们不会生成任何分支,有意义吗?,顺便说一下,它们是纯数值节点。
我们要删除所有具有叶节点值的行。 在这种情况下,我们删除所有阴天行。
//--- Search if there is zero entropy in the Array int zero_entropy_index = 0; bool zero_entropy = false; for (int e=0; e<ArraySize(P_EntropyArr); e++) if (P_EntropyArr[e] == 0) { zero_entropy = true; zero_entropy_index=e; break; } if (zero_entropy) //if there is zero in the Entropy Array { MatrixRemoveRow(m_dataset,p_Classes[zero_entropy_index],cols); rows_total = ArraySize(m_dataset); //New number of total rows from Array if (m_debug) { printf("%s is A LEAF NODE its Rows have been removed from the dataset remaining Dataset is ..",p_Classes[zero_entropy_index]); ArrayPrint(DataColumnNames); MatrixPrint(m_dataset,cols,rows_total); } //we also remove the entropy from the Array and its information everywhere else from the parent Node That we are going to build next ArrayRemove(P_EntropyArr,zero_entropy_index,1); ArrayRemove(p_Classes,zero_entropy_index,1); ArrayRemove(p_ClassNumbers,zero_entropy_index,1); } if (m_debug) Print("rows total ",rows_total," ",p_Classes[zero_entropy_index]," ",p_ClassNumbers[zero_entropy_index]);
运行此代码模块后的输出将是
NQ 0 13:47:20.574 TestScript (EURUSD,H1) Overcast is A LEAF NODE its Rows have been removed from the dataset remaining Dataset is .. GP 0 13:47:20.574 TestScript (EURUSD,H1) "Outlook" "Temp" "Humidity" "Wind" "PlayTennis " KG 0 13:47:20.574 TestScript (EURUSD,H1) [ FS 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Weak" "No" GK 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Hot" "High" "Strong" "No" EI 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Mild" "High" "Weak" "No" IP 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Cool" "Normal" "Weak" "Yes" KK 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Mild" "Normal" "Strong" "Yes" JK 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Weak" "Yes" FL 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Weak" "Yes" GK 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Cool" "Normal" "Strong" "No" OI 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Mild" "Normal" "Weak" "Yes" IQ 0 13:47:20.575 TestScript (EURUSD,H1) "Rain" "Mild" "High" "Strong" "No" LG 0 13:47:20.575 TestScript (EURUSD,H1) ] IL 0 13:47:20.575 TestScript (EURUSD,H1) columns = 5 rows = 50 HE 0 13:47:20.575 TestScript (EURUSD,H1) rows total 50 Rain 5
太厉害了
最后,但在此刻并不太重要的过程是:
从数据集中删除父节点列或根节点列
由于我们已经检测到其为根节点,并将其绘制到树中,故数据集;里不再需要它,我们数据集只需保留未分类的值
//--- REMOVING THE PARENT/ ROOT NODE FROM OUR DATASET MatrixRemoveColumn(m_dataset,max_gain,cols); // After removing the columns assign the new values to these global variables cols = cols-1; // remove that one column that has been removed rows_total = rows_total - single_rowstotal; //remove the size of one column rows // we also remove the column from column names Array ArrayRemove(DataColumnNames,max_gain,1); //--- printf("Column %d removed from the Matrix, The remaining dataset is",max_gain+1); ArrayPrint(DataColumnNames); MatrixPrint(m_dataset,cols,rows_total);
此代码模块的输出将是
OM 0 13:47:20.575 TestScript (EURUSD,H1) Column 1 removed from the Matrix, The remaining dataset is ON 0 13:47:20.575 TestScript (EURUSD,H1) "Temp" "Humidity" "Wind" "PlayTennis " HF 0 13:47:20.575 TestScript (EURUSD,H1) [ CR 0 13:47:20.575 TestScript (EURUSD,H1) "Hot" "High" "Weak" "No" JE 0 13:47:20.575 TestScript (EURUSD,H1) "Hot" "High" "Strong" "No" JR 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "High" "Weak" "No" NG 0 13:47:20.575 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" JI 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "Normal" "Strong" "Yes" PR 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "High" "Weak" "Yes" JJ 0 13:47:20.575 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" QQ 0 13:47:20.575 TestScript (EURUSD,H1) "Cool" "Normal" "Strong" "No" OG 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "Normal" "Weak" "Yes" KD 0 13:47:20.575 TestScript (EURUSD,H1) "Mild" "High" "Strong" "No" DR 0 13:47:20.575 TestScript (EURUSD,H1) ]
太厉害了
现在,我们之所以能够自信地保留数据集的某些部分,原因在于函数库正在绘制一棵树,它保留了数据集去往何处的线索,这是此刻我们已绘制的树。
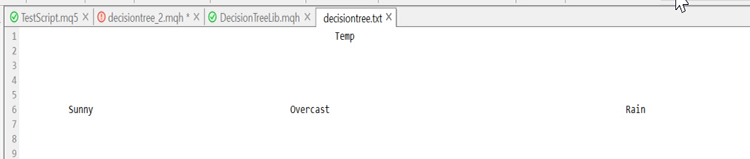
看起来很丑陋,但出于演示目的,它已经足够优秀了。我们将在下一篇文章系列中尝试利用 HTML 创建它,帮助我在 GitHub 存储库中达成如下链接的这一点,现在我要讲述构建树的剩余过程,来结束本话题,我们迭代此过程,直到没有任何可拆分的项目,日志记录如下:
HI 0 13:47:20.575 TestScript (EURUSD,H1) Final Parent Entropy Array and Class Numbers RK 0 13:47:20.575 TestScript (EURUSD,H1) "Sunny" "Rain" CL 0 13:47:20.575 TestScript (EURUSD,H1) 0.9710 0.9710 CE 0 13:47:20.575 TestScript (EURUSD,H1) 5 5 EH 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<<<< Parent Entropy 0.97095 A = 1 >>>>>>>> OF 0 13:47:20.575 TestScript (EURUSD,H1) <<<<< C O L U M N Temp >>>>> RP 0 13:47:20.575 TestScript (EURUSD,H1) << Hot >> total > 2 MD 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" MQ 0 13:47:20.575 TestScript (EURUSD,H1) 2 0 QE 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Hot = 0.00000 FQ 0 13:47:20.575 TestScript (EURUSD,H1) << Mild >> total > 5 KJ 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" NO 0 13:47:20.575 TestScript (EURUSD,H1) 2 3 DH 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Mild = 0.97095 IS 0 13:47:20.575 TestScript (EURUSD,H1) << Cool >> total > 3 KH 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" LM 0 13:47:20.575 TestScript (EURUSD,H1) 1 2 FN 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Cool = 0.91830 KD 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.20999 >>>>>> EF 0 13:47:20.575 TestScript (EURUSD,H1) DJ 0 13:47:20.575 TestScript (EURUSD,H1) <<<<< C O L U M N Humidity >>>>> HJ 0 13:47:20.575 TestScript (EURUSD,H1) << High >> total > 5 OS 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" FD 0 13:47:20.575 TestScript (EURUSD,H1) 4 1 NG 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of High = 0.72193 KM 0 13:47:20.575 TestScript (EURUSD,H1) << Normal >> total > 5 CP 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" JR 0 13:47:20.575 TestScript (EURUSD,H1) 1 4 MD 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Normal = 0.72193 EL 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.24902 >>>>>> IN 0 13:47:20.575 TestScript (EURUSD,H1) CS 0 13:47:20.575 TestScript (EURUSD,H1) <<<<< C O L U M N Wind >>>>> OS 0 13:47:20.575 TestScript (EURUSD,H1) << Weak >> total > 6 CK 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" GM 0 13:47:20.575 TestScript (EURUSD,H1) 2 4 OO 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Weak = 0.91830 HE 0 13:47:20.575 TestScript (EURUSD,H1) << Strong >> total > 4 GI 0 13:47:20.575 TestScript (EURUSD,H1) "No" "Yes" OJ 0 13:47:20.575 TestScript (EURUSD,H1) 3 1 EM 0 13:47:20.575 TestScript (EURUSD,H1) Entropy of Strong = 0.81128 PG 0 13:47:20.575 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.09546 >>>>>> EG 0 13:47:20.575 TestScript (EURUSD,H1) HK 0 13:47:20.575 TestScript (EURUSD,H1) Parent Noce will be Humidity with IG = 0.24902 OI 0 13:47:20.578 TestScript (EURUSD,H1) Parent Entropy Array and Class Numbers JO 0 13:47:20.578 TestScript (EURUSD,H1) "High" "Normal" "Cool" QJ 0 13:47:20.578 TestScript (EURUSD,H1) 0.7219 0.7219 0.9183 QO 0 13:47:20.578 TestScript (EURUSD,H1) 5 5 3 PJ 0 13:47:20.578 TestScript (EURUSD,H1) Classified matrix dataset NM 0 13:47:20.578 TestScript (EURUSD,H1) "Temp" "Humidity" "Wind" "PlayTennis " EF 0 13:47:20.578 TestScript (EURUSD,H1) [ FM 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "High" "Weak" "No" OD 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "High" "Strong" "No" GR 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "High" "Weak" "No" QG 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "High" "Weak" "Yes" JD 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "High" "Strong" "No" KS 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" OJ 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Normal" "Strong" "Yes" CL 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Normal" "Weak" "Yes" LJ 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Normal" "Strong" "No" NH 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Normal" "Weak" "Yes" ER 0 13:47:20.578 TestScript (EURUSD,H1) ] LI 0 13:47:20.578 TestScript (EURUSD,H1) columns = 4 rows = 40 CQ 0 13:47:20.578 TestScript (EURUSD,H1) rows total 36 High 5 GH 0 13:47:20.578 TestScript (EURUSD,H1) Column 2 removed from the Matrix, The remaining dataset is MP 0 13:47:20.578 TestScript (EURUSD,H1) "Temp" "Wind" "PlayTennis " QG 0 13:47:20.578 TestScript (EURUSD,H1) [ LL 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "Weak" "No" OE 0 13:47:20.578 TestScript (EURUSD,H1) "Hot" "Strong" "No" QQ 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Weak" "No" QE 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" LQ 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Strong" "No" HE 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" RM 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Strong" "Yes" PF 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" MR 0 13:47:20.578 TestScript (EURUSD,H1) "Cool" "Strong" "No" IF 0 13:47:20.578 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" EN 0 13:47:20.578 TestScript (EURUSD,H1) ] ME 0 13:47:20.578 TestScript (EURUSD,H1) columns = 3 rows = 22 ER 0 13:47:20.578 TestScript (EURUSD,H1) Final Parent Entropy Array and Class Numbers HK 0 13:47:20.578 TestScript (EURUSD,H1) "High" "Normal" "Cool" CQ 0 13:47:20.578 TestScript (EURUSD,H1) 0.7219 0.7219 0.9183 OK 0 13:47:20.578 TestScript (EURUSD,H1) 5 5 3 NS 0 13:47:20.578 TestScript (EURUSD,H1) <<<<<<<< Parent Entropy 0.91830 A = 2 >>>>>>>> JM 0 13:47:20.578 TestScript (EURUSD,H1) <<<<< C O L U M N Temp >>>>> CG 0 13:47:20.578 TestScript (EURUSD,H1) << Hot >> total > 2 DM 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" LF 0 13:47:20.578 TestScript (EURUSD,H1) 2 0 HN 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Hot = 0.00000 OJ 0 13:47:20.578 TestScript (EURUSD,H1) << Mild >> total > 5 JS 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" GD 0 13:47:20.578 TestScript (EURUSD,H1) 2 3 QG 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Mild = 0.97095 LL 0 13:47:20.578 TestScript (EURUSD,H1) << Cool >> total > 3 JQ 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" IR 0 13:47:20.578 TestScript (EURUSD,H1) 1 2 OE 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Cool = 0.91830 RO 0 13:47:20.578 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.15733 >>>>>> PO 0 13:47:20.578 TestScript (EURUSD,H1) JS 0 13:47:20.578 TestScript (EURUSD,H1) <<<<< C O L U M N Wind >>>>> JR 0 13:47:20.578 TestScript (EURUSD,H1) << Weak >> total > 6 NH 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" JM 0 13:47:20.578 TestScript (EURUSD,H1) 2 4 JL 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Weak = 0.91830 QD 0 13:47:20.578 TestScript (EURUSD,H1) << Strong >> total > 4 JN 0 13:47:20.578 TestScript (EURUSD,H1) "No" "Yes" JK 0 13:47:20.578 TestScript (EURUSD,H1) 3 1 DM 0 13:47:20.578 TestScript (EURUSD,H1) Entropy of Strong = 0.81128 JF 0 13:47:20.578 TestScript (EURUSD,H1) <<<<<< Column Information Gain 0.04281 >>>>>> DG 0 13:47:20.578 TestScript (EURUSD,H1) LI 0 13:47:20.578 TestScript (EURUSD,H1) Parent Noce will be Temp with IG = 0.15733 LH 0 13:47:20.584 TestScript (EURUSD,H1) Parent Entropy Array and Class Numbers GR 0 13:47:20.584 TestScript (EURUSD,H1) "Hot" "Mild" "Cool" CD 0 13:47:20.584 TestScript (EURUSD,H1) 0.0000 0.9710 0.9183 GN 0 13:47:20.584 TestScript (EURUSD,H1) 2 5 3 CK 0 13:47:20.584 TestScript (EURUSD,H1) Classified matrix dataset RL 0 13:47:20.584 TestScript (EURUSD,H1) "Temp" "Wind" "PlayTennis " NK 0 13:47:20.584 TestScript (EURUSD,H1) [ CQ 0 13:47:20.584 TestScript (EURUSD,H1) "Hot" "Weak" "No" LI 0 13:47:20.584 TestScript (EURUSD,H1) "Hot" "Strong" "No" JM 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "No" NI 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" CL 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "No" KI 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "Yes" LR 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" KJ 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" IQ 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" DE 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Strong" "No" NR 0 13:47:20.584 TestScript (EURUSD,H1) ] OI 0 13:47:20.584 TestScript (EURUSD,H1) columns = 3 rows = 30 OO 0 13:47:20.584 TestScript (EURUSD,H1) Hot is A LEAF NODE its Rows have been removed from the dataset remaining Dataset is .. HL 0 13:47:20.584 TestScript (EURUSD,H1) "Temp" "Wind" "PlayTennis " DJ 0 13:47:20.584 TestScript (EURUSD,H1) [ DL 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "No" LH 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" QL 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "No" MH 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Strong" "Yes" RQ 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Weak" "Yes" MI 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" KQ 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Weak" "Yes" FD 0 13:47:20.584 TestScript (EURUSD,H1) "Cool" "Strong" "No" HQ 0 13:47:20.584 TestScript (EURUSD,H1) ] NN 0 13:47:20.584 TestScript (EURUSD,H1) columns = 3 rows = 24 IF 0 13:47:20.584 TestScript (EURUSD,H1) rows total 24 Mild 5 CO 0 13:47:20.584 TestScript (EURUSD,H1) Column 1 removed from the Matrix, The remaining dataset is DM 0 13:47:20.584 TestScript (EURUSD,H1) "Wind" "PlayTennis " PD 0 13:47:20.584 TestScript (EURUSD,H1) [ LN 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "No" JI 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" EL 0 13:47:20.584 TestScript (EURUSD,H1) "Strong" "No" GO 0 13:47:20.584 TestScript (EURUSD,H1) "Strong" "Yes" JG 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" JN 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" JE 0 13:47:20.584 TestScript (EURUSD,H1) "Weak" "Yes" EP 0 13:47:20.584 TestScript (EURUSD,H1) "Strong" "No" HK 0 13:47:20.584 TestScript (EURUSD,H1) ] PP 0 13:47:20.584 TestScript (EURUSD,H1) columns = 2 rows = 10 HG 0 13:47:20.584 TestScript (EURUSD,H1) Final Parent Entropy Array and Class Numbers FQ 0 13:47:20.584 TestScript (EURUSD,H1) "Mild" "Cool" OF 0 13:47:20.584 TestScript (EURUSD,H1) 0.9710 0.9183 IO 0 13:47:20.584 TestScript (EURUSD,H1) 5 3
此处是构建决策树的函数概述,我发现这段代码很难理解且易混淆,尽管手工计算数值的过程看起来很简单,既如此我还是决定在本章节加以详细解释。
void CDecisionTree::BuildTree(void) { int ClassNumbers[]; int max_gain = 0; double IGArr[]; //double parent_entropy = Entropy(p_ClassNumbers,single_rowstotal); string p_Classes[]; //parent classes double P_EntropyArr[]; //Parent Entropy int p_ClassNumbers[]; //parent/ Target variable class numbers GetClasses(TargetArr,m_DatasetClasses,p_ClassNumbers); ArrayResize(P_EntropyArr,1); P_EntropyArr[0] = Entropy(p_ClassNumbers,single_rowstotal); //--- temporary disposable arrays for parent node information string TempP_Classes[]; double TempP_EntropyArr[]; int TempP_ClassNumbers[]; //--- if (m_debug) Print("Default Parent Entropy ",P_EntropyArr[0]); int cols = m_colschosen; for (int A =0; A<ArraySize(P_EntropyArr); A++) { printf("<<<<<<<< Parent Entropy %.5f A = %d >>>>>>>> ",P_EntropyArr[A],A); for (int i=0; i<cols-1; i++) //we substract with one to remove the independent variable coumn { int rows = ArraySize(m_dataset)/cols; string Arr[]; //ArrayFor the current column string ArrTarg[]; //Array for the current target ArrayResize(Arr,rows); ArrayResize(ArrTarg,rows); printf(" <<<<< C O L U M N %s >>>>> ",DataColumnNames[i]); int index_target=cols-1; for (int j=0; j<rows; j++) //get column data and its target column { int index = i+j * cols; //Print("index ",index); Arr[j] = m_dataset[index]; //printf("ArrTarg[%d] = %s m_dataset[%d] =%s ",j,ArrTarg[j],index_target,m_dataset[index_target]); ArrTarg[j] = m_dataset[index_target]; //printf("Arr[%d] = %s ArrTarg[%d] = %s ",j,Arr[j],j,ArrTarg[j]); index_target += cols; //the last index of all the columns } //--- Finding the Entropy //The function to find the Entropy of samples in a given column inside its loop //then restores all the entropy into one array //--- Finding the Information Gain //The Function to find the information gain from the entropy array above //--- if (i == max_gain) { //Get the maximum information gain of all the information gain in all columns then //store it to the parent information gain } //--- ZeroMemory(ClassNumbers); ZeroMemory(SamplesNumbers); } //---- Get the parent Entropy, class and class numbers // here we store the obtained parent class from the information gain metric then we store them into a parent array ArrayCopy(p_Classes,TempP_Classes); ArrayCopy(P_EntropyArr,TempP_EntropyArr); ArrayCopy(p_ClassNumbers,TempP_ClassNumbers); //--- string Node[1]; Node[0] = DataColumnNames[max_gain]; if (m_debug) printf("Parent Node will be %s with IG = %.5f",Node[0],IGArr[max_gain]); if (A == 0) DrawTree(Node,"parent",A); DrawTree(p_Classes,"child",A); //--- CLASSIFY THE MATRIX MatrixClassify(m_dataset,p_Classes,cols); //--- Search if there is zero entropy in Array if there is any remove its data from the dataset if (P_EntropyArr[e] == 0) { zero_entropy = true; zero_entropy_index=e; break; } if (zero_entropy) //if there is zero in the Entropy Array { MatrixRemoveRow(m_dataset,p_Classes[zero_entropy_index],cols); rows_total = ArraySize(m_dataset); //New number of total rows from Array //we also remove the entropy from the Array and its information everywhere else from the parent Node That we are going to build next ArrayRemove(P_EntropyArr,zero_entropy_index,1); ArrayRemove(p_Classes,zero_entropy_index,1); ArrayRemove(p_ClassNumbers,zero_entropy_index,1); } if (m_debug) Print("rows total ",rows_total," ",p_Classes[zero_entropy_index]," ",p_ClassNumbers[zero_entropy_index]); //--- REMOVING THE PARENT/ ROOT NODE FROM OUR DATASET MatrixRemoveColumn(m_dataset,max_gain,cols); // After removing the columns assing the new values to these global variables cols = cols-1; // remove that one column that has been removed rows_total = rows_total - single_rowstotal; //remove the size of one column rows // we also remove the column from column names Array ArrayRemove(DataColumnNames,max_gain,1); //--- } }
底线
现在,您已经了解了分类树中涉及的基本计算,尽管函数库中拥有让您开始构建决策树算法所需的几乎任何内容,并可帮助您解决您关心的交易问题,但这是本文中涉及的一个艰难而漫长的主题,我依然希望能在下一篇或两篇文章中完结。
感谢阅读,我的 GitHub 存储库链接在这里 https://github.com/MegaJoctan/DecisionTree-Classification-tree-MQL5。
本文由MetaQuotes Ltd译自英文
原文地址: https://www.mql5.com/en/articles/11061
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 神经网络变得轻松(第十八部分):关联规则
神经网络变得轻松(第十八部分):关联规则
 从头开始开发智能交易系统(第 20 部分):新订单系统 (III)
从头开始开发智能交易系统(第 20 部分):新订单系统 (III)
 您应该知道的 MQL5 向导技术(第 01 部分):回归分析
您应该知道的 MQL5 向导技术(第 01 部分):回归分析
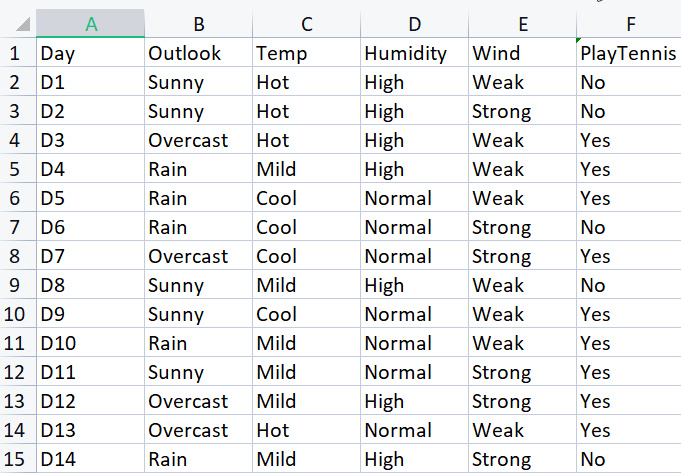
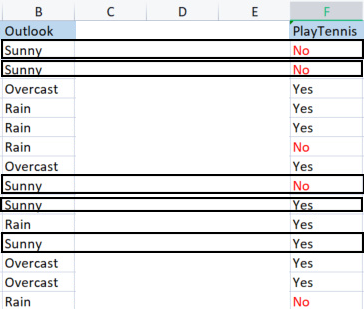

你好,欧米茄先生、
非常感谢你的 ID3 解决方案。不过,我提供并附上了一份有关这方面的 excel 表,我想这对您的解释会很清楚。
再次感谢、
F.Mahmoudian
你好,欧米茄先生、
非常感谢你的 ID3 解决方案。不过,我提供并附上了一份有关这方面的 excel 表,我认为这对您的解释很清楚。
再次感谢、
F.Mahmoudian
非常感谢,我还在想如何让脚本自己画出树来
many thanks to it, I'm still trying to figure out how to let the script draw the tree itself
非常感谢
对了,为什么大家都如此痴迷于 MO、AI 和 DeepLearning?有一件被人遗忘的旧事,专题启动器提醒了我们。有专家系统和各种加权评估。当然,这些方法已有 30-50 年历史,并不时髦,但它们坚持物理模型和因果关系,其结果是可以解释的。我得深入研究一下。
这是唯一有可能成为已计算信号过滤器的方法。这个方向上的其他方法都很糟糕。
对了,为什么大家都如此痴迷于 MO、AI 和 DeepLearning?有一件被人遗忘的旧事,专题启动器提醒了我们。有专家系统和各种加权评估。当然,这些方法已有 30-50 年历史,并不时髦,但它们坚持物理模型和因果关系,其结果是可以解释的。我得好好研究研究。
这是唯一有可能成为已计算信号过滤器的方法。这个方向上的其他方法都被搞砸了。